Abstract
In vertebrate muscles, Z-bands connect adjacent sarcomeres, incorporate several cell signaling proteins, and may act as strain sensors. Previous electron microscopy (EM) showed Z-bands reversibly switch between a relaxed, “small-square” structure, and an active, “basketweave” structure, but the mechanism of this transition is unknown. Here, we found the ratio of small-square to basketweave in relaxed rabbit psoas muscle varied with temperature, osmotic pressure, or ionic strength, independent of activation. By EM, the A-band and both Z-band lattice spacings varied with temperature and pressure, not ionic strength; however, the basketweave spacing was consistently 10% larger than small-square. We next sought evidence for the two Z-band structures in unfixed muscles using x-ray diffraction, which indicated two Z-reflections whose intensity ratios and spacings correspond closely to the EM measurements for small-square and basketweave if the EM spacings are adjusted for 20% shrinkage due to EM processing. We conclude that the two Z-reflections arise from the small-square and basketweave forms of the Z-band as seen by EM. Regarding the mechanism of transition during activation, the effects of Ca2+ in the presence of force inhibitors suggested that the interconversion of Z-band forms was correlated with tropomyosin movement on actin.
Introduction
In the Z-bands of vertebrate skeletal and cardiac muscles, antiparallel thin filaments from adjacent sarcomeres form a square array that is densely cross-linked (1). At a minimum, the Z-band must transmit the force of contraction between sarcomeres, but there is increasing recognition that the Z-band also hosts a multitude of signaling proteins and may act as a strain sensor (2). Unlike the A-band, relatively few structure-function studies have examined the Z-band.
Early electron microscopy (EM) studies (3,4) noted that the Z-band could display two distinct forms that came to be called small-square and basketweave, the names being descriptive of their appearance in transverse sections. Relaxed muscles show predominantly small-square Z-bands, whereas active muscles reversibly show the basketweave form (5–7). Passively stretched relaxed muscles do not show the basketweave form, nor do active muscles if stretched beyond a sarcomere length of 2.7 μm (8). In rat soleus and cardiac muscles, the basketweave Z-band lattice spacing is ∼20% larger than the small-square form, as measured by EM (7,8). Thus far, the small-square and basketweave forms of the Z-band have only been directly observed by EM, although an ∼8% increase in Z-band lattice spacing has been observed by x-ray diffraction (XRD) during contraction of frog muscle at normal osmolarity (9).
To date, the mechanism of the small-square to basketweave transition, as well as its relationship to calcium, thin filament activation, cross-bridge binding, or eventual force production by the cross-bridges during normal contraction remains unknown. To address these questions, we sought to explore the small-square to basketweave transition in skinned rabbit psoas muscle, for which there is a wealth of published XRD and biochemical data available. We used EM to map out the conditions where we could reliably observe the two lattice forms in fibers that were mechanically relaxed, and found in particular that lowering the ionic strength varied the proportion of small-square to basketweave but did not significantly change the lattice spacing of either form. We then sought XRD evidence for the two lattice forms in unfixed muscles. Finally, we took advantage of the skinned fiber preparation to correlate specific stages of contraction to Z-band structure, by treating with calcium while inhibiting active force via vanadate, aluminum fluoride, or troponin C extraction.
Materials and Methods
Solutions and preparations of muscles
Standard relaxing solution contained (in mM) 100 potassium methane sulfonate, 20 MOPS, 5 EGTA, 5 ATP, 6 MgCl2, 5 potassium phosphate, 1 DTT, and 3% dextran T-500, pH 6.8 adjusted with KOH. Low ionic strength relaxing solution lacked potassium methane sulfonate, rigor solution lacked ATP, calcium activating solutions contained 5 CaCl2 (pCa ∼4.5), vanadate solutions contained 2.5 mM vanadate, and aluminum fluoride solutions contained 2.5 mM AlF3, but solutions were otherwise identical to standard relaxing solution. Troponin C extraction solution contained: (in mM) 100 potassium methane sulfonate, 20 MOPS, 5 EDTA, 1 DTT, 1 trifluoperazine, 1% Triton X-100, and 3% dextran T-500, pH 6.8. Small bundles of rabbit psoas fibers were dissected, tied to Lucite rods at body length, chemically skinned on a rotator in 50% glycerol-relaxing solution with antiprotease cocktail at 2°, with 3 solution changes, equilibrated 12 h in 75% glycerol/relaxing solution, removed from the Lucite rod, cut into 2 cm long pieces, separated into fascicles ∼0.5 mm in diameter, placed in individual plastic vials with 1 ml of 75% glycerol/relaxing solution, and stored at −100° until use. Fibers stored at −100° in 75% glycerol appear effectively immortal, whereas their mechanical response and filament order begin to degrade within 1–2 weeks if stored at –20°.
Physiology
To measure force and stiffness under various experimental conditions, single fibers were mounted in a physiology apparatus previously described (10). Stiffness was measured by analyzing the peak-to-peak force variation resulting from a 0.15% length oscillation at 500 Hz. Fiber lengths, force, and stiffness were sampled at 1 kHz and recorded by custom LabVIEW (National Instruments, Austin, TX) routines. Force is reported as percent maximal calcium-activated force, and stiffness as percent rigor stiffness. Physiology experiments were conducted at 22°.
Electron microscopy
Single fibers were dissected in 75% glycerol and glued with cellulose nitrate glue onto stainless steel “U-pins” (0.305 mm dental wire bent into a U-shape, ∼4 × 10 mm). The U-pin serves as a convenient handle and marker for the single fiber during EM processing, and prevents the fiber from shortening. Sarcomere length was checked by laser diffraction, and only samples with a sarcomere length of 2.4 μm were used. Fibers were fixed for 5 min at 38° with 2.5% glutaraldehyde (Tousimis, Rockville, MD) and 0.2% tannic acid No. 1674 (Mallinckrodt, St. Louis, MO) made up in experimental variations of the standard relaxing solution, pH 6.8. Some fixations were also done at 0° or 20°. After fixation, fibers were rinsed, post-fixed on ice for 5 min with 1% osmium tetroxide in 100 mM phosphate buffer (pH 6.0) with 10 mM MgCl2, rinsed, stained en bloc with 2% aqueous uranyl acetate for 12 h at 2°, rinsed, dehydrated in a graded series of ethanol, and infiltrated at 60° with freshly prepared epoxy resin mixture (in grams, 10 Araldite-506, 15 DDSA, 2 DER-736, and 0.54 DMP-30). Fibers were then cut off their U-pins and assembled into “rafts” of parallel fibers from different experimental groups in a minimum of resin, keeping careful maps of the assembled rafts while intentionally selecting fiber segments of different lengths and avoiding symmetric arrays. Rafts were prepolymerized ∼12 h at 60°, then covered with fresh resin to fill the embedding molds, and the final polymerization carried out at 80° for 48 h. Thus assembled, these rafts of co-embedded fibers allow 4–6 experimental groups to be examined in a single section. Transverse sections ∼40–60 nm thick were stained with potassium permanganate and lead, and photographed at 18,500–30,000× on a Philips 420 electron microscope at 100 kV. During microscopy, we minimized variations in magnification by bringing the first specimen into view, adjusting it to be eucentric, focusing the objective lens, and then doing all subsequent focusing by adjusting the height of the specimen to be eucentric, rather than by the normal means of changing the objective lens current. With each set of images, we also photographed calibration images of negatively stained tropomyosin tactoids, at the same magnification, and focused as above, with the spacing of the tactoid taken as 39.5 nm (11).
Image analysis
Lattice spacings of the A-band and Z-band were measured from EM cross sections using CRISP (Calidris, Sollentuna, Sweden). A well-ordered region of each myofibril was manually outlined and the outlying area was deleted, given a 5 pixel soft edge, and floated to the mean density value of the region selected. CRISP was then used to calculate the Fourier transform, refine the lattice from the transform, and report the lattice constants and included angle, a∗, b∗, and γ∗, which were manually recorded in a spreadsheet. For Z-bands, square symmetry was assumed and a∗ and b∗ were averaged together. For A-bands, hexagonal symmetry was assumed, and a∗, b∗, and the third hexagonal spot (which is geometrically fixed by a∗, b∗, and γ∗) were averaged together. Images of both the Z-band and the A-band depart from true square or hexagonal symmetry, presumably due to section compression. Averaging in this way will remove bias in any particular direction, but will result in values expected to be slightly smaller due to section compression. For the Z-band lattice spacings, each region measured was manually scored by visual appearance as either small-square or basketweave, and average spacings were separately calculated. To quantify the ratio of small-square to basketweave in each condition, the fraction of measurements scored as small-square are reported as percent small-square (Table 1, % SS). We expect this number fraction to approximate the relative area fraction, because Z-bands are approximately a constant diameter, and the areas selected for diffraction were within a limited size range (25–100% of Z-band area).
Table 1.
EM data for varying ionic strength, temperature, and osmotic pressure
| μ | °C | [Dex.] | SA (nm) | SSS (nm) | SBW (nm) | % SS |
|---|---|---|---|---|---|---|
| Std | 38 | 0% | 33.3 ± 1.3 (19) | 23.2 ± 1.2 (14) | 25.5 ± 1.3 (14) | 50 |
| ” | ” | 3% | 28.1 ± 2.5 (40) | 19.1 ± 1.2 (46) | 21.5 ± 1.1 (4) | 92 |
| ” | ” | 6% | 28.2 ± 1.7 (44) | 17.6 ± 0.7 (17) | ∗ | 100 |
| ” | ” | 12% | 27.7 ± 1.4 (19) | 17.3 ± 0.7 (40) | ∗ | 100 |
| LIS | ” | 0% | 33.3 ± 1.8 (18) | 23.4 (1) | 25.8 ± 1.8 (18) | 5 |
| ” | ” | 3% | 28.8 ± 2.2 (43) | 19.3 ± 0.8 (30) | 21.3 ± 0.8 (42) | 42 |
| ” | ” | 6% | 28.5 ± 1.5 (43) | 18.2 ± 1.0 (16) | 20.3 ± 1.2 (11) | 59 |
| ” | ” | 12% | 27.7 ± 1.4 (12) | 17.8 ± 1.2 (22) | ∗ | 100 |
| Std | 38 | 3% | 28.1 ± 2.3 (52) | 19.0 ± 1.1 (64) | 21.5 ± 1.1 (4) | 94 |
| ” | 20 | ” | 28.7 ± 1.1 (26) | 20.1 ± 0.8 (31) | 22.3 ± 1.4 (13) | 70 |
| ” | 0 | ” | 30.7 ± 1.9 (23) | 21.0 ± 1.3 (13) | 23.3 ± 0.9 (19) | 41 |
EM measurements of A-band lattice spacing (SA), small-square Z-band lattice spacing (SSS), basketweave Z-band lattice spacing (SBW), and ratio of small-square to basketweave within the Z-band (%SS) as a function of ionic strength (μ), temperature (°C), and dextran concentration ([Dex.]). Ionic strength is either standard (Std), or low ionic strength (LIS). Values presented as mean ± standard deviation (number of measurements (nm)).
” Indicates same as above.
No areas of basketweave large enough for diffraction observed.
X-ray diffraction
XRD experiments were conducted in the laboratory of Dr. Leepo Yu in the National Institutes of Health, Bethesda, MD. Dissection and skinning of rabbit fibers and the x-ray apparatus are described in detail elsewhere (12). Patterns were recorded on a 1D wire detector with a semitransparent backstop that recorded the attenuated direct beam, which was used to normalize each pattern for total exposure. Equatorial patterns were collected from 2000-s long exposures of single rabbit fibers in standard or low ionic strength relaxing solutions while fibers were thermostatically held at 38°. Up to four patterns could be collected from fresh regions of each fiber, with six different fibers being examined. As a calibration for specimen to detector distance, one pattern was recorded at 5° in Dr. Yu's standard solution (in mM, 1 ATP, 1 EGTA, 3 MgCl2, 10 imidazole, 1 DTT, pH 7.0), and the A-band spacing for this pattern was assumed to be 38.4 nm (12). One pattern each was also recorded at 2–4° in our standard or low ionic strength solutions to examine the effect of temperature on lattice spacing. A background pattern, with the x-ray chamber in place and filled with solution but no fiber, was subtracted from each fiber pattern. Individual x-ray patterns were noisy and the Z-reflections were consequently difficult to identify. To increase the signal/noise ratio, each pattern was normalized and folded and the half-patterns were averaged together to give two average patterns, one for standard and one for low ionic strength, which were then analyzed. The region encompassing the 10 and 11 A-band reflections from the two average patterns was curve-fitted using a least squares fitting routine that specified four independent Lorentzian peaks. The positions of the A-band 10 reflection and the two observed Z-band reflections were allowed to vary freely, whereas the position of the A-band 11 reflection was constrained with respect to the 10 position as would be expected for a hexagonal lattice. Integrated peak intensities were calculated from the fitted parameters for peak width and amplitude.
Results
We found that rabbit psoas Z-bands were generally a mixture of small-square and basketweave forms, with even a single Z-band exhibiting discrete domains of either form. We found experimental conditions that could drive one form or the other to predominate (Fig. 1 and Fig. S1 in the Supporting Material). In our standard relaxing condition (38°, 3% dextran, 100 mM KMeSO3), which was designed to mimic the in vivo environment, the Z-band was predominantly small-square (Fig. 1 A), similar to the results of Goldstein et al. (6) for relaxed, intact, soleus muscle. Reducing the fixation temperature, dextran concentration, or ionic strength favored a greater proportion of the basketweave form (Figs. 1 B, 2, A and B, and S1). The tendency of low ionic strength to give basketweave could be overcome by increasing the dextran concentration, and 12% dextran gave 100% small-square, confirming total interconvertibility (Fig. S1 N).
Figure 1.
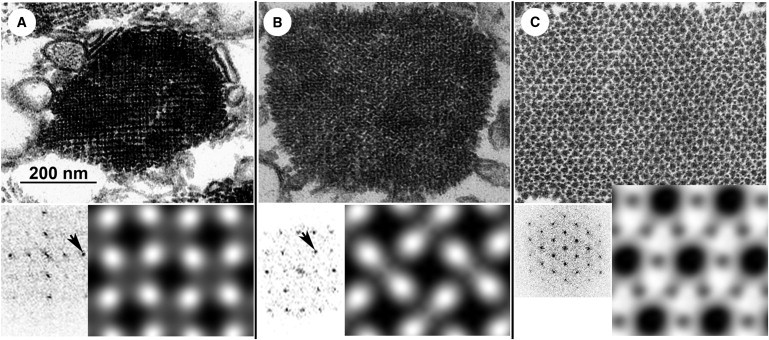
Transverse sections of Z-bands showing the small-square (A) and basketweave (B) forms, together with A-band (C). Each panel consists of an electron micrograph (top), Fourier transform (bottom left), and filtered images (bottom right). Scale bar in A applies also to micrographs in B and C. Computed diffraction patterns from Z-bands show typical differences, with the small-square form having strong 2,0 diffraction spots (A, arrow), whereas the basketweave form typically has strong 11 spots (B, arrow). Filtered images in A and B show diamond-shaped profiles of cross-cut actin filaments, connected by Z-links. Filtered image in C (not the same scale as those in A and B) shows profiles of thick and thin filaments in hexagonal array.
Figure 2.
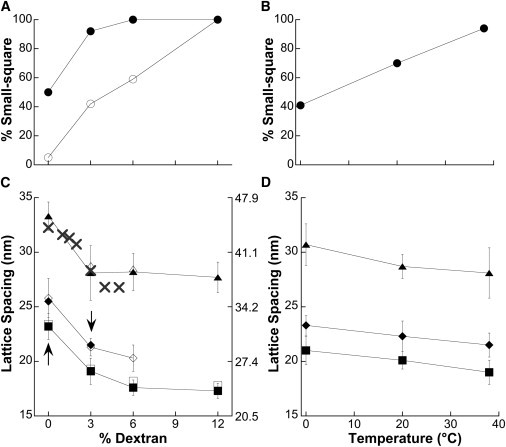
EM measurements on the effect of ionic strength, dextran concentration, and temperature on the ratio of small-square to basketweave (circles, A and B), A-lattice spacing (triangles, C and D), basketweave Z-lattice spacing (diamonds, C and D) and small-square Z-lattice spacing (squares, C and D). In A and C, solid symbols = standard ionic strength and open symbols = low ionic strength, which in C nearly or completely overlap. In A and C, dextran concentration and ionic strength were varied while temperature was held constant (38°). In B and D, temperature was varied while ionic strength (standard) and dextran concentration (3%) were held constant. (C) Left vertical axis represents actual EM measurements reported in Table 1, while right-hand axis represents the same values divided by a factor of 0.73 for comparison with previously published XRD data taken at 5°C (15). Corrected EM measurements for the A-lattice (triangles3 right-hand scale) closely match published XRD data (X, right-hand scale). Error bars represent standard deviation.
Both the Z- and A-band lattice spacings measured by EM varied with dextran concentration and temperature, but were relatively insensitive to ionic strength (Fig. 2, C and D, Table 1). Lowering the fixation temperature from 38° to 0° increased both Z- and A-band lattice spacings by ∼8%, whereas lowering the dextran concentration from 3% to 0% increased both by ∼20%. Increasing the dextran concentration from 3% to 6% decreased the Z-band lattice spacing by ∼6%, with no further decrease observed at 12% dextran. By contrast, there was no significant change in the measured A-band spacing between 3% and 12% dextran concentrations, indicating that to some extent, Z-band lattice spacing can be varied independent of A-band spacing, although they generally parallel one another. In all cases where both small-square and basketweave Z-bands could be observed, the basketweave lattice spacing was ∼10% larger than the small-square spacing (Fig. 2, C and D). This 10% increase is in the same direction but smaller than the 20% increase seen by Goldstein et al. (7,8). We do not currently know the source of the discrepancy, but several experimental differences stand out: intact versus skinned muscle here; rat soleus, a slow twitch muscle with wide Z-bands versus rabbit psoas, a fast twitch muscle with narrow Z-bands here; the use of tannic acid here; and finally the embedding resin, Epon versus Araldite here. It has been suggested that the structural transition from small-square to basketweave may simply be the result of the lattice spacing change (6,13). However, we note that the basketweave spacing in 3% dextran (down arrow, Fig. 2 C) is actually smaller than the small-square spacing at 0% dextran (up arrow, Fig. 2 C), but the two forms are still visibly distinct. Thus, our results imply that the 10% lattice spacing change is the result of the structural transition from small-square to basketweave, and not the other way around.
The results presented thus far indicate that at least relative spacing changes can be measured by EM in both the A-band and the Z-band under a variety of experimental conditions. Others have argued that EM cannot reliably measure lattice spacing (14), but we suspected that previously published discrepancies between EM and XRD results stemmed from comparing different muscle under different experimental conditions. Although we did expect a certain amount of shrinkage during EM processing, we hypothesized that this would be a uniform shrinkage. To address this question, we conducted XRD experiments comparing rabbit psoas muscles in both our standard and low ionic strength solutions. Our purpose was twofold. Most importantly, we sought XRD evidence for the two discrete Z-band lattice forms, which heretofore had only been observed by EM of fixed muscles. Secondarily, by comparing the A-band lattice spacings as measured by XRD and EM, we could calculate the amount of shrinkage in the EM results and determine whether consistent results could be achieved between the two techniques when comparing similar experimental conditions.
Regarding XRD evidence for the two discrete Z-band forms observed by EM, we initially only expected to see a Z-lattice spacing change, as low or standard ionic strength favored the basketweave or small-square Z-band forms. However, to our surprise, the low ionic strength pattern clearly showed two Z-reflections, and the standard ionic strength similarly suggested the presence of two Z-reflections, which we call Z1 and Z2 (Fig. 3). The spacing of Z2 was ∼10% larger than Z1, and the two reflections maintained very similar spacings in the standard and low ionic strengths (Table 2). Ionic strength did however change the relative intensities of the two Z-reflections, being ∼89% Z1 in standard ionic strength and ∼36% Z1 in low ionic strength. Thus our XRD results, like our EM results, provide evidence for the existence of two discrete lattice forms in the psoas Z-band, with one form ∼10% larger than the other and with ionic strength varying the relative proportion of the two lattice forms but not their spacing. We therefore identify Z1 as arising from the small-square form of the Z-band, and Z2 as arising from the basketweave form.
Figure 3.
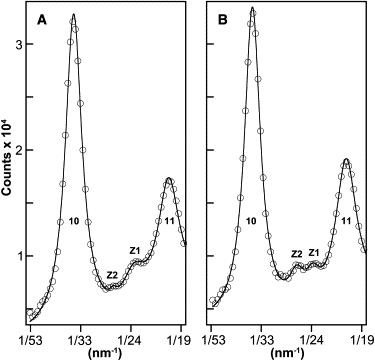
Averaged equatorial x-ray patterns in standard (A) and low ionic strength (B) show two Z-reflections, labeled Z1 and Z2, between the 10 and the 11 reflections from the A-band.
Table 2.
XRD data for varying ionic strength and temperature
| μ | °C | SA (nm) | I10/I11 | SZ1 (nm) | SZ2 (nm) | IZ1/IZ2 |
|---|---|---|---|---|---|---|
| Std | 38 | 34.9 | 1.3 | 24.0 | 26.7 | 8.05 (89%) |
| LIS | 38 | 35.5 | 1.3 | 24.2 | 26.3 | 0.56 (36%) |
| Std | 2–4 | 38.3 | 0.8 | ∗ | ∗ | ∗ |
| LIS | 2–4 | 38.4 | 0.4 | ∗ | ∗ | ∗ |
XRD measurements of A-band lattice spacing (SA), intensity ratio of A-band 10 and 11 reflections (I10/I11), spacing of two Z-reflections (SZ1 and SZ2), and intensity ratio of two Z-reflections (IZ1/IZ2) as a function of ionic strength (μ) and temperature.
Data for 2–4°C come from single patterns (Fig. S2), therefore Z-reflections could not be resolved from background.
Regarding the A-band spacings as measured by XRD, the A-band spacing is ∼35 nm and lowering the ionic strength causes little change in either the spacing (SA) or the intensity ratio (I10/I11) at our standard temperature of 38° (Table 2). Lowering the temperature to 2–4° increases the lattice spacing to ∼39 nm (Table 2, Fig. S2), an increase of ∼8% that exactly parallels the 8% increase seen by EM. At 2–4°, lowering the ionic strength decreases I10/I11, but causes little additional spacing change (Table 2), consistent with previous XRD results (15). Comparing our XRD data to our EM data, we find that the A-band spacing measured by EM is consistently ∼20% smaller than that measured by XRD at either temperature or ionic strength indicating that EM processing has caused ∼20% shrinkage, similar to previous reports (16). The EM spacings from our osmotic pressure experiments (Fig. 2 C) can be directly compared to previously published XRD data results (15) if we take into account the 20% shrinkage due to EM processing and the 8% spacing difference due to the different temperatures in the two experiments. Applying a correction factor of 0.73 (= 0.8 × 0.915) to our data (Fig. 2 C, right-hand scale), we find that the A-band spacings are very similar to published XRD spacings (Fig. 2 C, X symbols). Thus, it appears that, at least for these cases and in the A-band, EM is able to faithfully preserve relative differences in lattice spacing. Although there is no a priori reason to assume that the shrinkage caused by EM processing would be the same in both the A-band and the Z-band neither is there any reason to assume it would not. Correcting our small-square and basketweave EM measurements for 20% shrinkage gives a spacing of ∼24 nm for small-square and ∼27 nm for basketweave, which are very similar to the spacings measured by XRD for Z1 and Z2 (Table 3). This close correlation between the corrected EM spacings and the measured XRD spacings further supports our identification of the Z1 and Z2 reflections as arising from the small-square and basketweave forms of the Z-band.
Table 3.
Comparison of EM spacing data to XRD data
| A-band |
Z-band |
||||||||
|---|---|---|---|---|---|---|---|---|---|
| EM |
XRD |
EM |
EM/f |
XRD |
|||||
| μ | SA | SA | f | SSS | SBW | S∗SS | S∗BW | SZ1 | SZ2 |
| Std | 28.1 | 34.9 | 0.8 | 19.1 | 21.5 | 23.9 | 26.9 | 24.0 | 26.7 |
| LIS | 28.8 | 35.5 | 0.8 | 19.3 | 21.3 | 24.1 | 26.6 | 24.2 | 26.3 |
Comparison of lattice spacings measured by EM versus XRD in standard and low ionic strength, at 38° and with 3% dextran. EM and XRD data are repeated from Tables 1 and 2, respectively. Shrinkage factor, f, due to EM processing is derived by dividing A-band EM spacing by XRD spacing. This shrinkage factor is then applied to the Z-band EM spacings to give corrected values for small-square or basketweave (S∗SS or S∗BW), which correspond closely to the XRD measured spacings for the Z1 and Z2 reflections.
Whereas the above results were all obtained with skinned muscles that were mechanically relaxed, Goldstein et al. (6–8) had previously shown that the Z-band structure is also correlated to active tension, being predominantly small-square in relaxed muscles and basketweave in tetanized muscles. Our attempts to examine skinned fibers during full calcium activation, analogous to tetanized muscles (6), were not successful because the sarcomere pattern is rapidly lost when skinned psoas fibers are activated at 38°. Periodic isotonic shortening can stabilize the sarcomere pattern, but only at lower temperatures (17), and we did not pursue activation at lower temperatures because relaxed controls described above indicated temperature alone shifted the Z-band to the basketweave form. Nevertheless, our skinned muscle prep allowed us to dissect some of the steps that occur during active contraction and test for their individual effects on the Z-band structure. To rule out a direct effect of calcium on the Z-band, in the absence of tropomyosin movement, myosin binding, or active force, we extracted troponin C from fibers (18,19), and examined the Z-band fixed in the presence or absence of calcium. In both cases, the Z-bands were 100% in the small-square form (Fig. S3, A and B), with no significant difference found in the lattice spacing (Table 4), thus ruling out a direct effect of calcium on the Z-band.
Table 4.
EM data for calcium effects with force inhibition
| Condition | SA (nm) | SSS (nm) | SBW (nm) | % SS |
|---|---|---|---|---|
| TnC− Rlx | 27.9 ± 2.2 (28) | 19.1 ± 0.8 (22) | ∗ | 100 |
| TnC− Act | 28.4 ± 2.5 (22) | 19.3 ± 1.1 (26) | ∗ | 100 |
| AlF3 Rlx | 27.7 ± 2.0 (24) | 19.2 ± 0.8 (41) | ∗ | 100 |
| AlF3 Act | 28.6 ± 2.3 (23) | 19.4 ± 0.5 (29) | ∗ | 100 |
| Vi Rlx | 28.5 ± 2.5 (30) | 19.3 ± 0.5 (37) | ∗ | 100 |
| Vi Act | 28.5 ± 1.9 (23) | 19.6 ± 0.7 (17) | 21.7 ± 0.6 (16) | 52 |
EM measurements of A-band lattice spacing (SA), small-square Z-band lattice spacing (SSS), basketweave Z-band lattice spacing (SBW), and ratio of small-square to basketweave within the Z-band (%SS) as a function of the presence or absence of Ca2+(Act or Rlx, respectively) when force is inhibited by troponin C extraction (TnC−), aluminum fluoride (AlF3), or vanadate (Vi). Values presented as mean ± standard deviation (number of measurements).
No areas of basketweave large enough for diffraction observed.
To further explore the relation between active contraction and Z-band structure, we treated fibers with the force inhibitors aluminum fluoride or vanadate and again examined the Z-bands in the presence or absence of calcium. Both aluminum fluoride and vanadate are thought to act as phosphate analogs, forming a complex with ADP, which binds tightly to the myosin heads to inhibit force (20). However, there are subtle differences in the effects of the two inhibitors. Aluminum fluoride suppressed calcium-activated force to <1% of control values (Fig. S4, Table S1), whereas vanadate suppressed force less effectively, leaving ∼9% calcium-activated force. Both force inhibitors suppressed stiffness similarly, to ∼11% of rigor stiffness. In the presence of aluminum fluoride, the Z-bands were 100% small-square, regardless of the presence or absence of calcium (Fig. S3, C and D), similar to the troponin C extracted fibers. By contrast, in the presence of vanadate and calcium the Z-bands were a 52% mix of small-square and basketweave forms (Table 4, Fig S3, E and F).
Discussion
We have shown that the structure of the Z-band can be manipulated by temperature, ionic strength, or osmotic pressure to favor either the small-square or the basketweave form, and the known structure of the Z-band suggests why this might be so. Fig. 4, A and B, show four actin filaments as vertical cylinders, two from one sarcomere (black) and two from the adjacent sarcomere (yellow). “Z-links” (green or magenta) connect antiparallel (black-yellow) pairs of filaments. In the small-square structure (Fig. 4 A) the Z-links are sharply kinked so that their central regions lie back to back, whereas in the basketweave structure (Fig. 4 B) the Z-links are separate and curve smoothly between the actin filaments. Each actin filament would have multiple Z-links arranged with fourfold screw symmetry (21,22), although for clarity only two Z-links are drawn. When viewed in projection, the Z-links give rise to either the small-square or the basketweave appearance of the Z-band (Fig. 4, C and D).
Figure 4.
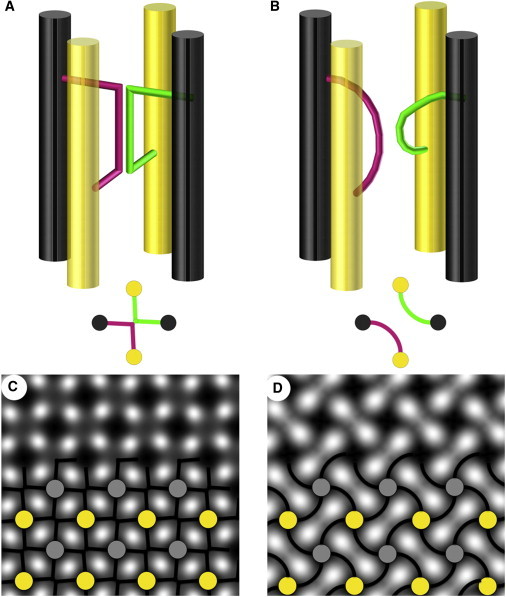
Models of Z-band structure based on 3D reconstructions from the Squire lab (21,22) showing the small-square (A) and basketweave (B) structures. Below each perspective drawing is a projection image as viewed down the filament axis. In C and D the projection image is repeated with fourfold rotational symmetry and superimposed on the filtered Z-band images from Figure 1.
The Z-links are widely believed to be composed of α-actinin (1) and several lines of evidence support this assumption. α-Actinin cross-links actin (23) and its dimensions (24) are consistent with the Z-link dimensions (21,22). The central rod portion of α-actinin exhibits a 90° left-handed twist (25), as required for the Z-links. MD simulations (26) indicate that α-actinin possesses both the rigidity in the central region and the flexibility nearer the ends that would be necessary to adopt the kinked structure shown in Fig. 4 A. Z-links may not be composed solely of α-actinin but probably also involve the elastic protein titin, to which α-actinin also binds (27), because proteolysis by calpain releases α-actinin from the Z-band without cleaving α-actinin itself (28), whereas calpain does cleave titin (29,30). Currently, 3D reconstructions lack sufficient resolution to resolve titin within the Z-band, although some details about titin's structure within the Z-band are beginning to emerge (27,31–33).
Because α-actinin is a dimer, the back-to-back association drawn in Fig. 4 A represents an effective “tetramer” of α-actinin, presumably stabilized by low-affinity protein-protein binding. Such protein binding would be entropically favored at high temperature, ionic strength, or osmotic pressure due to the release of solvation water from the protein interfaces (the hydrophobic effect, see (34–36)), and we thus interpret the prevalence of the small-square form under these conditions as a direct effect on the molecular interactions within the Z-band. Likewise, low temperature, ionic strength, or osmotic pressure would disfavor protein-protein binding, and these are the very same conditions that we have shown to favor the basketweave form of the Z-band, where the Z-links are not interacting with each other. Biochemically, α-actinin is also well known to form aggregates unless held at low ionic strength (37), again consistent with our finding that low ionic strength favors the basketweave form of the Z-band. Evidence for an α-actinin tetramer has also been seen by negative stain, where rods 7–8 nm wide, twice the usual width of the dimer, were observed (38).
The work of Goldstein et al. (6–8) suggested that the conversion from small-square to basketweave required active tension, but our results effectively rule out that hypothesis because we observed the basketweave form even in muscles that were fully relaxed. Instead, our results with vanadate and aluminum fluoride inhibition of calcium-activated force suggest that, in addition to direct effects of temperature, ionic strength, and osmotic pressure, the transition from small-square to basketweave in active fibers may be associated with tropomyosin movement on the thin filaments. It is now well established that in vertebrate skeletal muscle tropomyosin can adopt three different positions, called “blocked”, “closed”, and “open” (see (39) and references therein). Because vanadate suppressed active tension less effectively than aluminum fluoride under our conditions, a greater portion of the cross-bridges must be able to complete the force-generating step to strong binding, which in turn implies that a greater portion of the tropomyosin molecules would be in the fully open position. In contrast, the almost complete suppression of calcium-activated force in the presence of aluminum fluoride suggests that tropomyosin would be predominantly in the closed position. It is unlikely that the small residual force present during vanadate inhibition is responsible for the different Z-band response to calcium compared to aluminum fluoride inhibition, because Z-bands fail to show the basketweave form when intact muscles are stretched to sarcomere lengths beyond 2.7 μm and then tetanized (8), despite sufficient overlap between the thick and thin filaments to generate as much as 60% of the force at full overlap. Because the basketweave form of the Z-band was seen in the presence of calcium when force was inhibited by vanadate, but not when inhibited by aluminum fluoride, suggests instead that the basketweave form is associated with tropomyosin being in the open position, but not in the closed or blocked position. Consistent with this hypothesis is the observation that Z-bands are 100% in the basketweave form in rigor (40), where strong cross-bridge binding and displacement of tropomyosin to the fully open position should be maximal.
Communicating tropomyosin movement from within the A-band to the Z-band requires cooperative coupling between overlapping tropomyosins and a long persistence length to cross the I-band, which is ∼0.33 μm long in our experiments. Direct electron microscopic visualization of the blocked, closed, and open states of thin filaments indicated that tropomyosin movement could propagate into regions free of myosin heads, but never beyond 0.5 μm (41). MD simulations indicate that tropomyosin is inherently curved and has a dynamic persistence length of ∼0.5 μm (42), consistent with the observations of Vibert et al. (41), and sufficient to span the I-band in our experiments. The dynamic persistence length of tropomyosin may explain why Z-bands did not show basketweave in tetanized muscles stretched beyond 2.7 μm (8). In rat soleus muscle stretched to a sarcomere length of 2.7 μm, the edge of the Z-band is 0.5 μm from the edge of the A-band, and the Z-band may simply be too far away from the overlap zone for the tropomyosin movement to be communicated to the Z-band. Thus, the results presented here and by others (8,41) lend support to the idea that when tropomyosin is either in the blocked or closed position the Z-band is small-square, but when the tropomyosin is in the open position the Z-band is basketweave. Tropomyosin has previously been shown to affect the axially repeating structure of the Z-band (43,44), but intriguingly, tropomyosin does not appear to be a component of the Z-band (45). The correlation we find, between tropomyosin position and the transverse structure of the Z-band, requires some other mediating protein, and we suggest titin as a likely candidate because titin is a Z-band component that also binds to tropomyosin (46), as well as calcium (47,48) and calpain (49,50).
Acknowledgments
The authors thank Dr. Leepo Yu for use of the XRD facility, Dr. Sengun Xu for help with XRD experiments, and Carmen Lucaveche for help with EM experiments.
This work was supported by grant AR-14317 to M.K.R.
Supporting Material
References
- 1.Luther P.K. The vertebrate muscle Z-disc: sarcomere anchor for structure and signalling. J. Muscle Res. Cell Motil. 2009;30:171–185. doi: 10.1007/s10974-009-9189-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Pyle W.G., Solaro R.J. At the crossroads of myocardial signaling: the role of Z-discs in intracellular signaling and cardiac function. Circ. Res. 2004;94:296–305. doi: 10.1161/01.RES.0000116143.74830.A9. [DOI] [PubMed] [Google Scholar]
- 3.Landon D.N. The influence of fixation upon the fine structure of the Z-disk of rat striated muscle. J. Cell Sci. 1970;6:257–276. doi: 10.1242/jcs.6.1.257. [DOI] [PubMed] [Google Scholar]
- 4.Macdonald R.D., Engel A.G. Observations on organization of Z-disk components and on rod-bodies of Z-disk origin. J. Cell Biol. 1971;48:431–437. doi: 10.1083/jcb.48.2.431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Landon D.N. Change in Z-disk structure with muscular contraction. J. Physiol. 1970;211:44–45. [PubMed] [Google Scholar]
- 6.Goldstein M.A., Michael L.H., Sass R.L. The Z-band lattice in skeletal muscle before, during and after tetanic contraction. J. Muscle Res. Cell Motil. 1986;7:527–536. doi: 10.1007/BF01753569. [DOI] [PubMed] [Google Scholar]
- 7.Goldstein M.A., Michael L.H., Sass R.L. Two structural states of Z-bands in cardiac muscle. Am. J. Physiol. 1989;256:H552–H559. doi: 10.1152/ajpheart.1989.256.2.H552. [DOI] [PubMed] [Google Scholar]
- 8.Goldstein M.A., Michael L.H., Sass R.L. Z band dynamics as a function of sarcomere length and the contractile state of muscle. FASEB J. 1987;1:133–142. doi: 10.1096/fasebj.1.2.3609610. [DOI] [PubMed] [Google Scholar]
- 9.Irving T.C., Li Q., Millman B.M. Z/I and A-band lattice spacings in frog skeletal muscle: effects of contraction and osmolarity. J. Muscle Res. Cell Motil. 1998;19:811–823. doi: 10.1023/a:1005459605964. [DOI] [PubMed] [Google Scholar]
- 10.Güth K., Wojciechowski R. Perfusion cuvette for the simultaneous measurement of mechanical, optical and energetic parameters of skinned muscle fibres. Pflugers Arch. 1986;407:552–557. doi: 10.1007/BF00657515. [DOI] [PubMed] [Google Scholar]
- 11.Caspar D.L., Cohen C., Longley W. Tropomyosin: crystal structure, polymorphism and molecular interactions. J. Mol. Biol. 1969;41:87–107. doi: 10.1016/0022-2836(69)90128-4. [DOI] [PubMed] [Google Scholar]
- 12.Yu L.C., Brenner B. Structures of actomyosin crossbridges in relaxed and rigor muscle fibers. Biophys. J. 1989;55:441–453. doi: 10.1016/S0006-3495(89)82838-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Yamaguchi M., Izumimoto M., Stromer M.H. Fine structure of wide and narrow vertebrate muscle Z-lines. A proposed model and computer simulation of Z-line architecture. J. Mol. Biol. 1985;184:621–643. doi: 10.1016/0022-2836(85)90308-0. [DOI] [PubMed] [Google Scholar]
- 14.Irving T.C., Millman B.M. Z-line/I-band and A-band lattices of intact frog sartorius muscle at altered interfilament spacing. J. Muscle Res. Cell Motil. 1992;13:100–105. doi: 10.1007/BF01738433. [DOI] [PubMed] [Google Scholar]
- 15.Brenner B., Yu L.C., Podolsky R.J. X-ray diffraction evidence for cross-bridge formation in relaxed muscle fibers at various ionic strengths. Biophys. J. 1984;46:299–306. doi: 10.1016/S0006-3495(84)84026-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Reedy M.K., Goody R.S., Rosenbaum G. Co-ordinated electron microscopy and x-ray studies of glycerinated insect flight muscle. I. X-ray diffraction monitoring during preparation for electron microscopy of muscle fibres fixed in rigor, in ATP and in AMPPNP. J. Muscle Res. Cell Motil. 1983;4:25–53. doi: 10.1007/BF00711957. [DOI] [PubMed] [Google Scholar]
- 17.Brenner B. Technique for stabilizing the striation pattern in maximally calcium-activated skinned rabbit psoas fibers. Biophys. J. 1983;41:99–102. doi: 10.1016/S0006-3495(83)84411-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Hannon J.D., Chase P.B., Gordon A.M. Calcium-independent activation of skeletal muscle fibers by a modified form of cardiac troponin C. Biophys. J. 1993;64:1632–1637. doi: 10.1016/S0006-3495(93)81517-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Brandt P.W., Diamond M.S., Schachat F.H. Co-operative interactions between troponin-tropomyosin units extend the length of the thin filament in skeletal muscle. J. Mol. Biol. 1987;195:885–896. doi: 10.1016/0022-2836(87)90492-x. [DOI] [PubMed] [Google Scholar]
- 20.Chase P.B., Martyn D.A., Gordon A.M. Effects of inorganic phosphate analogues on stiffness and unloaded shortening of skinned muscle fibres from rabbit. J. Physiol. 1993;460:231–246. doi: 10.1113/jphysiol.1993.sp019469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Luther P.K., Barry J.S., Squire J.M. The three-dimensional structure of a vertebrate wide (slow muscle) Z-band: lessons on Z-band assembly. J. Mol. Biol. 2002;315:9–20. doi: 10.1006/jmbi.2001.5217. [DOI] [PubMed] [Google Scholar]
- 22.Morris E.P., Nneji G., Squire J.M. The three-dimensional structure of the nemaline rod Z-band. J. Cell Biol. 1990;111:2961–2978. doi: 10.1083/jcb.111.6.2961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Blanchard A., Ohanian V., Critchley D. The structure and function of alpha-actinin. J. Muscle Res. Cell Motil. 1989;10:280–289. doi: 10.1007/BF01758424. [DOI] [PubMed] [Google Scholar]
- 24.Tang J., Taylor D.W., Taylor K.A. The three-dimensional structure of alpha-actinin obtained by cryoelectron microscopy suggests a model for Ca(2+)-dependent actin binding. J. Mol. Biol. 2001;310:845–858. doi: 10.1006/jmbi.2001.4789. [DOI] [PubMed] [Google Scholar]
- 25.Ylänne J., Scheffzek K., Saraste M. Crystal structure of the alpha-actinin rod reveals an extensive torsional twist. Structure. 2001;9:597–604. doi: 10.1016/s0969-2126(01)00619-0. [DOI] [PubMed] [Google Scholar]
- 26.Golji J., Collins R., Mofrad M.R. Molecular mechanics of the alpha-actinin rod domain: bending, torsional, and extensional behavior. PLOS Comput. Biol. 2009;5:e1000389. doi: 10.1371/journal.pcbi.1000389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Young P., Ferguson C., Gautel M. Molecular structure of the sarcomeric Z-disk: two types of titin interactions lead to an asymmetrical sorting of alpha-actinin. EMBO J. 1998;17:1614–1624. doi: 10.1093/emboj/17.6.1614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Goll D.E., Dayton W.R., Robson R.M. Studies of the alpha-actinin/actin interaction in the Z-disk by using calpain. J. Biol. Chem. 1991;266:8501–8510. [PubMed] [Google Scholar]
- 29.Lim C.C., Zuppinger C., Sawyer D.B. Anthracyclines induce calpain-dependent titin proteolysis and necrosis in cardiomyocytes. J. Biol. Chem. 2004;279:8290–8299. doi: 10.1074/jbc.M308033200. [DOI] [PubMed] [Google Scholar]
- 30.Taveau M., Bourg N., Richard I. Calpain 3 is activated through autolysis within the active site and lyses sarcomeric and sarcolemmal components. Mol. Cell. Biol. 2003;23:9127–9135. doi: 10.1128/MCB.23.24.9127-9135.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Zou P., Pinotsis N., Wilmanns M. Palindromic assembly of the giant muscle protein titin in the sarcomeric Z-disk. Nature. 2006;439:229–233. doi: 10.1038/nature04343. [DOI] [PubMed] [Google Scholar]
- 32.Knupp C., Luther P.K., Squire J.M. Titin organisation and the 3D architecture of the vertebrate-striated muscle I-band. J. Mol. Biol. 2002;322:731–739. doi: 10.1016/s0022-2836(02)00819-7. [DOI] [PubMed] [Google Scholar]
- 33.Luther P.K., Squire J.M. Muscle Z-band ultrastructure: titin Z-repeats and Z-band periodicities do not match. J. Mol. Biol. 2002;319:1157–1164. doi: 10.1016/S0022-2836(02)00372-8. [DOI] [PubMed] [Google Scholar]
- 34.Timasheff S.N. The control of protein stability and association by weak interactions with water: how do solvents affect these processes? Annu. Rev. Biophys. Biomol. Struct. 1993;22:67–97. doi: 10.1146/annurev.bb.22.060193.000435. [DOI] [PubMed] [Google Scholar]
- 35.Tsai C.J., Nussinov R. Hydrophobic folding units at protein-protein interfaces: implications to protein folding and to protein-protein association. Protein Sci. 1997;6:1426–1437. doi: 10.1002/pro.5560060707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Keskin O., Gursoy A., Nussinov R. Principles of protein-protein interactions: what are the preferred ways for proteins to interact? Chem. Rev. 2008;108:1225–1244. doi: 10.1021/cr040409x. [DOI] [PubMed] [Google Scholar]
- 37.Masaki T., Takaiti O. Some properties of chicken alpha-actinin. J. Biochem. 1969;66:637–643. [PubMed] [Google Scholar]
- 38.Suzuki A., Goll D.E., Stromer M.H. Some properties of purified skeletal muscle alpha-actinin. J. Biol. Chem. 1976;251:6860–6870. [PubMed] [Google Scholar]
- 39.Poole K.J., Lorenz M., Holmes K.C. A comparison of muscle thin filament models obtained from electron microscopy reconstructions and low-angle x-ray fibre diagrams from non-overlap muscle. J. Struct. Biol. 2006;155:273–284. doi: 10.1016/j.jsb.2006.02.020. [DOI] [PubMed] [Google Scholar]
- 40.Edwards R.J., Goldstein M.A., Sass R.L. The Z-band lattice in skeletal muscle in rigor. J. Ultrastruct. Mol. Struct. Res. 1989;102:59–65. doi: 10.1016/0889-1605(89)90033-5. [DOI] [PubMed] [Google Scholar]
- 41.Vibert P., Craig R., Lehman W. Steric-model for activation of muscle thin filaments. J. Mol. Biol. 1997;266:8–14. doi: 10.1006/jmbi.1996.0800. [DOI] [PubMed] [Google Scholar]
- 42.Li X.E., Holmes K.C., Fischer S. The shape and flexibility of tropomyosin coiled coils: implications for actin filament assembly and regulation. J. Mol. Biol. 2010;395:327–339. doi: 10.1016/j.jmb.2009.10.060. [DOI] [PubMed] [Google Scholar]
- 43.Schachat F.H., Canine A.C., Reedy M.C. The presence of two skeletal muscle alpha-actinins correlates with troponin-tropomyosin expression and Z-line width. J. Cell Biol. 1985;101:1001–1008. doi: 10.1083/jcb.101.3.1001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Laing N.G., Wilton S.D., Haan E. A mutation in the alpha tropomyosin gene TPM3 associated with autosomal dominant nemaline myopathy. Nat. Genet. 1995;9:75–79. doi: 10.1038/ng0195-75. [DOI] [PubMed] [Google Scholar]
- 45.Trombitás K., Baatsen P.H., Pollack G.H. Immunoelectron microscopic observations on tropomyosin localization in striated muscle. J. Muscle Res. Cell Motil. 1990;11:445–452. doi: 10.1007/BF01739764. [DOI] [PubMed] [Google Scholar]
- 46.Raynaud F., Astier C., Benyamin Y. Evidence for a direct but sequential binding of titin to tropomyosin and actin filaments. Biochim. Biophys. Acta. 2004;1700:171–178. doi: 10.1016/j.bbapap.2004.05.001. [DOI] [PubMed] [Google Scholar]
- 47.Yarom R., Meiri U. N lines in striated muscle: a site of intracellular Ca2+ Nat. New Biol. 1971;234:254–256. doi: 10.1038/newbio234254a0. [DOI] [PubMed] [Google Scholar]
- 48.Vignon X., Beaulaton J., Ouali A. Ultrastructural localization of calcium in post-mortem bovine muscle: a cytochemical and x-ray microanalytical study. Histochem. J. 1989;21:403–411. doi: 10.1007/BF01789738. [DOI] [PubMed] [Google Scholar]
- 49.Coulis G., Becila S., Ouali A. Calpain 1 binding capacities of the N1-line region of titin are significantly enhanced by physiological concentrations of calcium. Biochemistry. 2008;47:9174–9183. doi: 10.1021/bi800315v. [DOI] [PubMed] [Google Scholar]
- 50.Raynaud F., Fernandez E., Ouali A. Calpain 1-titin interactions concentrate calpain 1 in the Z-band edges and in the N2-line region within the skeletal myofibril. FEBS J. 2005;272:2578–2590. doi: 10.1111/j.1742-4658.2005.04683.x. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


