Models of HERG Gating

Abstract

HERG (Kv11.1, KCNH2) is a voltage-gated potassium channel with unique gating characteristics. HERG has fast voltage-dependent inactivation, relatively slow deactivation, and fast recovery from inactivation. This combination of gating kinetics makes study of HERG difficult without using mathematical models. Several HERG models have been developed, with fundamentally different organization. HERG is the molecular basis of I_Kr, which plays a critical role in repolarization. We programmed and compared five distinct HERG models. HERG gating cannot be adequately replicated using Hodgkin-Huxley type formulation. Using Markov models, a five-state model is required with three closed, one open, and one inactivated state, and a voltage-independent step between some of the closed states. A fundamental difference between models is the presence/absence of a transition directly from the proximal closed state to the inactivated state. The only models that effectively reproduce HERG data have no direct closed-inactivated transition, or have a closed-inactivated transition that is effectively zero compared to the closed-open transition, rendering the closed-inactivation transition superfluous. Our single-channel model demonstrates that channels can inactivate without conducting with a flickering or bursting open-state. The various models have qualitative and quantitative differences that are critical to accurate predictions of HERG behavior during repolarization, tachycardia, and premature depolarizations.

Introduction

Gating of the Kv11.1 (Human Ether-à-Go-Go related gene, HERG, KCNH2) voltage-gated K⁺ channel is remarkably different from most other V_m-gated K⁺ channels. HERG is the major molecular basis underlying native cardiac I_Kr current (1–3), and plays a crucial role in repolarization. Even moderate changes in I_Kr can have considerable effects on the shape and duration of the cardiac action potential (AP), resulting in AP lengthening, long QT syndrome, and increasing the likelihood of arrhythmic events and sudden cardiac death (4,5). Understanding HERG gating kinetics is therefore of critical clinical importance and its behavior is a frequent subject of investigation in mathematical models of the cardiac AP (6–40). Several different formulations for the gating of I_Kr/HERG have been used in these AP models. However, little or no attention has been paid to the qualitative and quantitative behavior produced by these different formulations of HERG.

In this article, we examine in detail the relative behavior of several HERG models frequently employed in mathematical modeling and adapted for the study of AP repolarization. These models have been derived using different preparations (e.g., myocytes from different species or regions, or channels expressed in different expression systems) or to match data under different experimental conditions (e.g., different temperature). Nonetheless, there are qualitative differences in the performance of the various models, some of which deviate substantially from known biophysical behavior under any conditions. Many of the quantitative differences produce large and perhaps unexpected differences that are of potentially major consequence to those using cellular model simulations.

HERG exhibits some distinct and unusual gating behavior. HERG has slow activation (with a V_m-insensitive step that becomes rate-limiting under physiological conditions), V_m-dependent inactivation, and strong V_m-dependent inward rectification (41–43). HERG rectification is a result of gating, and therefore is distinct from the rectification observed in K_ir channels that results from open channel block by intracellular Mg²⁺ and polyamines (44–46). Development of, and recovery from, inactivation is very rapid relative to the much slower processes of activation and deactivation. This property makes HERG very efficient in producing repolarizing current in the later phases of repolarization. HERG inactivation is sometimes categorized as “C-type” (41), a mechanism found in a variety of K⁺ channels, which may be related to “slow” inactivation in Na⁺ and Ca²⁺ channels (47). However, there are distinct differences between HERG inactivation and classic C-type inactivation. For example, the development of HERG inactivation is intrinsically V_m-dependent and at depolarized potentials inactivation becomes faster than activation (41,43,48), resulting in steady-state rectification at positive voltages.

Mathematical representations of HERG fall into two groups. The first are the oldest and most computationally convenient, using conventional Hodgkin and Huxley (HH) type formulations with independent activation and inactivation gating variables (49). These models have a very simple first-order activation process. The second group uses Markov processes, enabling more complex activation schemes. Within the Markov group, there is diversity in the nature of the activation process and in the coupling of activation to inactivation, as well as quantitative differences in kinetics. This modeling study suggests that the particular activation and inactivation components used in the model are critical determinants of whether the model will be able to reproduce HERG voltage-clamp data. It is also important in determining HERG current development during the AP; the inactivation formulation used produces critical differences in behavior during the AP, and premature APs.

Materials and Methods

Model formulations

Simulations were calculated using a fourth-order Runge-Kutta algorithm with a variable step size implemented in Microsoft Visual C++ 2008. Numerical accuracy was confirmed by demonstrating insensitivity to step size. Computations were performed on a Dell Precision T7500 (Round Rock, TX) with two Intel Xeon E5520 CPUs (Santa Clara, CA). All voltage protocols used are detailed in the text. Model parameters are from the original publications. Whole-cell current is proportional to whole-cell conductance, g; the number of channels in the open state, O; membrane potential, V; and reversal potential E_k (84.3 mV):

$$I=gO\left(V-E_K\right).$$

ZLRR (Zeng, Laurita, Rosenbaum, and Rudy) model

Zeng et al. (50) used an HH gating particle formalism where the open state is calculated as the fraction of channels that are activated, but not inactivated:

$$O=XR,$$

$$R=\frac{1}{1+\mathit{exp}\left(\frac{V+9}{22.4}\right)},$$

$$X_{r\infty }=\frac{1}{1+\mathit{exp}\left(-\frac{V+21.5}{7.5}\right)},$$

$${\tau }_{Xr}=\frac{1}{\left(\frac{0.00138\left(V+14.2\right)}{1-\mathit{exp}\left(-0.123\left(V+14.2\right)\right)}\right)+\left(\frac{0.00061\left(V+38.9\right)}{\mathit{exp}\left(0.145\left(V+38.9\right)-1\right)}\right)}.$$

WLMSR (Wang, Lu, Morales, Strauss, and Rasmusson) model

Wang et al. (43) developed a Markov model with three closed states, and introduced the V_m-insensitive transition necessary to model activation:

$${\text{C}}_1\underset{{\beta }_1}{\overset{{\alpha }_1}{\rightleftarrows }}{\text{C}}_2\underset{K_b}{\overset{K_f}{\rightleftarrows }}{\text{C}}_3\underset{{\beta }_2}{\overset{{\alpha }_2}{\rightleftarrows }}\text{O}\underset{{\beta }_1}{\overset{{\alpha }_1}{\rightleftarrows }}\text{I}.$$

CR (Clancy and Rudy) model

The model of Clancy and Rudy (51) used the formulation of Wang et al. (43), with the addition of a direct transition from the C3 closed state to the inactivated state. Note that the C₃-I and C₃-O transition rates are identical:

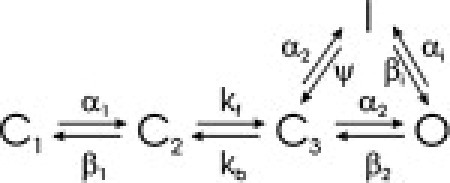
MGWMN (Mazhari, Greenstein, Winslow, Marban, and Nuss) model

The formulation of Mazhari et al. (52) is also based on the Wang V_m-insensitive step model, but introduces a direct transition from the C₃ to I that has different rate constants from the C₃-O transition:

OGD (Oehmen, Giles, and Demir) model

The formulation of Oehmen et al. (53) has a linear model with the V_m-insensitive step, but only two closed states:

$${\text{C}}_2\underset{K_{\text{b}}}{\overset{K_{\text{f}}}{\rightleftarrows }}{\text{C}}_3\underset{{\beta }_2}{\overset{{\alpha }_2}{\rightleftarrows }}\text{O}\underset{{\beta }_1}{\overset{{\alpha }_1}{\rightleftarrows }}\text{I}.$$

Gating parameters

The equations defining the gating transitions for each of the Markov models are given in Table 1. Where needed, ψ is defined by the other parameters to ensure thermodynamic reversibility, i.e.,

$$\psi ={\alpha }_{i2}{\beta }_i{\beta }_2/{\alpha }_2{\alpha }_i\left(\text{MGWMN}\right);\psi ={\beta }_i{\beta }_2/{\alpha }_i\left(\text{CR}\right).$$

Table 1.

Equations and parameter values for transitions in each model

	WLMSR (ms−1)	MGWMN (ms−1)	CR (ms−1)	OGD (ms−1)
kf	0.023761	0.0266	2.172	0.0176
Kb	0.036778	0.1348	1.077	0.684
α1	0.022348exp(0.01176Vm)	0.0069exp(0.0272 Vm)	0.0555exp(0.05547153(Vm−12))	—
β1	0.047002exp(−0.0631Vm)	0.0227exp(−0.0431 Vm)	0.002357exp(−0.036588 Vm)	—
α2	0.013733exp(0.038198Vm)	0.0218exp(0.0262 Vm)	0.0655exp(0.05547153(Vm−36))	0.0787exp(0.0378(Vm+10))
β2	0.0000689exp(−0.04178Vm)	0.0009exp(−0.0269 Vm)	0.0029357exp(−0.02158 Vm)	0.0035exp(−0.0252(Vm+10))
αi	0.090821exp(0.023391Vm)	0.0622exp(0.0120 Vm)	0.656(4.50.3/[K+]o0.3)exp(0.000942 Vm)	0.264/([K+]o/5.4)0.4exp(0.0164(Vm+10))
βi	0.006497exp(−0.03268Vm)	0.0059exp(−0.0443 Vm)	0.439 (4.5/[K+]o)exp(−0.02352(Vm+25))	0.0849/([K+]o/5.4)0.05exp(−0.0454(Vm+10))
αi2	—	1.29E-5exp(2.71E-6 Vm)	0.0655exp(0.05547153(Vm−36))	—

Results

Steady-state activation

All models exhibit similar steady-state activation versus voltage. Fig. 1 shows computed traces from a standard two-pulse protocol: P1 (to a variety of depolarizing potentials) activates the channel, then the channel rapidly enters the inactivated state, which gives rise to the rectification of outward current at positive potentials. The P2 pulse, to –40 mV, results in rapid recovery from inactivation, but deactivation is relatively slow, so the peak outward current is a reflection of the number of channels in the open state at the end of the initial P1 depolarizing pulse. The values for V_1/2 for all models are within the experimental range, between −28 and −15 mV. However, there are significant differences in the relative magnitude of outward current generated by P1 and P2, suggesting that the time-dependent nature of rectification is very different between the various models. WLMSR, MGWMN, and OGD models exhibit the expected strong rectification, with the P2 pulse passing much greater current than the P1 pulse, whereas ZLRR and CR models do not exhibit rectification, and in some cases have larger current flowing in the P1 pulse than in the P2 pulse (see Supporting Material).

Figure 1.

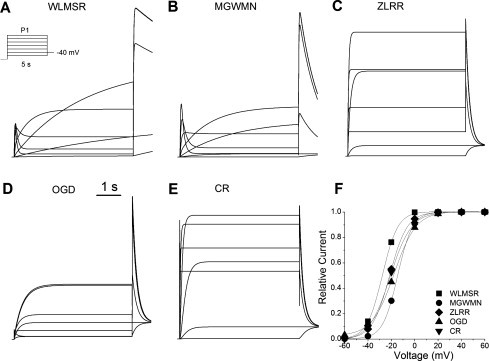
Steady-state activation. (A–E) A P1 pulse was applied from the holding potential of −90 mV to voltages between −60 and +60 for 5 s, followed by a P2 pulse to −40 mV (see inset) for all models. (F) Relative magnitude of the peak P2 current versus P1 voltage. (Lines) Fits to Boltzmann relationship (1/(1 + exp((V–V_1/2)/k))). V_1/2 values were similar for all models: WLMSR −27.7 mV; MGWMN −14.6 mV; ZLRR −21.5 mV; OGD −17.7 mV; CR −21.0 mV.

The onset of current flow is clearly very different between the models. Fig. 2 shows the details of the beginning of P1 pulse, during which a transient current is described experimentally for both HERG and endogenous I_Kr. This transient current reflects the molecular coupling between activation and inactivation. The transient behavior and its decay reflects the delayed delivery of the channel to the open state, followed by rapid inactivation, which is a phenomenon first reported for Na⁺ currents by Aldrich et al. (54). The WLMSR and MGWMN models exhibit the expected initial transient current. The ZLRR model shows no transient current, and the CR and OGD models only have a transient component at extreme potentials. The ZLRR model has independent first-order HH gating variables, and as inactivation can proceed independently, no transient is generated by this formulation. The differences in the magnitude of the transient in the Markov type models reflect significant differences in both activation and coupling between activation and inactivation.

Figure 2.

Initial activation phase. (A–E) Detail of current traces subject to activation protocol from Fig. 1 for all models. Differences are clearly seen in the initial response to depolarization, when a transient current is expected due to the rapid inactivation following activation.

Deactivation

Deactivation experiments were simulated using a two-step protocol. A first 5-s (P1) pulse activated then inactivated channels. This was followed by the test step (P2) to a range of voltages between −120 and −40 mV. Recovery from inactivation was rapid in all models, and deactivation is relatively slow, so deactivation was measured by directly fitting current decay. The process of deactivation is qualitatively consistent across all models, being well separated in time from the rapid recovery from inactivation (Fig. 3). Quantitatively, there are very large differences in speed. These quantitative differences in time constant reflect several factors. The two most important are species/isoform (HERG1a or 1b) and temperature (e.g., room temperature versus 37°C). When normalized, there are only minor variations in the V_m-dependence of the time constants, consistent with the minor variations in the steepness of the steady-state activation curve. Fig. 3 shows a significant qualitative difference evident between models. In the ZLRR and CR models the ratio of the magnitude of the current at the end of the P1 pulse to the peak P2 current is much larger compared to all other models. This suggests that the ZLRR and CR models may make similar predictions of current magnitude and rectification despite having different gating structures.

Figure 3.

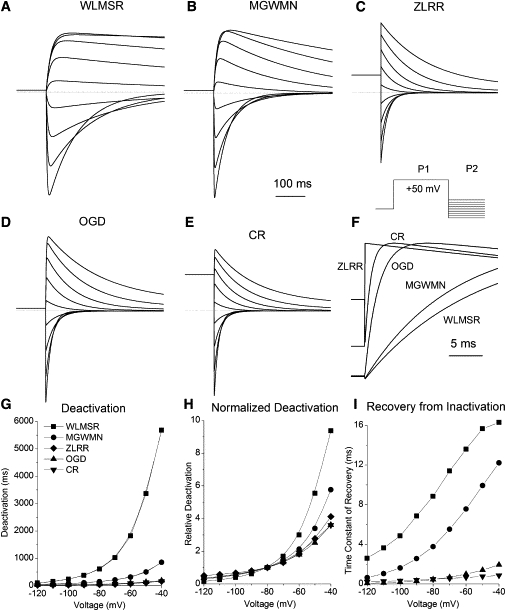
Deactivation. (A–E) Traces obtained with a standard two-pulse deactivation protocol. P1 is from −90 to +50 mV for 5 s, P2 is between −120 and −40 mV. (Dotted lines) Zero current level. (F) Comparison of recovery from inactivation for the P2 step to −40 mV. (G) Deactivation versus voltage. (H) Normalized (at −80 mV) deactivation versus voltage. (I) Apparent recovery from inactivation was determined by fitting a single exponential to the current. This method counts only recovery of the channels to the open state, so in models with inactivated-closed state transitions, these will not be included. ZLRR recovery is instantaneous.

Activation rate

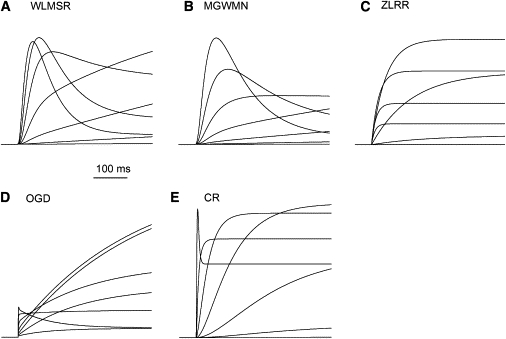
Examining the rate of activation demonstrated substantial differences between models. Activation kinetics cannot be measured through direct fitting of the onset of current. A activation was therefore measured with a modified tail current protocol (Fig. 4), in which the growth of the tail currents reflects the activation process (43,48). Three of the Markov type models (WLMSR, MGWMN, and OGD) show qualitatively similar behavior, with sigmoid activation kinetics and time constants reaching an asymptotic relatively slow activation rate (Fig. 5). In contrast, activation in the ZLRR model is rapid at all potentials. This is consistent with the assumptions of a single step V_m-dependent HH formalism. The CR model again is very distinctive, having the rapid voltage dependence of the ZLRR model over most of the voltage range, becoming nearly instantaneous at positive potentials, and having an initial atypical “overshoot” fast transient at very positive potentials on the initial depolarization, which is larger than the tail current.

Figure 4.

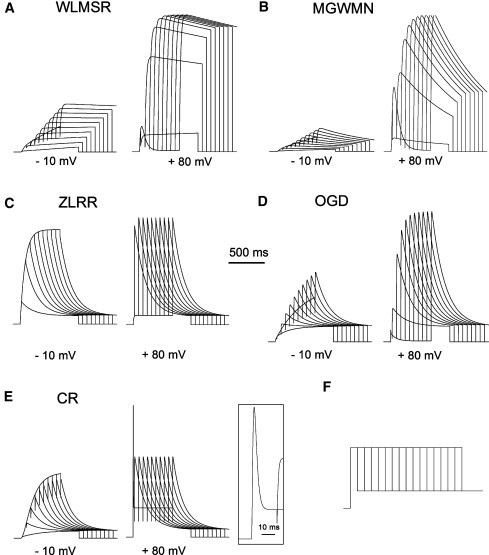
Activation rate was measured using an envelope of tails protocol. V_m was depolarized from the holding potential of −90 mV to the test potential for durations between 20 and 500 ms in 60 ms increments. The membrane potential was then returned to −40 mV, which elicited an outward tail current, the peak of which indicates the degree of activation. Traces are shown for activation to −10 and +80 mV for all models (A–E). (E) The CR model has a large transient current flux immediately after depolarization to +80 mV, which is shown in detail (inset). (F) Voltage protocol.

Figure 5.

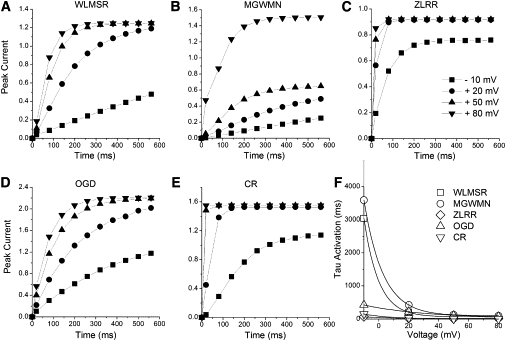
Activation rates. (A–E) The peak current on repolarization to −40 mV from the activation rate protocol (Fig. 4) versus pulse duration for all models. (F) Activation rate, measured by fitting a single exponential to the late phase of activation, versus voltage for all models. (Lines) Exponential fits to activation.

Inactivation

In all models, inactivation has intrinsic and steep voltage dependence. The ZLRR model is an HH type model, and so inactivates equally from all preactivated closed states when considered as an expanded Markov model. The remaining models inactivate either from the open state or the open and proximal closed state. Depending on the formulation, there were significant differences in inactivation between models, and important differences in the ability of the models to reproduce experimental data. Fig. 6 shows the model responses to a protocol designed to measure inactivation directly (41,43,48). The P1 pulse activates and inactivates the channel, and the brief return to −90 mV rapidly relieves inactivation, but little of the slow deactivation occurs. In the P2 pulse, the channels are open, and so the process of inactivation can be observed directly before the slower deactivation process occurs.

Figure 6.

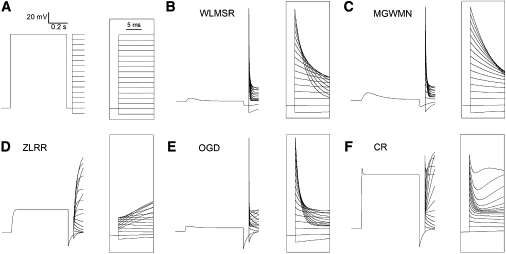
Inactivation. (A) Voltage protocol: a P1 depolarization to +50 for 600 ms to activate the channels was followed by a repolarizing pulse to −90 mV for 60 ms to remove inactivation, then a P2 pulse to a range of potentials between −100 and +50 mV to allow direct observation of inactivation. (Inset) Details of P2 pulse. (B–F) The inactivation protocol was applied to all models.

Using this protocol reveals important differences between models (Fig. 6). The WLMSR, MGWMN, and OGD models are qualitatively similar both to each other and to previously published experimental results obtained using this protocol (43,48). The ZLRR and CR models produce distinctively different results, which have not been observed experimentally. The ZLRR and CR models fail to reproduce the expected transient in P2. In the ZLRR model, no inactivation is observed at all. This is due to the instantaneous inactivation in the ZLRR model. Time-dependent inactivation was not a phenomenon that this model was designed to reproduce. In the CR model, there is a brief small inactivation, followed by reactivation of the current. This behavior results from the very strong voltage dependence and parameter choice for the kinetics of activation, as well as the nature of the coupling of inactivation to the preopen closed state in the CR model (see Discussion, below).

Action potentials

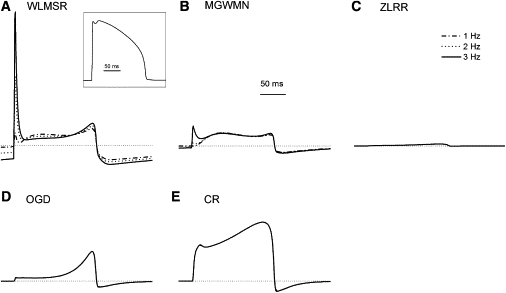
Under voltage-clamp conditions, the various models offer significantly different predictions of behavior. We therefore examined the predicted current during AP clamp for each model. All models predict changes in HERG current during the course of an AP. We also examined the frequency response of the models. An experimentally recorded AP was digitized and used as a voltage-clamp input at different frequencies. Most models have very rapid gating, and so showed no frequency-dependent change in current (Fig. 7). The only frequency-dependent responses were the WMLSR and MGWMN models. The most marked effect was the development of a transient-outward-like behavior at rapid rates, which is consistent with the experimental recordings obtained studying HERG via dynamic AP clamp (55). The WMLSR and MGWMN models also produced a slight decrease in outward current during the early plateau with increasing rate, followed by an augmentation of outward current in the later phases.

Figure 7.

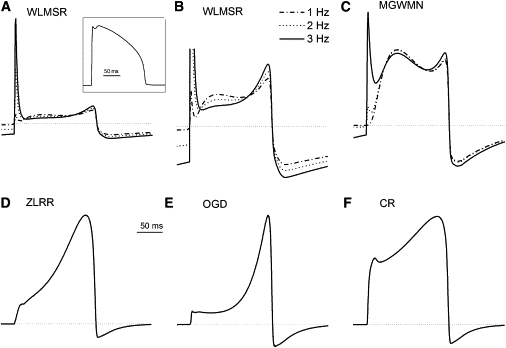
Kinetic changes in response to AP clamp. AP clamp (inset) was applied to all models for 10 s. (A–F) The final AP is shown for stimulation frequencies of 1, 2, and 3 Hz for all models. (Dotted lines) Zero current level. (B) Detailed view of frequency-dependent changes in WLMSR model.

Mutations in HERG and drug suppression of I_Kr have been associated with early after-depolarizations. An important question then becomes, how do different models behave during a second premature AP? Fig. 8 shows simulations of AP clamp showing an AP interrupted by a second AP near the foot of repolarization of the first AP. The ZLRR and CR models show no change in the second peak of current and only minor changes in time course. The WLMSR, MGWMN, and OGD models all show an augmentation of the second peak of current during the late repolarization phase of the second AP. None of the models showed significant frequency dependence of I_Kr behavior during this second AP.

Figure 8.

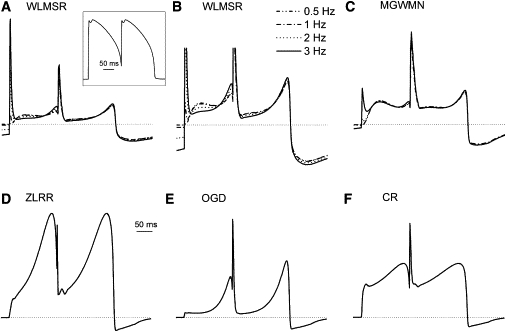
Kinetic changes in response to a premature AP during AP clamp. (A–F) All models were subjected to the voltage protocol (inset) for 10 s. The final AP is shown for stimulation frequencies of 0.5, 1, 2, and 3 Hz. (Dotted line) Zero current level.

Discussion

The unusual gating properties of I_Kr and HERG have long presented a challenge for computer modelers of ion channel behavior. Clay et al. (56) noted that the HH formalism or very simple models cannot reproduce the observed behavior of this current under voltage-clamp. The HERG activation process at many voltages is obscured by the overlap with fast inactivation, and cannot be fit directly to the rising phase of the current. Using the tail current protocol (see Fig. 4), HERG activation has complex sigmoidicity and voltage-dependent saturation. For HERG and I_Kr currents, activation appears exponential up to ∼+20 mV, but above that range the transient component of the current precludes direct analysis of activation, and extrapolation of the activation trend using an HH set of assumptions can lead to an unrealistically fast activation process. Activation therefore cannot be adequately represented by a Hodgkin-Huxley (49) single gating variable raised to a power. The ZLRR formulation has a Hodgkin-Huxley gating approximation (50) that was developed before most of the gating properties of I_Kr and HERG had been experimentally established. It is not surprising, therefore, that the ZLRR model fails to reproduce many of the phenomena associated with I_Kr behavior under voltage-clamp. Even though the ZLRR model reproduces some key features of I_Kr (e.g., steady-state activation, qualitative deactivation), the activation process in the ZLRR model (and its instantaneous inactivation) predicts very different current magnitudes and behavior during the AP in response to changes in rate and to premature stimulation. In sum, HERG is not adequately modeled with an HH representation.

Clearly, the activation process is an important feature of HERG. The Markov-type models have either two (OGD) or three (WLMSR, MGWMN, CR) closed states in the activation pathway. The two-closed-state OGD model closely parallels the model of Liu et al. (48) that examined I_Kr in ferret atrial myocytes. The experimental data for the model of Liu et al. (48) were the first to demonstrate sigmoidicity of activation and a voltage-insensitive step in the activation sequence. At high potentials, this put a limit on how fast the I_Kr current could activate. Because deactivation was highly voltage-sensitive and did not show saturation, it was assumed that the voltage-sensitive step communicated directly with the open state, whereas the voltage-insensitive step occurred earlier in activation. The OGD model retains these properties, and matches the experimental voltage-clamp data well. However, it should be noted that the limitations of studies in native myocytes require holding or a prepulse to ∼−40 mV to eliminate the large and overlapping I_to K⁺ current (48,53). As a result, transitions occurring near the resting membrane potential were not probed.

Currents recorded from heterologously expressed HERG channels are much more readily isolated from overlapping currents than I_Kr, and can be studied over a wide range of potentials. Wang et al. (43) quantitatively analyzed HERG expressed in Xenopus oocytes and found that a minimum of three closed states was required to reproduce the sigmoidicity of activation from normal resting membrane potentials. Similar to the earlier analysis of I_Kr by Liu et al. (48) and Wang et al. (43), we found evidence for a rate-limiting voltage-insensitive step. They also fit a comprehensive set of experiments and demonstrated an additional voltage-sensitive step preceding the voltage-insensitive step. This study (43) formed the experimental basis for the use of three steps with the middle step being voltage-insensitive, which is incorporated into the WLMSR, MGWMN, and CR models examined here. Inclusion of this step is crucial for the rate-dependent changes observed in the WLMSR and MGWMN models.

Despite inclusion of this step, the CR model does not predict rate-dependent changes in activation. This is due to some of the parameter choices in the CR model. The single most obvious and extreme difference between CR and the other models is in the voltage-insensitive step. The forward transition rate, K_f, is two orders-of-magnitude faster than the next largest value of K_f (in the OGD model). This is despite the OGD model representing I_Kr behavior at physiological temperatures (35°C). With respect to the voltage-insensitive step, there are quantitative differences that are related to temperature and the expression system, but none of the experimental data that estimated this step from tail current protocols are as large as in the CR model (53,57). The rapid onset kinetics of the CR model parallel the activation properties of the older ZLRR model and result in a model with similarly inappropriate activation.

In the Markov models, activation and inactivation are coupled. Two of these models (WLMSR and OGD) have a linear scheme in which HERG must proceed obligatorily through the open state to inactivate. The experimental basis for this was originally described for I_Kr in ferret atrial cells and for HERG expressed in Xenopus oocytes (43,48). There were two key observations that led to this scheme. The first was the need to quantitatively reproduce the transient behavior seen above +20 mV in both systems. The second constraint leading to this model structure was the relative ratio of the peak currents recorded during the P1 and P2 pulses to the protocol shown in Fig. 1. In experimental conditions, the P1 peak at positive potentials is much smaller than the P2 peak. This constrained the possible transitions between activation and inactivation. The P2 peak in the WLMSR, MGWMN, and OGD models replicates this experimentally observed phenomenon. For further analysis of peak P1 and P2 currents, see Supporting Material.

The MGWMN and CR models are not linear schemes, but instead include a direct transition to the inactivated state from the closed state immediately preceding the open state. In the MGWMN model, the direct transition from the closed state to the inactivated state is negligible compared to the transition to the open state, due to the constraints macroscopic data place upon transitions. For example, at +50 mV, the ratio α₂/α_i2 is 6262:1 (see Supporting Material). Thus, the MGWMN model has an effectively zero transition between the closed and inactivated state, and so numerically the MGWMN model is in practice a linear scheme.

In contrast, the CR model has significant transitions directly to the inactivated state from the preactivated closed state. In the CR formulation, the transition from the final closed state to the inactivated state is the same magnitude as the transition to the open state. The experimental basis for this transition arises from the single channel analysis of Kiehn et al. (58) on HERG expressed in Xenopus oocytes. This study noted that at very positive potentials, it was possible for the channel to inactivate without having passed current. However, it also showed that recovery from inactivation followed by deactivation effectively always proceeded through the open state, consistent with a linear model. Some transition schemes at specific potentials were examined in this study, but a comprehensive model was not proposed. The CR model includes significant transitions based on these measurements directly from the preactivated closed state to the inactivated state. However, our simulations here show that this scheme leads to inconsistencies with observations of transient behavior and other experimentally reported behavior, and that this model is not capable of reproducing experimental data.

Examination of the data of Kiehn et al. (58) gives one possible explanation for the apparent difference between the single channel and macroscopic current data. After depolarization, single channels open, but flicker rapidly between conducting and nonconducting states (58). Such a flicker state may represent a rapid on and off of the conductance that is related to neither the process of activation or inactivation and instead may represent unrelated physical changes such as fluctuations in the selectivity filter or blocking by divalent ions. This independent flickering process is modeled in Fig. 9 for the WLMSR model. The average duration of the simulated flickering bursts is still consistent with the open dwell time from the Markov models, but at positive potentials (+100 mV) as measured by Kiehn et al. (58) the inactivation rate is so fast relative to the median closed state duration that the single channel very frequently inactivates without conduction. The single channel open- and closed-times likely occur by a mechanism that is independent of the conformational changes associated with voltage-dependent activation and inactivation. This mechanism can account for the apparent contradictions between macroscopic data and single channel measurements.

Figure 9.

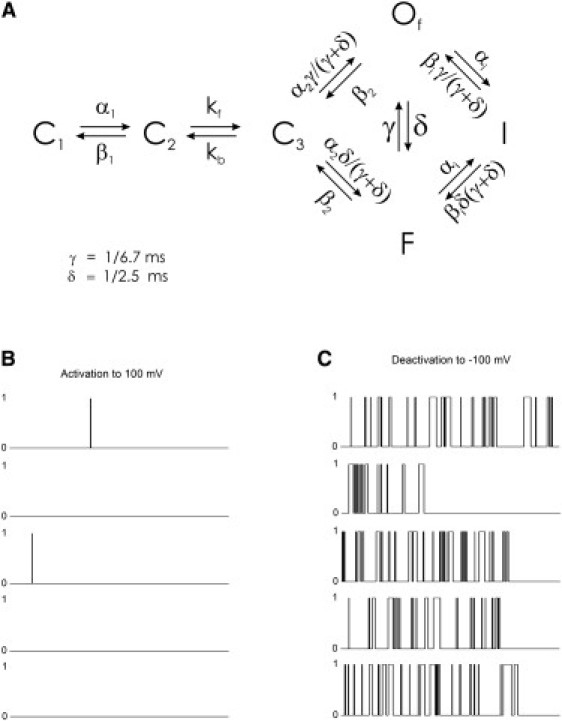
Simulated flickering open state. (A) Markov model of a burst open state. The open state of the WLMSR model was split into two states with rate constants consistent with this process being independent of activation/inactivation gating transitions. The values δ and γ correspond to open and intermediate closed dwell times at +100 mV (58). Simulated single channel events (300 ms) for (B) activation to +100 mV. (C) Deactivation from I at −100 mV. For activation to 100 mV, 58/100 were blank traces, 12/100 were early openings in the first 30 ms, and 30/100 were late openings. This compares well with the 55%, 24%, and 21% for blank, early, and late openings observed by Kiehn et al. (58). During deactivation, the O_f state was frequently visited illustrating how the observation of inactivation without prior opening by Kiehn et al. (58) can be reconciled with the model of Wang et al. (43).

The CR model sets the transition between the final closed state and the open state to be identical to the transition to the inactivated state. This, and the other parameter choices, results in a model that has many of the shortcomings of the HH type model—i.e., there is little rectification (compare to Fig. 1), instantaneous activation at positive potentials (Fig. 5), and almost instantaneous recovery from inactivation (Fig. 3). In sum, the CR model is not able to reproduce many of the significant characteristics of HERG gating.

The different model predictions of current time courses during the AP are obviously very different between models. This is important for studies of drug binding, and in particular drug binding to the open state. The most striking difference in open channel probability occurs with the ZLRR model, in which the shape of the time course is qualitatively similar to some of the other models, but the HH model does not force transition through the open state, resulting in very low open probabilities (Fig. 10). The problems of using the HH approximation instead of coupled inactivation for open channel drug binding have been illustrated for Kv1.4 previously (59). The simulations presented here indicate that the HH approximation will be severely defective for studies of open channel drug binding to I_Kr/HERG.

Figure 10.

Relative probability of the channel being open during the AP. (A–E) All traces are to scale and show the currents at a constant E_k and conductance during the AP. The low currents during the AP of the ZLRR result from the extremely low open channel probability, whereas the CR model has a higher open probability than the other models during most phases of the AP. (Dotted line) Zero current level.

In conclusion, diverse models of I_Kr and HERG gating are currently in use in AP and voltage-clamp simulations. These formulations have significant differences in their predictions of HERG behavior and magnitude. Our analysis indicates that although under limited conditions an HH model may appear similar to a Markov formulation (14), HERG cannot be adequately modeled with an HH style formulation. In a Markov chain, HERG requires representation by three closed states, an open state, and an inactivated state. The rate dependence of current magnitude is predicted to be strongly dependent upon inclusion of the third closed state, farthest from the open state. Experimental work on I_Kr in myocytes has been limited to more positive potentials due to overlap with other currents, resulting in models with only two closed states. New myocyte experiments are needed to examine activation behavior at lower potentials to define the kinetic behavior of the third closed state. This comparison between models and the apparent importance of the early voltage-dependent steps underscores the importance of reconciling macroscopic currents with gating measurements (e.g., (60)). This will require more careful evaluation of the physical changes involved in sequential slow steps of activation and inactivation that are dominant in determining macroscopic behavior. Despite having independent voltage sensors as Indicated by mutagenesis experiments and biophysical measurements, the coupled sequential nature of activation and inactivation suggest that HERG gating shares a common structure-function relationship that constrains gating models of C-type inactivation in other Kv channels (61).

Some HERG model formulations include a direct transition between the closed and inactivated states. The only model that included this transition that was able to adequately reproduce experimental data had a transition rate that was effectively zero. Diverse models of I_kr/HERG are used for in silico approaches to the development of new and safer drugs and for understanding the molecular basis of arrhythmias. The underlying models have very different properties that give very different predicted results.

In summary, our analysis indicates that HERG is best represented by a linear Markov model with three closed states, one open state, and one inactivated state.