A Model of Cellular Cardiac-Neural Coupling That Captures the Sympathetic Control of Sinoatrial Node Excitability in Normotensive and Hypertensive Rats

Abstract

Hypertension is associated with sympathetic hyperactivity. To represent this neural-myocyte coupling, and to elucidate the mechanisms underlying sympathetic control of the cardiac pacemaker, we developed a new (to our knowledge) cellular mathematical model that incorporates signaling information from cell-to-cell communications between the sympathetic varicosity and sinoatrial node (SAN) in both normotensive (WKY) and hypertensive (SHR) rats. Features of the model include 1), a description of pacemaker activity with specific ion-channel functions and Ca²⁺ handling elements; 2), dynamic β-adrenergic modulation of the excitation of the SAN; 3), representation of ionic activity of sympathetic varicosity with NE release dynamics; and 4), coupling of the varicosity model to the SAN model to simulate presynaptic transmitter release driving postsynaptic excitability. This framework captures neural-myocyte coupling and the modulation of pacemaking by nitric oxide and cyclic GMP. It also reproduces the chronotropic response to brief sympathetic stimulations. Finally, the SHR model quantitatively suggests that the impairment of cyclic GMP regulation at both sides of the sympathetic cleft is crucial for development of the autonomic phenotype observed in hypertension.

Introduction

The heart is an efficient and effective electromechanical pump for supplying the continuous flow of blood that is fundamental for life. This crucial function is highly dependent on the autonomic modulation of cardiac pacemaking, and impaired sympathetic β-adrenergic signaling has been coupled to the onset of hypertension and arrhythmia (1,2). Critical to this coupling is the communication between the varicosity and the cardiomyocyte. The action potential (AP) that arrives at the prejunctional sympathetic varicosity triggers the release of neurotransmitter from the vesicles in a fast, calcium-dependent manner (3). Norepinephrine (NE) then diffuses across the neuromuscular cleft and binds to β-receptors, where it initiates a signaling cascade that is coupled to biochemical pathways that in turn regulate cardiomyocyte excitation-contraction coupling. The ionic activity, biochemical signaling, and cell-cell communication between the neuron and the myocyte add significant complexity to our understanding of how the cardiac-neural axis controls myocardial excitability. For these reasons, reassembling these processes represents both an important goal and a major challenge.

Computational modeling provides an effective approach for tackling the problem of reassembly quantitatively. Studies over the last few decades led to increasingly detailed biophysically based cell models of neural and cardiac electrophysiology, β-adrenergic signaling, transmitter release and regulation, and Ca²⁺-dependent vesicle fusion (4–9). However, in each of these studies, only part of the cardiac-neural axis in the control of myocardial excitability was represented, and thus no cellular model is currently available that captures neural-myocyte coupling. Our goal in this study was to provide a fully coupled cardiac-neural cell model, and test its robustness against actual physiological data from an animal model of impaired sympathetic regulation.

Sympathetic hyperresponsiveness resulting in increased transmitter turnover and hyperactive cardiac myocytes is a hallmark of hypertension (10–12). The mechanisms that produce hyperactivity on both sides of the neuromuscular junction remain to be elucidated, but may involve 1), increased NE efflux (Ca²⁺ channel related); 2), weaker NE reuptake; 3), higher sensitivity of adrenoceptors; or 4), enhanced β-adrenergic signaling. Previous studies reported that the sensitivity of adrenoceptors does not change between SHR and WKY rat atrial cells (13). The function of neuronal reuptake is also controversial, with weak activity of the NE transporter (NET) being observed in human hypertension (14), and an increased reuptake of NE found in several animal studies (15,16). This raises the possibility that the role of neuronal reuptake in hypertension is dependent on the species studied.

Aiming for increased internal consistency within modeling frameworks (17), we chose to use data from the spontaneously hypertensive rat to validate our model, given its relevance for the specific study of impaired autonomic regulation of cardiac excitability. Studies on the right atrium of WKY and SHR rats suggested that NE reuptake activities were unchanged (13). This result is also consistent with observations in our laboratory that there is no significant difference between WKY and SHR in terms of NET (D. Li and D. J. Paterson, unpublished data). Enhanced Ca²⁺ influx in sympathetic neurons and β-adrenergic signaling in the sinoatrial (SA) node has been observed in SHR rats (11,12). Increased Ca²⁺ influx and elevated cAMP levels will directly enhance NE release and hyperactivity of atrial cells. This is thought to be related to oxidative stress causing dysregulation of cyclic nucleotides, in particular, impairment of the NO-sCG-cGMP dependent pathways that couple to the regulation of intracellular calcium. This pathway appears to play an important role in determining peripheral noradrenergic activity at both pre- and postjunctional sides during the development of hypertension (11). Such experimental measurements now provide data for parameterizing both a mathematical model for the SHR and the model perturbations required to map the SHR framework to the WKY phenotype. Using these models, our goal was to isolate the individual factors that control transmitter turnover and heart rate, and identify a mechanism on both sides of the cardiac-neural axis that might explain the enhanced adrenergic phenotype seen in the hypertensive rat.

Materials and Methods

Computational parameterization

Fig. 1 shows a schematic of the components and their interactions in the sympathetic neuron-cardiomyocyte coupled model. In response to an AP, the membrane ion channels in the varicosity open. Ca²⁺ influx dramatically increases the local Ca²⁺ concentration near the inner mouth of the Ca²⁺ channel and the vesicles, which are specialized as the active zone in the model. Increased [Ca²⁺] causes Ca²⁺ sensors on the vesicle to trigger vesicle fusion and neurotransmitter release, after which the released transmitters diffuse across the cleft and bind to β-adrenergic receptors distributed along the postjunctional SAN cell membrane. This initiation of the intracellular signal transduction modulates the spontaneous excitability of the SAN through a variety of functional ion channel and ion transporter modifications. Further details of the individual steps and the modeling framework required to represent this pathway are outlined in the following sections.

Figure 1.

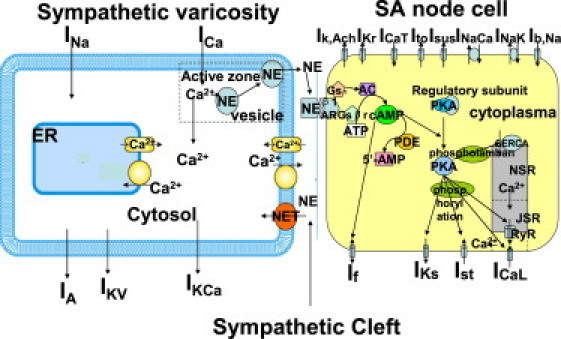
Schematic diagram of a rat SAN cell model and its sympathetic control.

SAN cell membrane current and AP

We formulated a mathematical model of the AP of a rat SAN to describe the essential properties of a pure pacemaker cell at 37°C using the classical Hodgkin-Huxley formalism.

Figs. 2 and 3 show a good agreement between experimental and model results for normalized I/V relations and simulated current transients, respectively, for the major individual currents (I_CaL, I_Kr, I_Ks, and I_f). Further details regarding the model development, parameter justification, and component validation are included in the Supporting Material.

Figure 2.

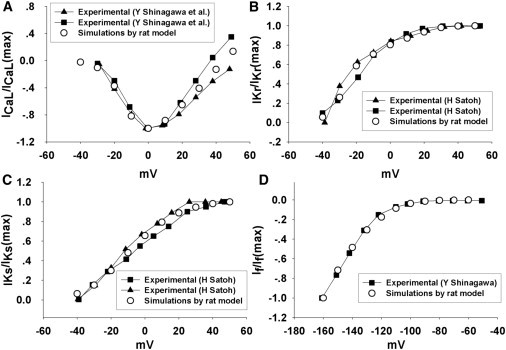
(A) Normalized I/V relationship curves for L-type Ca²⁺ current in response to a series of 100 ms testing potentials ranging from −40 mV to 50 mV. (B) Normalized I/V relationship curves for I_Kr in response to a series of 200 ms testing potentials ranging from −40 mV to 50 mV. (C) Normalized I/V relationship curves for I_Ks in response to a series of 1000 ms testing potentials ranging from −40 mV to 50 mV. (D) Normalized I/V relationship curves for I_f in response to a series of 300 ms testing potentials ranging from −160 mV to −60 mV. The holding potential is −40 mV; the peak values of the currents were measured.

Figure 3.

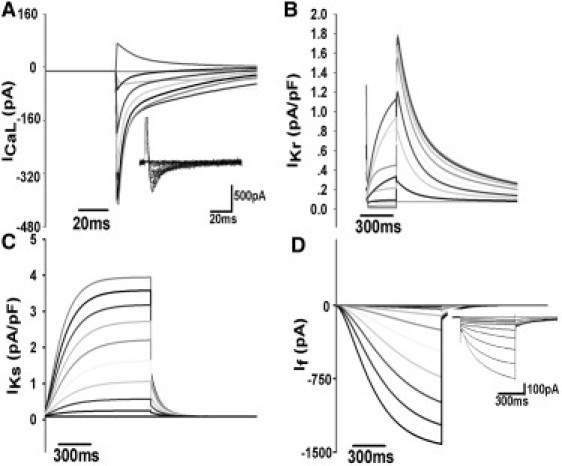
(A–C) Simulated ion current transients under the same voltage-clamp condition as in Fig. 2. (D) Simulated I_f current transients in response to a series of 1000 ms testing pulses ranging from −30 to −120 mV. The holding potential is −40 mV, and the experimental recordings of I_CaL and I_f are superimposed in the figure as a comparison.

Neuron membrane current and AP

To simulate the AP in a presynaptic neuron, we adopt the modeling framework proposed by Belluzzi and Sacchi (4) of a sympathetic neuron, which was based on experimental data from isolated rat superior cervical ganglion. Within this framework, six separate types of voltage-dependent membrane ion channels are involved in the genesis of AP in this model: 1), the sodium current, I_Na, the fast inward current that makes the major contribution to the depolarization; 2), the calcium current, I_Ca; 3), the transient I_A, the outward current (carried by K⁺) that sustains the membrane repolarization; 4), the delayed rectifier potassium current, I_KV, a small and slow current that makes a minor contribution to the development of AP; and 5), the Ca²⁺-dependent K⁺ current, I_KCa, which plays a important role in the genesis of the AP; and 6) I_stim, a stimulating current in the neuron cell model, specifically, a 2-ms stimulus of 20 pA applied to trigger an AP.

As with the myocyte model, each current is kinetically characterized by a set of ordinary differential equations of the Hodgkin-Huxley type, including gating mechanisms, together with the maximum conductance values measured. As described above, the AP can be arranged for numerical integration as follows:

$$\frac{dV}{dt}=\frac{-\left(I_{Na}+I_{Ca}+I_A+I_{KV}+I_{KCa}+I_{stim}\right)}{C_m}.$$ (1)

Although there is significant evidence that Ca²⁺ influx across the neuron membrane is involved with multiple Ca²⁺ channel types, including L, P/Q, N, and T types, the contribution of specific Ca²⁺ channel types to the initiation of transmitter release differs among different species and synapses (18–21).

There is no experimental evidence showing a dominant Ca²⁺ channel type in sympathetic varicosity of rat heart, and we cannot provide a direct correspondence between the present Ca²⁺ current and any of the individual classical L, P/Q, N, T types. However, in the context of no significant difference in the time courses of Ca²⁺ entry through these subtypes (22), the nonspecific Ca²⁺ current is satisfactorily simulated using the parameters of Belluzzi and Sacchi (4).

Ca²⁺ transient and transmitter release

In response to an AP, the fast release of neurotransmitter from the vesicles is triggered in a few milliseconds by a brief, localized intracellular Ca²⁺ increase through the opening of the Ca²⁺ channel. The elevation of intracellular Ca²⁺ concentration that is needed for exocytosis is thought to be as high as 100 μM. The spatial-temporal scales indicate that the vesicles have to be located sufficiently close to Ca²⁺ channels. Following Soto and Othmer's study (8) on rat neuron synapse, we adopt a functional area underlying the presynaptic face as the active zone, in which both the transmitter release machinery and voltage-dependent Ca²⁺ channel are assumed to be colocalized. The size of the active zone is defined as 0.052 ± 0.024 μm² with a mean radius of 125 nm based on electron microscopy measurements (23) of the rat neuron. The evolution of the calcium concentration in the active zone is modeled according to

$$\frac{dC{a}_Z}{dt}=-i_{Ca}\times \frac{C_m}{2\times F\times V_Z}-C{a}_Z\times K_{\left[Ca\right]},$$ (2)

where i_Ca is the membrane Ca²⁺ current, V_Z represents the volume of active zone, C_m is the neuron cell capacitance, and F is Faraday's constant. The calcium difference between the bulk cytoplasm and the active zone is described by the term Ca_Z × K_[Cz], where K_[Cz] is the time constant. Further details are provided in the Supporting Material.

In the neuron, there are other possible regulatory organelles involved in Ca²⁺ handling, including the ER and mitochondria. However, in the anatomical study of Lysakowski et al. (24), the ER and mitochondria were observed to be too far away from the active zone to affect the fast neurotransmitter release process. Smith and Cunnane (25) also reported that blocking of RyR did not affect the neurotransmitter release in postganglionic sympathetic nerve terminals. This observation is consistent with recent data from our own laboratory (unpublished) obtained from rat sympathetic neurons that showed only a minor contribution of Ca²⁺ release from the ER to the intracellular Ca²⁺ transient. Thus, focusing on the exocytosis-related Ca²⁺ transient, we did not include the intracellular Ca²⁺ regulation by RyR and mitochondria in the model.

The mathematical description of the process of Ca²⁺-triggered fusion of vesicles and neurotransmitter release is based on experimental data from the calyces of Held in the rat (9). (A schematic representation of the kinetics of Ca²⁺ binding and vesicle fusion is shown in the lower panel of Fig. 5.) The kinetic parameters K_on and K_off represent Ca²⁺ binding and dissociated rate constants, respectively, and γ is the rate at which vesicle with full Ca²⁺ ions bound fuse.

Figure 5.

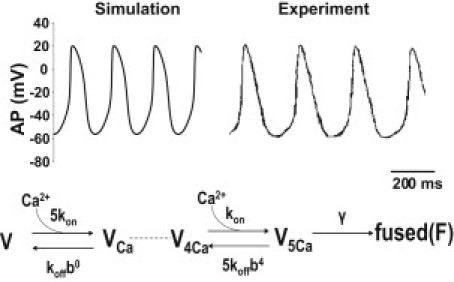
Upper panel: Illustration of the traces generated by rat SAN model for spontaneous AP and recorded AP in the experiment with rat SAN. Lower panel: Scheme of the kinetic model for binding of Ca²⁺ to the vesicle and the vesicle fusion.

The sympathetic varicosity communicates with the SAN cell via the neuro-effector junction, which is formed by the membranes of the pacemaker cell and the sympathetic varicosity. The contact area is ∼0.15 ± 0.03 μm² and the width of the cleft is <100 nm (26), resulting in a cleft volume of 1.5 × 10⁻¹⁵ l.

In the sympathetic cleft, the released transmitters transported back to neuron terminals by NET or spilled over into plasma. Approximately 90% of the transmitters released from the sympathetic nerve were reported to be recaptured by NET (27), so the clearance of NE in the cleft is largely dependent on the neuronal NET. The regulation of NE in the neuroeffector junction is modeled with the following equation:

$$\frac{dNE}{dt}=\frac{E\times n\times a}{V_{cleft}}-\left[NE\right]\times P_{up},$$ (3)

where n, the number of the releasable vesicles, is set to 12 for the single adrenergic varicosity contact (26); a is the number of transmitter molecules contained in a single vesicle (a value of 4000 is used in the model) (28); and E is defined as the rate of the fusion for the releasable vesicles. Because the volume of the cleft is small (V_cleft = 1.5×10⁻¹⁵ l), the concentration of the neurotransmitter in the cleft is assumed to be spatially uniform. The transport rate of NE by NET is represented by P_up.

The free NE released from the prejunctional varicosity binds to the β-adrenergic receptors on the membrane of the pacemaker myocytes to initiate the β-adrenergic signaling cascade in SAN myocytes. To represent the β-adrenergic signaling components and regulation of myocyte electrophysiology, a kinetic model integrating β-adrenergic signaling with cell excitability was developed based on previous modeling studies (7,29,30).

Specifically, the formulas for the No-cGMP pathway of β-adrenergic signaling were adopted from Saucerman et al.'s (7) model of rat ventricle, and the equations for modulating the activities of β-adrenergic sensitive ion channels and transporters were based on studies of guinea pig SAN (I_CaL, I_st, and I_f) (30) and rat ventricle (I_Ks and SERCA (29). The values for the concentrations of cAMP and PKA without β1-adrenergic stimulation, 0.0002268 mM and 0.00005868 mM, were adopted from studies on rat SAN (12) and rat ventricle (7), respectively. The parameters for the equilibrium constants for cAMP and PKA were updated to fit the experimental records for individual membrane currents I_CaL, I_st, and I_Ks. The fitted I/V curves are plotted in Fig. 4, A–E. However, only the experimental data for I_CaL are from rat SAN; other components are based on data from guinea pig SAN (31,32). (The model rate response to a series of NE concentrations is shown in Fig. 6 A in comparison with experimental data (12).)

Figure 4.

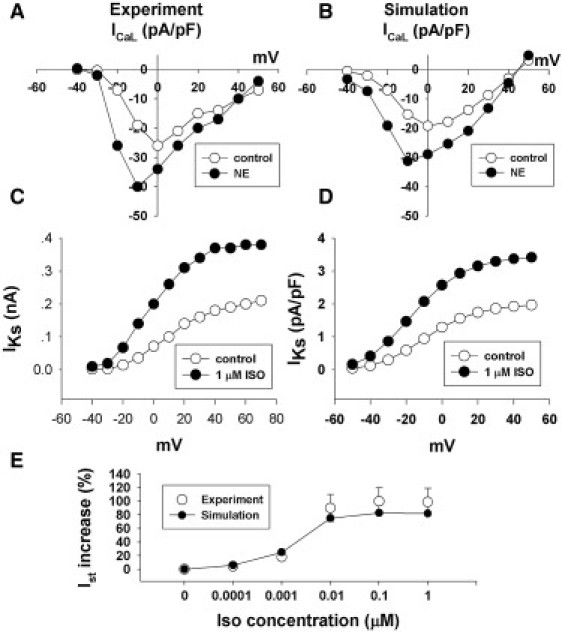
(A) I/V relationship curves for the peak of an L-type Ca²⁺ current recorded from isolated SAN cells of rat under control condition and exposure to 2 μM of NE. (B) I/V relationship curves for peak of L-type Ca²⁺ current simulated by the model under the same conditions described above. (C) I/V relationship curves for the peak of I_Ks recorded from isolated SAN cells of guinea pig under the control condition and exposure to 1 μM of ISO. (D) I/V relationship curves for the peak I_Ks current simulated by the model under the same conditions described above. (E) The simulated curve of percent changes of I_st in response to a series of ISO concentrations is fitted to the experimental data of guinea pig SAN (circles with error bar).

Figure 6.

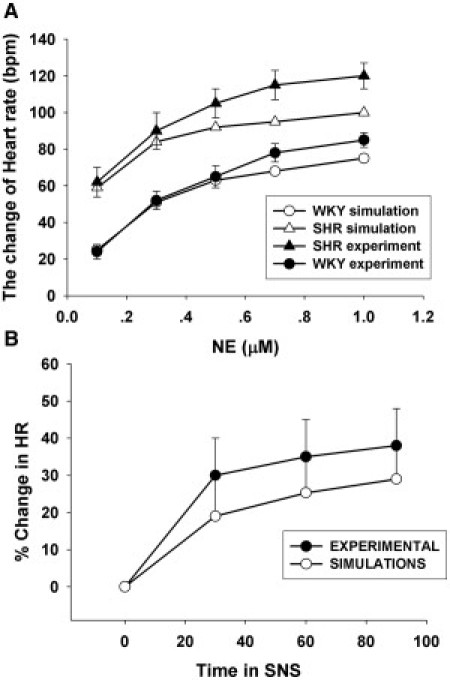
(A) Comparison of chronotropic responses to a series of NE concentrations in WKY and SHR. The black circles represent the experimental recordings (12), and white circles indicated the simulated results. (B) Comparison of the percent changes in the heart rate during SNS of 3 Hz between the experiment (black circles with error bar) and the simulation (white circles).

SHR model

Our goal in developing the neural-cardiac myocyte coupling model for SHR was to capture the observed increased NE level in the prejunctional neuron and the enhanced β1-adrenergic signaling in the postjunctional SAN cell.

Ca²⁺-dependent NE release is directly induced by Ca²⁺ influx through neural Ca²⁺ channels. The conductance of the Ca²⁺ channel is controlled by cAMP-dependent phosphorylation, which in turn is downregulated by cGMP-dependent protein kinase and phosphodiesterases. Because the lower cGMP level is found in SHR tissue (11), impaired cGMP downregulation of the cAMP-dependent phosphorylation of the Ca²⁺ channel results in increased exocytosis of the neurotransmitters.

Data recently obtained from the superior cervical ganglia of SHR in our laboratory showed that the cytoplasmic Ca²⁺ transient was ∼40% larger in SHR than in WKY (D. Li and D. J. Paterson, unpublished data). Consistent with this observation, the conductance of the neural Ca²⁺ channel was increased by 40% in the SHR model. In the SAN cell, through the same pathway the weaker cGMP-dependent stimulation of phosphodiesterase 2 (PDE2) increases cAMP- and protein kinase A-dependent stimulation of β1-adrenergic-sensitive membrane currents and pumps. Therefore, the postsynaptic hyperactivity of SHR is simulated by reducing the amount of PDE2 by 26% in the model.

Results

The upper panel of Fig. 5 shows the spontaneous APs produced by the rat SAN model presented here and recorded in a rat SAN cell. All of the critical parameters of AP are in the physiological range and comparable to the previous SAN models.

The model generated CL and APD₅₀ = 257 and 77 ms, respectively; APA, MDP, and MOP = 76.18, −56.28, and 19.9 mV, respectively; and V_max = 6.5 V/s. All of these results are in close agreement with experimental observations (33).

Compared with the WKY rat, SHR has a ∼50% higher plasma NE concentration and 21% faster heart rate under the resting condition, as measured in the experimental study by Girouard et al. (34). Our SHR model demonstrates close agreement: the HR is increased by 12% and the NE concentration in the cleft is elevated by 80% compared with the WKY model.

Under the sympathetic modulation through the β1-adrenergic signaling pathway, the SAN's chronotropic response to the variation of NE concentration was simulated in the WKY and SHR model. The results, shown in Fig. 6 A, are comparable to the experimental data (12).

Fig. 7 A presents results from the WKY model after a series of stimuli with frequencies ranging from 0.2 Hz to 3 Hz. The simulated results of the changing heart rate (white circles) are consistent with the experimental records (black circles with error bar) (35). The responses of SHR in the experiment (35) and in the model are presented in Fig. 7 B. The simulation (white circles) shows a more sensitive response than the experiment. The experimental and simulated results show the same slowing trend with an increase in stimulating frequency.

Figure 7.

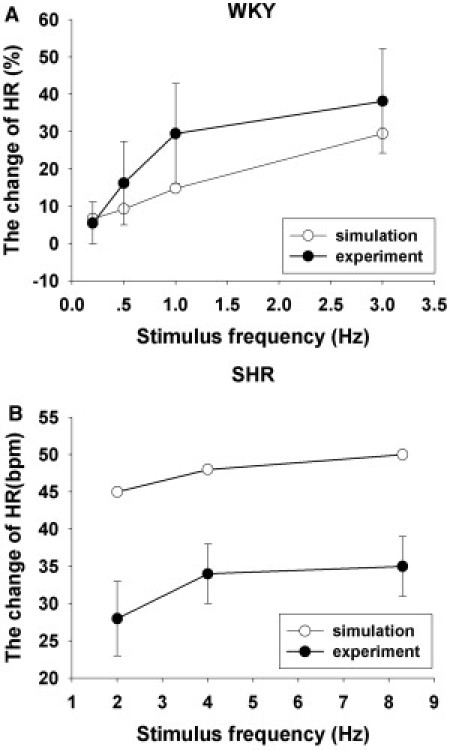
(A) Percent changes in heart rate of WKY rat in response to a series of sympathetic stimulus frequencies. (B) Changes in the heart rate of SHR rats under the different stimulating rates. All experimental data are indicated in red, and simulation results are shown in black.

The heart rate is recorded at 0, 30, 60, and 90 s during sympathetic nervous stimulation (SNS) of 3 Hz and presents a continuous increase, as plotted in Fig. 6 B (black). Our WKY model presents a similar increasing change of heart rate, and the simulated curve (white circles) of the percent changes in heart rate during SNS shows close agreement with the time courses in heart rate observed by Onuki et al. (35).

Because of the small size of the sympathetic cleft, the NE concentration cannot be measured directly. The neural transmitter turnover is typically recorded to reflect the concentration of transmitter in the cleft. Using the above protocol, we recorded the NE changes produced by a series of stimuli at a range of frequencies in rat SAN (36), the responses to which are well represented by the WKY model, shown in Fig. 8 A. In our laboratory, the stimulation-evoked release of NE was studied in WKY and SHR rat atria at a 5 Hz stimulating rate. Approximately 50% more NE release was observed in SHR compared with WKY (11). The enhanced NE release is also produced in our SHR model; however, it is about twice as large as that observed experimentally. This difference could be due to the limitation of the measurement, as mentioned above.

Figure 8.

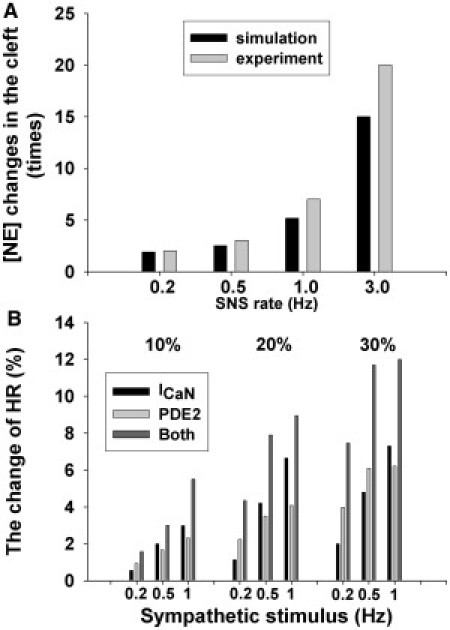
(A) Bar chart of the changes of NE concentration in the neuromuscular junction in response to a series of SNSs. (B) Bar chart of the chronotropic response to a 10%, 20%, and 30% increase of Ca²⁺ influx and PDE2 at a series of sympathetic stimulus frequencies.

We applied a range of sympathetic stimulation rates in the model, from 0.2 Hz to 8 Hz, to assess whether there were any changes in the sympathetic APD and varicosity Ca concentration over such a wide range of stimulating rates. The results show no significant change in the varicosity calcium concentration or the sympathetic APD until the 5 Hz stimulation. From 5 Hz to 8 Hz, the APD increased slowly from 5.8 ms to 6.1 ms.

Discussion

In this study, we have described the first (to our knowledge) biophysically detailed model of the membrane AP in rat SAN cells modulated by the sympathetic nervous system. Whenever possible, published data obtained via patch-clamp, biochemical, and imaging experiments from rat atrium tissue and isolated rat SAN cells were used to validate the model development.

This model provides a comprehensive description of the role played by the cellular cardiac-neural axis in the controlling the myocardial excitability of the rat SAN. A rat SAN model was developed to reproduce the waveform of the SAN cell pacemaker AP. The model reproduces the voltage-clamp data from rat SAN cells for I_CaL, I_Kr, I_Ks and I_f. A β-adrenergic model was coupled to this SAN, demonstrating that the response of neurotransmitter changes to excitation can mimic actual physiology. The model of sympathetic varicosity also mimics the NE release at varying rates of field stimulation, with simulations predicting behavior. The coupling of the neural and myocyte cells shows good agreement with experimental recordings after a different prejunctional stimulus. The developed framework was reparameterized to produce a SHR model with which the effects of the mechanisms underlying the sympathetic neural phenotype seen in hypertension were quantified.

To validate the model, we simulated the effects of blocking membrane currents, and the results show a good agreement with experiments, as outlined below.

Effects of I_CaL

I_CaL is believed to be the most important pacemaking current, as evidenced by the observation that spontaneous beating is stopped by Ca²⁺ antagonists (37). The model behavior is consistent with this experimental observation demonstrated by a simulated block of I_CaL by decreasing the maximum current conductance to 0, which produced an abrupt cessation in pacemaker activity.

Effects of I_Kr

I_Kr is another important pacemaker current. During diastole, I_Kr was slowly deactivated and the decreased outward current potentiated the self-activated depolarization. Depressed spontaneous activity and sinus arrest were observed in the rat SAN cell when I_Kr was completely blocked by E-4031 (38). After I_Kr was blocked in our model, the spontaneous beating was first depressed and then slowly abolished. This simulated cell behavior is consistent with experimental observations (33).

Effects of I_st

The sustained inward current is specific to the pacemaker SAN cells (39), and was suggested to be a key pacemaker current by Shinagawa et al. (33) and Guo et al. (40) based on the production of sinus arrest with the application of nicardipine (the blocker of I_st) on rat SAN tissue. The model behavior is consistent with this experimental observation, with the blocking of I_st also stopping the spontaneous pacemaker activity.

Effects of I_f

The hyperpolarization-activated current's role in generating spontaneous depolarization is hard to quantify because of the heterogeneity in current density, as well as the large variation in the threshold potential of activation ranging from −30 mV to −70 mV (41–47). Bers (48) suggested that the role of I_f might be minor in the central SAN cells but more important in peripheral SAN cells. Shinagawa et al. (33) reported an even more negative threshold of activation (≤ −90 mV) in rat SAN cells. Such a negative potential of activation eliminates the contribution of I_f to the diastolic depolarization under normal conditions. However, because all of these experiments were performed with Tyrode buffered solution and not full blood products (i.e., cAMP), the actual membrane potential may be more positive than indicated by these experiments (49,50).

Applying the negative potential (∼−90 mV) for the activation of I_f in our rat SAN model, the hyperpolarization-activated channel remains inactivated under a so-called normal range of AP, suggesting that the variation in the current density of I_f had no effect on the pacemaker activity.

Effects of I_b,Na

The background Na⁺ current provides an inward current in the pacemaker potential range, as reported by Hagiwara et al. (51,52). However, the significance of the role of I_b,Na in generating spontaneous depolarization is not clear. In our model, the blocking of I_b,Na caused a sinus arrest. A similar large impact of I_b,Na was reported by Noble et al. (53) when I_f was blocked in a study of rabbit pacemaking, demonstrating that I_b,Na provided a compensating current for the reduction in I_f. In our rat SAN model, the I_f current is negligibly small under normal conditions due to the lower activation potential (−90 mV), so the compensation by I_b,Na plays a important role in the generation of spontaneous depolarization.

I_CaT

The T-type Ca²⁺ current as an inward current is involved in pacemaker depolarization, as demonstrated by the slowdown in pacemaker activity when it is blocked (54,55). The blockade of I_CaT increased the CL of the AP by only 15.6% in the model, a result that is consistent with the experimental data from Hagiwara et al. (51,52) and Satoh (56). However, it is important to note that the contribution of I_CaT to pacemaker activity is controversial, and a wide range of experimental results have been reported (55,57–59).

I_Ks

In previous studies (6,60), it was assumed that the slow delayed rectifying potassium current does not make a significant contribution to pacemaker activity. However, I_Ks is sensitive to β-adrenergic agonists, which enhance the effect of I_Ks to produce a positive chronotropic effect on SAN cells (38). The full blocking of I_Ks predicts a 6.6% increase of CL in our rat SAN model.

I_K,Ach

The muscarinic K⁺ current is an inwardly rectifying current that under physiological conditions behaves like background current in the absence of acetylcholine (61). Additionally, I_K,Ach is the main target of the neurotransmitter (acetylcholine) released from parasympathetic nerves for depressing the spontaneous activity of SAN cell (62,63). In our model, the blockade of I_K,Ach shortened the CL of AP by only 3.5%.

I_sus and I_to

The changes of CL by the blockade of I_sus and I_to were only 6% and 1.17%, respectively.

The role of Ca²⁺ regulation in pacemaker activity is a controversial issue in the literature. Supported by the experimental observations of Janvier and Boyett (64), in this study we assume that the contribution of SR Ca²⁺ release to pacemaker activity is small due to the poor development of the SR in central SAN cells. Applying this assumption means that abolishing Ca²⁺ release of SR in our model only produced a 3.5% increase on CL, which is in good agreement with the observations of Miyamae and Goto (65).

In addition to this additional individual current information, we note that the simulated voltage-clamp data (Fig. 2) compare well with the major pacemaking currents I_CaL, I_st, I_Kr, I_Ks, and I_f. Furthermore, we have demonstrated that in the model I_CaL, I_st, and I_Kr are fundamental to the spontaneous activity experimentally, consistent with the experimental blockade of each of these currents shown to induce sinus arrest (33,40,42). Although other currents make variable contributions to the AP, there is no evidence that they play substantial roles in the process of spontaneous depolarization (38,58,61,66–68).

Consistent with the link between elevated NE levels and the hyperactivity of cardiac myocytes, the increased Ca²⁺ influx through prejunctional neurons and the lower amount of PDE2 in postjunctional SAN cells were shown to be fundamental differences between the WKY and SHR models developed in this study. The simulated results in the SHR model are in good agreement with the experimental data on both sides of the neural-muscular junction, and suggest that these two factors are important for the development of hypertension. Furthermore, these simulations support our previous conclusions regarding the role of nNOS-sGC-cGMP in modulating noradrenergic activity at both pre- and postsynaptic levels (11), given that the changes for the SHR model are both related to the weak cGMP regulation. This result brings into focus the identification of the relative contribution of these two factors to heart rate regulation. To address this issue, we investigated the chronotropic response of the heart to these two factors separately through a sensitivity analysis of the model results. Specifically, we assessed the chronotropic response to a 10%, 20%, and 30% increase of Ca²⁺ influx and PDE2 both separately and combined (Fig. 8 B). The results show that the sensitivities of these two mechanisms are rate-dependent. At the lower stimulating frequency, PDE2 shows a higher sensitivity. In contrast, with an increasing stimulus rate, the sensitivity of Ca²⁺ influx increased more quickly at the higher frequency. However, it is important to note that these two mechanisms are inherently coupled, given that neither Ca²⁺ influx nor PDE2 plays a dominant role in isolation, with the alternation of HR ultimately modulated by both of these factors.

Quantitatively, there are some differences between the simulations and experiments. Such inconsistencies are an inevitable result of both the shortcomings of the model and the incomplete experimental data. In the SAN cell model, we have to use the voltage-clamp data from rat SAN cells with different capacitances and incomplete experimental data on the kinetics of membrane currents. Furthermore, because there are no significant specific clamp data for the β-adrenergic modulation on individual membrane currents, I_st and I_f are based on guinea pig SAN data, and I_Ks and Ca²⁺ uptake are based on data from rat ventricles. In the cleft, there is a lack of geometry data for the neuro-effector junction, and indirect measurements were thus used to parameterize the model of transmitter regulation in the cleft. In the sympathetic neuron model, nonspecific Ca²⁺ influx is applied to initiate exocytosis. The simulations of membrane AP, Ca²⁺-dependent vesicle fusion and the NE release process are based on studies of rat brain tissue.

Despite these limitations, the rat SAN model and the fully coupled model successfully captured many of the fundamental features of pacemaker activity and β-adrenergic control of myocardial excitability. Following in silico stimulus protocols, we were able to reproduce both prejunctional NE release and postjunctional cardiac myocyte response well in the model. This framework provides a means of comparing and investigating interactions between pre- and postjunctional functions. In addition, the SHR model successfully replicated the basic behavior of spontaneous hypertensive rat and responses under a range of different conditions. Finally, and perhaps most significantly, within the quantitative framework provided by the model, the weaker cGMP regulation was shown to be a likely candidate for underpinning the hypertensive phenotype. Based on our results, we suggest that the increased Ca²⁺ influx in neurons and the enhanced β-adrenergic signaling in SANs play a crucial role in the development of the sympathetic neural phenotype caused by hypertension.