Quantifying the Uncertainty of Spontaneous Ca²⁺ Oscillations in Astrocytes: Particulars of Alzheimer's Disease

Abstract

The quantification of spontaneous calcium (Ca²⁺) oscillations (SCOs) in astrocytes presents a challenge because of the large irregularities in the amplitudes, durations, and initiation times of the underlying events. In this article, we use a stochastic context to account for such SCO variability, which is based on previous models for cellular Ca²⁺ signaling. First, we found that passive Ca²⁺ influx from the extracellular space determine the basal concentration of this ion in the cytosol. Second, we demonstrated the feasibility of estimating both the inositol 1,4,5-trisphosphate (IP₃) production levels and the average number of IP₃ receptor channels in the somatic clusters from epifluorescent Ca²⁺ imaging through the combination of a filtering strategy and a maximum-likelihood criterion. We estimated these two biophysical parameters using data from wild-type adult mice and age-matched transgenic mice overexpressing the 695-amino-acid isoform of human Alzheimer β-amyloid precursor protein. We found that, together with an increase in the passive Ca²⁺ influx, a significant reduction in the sensitivity of G protein-coupled receptors might lie beneath the abnormalities in the astrocytic Ca²⁺ signaling, as was observed in rodent models of Alzheimer's disease. This study provides new, to our knowledge, indices for a quantitative analysis of SCOs in normal and pathological astrocytes.

Introduction

After finding intra/intercellular calcium (Ca²⁺) events induced in cultured astrocytic syncytium by exogenous application of glutamate (1), astrocytes were no longer thought of as passive cytoarchitectonic supports of neuronal structures (2–5). Recent observations bring to light the existence of similar Ca²⁺ signaling in vivo under external somatosensory stimulations (6) which could also exhibit the same complex temporal patterns (7) as those reported previously in vitro. Interestingly, astrocytic Ca²⁺ signaling also occurs, both in situ (8) and in vivo (9), without the application of either exogenous agonists or external stimuli—i.e., a phenomenon called “spontaneous Ca²⁺ oscillations” (SCOs). Under several experimental protocols, it has been demonstrated that SCOs can emerge in this type of cell even in the absence of neuronal activity (8,10–12) but are mediated by the activation of inositol 1,4,5-trisphosphate (IP₃) receptors (IP₃R) (8,10). Accordingly, a minimal basal level of cytosolic IP₃ in astrocytes is thought to underlie the SCOs.

In three experimental mice models of Alzheimer's disease (i.e., APP mice, which are transgenic mice overexpressing the 695-amino-acid isoform of human Alzheimer β-amyloid precursor protein, harboring the double Swedish mutation “Tg2576”; triple transgenic mice 3XTg-AD; and mice expressing Dutch/Iowa mutation), Takano et al. (13) found an increase in the frequency of SCOs in live intact astrocytes of the barrel cortex. These transgenic mice, even at an early stage (2–4 months), exhibited both poor vasodilation in response to sensory stimulation and instability in vascular tone. These results provided a physiological explanation for the previously observed reductions of regional cerebral blood volume in similar transgenic murine APP models (V717F, K670N/M671L) (14).

Using multiphoton fluorescence lifetime imaging microscopy in vivo, Kuchibhotla et al. (12) reported a global elevation of resting Ca²⁺ inside the astrocytes of Swedish APP transgenic mice expressing mutant presenilin 1 in neurons (APPswe:PS1ΔE9), which was independent of the astrocytes' proximity to individual β-amyloid plaques. For such double-transgenic mice, SCOs were more frequent and synchronized across long distances. Chow et al. (15) recently verified that exogenous application of β-amyloid on isolated astrocytes in purified cultures induced Ca²⁺ transient activity with a high probability for the emergence of delayed intercellular Ca²⁺ waves. Unfortunately, transient Ca²⁺ events during SCOs show very irregular patterns and unpredictability in terms of their amplitudes, durations, and initiation times. That is the reason why physiologists have oversimplified the analysis of SCOs in astrocytes through two basic indices (12,13,15): 1), type/percent of cells (e.g., inactive and active); and 2), their response frequency (i.e., number of events in a time window). These purely descriptive indices are not quite useful while evaluating the physiological mechanisms underlying astrocytic Ca²⁺ signaling in both normal and pathological situations.

Having quantitative indices of the Ca²⁺ dysregulation in astrocytes will be of great value for studying the pathogenesis of the Alzheimer's disease at both the molecular and cellular levels. In this article, we propose a strategy to quantify the astrocytic Ca²⁺ signaling based on a biophysical model for SCOs. Our model is based on the assumption that the following statements are valid:

• 1.The Li-Rinzel simplification (16) of the De Young-Keizer model accounts well for the kinetics of the IP₃R.
• 2.An additive Wiener process represents adequately the stochastic character of the IP₃R h-open gate probability for small numbers of interacting channels inside a cluster (17).
• 3.A strong cluster coupling in the astrocyte somas originates from the small size of this cell type, the large dimension of its clusters, and the absence of large exogenous buffering mechanisms in our experimental protocol.
• 4.A basal level of cytosolic IP₃ production, with its intrinsic fluctuations, exists in the astrocytes via the action of a diversity of receptor-agonists.
• 5.The subtype δ1 of membrane phospholipase C (PLC) causes a considerable Ca²⁺-dependent feedback in the IP₃ production.
• 6.There is a Ca²⁺ influx from the extracellular space due to both passive leakage channels (which are allowed to fluctuate in terms of their permeability) and a mechanism of capacitative Ca²⁺ entry (CCE).
• 7.The Ca²⁺ extrusion by the plasma membrane and the ATPase Ca²⁺-pump “SERCA” in the endoplasmic reticulum (ER) are accurately represented by linear and Hill-type kinetics, respectively.

By changing the amount of Ca²⁺ influx through passive leakage channels in our model, we were able to reproduce the dissimilar resting Ca²⁺ levels reported by Kuchibhotla et al. (12) for wild-type (WT) and APPswe:PS1ΔE9 mice. By means of a filtering strategy and a maximum-likelihood criterion (i.e., the innovation method), we estimated both the basal levels of IP₃ production and the number of IP₃R channels clustered in each astrocyte soma using two-photon fluorescent Ca²⁺ images from hippocampal slices of both WT and Tg2576 mice. Finally, through simulations, we discussed the impact of these parameters on the abovementioned basic indices for Ca²⁺ signaling, which were compared with estimations from actual Ca²⁺ events in both types of mice.

Materials and Methods

Astrocytic Ca²⁺ imaging

We used eleven C57BL/6 mice in this study with an approximate age-match (0.5–1.5 y/o), i.e., WT (N = 6) and Tg2576 (N = 5 (18)) mice. After the anesthetized mice (diethyl ether) were sacrificed, their brains were rapidly removed and briefly submerged in ice-cold cutting solution. The solution was saturated with 95% O₂ and 5% CO₂. The right hemispheres were mounted on a platform and cut into transverse 300-μm-thick slices using a vibratome (VT1200S; Leica, Nussloch, Germany). The slices were first incubated for 30 min at 34°C in a mixed solution (50% cutting solution and 50% artificial cerebrospinal fluid (aCSF) solution), and latter were kept for at least 30 min at room temperature in aCSF solution gassed with 95% O₂ and 5% CO₂. Slices were transferred into a 24-well plate filled with 1 ml of dye solution, and incubated for 45 min at 34°C during which 95% O₂ and 5% CO₂ were continuously supplied. The dye solution was aCSF containing fluorescent Ca²⁺ indicator (Fluo 4-AM, 22.8 μM; Dojin Chemical, Kumamoto, Japan), sulforhodamine 101 (SR101, 0.824 μM, Invitrogen, Carlsbad, CA), pluronic F-127 (Invitrogen) at 0.01%, and cremophor EL (Sigma Aldrich, St. Louis, MO) at 0.005%.

After loading, slices were washed out in oxygenated aCSF solution at room temperature for at least 30 min, mounted in a recording chamber and perfused with oxygenated aCSF at 30°C to simulate similar conditions to those from the in vivo recordings. Two-photon images from astrocytes at CA1 stratum radiatum in the hippocampus (see Fig. S1 in the Supporting Material) were collected with FluoView 10-ASW software (Olympus, Shinjoku, Tokyo, Japan) and an upright microscope (BX61WI, LUMPlanFI/IR 60×/0.90 N.A. water-immersion objective; Olympus). Fluo 4-AM and SR101 dyes were excited at 810 nm with a mode-lock Ti:sapphire femtosecond laser (MaiTai; Spectra-Physics, Newport, Irvine, CA). Structural SR101 and functional Ca²⁺ images of astrocytes were collected using red and green filters, respectively. For each slice, 10 min of two-photon Ca²⁺ fluorescent images, at a sampling frequency of 2.33 Hz, were recorded at different depths and averaged at each time instant over particular regions of interest. These regions of interest entirely covered the astrocyte somas as defined from the SR101 fluorescent images. To estimate the Fluo 4-AM relative fluorescent change, the two-photon fluorescent time series for each region of interest was preprocessed (see Fig. S2). All animal procedures were reviewed and approved by the Tohoku University Animal Studies Committee.

The biophysical model

The model proposed to describe SCOs in astrocytes covers the following mechanisms (see Fig. S3):

Generation/degradation of cytosolic IP₃

A constant production $X_{I{P}_3}$ (μM/s) of IP₃ (μM) originates from fluctuations in the action of a plethora of receptor-agonists over G-protein-coupled receptors located in the astrocytic membrane. In this way, a basal cytosolic level of IP₃ is created by the activation of the PLC (type β) through the GTP-bound in the G-proteins. The local IP₃ signal inside the cell degrades rapidly, with a relatively short lifetime τ ≈ 1 s, by the 5-phosphomonoesterase (i.e., IP₃ phosphatase) and the 3-kinase. In this study, we have neglected the effect of IP₃ molecule diffusion on the local cellular signaling. In astrocytes, IP₃ could also be produced by the subtype δ1 of membrane PLC, a mechanism regulated by cytosolic Ca²⁺ that might contribute to the basal levels of IP₃. The Ca²⁺-dependent regulation of the PLC_δ1 enzyme activity was better fitted by the Hill's kinetic model (19), as

$$PL{C}_{\delta 1}={\nu }_{\delta }\frac{{\left({\left[C{a}^{2+}\right]}_c\right)}^2}{{\left({\left[C{a}^{2+}\right]}_c\right)}^2+{\left(K_{\delta Ca}\right)}^2}.$$ (1a)

The random activation of membrane G-proteins-coupled receptors through extracellular receptor-agonists might be a source for stochasticity in IP₃ basal production, an effect modeled by the Wiener fluctuations ${\sigma }_{I{P}_3}^{2}d{\omega }_{I{P}_3}$. Therefore, the final dynamic equation for IP3 is,

$$d\left[I{P}_3\right]=\left(X_{I{P}_3}+PL{C}_{\delta 1}-K_{I{P}_3}\left[I{P}_3\right]\right)dt+\stackrel{I{P}_3\text{fluctuations}}{\overbrace{{\sigma }_{I{P}_3}d{\omega }_{I{P}_3}}}.$$ (1b)

Sources of Ca²⁺ signaling

Ca²⁺ concentration (μM) in the cytosol [Ca²⁺]_c changes due to a diversity of sources flowing in and out. Ca²⁺ ion release v_Rel from ER through opened IP₃R channels constitutes the main source of Ca²⁺ flow into the cytosol. The ATPase Ca²⁺-pump “SERCA” represents the major mechanism v_SERCA for Ca²⁺ uptake into the ER. Ca²⁺ entry into the astrocytes from the extracellular space has been suggested to play a protagonist role in the generation of spontaneous Ca²⁺ oscillations in astrocytes (11). Previous theoretical studies have assumed, not only a constant Ca²⁺ influx j_in (μM/s) through passive channels, but also the existence of a CCE v_CCE mediated by store-operated Ca²⁺ channels (19). In models that include Ca²⁺ influxes from the extracellular space, the extrusion of this ion across the plasma membrane v_out is needed to warrant lasting steady-state behaviors:

$$d{\left[C{a}^{2+}\right]}_c=\left(v_{Rel}-v_{SERCA}+\varepsilon \left(j_{in}+v_{CCE}-v_{out}\right)\right)dt+\stackrel{C{a}^{2+}fluctuations}{\overbrace{{\sigma }_{C{a}^{2+}}d{\omega }_{C{a}^{2+}}}}.$$ (2a)

The scaling factor ɛ = A_pm/A_ER is introduced to emphasize that the total surface area of the plasma membrane A_pm is much smaller than the ER membrane area A_ER (16). In Eq. 2a, we have added a Wiener process ${\sigma }_{C{a}^{2+}}d{\omega }_{C{a}^{2+}}$ to account for random dislocations of the Ca²⁺ ions across the plasma membrane through leakage channels. To represent the kinetics of the IP₃R, we used the Li-Rinzel simplification (16) of the De Young-Keizer model:

$$v_{Rel}=c_1\left\{v_1{m}_{\infty }^3{h}^3+v_2\right\}\left({\left[C{a}^{2+}\right]}_{ER}-{\left[C{a}^{2+}\right]}_c\right).$$ (2b)

The kinetics of the IP₃R are written in an analogy of Hodgkin-Huxley's model for electrically excitable neurons (Eq. 2b), where the driving force for Ca²⁺ fluxes is created by the concentration gradient between the ER and the cytosol. Temporal changes in the Ca²⁺ concentration inside the ER occur by depletion and repletion of this internal store through the activity of IP₃R and the SERCA pumping, respectively. To characterize the instantaneous Ca²⁺ ion gradient between the ER and the cytosol, these changes need to be modeled. To that end, a state variable, the total free Ca²⁺ ions per astrocyte volume c_o (μM), is usually introduced such that [Ca²⁺]_ER = (c_o − [Ca²⁺]_c)/c₁.

The open probability for three independent gates m is approached by their values at the equilibrium m_∞ = [IP₃][Ca²⁺]_c/(([IP₃] + d₁)([Ca²⁺]_c + d₅)). Each gate h has an inactivation binding site for Ca²⁺ ions that could be either occupied (closed) or nonoccupied (open). IP₃R channels on the ER membrane are organized in clusters and these clusters form arrays spatially distributed inside the cells. We assumed that the interactions between clusters of IP₃R channels in astrocytes are strong enough to ignore the effect of dynamic Ca²⁺ diffusion inside such small cells (∼7–9 μm in diameter (20)). Hence, the somatic epifluorescent Ca²⁺ images observed in our experiments are, as a first approximation, described sufficiently well by a model for a larger Ca²⁺ cellular domain comprising strongly coupled clusters (17). This model is also able to reproduce transient Ca²⁺ events originating from single clusters (puffs) (21). For a small number N_cluster of IP₃R channels inside a cluster, asymptotic theoretical formulas for the open/closed probabilities are inadequate to describe Ca²⁺ release from the ER, i.e., the deterministic model is insufficient. In such a case, the open probability for h-gates has to be modeled by means of Markov processes (17), i.e., the stochastic model. If the number of IP₃R channels in the Ca²⁺ signaling microdomains is relatively large, we can alternately employ the equivalent Fokker-Plank formalism with opening α_h = ad₂([IP₃] + d₁)/([IP₃] + d₃) and closing β_h = a[Ca²⁺]_c rates for three independent gates h, as

$$dh=\left[{\alpha }_h\left(1-h\right)+{\beta }_{h}h\right]dt+{\sigma }_{h}d{\omega }_h.$$ (2c)

The variance of zero-mean Gaussian white noise ${\sigma }_h^2$ was defined in Shuai and Jung (17):

$${\sigma }_h^2=\left(\frac{{\alpha }_h\left(1-h\right)+{\beta }_{h}h}{N_{cluster}}\right).$$

Note that the stochastic model transforms into a deterministic one for an infinitely large number of channels. Because variance ${\sigma }_h^2$ depends on state variables [IP₃], [Ca²⁺]_c, and h, the diffusion Wiener process in the stochastic differential equation (Eq. 2c) is multiplicative. Integration, filtering hidden state variables, and making statistical inferences (i.e., parameter estimations) of this particular type of Itô stochastic differential equation require a high computational cost. In this article, we evaluate the behaviors of the proposed biophysical model for constant values of ${\sigma }_h^2$, which were defined from its physiological bounds. Therefore, we approximate the dynamics of the state variable h by a stochastic differential equation with an additive Wiener noise.

The lower 0.8 × 10⁻³ s⁻¹ and upper 6.0 × 10⁻³ s⁻¹ bounds for the variance ${\sigma }_h^2$ were established from assumptions of the following: IP₃R opening rate 0.031 s⁻¹ ≤ α_h ≤ 0.092 s⁻¹ (a consequence of 0.01 μM ≤ [IP₃] ≤ 0.5 μM); IP₃R closing rate 0.016 s⁻¹ ≤ β_h ≤ 12 s⁻¹ (a consequence of 0.080 μM ≤ [Ca²⁺]_c ≤ 0.6 μM); N ≈ 20 (although there is still some discrepancy, it has been postulated that a single cluster comprises ∼10–30 IP₃R channels); and 0 ≤ h ≤ 1.

The SERCA pumping in astrocytes has been consistently modeled through a Hill-type kinetic model:

$$v_{SERCA}=V_{serca}\frac{{\left({\left[C{a}^{2+}\right]}_c\right)}^2}{{\left({\left[C{a}^{2+}\right]}_c\right)}^2+{\left(K_p\right)}^2}.$$ (2d)

In this article, we used a phenomenological model proposed by Di Garbo et al. (22) to describe the CCE effect in astrocytes, i.e.,

$$v_{CCE}=x_{CCE}\frac{{\left(H_{CCE}\right)}^2}{{\left({\left[C{a}^{2+}\right]}_{RE}\right)}^2+{\left(H_{CCE}\right)}^2}.$$ (2e)

A simple linear kinetic model has been consistently used in the past to represent the Ca²⁺ extrusion across the plasma membrane:

$$v_{out}=k_{out}{\left[C{a}^{2+}\right]}_c.$$ (2f)

Obviously, changes in the total free Ca²⁺ concentration c_o are only caused by Ca²⁺ fluxes and extrusion across the plasma membrane; hence, this state variable must satisfy

$$d{c}_o=\varepsilon \left(j_{in}+v_{CCE}-v_{out}\right)dt.$$ (3)

The effect of random dislocations of the Ca²⁺ ion across the plasma membrane were considered too small to cause any perturbation in the state variable c_o, which varies in the range of 1 ≤ c_o (μM) ≤ 3 because of the high Ca²⁺ concentration in the ER.

The values of the parameters for the proposed biophysical model and the ranges for the variances in the Wiener processes are reported in Table S1 and Table S2 in the Supporting Material. In Ca²⁺ imaging with the Fluo 4-AM dye, the baseline fluorescence F_o cannot be used to determine the basal Ca²⁺ concentration C_basal in the cytosol. Therefore, the Fluo 4-AM relative fluorescent change was defined in this article for a given C_basal, i.e., observation equation,

$$\frac{\Delta F}{F_0}=\gamma \left({\left[C{a}^{2+}\right]}_c-C_{basal}\right)+\xi .$$ (4)

The factor γ ≈ 1 μM⁻¹ was estimated by Shigetomi et al. (11) (see Fig. 2 b in (11)) for the Fluo 4-AM dye. We assumed an instrumental fluorescent noise with a Gaussian distribution, i.e., ξ ∼ N(0,${\sigma }_F^2$). In this study, the stochastic differential equations, Eqs. 1–3, were numerically solved using the local linearization method (23), with integration step Δt = 0.1 s. The statistical inference about the model parameters was performed by combining the local linearization filter and the innovation method (24), an approach that was previously validated for the particular case of astrocytic Ca²⁺ signaling (19).

Figure 2.

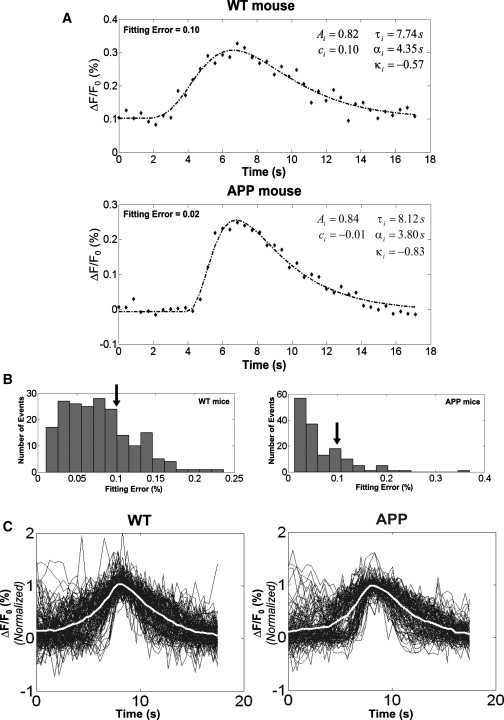
Procedure to characterize single Ca²⁺ events. (A) Examples of fitting a generalized-Gaussian function to a particular Ca²⁺ event in both WT (top) and Tg2576 (APP) (bottom) mice. The respective values for location τ_i, shape κ_i, scale α_i, amplitude A_i, and baseline c_i are also shown. (B) A least-square criterion was used to fit the generalized-Gaussian function to the actual ΔF/F₀ waveforms. Ca²⁺ events with fitting errors >0.1 (solid arrows) were considered doubtful, and therefore, excluded from the analysis. (C) The normalized Ca²⁺ events (solid, single trials; open, mean). The total numbers of well-fitted events for WT and Tg2576 (APP) mice, which additionally were required to have amplitudes >15%, were n = 147 and n = 121, respectively.

Results

Basic indices: cell type/percent and response frequency

Typical time courses of the Fluo 4-AM relative fluorescent changes in astrocytes of WT (left) and Tg2576 (right) mice are shown in Fig. 1. We quantified the SCOs in astrocytes using the basic indices proposed in the past (12,13,15). According to the SCO characteristics, SR101-labeled astrocytes were further classified into: inactive (a stable Ca²⁺ baseline); active (irregular Ca²⁺ events); and hyperactive (highly fluctuating Ca²⁺ baseline). To be consistent with a previous study (12), our classification of the astrocyte-type was based on: 1), 5 min of two-photon Ca²⁺ fluorescent images and 2), transient events with relative fluorescence change >15%.

Figure 1.

Examples of the relative fluorescent changes ΔF/F₀ obtained from astrocytes of both WT and Tg2576 (APP) mice. In both types of mice, we are able to distinguish three kinds of Ca²⁺ signaling states: inactive, a stable Ca²⁺ baseline; active, irregular Ca²⁺ events; and hyperactive, a highly fluctuating Ca²⁺ baseline.

In hyperactive astrocytes, trains of Ca²⁺ events (i.e., bursts) were frequently observed. To automatically identify the time instants of possible Ca²⁺ events, we developed an algorithm that combines a thresholding method and a maximum time-derivative strategy. By means of a least-square criterion, we fitted a generalized-Gaussian function (Eq. 5), with location τ_i, shape κ_i, scale α_i, amplitude A_i, and baseline c_i, to the ΔF/F₀ data corresponding to each identified Ca²⁺ event. Fig. 2 A exemplifies the fitting results for a particular cell of a WT (deficient fitting 0.10) and an APP (excellent fitting 0.02) mouse. Ca²⁺ events with large fitting errors (≥0.1, solid arrows in Fig. 2 B) were disregarded. The final normalized waveforms of Ca²⁺ events for WT (147 events) and APP (121 events) mice are shown in Fig. 2 C:

$$\begin{array}{l}{s}_i\left(t\right)=\frac{A_i\exp \left[-{\left(x_i\left(t\right)\right)}^2\right]}{{\alpha }_i-{\kappa }_i\left(t-{\tau }_i\right)}+c_i,\hfill \\ t\in \{\begin{array}{cc}\left(-\infty ,{\tau }_i+{\alpha }_i/{\kappa }_i\right)& {\kappa }_i>0\\ \left(-\infty ,\infty \right)& {\kappa }_i=0\\ \left({\tau }_i+{\alpha }_i/{\kappa }_i,\infty \right)& {\kappa }_i<0,\end{array}\hfill \\ x_i\left(t\right)=\{\begin{array}{cc}-\frac{1}{{\kappa }_i}\log \left(1-\frac{{\kappa }_i\left(t-{\tau }_i\right)}{{\alpha }_i}\right)& {\kappa }_i\ne 0\\ \frac{t-{\tau }_i}{{\alpha }_i}& {\kappa }_i=0.\end{array}\hfill \end{array}$$ (5)

Note that epifluorescence unique Ca²⁺ events (ΔF/F₀ ≃ 5 ± 4% (11)), which may represent isolated somatic puffs, were ignored in this study. Therefore, the Ca²⁺ spikes detected by our algorithm must reflect synchronized activity in all somatic microdomains. In agreement with a previous study for in vivo cortical astrocytes (12), the percent of active astrocytes was higher, although nonsignificant, in the hippocampal acute slices obtained from APP mice (Table 1). The discrepancy may be attributable to the differences in the production of β-amyloid peptides between these two mutant mice: Tg2576 (11–13-months-old) Aβ(1–42/43) → 175 ± 26 pmol/g (18) and APPswe:PS1ΔE9 (12-months-old) insoluble Aβ42 → 1009.53 ± 115.56 pmol/g (25).

Table 1.

The percentages of different cell types in WT and APP mice

Type of cell	WT mice (%)	APP mice (%)
Inactive	38.33 ± 29.10	35.91 ± 15.52
Active	20.98 ± 18.77	42.13 ± 16.78
Hyperactive	40.69 ± 38.61	21.95 ± 5.48
Total active (active + hyperactive)	61.66 ± 29.10	64.08 ± 15.51

Cell types are for both WT (six mice, total number of cells = 67) and Tg2576 mice (four mice, total number of cells = 85), with the corresponding standard deviations. (Note that, as a consequence of the small amount of recorded cells (n = 2), one mouse was not included in this analysis.) Classification: inactive, astrocytes with stable Ca²⁺ baseline; active, astrocytes showing irregular Ca²⁺ events; and hyperactive, astrocytes with a highly fluctuating Ca²⁺ baseline.

When comparing results in the study by Kuchibhotla et al. (12) with those in Table 1, readers must bear in mind the dependency of astrocytic Ca²⁺ signaling on temperature (26). Albeit having a high intermouse variability, hyperactive astrocytes were more common in WT mice, a fact that was not significant. We found a significant reduction (two-sample t-test with unequal variances, p = 0.001) in the response frequency of the astrocytes which were not inactive in APP mice (0.90 ± 0.62 events/min, n = 87) with respect to that of WT mice (1.65 ± 1.01 events/min, n = 67). This result is inconsistent with the increase in the response frequency reported earlier by Takano et al. (13) for young (2–4 months/old) APP (Tg2576) mice in vivo, i.e., WT (0.4 ± 0.1 events/min) and APP (2.3 ± 0.6 events/min). Differences in the technique employed (i.e., acute slices versus in vivo), the brain tissue (i.e., hippocampus vs. neocortex), and the detection method of Ca²⁺ events (i.e., automatic versus manual) might underlie such discrepancy.

Basal Ca²⁺ levels in the cytosol: a key physiological parameter

By means of the proposed biophysical model, we examined whether the basal Ca²⁺ levels in the cytosol were determined by the activity of receptor-agonists $X_{I{P}_3}$ or by the amount of passive Ca²⁺ influx j_in. By solving a nonlinear equation system (fsolve.m function, MATLAB R2006b; The MathWorks, Natick, MA), we were able to determine C_basal numerically for each pair of physiological parameters $\left\{X_{I{P}_3},j_{in}\right\}$ (Fig. 3 A). Surprisingly, large increases in $X_{I{P}_3}$ caused small changes in C_basal, with a slight tendency for the interval 0.02 μM/s ≤ $X_{I{p}_3}$ ≤ 0.5 μM/s to rise. However, C_basal was more sensitive to changes in j_in, with an approximately linear dependency. We found that, to replicate the corresponding values of C_basal reported for WT (0.081 μM) and APPswe:PS1ΔE9 (0.149 μM) mice (12), the Ca²⁺ influx must be roughly j_in = 0.036 μM/s and j_in = 0.070 μM/s, respectively. The baseline for the total free Ca²⁺ ions per astrocyte volume c_o,b also depended on both $X_{I{P}_3}$ and j_in, with rapid increases for high values of j_in ≥ 0.04 μM/s (Fig. 3 B). Increasing the level of IP₃ brought about a decrease of c_o,b, probably caused by depletion of the intracellular stores and the associated enhancement of Ca²⁺ extrusion across the plasma membrane. There were no perceivable changes in either C_basal or c_o,b for values of $X_{I{P}_3}$≥ 0.3 μM/s.

Figure 3.

Dependency of the basal Ca²⁺ concentration in the cytosol C_basal (A) and the baseline for the total free Ca²⁺ ions per astrocyte volume c_o,b (B) with the physiological parameters $X_{I{P}_3}$ and j_in. (Dashed lines) Corresponding mean levels of these parameters for the experimentally observed C_basal in WT (0.081 μM) and APP(PS1) (0.149 μM) mice.

The initial conditions (note that the initial conditions represent the steady-state solutions of the differential equation system) for the state variables were recalculated in each analysis performed in our study as a function of $X_{I{P}_3}$ and j_in. Based on the fact that the nonlinear function in the stochastic differential equations (Eqs. 1–3) represents a contraction mapping, there is no possibility for SCOs (i.e., at low IP₃ levels) without the presence of external diffusive forces, i.e., the Wiener processes. Unfortunately, as a result of the uncertainty in determining C_basal, we found ourselves unable to estimate j_in from the Fluo 4-AM relative fluorescent changes. Instead, we used the following heuristic strategy to determine C_basal for our particular mice: 1), we assume a linear dependency of C_basal in astrocytes and the β-amyloid concentrations in the tissue, i.e., C_basal = m[Aβ₄₂] + l; 2), we estimated the slope m = 0.067 nM (pmol/g)⁻¹ and intercept l = 80.9 nM from measured data of C_basal (12) and β-amyloid concentrations in the tissue (18,25) for both WT and APPswe:PS1ΔE9 mice (∼12 months/old); 3), we calculated the C_basal = 92.6 nM value for the Tg2576 mice (11–13 months/old) from their particular β-amyloid concentrations (18); and then, 4), we estimated approximately j_in = 0.043 μM/s for the Tg2576 mice from Fig. 3 A.

Statistical inference: IP₃ production levels and number of clustered IP₃R channels

From the whole time series of relative fluorescent changes ΔF/F₀ in each cell, we estimated the respective hidden state variables {[IP₃], h, c_o} and the model parameters $\left\{X_{I{P}_3},{\sigma }_h\right\}$ for given values of C_basal. Based on the Bayesian model selection strategy (i.e., the evidence), we verified that the model resulting from fitting these two parameters was more likely than those fitting other combinations of parameters. Also, we confirmed that: 1), changes in the variances ${\sigma }_{C{a}^{2+}}^2$ and ${\sigma }_{I{P}_3}^2$ do not have a significant impact on the astrocytic Ca²⁺ signaling and 2), the temporal characteristics of the astrocytic Ca²⁺ events is appreciably dependent on the number of IP₃R channels per cluster.

Therefore, variances $\left\{{\sigma }_{C{a}^{2+}}^2,{\sigma }_{I{P}_3}^2\right\}$ were both set low (1 × 10⁻⁴ μM/s) and variance ${\sigma }_h^2$ was estimated from actual data for each particular cell. For each time series, we estimated the variance of the instrumental noise (0.1 × 10⁻⁵ ≤ σ²_F ≤ 2.5 × 10⁻⁵) as a genuine Gaussian process superimposed on the eventlike Ca²⁺ signaling. To avoid any ambiguity in our conclusions caused by a lack of information about the basal Ca²⁺ concentration in the cytosol for Tg2576, we performed a statistical analysis for four different values of j_in. The minimal and maximal values of j_in were set from the observed C_basal in WT and APPswe:PS1ΔE9 mice (12), respectively. We introduced two extra values of Ca²⁺ influx, i.e., the value j_in = 0.043 μM/s, to represent our estimated C_basal for the Tg2576 mice, and the in-between value of j_in = 0.053 μM/s.

Fig. 4 shows results from the statistical inference for a particular cell of a WT (left) and an APP (right) mouse, using the most likely value of C_basal for each. The relative fluorescent changes ΔF/F₀ (solid) and the resulting innovations η (shaded) after model fitting are shown for each cell (top). The estimated hidden state variables $\left\{\widehat{\left[I{P}_3\right]},\widehat{h},{\widehat{c}}_o\right\}$ are displayed on independent panels below. The distribution of the innovations η was confirmed to be approximately Gaussian, an assessment based on the Kolmogorov-Smirnov test. The estimated parameters $\left\{{\widehat{X}}_{I{P}_3},{\widehat{\sigma }}_h\right\}$ for both particular cells were {0.32 μM/s, 0/018 s^−1/2} for the WT mouse and {0.31 μM/s, 0.021 s^−1/2} for the APP mouse. The mean values 〈h〉 and 〈[IP₃]〉 in the observation time window, together with C_basal and the estimated variance ${\widehat{\sigma }}_h^2$, were used to calculate the approximate number of IP₃R channels clustered in the astrocyte soma for each mice-type using

$${\widehat{N}}_{cluster}\approx \left(\frac{{\overline{\alpha }}_h\left(1-\langle h\rangle \right)+{\overline{\beta }}_h\langle h\rangle }{{\widehat{\sigma }}_h^2}\right),$$ (6)

with ${\overline{\alpha }}_h=a{d}_2\left(\langle \left[I{P}_3\right]\rangle +d_1\right)/\left(\langle \left[I{P}_3\right]\rangle +d_3\right)$ and ${\overline{\beta }}_h=a{C}_{basal}$.

Figure 4.

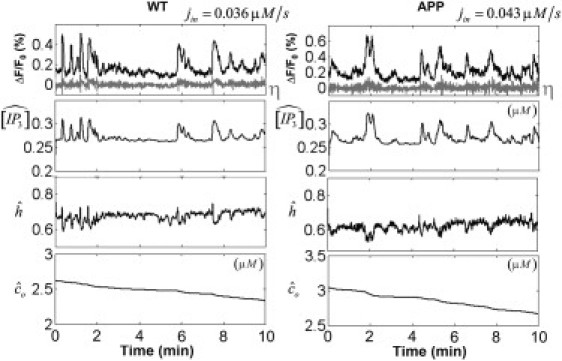
Statistical inference for a particular cell of a WT (left) and an APP (right) mouse. We used the most likely value of C_basal for each mouse type, i.e., j_in = 0.036 μM/s (WT mice) and j_in = 0.043 μM/s (Tg2576 mice). (Upper panel) Relative fluorescent changes ΔF/F₀ (solid) and the resulting innovations η (shaded) after model fitting for each cell. The estimated hidden state variables $\left\{\widehat{\left[I{P}_3\right]},\widehat{h},{\widehat{c}}_o\right\}$ are shown in three separated panels below.

The same procedure was applied to ΔF/F₀ data from all recorded-cells of both WT (n = 67) and APP (n = 84) mice (the algorithm had convergence problem in three cells of APP mice, which were not considered in the statistical analysis). The results are summarized in Fig. 5. The IP₃ production levels were significantly smaller (two-sample t-test with unequal variances) in the Tg2576 mice, which was consistent no matter which value of passive Ca²⁺ influx we used in the estimation procedure (top left). For Tg2576 mice, the variance ${\widehat{\sigma }}_h^2$ decreases as a function of the value in use for the parameter j_in. We found no significant difference for this variance between WT and Tg2576 mice when the estimated j_in for this particular mutation was used. The number of IP₃R channels in a single cluster of the astrocytes from WT mice was ${\widehat{N}}_{cluster}$= 131 ± 29 (note that mean ± 1.96 × SE). For the Tg2576 mutant mice, we conjecture a nonsignificant decrease in the total number of channels per cluster (${\widehat{N}}_{cluster}$= 105 ± 14; note that mean ± 1.96 × SE). These numbers are much larger than those associated with actual channels recruitment during puff events in healthy Xenopus oocytes (27) and human neuroblastoma SH-SY5Y cells (28). They are also incompatible with lower/upper bounds theoretically predicted to underlie, in terms of efficiency, a single puff from wide-ranging biophysical models of Ca²⁺ signaling (29,30).

Figure 5.

Summary of parameter estimation and statistical tests for all cells in both WT (n = 67, solid bars) and Tg2576 (APP) (n = 84, shaded bars) mice. Though we provided an empirical estimation in this study, C_basal is experimentally unknown for Tg2576 mice. Therefore, the statistical inference in the particular case of using data from our APP transgenic mice was performed for different values of C_basal (i.e., mice with no β-amyloid accumulation, 81 nM; mice with a slight number of plaques, Tg2576, 92 nM; mice with a moderate number of plaques, 110 nM; and mice with a severe number of plaques, APP(PS1), 149 nM). The IP₃ production levels $X_{I{P}_3}$ were significantly higher in WT mice. While raising the value of C_basal, the estimators of variance ${\widehat{\sigma }}_h^2$ and the average number of IP₃R channels in a single cluster ${\widehat{N}}_{cluster}$ reduced and increased, respectively. For the predicted C_basal in Tg2576 mice, there were no significant differences with the corresponding estimators of these two parameters for WT mice. A bar represents the mean value of the estimated parameter and the 1.96 × SE.

Actual and predicted Ca²⁺ event statistics

From the synthetic ΔF/F₀ data, created by integrating our biophysical model with the estimated ${\widehat{X}}_{I{P}_3}$ and ${\widehat{\sigma }}_h$ values for both WT and Tg2576 mice, we calculated the basic indices commonly used to quantify the SCOs. In these simulations, the variances of the Wiener fluctuations for IP₃ and Ca²⁺ signaling were also small (i.e., ${\sigma }_{I{P}_3}^2$= 1 × 10⁻⁴ μM/s, ${\sigma }_{C{a}^{2+}}^2$= 1 × 10⁻⁴ μM/s) and the same for all trials. We used the respective values of j_in for each mouse type. For practical reasons, we did not add instrumental fluorescent noise. Consistent with our statistical analysis of Ca²⁺ events from actual data, synthetic Ca²⁺ events with amplitudes <15% were not considered. We reproduced the tendency of APP transgenic mice to have more computer-generated active cells (67%) than WT mice (41%). However, the response frequencies for astrocytes in these two virtual mice were lower, i.e., WT (0.26 ± 0.08 events/min) and Tg2576 (0.29 ± 0.10 events/min) mice, than those observed experimentally. For both mouse types, we were unable to generate hyperactive cells from the estimated model parameters, which might be one of the reasons for the mismatch in their actual/predicted response frequencies through a population analysis. If the hyperactive cells are not included, the response frequencies for astrocytes in WT and Tg2576 mice were 0.96 ± 0.41 events/min and 0.61 ± 0.30 events/min, respectively. The estimated models for WT and Tg2576 mice were able to reproduce the respective distributions of Ca²⁺ event amplitudes reconstructed from the actual data, which were bimodal in the particular case of the Tg2576 mice (see Fig. S4).

Discussion

Based on a biophysical model, we proposed what we believed to be novel indices to quantify the SCO in astrocytes. We performed a statistical inference from actual experimental data to determine the particulars of our model for WT and Tg2576 mice. We concluded that abnormalities in astrocytic Ca²⁺ signaling observed in APP transgenic mice might result from a strengthening of the passive Ca²⁺ influx from the extracellular space and a significant reduction of the IP₃ production levels. We found a large number of channels inside astrocytic IP₃R clusters. Our conclusions rely on parameter estimates that are model-specific (e.g., just three subunits for IP₃R channels in the Li-Rinzel model, strong cluster interactions in the soma), and even depend on those parameter values which have been kept fixed through the study. The strategy proposed in this study can also be used to quantify Ca²⁺ signaling in other cell types.

Possible mechanisms for Ca²⁺ influx in astrocytes

By simulations, we have found that a change in the passive Ca²⁺ influx is needed to explain the significant differences (∼70 nM) in the basal Ca²⁺ levels between WT and APPswe:PS1ΔE9 mice found by Kuchibhotla et al. (12). We verified also (data not shown) that it is possible to switch an astrocyte from an inactive to a more active physiological state by just increasing the Ca²⁺ influx from the extracellular space. This suggests that astrocytes in APP transgenic mice, which showed a larger probability for having SCOs, possess plasma membranes with more permeability to Ca²⁺ ions—a situation that might cause an abnormal increase in the resting cytosolic levels for this ion and hence possible dysfunctions of important intracellular signaling mechanisms. Increases in the Ca²⁺ influx might not only result from changes in the permeability of leakage channels, but also from alterations in the active channels (e.g., store-operated and ligand-gated channels). A specific Ca²⁺-independent phospholipase 2 has been suggested to cause Ca²⁺ influx through store-operated Ca²⁺ entry channels during depletion of internal stores (31), a pathway that could be enhanced in the presence of oligomeric β-amyloid peptides (32).

An alternative pathway involves nitric oxide as a possible modulator for refilling internal stores (33). Also, the role played by several types of voltage-gated Ca²⁺ channels in astrocytic Ca²⁺ signaling was recently evaluated theoretically by Zeng et al. (34). However, blocking the L-type of Ca²⁺ channels has, in practice, produced no effect on SCOs in astrocytes (35). Rojas et al. (36) proposed that an influx of Na⁺ through high-affinity trans-membrane glutamate transporters GLAST and GLT-1 can activate the reverse Na⁺/Ca²⁺ exchange in cortical astrocytes, a mechanism that may be abnormal in Alzheimer's disease (37). In agreement with that, Wang et al. (35) have reported an enhancement of SCO when astrocytes are exposed to both a low Na⁺ and a high Ca²⁺ solution. Paradoxically, ethylenediamine tetraacetic acid (a “sequesterer” of Ca²⁺ ions) bathing did not affect SCO (35), whereas this type of activity was suppressed in the prolonged absence of external Ca²⁺ (8). More studies are required at some point to clarify which particular mechanisms underlie the amplification of the Ca²⁺ influx in APP transgenic mice and how the β-amyloid plaques up/downregulate them.

Characterizing astrocytic Ca²⁺ microdomains

Many neurotransmitters have been confirmed to generate IP₃ signal through the activation of G-proteins-coupled receptors. Based on our results, we foresee a significant reduction in the sensitivity of these receptors in hippocampal astrocytes that might occur along with the β-amyloid accumulation. This conjecture is somehow in disagreement with a previous study suggesting an upregulation of the metabotropic glutamate receptor 5 by the β-amyloid (1–40) peptides (38). In weakly stimulated astrocytes or under conditions of very low IP₃ levels, SCOs might originate mostly from an increase in IP₃R responsiveness as a result of the existence of clusters of IP₃R channels along the ER membrane. Models assuming strong interactions between the channels inside a single cluster have been used to represent local pufflike events (17,39,40).

As demonstrated in these previous theoretical works, a small number of IP₃R channels clustered within a tiny cytosolic region brings about stochasticity in the mechanisms for Ca²⁺ ion release from the ER. The full width at half-maximum (FWHM) and the full duration half-maximum (T_0.5) of a puff event are magnitudes that may be robustly affected by the channels' organization inside a single cluster. For example, the numbers of recruited channels inside a cluster during a puff event have been estimated as ∼8 and ∼6 for healthy Xenopus oocytes (27) and human neuroblastoma SH-SY5Y cells (28), respectively. These numbers are compatible with the similarities found in the FWHM and the T_0.5 for puff events in these two different cells (41), i.e., Xenopus oocytes (FWHM = 3.4 μm and T_0.5 ≈ 260 ms) and human neuroblastoma SH-SY5Y cells (FWHM = 3.5 μm T_0.5 ≈ 300 ms). However, puff events in astrocytes have both larger sizes (FWHM = 5.1 ± 0.1 μm) and considerably slower temporal dynamics (T_0.5 = 3900 ± 300 ms) (11). Therefore, the number of IP₃R channels recruited during a puff event must be different for this particular cell type.

Based on our data, we predict a relative large number of IP₃R channels (${\widehat{N}}_{cluster}\simeq 131$) inside a single cluster of healthy hippocampal astrocytes. For the Tg2576 mutant mice, we observed a nonsignificant decrease in the number of channels inside a cluster (${\widehat{N}}_{cluster}\simeq 105$). Assuming a maximal interchannel distance d_c inside a cluster of 100 nm, we anticipate an upper bound for the effective cluster volume $V_{cluster}={\widehat{N}}_{cluster}\left(4\pi /3\right){\left(d_c/2\right)}^3$ in healthy hippocampal astrocytes of ∼0.069 μm³, whereas for cells comprising few tens of channels this bound will be nearly 0.018 μm³. We found it interesting that the cluster volume's rate (3.8) predicted from these theoretical bounds is consistent with that rate (3.2) determined from the actual FWHM values of Ca²⁺ puffs in these cells.

Possible role of Ca²⁺ diffusion

The existence of steep concentration gradients for Ca²⁺ ions inside many cells causes weak connections between adjacent clusters which justifies the need to include diffusion mechanisms in the biophysical models of their Ca²⁺ signaling. Models founded on the reaction-diffusion theory have been suggested to represent the transition between stochastic localized pufflike (T_0.5 ∼100 ms) and deterministically appearing global-spike-like (T_0.5 of approximately few seconds) events in several cell types (42). This emerging family of models also aims to provide an explanation, through the random wave nucleation hypothesis, for the linear relationship between the average and the standard deviation of the interspike-intervals observed in a number of cells (43), which constitutes a type of frequency encoding robust against cell variability (44). Similar linear relationships have been reproduced using models for single clusters with different channel numbers (45), diminishing the prerequisite of multiscale channel interactions as defined in reaction-diffusion systems. However, we hypothesized that coupling among somatic clusters in astrocytes is very strong. Our hypothesis is based on the fact that: 1), under physiological conditions (i.e., negligible buffering systems), the diffusion of Ca²⁺ ions occurs rapidly within the very small soma; and 2), having merely a few microdomains in the soma, which are indeed in very close proximity due to their large FWHM, would facilitate Ca²⁺ signal synchronization.

As suggested from the results by Shigetomi et al. (11), those Ca²⁺ transients in astrocytes detectable by epifluorescence microscopy (i.e., with amplitudes ΔF/F > 15%) might reflect whole-soma synchronized events. Therefore, in this study we used the theoretical framework proposed by Shuai and Jung (17) to describe Ca²⁺ release from strongly coupled clusters of IP₃R channels. Similar approaches have been used in the past to successfully explain observable Ca²⁺ spikes in astrocytes without the need of including diffusion phenomena (46,47). Ca²⁺ diffusion phenomena may underlie the existence of burstlike activity as seen in hyperactive astrocytes (48) and hence give an explanation for the mismatch found in the actual/predicted response frequencies for both WT and Tg2576 mice. However, these models must definitely be based on particular characteristics for astrocytes. For example, the conclusions by Skupin et al. (48) rely on the validity of their assumptions about the number of channels per cluster (i.e., 4–16 channels) and the number of clusters per astrocyte (i.e., 47 clusters).