Using Covalent Dimers of Human Carbonic Anhydrase II to Model Bivalency in Immunoglobulins

Abstract

This paper describes the development of a new bivalent system comprising synthetic dimers of carbonic anhydrase linked chemically through thiol groups of cysteine residues introduced by site-directed mutagenesis. These compounds serve as models with which to study the interaction of bivalent proteins with ligands presented at the surface of mixed self-assembled monolayers (SAMs). Monovalent carbonic anhydrase (CA) binds to benzenesulfonamide ligands presented on the surface of the SAM with K_d^surf = 89 nM. The synthetic bivalent proteins—inspired by the structure of immunoglobulins—bind bivalently to the sulfonamide-functionalized SAMs with low nanomolar avidities (K_d^{avidity, surf} = 1 – 3 nM); this difference represents a ~50-fold enhancement of bivalent over monovalent association. The paper describes dimers of CA having i) different lengths of the covalent linker that joined the two proteins, and ii) different points of attachment of the linker to the protein (either near the active site (C133) or distal to the active site (C185)). Comparison of the thermodynamics of their interactions with SAMs presenting arylsulfonamide groups demonstrated that varying the length of the linker between the molecules of CA had virtually no effect on the rate or avidity of association, or on the avidity of these dimers with ligand-presenting surfaces. Varying the point of attachment of the linker between monomeric CA’s also had almost no effect on the avidity of the dimers, although changing the point of attachment affected the rates of binding and unbinding. These observations indicate that the avidity of these bivalent proteins, and by inference the avidities of structurally similar bivalent proteins such as IgG, are unexpectedly insensitive to the structure of the linker connecting them.

Introduction

Bivalency is the simultaneous association of two ligands that are linked together with two binding sites on a receptor. Although bivalent receptors typically show an enhancement in binding over the constituent monovalent system, the molecular details of this enhancement remain incompletely understood.^{1, 2} We cannot rationalize, for example, whether antibodies evolved to be bivalent to enhance binding to antigen, and whether the presence of the Fc domain influences the free energy of the bivalent interaction. One approach to answering these questions—the one we describe here—is to design a model system that facilitates the systematic study of structure-function relationships in series of bivalent receptors.

This paper describes a model system that we are using to study the interaction of bivalent proteins—synthetic dimers of mutants of human carbonic anhydrase II (HCAII, EC 4.2.1.1, or “CA” for brevity)—and mixed self-assembled monolayers (SAMs) presenting ligands (para-substituted benzenesulfonamides) that bind at the active site of CA (Scheme 1). We intend this system to serve as a model with which to examine the biophysics and physical-organic chemistry of bivalency in systems of proteins and ligands. We are interested particularly in the structure of antibodies, and have been trying to understand: i) the structural features required for bivalency to lead to a tight association (e.g., high avidity) in the binding of antigen (especially when presented on surfaces) to antibody, ii) the range in the strength of associations between antibodies and antigens,³ and iii) the thermodynamic constraints on bivalent interactions that may have influenced the evolution of the multivalent structures of antibodies that we now observe.⁴

Scheme 1.

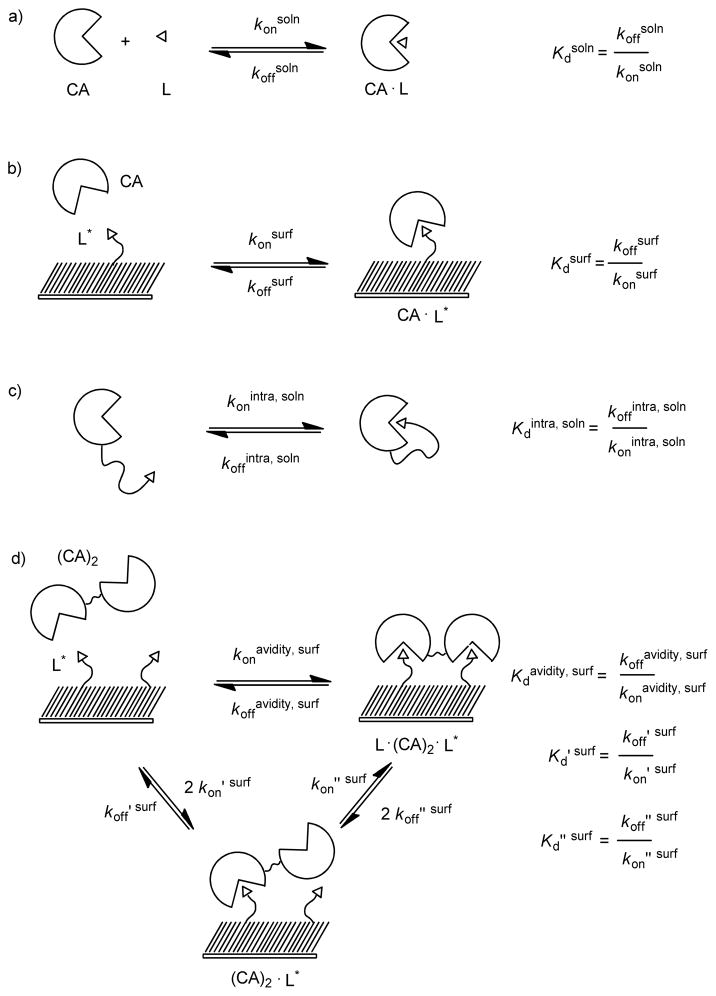
Thermodynamic schemes describing the binding of monovalent carbonic anhydrase CA and bivalent carbonic anhydrase (CA)₂ to surfaces presenting benzensulfonamides (L). a) The binding of CA to a monovalent ligand in solution (L) forms a receptor-ligand complex (CA·L) that is characterized by rate constants for association and dissociation, k_on^soln and k_off^soln_, respectively. The ratio k_off^soln to k_on^soln is the dissociation constant K_d^soln. b) The binding of CA to a mixed SAM presenting multiple ligands forms a receptor-ligand complex (CA·L*) that is characterized by rate constants for association and dissociation, k_on^surf and k_off^surf. The ratio k_off^surf to k_on^surf is the dissociation constant K_d^surf (eq 2). c) The rate of association and dissociation between the binding site of CA and a ligand covalently attached to CA by a flexible tether is characterized by rate constants for association and dissociation, k_on^{intra, soln} and k_off^{intra, soln}_, respectively. The ratio k_off^{intra, soln} to k_on^{intra, soln} is the unitless dissociation constant K_d^{intra, soln}. d) The association of (CA)₂ to two ligands (L*) can be conceptualized as a process involving two steps. The initial step—the association of (CA)₂ to L*—is characterized by rate constants k_off ′ ^surf and k_on′ ^surf. The second step—the association of an additional ligand to the unbound active site of (CA)₂ forms a complex consisting of one (CA)₂ and two ligands (L*· (CA)₂·L)* —is characterized by rate constants k_off ″ ^surf and k_on ″ ^surf. The ratio k_off ″ ^surf to k_on ″ ^surf is the dissociation constant K_d″ ^surf (eq 6). The rate of binding of (CA)₂ to two ligands is characterized by rate constants k_off^{avidity, surf} and k_on^{avidity, surf}. The ratio of k_off^{avidity, surf} and k_on^{avidity, surf} is the avidity (K_d^{avidity, surf}) and characterizes the strength of (CA)₂ binding to L* in the form of L*·(CA)₂·L* (eq 8).

Monoclonal antibodies are, in practice, difficult for many biophysicists and physical-organic chemists to obtain in the quantities and varieties needed for physical biochemistry, and it is impractical to vary the elements of their structure (e.g., the length and flexibility of the linker between the Fab and Fc regions) relevant to our inquiry. We wished to develop a class of molecules that would serve as models of antibodies, and that would be more convenient to use than antibodies themselves. Our objective in this research was to construct, evaluate, and use covalent dimers of human carbonic anhydrase II (collectively referred to as “dimers of CA” or “(CA)₂” ) as one such model, and to characterize the structural features of the linker (distance between binding sites, flexibility, and position of attachment to the protein) between the two molecules of CA required for bivalency to lead to enhanced binding (ΔG°_{avidity, surf} < ΔG°_surf) to multivalent ligands. We found that dimers of CA bind bivalently to mixed SAMs presenting benzensulfonamide groups with a free energy that was modestly more favorable (~2 ± 0.4 kcal mol⁻¹) than the monovalent interaction. Surprisingly, over the range of structures we examined, the length, flexibility, and position of attachment of the linker between the two equivalents of CA did not influence the free energy of bivalent association with the surface.

The Structure of Bivalent Antibodies and Their Binding to Ligands

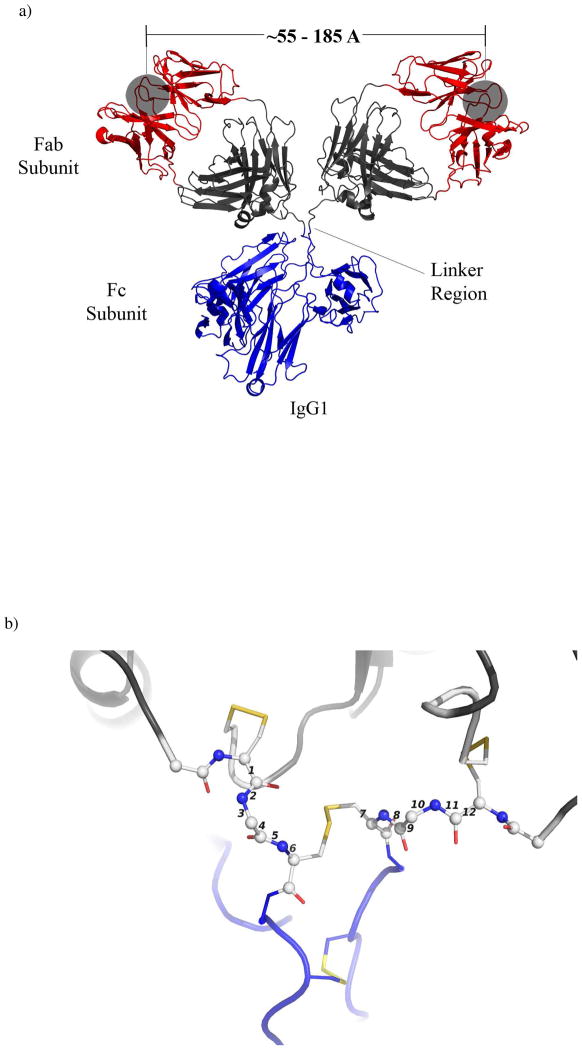
Antibodies (immunoglobulins) are one of the most important elements of recognition in the immune system of vertebrates: antibodies recognize non-self antigens.⁴ Antibodies exist in five major classes, grouped by their primary structure: bivalent (IgD, IgE, and IgG), tetravalent (IgA), or decavalent (IgM). Immunoglubulin G (IgG) is the most common class of antibody found in human serum; ~75% of all antibodies in serum are IgGs.⁵ The structure of an IgG (~152 kDa protein) comprises three globular subunits — two identical Fab subunits and one Fc subunit — with the Fab and Fc moieties joined by flexible linkers (Figure 1). In IgG, this linker consists of four amino acids with eight rotatable bonds (Figure 1b). The Fab subunits (~ 50 kDa each) present the domains that bind the antigen — typically a small molecule ligand, or a sequence of amino acids (an epitope) present in a protein or peptide. The Fc subunit (~ 50 kDa) can be recognized by receptors on the exteriors of B- and T-cells of the immune system; these elements provide a “bridge” between the binding of ligands to the Fabs and the activation of B- and T-cells.

Figure 1.

A monoclonal murine IgG1 specific for phenolbarbital showing subunits and key distances (the ribbon diagram was generated using PyMol and the atomic coordinates: PDB 1IGY). a) The subunits are depicted by color – blue represents the Fc subunit, red and black represent the Fab, with the red ribbons depicting the binding pocket of the antibody (grey shaded region). The open circles designate the opening to the antigen binding sites. b) Expanded view of the linker region. Spheres represent atoms and sticks represent bonds between atoms. Disulfide bonds between Cys residues appear as yellow sticks. Numbers indicate the rotatable bonds.

Crystal structures and measurements in solution suggest that distances between the two Fab binding sites ranging from ~5.5 nm to ~18.5 nm are accessible.^{6, 7} This distance varies, probably with little energetic penalty, because the linker (or hinge) region between the Fab and Fc regions is flexible. Wilson and coworkers have performed detailed studies on the structure of antibodies, and have characterized the linker region as “more like a loose tether than door hinges”.⁷

Many biological functions of the Fab and Fc subunits are known, but it is unclear, quantitatively, what advantage the particular arrangement of two Fab’s and one Fc, connected by a flexible linker, affords in binding to multivalent antigens. In particular, in understanding why IgG and similar proteins have the bivalent, tripartite structure that has given organisms with them a selective advantage, it would be useful to know the answers to three questions: i) How do size, rigidity, and flexibility of the Fab and Fc subunits influence their binding to antigens (particularly when displayed on the surfaces of cells and viruses)? ii) What is the importance of the location, structure, and flexibility of the linker that joins Fab to Fc? iii) How does the bivalency of the system relate to the kinetics and thermodynamics of association with, and dissociation from, the antigen?

Monoclonal antibodies are themselves difficult subjects for biophysical studies because they are difficult to obtain in the variety needed for physical biochemistry, can be expensive, and are not generally available in large quantities. The antibodies most suitable for biophysical studies are not necessarily the antibodies prepared in the largest quantities. As a consequence, techniques such as isothermal titration calorimetry (ITC)—one of the most powerful techniques for studying binding—cannot be readily applied to the study of binding of antibodies, since ITC typically requires 0.5 to 1.0 milligrams of protein per experiment.⁸ Further, it is impractical to make large changes to the structure of the Fab, Fc, and linker regions using the techniques of molecular biology. We wished to design a bivalent biochemical system in which the important structural components were under our synthetic control, and in which a synthetic route could yield milligram quantities of bivalent protein.

Bivalent Dimers of Carbonic Anhydrase as a Model of Bivalency in Proteins

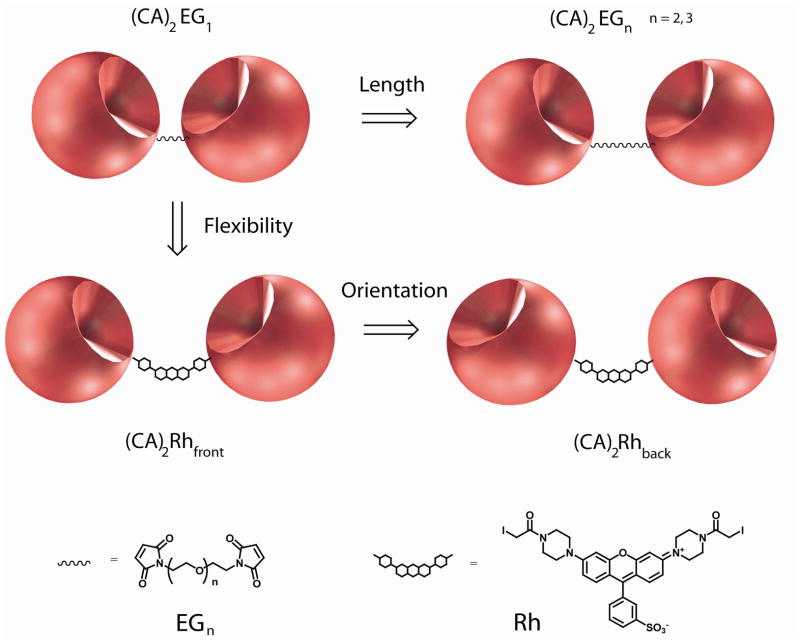
As a first approximation, and to work out techniques, we developed covalent dimers of human carbonic anhydrase (CA)₂ to study the structural features of bivalent proteins that relate structure and free energy of monovalent binding to the free energy of bivalent binding (Figure 2). This model system has six useful characteristics: i) Both CA and the Fab regions of IgG are similar in size (~ 30 kDa for HCAII and ~50 kDa for the Fab of IgG). Binding of ligands to the two systems might therefore be expected to be similar, although the active site in CA is probably more buried than the binding site in a typical antibody. ii) It is possible to omit or to include the equivalent of an “Fc” subunit in synthetic dimers of CA. In these initial studies, we chose to omit an equivalent of the Fc from the dimers for simplicity, and to provide a baseline value for bivalent avidity. iii) The linker region that joins the two Fab subunits to the Fc subunit in an antibody is a peptide. The linker in synthetic dimers of CA can be any of a large number of classes of compounds. Here, we have selected as cross-linkers either oligoethylene glycol (EG, a flexible linker) or rhodamine (a more rigid one) (Figure 2). The range of distances accessible between the binding sites and the flexibility of the linker are, in principle, larger for synthetic dimers of CA than for antibodies. iv) It is easy to change the point of attachment of the linker to CA by site-specific mutagenesis to introduce a cysteine in the desired location. v) The strategy used to prepare dimers of CA should be applicable to many other monomeric proteins, and thus lead into a large family of semi-synthetic, covalently linked protein dimers. vi) The interaction between CA and sulfonamides is extensively characterized; this background makes this system particularly suitable for biophysical studies.⁹

Figure 2.

Cartoon models of synthetic dimers of human carbonic anhydrase II showing the relationship between flexibility and orientation of the linker. (CA)₂EG_n contain a flexible linker comprising ethylene-glycol and (CA)₂Rh_front and (CA)₂Rh_back contain a rigid rhodamine linker.

The CA-Sulfonamide Interaction

Carbonic anhydrase binds a wide range of substituted sulfonamides with dissociation constants in solution (K_d^soln) in the range of micromolar to picomolar (Scheme 1a).⁹ Arylsulfonamides—of which 1 and 2 (Chart 1) are representative examples—bind to CA by coordination of the sulfonamide (-SO₂NH₂) moiety as an anion (-SO₂NH⁻) to the Zn^II ion located in the active site, and association of the aromatic ring with the hydrophobic “shell” of the binding site. The structure and thermodynamics of this conserved interaction have been characterized using a variety of experimental techniques, including crystallography, spectroscopy, calorimetry, and surface plasmon resonance.⁹ Typical values for the enthalpy of binding in solution (ΔH°_soln) are in the range of −6 to −12 kcal mol⁻¹; typically values for the entropy of binding in solution (−TΔS° _soln) are in the range of +3 to − 3 kcal mol⁻¹.

Chart 1.

Monomeric CA Binding to Ligands Covalently Attached to Surfaces

Mrksich et al. demonstrated that bovine CA (BCA) adsorbs specifically to mixed SAMs presenting para-substituted benzenesulfonamide ligands (2) at an interface composed otherwise of tri(ethylene glycol) groups (3) (Chart 1).¹⁰ This particular group of mixed SAMs has two properties: i) they resist nonspecific adsorption of CA, and ii) they present the sulfonamide portion of 2 in a form that allows it to bind to the active site of CA (Figure 3). For this study, the mixed SAMs were prepared by the common-intermediate method described by Lahiri et al.¹¹ Benzensulfonamide 1 was coupled to the carboxylic acid groups of a preformed SAM of thiols 3 and 4 through an activated ester to obtain the benzenesulfonamide (2) tethered to the surface.

Figure 3.

Schematic drawing of CA bound the immobilized benzenesulfonamide (2) of a mixed SAM of 2 and 3. Benzenesulfonamides (indicated in the ball-and-stick representation) bind specifically to CA and ethylene-glycol resists the non-specific adsorption of proteins. The components of the figure are drawn to scale, and the conformations of the ethylene-glycol chains were arbitrarily assigned.

The binding of CA to a ligand (L*) tethered to a surface forms a protein-ligand complex bound to the surface (CA·L*, Scheme 1b). (We indicate species that are bound covalently to the surface of the SAM with an asterisk, *.) The rate of change of the surface density of CA·L* (d[CA·L*] / dt, units of moles area⁻¹ s⁻¹) depends on the concentrations of CA (in molar units) and L* (units of moles area⁻¹) and the rate constants for the intermolecular association (k_on^surf, M⁻¹ s⁻¹) and dissociation (k_off^surf, s⁻¹) (eq 1). This treatment assumes that mass transport does not limit the rates of association

$$\frac{d[\text{CA}·\text{L}\ast ]}{d\text{t}}={k_{\text{on}}}^{\text{surf}}[\text{CA}][\text{L}\ast ]-{k_{\text{off}}}^{\text{surf}}[\text{CA}·\text{L}\ast ]$$ (1)

and dissociation.^{12, 13} At equilibrium, [CA·L*] does not change with time (i.e., d[CA·L*] / d t = 0), and the rate at which CA associates with L* equals the rate at which CA·L* dissociates to form CA and L*. The affinity of this monovalent interaction (K_d^surf, M) is the ratio of k_off^surf, to k_on^surf and it provides a measure of the strength of the association between CA and L* (eq 2).

$${K_{\text{d}}}^{\text{surf}}=\frac{{k_{\text{off}}}^{\text{surf}}}{{k_{\text{on}}}^{\text{surf}}}=\frac{[\text{CA}][\text{L}\ast ]}{[\text{CA}·\text{L}\ast ]}$$ (2)

At equilibrium, K_d^surf can be interpreted as the concentration of CA at which half of the laterally non-interacting sulfonamides on a surface would be bound by CA. Equation 3 gives the change in the free energy corresponding to the association of CA to L*. At the low mol fractions of

$${\mathrm{\Delta }\text{G}°}_{\text{surf}}=\text{RT}ln({K_{\text{d}}}^{\text{surf}})$$ (3)

benzenesulfonamide (2) used by Mrksich et al. to prepare mixed SAMs (χ = 0.05), the adsorption of bovine CA (BCA) was ~90% reversible, and the rate constants reported for binding of BCA were k_on^surf = 1.9 × 10⁴ M⁻¹ s⁻¹, k_off^surf = 5.4 × 10⁻³ s⁻¹; these values give a monovalent affinity K_d^surf = 2.6 × 10⁻⁷ M (Table 1); the value of K_d^soln for a corresponding ligand in solution is 5 × 10⁻⁸ M. These values are similar to those reported by Lahiri et al. for the binding of BCA to mixed SAMs of 2 and 3 (χ = 0.02) (Table 1).^{11, 14}

Table 1.

Rate constants (k), dissociation constants (K_d), and free energies (ΔG°) for the association and dissociation of CA and (CA)₂’s to benzensulfonamide 1 in solution and SAMs of 2 and 3 as determined with SPR. This table also contains entries from the literature.

protein	ligand	kon′ surf(104 M−1 s−1) a	koff′ surf (10−3 s−1) a	koffavidity, surf (104 s−1)b	A / (A +B)c	ΔG°′surf, kcal mol−1	Kd′ surf, nM	ΔG°avidity, surf, kcal mol−1	Kdavidity, surf, nM	Enhancement (Kdsurf / Kdavidity surf)	Ref
HCAII (C206S,K133C)	1 solution	--	--	--	--	−10.6 ± 0.1d	15d	--	--	--
HCAII (C206S,K133C)	6 solution	--	--	--	--	−13.2 ± 0.1d	0.2d	--	--	--
BCA	2	1.9 e	5.4 e	--	--	−9.0 e	260 e	--	--	--	Mrskich, 1995
BCA	2	3.5 e	5.3 e	--	--	−9.3 e	150 e	--	--	--	Lahiri, 1999a
BCA	2	0.9 e	5.4 e	--	--	−8.5 e	560 e	--	--	--	Lahiri, 1999b
HCAII (C206S,K133C)	2	5.6 ± 0.6 e	5.0 ± 0.7 e	--	--	−9.6 ± 0.2 e	89 e	--	--	--
HCAII (C206S,E187C)	2	5.6 ± 0.8 e	4.8 ± 0.5 e	--	--	−9.6 ± 0.2 e	86 e	--	--	--
(CA)2EG1	2	3.4 ± 0.6	5.5 ± 0.6	1.2 ± 0.1	0.14 ± 0.05	−9.3 ± 0.1	160	−11.9 ± 0.1	1.8	50 ± 14
(CA)2EG2	2	3.8 ± 0.8	5.3 ± 0.8	1.3 ± 0.4	0.15 ± 0.04	−9.4 ± 0.2	140	−12.0 ± 0.2	1.7	50 ± 20
(CA)2EG3	2	3.9 ± 0.6	5.7 ± 0.5	1.2 ± 0.3	0.13 ± 0.04	−9.3 ± 0.1	150	−12.0 ± 0.2	1.5	60 ± 20
(CA)2Rhfront	2	2.2 ± 0.8	4.5 ± 0.3	1.0 ± 0.4	0.11 ± 0.03	−9.1 ± 0.1	200	−11.8 ± 0.3	2.2	40 ± 20
(CA)2Rhback	2	6.5 ± 1.0	5.0 ± 0.4	3.0 ± 0.2	0.12 ± 0.02	−9.7 ± 0.1	78	−11.8 ± 0.1	2.3	37 ± 9

^ak_on′ ^surf and k_off ′ ^surf corresponds to the average of three independent experiments. k_off′ ^surf determined from fitting eq 11 to the sensorgrams with 221 μM ethoxzolamide. The errors correspond to 90% confidence intervals according to t-statistics.

^bk_off^{avidity, surf} corresponds to the average of three independent experiments determined from fitting eq 12 to the sensorgrams with 0 μM ethoxzolamide. The errors in k_off^avidity correspond to 90% confidence intervals according to t-statistics.

^cThe fraction of protein bound monovalently to the SAM is given by the ratio of the pre-exponential factors A and B obtained from non-linear curve fitting of eq 12 to the dissociation phase of the sensorgrams.

^dThese values correspond to binding of monovalent CAs to ligands in solution; K_d^soln, and ΔG°_soln.

^eThese values correspond to binding of monovalent CAs to the SAM; k_on^surf, k_off^surf, K_d^surf, and ΔG°_surf according to eq 1, 2, and 3.

Intramolecular Binding of a Tethered Ligand-CA System

In separate studies aimed at understanding intramolecular interactions, we characterized the thermodynamics of binding for the association between the active site of HCA and an arylsulfonamide ligand that was covalently tethered to the surface of HCA by oligo(ethylene glycol) linkers of different length 5 (EG_n, n = 0, 2, 5, 10, and 20; Chart1 and Scheme 1c).¹⁵ In that system, the relationship between the intramolecular dissociation constant (K_d^intra) and the length of the flexible linker was quantitatively well-explained by a model that describes the linker as a random-coil polymer. We inferred from calorimetric studies that the length of the linker—in the range of 0.5 to 2.6 nm (rms distances)—influences the thermodynamics of binding exclusively entropically. In the work we describe in the current paper, we employ crosslinkers of EG and crosslinkers of rhodamine to connect the monomers of CA to form dimers of CA.

Multivalent Interactions in Protein-Ligand Systems

Multivalency is associated, in biochemistry, with a number of mechanisms for the control of biological processes that do not exist in monovalent systems: “tighter binding” and “clustering of ligands” are among these mechanisms, although the thermodynamic basis of neither is completely understood.^{2, 16, 17} Examples of multivalent interactions in biology include antibody-antigen associations, interactions of some multi-subunit toxins (shiga toxin, shiga-like toxin, cholera toxin) with their target cells, and interactions of certain classes of cell-surface receptors with their cytokines.^18–21 Bivalent interactions, a subset of multivalent interactions, are those that involve the binding of a bivalent receptor to multivalent ligands, or to a surface presenting multiple monovalent ligands. Bivalency is the simplest example of multivalency, and the type used predominantly in pharmaceutical chemistry.²²

The thermodynamics of the interaction of antibodies with ligands tethered to (or embedded in) a surface has been the subject of a few experimental reports. Karush et al. measured the binding of polyclonal IgGs to viral particles that were covalently labeled with DNP (K_d = 10⁻⁷ M for monovalent DNP, K_d^apparent = 10⁻¹⁰ M for IgG) and found, assuming K_d^apparent = K_d^avidity, that antibodies bound approximately 1,000 more strongly to the virus than the Fab fragments.²³ Karulin and Dzantiev found that the bivalent affinity of polyclonal IgG’s to antigens on the surface of Bacillus sp. (K_d^avidity = 10⁻¹¹ M) was 110 times stronger than the monovalent Fab (K_d = 1.1 × 10⁻⁹ M).²⁴ Thompson et al. used total internal reflection fluorescence (TIRF) microscopy to measure the association of a monoclonal anti-dinitrophenyl (DNP) IgG (K_d^apparent = 3.3 × 10⁻⁷ M) and its Fab fragment (K_d = 3.2 × 10⁻⁶ M) to a supported phospholipid monolayer presenting DNP-conjugated phospholipids.²⁵ They found (assuming that K_d^apparent is equal to K_d^avidity) that the antibodies bound ~10 times more tightly to the DNP groups on a surface than did the monovalent Fab fragments. The Cremer group developed a microfluidic device in combination with TIRF microscopy to investigate the binding of polyclonal anti-DNP IgG antibodies and their Fabs to membranes of phospholipids containing DNP-conjugated lipids. They found that antibodies bound bivalently to ligands at the surface (K_d^apparent = 1.8 × 10⁻⁵ to 1.8 × 10⁻⁶ M) 3- to 30- times more strongly than did the monomeric Fab (K_d = 5 × 10⁻⁵ M), assuming that the range of K_d^apparent represented the range of K_d^avidity.26 The results of these studies suggest that IgG’s bind more strongly to ligands than the Fabs, and that the enhancement in binding is in the range from 10 to 1,000, but with unknown accuracy and variability with structure. Unfortunately, these studies do not resolve the question of whether this range represents typical values, or an idiosyncratic selection (with unquantified uncertainties).

In this paper, we focus on differences in free energy (ΔG°) of binding of CA and dimers of CA to ligands covalently tethered to a surface (Scheme 1); in subsequent papers we will examine ΔH° and −TΔS°. We used surface plasmon resonance (SPR), which measures the kinetics of association and dissociation of proteins on surfaces, to estimate the changes in free energies, because it is a well-established technique for studying multivalent interactions.²⁷ Scheme 1d diagrams the bivalent association and dissociation of (CA)₂’s to SAMs as a process that involves two steps—although, in principle, comparison of the thermodynamics of monovalent and bivalent binding does not require separate analysis of these steps. An equation analogous to equation 3 describes the equilibrium constant for the monovalent association of a bivalent receptor (CA)₂ to a ligand tethered to a surface (eq 4). A dimer of CA is statistically twice as likely to bind to a ligand

$${{K_{\text{d}}}^{\prime }}^{\text{surf}}=\frac{{{k_{\text{off}}}^{\prime }}^{\text{surf}}}{{{k_{\text{on}}}^{\prime }}^{\text{surf}}}=\frac{2[{(\text{CA})}_2][\text{L}\ast ]}{[{(\text{CA})}_2·\text{L}\ast ]}$$ (4)

as monomeric CA, because it possesses two binding sites; we include a factor of two in the numerator of equation 4.²⁸ The value of K_d′^surf determines the change in free energy for the monovalent binding of (CA)₂ to the surface (eq 5). CA and (CA)₂ have different molecular weights

$${\mathrm{\Delta }G°}^{\prime }=\text{RT}ln({{K_{\text{d}}}^{\prime }}^{\text{surf}})$$ (5)

and therefore different translational and rotational entropies in solution. One may expect the monovalent dissociation constants K_d^surf and K_d′^surf to be similar, but should not expect them to be identical.

Bivalent receptors can also form non-covalent bonds with the ligand-presenting surface in which the species (CA)₂·L* binds a second monovalent ligand (L*) tethered to the surface and forms (L*·(CA)₂·L*) (Scheme 1d). The change in the surface density of L*· (CA)₂·L* (units of moles area⁻¹) with time (d[L*· (CA)₂·L]* / dt) is determined by the surface densities of (CA)₂·L* and L*· (CA)₂·L*, and the rate constants for association (k_on ″ ^surf, s⁻¹ ) and dissociation, (k_off ″ ^surf, s⁻¹). At equilibrium (i.e., when d[L*· (CA)₂·L]*/d t = 0), K_d ″ ^surf is equal to the concentration of (CA)₂·L*; divided by twice the concentration of L*·(CA)₂·L* (eq 6). The corresponding change in the free

$${{K_{\text{d}}}^{″}}^{\text{surf}}=\frac{{{k_{\text{off}}}^{″}}^{\text{surf}}}{{{k_{\text{on}}}^{″}}^{\text{surf}}}=\frac{[{(\text{CA})}_2·\text{L}\ast ]}{2[\text{L}\ast ·{(\text{CA})}_2·\text{L}\ast ]}$$ (6)

energy for the binding is calculated from equation 7. The overall strength of association between

$${\mathrm{\Delta }G°}^{″}=\text{RT}ln({{K_{\text{d}}}^{″}}^{\text{surf}})$$ (7)

(CA)₂ and the ligands tethered to the surface is characterized by the avidity of this bivalent interaction (K_d^{avidity, surf}, M); the ratio of k_off^{avidity, surf} to k_on^{avidity, surf} (eq 8 and Scheme 1d). It follows from equations 3 and 7 that the change in the free energy for the formation of a complex of one

$${K_{\text{d}}}^{\text{avidity},\text{surf}}=\frac{{k_{\text{off}}}^{\text{avidity},\text{surf}}}{{k_{\text{on}}}^{\text{avidity},\text{surf}}}=\frac{[{(\text{CA})}_2][\text{L}\ast ]}{[\text{L}\ast ·{(\text{CA})}_2·\text{L}\ast ]}$$ (8)

(CA)₂ and two ligands (ΔG°_{avidity, surf}) is given by equation 9.

$${\mathrm{\Delta }G°}_{\text{avidity},\text{surf}}=\text{RT}ln({K_{\text{d}}}^{\text{avidity},\text{surf}})$$ (9)

We estimate—based on the size of CA (diameter ~ 2.1 nm), the packing of alkanethiols of the SAM (0.5 nm sulfur-to-sulfur), and a mol fraction of 0.02—that each (CA)₂ bound to the surface (that is, (CA)₂·L*)—has access, on average, to five ligands on the SAM. The Supporting Information details this calculation. We assume that the ligands are randomly distributed across the SAM, and that the distances between ligands on the SAM are, therefore, described by a distribution of distances with an average distance between ligands. It is likely that the rates of dissociation we measure for dimers by SPR are average rates of dissociation and, as a result, the rate constant k_off^{avidity, surf} represents an average of rate constants for dimers dissociating from ligands on the surface.

Equations 2, 4, 6, and 8 are true when the thermodynamic activities of (CA)₂ and L* equal their concentrations or surface densities. This assumption is often not valid for concentrated solutions and for molecules closely packed on a surface. We employed conditions—low concentrations of receptors (nM) and low densities of ligands on the surface (the mol fraction of 2 was χ = 0.02)—that minimized lateral interactions between the receptors bound to surfaces and that allowed us to assume that the concentrations of the proteins equal their activities.¹⁴

The enhancement (β) is the ratio of the monovalent dissociation constant to the avidity and describes the increase in the strength of binding of (CA)₂ over that of CA (eq 10). Values of β > 1

$$\beta =\frac{{K_{\text{d}}}^{\text{surf}}}{{K_{\text{d}}}^{\text{avidity},\text{surf}}}$$ (10)

indicate that (CA)₂ binds to ligands on the surface more strongly than does CA.

Experimental Design

We wanted to estimate values of ΔG°_{avidity, surf} because comparison of this parameter with ΔG°_surf describes the energetic consequence of tethering together receptors. In particular, we wanted to determine whether ΔG°_{avidity, surf} depended on the length or rigidity of the linker, or on the geometric presentation of the binding sites of the dimer.

We prepared five synthetic dimers of CA from two double mutants of HCAII (collectively referred to as CA’s) and used the system of dimers and SAMs presenting benzenesulfonamides to explore the thermodynamics of bivalent binding. These synthetic dimers are particularly well-suited to study the free energies of association for at least four reasons: i) HCAII is an exceptionally stable, monomeric protein, and many mutants of it are also very stable.²⁹ ii) Wild-type HCAII and its mutants are available by overexpression in E.coli (~30 mg / L of culture).^{29, 30} iii) The structure of HCAII has been well-characterized by X-ray crystallography, and the protein has been characterized extensively in numerous biophysical assays (i.e., capillary electrophoresis, calorimetry, circular dichroism, and other methods).⁹ iv) Many arylsulfonamides bind to the active site of HCAII, and synthetic manipulation of these sulfonamides is practical.⁹

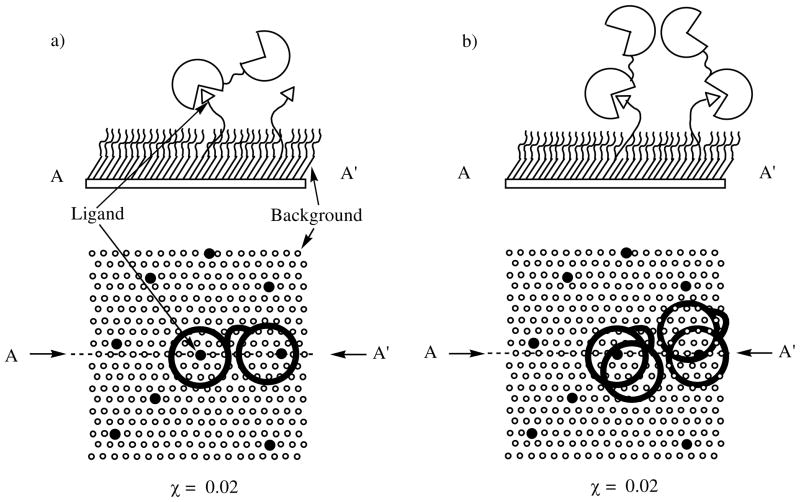
We used SPR to characterize the kinetics of binding of the mono- and dimeric CA’s to SAMs presenting arylsulfonamides. SAMs of alkanethiolates are easy to prepare and to functionalize with arylsulfonamides,³¹ and the binding of proteins to SAMs is subject to fewer mass-transport limitations than those inherent in the use of dextran gels.¹¹ The density of arylsulfonamides in SAMs can be varied easily, although we have not done so in this work. We assume the mole fraction of benzenesulfonamide ligands in the SAM is the mole fraction of benzenesulfonamide ligands in the solution from which it is prepared. To minimize lateral interactions, we did not saturate the SAMs with dimers during our SPR experiments (Figure 4).

Figure 4.

Schematics showing (CA)₂ bound to mixed SAMs presenting arylsulfonamide ligands 2 (triangles and solid circles) in a background of ethylene-glycol 3 (open circles). a) Cross section and top-down view of a mixed SAM (χ = 0.02) with a dimer of CA bound to one benzenesulfonamide. The probability that two dimers bound to the surface will touch one another will be minimal when the density of dimers bound to the surface is much lower than the total surface density of ligands (moles area⁻¹). b) Cross section and top-down view of a mixed SAM (χ = 0.02) with two dimers of CA bound to ligands which are close to one another. The probability that two dimers will touch increases as the density of dimers bound to the surface approaches the total density of benzenesulfonamides.

The rates of association and dissociation that determine K_d ^{avidity, surf} are not directly observable by SPR. The SPR instrument measures the change in refractive index near the SAM; the change in the refractive index is proportional to the change in the total amount of protein near the SAM and not the type of species bound to the surface. A (CA)₂ dimer bound to the surface as (CA)₂·L* provides the same change in the refractive index as L*· (CA)₂·L* and as a result, (CA)₂·L* and L*· (CA)₂·L* are indistinguishable to an SPR instrument. We reasoned that we could estimate the value of K_d^{avidity, surf} by measuring the rates of dissociation of (CA)₂ from the SAMs in the presence and absence of the soluble, monovalent inhibitor ethoxzolamide, which competes with L* for the binding sites of the dimers. We developed an assay that comprises four steps: i) We measured the rates of association and dissociation of monovalent CA binding to mixed SAMs of 2 and 3 by SPR. ii) We determined the dissociation constant of (CA)₂·L*—that is K_d′ ^surf—from the sensorgrams of dimers unbinding from the SAM in the presence of a high concentration of ethoxzolamide. iii) We determined the dissociation constant of L*· (CA)₂·L* to form (CA)₂·L*, that is K_d″ ^surf, from the sensorgrams of dimers unbinding from the SAM in the absence of ethoxzolamide. iv) We calculated the avidity of the system (K_d^{avidity, surf}) using the experimentally determined values of K_d′ ^surf and K_d″ ^surf.

Results and Discussion

Synthesis and Characterization of dimers of CA

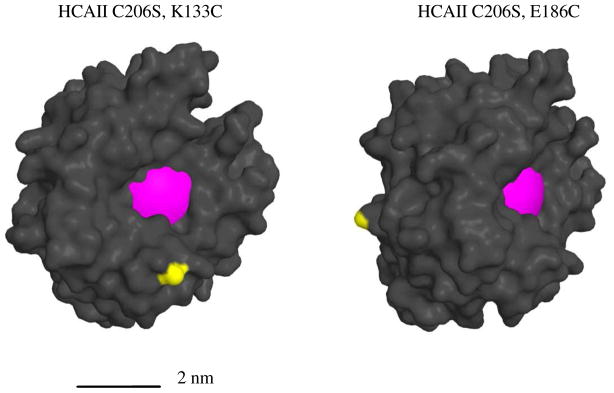
We prepared dimers starting from double mutants of human carbonic anhydrase II. We previously described one of the double mutants of HCAII that we use here to construct several dimers, HCAII(C206S, K133C).¹⁵ Briefly, we mutated Lys-133, which is located near but outside the active site in wild-type HCAII, to a cysteine. This cysteine provides a reactive thiol, which can be used for thiol-selective coupling. We mutated the wild-type cysteine at position 206 to a serine to preclude a side reactions leading to a mixture of coupling sites. The other double mutant, HCAII(C206S, E187C), has the reactive thiol located opposite to the active site and on the surface of the protein (Figure 5).

Figure 5.

Molecular models of double mutants HCAII(C206S, K133C) and HCAII(C206S, E187C). The magenta surface indicates the binding pocket and the yellow surface represents the sulfur atom of the Cys residue introduced by mutation. The surface diagrams were modeled from a high-resolution structure of HCAII (PDB ID: 2ILI). The two proteins are shown from different perspective.

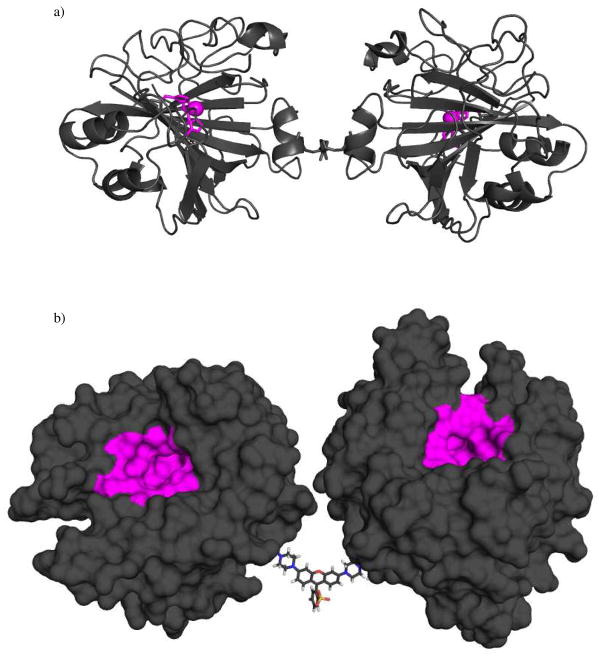
We conjugated two double mutants of HCAII using commercially available cross-linkers: i) flexible cross-linkers of bis-maleimides with ethylene-glycol linkers (EG₁, EG₂, and EG₃), and ii) a more rigid cross-linker of bis-α iodo-rhodamine (Rh) (Figures 2). Although the EG₁ crosslinker does not contain -OCH₂CH₂O- (an ethylene glycol unit), we employ the EG nomenclature for simplicity. Isothermal titration calorimetry (ITC) revealed a stoichiometry of binding of acetazolamide (a ligand that binds to monomeric CA, K_d^inter = 25 nM with a stoichiometry of one mole of protein to one mole of ligand) of 1.9 acetazolamides per (CA)₂ (or 0.95 ± 0.5 acetazolamides per active site). This result indicated that both binding sites of (CA)₂ were active. X-ray crystallography confirmed that the structure of the monomers was intact (Figure 6a) (Data not shown).

Figure 6.

a) X-ray crystal structure of (CA₂)EG₁. (CA₂)EG₁ is depicted as a grey-colored ribbon diagram with the Zn²⁺ ions and three coordinating histidine residues comprising the active sites rendered as a magenta sphere and sticks, respectively. b) Surface rendering of a model of (CA)₂Rh_back. The model represents an idealized structure built from the crystal structure of native CA and from the minimum energy structure of rhodamine. To provide the pose presented here, the rotatable bonds in the linker region were adjusted to allow the active sites of the CA monomers (indicated with magenta surfaces) to point in the same direction.

We modeled the structure of (CA)₂Rh_back using the crystal structure of native HCA and the structure of the rhodamine crosslinker: we converted E187 to a cysteine by deleting the atoms of the carbonyl and Δ-carbon, and created a single bond between the γ and the acetamide of the linker. To demonstrate that the active sites of this dimer could, in principle, simultaneously interact with the surface, we adjusted the rotatable bonds of the linker to point the active sites of the monomers in the same direction (Figure 6b).

Preparation of Mixed Self-Assembled Monolayers (SAMs) for SPR

In our previous work, Mrskich et al. described the combination of SPR and mixed SAMs presenting benzenesulfonamides to measure the binding of bovine carbonic anhydrase (BCA) to surfaces,¹⁰ and Lahiri et al. described an improved method for the preparation of SAMs that present benzenesulfonamides and characterized the binding of HCAII to these surfaces.¹¹ For the current study, we prepared mixed SAMs of ethylene-glycol-terminated alkanethiolate 3 and benzenesulfonamide 2 in which χ = 0.02, according to the procedure of Lahiri et al. (Chart 1).¹¹ We performed no additional characterization of the surfaces.

An SPR-based assay to study the binding of (CA)₂ to SAMs

The following discussion describes the SPR experiments we developed to estimate values of ΔG°_surf, ΔG° _{avidity, surf}, and the enhancement (β). We refer, here, to the interval of time when protein is allowed to adsorb to the SAM as the “association phase” and the interval of time when the protein desorbs from the surface as the “dissociation phase”.

(1) CA binding to SAMs

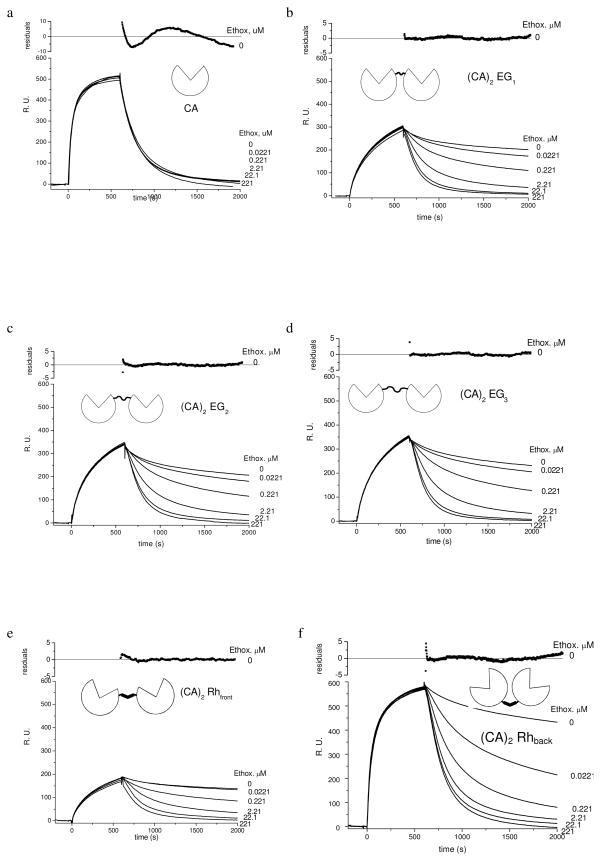
We exposed SAMs of 2 and 3 (χ = 0.02) to a solution of CA (438 nM) for 10 min (association phase) followed by buffer or a solution of the inhibitor ethoxzolamide in buffer—at concentrations ranging from 0.0221 to 221 μM—for 25 min (dissociation phase). The presence of ethoxzolamide (Figure 7a) did not affect the rate of dissociation of CA from the SAMs—differences between the sensorgrams at different concentrations of ethoxzolamide are smaller than the variations obtained from repetitions of the experiment (experimental error). A rate of dissociation that is independent of the concentration of ethoxzolamide is consistent with a mechanism for the dissociation that involves a single dissociation event of the monovalent CA from the SAM (Scheme 1b)—in other words, the result indicates that once CA dissociates from the SAM, it does not rebind.

Figure 7.

Sensorgrams of HCAII(C206S, K133C) (438 nM) and (CA)₂’s (219 nM) binding to SAMs presenting arylsulfonamides 2 (χ = 0.02) obtained with surface plasmon resonance (SPR). (CA)₂EG_n contain a flexible linker comprising ethylene-glycol and (CA)₂Rh_front and (CA)₂Rh_back contain a rigid rhodamine linker. These sensorgrams show the three phases of each experiment: i) equilibration of the surface of the surface with buffer, ii) association of the protein with the surface, and iii) dissociation in the absence (0 μM) or the presence of ethoxzolamide (an inhibitor for CA, K_d^ethox = 0.0002 μM). These data have been corrected for changes in the bulk refractive index that occur due to protein in the solution that is not bound to the surface. The residuals for CA correspond to fitting a single exponential function (eq 11) to the sensorgrams with 0 μM of ethoxzolamide and show ~5% deviation of the model from the data. The residuals for (CA)₂’s correspond to fitting a double exponential function (eq 12) to the sensorgrams with 0 μM and show < 5% deviation of the model from the data ethoxzolamide.

We estimated the rate constants for the reversible binding of double mutants of CA to SAMs presenting benzenesulfonamides following the procedure of Lahiri et al.¹⁴ Briefly, integrating equation 1 with d[CA · L*] d t ≈ –k_off^surf[CA·L*] (in agreement with the result that CA does not rebind to the SAM) and replacing [CA·L*] by the reading of the SPR (measured in response units, R.U.) yields equation 11. We used non-linear curve-fitting of the single exponential function (eq 11) to the dissociation phase of sensorgrams (Figure 7a) with the pre-exponential factor A and the rate constant k_off^surf as the only adjustable parameters. R.U._t (in response units) is the signal recorded

$${\text{R}.\text{U}.}_{\text{t}}=\text{A}{e}^{-{{\text{k}}_{\text{off}}}^{\text{surf}}(\text{t}-{{\text{t}}_0}^{\text{diss}})}$$ (11)

by the instrument at time t (Figure 7a) where t corresponds to the time on the horizontal axis and t₀^diss is the time at the beginning of the dissociation phase. The variations of roughly 10% seen in Figure 7a are less than the error of 14% in the value of k_off^surf obtained from repeating the experiment three times (Table 1). We estimated k_off^surf for HCAII(C206S, K133C) (438 nM) and a SAM of 2 and 3 (χ = 0.02) to be (5.0 ± 0.7) × 10⁻³ s⁻¹, a value that was indistinguishable from that measured by Lahiri et al. for wild type BCAII.

We estimated a value of (5.6 ± 0.6) × 10⁴ M⁻¹ s⁻¹ for k_on^surf using the procedure of Lahiri et al.¹⁴ Briefly, we estimated the value of k_on^surf by measuring d[CA·L*] / d t at several values of [CA]. (Other assumptions might be possible, but the assumption of two states is the simplest and provides good fits of experiment to theory.) The values of k_on^surf and k_off^surf estimate K_d^surf = 89 ± 20 nM by equation 2; this dissociation constant is indistinguishable from that measured by Lahiri et al. for the wild type BCAII and only slightly less favorable than the association in solution K_d^soln = 15 nM for the closely related sulfonamide 1 (Chart 1). In analogous experiments involving HCAII(C206S, E187C), we determined values for k_off^surf (4.8 ± 0.5) × 10⁻³ s⁻¹ and K_d^surf (86 ± 15 nM), which are indistinguishable from those of HCAII(C206S, K133C) (Table 1).

(2) (CA)₂’s dissociate rapidly from SAMs in the presence of high concentrations of ethoxzolamide

We caused dilute solutions of the (CA)₂’s (219 nM in 10 mM PBS) to flow over SAMs of 2 and 3 (χ = 0.02). Solutions of (CA)₂ were followed by a solution of ethoxzolamide in buffer (Figure 7b – f). We included ethoxzolamide only during the dissociation phase because inclusion of ethoxzolamide throughout the course of experiments prevents the association of (CA)₂ with the SAM.

The rates of dissociation of dimers from the SAM increase as the concentration of ethoxzolamide increases, and the rates approach an asymptotic value at the highest concentrations of ethoxzolamide (Figure 7b–f). We attribute this observation to evidence that dimers bind bivalently to the SAM. We propose a mechanism consisting of several steps for dimers to dissociate from the SAM in the presence of ethoxzolamide (Scheme 2). Ethoxzolamide competes with L* for the open binding site of (CA)₂·L*. Hence, as the concentration of ethoxzolamide increases, the rate at which ethoxzolamide binds to the open binding site of (CA)₂·L* (characterized by k_on^ethox [ethox], Scheme 2) becomes larger than the rate of L* binding to the open binding site of (CA)₂·L* (characterized by k_on″ ^surf) increasing the apparent rate of dissociation. When the product (k_on^ethox·[ethox]) is much larger than k_on″ ^surf, rebinding of (CA)₂·L* to form L*·(CA)₂·L* is prevented—i.e., d[(CA)₂·L*]/d t ≈ k_off′ ^surf[(CA)₂·L*] and the dimer rapidly dissociates from the surface. We estimated values for the rate constant of dissociation at the highest concentration of ethoxzolamide (in this case ~221 μM) using the same method we used for monomeric CA: we fit a single exponential function (eq 11 with k_off′ ^surf substituting k_off ^surf) to the sensorgrams with 221 μM ethoxzolamide (Table 1). Values of k_off′ ^surf (~ 5 × 10⁻³ s⁻¹) are indistinguishable from the value of k_off^surf that we determined for the dissociation of monovalent CA ((5.0 ± 0.9) × 10⁻³ s⁻¹). This result suggests that, at high concentrations of ethoxzolamide, the monovalent dissociation of (CA)₂·L* to form (CA)₂ and L* is the rate-limiting step for dissociation of (CA)₂ from the SAMs. This conclusion is only true when the dissociated dimer does not rebind to the SAM, which is the behavior we observed for monomeric CA (Figure 7a).

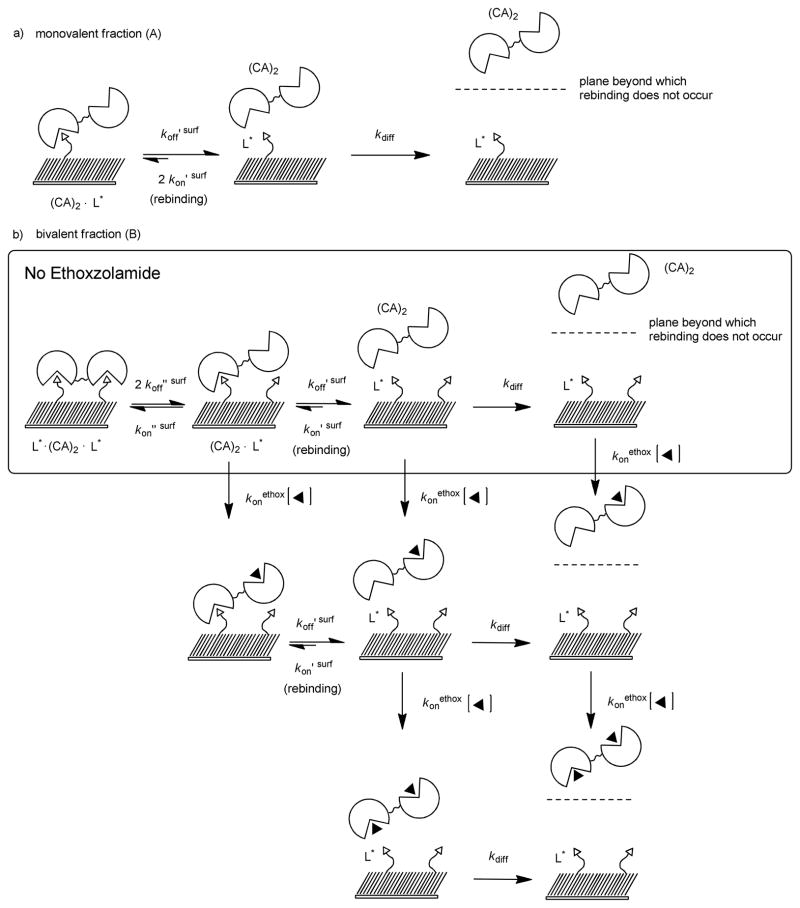
Scheme 2.

Thermodynamic schemes describing the dissociation of dimers of CA—bound monovalently and bivalently—from surfaces presenting benzensulfonamides (L*) in the absence and presence of ethoxzolamide (◂). a) The rate of dissociation of (CA)₂ bound to a single L* is characterized by rate constant k_off ′ ^surf. Once dissociated, (CA)₂ near the surface can rebind to L* or diffuse away from the surface with a rate characterized by rate constant k_diff. b) A binding site of L*·(CA)₂·L* can dissociate from one L* with a rate characterized by rate constant 2 k_off″ ^surf. (CA)₂·L* can rebind to L* (k_on″ ^surf) forming L*· (CA)₂·L* or the second binding site can dissociate from L* with a rate characterized by k_off′ ^surf. In the presence of ethoxzolamide the open binding site of (CA)₂·L* can bind a molecule of ethoxzolamide preventing the formation of L*· (CA)₂·L* and leading, ultimately, to (CA)₂ in solution associated with one or two molecules of ethoxzolamide.

We estimated values of k_on′ ^surf for dimers in the same way we did for monomeric CA. After determining the values of k_on′ ^surf and k_off′ ^surf for each dimer, we calculated K_d′ ^surf using equation 2. The values of ΔG° ′ ^surf are similar to each other and indistinguishable from those of monovalent CA (−9.6 kcal mol⁻¹) (Table 1).

(3) (CA)₂’s dissociate slowly from SAMs in the absence of ethoxzolamide

We delivered solutions of (CA)₂’s (219-nM solutions) over SAMs of 1 and 4 ( χ = 0.02) and allowed the dimers to associate with the SAM. The dissociation phase was triggered by exposing the surface to buffer lacking (CA)₂ (curves labeled 0 μM in Figures 7b–f). In the absence of ethoxzolamide the rates of dissociation of dimers from the SAM were slower than the rate of dissociation for CA from the surface under analogous conditions (curve labeled 0 μM in Figure 7a). The dissociation phase of dimers in the absence of ethoxzolamide was described poorly (R² < 0.9) by a single exponential function—equation 11. We estimated values for k_off^{avidity surf} from fitting a biexponential function (eq 12) to the dissociation phase of the 0 μM curves, using A, B, and k_off ^{avidity surf} as the three adjustable parameters, and substituting k_off′ ^surf by the values determined previously for each dimer (section (2)). This curve-fitting procedure provided values of R² between 0.92 and 0.96, suggesting

$${\text{R}.\text{U}.}_{\text{t}}=\text{A}{\text{e}}^{-{{{\text{k}}_{\text{off}}}^{\prime }}^{\text{surf}}(\text{t}-{\text{t}}_0)}+\text{B}{\text{e}}^{-{{\text{k}}_{\text{off}}}^{\text{avidity}\text{surf}}(\text{t}-{\text{t}}_0)}$$ (12)

that the dissociation of all dimers is adequately described by equation 12; plots of the residuals of the least-squares fit appear in the upper section of each panel in Figure 7 and show less than 5% deviation between equation 12 and the ‘0-μM’ data.

Fitting the dissociation phase of the 0 μM curves to equation 12 assumes that two distinct populations of dimer are bound to the surface. We suggest that the first exponential A e^{−k_off′surf(t-t₀)} plausibly corresponds to the fraction of protein that is bound monovalently to the surface—that is, (CA)₂·L*. It is unlikely the solutions contained monomeric CA, or dimers with a single defective binding site, as the solutions were exhaustively purified by size-exclusion chromatography, and ~95% of the binding sites of (CA)₂ are active as judged by ITC. This fraction of protein represents, we presume, dimers bound to an area of the SAM with only one ligand accessible for any of several reasons: i) blocking of some ligands by dimers that are bivalently bound to the surface, ii) defects (e.g., at grain boundaries in the gold layer) in the SAMs, and iii) heterogeneously distributed distances between the ligands on the surface. This assumption is consistent with the observation that the rate of dissociation is rapid (Figure 7, panels b–f) at high concentrations of ethoxzolamide. The population of dimers that dissociate quickly is bound monovalently to the surface and not capable of bivalent binding.

Once the monovalently bound dimer dissociates from the ligand it diffuses through a stationary boundary layer into a moving stream of buffer and is not able to rebind to the surface (Scheme 2a). The fraction of monovalently bound protein represents at most 15 % of the total protein on the surface as judged by the ratio of pre-exponential factors A / (A + B) (Table 1).

The second term in equation 12, B e^{−k_offavidity surf(t-t₀)}, corresponds to a fraction of (CA)₂ that dissociates more slowly than the monovalently bound fraction; we assume that this fraction of protein corresponds to bivalently bound dimer, L*·(CA)₂·L*. We propose a step-wise mechanism to describe the dissociation of L*· (CA)₂·L* from the surface in the absence of ethoxzolamide (Scheme 2b). Dissociation of (CA)₂ begins with one binding site of L*·(CA)₂·L* dissociating to form (CA)₂·L*, which can then either rebind to L* to form L*·(CA)₂·L*, or the second binding site of (CA)₂·L* can dissociate from the SAM yielding (CA)₂ in solution. We assumed that after dissociating from the SAM, (CA)₂ rarely (if ever) rebinds: d[(CA)₂]/d t ≈ k_off′^surf[(CA)₂· L]*; this assumption is in agreement with the experiments using monomeric CA (section 2) and (CA)₂ in the presence of large concentrations of ethoxzolamide. We propose that once dissociated from the ligands on the surface, (CA)₂ diffuses away from the surface through a stationary boundary layer and is swept away by a continuously flowing stream of buffer, which ultimately prevents rebinding.

We approximate the value of k_off^{avidity surf} as two times the product of K_d″ ^surf and k_off ′ ^surf (eq 13). (Details of the derivation of equation 13 are in the Supporting Information.) This equality, combined with the experimentally determined values of k_off ^{avidity surf} and k_off ′ ^surf, makes it possible to estimate K_d ″ ^surf and, ultimately, ΔG°_{avidity surf} from the binding sensorgrams (Table 1).

$${k_{\text{off}}}^{\text{avidity},\text{surf}}\approx 2{{K_{\text{d}}}^{″}}^{\text{surf}}{{k_{\text{off}}}^{\prime }}^{\text{surf}}$$ (13)

(4) Calculation of the Avidity Dissociation Constant

The avidity corresponds to the product of K_d′ ^surf and K_d″ ^surf, according to Scheme 1c (eq 14). Substituting the values of K_d′ ^surf (determined

$${K_{\text{d}}}^{\text{avidity}\text{surf}}=\left({{K_{\text{d}}}^{\prime }}^{\text{surf}}/2\right)·\left(2{{K_{\text{d}}}^{″}}^{\text{surf}}\right)$$ (14)

in section (2)) and K_d″ ^surf (determined in section (3)) into equation 14 yields K_d^{avidity surf} (Table 1).

Structure-Energy Relationships for the Dimers of Carbonic Anhydrase (the (CA)₂’s)

(1) Length of the Linker

(CA)₂EG₁, (CA)₂EG₂, and (CA)₂EG₃ are linked together near the active site of CA by oligoethylene-glycol linkers of increasing length. The sensorgrams for these three dimers are qualitatively similar in that they reach similar values of R.U._max (~300 R.U.) and decay to zero R.U. over roughly the same period of time (Figure 7b–d). The rates of association of these dimers with the SAMs are similar to each other and slightly slower than the rate of association of CA with the SAM (characterized by values of k_on ′ ^surf of (3.4 ± 0.6) × 10⁴ M⁻¹ s⁻¹, (3.8 ± 0.8) × 10⁴ M⁻¹ s⁻¹, (3.9 ± 0.6) × 10⁴ M⁻¹ s⁻¹ for dimers, and 5.6 ± 0.6) × 10⁴ M⁻¹ s⁻¹ for CA ). The rates of dissociation of these dimers from the SAMs are statistically indistinguishable from each other (characterized by values of k_off ^{avidity surf} of (1.2 ± 0.1) × 10⁻⁴ s⁻¹, (1.3 ± 0.4) × 10⁻⁴ s⁻¹, (1.2 ± 0.3) × 10⁻⁴ s⁻¹). The avidities for each of these dimers are indistinguishable from one another (ΔG°_{avidity surf} = −11.9 kcal mol⁻¹), and the avidities are ~2 kcal mol⁻¹ more favorable than the monovalent affinity (−9.6 kcal mol⁻¹) (Table 1). This difference in free energy represents a roughly 50-fold enhancement in the binding of the dimers over that of monovalent CA.

(2) Flexibility of the Linker

We constructed a dimer using a crosslinker of rhodamine (CA)₂Rh_front to examine the contributions of flexibility of the linker to the thermodynamics of binding. Interestingly, we found that the rates of association and dissociation of (CA)₂Rh_front were similar to those of (CA)₂EG₁, (CA)₂EG₂ and (CA)₂EG₃. This similarity suggests that the flexibility of the linker does not play a dominant role in the binding of these dimers to the SAM. (CA)₂Rh_front associates with the SAM slightly more slowly (k_on ′ ^surf = (2.2 ± 0.8) × 10⁴ M⁻¹ s⁻¹) than the EG dimers (k_on ′ ^surf ≥ = (3.7 ± 0.6) × 10⁴ M⁻¹ s⁻¹), although it binds as tightly as the other dimers (ΔG°_{avidity surf} of −11.8 kcal mol⁻¹). As was the case for the EG_n-linked dimers, the avidity of binding for (CA)₂Rh_front is a ~40 fold enhancement over that of monovalent CA.

(3) Orientation of Binding Sites of (CA)₂

We constructed a CA dimer (CA)₂Rh_back from two building blocks of CA with a reactive thiol located on the surface of the protein and opposite to the active site. Our goal was to explore the importance of the position of attachment of the linker that joins monomeric CA in dimers—that is, the orientation of the binding sites of (CA)₂ (Figure 2). The rate of association of (CA)₂Rh_back with the SAM is the fastest of all (CA)₂’s (k_on ′ ^surf = (6.5 ± 1.0) × 10⁴ M⁻¹ s⁻¹), and it is similar to the rate of association of the CA monomer from which it was constructed (k_on^surf = (5.6 ± 0.8) × 10⁴ M⁻¹ s⁻¹) (Figures 7a and f). The amount of (CA)₂Rh_back bound to the surface—which is proportional to the response units in the SPR experiment—at the end of the association phase (550 R.U.) is also similar to that of the CA monomer bound to the surface (500 R.U.). The active sites of (CA)₂Rh_back thus appear to be as accessible to ligand as is the active site of a CA monomer.

Although (CA)₂Rh_back associates with the SAM as rapidly as the monomer, unlike the CA monomer, which binds monovalently to the SAM, (CA)₂Rh_back binds bivalently to the SAM. The rate of dissociation of (CA)₂Rh_back increases with increasing concentrations of ethoxzolamide, and the rate of dissociation in the absence of ethoxzolamide (k_off^avidity = (3.0 ± 0.2) × 10⁻⁴ s⁻¹) is ~ 10 times slower than that of the monomeric CA (k_off^surf = (4.8 ± 0.5)× 10⁻³ s⁻¹). Curve fitting of the decrease in R.U. during the dissociation phase of the experiment indicates that roughly 88% of (CA)₂Rh_back is bound bivalently to the SAM, and that roughly 12% of (CA)₂Rh_back is bound monovalently to the SAM.

The structure of (CA)₂Rh_back differs from (CA)₂Rh_front only by the point of attachment of the rhodamine crosslinker. The rate constant of binding of (CA)₂Rh_back (k_on ′ ^surf = (6.5 ± 1.0) × 10⁴ M⁻¹ s⁻¹) is roughly three times that of (CA)₂Rh_front (k_on ′ ^surf = (2.2 ± 0.8) × 10⁴ M⁻¹ s⁻¹). The concentrations of (CA)₂Rh_back and (CA)₂Rh_front were the same (219 nM), and since the length of the association phases were also identical in each experiment (600 s), the amount of (CA)₂Rh_back bound to the surface at the end of the dissociation phase is roughly three times that of (CA)₂Rh_front. This result suggests that the active sites of (CA)₂Rh_front may be less sterically accessible for binding to ligands than the active sites of (CA)₂Rh_back and the active sites of the monomer. The active sites of (CA)₂Rh_back may be more accessible to ligands than are the other dimers because the binding sites of the former are oriented away from one another as opposed to adjacent to one another. At the beginning of the dissociation phase ~ 88% of the total amount of (CA)₂Rh_back and 89% of (CA)₂Rh_front are bound bivalently to the SAM ( A / (A+B), Table 1). This similarity suggests that the two dimers both bind bivalently to the SAM.

The rate of dissociation of (CA)₂Rh_back increases with increasing concentrations of ethoxzolamide as observed with all dimers, but unlike the other dimers k_off^avidity for (CA)₂Rh_back is roughly three times larger than the other dimers. The rates of association and dissociation combine to a yield an avidity for (CA)₂Rh_back indistinguishable from the other dimers. An enhancement of only 37 fold over that of the corresponding monovalent CA is observed for the binding for (CA)₂Rh_back.

Conclusions

(CA)₂ is a tractable, flexible model for bivalency in proteins

This model system enabled us to approach systematically the binding of bivalent receptors to surfaces presenting multiple ligands. The SPR techniques described in this paper are directly applicable to the characterization of other bivalent receptors: for example, engineered antibodies. A model bivalent system based on CA is particularly attractive for biophysical and physical organic studies because this protein is readily overexpressed in and purified from E. coli, especially easy to be modifed by site directed mutagenesis, and is bound by numerous arylsulfonamide ligands with a wide range of monovalent affinities.

The dimers of CA are capable of binding bivalently to the SAMs

The dissociation phase of the SPR experiments with (CA)₂’s in the presence of ethoxzolamide is not a process that occurs under equilibrium conditions: soluble ethoxzolamide competes for the active sites of the (CA)₂ with ligand tethered to the surface. Thus as the concentration of soluble ethoxzolamide increases, the apparent rate of dissociation of dimer from the surface increases, and in the absence of ethoxzolamide, the dissociation data are described by a biexponental function. We interpret this behavior to result from two populations of (CA)₂’s adsorbed to the surface: i) the majority of the protein (~85%) can simultaneously access two ligands and thus binds bivalently to the surface, and ii) a small amount of the protein (~15%) can access only one molecule of ligand and binds monovalently to the surface.

The geometries of the active sites may be the most important factor in determining the strength of binding

Varying the length and flexibility of the linker connecting monomeric CA’s did not affect significantly the rates of association and dissociation of the dimers to and from the SAM—the sensorgrams for dimers with EG linkers and (CA)₂Rh_front are similar. Interestingly, increasing the number of bonds (rigid rotors) in the linker between monomeric CA’s did not diminish the value of β for the dimers of CA as would be expected if the rotations about the bond become restricted. This result suggests that the number and identity of the amino acids comprising the peptide linker connecting the Fab domain to the Fc domain in IgG may not determine the rates of binding for antibodies.

Varying the point of attachment of the linker between monomeric CA’s affected the rates of binding and unbinding, although changing the point of attachment had virtually no effect on the avidity of the dimers. The rate of association of (CA)₂Rh_back with the SAM is the fastest of all (CA)₂’s and is similar to the rate of association of the CA monomer from which it was constructed. The active sites of (CA)₂Rh_back may be sterically less hindered for binding to ligands than the other dimers because the binding sites should be oriented away from one another as opposed to adjacent to one another. We infer, from the crystal structures of antibodies and the binding of (CA)₂Rh_back, that the geometry of the Fab domains relative to each other may be more important than length and flexibility of the peptide linker for determining the binding of antibodies to ligands on a surface. When one Fab of the antibody is bound to one antigen of a surface, the point of attachment may allow both Fab domains to achieve an unstrained conformation that directs the remaining Fab toward the surface and, presumably, bind another antigen.

Dimers bind with much lower enhancements than would be predicted based on monovalent enthalpies of binding

The simplest level of theory predicts the change in enthalpy (ΔH°_avidity) for the bivalent association of (CA)₂ to ligands on the SAM would be twice the change in enthalpy for the monovalent interaction (ΔH°_surf) (eq 20).³² The value of enthalpy of binding for monomeric CA to benzenesulfonamide 7 is ΔH°_soln = −9.8 kcal mol⁻¹.

$${\mathrm{\Delta }\text{H}°}_{\text{avidity}}\approx 2{\mathrm{\Delta }\text{H}°}_{\text{surf}}$$ (20)

If we assume the same value for the change in enthalpy for a surface as for solution and we assume the change in entropy is zero, which is typical for this interaction, we would estimate an enhancement of 10⁷ (K_d^{avidity surf} ~ 4 × 10⁻¹⁵ M).We observe only an enhancement of ~50. Although more sophisticated theories for the entropy of multivalent interactions at interfaces exist,^{33, 34} the enthalpies and entropies for the binding of CA and (CA)₂ to these surfaces, unfortunately, are not available experimentally, and the thermodynamic basis for the difference between these values remains undefined. Thus, at present, the redistribution of enthalpy and entropy from monomers (CA or Fab) to dimers of ((CA₂) or IgG) remains unresolved.

The value of the enhancement that we observe on going from CA to (CA)₂ and some of the corresponding values that we and others infer for going from Fab to IgG, seem small, but it is hard to judge the importance of a factor 10 – 1000 in enhancement of a bivalent species for the epitopes on the surface of, for example, a pathogen. Very high avidity would lead to effectively irreversible binding, with consequences for efficient use of antibodies that might be detrimental to the organism. The value of a significant but relatively small increase in affinity is not one we can resolve, but our results do suggest that the reason for bivalency in immunoglobulins is not simply achieving a large increase in avidity.

(CA)₂’s show values of β similar to antibodies

The 50-fold enhancements in binding for (CA)’s are within the range of enhancements from 10 to 1,000 we estimate for antibodies based on examination of the literature. We are interested in studying the role of the Fc domain—the addition of which should be reasonably tractable with our model system—in determining the values of β for antibodies. It is plausible that including an analog of the Fc subunit could increase the enhancement in bivalent association by reducing the volume of space accessible to the Fabs, and we aim to test this hypothesis using dimers of CA. The preparation of antibody mimics that incorporate an analog of the Fc unit are tractable, we feel, because of our successful semi-synthesis that begins with readily available mutants of CA. As our understanding of bivalency increases, we anticipate that model systems, such as dimers of CA, will allow us to examine the thermodynamic basis for the range of enhancements observed in antibodies.

Experimental Section

General Methods

Chemicals were purchased from Aldrich, Alfa Aesar, and Novabiochem. NMR experiments were carried out on a Varian INOVA 500 MHz. Isothermal titration calorimetry (ITC) was performed using a VP-ITC microcalorimeter (MicroCal). Analytical HPLC was run on a Varian instrument with a C18 column, 5 μm (4.6 × 250 mm), from Vydac using a linear gradient of water with 0.1% TFA (A) and acetonitrile containing 0.08% TFA (B), at a flow rate of 1 mL min⁻¹ (UV detection at 218 and 280 nm). Preparative reverse-phase HPLC was performed using a Varian HPLC instrument equipped with a C18 column, 5 μm (22 × 250 mm), from Vydac at a flow rate of 15 mL min⁻¹ with UV detection at 218 and 280 nm.

Synthesis of dimers of CA

Methods for the overexpression and purification of the HCAII double mutants from E. coli have been reported previously. To a solution of mutant HCAII (11.5 mg, 0.38 μmoles) in 10 mM phosphate buffer (5.0 mL) at pH 7.2, was added a solution of bis-maleimidomethyl ether (40 μg, 0.17 μmoles) in like buffer (0.085 mL) over the course of 20 h in 8.5 μL equal portions. The crude reaction mixture was purified by size-exclusion chromatography using a column of Superdex 75 (16 × 600 mm) eluting with 10 mM tris-sulfate buffer at a constant flow rate of 0.5 mL min⁻¹. The appropriate fractions were pooled to yield (CA)₂’s. Purity and molecular weight were consistent with the proposed structure as assessed by SDS-PAGE and ESI-MS.

• (CA)₂EG₁ ESI-MS m/z found 58,385 Da; calcd. 58,386 Da (apo- + 2H₂O from the hydration of the maleimide during ionization).

• (CA)₂EG₂ ESI-MS m/z found 58,456 Da; calcd. 58,458 Da (apo- + 2H₂O)

• (CA)₂EG₃ ESI-MS m/z found 58,503 Da; calcd. 58,502 Da (apo- + 2H₂O)

• (CA)₂Rh_front ESI-MS m/z found 58,699 Da; calcd. 58,698 Da (apo-)

• (CA)₂Rh_back ESI-MS m/z found 58,698 Da; calcd. 58,696 Da (apo-)

Isothermal Titration Calorimetry

To determine the stoichiometry of binding of monovalent ligands to the active sites of (CA)₂ in solution, 5.24 μM (CA)₂ (concentration determined by UV spectroscopy, assuming ε₂₈₀ = 109,400 M⁻¹ cm⁻¹) in 10 mM sodium phosphate buffer pH 7.5 (with 1.4% DMSO-d₆) was titrated with 22 mM acetazolamide (concentration determined by ¹H NMR) in the same buffer at T = 298 K. Thirty-nine injections of 7.0 μL were preceded by one injection of 2.0 μL, which was omitted for data analysis. After subtraction of background heats, the data were analyzed by a single-site binding model using the Origin software (provided by MicroCal) with the values of binding stoichiometry, ΔH°, and K_d being allowed to vary to optimize the fit.

Preparation of SAMs

The gold surfaces were purchased from the manufacturer of the SPR instrument (Biacore 3000 from GE Healthcare). The surfaces were cleaned by immersing them in freshly prepared piranha solution, rinsing thoroughly with water followed by rinsing with ethanol. The surfaces were then immediately immersed in a solution of 1 and 2 (2 mM total thiol in EtOH) at a mole fraction (χ = [1]/ [2]) of 0.02 for 10 h, rinsed with EtOH and dried with a stream of N₂. We coupled benzenesulfonamide 3 to the carboxylic acid of 2 via the activated ester of 2 (EDC / NHS) to form conjugate 4 in the SPR.

SPR assay

Solutions of protein in 50 mM tris-sulfate buffer were prepared with a concentration of 438 nM in binding sites (438 nM for monovalent CA and 219 nM for bivalent CA). Solutions of ethoxzolamide in 10 mM tris-sulfate buffer were prepared from serial dilution of a 0.221 mM stock solution prepared gravimetrically. Solutions of buffer were injected over the surface (10 μL min⁻¹) until a stable a baseline was obtained. Solutions of buffer were followed by solutions of protein (10 μL min⁻¹ for 10 min) then solutions of buffer or ethoxzolamide in buffer (10 μL min⁻¹ 25 min).