On the mechanism of protein fold-switching by a molecular sensor

Abstract

Alternate frame folding (AFF) is a mechanism by which conformational change can be engineered into a protein. The protein structure switches from the wild-type fold (N) to a circularly-permuted fold (N′), or vice versa, in response to a signaling event such as ligand binding. Despite the fact that the two native states have similar structures, their interconversion involves folding and unfolding of large parts of the molecule. This rearrangement is reported by fluorescent groups whose relative proximities change as a result of the order–disorder transition. The nature of the conformational change is expected to be similar from protein to protein; thus, it may be possible to employ AFF as a general method to create optical biosensors. Toward that goal, we test basic aspects of the AFF mechanism using the AFF variant of calbindin D_9k. A simple three-state model for fold switching holds that N and N′ interconvert through the unfolded state. This model predicts that the fundamental properties of the switch—calcium binding affinity, signal response (i.e., fluorescence change upon binding), and switching rate—can be controlled by altering the relative stabilities of N and N′. We find that selectively destabilizing N or N′ changes the equilibrium properties of the switch (binding affinity and signal response) in accordance with the model. However, kinetic data indicate that the switching pathway does not require whole-molecule unfolding. The rate is instead limited by unfolding of a portion of the protein, possibly in concert with folding of a corresponding region.

INTRODUCTION

In two earlier studies, we introduced the concept of alternate frame protein folding (AFF) as a potentially general mechanism for creating biosensors¹ and artificial zymogens.² The method was applied to the small protein calbindin D_9k to convert it into calbindin-AFF, a calcium- driven molecular switch. Calbindin-AFF is able to fold in one of two frames within the same polypeptide chain. The first frame consists of the normal sequence of amino acids and folding results in the wild-type (WT) structure (N) [Fig. 1(A)]. The second frame is comprised of a permuted amino acid sequence and folding produces a circularly-permuted structure (N′). The N and N′ conformations are mutually exclusive because they share a common stretch of amino acids. We previously suggested that the AFF mechanism is specified by the same thermodynamic and kinetic considerations that govern protein folding and ligand binding. The purpose of this study is to test that hypothesis.

Figure 1.

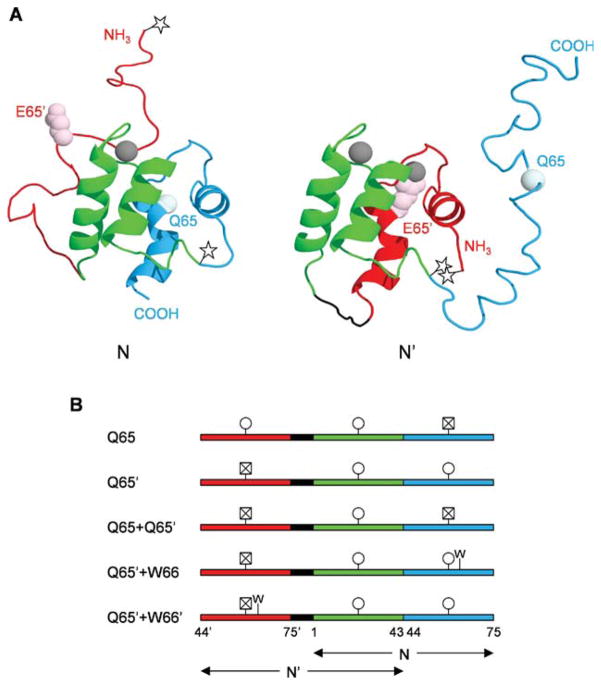
Structures and amino acid sequences of calbindin-AFF variants. (A) Predicted structures of N and N′ conformations. The color scheme is as follows: red, hand-2′ (residues 44′–75′); green, hand-1 (residues 1–43); blue, hand-2 (residues 44–75). The side chain of E65′ is shown in light pink and the alpha carbon of Q65 is shown in pale cyan. Calcium ions are depicted as gray spheres. The Q65 variant is shown in which calcium binding induces the red region to fold and the blue region to unfold. The stars mark the location of Cys residues to which fluorophores are attached, to track the N–N′ conformational change. (B) Amino acid sequences of calbindin-AFF variants showing the shared sequence in green and the duplicated sequences in red and blue, as in Panel A. The black segment is a six-amino acid linker. Circles indicate viable calcium binding sites; crossed-out squares denote calcium binding sites made nonfunctional by the presence of the Q65 or Q65′ mutation. The presence of the F66W mutation is marked by W.

The general approach for engineering the N ⇄N′ conformational change into a given protein is to duplicate a segment from the C-terminus and append it to the N-terminus, or to copy a segment from the N-terminus and ligate it to the C-terminus. Which segment is chosen depends on the location of key functional residues. For the biosensor application described here, the replicated segment must contain at least one amino acid which, when mutated, eliminates ligand binding. Beyond that criterion, the length of the duplicate polypeptide is dictated by preference for the termini of the circularly permuted protein to be located at a surface loop of the WT structure. Choosing the duplication to begin at the loop closest in sequence to the binding residue will minimize overall length and help to avoid potential aggregation and/or degradation problems.

Figure 1(B) illustrates how we modified the amino acid sequence of WT calbindin (75 amino acids) to generate calbindin-AFF. WT calbindin consists of two calcium-binding EF-hands: hand-1 (residues 1–43) and hand-2 (residues 44–75). Calbindin contains three surface loops. Two are used to coordinate calcium, leaving the loop connecting hand-1 and hand-2 as the only possible site for circular permutation. Calbindin-AFF is generated by duplicating residues 44–75 and appending them to the N-terminus of WT calbindin. This peptide equates to hand-2, although for a typical protein the duplicate sequence need not correspond to a functional domain. The duplicate sequence is designated by prime superscripts (44′–75′) but is otherwise numbered identically to the parent sequence. Calbindin-AFF is thus comprised of three EF-hands: hand-2′ (colored red in Fig. 1), hand-1 (green), and hand-2 (blue). Finally, a six-amino acid linker is inserted between hand-2′ and hand-1 to bridge the original N- and C-termini of the circularly permuted fold.

Conformation N is produced by folding of hand-1 and hand-2 [Fig. 1(A)]. N′ is generated by folding of hand-2′ and hand-1. N and N′ cannot exist simultaneously because they compete for hand-1. We introduce mutations into each frame to: (i) drive the N → N′ and N′ → N fold shifts using binding energy (E65Q calcium binding mutation), or (ii) to selectively destabilize one of the folds (F66W hydrophobic core mutation). To illustrate the nomenclature of mutants, Q65 indicates the E65Q mutation at position 65 in fold N, while W66′ denotes the F66W mutation in position 66′ of fold N′.

We predict that the “orphan” regions of an AFF-modified protein, that is, one of the two duplicate segments, will be disordered in either native conformation. For example, N will contain a disordered N-terminal tail and N′ will contain a disordered C-terminal tail [Fig. 1(A)]. This expectation is general and it should hold true for calbindin-AFF, because hand-2 is largely unstructured in isolation.³ In that respect, calbindin-AFF is reminiscent of intrinsically disordered proteins found in nature.^4–6 Intrinsically disordered proteins are chiefly unfolded in the cell until they bind their ligands. Favorable interactions between the protein and the substrate provide the energetic contributions necessary to drive folding.⁷ Similarly, calcium binding is the driving force for a disorder–order transition within the calbindin-AFF molecule. A notable difference is that calbindin-AFF is native in both bound and free forms, and binding-induced folding is coupled to unfolding of another region of the molecule. Thus, no net folding or unfolding takes place; rather, the structure is remodeled.

The goal of this study is to define basic thermodynamic and kinetic principles that underlie the AFF mechanism. By doing so we address the following questions: (i) Does the entire calbindin-AFF molecule have to unfold to refold using a different set of amino acids? (ii) Are the N- and C-terminal tails folded or unfolded? (iii) Can we manipulate the populations of N and N′ to control ligand binding affinity and the signal response of the switch? (iv) Can we modulate the rate of switching between the two conformations? This information will provide insight to this unique binding/folding/unfolding mechanism and help guide future design of biosensors based on the AFF principle.

MATERIALS AND METHODS

Gene construction, protein expression, and dye labeling

Genes were constructed and proteins were expressed and purified as described.¹ All genes were fully sequenced. To label the proteins, we first removed residual β-mercaptoethanol (which was added during purification) by desalting lyophilized protein into 10 mM Tris (pH 7.5) using a Sephadex G25 spin column. Protein concentration was measured by absorbance (ε₂₇₈ =1400 M⁻¹ cm⁻¹) and samples were precipitated using 10% trichloroacetic acid. Pellets were resuspended in 7M guanidine hydrochloride (GdnHCl), 10 mM Tris (pH 8.0) to a final protein concentration of 1 mM. Cys groups were reduced by adding a 10-fold excess of Tris (2-carboxyethyl) phosphine HCl (TCEP) and incubating for 30 m at room temperature. Protein was refolded by rapid 20-fold dilution into 0.1M Tris (pH 8.0). BODIPY-FL maleimide (Molecular Probes) or N-1-pyrene maleimide (Anaspec) was added in two-fold excess of Cys concentration and labeling was allowed to proceed for 1 h at room temperature and in the dark. Protein was desalted into 20 mM Tris (pH 7.5), 0.1M NaCl using a PD10 column (Bio-Rad). Fluorophore concentration was estimated using absorbance (BODIPY ε₅₀₃ = 80,000 M⁻¹ cm⁻¹, pyrene ε₃₄₅ =24,000 M⁻¹ cm⁻¹). Despite increasing the dye concentration and the duration of the labeling step, MALDI mass spectrometry (not shown) revealed that the labeling reactions were incomplete. A typical experiment resulted in ~30% double-labeled protein, ~60% single-labeled, and ~10% unlabeled.

Equilibrium denaturation and calcium binding experiments

All data were recorded at 20°C. Protein samples for denaturation experiments were prepared by mixing a solution of protein (7–10 μM) in 20 mM Tris (pH 7.5), and either 200 μM CaCl₂ (holo samples) or 400 μM EDTA (apo samples) with an identical solution containing the highest concentration of denaturant used in the experiment. Unlabeled protein samples contained 0.15 mM TCEP. Dilutions were made using a Hamilto-nian Microlab 540B dispenser and denaturant concentrations were measured by refractive index.⁸ Samples were equilibrated overnight at 20°C. CD data were collected on an Aviv Model 202 spectropolarimeter. BODIPY fluorescence data were recorded on a Horiba Jobin-Yvon Fluoromax-3 fluorimeter with excitation at 503 nm and emission from 507 to 600 nm. Equilibrium calcium binding experiments were performed as described.¹ Pyrene excimer fluorescence was calculated by normalizing the spectra to the highest intensity peak (374 nm), adding the excimer emission values from 460 to 500 nm, and dividing by monomer fluorescence at 383 nm.⁹ Calcium binding by calbindin can be specified by two macroscopic association constants which reflect binding of the first calcium to either hand, then binding of the second ion to the remaining hand. These values are ~10⁶ M⁻¹ and 10⁷ M⁻¹, respectively, for WT calbindin.¹⁰ Our experiments do not permit these macroscopic constants to be determined individually. We instead fit the data to the Hill equation (Y = A + B[Ca²⁺]ⁿ/([Ca²⁺]ⁿ + (1/K_a,obs)ⁿ)) where A is initial fluorescence, B is the amplitude, and n is the cooperativity coefficient.

Rapid kinetic experiments

Stopped-flow fluorescence data were recorded at 20°C using a Bio-Logic SFM4-Q/S rapid mixing device. All stopped-flow fluorescence experiments employed BOD-IPY-labeled proteins; excitation was at 485 nm and a 497-nm high-pass filter was employed on detection. Unfolding experiments were performed by mixing native (Q65+Q65′) (3–6 μM in 20 mM Tris, pH 7.5) with 0.5 mM CaCl₂ (1:1 ratio) in Mixer 1, then diluting the product with 9.8M urea in Mixers 2 and 3 to achieve the final urea concentration shown in the figures. For Ca²⁺-binding experiments, 50 μM EDTA was added to the protein samples to ensure apo conditions. Apo-proteins were first diluted with various volumes of 6M urea (up to 2.5 M final concentration, using Mixer 1), then mixed with CaCl₂ to a final concentration of 300 mM.

Stopped-flow CD data were acquired on an Aviv model 400 spectropolarimeter. Calcium binding experiments were performed as above, except unlabeled proteins were used. Data were recorded at 222 nm.

RESULTS

General model of fold switch

The AFF mechanism can be represented using an allosteric coupling model described by Hilser and Thompson (HT)¹¹ and by ourselves.¹² The HT model shares similarities with the longstanding Monod-Wyman-Changeux¹³ and Koshland-Nemethy-Filmer¹⁴ models of allostery; however, it is different in that the binding-incompetent conformations are unfolded. The HT formulation describes site-to-site communication within a single two-domain protein in which both domains are intrinsically disordered. Each folded domain recognizes a separate ligand and binding drives folding in both cases. The effect of binding to one domain on folding of the other is determined by an energy term (g_int) which describes the interaction between the two-folded domains. If g_int is positive then the two domains interact favorably and binding to the first domain increases the probability that the second will fold. The model that we introduced previously, which describes the coupled folding–unfolding equilibrium between two protein domains that fold in a mutually exclusive fashion, is similar to the HT model except the coupling energy is always unfavorable.¹²

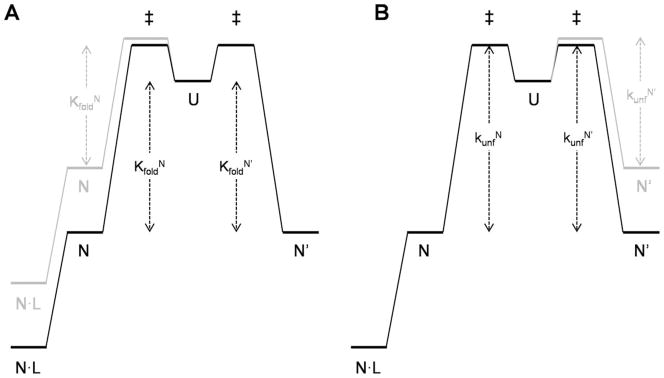
The AFF mechanism is a special case of the HT model in which g_int is negative and effectively infinite. In this case the two domains correspond to N and N′. Because N and N′ compete for a shared sequence, folding of N precludes folding of N′ and vice versa. The resulting mechanism contains only states N, N′, and U (the globally unfolded conformation) as described by Eq. (1):

$$N·\text{L}\stackrel{K_{\text{a}}^N[\text{L}]}{\iff }N\stackrel{K_{\text{fold}}^N}{\iff }\text{U}\stackrel{K_{\text{fold}}^{N^{\prime }}}{\iff }{N}^{\prime }\stackrel{K_{\text{a}}^{N^{\prime }}[\text{L}]}{\iff }{N}^{\prime }·\text{L}$$

where L is ligand, K_a is the association constant, and K_fold is the equilibrium constant for folding. For N to convert to N′ (and vice versa), at least a portion of the molecule must unfold and a corresponding portion must fold. The interconversion is not required to proceed through U (e.g., the shared region need not unfold); U is included simply to provide a common reference point for free energy changes.

The three fundamental properties of the sensor are ligand binding affinity, output signal response (e.g., fluorescence change), and response rate. The thermodynamic stabilities of N and N′ dictate the equilibrium aspects of the switch; namely, binding affinity and fluorescence change. Consider the case where a binding mutation is introduced into N′ so that $K_{\text{a}}^{N^{\prime }}=0$. The observed association constant (K_a,obs^N) is given by Eq. (2):

$$K_{\text{a}.\text{obs}}^N=\frac{[\text{bound}\text{species}]}{[\text{free}\text{species}][\text{L}]}=\frac{[N·\text{L}]}{([N^{\prime }]+[\text{U}]+[N])[\text{L}]}$$

Equation (2) can be rearranged to yield the following relationship between $K_{\text{a},\text{obs}}^N$ and $K_{\text{a}}^N$:

$$K_{\text{a}.\text{obs}}^N=\left[\frac{K_{\text{fold}}^N}{1+K_{\text{fold}}^N+K_{\text{fold}}^{N^{\prime }}}\right]K_{\text{a}}^N$$

If N is much more stable than N′ then $K_{\text{a},\text{obs}}^N\cong K_{\text{a}}^N$. If the stability of N′ is comparable to or greater than that of N, then a portion of binding energy is used to drive the N′→ N conformational change and the observed association constant drops. The magnitude of the observed fluorescence change is similarly determined by the extent to which the populations of N and N′ change upon binding. Figure 2 illustrates how these properties can be manipulated by selectively destabilizing one of the two possible native conformations. The black energy levels depict N and N′ as being equal in free energy; this is approximately true for calbindin-AFF (vide infra). When N and N′ are isoenergetic then $K_{\text{a},\text{obs}}^N\cong 0.5\times K_{\text{a}}^N$. The fraction of N equals 0.5 and it can increase by as much as a factor of two upon binding. Introducing a destabilizing mutation into N (Δ ΔG = −2 kcal mol−¹; gray energy levels) drops the observed binding affinity by 16-fold (from 0.5 ×K_a^N to 0.03 ×K_a^N), reflecting the fact that the conversion of N′ to N is thermodynamically uphill. The fraction of N can increase by a factor of 33 (from 0.03 to 1.0), which allows the fluorescence change to increase almost to its maximum value (given by the ratio of the fluorescence intensities of N and N′).

Figure 2.

Free energy diagrams of the minimal three-state model for fold switching. Vertical arrows indicate free energy changes; RT and logarithm terms are omitted for clarity. Represented in black are the free energy levels of Q65 and Q65′, in which the stabilities of N and N′ are approximately equal(K_fold^N =K_fold^N′). Ligand binding to N is shown (e.g., the Q65′ variant). (A) The effect of introducing a destabilizing mutation into N, depicted in gray, is to decrease binding affinity and increase fluorescence change. (B) The effect of introducing a destabilizing mutation into N′, shown in gray, is to decrease the height of the rate-limiting barrier (K_unf^N′).

What determines the rate of switching? The three-state mechanism shown in Figure 2(B) postulates that the N →N′ and N′ → N rates are largely limited by global unfolding of N and N′ (k_unf ^N and k_unf ^N′, respectively). If so, then the observed rate of ligand binding can be modulated as well. The height of the rate-limiting barrier in Figure 2 can be reduced by a mutation (shown in gray) that raises the free energy of N′ without proportionally raising the free energy of the N′ → U transition state. This type of behavior, which is categorized as φ < 1.0 in the φ-analysis methodology of Fersht,¹⁵ is common among destabilizing mutations. It should be noted that both the N→N′ and N′→ N rates can in principle be accelerated without affecting K_a,obs. This can be achieved by introducing a mutation into the shared region [colored green in Fig. 1(A)], which would be expected to destabilize N and N′ to similar extents.

Selection of mutants and method of fluorescence detection

We previously determined that WT and circularly permuted calbindin are of similar stability in their calcium-free (apo) as well as calcium-bound (holo) states.¹ Though WT and permuted calbindin lack the N- and C-terminal extensions found in calbindin-AFF, they nevertheless serve as reasonable models of the N and N′ states of calbindin-AFF, respectively. Given this assumption, calbindin-AFF is expected to exist in a roughly 1:1 ratio of the two native conformations. We chose the hydrophobic core mutation F66W to perturb that ratio. This mutation destabilizes WT apo-calbindin by 2.3 kcal mol⁻¹.¹⁶ Interestingly, the F66W mutation increases the macroscopic association constant of binding the first Ca²⁺ to either site (by 10-fold) without affecting binding to the remaining site.¹⁷ The net result is that overall calcium affinity is increased but cooperativity is decreased. To estimate the effect of the F66W mutation on N′, we used circular dichroism (CD) to monitor GdnHCl-induced unfolding of circularly permuted calbindin (Supporting Information Fig. S1(A,B)]. Thermodynamic parameters are obtained by fitting the data to the two-state linear extrapolation equation ΔG = ΔG^H2O–m[denaturant], where m is the cooperativity parameter and ΔG^H2O is the folding free energy extrapolated to zero denaturant. Table I indicates that the F66W mutation reduces stability of permuted apo-calbindin by 1.97 kcal mol⁻¹ and permuted holo-calbindin by 1.50 kcal mol⁻¹.

Table I.

Stability and Calcium Binding Parameters of Calbindin Variants

Variant	Cm (M)		DG H2O(kcal mol−1)		m (kcal mol−1 M−1)		Ka,obs (M−1) n		Ka,obs (M−1) n
	Apo	Holo	Apo	Holo	Apo	Holo	Pyrene		BODIPY
Permuted calbindin	2.78	4.49	5.54	7.98	1.99	1.78	N.A.a	N.A.	N.A.	N.A.
Permuted calbindin F66W	1.70	3.93	3.57	6.48	2.10	1.65	N.A.	N.A.	N.A.	N.A.
Q65′	2.65	5.64	3.90	7.95	1.47	1.41	5.50 × 105	2.43	8.55 × 105	2.75
(Q65′1W66)	2.51	4.78	3.67	3.02	1.55	0.63	3.88 × 105	1.76	5.99 × 105	2.65
(Q65′1W66′)	2.61	5.54	3.85	8.55	1.48	1.54	N.M.b	N.M.	1.42 × 106	1.81

Standard deviations are: ±0.05 M (C_m), ± 0.4 kcal mol⁻¹ (ΔG^H2O), ± 0.1 kcal mol⁻¹M⁻¹ (m), ± 5 × 10⁴ (K_a,obs), and ± 0.1 (n).

^aN.A., not applicable.

^bN.M., not measured due to insufficient amplitude.

Calbindin-AFF is comprised of three EF-hands: hand-2′, hand-1, and hand-2 (see Fig. 1). The E65Q mutation reduces binding affinity of hand-2 of WT calbindin by 10⁵-fold.¹⁸ We employed this mutation to inactivate hand-2 of Q65 and hand-2′ of Q65′. Because the E65Q mutation does not dramatically perturb stability of WT calbindin (Δ ΔG = 0.36 kcal mol⁻¹),¹ apo-Q65 and apo-Q65′ are still expected to consist in an ~1:1 ratio of N and N′. Binding of two calcium ions causes Q65 and Q65′ to fully adopt conformations N′ and N, respectively. It is important to note that both variants can coordinate one Ca²⁺ with hand-1. As a result, the driving force for the conformational change is provided by the free energy change of ligating the second calcium ion to hand-2 (or hand-2′) once the first has already bound to hand-1.

The calcium-induced fold shift of calbindin-AFF is monitored by placing either BODIPY-FL or pyrene groups at the two positions indicated in Figure 1(A). In conformation N′, the fluorophores adopt the equivalent of sequential positions in the surface loop and are hence in close proximity. In conformation N they are separated by residues 44′–75′ [Fig. 1(A)] and are expected to be distant from one another. The distance increase is reported either as an increase in BODIPY fluorescence at 513 nm (due to reduction of BODIPY self-quenching) or as a decrease in pyrene fluorescence from 460–500 nm (due to loss of pyrene excimer formation). Thus, calcium binding can be linked to an increase or a decrease in fluorescence depending on the choice of calbindin-AFF variant (Q65 or Q65′) or selection of fluorophores (BODIPY or pyrene). All calcium binding experiments in this study are performed using Q65′ and mutants thereof. Since binding triggers the N′ → N conformational change in Q65′, addition of calcium is predicted to increase and decrease fluorescence of the BODIPY- and pyrene-labeled proteins, respectively.

Equilibrium denaturation experiments

We tested the mechanism outlined in Figure 2 by determining the effect of W66 and W66′ on equilibrium unfolding of Q65′. If apo-Q65′ consists of comparable fractions of N and N′, as expected, then its GdnHCl unfolding curve will be the superposition of two closely-spaced transitions. The two transitions can be isolated, however, using the F66W mutation. W66 destabilizes N by ~2 kcal mol⁻¹ but it has no effect on N′. This causes N′ to become almost fully populated, and the unfolding curve of apo-(Q65′1W66) approximates that of the pure N′ state. Similarly, the unfolding curve of apo-(Q65′+W66′) corresponds to that of the pure N state. Apo-(Q65′+W66) and apo-(Q65′+W66′) have similar ΔG^H2O values and midpoints of denaturation (C_m) (Table I) and their unfolding curves are nearly superimposable [Supporting Information Fig. S1(D,E)]. The two transitions that make up the observed unfolding curve of apo-Q65′ should be almost superimposable as well, leading to the prediction that all three apo-Q65′ variants will produce similar ΔG^H2O and C_m values. Table I shows this to be the case. These findings confirm that N and N′ are approximately isoenergetic in apo-Q65′, as depicted in Figure 2.

We next employed the W66 and W66′ mutations to test whether calcium induces the fold shift. W66 strongly destabilizes holo-Q65′ (ΔΔG = −4.9 kcal mol⁻¹, ΔC_m = −0.86 M GdnHCl), suggesting that position 66 is structured in the calcium-bound state. By contrast, W66′ has little effect on holo-Q65′ (Δ ΔG = +0.6 kcal mol⁻¹, ΔC_m = −0.10 M GdnHCl), revealing that position 66′ is in an unstructured environment. These data indicate that calcium binding drives holo-Q65′ to adopt conformation N exclusively.

Residual structure of N- and C-terminal tails

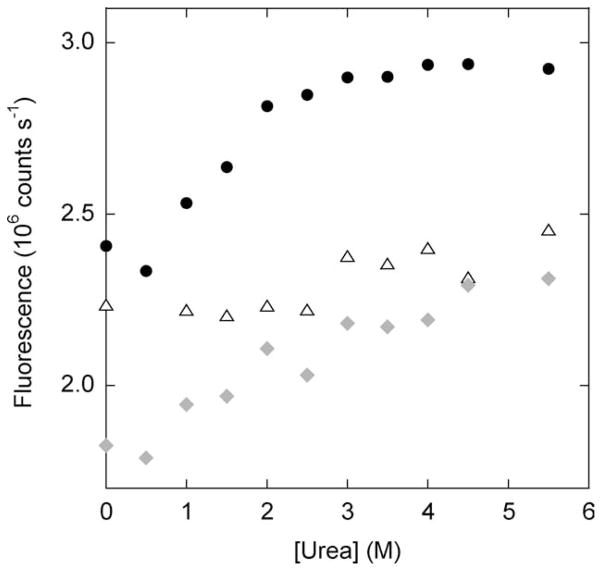
The magnitude of the fluorescence change between N and N′ is likely to depend on the extent to which the duplicated polypeptide is structured or disordered. In N′, the fluorophores are held in close proximity regardless of the structure of the C-terminal tail, because the two Cys residues adopt what would be consecutive positions in the WT structure [Fig. 1(A)]. In conformation N, we anticipate that the two fluorophores will be maximally distant from one another if the N-terminal tail is completely unstructured and flexible. CD studies find that isolated hand-2 is largely disordered in the absence of calcium,³ and thioldisulfide exchange experiments suggest that hand-2 is disordered in holo-Q65.¹ As an additional test we measured fluorescence of BODIPY-labeled holo-Q65, holo-Q65′, and holo-(Q65+Q65′) as a function of urea. We employed urea (instead of GdnHCl) because all of the above species possess C_m values in excess of 7 M urea (not shown). We can therefore monitor structural changes over a wide range of urea concentrations in which the proteins remain native. Figure 3 indicates that fluorescence of holo-Q65′ increases significantly from 0 to 2 M urea while that of holo-Q65 remains relatively constant up to 6 M urea. The holo-Q65′ data suggest that the hand-2′ is partially ordered in conformation N, causing fractional quenching of the BODIPY groups. The residual structure appears to melt gradually between 0 and 2 M urea. Hand-2 is presumably likewise partially ordered in N′ but its unfolding does not seem to alter the proximity of the fluorophores, consistent with the predicted structure in Figure 1(A). The fluorescence change of holo-(Q65+Q65′) is in between that of holo-Q65 and holo-Q65′, reflecting the 31:1 ratio of N′ and N believed to be present in holo-(Q65+Q65′).

Figure 3.

Dependence of BODIPY fluorescence on subdenaturing concentrations of urea. Holo-Q65 is shown in triangles, holo-Q65′ in circles, and holo-(Q65+Q65′) in diamonds.

Equilibrium calcium binding experiments

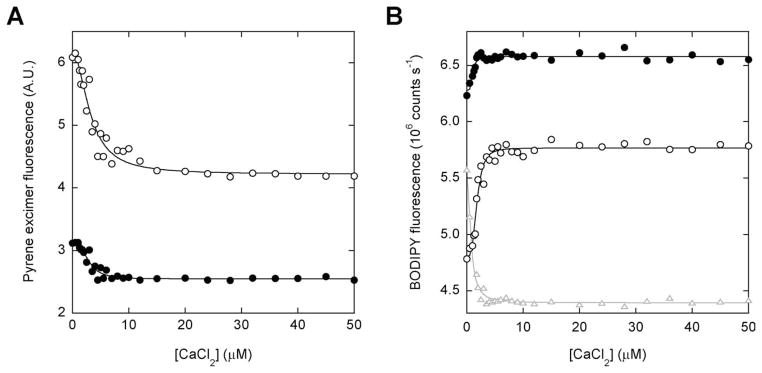
We next tested whether W66 and W66′ modulate calcium binding affinity and fluorescence change of Q65′ in accordance with the model. Figure 4 shows results obtained for Q65′, (Q65′+W66), and (Q65′+W66′) labeled with pyrene [Fig. 4(A)] and BODIPY [Fig. 4(B)]. Table I summarizes the fitted binding parameters. As forecasted by Figure 1(A), addition of calcium to Q65′ decreases pyrene fluorescence and increases BODIPY fluorescence. Equation (3) calculates that W66 will decrease K_a,obs of Q65′ by a factor of 16 and increase the amplitudes of the fluorescence change. We observe that this mutation lowers K_a,obs by a factor of 1.4 for both pyrene and BODIPY-labeled Q65′. The discrepancy likely arises from the fact that the F66W mutation is known to increase the intrinsic calcium binding affinity of WT calbindin by 10-fold.¹⁷ This effect may mask a larger than apparent reduction in K_a,obs. In agreement with the model, the W66 mutation increases the amplitudes of the pyrene and BODIPY fluorescence changes.

Figure 4.

Equilibrium calcium binding of calbindin-AFF variants. (A) Binding of calcium to Q65′ (●) and (Q65′+W66) (○), detected by pyrene excimer fluorescence. (B) Binding of calcium to Q65′ (●), (Q65′+W66) (○), and (Q65′+W66′) (gray triangles) monitored by BODIPY fluorescence. Lines are best fits of the data to the Hill equation.

Equation (3) estimates that the W66′ mutation will increase K_a,obs of Q65′ by a factor of ~2 (from 0.5 × K_a to ~K_a) and decrease the amplitude change. The pyrene fluorescence change of (Q65′+W66′) diminishes to the point where K_a,obs cannot be determined accurately (data not shown). Unexpectedly, the W66′ mutation inverts the sign of the BODIPY fluorescence change [Fig. 4(B)]. The probable cause is a new quenching interaction formed between BODIPY and W66′ in conformation N. Residues 44′–75′ are principally disordered in N and Trp is known to quench BODIPY in unfolded proteins.¹⁹ Regardless of the nature of the fluorescence change, the W66′ mutation increases K_a,obs by a factor of 4.2.

Kinetic measurements

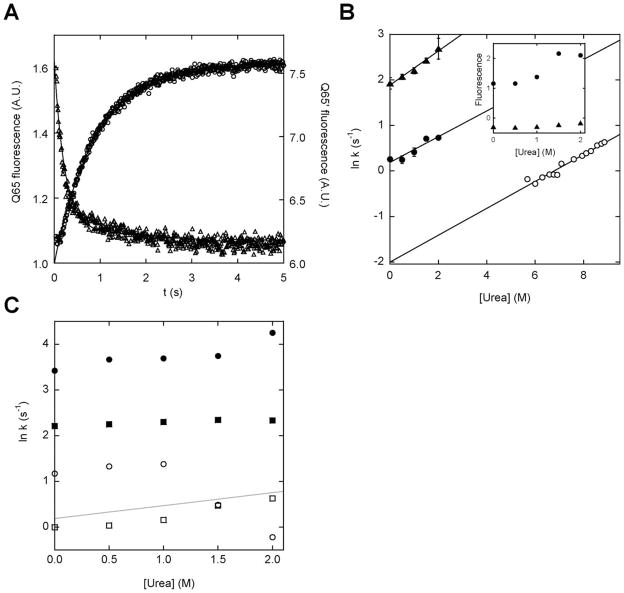
We measured rates and amplitudes of calcium-induced fold switching using BODIPY-labeled calbindin-AFF variants. The rates are faster than those we reported earlier using pyrene-labeled protein.¹ The reason is not clear; it may be attributable to a kinetic barrier imposed by pyrene dimer formation. Figure 5(A) shows calcium binding data for BODIPY-labeled Q65 and Q65′ monitored by stopped-flow fluorescence. The data fit adequately to one-exponential functions, and the amplitudes of Q65 and Q65′ exhibit the expected inversion of sign as the switch is driven in opposite directions. The N →N′ rate is four-fold faster than the N′ → N rate (6.85 and 1.29 s⁻¹, respectively).

Figure 5.

Rates and amplitudes of calcium-induced fold switching monitored by BODIPY fluorescence. (A) Representative stopped-flow fluorescence traces of calcium binding to Q65 (triangles) and Q65′ (circles). The lines are best fits of the data to single-exponential functions. (B) Rates of fold switching (filled symbols) and global unfolding (open symbols) plotted as a function of urea. Symbols are: (▲), Q65; (●), Q65′; (○), holo (Q65+Q65′). The slopes of the fitted lines are (in units of M⁻¹ s⁻¹): 0.38 (Q65), 0.28 (Q65′), and 0.30 (Q65+Q65′). The inset shows the fitted fluorescence amplitudes plotted as a function of urea, using the same symbols. (C) Fold-switching rates of (Q65′+W66) (squares) and (Q65′+W66′) (circles). Closed and open symbols denote the faster and slower rates, respectively. The gray line shows the linear fit of the Q65′ data from panel B for comparison.

To test whether these rates are limited by whole-molecule unfolding, we measured the global unfolding rate of BODIPY-labeled holo-(Q65+Q65′) as a function of urea concentration [Fig. 5(B)]. Holo-(Q65+Q65′) contains a single calcium ion bound to hand-1 [Fig. 1(A)]. Because hand-1 is folded in both conformations, and because calcium binds to this site in folded calbindin extremely rapidly (k = 10⁹ M⁻¹ s⁻¹),²⁰ the singly-bound species will form within the mixing time of Ca²⁺-binding experiments. Thus, the observed signal in Figure 5(A) corresponds to folding/unfolding of hand-2/hand-2′ in the context of holo-(Q65+Q65′). Figure 5(B) reveals that these events do not require global unfolding. The urea-induced unfolding rate of holo-(Q65+Q65′) extrapolates to 0.13 s⁻¹ in the absence of denaturant. This figure is 10-fold and 53-fold slower than the observed N′ → N and N →N′ rates, respectively.

Although conformational switching of Q65 and Q65′ does not appear to proceed via global unfolding, Figure 5(B) suggests that both transition states involve partial unfolding. The N′ → N and N → N′ rates both accelerate with increasing concentrations of urea. The slopes of the lines are similar to that of the global unfolding line, suggesting that the transition states of all three reactions expose comparable amounts of additional surface area. The corresponding amplitudes of the N′ → N and N → N′ reactions are shown in the inset to Figure 5(B). In agreement with the sub-denaturing urea experiments (see Fig. 3), the Q65′ amplitude increases with urea and the Q65 amplitude remains constant.

The W66 and W66′ mutations give insight into the nature of the N′ → N transition state of Q65′. The conversion of N′ to N requires unfolding of hand-2′ and folding of hand-2 [Fig. 1(A)]. If the N′ → N rate is limited by one of these processes, then W66 and W66′ may decrease and increase the observed rate, respectively. Both mutations unexpectedly result in bi-phasic kinetics. For each variant, the two amplitudes are of the same sign and are similar in magnitude (Supporting Information Fig. S2). Figure 5(C) compares the rate constants of Q65′, (Q65′+W66), and (Q65′+W66′). It can be seen that the slow rate of (Q65′+W66) is less than that of Q65′, and the slow rate of (Q65′+W66′) is greater than that of Q65′. Although the mechanism cannot be derived unambiguously from these data, a simple interpretation is that the faster phase corresponds to formation of an intermediate and the slower phase is the rate-limiting conversion of the intermediate to N. If so, then the W66 mutation increases the transition state barrier slightly while the W66′ mutation lowers it significantly. This result is consistent with the physical picture of folding and unfolding.

Finally, we monitored calcium binding by stopped-flow CD to identify any intermediates that may accumulate during the fold switch. No change in ellipticity at 222 nm was observed for either Q65 or Q65′ (data not shown). This result indicates that the conformational change proceeds without populating species which contain either extra or missing α-helical structure.

DISCUSSION

In this study we establish a framework for understanding basic thermodynamic and kinetic aspects of the AFF switching mechanism. There are two main findings. The first is that the equilibrium properties of the switch—binding affinity and signal response—can be manipulated using well-established principles of protein stability. The second is that the conformational change which underlies AFF appears to involve limited remodeling of the structure rather than global unfolding/refolding. With respect to the first point, it is particularly useful in biosensor applications to be able to tune binding affinity to match the concentration of analyte present in, for example, a cell or subcellular compartment. The degree to which K_a,obs can be decreased is limited only by the extent to which one conformation can be destabilized relative to the other. In practice, the concentration range in which the sensor can effectively operate depends on the ratio of fluorescence intensities of N and N′. Consider the case of N′ → N where binding is reported as an increase in fluorescence. If one wishes to set K_a,obs to 1% of K_a, then K_fold ^N′ is adjusted to ~100 × K_fold^N. The fraction of N increases from 0.01 to 1.0 upon ligand binding. The observed fluorescence change approaches its maximum value, which is specified by the intensity ratio of N and N′. This increase can be readily detected even if N is only moderately more fluorescent than N′. If one desires K_a,obs to be 90% of K_a then the fraction of N is initially 0.9. To realize the maximum fluorescence increase of 1.1-fold, it becomes important to make the intensity ratio of N and N′ as large as possible.

In our experiments, K_a,obs increases and decreases in response to mutation as predicted. The magnitude of the change is in quantitative agreement with the model for (Q65′+W66′), but it is smaller than expected for (Q65′+W66) (Table I). As mentioned, the discrepancy can be at least partially reconciled by noting that the F66W mutation raises the intrinsic calcium binding affinity of WT calbindin by 10-fold.¹⁷ The amplitude and sign of the calcium-induced fluorescence change also follow the expected pattern, with W66 and W66′ enhancing and diminishing (respectively) the negative change in pyrene fluorescence (see Fig. 4). W66 similarly boosts the positive fluorescence change of BODIPY-labeled Q65′. BODIPY-labeled (Q65′+W66′) is an exception. We anticipated that BODIPY fluorescence would be quenched in N′ and not quenched in N. The data unexpectedly indicate that the BODIPY groups are most strongly quenched in N [Fig. 4(B)]. We attribute quenching to interaction with W66′ (the only Trp residue in the sequence), which may be facilitated by the disorder and flexibility of residues 44′–75′ in N. This putative interaction actually proved fortuitous, because it allowed us to measure K_a,obs even when the fractional change in N was expected to be minor (as was observed for the pyrene-labeled protein). The important point is that the optical properties of N and N′ can be unpredictable, but within a given pair of chromophores, the signal output can be altered in a rational manner.

Response time is the third key property of a sensor. Q65′, (Q65′+W66), and (Q65′+W66′) all appear to bind calcium ions much more slowly than WT calbindin [Fig. 5(A)], in which the rate is diffusion controlled. The reason is that our experiments detect binding by observing the comparatively slow fold shift. The fraction of molecules already in the binding-competent conformation (~50%) may coordinate Ca²⁺ rapidly, but this event is optically invisible. Nevertheless, calbindin-AFF switches native conformations within a few seconds. This rate is substantially faster than that of global unfolding [Fig. 5(B)]. This finding speaks favorably to the use of AFF in other binding proteins, because global unfolding can be very slow for stable proteins.

The nature of the transition state for the fold change remains to be elucidated. We can, however, suggest a reasonable physical picture in which hand-1 remains folded while hand-2 and hand-2′ fold/unfold and exchange positions. Consider the N′ → N transition in which hand-2 folds and hand-2′ unfolds. We envision that folding of hand-2 may be assisted by calcium binding because the isolated 44–75 fragment is known to be disordered in the absence of calcium and partially helical in its presence (K_a,obs = 4 × 10⁴ M⁻¹).³ Several findings imply that subsequent displacement of hand-2′ by hand-2, along with unfolding of the former and folding of the latter, occurs in a concerted fashion. First, stopped-flow CD experiments detect no transient change in ellipticity when calcium is added to Q65 or Q65′. Therefore, a super-helical intermediate (in which hand-2 and hand-2′ are both folded) does not accumulate; unfolding of hand-2′ is not likely to be the sole rate-limiting step. Second, the W66 and W66′ mutations respectively decrease and increase the slow rate of the N′ → N reaction [Fig. 5(C)]. This result is expected if folding of hand-2 as well as unfolding of hand-2′ contribute to the rate-limiting barrier. The N′ → N and N → N′ rates increase with urea concentration [Fig. 5(B)], suggesting that both transition states are more unfolded than the ground states.

CONCLUSIONS

AFF unites two aspects of protein folding. The first is the well-established linkage between folding and binding. The second is a newer concept of coupling folding to unfolding of another portion of the molecule.^2,12,21–24 AFF therefore constitutes a conformational switching mechanism that is driven by binding energy. Folding is itself a dramatic conformational change, and others have exploited binding-induced folding of unfolded proteins to create optical biosensors.¹⁹ Our mechanism is unique in that the bound and free proteins are both native; fold switching does not involve net folding or unfolding, only structural rearrangement. In this way, the globally unfolded state (which may present problems of solubility and degradation) is averted. Thus, binding affinity and switching rate can be tuned by manipulating the relative stabilities of the two native forms and the height of the energy barrier that separates them. This study demonstrates that it is possible to make such adjustments by varying the free energies of N and/or N′ according to established principles.