Using Free Energy of Binding Calculations to Improve the Accuracy of Virtual Screening Predictions

Abstract

Virtual screening of small molecule databases against macromolecular targets was used to identify binding ligands and predict their lowest energy bound conformation (i.e., pose). AutoDock4- generated poses were rescored using mean-field pathway decoupling free energy of binding calculations and evaluated if these calculations improved virtual screening discrimination between bound and non-bound ligands. Two small molecule databases were used to evaluate the effectiveness of the rescoring algorithm in correctly identifying binders of L99A T4 lysozyme. Self-dock calculations of a database containing compounds with known binding free energies and co-crystal structures largely reproduced experimental measurements, although the mean difference between calculated and experimental binding free energies increased as the predicted bound poses diverged from the experimental poses. In addition, free energy rescoring was more accurate than AutoDock4 scores in discriminating between known binders and non-binders, suggesting free energy rescoring could be a useful approach to reduce false positive predictions in virtual screening experiments.

INTRODUCTION

Structure-based virtual screening of chemical databases against macromolecular targets has identified bioactive compounds for the potential treatment of diseases such as dengue fever,¹ cancer,^2–4 bacterial infections,^{5, 6} inflammation,⁷ depression,⁸ and diabetes.⁹ Virtual screening approaches systematically utilize docking programs (e.g., EUDOC,¹⁰ Dock,¹¹ Glide,¹² GOLD,¹³ FlexX,¹⁴ AutoDock4¹⁵) to predict a small molecule’s lowest “energy” conformation and orientation (i.e., pose) when bound to a macromolecular binding site. The energy scoring function in conventional docking programs typically sums empirically-derived terms meant to describe intramolecular conformational energies and non-bonding interaction energies between the ligand and macromolecular target.^16–20 The degree to which the empirical energy function represents the observed free energy of binding (FEB) influences the accuracy of the relative energy difference between bound potential ligands, and therefore the correct identification of molecules that bind to the macromolecular target. Recent comparative evaluations of several widely used docking programs concluded that no docking program showed a significant performance advantage with respect to pose accuracy and chemical database enrichment.^21–24 Moreover, the pose accuracies of each docking program were dependent on the protein target and no program had a significant advantage in terms of accurate pose predictions for all tested proteins. Encouragingly, the lowest energy docking pose of many programs typically differed from the known co-crystal structure by 1–2 Å root-mean-square deviation (rmsd).^21–24 In contrast, docking energy scores generally had poor agreements to experimental FEB, and were often biased by molecular weight, functional groups, and/or number of intermolecular contacts.^21–24

Consensus^{25, 26} and weighting²⁷ score methods have attempted to correct inaccuracies and bias in docking energy scores. However, significant errors persist in the docking scores due to incomplete enumeration of conformational states, inexact treatment of solvent and entropy contributions, and empirical parameterization of enthalpic energy terms. Thus, contemporary virtual screening calculations have high false positive rates that necessitate time-consuming laboratory validation to identify active (i.e., true positive) compounds from large numbers of false positive predictions.

In principle, the FEB between a ligand and protein can be accurately calculated from rigorous statistical mechanical (SM) theory.^{17, 28} Both endpoint and pathway algorithms have been developed to efficiently perform SM-FEB calculations. End point methods (e.g., linear interaction energy [LIE],²⁹ molecular mechanics Poisson-Boltzmann-and-surface-area [MM-PBSA]³⁰) compute FEB from the difference between unique states, whereas pathway methods (e.g., alchemical pathways,³¹ annihilation,³² intermolecular interaction decoupling³³) incrementally transfer a ligand-protein system between states and integrate energies along the transfer path to calculate FEB. Recent mean-field pathway decoupling FEB calculations^34–36 that used co-crystal structures for the starting states reproduced experimental FEB measurements with accuracies of ~1 kcal/mol.

SM-FEB calculations offer an alternative to empirical “energy” scoring approaches since they can appear to be able to largely reproduce observed ligand-protein FEBs.³⁷ However, these calculations are computationally demanding. One possible approach to improve the accuracy of virtual screening within the constraints of limited computing resources is to use conventional docking programs to predict poses and preliminary interaction “scores” for the compound library, and then perform rigorous calculations to determine FEB for the “best” (i.e., top-ranked) docked compounds. This FEB rescoring method is attractive because ligand poses can be rapidly determined with empirical energy functions, and SM-FEB calculations can be limited to a subset of the original virtual library. Moreover, compound databases can be examined with parallel calculations, and individual perturbation steps in SM-FEB calculations are amenable to parallel processing and distributed computing environments. For example, the perturbation sampling steps in pathway decoupling calculations^34–36 can be independently calculated in a distributed computing environment.³⁸

This study compared the accuracy of virtual screening a library of known binders and non-binders of L99A T4 lysozyme³⁹ using either FEB rescoring or empirical docking scores. The rescoring approach used the well-established AutoDock4^{15, 40} program to compute initial poses and empirical docking scores. Roux’ mean-field pathway decoupling FEB approach^34–36 was used to subsequently calculate FEBs. In addition, the sensitivity of these calculations to the initial docked structures was determined. Significantly, FEB calculations initiated with either crystal structures or AutoDock4 poses were in good agreement with experimental measurements. In a limited virtual screening experiment, false-positive rates were reduced and enrichment rates improved when libraries were evaluated with FEB rescoring as opposed to AutoDock4 scores. Moreover, rescoring allowed clear discrimination between ligands that were known binders and non-binders. These results suggest that FEB rescoring could be used to efficiently screen large virtual libraries for novel drug leads.

EXPERIMENTAL METHODS

Hardware

All calculations were performed at the Texas Advanced Computing Center (TACC; Austin, TX) using the “Lonestar” high-performance cluster that consisted of 1,300 dual core 64-bit 2.66 GHz Xeon (Intel) processors.

Atomic Coordinates

Atomic coordinates for L99A T4 lysozyme apo-enzyme and co-crystal structures were obtained from the Protein Data Bank. The reference codes were 2B6Y for the apo-enzyme and co-crystal structures were 1NHB (ethybenzene ligand), 188L (o-xylene ligand), 187L (p-xylene ligand), 182L (benzofuran ligand), 185L (indole ligand), 186L (n-butlybenznene ligand), and 184L (isobulbenzene ligand).^{41, 42} The benzene-lysozyme co-crystal coordinates were provided by Y. Deng (University of Chicago).

Docking Calculations

Ligand coordinates, if not available from co-crystal structures, were generated with PyMol 0.99.⁴³ Ligands were parameterized with Antechamber⁴⁴ using the generalized AMBER force field⁴⁵ and AM1-BCC charges.⁴⁶ The three-dimensional structures of all ligands were minimized with CHARMM using an adopted basis Newton-Raphson minimization.^{47, 48}

Ligands and lysozyme target proteins were prepared for docking using the program AutoDockTools⁴⁰ and its default parameters, including assigning of AutoDock’s atom types and charges. All lysozyme side-chains were treated as fixed entities. Dockings were performed using the program AutoDock 4.01.^{15, 40} Previously, this docking program had successfully predicted co-crystal conformations for a number of systems.¹⁵ Grid parameters were used with default settings, and the search areas were centered on the lysozyme-binding pocket. Docking parameters were optimized for large-scale virtual screening (data not shown), with the number of genetic algorithm runs set to 100, the maximum number of energy evaluations set to one million, and the population size set to 200; all other docking parameters were set tof default values. The most likely pose from a docking simulation was determined using a pose-based cluster analysis and a 1.5 Å cut-off. Based on previous work, poses that most closely mimicked the crystallographic structure typically had the lowest energy score within the largest pose cluster (data not shown). The most likely pose was protonated using PyMol and re-parameterized with Antechamber as described above; however these poses were not subjected to additional minimization.

Mean-field Free Energy of Binding (MF-FEB) Calculations

The calculations were applied as described previously.^34–36 Calculations were performed using the CHARMM package^{47, 48} with the CHARMM22 force field^{49, 50} used to describe the protein and TIP3 water parameters⁵¹ used to describe the explicit waters. Each binding calculation was done in triplicate using same equilibrated starting coordinates.

Statistics

All statistics were preformed using Microsoft’s Excel 2003. P-scores were calculated using the two-tailed Student T-test and varying standard deviation options. All other functions used the default settings.

RESULTS AND DISCUSSION

Test Systems

We tested the accuracy of the AutoDock scoring function and free energy calculations using the L99A T4 lysozyme³⁹ as a test system. The L99A mutation in T4 lysozyme created an ~150 A³ void in center of a helix bundle that can bind small hydrophobic molecules.⁵² Two collections of small molecules were used as test sets. The first set, or control set, consisted of eight lysozyme ligands (n-butlybenznene, i-butlybenzene, ethylbenzene, benzofuran, benzene, indole, p-xylene, and o-xylene), each with a known binding affinity and co-crystal structure.^{39, 42} Experimental binding energies (ΔG_exp) for the control set ranged from −6.70 to −4.60 kcal/mol. ³⁹ This set was used to examine the accuracy of MF-FEB predictions relative to the experimental energies. We used a second ligand set, or screening set, to examine the ability of MF-FEB predictions to discriminate between lysozyme binders and non-binders in a small-scale virtual screening experiment. The screening set consisted of 30 compounds selected from thermal shift experiments that categorized the compounds as either lysozyme binders (16 compounds) or non-binders (14 compounds).³⁹ Experimental binding energies for the known binders in the screening set ranged from −6.70 to −4.59 kcal/mol. ³⁹

Accuracy of MF-FEB Calculations Using AutoDock4-predicted Binding Poses

Three experiments were performed with the control set to test the accuracy of MF-FEB calculations. These experiments used as initial coordinates for the MF-FEB calculations the coordinates from co-crystal structures, AutoDock4-generated self-docked binding poses, and AutoDock4-generated cross-docked binding poses.

To minimize errors arising from inaccurate binding orientations between a ligand and target protein, the first set of MF-FEB calculations were completed using coordinates extracted from inhibitor-lysozyme co-crystal structures (Table 1). The implicit assumption was that these structures represented the biologically relevant docking result, and thus were good starting structures for MF-FEB (ΔΔG_binding) calculations. These calculations showed good agreement to ΔG_exp measurements, with a linear correlation coefficient r=0.85 and an average error of 1.3 kcal/mol (s.d.=0.99 kcal/mol; n=3) between calculated and experimental free energies (Table 1). In addition, these calculations were in good agreement (average error of 1.6 ± 1.2 kcal/mol) with previous MF-FEB calculations performed with ligand partial charges calculated with CHARMM.³⁴ During the molecular dynamics equilibration phase of the MF-FEB calculations the initial ligand positions shifted on average ~0.7 Å relative to the crystal structure coordinates (Table 1). The average position during equilibration was used as the reference pose for applying translation and conformation constraints to the ligand. These calculations were more accurate than MF-FEB calculations that used co-crystal structures as the constraint reference poses.³⁶

Table 1.

Comparison between MF-FEB Calculations and Experimental Binding Energies ^a

Ligands	Experimental	MF-FEB
	ΔGexp (kcal/mol)	rmsd* (Å)	ΔΔGbinding ( kcal/mol)
n-butylbenzene	−6.7 ± 0.02	0.9	−7.8 ± 0.5
i-butylbenzene	−6.5 ± 0.06	0.9	−9.5 ± 0.6
ethylbenzene	−5.8 ± 0.07	1.3	−8.0 ± 0.2
benzofuran	−5.5 ± 0.03	0.3	−6.5 ± 0.4
benzene	−5.2 ± 0.2	0.8	−5.2 ± 1.0
indole	−4.9 ± 0.06	0.7	−3.9 ± 0.2
p-xylene	−4.7 ± 0.06	0.6	−5.5 ± 0.8
o-xylene	−4.6 ± 0.06	0.3	−5.3 ± 0.2

^aInhibitor-lysozyme co-crystal structures were used as the starting poses for the ΔΔG_binding calculations. MF-FEB calculations were performed in triplicate. Root-mean-square deviation (rmsd) reflects the displacement of heavy atom positions between the final equilibrated pose and the starting structure.

Previous studies had observed that conformational bias in the T4 lysozyme binding site could reduce the accuracy FEB predictions.^{34, 53} To determine the sensitivity of MF-FEB calculations to the initial coordinates of the ligand-protein structure, ligands of the control set were self-docked into the binding site of their corresponding lysozyme structures using AutoDock4. The ligands were not energy minimized prior to the docking calculations and therefore the docking simulations inherited the information implicit in the co-crystal coordinates. Since Val111 in the T4 lysozyme binding pocket was observed to adopt ligand-dependent conformations,³⁹ self-docking was expected to reduce systematic bias arising from treating the protein binding site as a fixed structure.

The AutoDock generated structures and the MF-FEB constraint structures had average rmsd of 1.4 Å and 0.8 Å, respectively, relative to the co-crystal structures (Table 2). However, the constraint reference structures produced from either AutoDock or co-crystal starting structures differed by ~1 Å after the equilibration phase of the MF-FEB calculations. AutoDock scores for each ligand-lysozyme complex showed little correlation with ΔG_exp measurements (r = 0.52), while the MF-FEB ΔΔG_binding calculations correlated weakly with the ΔG_exp measurements (r=0.67) (Table 2). The average deviation between AutoDock scores and ΔG_exp measurements was 0.86 “kcal/mol”, whereas the average deviation between MF-FEB ΔΔG_binding and ΔG_exp measurements was 1.5 kcal/mol. However, these differences in the average deviation were not statistical different (two-tailed Student T-test, p=0.23). These results implied that AutoDock scores and MF-FEB calculations would likely be unable to correctly rank-order ligands with <10-fold differences in equilibrium dissociation constants.

Table 2.

MF-FEB Predictions Performed with Self-docked Poses ^a

Ligands	Experimental	AutoDock4		MF-FEB
	ΔGexp (kcal/mol)	rmsd (Å)	Score (kcal/mol)	rmsd (Å)	ΔΔGbinding (kcal/mol)
n-butylbenzene	−6.7 ± 0.02	1.0	−5.24	1.2	−11.3 ± 1.2
i-butylbenzene	−6.5 ± 0.06	1.7	−4.97	0.4	−7.3 ± 0.1
ethylbenzene	−5.8 ± 0.07	1.3	−4.46	0.4	−5.9 ± 0.1
benzofuran	−5.5 ± 0.03	2.2	−4.77	2.1	−6.2 ± 0.5
benzene	−5.2 ± 0.16	1.1	−4.00	0.7	−4.4 ± 0.7
indole	−4.9 ± 0.06	1.5	−5.05	0.6	−3.8 ± 0.2
p-xylene	−4.7 ± 0.06	1.3	−4.54	0.6	−7.0 ± 0.6
o-xylene	−4.6 ± 0.06	1.1	−4.51	0.7	−6.4 ± 0.2

^aThe listed root-mean-square deviation (rmsd) compared the co-crystal structures to either AutoDock-generated or MD-FEB poses. Only non-hydrogen atoms were used to tabulate rmsd values. The MF-FEB calculations were repeated 3 times with different starting seeds. The ΔG_exp data was included for ease of reference.

In more demanding experiments, the control set used the apo lysozyme structure as a target for AutoDock and MF-FEB calculations (Table 3). These simulations would be characteristic of approaches used for virtual screening where numerous ligand structures would be tested for binding to a single protein conformation. In these cross-docked experiments, the AutoDock program positioned the test ligands within the apo lysozyme structure in orientations that approximated the experimentally determined co-crystal structures (average rmsd ~1.6 Å) (Table 3). The MF-FEB molecular dynamics calculations typically repositioned the ligands so they more closely matched the co-crystal structures (average rmsd ~1.4 Å). The observed displacements of the docked ligands relative to the corresponding X-ray structures were largely due to the conformation of Val111 in the apo structure, which reduced the volume of the lysozyme apo binding site relative to the observed co-crystal structures. MF-FEB calculations performed with the AutoDock cross-docked poses as a starting conformation differed an average of ~1.4 kcal/mol from the ΔG_exp measurements (Table 3). However, the set of individual MF-FEB ΔΔG_binding calculations correlated poorly with ΔG_exp measurements (r = −0.16). As observed for MF-FEB calculations that used self-docked poses, these cross-docked MF-FEB results implied that MF-FEB calculations would likely be unable to correctly rank-order ligands with <10-fold differences in equilibrium dissociation constants.

Table 3.

MF-FEB Predictions using an Apo Lysozyme Protein Structure as the Docking Target ^a

Ligands	Experimental	Autodock4		MF-FEB
	ΔGexp (kcal/mol)	rmsd (Å)	Score (kcal/mol)	rmsd (Å)	ΔΔGbinding (kcal/mol)
n-butylbenzene	−6.7 ± 0.02	1.6	−6.20	1.6	−3.5 ± 0.4
i-butylbenzene	−6.5 ± 0.06	1.7	−5.50	1.7	−3.9 ± 0.6
ethylbenzene	−5.8 ± 0.07	1.4	−4.84	0.9	−7.3 ± 0.2
benzofuran	−5.5 ± 0.03	2.1	−4.69	2.1	−5.5 ± 0.6
benzene	−5.2 ± 0.2	1.3	−3.72	0.5	−4.5 ± 1.1
indole	−4.9 ± 0.06	1.3	−5.03	1.6	−3.0 ± 0.2
p-xylene	−4.7 ± 0.06	1.4	−4.37	1.8	−4.4 ± 1.0
o-xylene	−4.6 ± 0.06	1.8	−4.50	0.8	−5.9 ± 2.4

^aFor the MF-FEB calculations, three replicate calculations were performed. The experimental binding data is repeated for ease of reference. The root-mean-square deviation (rmsd) compared the co-crystal structures to either AutoDock-generated or MD-FEB poses.

MF-FEB calculations initiated with either AutoDock-generated or co-crystal ligand conformations generally produced similar values. On average, more accurate MF-FEB ΔΔG_binding calculations occurred in cases where the AutoDock structures most closely reproduced the available co-crystal structures. Docking against an apo protein that had binding site conformational differences relative to the co-crystal structure produced ligand structures that were displaced from the co-crystal structure and generally produced less accurate agreements between MF-FEB ΔΔG_binding and ΔG_exp values.

Receptor binding site flexibility is a challenge for docking programs.^{16, 19, 20, 54, 55} Some approaches have modeled receptor flexibility by combining docking calculations with receptor molecular dynamics (MD).⁵⁶ However, the MD performed during the above MF-FEB calculations was not sufficiently lengthy to enable significant changes in the receptor binding site conformation. More accurate MF-FEB predictions may result from calculations that incorporate receptor flexibility.^57,58

Enrichment and Discrimination Characteristics of MF-FEB-based Virtual Screening

Although relatively accurate binding free energies could be calculated using the bound conformations that resulted from docking ligands in the control set to the apolysozyme, the average error of ~1.4 kcal/mol for these calculations was not sufficiently accurate to produce a high correlation to the experimental binding energies that spanned only 2.1 kcal/mol. Since virtual screening experiments require discrimination between molecules that bind to the target protein (binders) and molecules that do not bind to the target protein (non-binders), the free energy range for these molecules includes both positive and negative values and likely spanned a larger range of free energies than existed in the control set. Thus, a small-scale virtual screening experiment was performed to determine if the accuracy of MF-FEB calculations would be sufficient to distinguish between binding and nonbinding molecules. This experiment used apo T4 lysozyme L99A as the target protein and a library of 16 known binders and 14 known non-binders known as the screening set (Table 4). In this experiment, a correlation coefficient between experimental and calculated FEB could not be determined as the ΔG_exp for the non-binders was unknown. However, this experiment provided insight on library enrichment, ligand discrimination, the responsiveness of the energy functions, and the role of solvation in binding predictions.

Table 4.

Small-scale Virtual Screening of T4 Lysozyme L99A against a Library of 30 Ligands ^a

Ligand	Experimental	AutoDock4	MF-FEB
	ΔGexp (kcal/mol)	Score (kcal/mol)	Δ ΔGbinding (kcal/mol)	ΔGsite (kcal/mol)	ΔGsolvation (kcal/mol)
n-butylbenzene	−6.70 ± 0.02	−6.20	−3.5 ± 0.4	−4.6 ± 0.2	−1.0 ± 0.5
propylbenzene	−6.55 ± 0.02	−5.46	−8.3 ± 0.6	−9.1 ± 0.7	−0.8 ± 0.1
isobutylbenzene	−6.51 ± 0.06	−5.50	−3.9 ± 0.6	−5.3 ± 0.5	−1.4 ± 0.3
ethylbenzene	−5.76 ± 0.07	−4.84	−7.3 ± 0.2	−8.5 ± 0.3	−1.2 ± 0.2
thianaphthene	−5.71 ± 0.05	−5.07	−7.0 ± 0.5	−10.0 ± 0.2	−3.0 ± 0.4
toluene	−5.52 ± 0.04	−4.19	−6.4 ± 0.4	−7.6 ± 0.06	−1.1 ± 0.4
benzofuran	−5.46 ± 0.03	−4.69	−5.5 ± 0.6	−9.5 ± 0.5	−4.0 ± 0.2
4-ethyltoluene	−5.42 ± 0.01	−5.77	−7.3 ± 0.1	−8.6 ± 0.06	−1.2 ± 0.03
benzene	−5.19 ± 0.16	−3.72	−4.5 ± 1.1	−5.2 ± 1.2	−0.7 ± 0.2
indene	−5.13 ± 0.01	−5.03	−6.1 ± 1.0	−9.3 ± 0.3	−3.2 ± 0.6
3-ethyltoluene	−5.12 ± 0.02	−5.72	−6.6 ± 0.4	−7.7 ± 0.2	−1.1 ± 0.3
indole	−4.89 ± 0.06	−4.85	−3.0 ± 0.2	−10.2 ± 0.2	−7.2 ± 0.3
m-xylene	−4.75 ± 0.15	−4.33	−5.2 ± 0.4	−6.1 ± 0.2	−0.9 ± 0.3
p-xylene	−4.67 ± 0.06	−4.37	−4.2 ± 1.0	−5.3 ± 1.2	−1.1 ± 0.4
o-xylene	−4.60 ± 0.06	−4.50	−5.9 ± 2.4	−6.9 ± 2.5	−1.2 ± 0.4
2-ethyltoluene	−4.56 ± 0.06	−5.53	−6.9 ± 0.9	−7.9 ± 0.5	−1.0 ± 0.7
pyridine	NB	−3.30	−1.0 ± 0.4	−5.4 ± 0.4	−4.4 ± 0.3
phenol	NB	−4.10	−1.1 ± 0.4	−7.4 ± 0.3	−6.2 ± 0.2
cyclohexane	NB	−4.07	−1.6 ± 1.1	−0.2 ± 1.6	1.4 ± 0.5
p-cresol	NB	−4.55	−2.0 ± 0.3	−7.9 ± 0.6	−5.9 ± 0.3
1,1-diethylurea	NB	−3.96	2.2 ± 0.5	−8.8 ± 0.4	−11.0 ± 0.8
aniline	NB	−3.99	−3.0 ± 0.8	−8.7 ± 0.5	−5.7 ± 0.3
benzyl alcohol	NB	−4.47	−0.02 ± 1.3	−7.4 ± 0.9	−7.4 ± 0.5
trans- cinnamaldehyde	NB	−5.56	−1.8 ± 0.4	−8.0 ± 0.12	−6.3 ± 0.4
tert- butylbenzene	NB	−5.09	−6.7 ± 1.3	−8.1 ± 1.2	−1.4 ± 0.3
ethanol	NB	−2.13	5.6 ± 0.1	2.3 ± 0.2	−3.4 ± 0.3
quinoline	NB	−5.01	−3.7 ± 0.5	−10.2 ± 0.7	−6.5 ± 0.2
1-heptoanol	NB	−5.19	−4.8 ± 0.6	−8.0 ± 0.9	−3.3 ± 0.6
azulene	NB	−5.38	−0.8 ± 0.3	−4.6 ± 0.3	−3.8 ± 0.1
furan	NB	−2.76	−3.7 ± 0.3	−4.2 ± 0.2	−0.4 ± 0.1

^aListed are ΔG_exp observations and calculated AutoDock scores and MF-FEB ΔΔG_binding. NB indicates a non-binding molecule (experimentally determined).

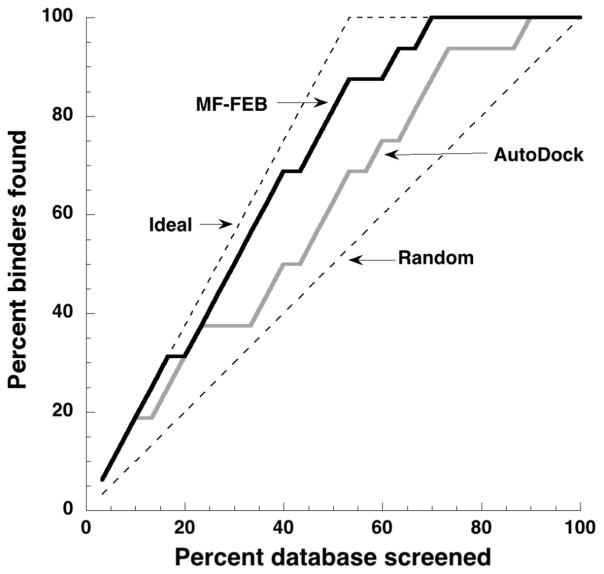
Enrichment curves (Fig. 1) that compared the percent of binders relative to the energy-ranked virtual database were constructed from the information in Table 4. Ranking the compound library by either AutoDock score or MF-FEB ΔΔG_binding identified known lysozyme binders as the first three hits (Table 4, Fig. 1). Moreover, the top scoring hit in each method corresponded to one of the strongest lysozyme binders in the screening set. However, after the initial three successful hits, the percentage of binders predicted by AutoDock scores began to approach a random distribution. In contrast, there were very few false positive hits using MF-FEB ΔΔG_binding calculations, and the percentage of binders identified relative to percentage of hits examined closely followed an ideal distribution. One of the few false positive MF-FEB predictions was tert-butylbenezene, which both scoring methods predicted to be a lysozyme binder. Tert-butylbenezene was an interesting non-binding ligand since it was chemically similar to the two strongest binders in the screening set. It is possible that tert-butylbenezene was experimentally classified as a non-binder because it could not enter the lysozyme binding site as opposed to having unfavorable interactions with the binding site; this restriction on binding would not be recognized by either the AutoDock or MF-FEB calculations.

Figure 1.

Enrichment curve showing AutoDock and MF-FEB results for small-scale virtual screening of T4 lysozyme L99A against a library of 16 known binders and 14 known non-binders. The ideal line represents a best-case prediction with no false positives. The random line corresponds to a random distribution of binders and non-binders.

The ΔG_exp for ligands in the co-crystal test set spanned 2.1 kcal/mol. In contrast, the range of free energies should be greater in the screening set since both non-binders and binders were included. The AutoDock calculations displayed similar scoring ranges for both binders and non-binders, with AutoDock scores for the screening set spanning ~4 kcal/mol (Table 4, Fig. 2) and scores for the bound ligands of the screening set spanning 2.5 kcal/mol (Table 4, Fig. 2). This small response range of AutoDock scores was consistent with previous virtual screening experiences in our laboratory (data not shown). In contrast, MF-FEB values calculated for the screening set spanned ~14 kcal/mol, and the majority of non-binders were predicted to have ΔG_binding > −2 kcal/mol. (Table 4, Fig. 2). MF-FEB energies were significantly better than AutoDock scores at discriminating between binders and non-binders. The average AutoDock score for lysozyme binders and non-binders was −5.0±0.3 and −4.3±0.5 kcal/mol, respectively. The p-score between these two groups was 0.015, which suggested a weak statistically relevant difference between the two groups. In contrast, the average MF-FEB ΔΔG_binding for lysozyme binders and non-binders was −5.7±0.7 and −1.6±1.6 kcal/mol respectively. The p-score between these groups was 0.00009, indicating the discrimination between the two groups based on MF-FEB energies was highly significant.

Figure 2.

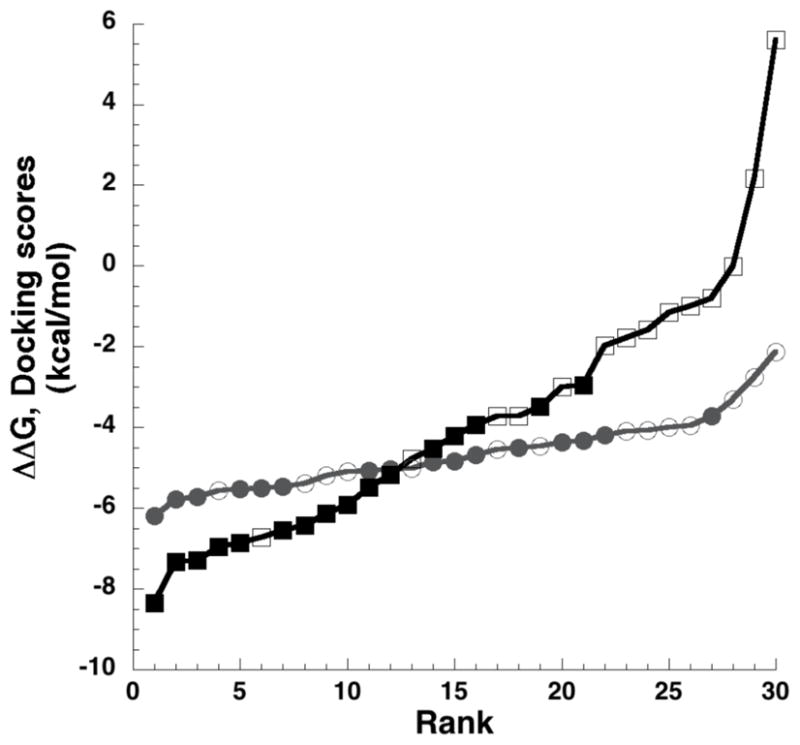
Energy distribution of ligands rank-ordered by AutoDock score (circles) or MF-FEB ΔΔG_binding (squares). Filled and unfilled markers represent lysozyme binders and non-binders, respectively.

Overall, the screening set was more highly enriched for lysozyme binders when ordered by MF-FEB energies instead of AutoDock scores. However, it was difficult to compare the enrichment observed in this MF-FEB study to previous comparative enrichment studies of docking programs^21–24 because the number of compounds in the screening set was small and contained similar numbers of binders and non-binders.

The high degree of discrimination observed with the MF-FEB calculations may arise from its accurate treatment of solvation effects. The majority (11 of 14) of non-binders in the screening set were weakly polar, whereas the T4 lysozyme L99A binding site was predominantly hydrophobic. The MF-FEB ΔΔG_binding was the differential energy for the ligand interacting with the protein (ΔG_site) and the solvent (ΔG_solvation) (Table 4). The average ΔG_site for binders and non-binders was -7.6±0.9 and −6.2±1.8 kcal/mol, respectively, and the p-score between these groups was 0.096. The average ΔG_solvation for binders and non-binders was −1.9±0.8 and −4.6±1.6 kcal/mol, respectively, with a p-score of 0.005 between these groups. Thus, it appeared that the discrimination between binders and non-binders observed with the MF-FEB calculations was largely driven by solvation calculations, which was consistent with the physical nature of ligands and binding site. The screening set contained 3 non-binders that lacked polar groups. Tert-butylbenzene, already discussed, ranked high (i.e., lower AutoDock score or MF-FEB energy relative to other ligands) in both docking and MF-FEB calculations. Cyclohexane and azulene non-binders had unfavorable MF-FEB energies due to steric constraints that resulted in weak ΔG_site contributions. The screening set highlighted the importance of determining both solvation and interaction energy contributions for the accurate calculation of the binding free energy.

Despite the promising discrimination observed with the lysozyme small-scale virtual screen, the MF-FEB calculations suffered from many of the drawbacks common to all molecular mechanical calculations. The available force fields were approximate, and could be improved by including polarizable force fields.^{37, 59} Convergence of the molecular dynamics simulations was a concern, since the variations in replicate MF-FEB calculations might suggest that some systems were not fully converged. In addition, the molecular dynamics simulations must sufficiently sample protein-ligand conformation space to ensure accurate calculation of solvation and interaction energies. Moreover, these simulations only permit local protein conformational changes and do not allow long-range protein motions or partial charge redistribution during protein-ligand interactions. However, in spite of these limitations, the use of MF-FEB energies with AutoDock-determined poses provided a powerful approach to discriminate between binders and non-binders in a virtual screening experiment.

CONCLUSIONS

MF-FEB energies correlated strongly with experimental binding energies when accurate structures of the lysozyme-ligand complex were used to initiate the MF-FEB calculations. As the deviation between the crystallographic and docked structures increased, the average error of the MF-FEB calculations only slightly increased. However, small-scale virtual screening results showed that rank-ordering libraries based on MF-FEB energies of docking poses could provide significant enrichment relative to rank-ordering based on AutoDock scores. The MF-FEB rescoring provided significant discrimination between micromolar binders and non-binders. These results suggested that rescoring docking poses with MF-FEB calculations could significantly reduce the false positive rate of conventional virtual screening projects.

Currently, limits on the accuracy of MF-FEB calculations initiated from docking poses may prevent these calculations from being used to design ligands with incremental improvements (e.g., 1.5 kcal/mol) in binding free energies. However, since these calculations can discriminate between binders and non-binders, they could be used to ensure that novel molecules proposed for chemical synthesis will bind to desired molecular targets. The results of this study were encouraging and merit further testing against larger virtual libraries.