Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2011 Dec 1.
Published in final edited form as: J Speech Lang Hear Res. 2010 Jul 19;53(6):1514–1528. doi: 10.1044/1092-4388(2010/09-0127)

Relation of vocal tract shape, formant transitions, and stop consonant identification

Brad H Story 1, Kate Bunton 1
PMCID: PMC3145491  NIHMSID: NIHMS309275  PMID: 20643794

Abstract

Purpose

The present study was designed to investigate the relation of formant transitions to place-of-articulation for stop consonants. A speech production model was used to generate simulated utterances containing voiced stop consonants, and a perceptual experiment was performed to test their identification by listeners.

Method

Based on a model of the vocal tract shape, a theoretical basis for reducing highly-variable formant transitions to more invariant formant deflection patterns as a function of constriction location was proposed. A speech production model was used to simulate vowel-consonant-vowel utterances for three underlying vowel-vowel contexts, and for which the constriction location was incrementally moved from the lips toward the velar part of the vocal tract. These simulated VCVs were presented to listeners who were asked identify the consonant.

Results

Listener responses indicated that phonetic boundaries were well aligned with points along the vocal tract length where there is a shift in the deflection polarity of either the second or third formant.

Conclusions

This study demonstrated that regions of the vocal tract exist that, when constricted, shift the formant frequencies in a predictable direction. Based on a perceptual experiment, the boundaries of these acoustically-defined regions were shown to coincide with phonetic categories for stop consonants.

Introduction

Stop consonants are produced by temporarily occluding the vocal tract at a specific location along its length. The ability of a talker to grade the shape, degree, and timing of the occlusion allows for production of a variety of acoustic events that may signal the place of articulation. These events can be roughly grouped into categories of bursts, periods of either silence or voicing that occur during an occlusion, and formant transitions.

The acoustic characteristics of bursts and silence result primarily from the location and duration of the consonantal occlusion, and its subsequent release. When the vocal tract is closed at a particular location, and the velopharyngeal port is closed, there is a cessation of radiated sound at the lip termination, thus creating a silent period that may be augmented with voiced sound radiated from the skin surfaces. Simultaneously, static pressure builds up in the cavity behind the constriction that, when released, will rapidly drop and generate a brief “burst” of turbulent sound. This burst primarily excites the upper resonances of the vocal tract shape that exists just following release of the constriction (Stevens & Blumstein, 1978), thus carrying information that could, at least partially, specify constriction location (Halle et al., 1957).

Formant transitions reflect the overall change in shape of the vocal tract during speech production. Vocal tract movements from one vowel to another tend to produce slowly-varying and continuous transitions of the formant frequencies, whereas the onset and offset of the vocal tract movements needed to impose and release consonantal constrictions result in rapidly changing transitions (Stevens & House, 1955, 1956; Lehiste & Peterson, 1961; Öhman, 1966). Although formant transitions are thought to play a role in specification of constriction location (Cooper et al., 1952; Delattre et al., 1955; Harris et al., 1958), the coarticulation of vowels and consonants causes their contributions to the formant transitions to be superimposed, thus creating highly context-dependent acoustic characteristics. Thus, the actual formant transitions produced by imposing a consonantal constriction at a particular location in the vocal tract will depend on the vowel context.

The relative perceptual significance of bursts and formant transitions as cues for place of articulation has been a frequent topic of investigation. Early experiments in speech perception (e.g., Cooper et al., 1952; Delattre et al., 1955; Harris et al., 1958) demonstrated the importance of direction and slope of the second and third formant transitions (F2 and F3). A curious, and widely cited, result of these early studies was that a rising F2 transition in the syllable/di/could evoke the same perceptual response for the initial consonant (i.e./d/) as a falling F2 transition in the syllable/du/(Liberman et al., 1954). Context dependence of this sort has often been used as an example of the presumed lack of acoustic invariance in the speech signal, and taken as evidence that perception of speech is referent to the speech production system.

A competing view is that place of articulation is invariantly-specified by the gross characteristics of a short-time spectrum sampled to include the burst and the initial portion of the formant transitions (Halle et al., 1957; Fant, 1960, 1973; Winitz et al., 1971; Stevens & Blumstein, 1978). This spectral representation is intended to integrate the consonant release and the initial vocalic portions that follow into a single invariant event rather than a sequence of events separated in time, perhaps in a manner similar to that of the auditory system (Stevens, 1975; Blumstein & Stevens, 1979). The formant transitions are thought to smoothly link the integrated onset spectrum with the following vowel such that discontinuities are minimized (Cole & Scott, 1974; Stevens & Blumstein, 1978), but do not provide the primary cues to place of articulation (Kewley-Port, 1982). Although acoustic analysis and some limited perceptual studies have supported this view (Blumstein and Stevens, 1979 & 1980), it is not clear that formant transitions are, in fact, secondary to the burst or integrated onset spectrum for processing connected speech. Based on transposition and recombination of portions of spoken syllables, Dorman et al. (1977) suggested that bursts and transitions are functionally equivalent for listeners. Blumstein et al. (1982) reported that the gross shape of the onset spectrum is apparently used by listeners for categorizing place of articulation but does not provide cues that are any more primary than the information provided by the formant frequencies present at the onset of voicing (i.e., the initial portions of the formant transitions). Similarly, Walley and Carrell (1983) demonstrated that, when presented with conflicting burst and formant transition information, listener responses tended to coincide with the formant transitions, thus indicating the importance of time-varying information for perceiving place of articulation. Both Kewley-Port (1983) and Lahiri et al. (1984) have also proposed that time-varying information following release of a constriction is important for distinguishing place of articulation, although formant transitions were not specifically implicated as the primary acoustic property.

Studies of consonants that include perceptual experiments typically use stimuli that are either generated with a formant-type synthesizer or based on manipulations of recorded natural speech. Formant synthesis is perhaps most common as it allows for construction of acoustic continua in which an individual acoustic feature, such as the onset frequency of a particular formant, is varied by some precise amount from stimulus to stimulus. In either case, the manipulation of acoustic properties is typically performed without consideration of how, or if, the resultant characteristics could actually be produced by a human vocal tract. That is, although the stimuli may follow some systematic change in acoustics, the acoustic patterns they contain may not be based on the realities of speech production. There are, in fact, few studies in which the stimuli for a perceptual experiment have been generated with even a simple simulation1 of the speech production process where, for example, the formant frequencies result directly from the resonant structure of the vocal tract tube rather than from idealizations of formant frequency patterns. Although some research in this direction has been reported by Carré and Divenyi (2000) and Carré et al. (2002) for vowel transitions and stop consonants, and by Scully and Allwood (1985) for fricatives, the contributions to the literature have been limited.

The purpose of the present study was to further investigate the relation of formant transitions to place-of-articulation for stop consonants. The approach was to use an area function model of the vocal tract in which a neutral configuration is modulated by two levels of superimposed movement (Story, 2005a). The first level supports overall vocal tract shape changes that produce vowel-to-vowel transitions, and in the second level localized constrictions can be imposed to occlude the vocal tract at a specific location. Resultant formant transitions, present in the speech signal, can thus be considered to originate first from perturbation of a neutral vowel formant pattern by the vowel-dependent modulations, and secondly from the perturbation of the intantaneous vowel-dependent formants by the localized constrictive modulations. Perhaps formant transitions can be “demodulated” such that their contribution to the speech signals is assessed relative to the underlying vowel-vowel transition. In this view, it is hypothesized that the pattern of time-varying formant deflections (i.e., deflection above or below the vowel transition) due to the consonantal modulation is systematically-related to place of articulation, and essentially removes the vowel-dependence of transitions.

The article is organized to achieve two specific aims. First, the theoretical basis for proposing formant deflection patterns as a potentially invariant relation is presented with regard to the structure of the vocal tract model. The second aim was to use speech signals produced by the model (as part of a more complete speech simulation system) to determine if listeners are sensitive to this particular form of invariance.

Kinematic model of the vocal tract area function

The area function model has been largely developed from analyses of data based on magnetic resonance imaging (MRI) of the vocal tract (Story et al., 1996, 1998; Story & Titze, 1998; Story, 2005b). The current form of the model, as described in Story (2005a), operates with respect to a functional division of the articulatory system into separate vowel and consonant components (e.g. Ohman 1966, 1967; and Perkell, 1969). It consists of multiple hierarchical tiers, each of which is capable of imposing particular types of perturbation on the vocal tract shape. In the first tier, vowel-to-vowel transitions can be produced by perturbing a mean vocal tract configuration with two shaping patterns called modes. According to the model, a time-dependent vowel-like area function V (x, t) is generated by,

V(x,t)=π4[Ω(x)+q1(t)φ1(x)+q2(t)φ2(x)]2 (1)

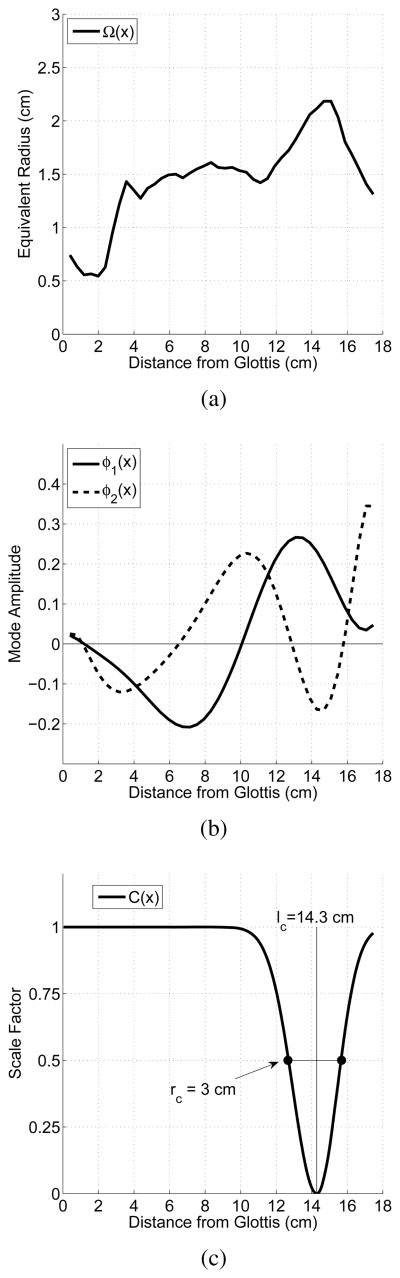
where x is the distance from the glottis and Ω(x), φ1(x), and φ2(x) are the mean vocal tract diameter function and modes, respectively, as defined in Story (2005a). The time-dependence is produced by the mode scaling coefficients q1(t) and q2(t). The squaring operation and scaling factor of π/4 converts the diameters to areas.

The mean diameter function and the two modes are shown in the upper and middle panels of Figure 1, respectively, for an adult male vocal tract (Story et al., 1996; Story & Titze, 1998) with a length of 17.5 cm. When q1 = q2 = 0, the area function ( π4Ω2(x)) produces nearly equally spaced formant frequencies, and thus is considered to be a “neutral” vocal tract configuration. Other combinations of q1 and q2 can generate a wide variety of vowel-like shapes (Story & Titze, 1998; Story, 2009a).

Figure 1.

Figure 1

Open in a new tab

Components of the area function model defined by Eqns. 1–2. (a) Equivalent diameter function representing the mean (or neutral) shape of the vocal tract, Ω(x), (b) two shaping modes φ1(x) and φ2(x), and (c) example constriction perturbation function with constriction location lc = 14.3 cm from the glottis, and constriction extent rc = 3 cm.

Production of consonants results from a second tier of perturbation that imposes constrictions on the underlying vowel or vowel-vowel transition. This is generated with a scaling function C(x) that extends along the length of the vocal tract. The value of C(x) is equal to 1.0 everywhere except in the region of the desired constriction location lc. An example is shown in the bottom panel of Figure 1 where the constriction location lc was specified to be 14.3 cm from the glottis, approximately the location for producing an alveolar consonant. The shaping of the constriction around lc is determined by a Gaussian function that includes control parameters for constriction extent along the tract length, and skewness. The extent rc is defined as the distance between the half maximum points of C(x) and a skewing factor sc dictates the degree of asymmetry of the constriction. For the case shown in the figure, these two parameters have been set to rc = 3 cm and sc = 1.17 (i.e., this causes the extent posterior to lc to be slightly larger than the anterior portion). When any vowel-like area function is multiplied by C(x), the region in the vicinity of lc will be reduced in area, thus superimposing the constriction. For velar consonants rc would typically be set to larger values to more accurately represent the extent of a constriction produced by the tongue body. The constriction function can be made time dependent with a temporal activation parameter called the consonant magnitude mc(t), such that it will impose the constriction at a specific time and location in the vocal tract.

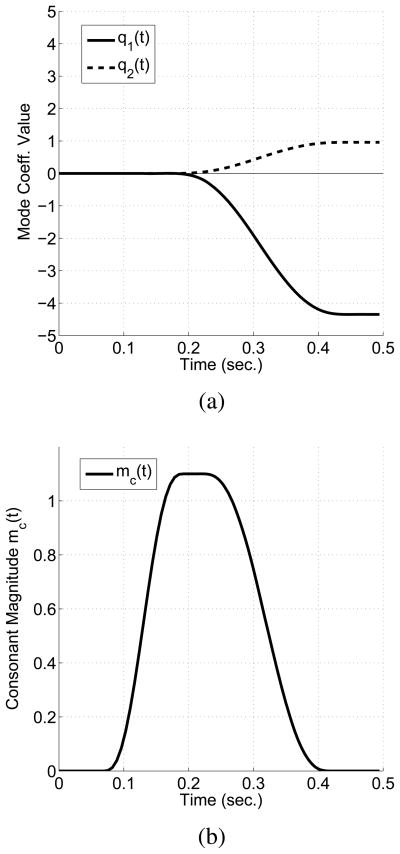
Shown in Fig. 2a is an example of time-varying mode coefficients that generate an area function change approximating a transition from the neutral shape (henceforth referred to as [ɑ]) to an [i] with a total duration of 0.5 seconds. Both q1(t) and q2(t) are held at zero for the initial 0.2 seconds and then transition toward values that generate the [i]. Other vowel shapes would require different contributions from each coefficient. The time-varying area function V (x, t) produced when these q1(t) and q2(t) are used in Eqn. 1, is displayed in Fig. 3a. The change in shape from a fairly uniform pharyngeal section and slightly expanded oral cavity to one where the oral cavity is constricted and the pharynx expanded, can be observed as time progresses over the 0.5 second duration. The magnitude of the consonant superposition function mc(t) that activates and then removes a constriction at a specified location (lc) is shown in Fig. 2b. When this function is equal to 1.0 the area at the constriction location is zero. Note that in the example, mc(t) exceeds 1.0 for a short time (between about 0.15–0.27 sec.). This is permitted so that the constriction can spread along a portion of the vocal tract length around the constriction location rather than be focused only at a single point (Story, 2005a). The time-varying constriction function C(x, t) produced with the combination of mc(t), and the C(x) shown previously in Fig. 1c, is plotted in Fig. 3b. It can be seen that the influence of the constriction spreads across time and space according to the chosen parameters of the function. This particular specification of the temporal activation and release of the consonant was roughly based on the constriction timing functions reported in Story (2009b) that were derived from articulatory data collected for vowel-consonant-vowel (VCV) utterances.

Figure 2.

Figure 2

Open in a new tab

Example time-dependent area function model parameters. (a) Time-varying mode coefficients q1(t) and q2(t) that produce an approximate [ɑi] transition, and (b) time-dependent consonant magnitude function that governs the onset, occlusion, and offset of the constriction perturbation.

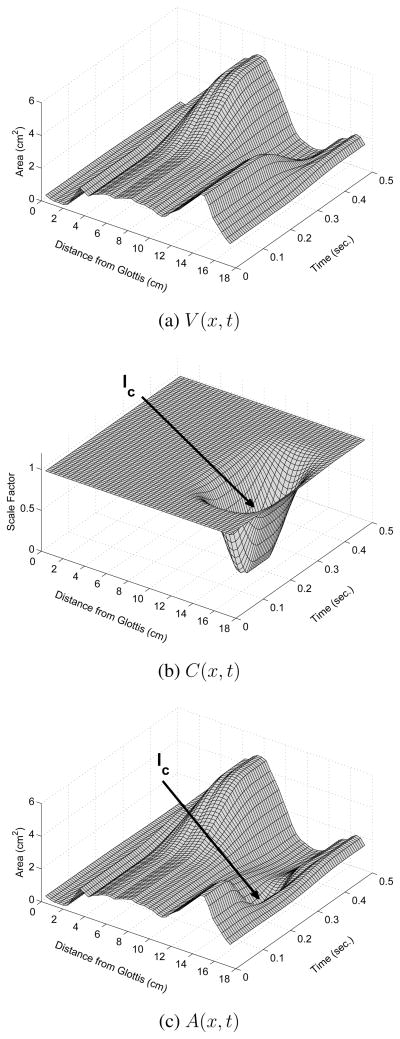
Figure 3.

Figure 3

Open in a new tab

Graphical illustration of generating a 3D time-varying area function for a VCV with Eqns. 1–2. In each plot, distance from the glottis is represented on the leftmost diagonal axis, time is on the rightmost diagonal axis, and area is on the vertical axis. (a) Time-varying mode coefficients q1(t) and q2(t) that produce an approximate [ɑi] transition, (b) time-dependent consonant perturbation function based on the functions in Figs. 1c and 2; the arrow points to the constriction location, and (c) composite area function resulting from the element-by-element and sample-by-sample product of the functions in (a) and (b).

A composite area function A(x, t) is generated by the vocal tract model as the product of each element along the x-dimension of V (x, t) and C(x, t) such that at any given time sample tn,

A(xi,tn)=∏i=1NxV(xi,tn)C(xi,tn) (2)

where Nx is the number of cross-sectional areas representing the complete area function. All area functions used in the present study consisted of Nx = 44 contiguous “tubelet” sections as defined in Story (2005a). The A(x, t) that results from combining the example vowel and consonant functions in Figs. 3a and 3b, is shown in Fig. 3c. The time-dependent consonant constriction is superimposed on the underlying vowel-vowel (VV) transition, thus producing a coarticulated VCV sequence.

Formant frequency patterns of time-varying area functions

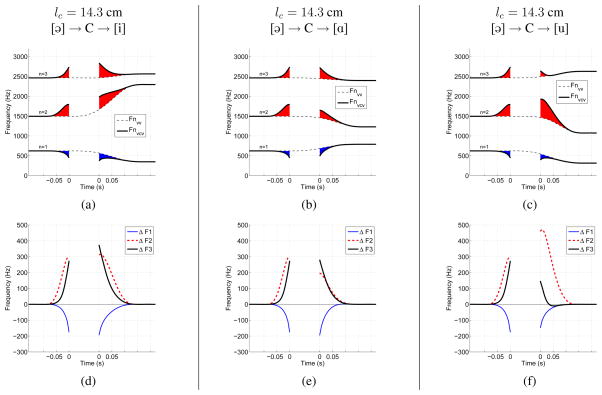
Formant frequencies were obtained over the time course of the VV transition in Fig. 3a and the composite VCV in Fig. 3c by calculating a frequency response for the area function associated with each time sample. This was carried out by exciting a one-dimensional waveguide with a flow impulse and transforming the response to a spectrum. The calculation included energy losses due to yielding walls, viscosity, heat conduction, and radiation, but to maintain simplicity did not include coupling of any side branch cavities such as the trachea, piriform sinuses or nasal tract. Formant frequencies resulting from the tract shape at a given time sample were determined by finding the peaks in the associated frequency response function. The resulting formant transitions are displayed in Fig. 4a where the VV is shown with dashed lines and the VCV as solid lines. The breaks in the VCV formants indicate the time period for which the vocal tract is occluded. Also note that the time axis has been modified such that the time points prior to the consonant occlusion are negative and end at zero, and times following the release of the occlusion are positive and begin at zero. This is similar to the time axis used by Stevens (2000, p. 367) for displaying formant contours of stop consonants.

Figure 4.

Figure 4

Open in a new tab

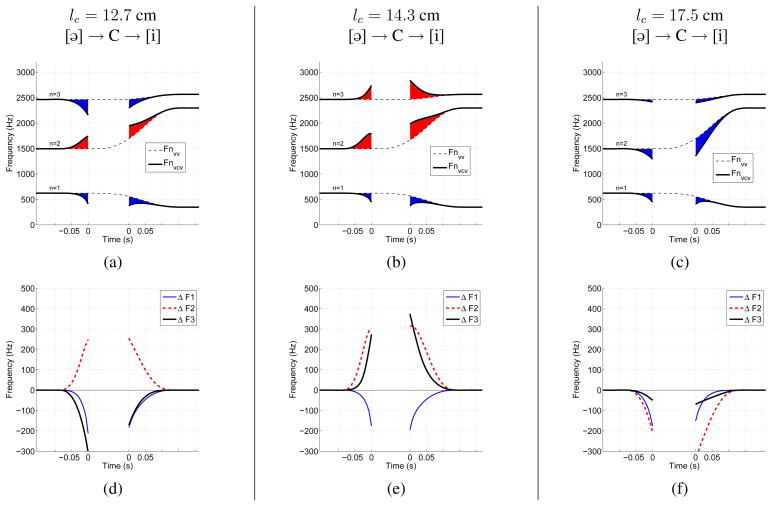
Formant frequencies and formant deflections calculated for time-varying area functions of VVs and VCVs, like those in Figs. 3a and 3c. For the plots in the top row (a,b,c), dashed lines indicate the calculated formants for each VV transition only, while the thick solid lines are the formants for the VCV. The shaded portions indicate the deflection of the formant frequencies generated by the VCV away from those generated by the VV alone (red indicates an upward deflection and blue a downward deflection). The plots in the bottom row (d,e,f) show time-dependent differences (deflections) between the formant frequencies generated by the VCV relative to those generated by the VV alone, based on Eqn. 3. Negative and positive time on the x-axis of each plot denotes the constriction onset and offset periods, respectively. The time between the two “zero” points is the period of vocal tract occlusion. Each column of plots corresponds to a VV context of [ɑi], [ɑ ə], or [ɑu], and the constriction location is lc = 14.3 cm for all three cases.

Observation of the VCV formants indicates that F1 falls during the onset of the consonant while F2 and F3 both rise. During the offset, F1 and F3 reverse course such that they rise and fall, respectively, but F2 continues to rise. This is a well known characteristic of an alveolar consonant (i.e., lc = 14.3 cm for this example) followed by an [i] vowel. With access to the VV transition, however, it can also be observed that during the period of time where the area function shape is influenced by the superimposed constriction (approx. −0.07 to 0.12 sec.), the formants along the time course of the VCV are effectively perturbed from the formants of the underlying vowel, as indicated by the shaded portions in the plot. That is, the presence of a constriction deflects the formants away from the path they would otherwise have followed. In both the onset and offset portions of this VCV, F2 and F3 are deflected above the corresponding VV transition formants, whereas F1 is perturbed downward. When viewed in this manner, the context dependence imposed by the underlying vowel is removed.

The magnitude of the deflection for each formant can be quantified by calculating the differences between the VCV formant tracks and those of the underlying VV during the onset and offset periods by,

ΔFn(t)=Fnvcv(t)−Fnvv(t)n=1,2,3. (3)

Time-dependent ΔFn(t)’s calculated for the example formants in Fig. 4a are shown directly below in Fig. 4d. When the VCV and VV formant tracks are equal, the corresponding ΔFn yields zero, but when they differ the deflection pattern is directed downward or upward away from zero. Fig. 4d indicates a downward F1 deflection of nearly 200 Hz, whereas F2 and F3 are deflected upward by about 300 Hz or more.

Invariant property of formant deflection patterns

Shown in the middle and rightmost columns of Fig. 4 are formant and formant deflection plots for two additional VCV area functions. The constriction location, extent, skewing factor, and timing of the consonant magnitude were exactly the same as for the previous case, but the mode coefficients were modified to produce a transition from the neutral tract shape [ɑ] to the final vowels ə] and [u], respectively. The VCV formant transition pattern during the consonant onset is identical in all three cases because the initial vowel is the same, but it is noted that F2 rises during the offset portion only when the final vowel is [i]. When either ə] or [u] follow the consonant, F2 falls. Although the context dependence of F2 is well known from acoustic analysis of [di], [də], and [du] syllables, the plots in the bottom row of Fig. 4 indicate that the formant deflection patterns demonstrate the same polarities (deflection directions). Thus, when formant transitions are assessed with reference to the underlying formants of the VV, the direction of the formant deflections appears to be directly related to the location of the constriction, regardless of the vowel context on which the consonant is imposed.

Effect of constriction location on formant deflection patterns

Based on the area function model and frequency response calculations described in the previous section, deflections of the F1, F2, and F3 formant frequencies due to a consonant perturbation of an underlying VV transition were quantified as a function of constriction location. Three sets of time-varying VCV area functions were created in which the underlying VV consisted of a transition from the neutral tract shape [ɑ] to either [i], ə] or [u]. Within each VV context, the constriction location was moved incrementally in discrete 0.4 cm steps beginning at the lips and progressing posteriorly into the vocal tract over a distance of 8 cm. This distance spans the region of the vocal tract length typically used for production of American English consonants (cf. Story et al., 1996). The time-course of the constriction magnitude was set to be that shown previously in Fig. 2b. This resulted in twenty separate VCV area functions for each VV context; i.e., [ɑCi], [ɑCə], and [ɑCu] where “C” represents twenty different constriction locations.

To account for the typically larger extent and different shape of a constriction in the velar region than in the lip and alveolar regions (cf. Story et al., 1996, 2005a; Fant, 1960), rc and sc were both varied as a function of constriction location such that,

rc={0.43(Lvt−lc)+1.59cmforlc≥11.5cm3.97cmfor9.92≤lc<11.5cm (4)
sc={0.054(Lvt−lc)+1.0forlc≥11.5cm1.3for9.92≤lc<11.5cm. (5)

In each equation, lc is one of the twenty locations between the velar region and the lips, and Lvt = 17.5 cm is the overall vocal tract length. These linear relations are based on results reported in Story (2005a, p. 3239) where constriction extent and skewing factor were determined for MRI-based area functions of stop consonants. They are intended to provide only a rough approximation of the changes to constriction shape with location, whereas a more complete description would require additional analysis of articulatory data.

With the methods described previously, time-varying formant frequencies and formant deflection patterns were calculated for each of the twenty VCV area functions generated within the three different VV contexts. To demonstrate the effect of constriction location on the formant patterns, an example is given in Fig. 5 where the VV context is a transition from [ɑ] to [i]. In the left column (Figs. 5a & 5d) are the formants and associated deflection patterns for a constriction located 12.7 cm from the glottis. This is approximately in the region of the vocal tract where a velar consonant ([g] or [k]) would be produced. In this case, F1 and F3 are deflected downward from the VV transition while F2 is deflected upward. As the constriction is moved into the alveolar region, as shown for lc = 14.3 cm in the middle column, the F1 and F2 deflections maintain the same polarities as for the velar case, but F3 is now deflected upward from the underlying VV formants. This case was also shown in the previous figure (Figs. 4a & 4d), but is repeated here as an example of the change in formant deflection pattern as a function of constriction location. Placing the constriction at the lip termination resulted in a downward deflection of all three formants, as indicated by the plots in the rightmost column. The formant deflection patterns for other constriction locations, and in the other VV contexts, indicate variants of the same patterns shown in Fig. 5. These patterns will be used in a later section to facilitate interpretation of a perceptual experiment.

Figure 5.

Figure 5

Open in a new tab

This figure has the same layout as Fig. 4, but the difference is that the vowel context was kept constant as [ɑi], and the constriction location was set to 12.7 cm, 14.3 cm, and 17.5 cm, respectively, across the three cases.

Identification of consonants as a function of constriction location

Based on the simulations of vocal tract shape and corresponding formant calculations, it is proposed that the formant deflection patterns, as defined here, may provide a relatively context-independent property that could signal place of articulation. Although it is not clear how a listener may reference the formant transitions in a speech signal to the underlying VV transitions (which are not directly available in the signal), it is of interest to determine if listeners are sensitive to this particular type of invariance. Toward that end, an experiment was conducted in which audio stimuli were generated based on the three sets of time-varying VCV area functions described in the previous sections. The goal was to find out if a change in listeners’ identification of consonants embedded in the VCVs corresponded to changes in the polarity of the formant deflection patterns.

Audio stimuli

An audio sample with a duration of 0.5 seconds was generated for each VCV area function in each of the three sets with a voice source model that was acoustically and aerodynamically-coupled to a wave-reflection model of the supraglottal vocal tract (Liljencrants, 1985; Story, 1995). This is the same wave propagation algorithm used in previous sections to calculate the formant frequencies but was excited by a periodic voice source rather than an impulse. Although a tracheal section can be incorporated into the model, it was not used for the present study in order to eliminate the effects of tracheal resonances. These are potentially interesting effects (e.g., Lulich, 2009; Stevens & Keyser, 2009) but were beyond the scope of this study. The vocal tract shape, which extended from glottis to lips, was dictated at every time sample by a specific VCV area function in a given series. As described previously for the formant calculations, the wave propagation algorithm included energy losses due to yielding walls, viscosity, heat conduction, and radiation at the lips (Story, 1995).

The voice source model was based on a kinematic representation of the medial surface of the vocal folds (Titze, 1984, 2006). Control parameters consisted of fundamental frequency, length and thickness of the vocal folds, degree of posterior adduction, bulging of the vocal fold surface, and the respiratory pressure. Based on acoustic analysis of audio recordings of VCVs available in the x-ray microbeam database (Westbury, 1994) the fundamental frequency (F0) was varied according to the contour shown in the top panel of Fig. 6. The sharp increase in F0 occurs while the vocal tract is occluded and provides intonational stress on the second syllable of each VCV. For each sample the respiratory pressure was ramped from 1000 to 7840 dyn/cm2 in the initial 5 ms with a cosine function, and then ramped down from to 7840 to 1000 dyn/cm2 over the final 50 ms of the utterance. This maintained vibration of the vocal folds over the duration of the utterance so that each consonant was “voiced.” The other parameters were set to constant values throughout the time course of each utterance. The output of the vocal fold model is a glottal area signal that was coupled to the pressures and air flows in the vocal tract through aerodynamic and acoustic considerations as prescribed by Titze (2002). The resulting glottal flow was determined by the interaction of the glottal area with the time-varying pressures present just superior to the glottis. In addition, a noise component was added to the glottal flow signal if the calculated Reynolds number within the glottis exceeded 1200.

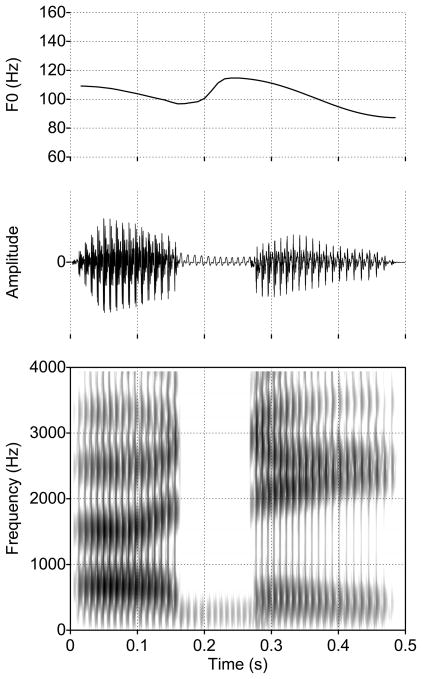
Figure 6.

Figure 6

Open in a new tab

Example of the fundamental frequency (F0) contour, waveform, and spectrogram of a synthetic speech sample produced in the [ɑCi] environment with lc = 14.3 cm. The top panel shows the F0 contour, the middle panel is the speech signal, and the bottom panel is the wide-band spectrogram of the the speech signal. Waveforms such as this were converted to an audio file for presentation in the listening experiment.

Shown in the middle panel of Fig. 6 is an example of a speech signal generated during production of a VCV. In this case the VV transition was [ɑi] and the consonant constriction was located 14.3 cm from the glottis. The corresponding wide-band spectrogram is shown in the bottom panel where the formant bands for F1, F2, and F3 can be observed to follow the same path as the formant contours in Fig. 5b. Extending from approximately 0.16–0.26 seconds is the duration of the occlusion, and the low-amplitude signal present during this period is sound radiated from the skin surfaces. Note that there is no apparent burst that occurs at the release of the consonant. This was deliberate since the focus for the present study was on formant transitions. It was assumed that an additional cue due to a transient noise source near the constriction would interfere with interpretation of the perceptual responses, even though the presence of a burst would have likely enhanced listener identification of consonants. Waveforms such as the one shown in Fig. 6 were generated for each VCV, converted to “wav” format audio files, and used as stimuli for the identification experiment. Three audio files containing all stimuli for the three different sets are available as supplemental online content associated with this article.

Listeners

Ten listeners (3 males and 7 females) with a mean age of 20.5 years (range = [18:22] years) participated in the perceptual experiment. Listeners passed a hearing screening (American Speech-Language-Hearing Association, 1997). They were all native speakers of American English and were undergraduate students at the University of Arizona. All procedures were approved by the Institutional Review Board at the University of Arizona.

Listening task

Individual listeners were seated in a sound treated room and audio samples were presented over a loudspeaker placed one meter in front of the listener. Sample presentation was controlled using the ALVIN interface (Hillenbrand & Gayvert, 2005). Each presentation consisted of a simulated VCV from one of the three VCV sets. The listeners were instructed to identify the consonant heard in a forced-choice paradigm, where the computer screen displayed buttons for the three English voiced stop consonants “b”, “d,” and “g.” Presentation of VCVs was blocked by set so that within each block listeners heard only VCVs relative to either the [ɑi], [ɑ ə], or [ɑu] VV transitions, and individual samples were randomly presented five times. Listeners participated in a single listening session that lasted no more than 45 minutes and they could take short breaks at their discretion.

Results

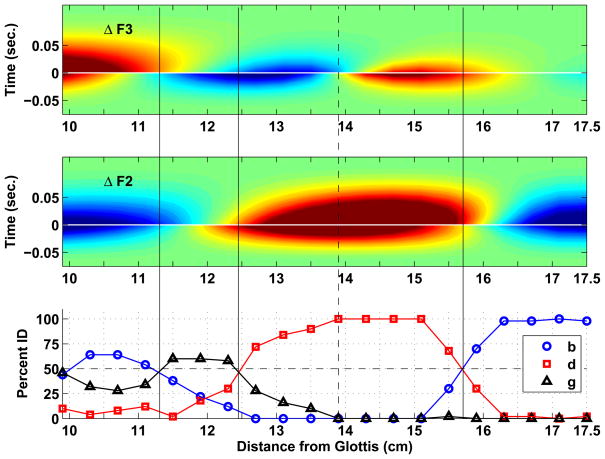
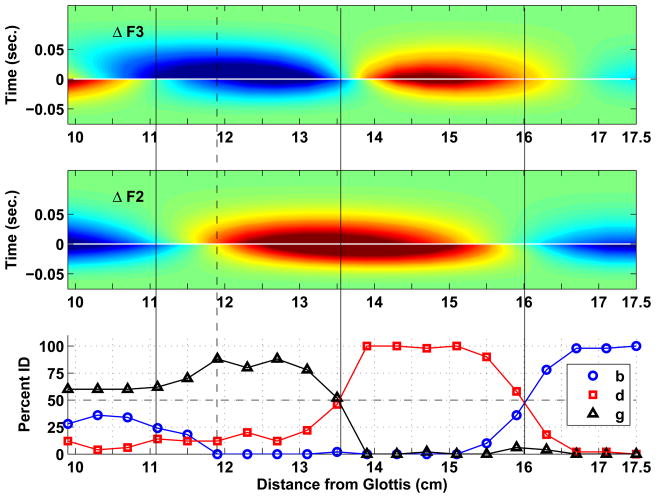
The identification results for the three sets of VCVs are presented in Figs. 7–9, along with plots that summarize the corresponding formant deflection patterns. In the middle and upper panels of each figure are contour plots constructed from the formant deflections calculated with Eqn. 3 for F2 and F3, respectively, for each of the twenty constriction locations. In each of these plots, the x-axis represents the range of constriction locations used to generate the VCVs (9.92–17.5 cm from the glottis), whereas the y-axis is time, where zero seconds represents the point of vocal tract closure and release, just as was shown in the formant deflection plots in the bottom rows of Figs. 4 and 5. The period of occlusion has been compressed and is indicated with a thin horizontal white line at zero seconds to conserve space. Negative and positive time correspond to the constriction onset and offset periods, respectively. Like color portions within each plot are contours representing constant magnitudes of formant deflection. Red indicates an upward deflection (positive) and blue a downward deflection (negative) relative to the formants of the underlying vowel, whereas light green is neutral and indicates no deflection. To enhance the representation of small formant deflections, the color map is scaled such the darkest blue corresponds to a deflection of −150 Hz and the darkest red to +150 Hz; deflections with absolute magnitudes greater than 150 Hz are set to the darkest blue or red value. When viewed along the y-axis of each plot, the contours indicate how the deflection of F2 and F3 from the underlying VV transition changes over the duration of the VCV for any given constriction location on the x-axis. It can also be observed along the vocal tract length (x-axis), that the deflection patterns alternate from “lobes” of red to blue, indicating a shift in polarity. Since the formant deflections for F1 were always negative in the oral part of the vocal tract, F1 contour plots are not presented.

Figure 7.

Figure 7

Open in a new tab

Contour plots based on the formant deflections determined with Eqn. 3 for all twenty time-varying area functions in the [ɑCi] set, and associated identification functions from the listening experiment. The middle and upper panels correspond to ΔF2, and ΔF3, respectively. The x-axis of each plot represents the portion of the vocal tract length within which constrictions were imposed to generate the set of VCVs. The y-axis in each plot is time, where zero seconds represents the point of vocal tract closure and release. Negative and positive time correspond to the constriction onset and offset periods, respectively. Like colors within each plot are contours where the formant deflections are constant. The solid vertical lines indicate phonetic boundaries defined by the 50 percent crossover points on the ID curves. The dashed lines are alternative boundaries discussed in the text.

Figure 9.

Figure 9

Open in a new tab

Contour plots based on the formant deflections determined with Eqn. 3 for all twenty time-varying area functions in the [ɑCu] set, and associated identification functions from the listening experiment.

The [b], [d], and [g] identification curves are plotted in the bottom panel of each figure as a function of the distance from the glottis, the same axis as the contour plots. This allows the identification of the stimuli to be compared directly to the formant deflection characteristics produced with constriction locations along the length of the vocal tract. The solid vertical lines drawn across all three plots in each figure represent the locations at which an identification curve crosses the 50 percent point. That is, the lines signify the locations within the vocal tract that correspond to a change in identification. The exceptions are the lines located near the left end of the plots where a crossover at 50 % identification was not achieved. Nonetheless, lines were positioned in these regions because a change did occur in identification. The dashed lines indicate features that are discussed with reference to each set of VCVs.

Identification curves for the [ɑCi] set shown in Fig. 7 indicate that the first three stimuli from the right side of the plot, representing points beginning at the lip termination and extending to 16.7 cm from the glottis, were almost always identified as the bilabial [b], whereas the fourth stimulus was similarly identified nearly 90 percent of the time. The identification shifts to [d] with stimuli produced by constrictions located at about 15.8 cm from the glottis. This corresponds precisely to the region of the vocal tract where the F2 deflection contour shifts from negative to positive (i.e., from blue to red), and is closely aligned with a similar shift in the F3 deflection pattern. The [d] category extends from this point posteriorly to about 13.4 cm from the glottis where the identification curves again cross the 50 percent point. This boundary is fairly well aligned with a shift from positive to negative polarity in the F3 deflection contour, although there is somewhat greater negative F3 deflection for the onset portion of the VCV than during the offset. All of the remaining stimuli were identified as [g] more than the other two choices, but the five stimuli that correspond to the portion of the vocal tract between 13.4 cm and the dashed vertical line at 11.5 cm were clearly the best representatives of the velar category. If taken as the category boundary, the dashed line is located exactly at a point where the F2 deflection polarity switches from positive to negative, and near a point where the polarity for F3 deflection switches from negative to positive. The stimuli associated with the most posterior constriction locations (i.e., 11.5 cm and 9.92 cm) seem to be fairly ambiguous with respect to the [b] and [g] categories.

Shown in Fig. 8 are results for the [ɑCə] set. Much like in the previous case, the boundary between the [b] and [d] categories in the identification plot is clearly aligned with a negative to positive polarity shift in the F2 deflection contour, as well as a similar shift in the deflection of F3. This boundary occurs at 16 cm from the glottis, essentially the same location as in the [ɑCi] context. Extending posteriorly from 16–13.6 cm is the [d] category, where the boundary between [d] and [g] (at 13.6 cm) is again aligned with the positive to negative shift in the F3 deflection pattern. Identification of the the remaining stimuli suggests that a fairly robust [g] category is associated with a region extending posteriorly from the 13.6 cm boundary to 11.5 cm which is indicated by the dashed line. As in the previous case, if the dashed line is assumed to be the phonetic boundary it is closely aligned with a polarity shift in the F2 deflection contour.

Figure 8.

Figure 8

Open in a new tab

Contour plots based on the formant deflections determined with Eqn. 3 for all twenty time-varying area functions in the [ɑCə] set, and associated identification functions from the listening experiment.

The results for the [ɑCu] set are shown in Fig. 9. The first four stimuli, associated with constriction locations near the lip end, were identified as [b] nearly 100 percent of the time. The boundary between [b] and [d] is located at 15.7 cm from the glottis, again aligned with the polarity shift in the F2 deflection contour but shifted slightly in the posterior direction relative to the [ɑCi] and [ɑCə] contexts. The [d] category extends from 15.7 cm posteriorly to [b/d] boundary at 12.5 cm, which is aligned primarily with the polarity shifts of the F2 and F3 deflection patterns on the offset side of the VCV. There is, however, an apparent division of responses within the [d] category. The four stimuli based on constrictions located between 13.9– 15.1 cm are identified as [d] 100 percent of the time, but the identification of those stimuli associated with locations posterior to 13.9 cm as [d] drops off as the boundary at 12.5 cm is approached, and the percentage of [g] responses increases. The dashed vertical line placed at 13.9 cm from the glottis indicates this change in identification, and is aligned with a polarity shift in the F3 deflection pattern that is similar to both [ɑCi] and [ɑCə] contexts. There is no range of stimuli in this set that is robustly identified as [g], however, the percentages for [g] responses in the region between 11.3–12.5 cm do exceed 50 percent. Perhaps the absence of a burst is more detrimental in this VV context than in the other two. Stimuli posterior to this range tend to be confused between [b] and [g].

It is of note that the stimuli based on a constriction location of lc = 14.3 cm in all three VV contexts, and corresponding to the examples in Fig. 4, were identified as [d] 100 percent of the time. This is not unexpected, but shows that the identification responses coincide with the formant deflection polarity pattern, which is the same in the three contexts, even though the F2 formant transition itself rises for [ɑCi] and falls in [ɑCə] and [ɑCu]. In addition, the stimuli corresponding to the three examples presented in Fig. 5, for a constriction imposed on the [ɑCi] context located 12.7 cm, 14.3 cm, and 17.5 cm, were identified more than 80 percent of the time as [g], [d], and [b], respectively. Again this is not unexpected but demonstrates that even though F2 rises in all three cases the identification responses coincide with the difference in the formant deflection patterns.

Discussion

The purpose of this study was to use a model of the vocal tract area function to investigate one aspect of voiced stop consonant production, the relation of formant transitions to place-of-articulation. The model is structured such that a neutral vocal tract configuration is modulated at one level by overall shape changes that produce vowel-to-vowel transitions, and at a second level by constrictions that occlude the vocal tract at a specific location. This view suggests that resulting formant transitions can be considered to originate first from perturbation of a neutral vowel formant pattern due to the vowel-dependent modulations, and secondly from a temporary “deflection” of the vowel-dependent formants by consonantal modulations. Analysis of time-varying area functions representative of VCVs produced with a wide range of constriction locations and vowel contexts supported the notion that formant deflection patterns (i.e., deflection above or below the underlying vowel transition) are systematically-related to place of articulation. Thus, it was hypothesized that listeners would be sensitive to this particular form of acoustic invariance. That is, perhaps at least a part of stop consonant perception involves a process that demodulates the time-varying formants present in the speech signal into separate contributions of the vowels and consonants.

Listener responses to VCV stimuli produced by the model indicated that phonetic boundaries between [b], [d] and [g] were, in most cases, aligned with a point in the vocal tract at which the formant deflection polarity of either F2 or F3 switched from negative to positive, or vice versa. This suggests that the formant deflection lobes (red and blue regions in Figs. 7–9) divide the vocal tract into regions that, when constricted, will produce a specific pattern of deflection polarity. For example, a constriction at 17.5 cm from the glottis (near or at the lips) will always produce negative deflection of F1, F2, and F3, whereas constricting the vocal tract at 15 cm (the alveolar region) will deflect F1 downward and F2 and F3 upward. These regions with the same deflection polarities were well aligned with the listeners’ identification of the voiced stops. Since in all the VCVs the underlying vowel was changing during the time the constriction was imposed, the deflection lobes shown in Figs. 7–9 were somewhat asymmetric with respect to the onset versus the offset portions. In particular, the vocal tract regions defined by deflection lobes in the offset portion were shifted toward or away from the lip end, relative to the onset. This may have had some effect on the identification responses at the edges of the phonetic boundaries. The onset/offset asymmetry may also have some implications for speech production in that a speaker could slide the constriction during the occlusion period to make optimal use of a particular deflection region (cf. Houde, 1968).

The results suggest that listeners are indeed sensitive to the form of relative invariance specified by the formant deflection patterns. Calculation of the deflection patterns, however, requires knowledge of the time-varying formant frequencies in the underlying VV transition, an abstract quantity that is not directly accessible from the acoustic properties in the speech signal. Note that this is not the same as determining the difference between the formant transition frequencies and the formants of the initial or following vowel, unless the VV context is maintained with a constant vowel shape (i.e., no transition). For example, in the offset portion of the [ɑCi] in Fig. 4a the polarity of the F2 deflection was positive (upward), whereas, the difference between the value of F2 at the consonantal release and the following vowel would be negative. Thus, if a listener is sensitive to the type of information in the deflection patterns there would need to exist some type of process to estimate the underlying VV formant frequencies from the available formant transitions. In their discussion of a study on stop consonants, Halle et al. (1957) wrote that “Formant transitions would then be intermediate structures whose assignment to the vowels or to the consonants is … dependent on their rate of change.” Perhaps an ongoing assessment of the time derivative of the formant transitions, as well as additional information provided by the burst, is a possible means by which to estimate contributions of both vowels and consonants to the formant characteristics of the speech signal.

In summary, this study has demonstrated that regions of the vocal tract exist that, when constricted, shift the formant frequencies in a predictable direction. Based on a perceptual experiment, the boundaries of these acoustically-defined regions were shown to closely coincide with phonetic categories for stop consonants. This is not to suggest, however, that perception is carried out with reference to the vocal tract structure, but rather that there are locations in the vocal tract that are optimal for imposing a constriction that produces particularly salient cues for a specific consonant. Although limited to constrictions imposed on three VV contexts, this study does demonstrate how a model of the vocal tract might be used to investigate the relation of vocal tract shape, acoustic characteristics, and perception of speech sounds. Future work will include investigating whether the effects shown here hold for a wider variety of time-varying vowel contexts, non-uniform vocal tract length scaling, more detailed representations of the constrictions based on articulatory data, and enhancement of the simulations with bursts. In addition, variations of the temporal aspects of the vowel-vowel transitions and the superposition of the consonantal constriction could be investigated.

Supplementary Material

SB2010_Set_a.wav. File: SB2010 Set a.wav.

Twenty stimuli generated in the [#x001DD;Cə] context. All VCVs are played in succession beginning at the lips and moving incrementally toward the glottis. There is 1.5 seconds of silence between each stimulus.

Download audio file (3.5MB, wav)
SB2010_Set_i.wav. File: SB2010 Set i.wav.

Twenty stimuli generated in the [#x001DD;Ci] context. All VCVs are played in succession beginning at the lips and moving incrementally toward the glottis. There is 1.5 seconds of silence between each stimulus.

Download audio file (3.5MB, wav)
SB2010_Set_u.wav. File: SB2010 Set u.wav.

Twenty stimuli generated in the [#x001DD;Cu] context. All VCVs are played in succession beginning at the lips and moving incrementally toward the glottis. There is 1.5 seconds of silence between each stimulus.

Download audio file (3.5MB, wav)

Acknowledgments

This research was supported by NIH grant number R01-DC04789.

Footnotes

1

Although any artificially-generated speech is strictly synthetic, the term simulated speech is used in this article to denote that it is produced, to some degree, by simulating the physical processes of human sound production. These consist primarily of vocal fold vibration, acoustic wave propagation in the tracheal, nasal, vocal tract systems, and the radiated acoustic output. In contrast, formant synthesis is an attempt to replicate the acoustic properties of the speech output signal, but not necessarily any of the physical processes that produce those properties.

References

  1. American-Speech-Language-Hearing Association (ASHA) Panel on Audiologic Assessment. Guidelines for Audiological Screening. Rockville, MD: 1997. [Google Scholar]
  2. Blumstein SE, Isaacs E, Mertus J. The role of gross spectral shape as a perceptual cue to place of articulation in initial stop consonants. J Acoust Soc Am. 1982;72(1):43–50. doi: 10.1121/1.388023. [DOI] [PubMed] [Google Scholar]
  3. Blumstein SE, Stevens KN. Acoustic invariance in speech production: Evidence from measurements of the spectral characteristics of stop consonants. J Acoust Soc Am. 1979;66(4):1001–1017. doi: 10.1121/1.383319. [DOI] [PubMed] [Google Scholar]
  4. Blumstein SE, Stevens KN. Perceptual invariance and onset spectra for stop consonants in different vowel environments. J Acoust Soc Am. 1980;67(2):648–662. doi: 10.1121/1.383890. [DOI] [PubMed] [Google Scholar]
  5. Carré R, Liénard JS, Marsico E, Serniclaes W. On the role of the ‘schwa’ in the perception of plosive consonants. 7th International Conf. on Spoken Lang. Proc; Denver, CO. 2002. pp. 1681–1684. [Google Scholar]
  6. Carré R, Divenyi P. Modeling and perception of “gesture reduction”. Phonetica. 2000;57:152–169. doi: 10.1159/000028469. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Cole RA, Scott B. Toward a theory of speech perception, Psych. Rev. 1974;81(4):348–374. doi: 10.1037/h0036656. [DOI] [PubMed] [Google Scholar]
  8. Cooper FS, Delattre PC, Liberman AM, Borst JM, Gerstman LJ. Some experiments on the perception of synthetic speech sounds. J Acoust Soc Am. 1952:597–606. [Google Scholar]
  9. Delattre PC, Liberman AM, Cooper FS. Acoustic loci and transitional cues for consonants. J Acoust Soc Am. 1955;27(4):769–773. [Google Scholar]
  10. Dorman MF. Stop-consonant recognition: Release bursts and formant transitions as functionally equivalent, context-dependent cues, Perc. and Psychophys. 1977;22(2):109–122. [Google Scholar]
  11. Fant G. Acoustic Theory of Speech Production. The Hague: Mouton; 1960. [Google Scholar]
  12. Fant G. Stops in CV-syllables. In: Fant Gunnar., editor. Speech Sounds and Features. MIT; Cambridge: 1973. pp. 110–139. [Google Scholar]
  13. Halle M, Hughes GW, Radley JPA, Radley Acoustic properties of stop consonants. J Acoust Soc Am. 1957;29(1):107–116. [Google Scholar]
  14. Harris KS, Hoffman HS, Liberman AM, Delattre PC, Cooper FS. Effect of third-formant transitions on the perception of the voiced stop consonants. J Acoust Soc Am. 1958a;30(2):122–126. [Google Scholar]
  15. Hillenbrand J, Gayvert RT. Open source software for experiment design and control. J Speech, Lang Hear Res. 2005;48:45–60. doi: 10.1044/1092-4388(2005/005). [DOI] [PubMed] [Google Scholar]
  16. Houde RA. Speech Comm Res Lab. Santa Barbara, CA: 1968. A study of tongue body motion during selected speech sounds, SCRL Monograph No. 2. [Google Scholar]
  17. Kewley-Port D. Measurement of formant transitions in naturally produced stop consonant-vowel syllables. J Acoust Soc Am. 1982;72(2):379–389. doi: 10.1121/1.388081. [DOI] [PubMed] [Google Scholar]
  18. Kewley-Port D. Time-varying features as correlates of place of articulation in stop consonants. J Acoust Soc Am. 1983;73:322–335. doi: 10.1121/1.388813. [DOI] [PubMed] [Google Scholar]
  19. Lahiri A, Gewirth L, Blumstein SE. A reconsideration of acoustic invariance for place of articulation in diffuse stop consonants: Evidence from a cross-language study. J Acoust Soc Am. 1984;76(2):391–404. doi: 10.1121/1.391580. [DOI] [PubMed] [Google Scholar]
  20. Lehiste I, Peterson GE. Transitions, glides, and diphthongs. J Acoust Soc Am. 1961;33(3):268–277. [Google Scholar]
  21. Liberman AM, Delattre P, Cooper FS, Gerstman L. The role of consonant-vowel transitions in the perception of the stop and nasal consonants, Psych. Monog. 1954;379:1–14. [Google Scholar]
  22. Liljencrants J. DS Dissertation. Dept. of Speech Comm. and Music Acous., Royal Inst. of Tech; Stockholm, Sweden: 1985. Speech Synthesis with a Reflection-Type Line Analog. [Google Scholar]
  23. Lulich SM. Subglottal resonances and distinctive features. J Phon. 2009 doi: 10.1016/j.wocn.2008.10. [DOI] [Google Scholar]
  24. Öhman SEG. Coarticulation in VCV utterances: Spectrographic measurements. J Acoust Soc Am. 1966;39:151–168. doi: 10.1121/1.1909864. [DOI] [PubMed] [Google Scholar]
  25. Öhman SEG. Numerical model of coarticulation. J Acoust Soc Am. 1967;41:310–320. doi: 10.1121/1.1910340. [DOI] [PubMed] [Google Scholar]
  26. Perkell J. Physiology of Speech Production: Results and Implications of a Quantitative Cineradiographic Study. MIT Press; Cambridge, MA: 1969. [Google Scholar]
  27. Scully C, Allwood E. Production and perception of an articulatory continuum for fricatives of English. Speech Comm. 1985;4:237–245. [Google Scholar]
  28. Stevens KN, House AS. Development of a quantitative description of vowel articulation. J Acoust Soc Am. 1955;27(3):484–493. [Google Scholar]
  29. Stevens KN, House AS. Studies of formant transitions using a vocal tract analog. J Acoust Soc Am. 1956;28(4):578–585. [Google Scholar]
  30. Stevens KN. The potential role of property detectors in the perception of consonants. In: Fant G, Tatham MAA, editors. Auditory Analysis and Perception of Speech. Academic Press; New York: 1975. pp. 303–330. [Google Scholar]
  31. Stevens KN, Blumstein SE. Invariant cues for place of articulation in stop consonants. J Acoust Soc Am. 1978;64:1358–1368. doi: 10.1121/1.382102. [DOI] [PubMed] [Google Scholar]
  32. Stevens KN. Acoustic Phonetics. MIT Press; Cambridge, MA: 2000. [Google Scholar]
  33. Stevens KN, Keyser SJ. Quantal theory, enhancement and overlap. J Phonetics. 2009;2009 doi: 10.1016/j.wocn.2008.10.004. [DOI] [Google Scholar]
  34. Story BH. Ph D Dissertation. University of Iowa; 1995. Physiologically-based speech simulation using an enhanced wave-reflection model of the vocal tract. [Google Scholar]
  35. Story BH, Titze IR, Hoffman EA. Vocal tract area functions from magnetic resonance imaging. J Acoust Soc Am. 1996;100(1):537–554. doi: 10.1121/1.415960. [DOI] [PubMed] [Google Scholar]
  36. Story BH, Titze IR, Hoffman EA. Vocal tract area functions for an adult female speaker based on volumetric imaging. J Acoust Soc Am. 1998;104(1):471–487. doi: 10.1121/1.423298. [DOI] [PubMed] [Google Scholar]
  37. Story BH. A parametric model of the vocal tract area function for vowel and consonant simulation. J Acoust Soc Am. 2005a;117(5):3231–3254. doi: 10.1121/1.1869752. [DOI] [PubMed] [Google Scholar]
  38. Story BH. Synergistic modes of vocal tract articulation for American English vowels. J Acoust Soc Am. 2005b;118(6):3834–3859. doi: 10.1121/1.2118367. [DOI] [PubMed] [Google Scholar]
  39. Story BH. A comparison of vocal tract perturbation patterns based on statistical and acoustic considerations. J Acoust Soc Am Exp Let. 2007a;122(4):EL107–EL114. doi: 10.1121/1.2771369. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Story BH. Time-dependence of vocal tract modes during production of vowels and vowel sequences. J Acoust Soc Am. 2007b;121(6):3770–3789. doi: 10.1121/1.2730621. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Story BH. Vocal tract modes based on multiple area function sets from one speaker. J Acoust Soc Am. 2009a;125(4):EL141–EL147. doi: 10.1121/1.3082263. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Story BH. Vowel and consonant contributions to vocal tract shape. J Acoust Soc Am. 2009b;126:825–836. doi: 10.1121/1.3158816. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Story BH, Titze IR. Parameterization of vocal tract area functions by empirical orthogonal modes. Journal of Phonetics. 1998;26(3):223–260. [Google Scholar]
  44. Titze IR. Parameterization of the glottal area, glottal flow, and vocal fold contact area. J Acoust Soc Am. 1984;75:570–580. doi: 10.1121/1.390530. [DOI] [PubMed] [Google Scholar]
  45. Titze IR. Regulating glottal airflow in phonation: Application of the maximum power transfer theorem to a low dimensional phonation model. J Acoust Soc Am. 2002;111:367376. doi: 10.1121/1.1417526. [DOI] [PubMed] [Google Scholar]
  46. Titze IR. The Myoelastic Aerodynamic Theory of Phonation. National Center for Voice and Speech; 2006. pp. 197–214. [Google Scholar]
  47. Walley AC, Carrell TD. Onset spectra and formant transitions in the adult’s and child’s percpetion of place of articulation in stop consonants. J Acoust Soc Am. 1983;73(3):1011–1022. doi: 10.1121/1.389149. [DOI] [PubMed] [Google Scholar]
  48. Westbury JR. X-ray microbeam speech production database user’s handbook, (version 1.0) UW-Madison; 1994. [Google Scholar]
  49. Winitz H, Scheib ME, Reeds JA. Identification of stops and vowel for the burst portion of/p,t,k/isolated from conversational speech. J Acoust Soc Am. 1971;51(4):1309–1317. doi: 10.1121/1.1912976. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

SB2010_Set_a.wav. File: SB2010 Set a.wav.

Twenty stimuli generated in the [#x001DD;Cə] context. All VCVs are played in succession beginning at the lips and moving incrementally toward the glottis. There is 1.5 seconds of silence between each stimulus.

Download audio file (3.5MB, wav)
SB2010_Set_i.wav. File: SB2010 Set i.wav.

Twenty stimuli generated in the [#x001DD;Ci] context. All VCVs are played in succession beginning at the lips and moving incrementally toward the glottis. There is 1.5 seconds of silence between each stimulus.

Download audio file (3.5MB, wav)
SB2010_Set_u.wav. File: SB2010 Set u.wav.

Twenty stimuli generated in the [#x001DD;Cu] context. All VCVs are played in succession beginning at the lips and moving incrementally toward the glottis. There is 1.5 seconds of silence between each stimulus.

Download audio file (3.5MB, wav)

RESOURCES