Density hysteresis of heavy water confined in a nanoporous silica matrix

Abstract

A neutron scattering technique was developed to measure the density of heavy water confined in a nanoporous silica matrix in a temperature-pressure range, from 300 to 130 K and from 1 to 2,900 bars, where bulk water will crystalize. We observed a prominent hysteresis phenomenon in the measured density profiles between warming and cooling scans above 1,000 bars. We interpret this hysteresis phenomenon as support (although not a proof) of the hypothetical existence of a first-order liquid–liquid phase transition of water that would exist in the macroscopic system if crystallization could be avoided in the relevant phase region. Moreover, the density data we obtained for the confined heavy water under these conditions are valuable to large communities in biology and earth and planetary sciences interested in phenomena in which nanometer-sized water layers are involved.

In many biological and geological systems, water resides in pores of nanoscopic dimensions, or close to hydrophilic or hydrophobic surfaces, comprising a layer of water, one or two molecules thick, with properties often different from the bulk. Such “confined” or “interfacial” water has attracted considerable attention, due to its fundamental importance in many processes, such as protein folding, concrete curing, corrosion, molecular and ionic transport, etc. (1–3). However, our understanding of the numerous physicochemical anomalies of confined water, and indeed of bulk water, is still incomplete. Basic gaps persist, among which the most interesting one is the origin of the unusual behavior of water in the supercooled region where water remains in the liquid state below the melting point (4–7). Recent studies have aimed at explaining anomalies such as the density maximum and minimum (8–10), and the apparent divergence of the thermodynamic response functions at 228 K at ambient pressure (11). The three major hypothesized scenarios currently under scrutiny are the “singularity-free (SF) scenario” (12, 13), the “liquid–liquid critical point (LLCP) scenario” (14, 15), and the “critical point-free (CPF) scenario” (16). It is hypothesized, by all these three scenarios, that in the low temperature range bulk water is composed of a mixture of two structurally distinct liquids: the low-density liquid (LDL) and the high-density liquid (HDL). They are respectively the thermodynamic continuation of the low-density amorphous ice (LDA) and high-density amorphous ice (HDA) into the liquid state. Evidence of a first-order phase transition between LDA and HDA has been reported since 1985 (17–20). Subsequently, several experimental findings have been interpreted as support of the hypothetical existence of two different structural motifs of liquid water (21–27). However, some of the interpretations have been questioned (28, 29). So far, direct evidence of a first-order liquid–liquid phase transition between LDL and HDL, as a thermodynamic extension of the first-order transition established in the amorphous solid waters, has not yet been observed.

An experimental challenge arises because the hypothesized first-order liquid–liquid phase transition exists in a region of the phase diagram, often called “no man’s land” (5), in which bulk water cannot exist in a liquid state. One method of overcoming this difficulty is to take advantage of confinement. By confining water in a nanoporous silica matrix, MCM-41-S with 15-Å pore diameter, the homogeneous nucleation process (crystallization) can be avoided, allowing us to enter no man’s land and investigate the properties of liquid water. There is still much debate on the differences and similarities between bulk and confined water (16, 30–32); however, even if the silica matrix, with its hydrophilic surfaces, might affect properties of water other than the suppression of homogeneous nucleation, confined water in MCM-41-S is representative of many environments of interest in biological and geological sciences where similar hydrophilic interfaces are intrinsic and important (1).

In this paper, we describe an efficient method for the density determination employing the cold neutron spin polarized inelastic neutron spectrometer (SPINS) at the National Institute of Standards and Technology (NIST) Center for Neutron Research (NCNR). Using this method, we are able to obtain sensitive measurements of the density of D₂O confined in MCM-41-S as a function of closely spaced temperatures (1-K interval) from 300 to 130 K in a range of pressures from ambient to 2,900 bars, achieving a remarkably good signal-to-noise ratio. The reliability and accuracy of the method are extensively discussed in Materials and Methods. There, we also estimate the extent of possible effects related to small amounts of helium from the pressurizing system being dissolved in the water, and the layering water distributions along the pore radius direction, showing that such effects are most likely negligible. Density plays a central role in many classical phase transitions. In particular, it is the order parameter in the gas–liquid and liquid–solid transitions. Therefore, its experimental determination assumes primary importance regarding the hypothesized liquid–liquid phase transition. In making such measurements, we are seeking evidence of a remnant of a first-order liquid–liquid phase transition of water that would exist in the macroscopic system if it were possible to avoid crystallization.

Results and Discussions

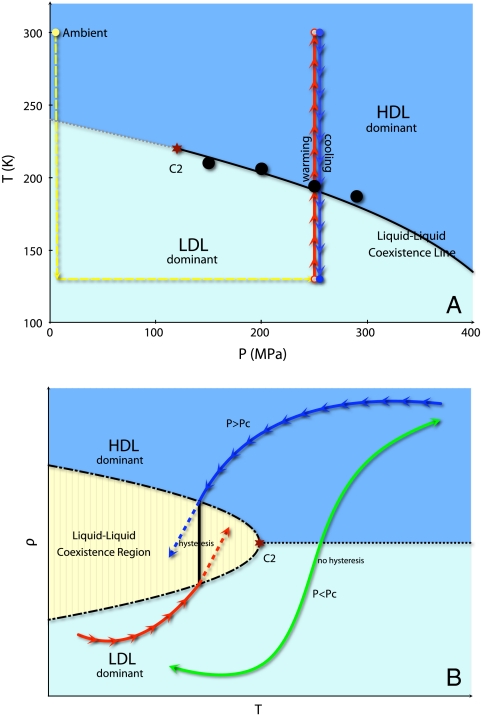
We begin by explaining the purpose of our experimental procedures using Fig. 1, which shows the hypothesized phase diagram of low temperature water in the presence of a first-order HDL-LDL transition. Normally, a discontinuous change of the state functions, such as density, associated with a first-order transition is difficult to detect directly. When the equilibrium phase boundary is crossed, due to the metastability or the kinetics of the phase transition, the phase separation may take very long time to happen, especially in confinement (33–35). However, a first-order line should still manifest itself with a significant hysteresis when it is crossed from opposite directions of the transition line, shown in Fig. 1B. Although a hysteresis phenomenon, if it exists, may not prove the existence of a first-order transition, the absence of hysteresis can serve to rule out a first-order phase change. Accordingly, we performed a series of warming and cooling scans over a range of pressures. For each pressure, the sample was cooled from 300 to 130 K at ambient pressure and then pressurized to the desired value (yellow dashed line in Fig. 1A). We then waited about 2 h for the system to equilibrate. The warming scan with 0.2 K/ min was first performed from 130 to 300 K (red line in Fig. 1A). When the warming scan was finished, we waited another 2 h at room temperature for system equilibration. After that, the cooling scan with 0.2 K/ min was performed from 300 to 130 K (blue line in Fig. 1A). When the full cycle was finished, the sample was brought back to ambient temperature and pressure before measuring another pressure. The system we choose to study is water confined in long cylindrical pores of silica with a diameter of 15 Å. In such confined water, two of its three dimensions are finite, leaving one along the pore axis that can be considered macroscopic. Thus, it is intrinsically difficult to observe a phase transition in such a restricted geometry. However, we may still find a remnant of a phase transition in a confined system, which in principle could be demonstrated by its size scaling.

Fig. 1.

The hypothesized (A) T-P and (B) ρ-T phase diagrams of water in the presence of a first-order liquid–liquid phase transition are used to explain the motivation of our experimental procedures. In order to detect the hypothesized transition, both warming (red) and cooling (blue) scans were performed. If a first-order HDL-LDL transition indeed exists at high pressures, a hysteresis phenomenon should be observed because of the long time required for the phase separation, shown as the difference between the red and blue curves in B. However, at relatively low pressures, when no first-order line is crossed, there should be no hysteresis, shown with the green curve in B. The four black points in A are determined from the temperature of the maximum density difference at each pressure described later in the text. Note that further studies are required to identify the hypothesized liquid–liquid critical point C2.

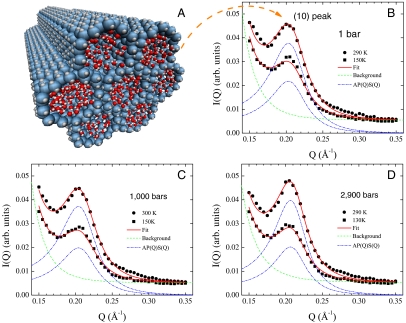
As described in Materials and Methods, the contrast of the neutron coherent scattering length density (SLD) of heavy water against that of the silica matrix gives rise to a strong signal in our experiment. Specifically, we observe a well-defined first Bragg diffraction peak arising from the (10) plane of a 2D hexagonal lattice of water cylinders in the grains of MCM-41-S silica matrix (Fig. 2A). Fig. 2 B–D illustrates the elastic neutron diffraction intensities measured at the highest and lowest temperatures at three representative pressures. One can immediately notice that the width and the position of the Bragg peak do not change with temperature. Hence, for our purposes, the structure of the confining matrix can be regarded as unaffected by temperature. Once the data are corrected for the temperature-independent background arising from the fractal packing of the MCM-41-S crystallites (grains) and the incoherent scattering, the only temperature-dependent quantity is the height of the Bragg peak, which is proportional to the square of the difference of SLD between the heavy water and the silica matrix, and therefore a sensitive indicator of the average mass density of the confined water. We can therefore sit at the Bragg peak position and monitor the peak intensity as a function of temperature, rather than performing a scan in Q at each temperature. Although our measurements are highly precise and sensitive with regard to relative changes, there is an overall uncertainty that we estimate (from the results of repeated measurements on the same and different sample batches) to be about 0.02 g/cm³ (standard deviation) in the overall density scale, arising from uncertainties in the scattering length density of the silica matrix, and the model we have used to analyze the data. Even after careful considerations of all these sources of uncertainties, the estimation of the uncertainty of the absolute density is still a challenge because of the possible systematic errors arising from the model used in the analysis. It should be pointed out, however, that this uncertainty can be considered as a scaling factor and that the relative shape of the density curves is almost directly related to the measured scattering intensity.

Fig. 2.

This figure demonstrates that the neutron diffraction intensities can be fitted with the model described in Materials and Methods. (A) Schematic representation of a D₂O hydrated MCM-41-S nanoporous silica crystallite (pore diameter 2R≈15 Å ± 2 Å). (B–D) The elastic neutron diffraction intensity I(Q) at three pressures measured by SPINS at NCNR. The structure factor peak at around 0.21 Å^-1 comes from the (10) plane of the 2D hexagonal arrangement of the water cylinders in the crystallite. The peak height is proportional to the square of the difference of neutron SLD between the confined D₂O and the silica matrix and therefore is a sensitive indicator of the average mass density of D₂O in the pores. By fitting with Eq. 1, the temperature-independent background (green dashed line) and the temperature-dependent elastic diffraction intensities (blue dash-dotted line) can be separated accordingly.

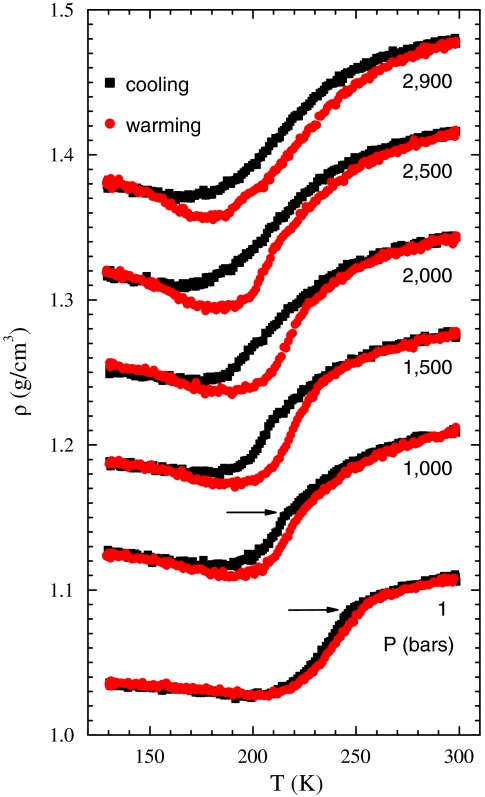
Fig. 3 shows the measured density of confined D₂O with both cooling and warming scans at a series of pressures. The fact that the warming and cooling curves join at both high and low temperature ends implies that the expansion–contraction processes are reversible. Up to 1,000 bars, the density difference between the cooling and warming scans is small, which could be attributed to the temperature lag when ramping the temperature continuously. The density difference due to this reason is small and relatively independent of pressure. However, above 1,000 bars, the density difference (hysteresis) opens up progressively as the pressure is increased. We expect the magnitude of the density difference might depend on the temperature ramping rate. Considering the feasibility of neutron scattering experiments, we chose a ramping rate of 0.2 K/ min. With such a slow rate, a rather uniform temperature distribution over the sample is assured, but the system may require much longer times to reach physical equilibrium after crossing a phase boundary. There seems to be a small regression of the opening up of the density difference at 2,900 bars between 190 and 210 K. Further investigations are needed to find out whether this regression is real or an experimental artifact. Nevertheless, the biggest density difference (confined D₂O) is found to be on the order of a few percent above 1,000 bars. In comparison to the density difference between high- and low-density amorphous H₂O ice (about 25%, measured at much lower temperatures), the observed difference is small. The reason, to our best speculation, might be a combined effect of confinement, isotopic difference, and temperatures. Note that the accuracy of the absolute density we determined depends on the background subtraction and the scaling. However, the relative shape of the density profiles is independent of the analysis.

Fig. 3.

The density profiles of confined D₂O in a hydrophilic substrate MCM-41-S are measured in both warming and cooling scans. The data are shifted by 0.05 g/cm³ between adjacent pressures for clarity. A hysteresis phenomenon becomes prominent above 1,000 bars. Error bars, due to counting statistics, in the density are smaller than the point size. The two horizontal arrows indicate the locations of the sudden change of slope in the density profiles (“kink”) at 1 bar and 1,000 bars.

Another remarkable feature of the density profiles is that a clear minimum is observed at each measured pressure. The minimum temperature T_min decreases from 210 to 170 K as the pressure is increased from ambient to 2,900 bars. Poole et al. have proposed that the occurrence of such a density minimum is an indication of full development of a defect-free random tetrahedral network (RTN) of the hydrogen bonds (36). Below T_min the completed RTN shows normal thermal contraction as the temperature is further lowered. Our results therefore imply that at higher pressures, the RTN can be reached only at lower temperatures. This is a consequence of the fact that the enthalpically favorable hydrogen-bonded RTN has a lower density compared to its less developed counterpart.

We now consider whether the observed density hysteresis can be related to a liquid–glass transition of confined heavy water (37–39), as distinct from a glass transition, in which the macroscopic observables may depend on the thermal history of the system. In the literature, the glass transition temperature of bulk H₂O at ambient pressure is commonly accepted to be around 130 K (40, 41) and is suggested to be modified to be about 160 K (42, 43). It is expected to be even lower at elevated pressures. Moreover, the structural relaxation time of the confined H₂O was reported to be in the order of a few nanoseconds at around 220 K at ambient pressure (44, 45) and even faster at elevated pressures (46). Note that in our experiments we scan at 0.2 K/ min, which is many orders of magnitude slower than the structural relaxation time of the confined water. Therefore, it is apparent that the maximum hysteresis we observe in confined D₂O at high pressures happens far above the glass transition.

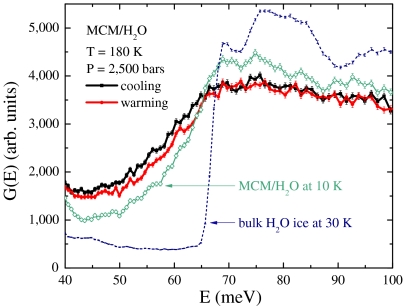
To further support our conclusion, we measured the Q-dependent generalized librational density of states G(E) of H₂O confined in MCM-41-S at ambient pressure. Here, we measured H₂O rather than D₂O because of the dominance of incoherent scattering from hydrogen. Many properties of D₂O differ from H₂O by a shift of about a few degrees, but the topologies of their phase diagrams are expected to be similar in the region under current investigation. Hence, for our purposes, it is reasonable to use H₂O rather than D₂O in this measurement. The G(E) was measured twice using the filter analyzer neutron spectrometer (FANS) at NCNR, both times at T = 180 K, P = 2,500 bars. This state point is presumably close to the maximum density difference between the cooling and warming scans of D₂O confined in MCM-41-S. The sample is prepared in such a way that it approaches the same T-P point from two different paths: a cooling approach and a warming approach as explained in Materials and Methods. The measurement time is 18 h per run. As one can see from Fig. 4, the difference between the two measured G(E) is slightly larger than their error bars. The same confined water sample is also measured at 10 K, at which temperature water should have already solidified in an amorphous form for the same reason that the homogenous nucleation is suppressed. For comparison, an additional measurement of the bulk crystalline ice is performed at 30 K, 1 bar. The G(E) of crystalline ice is characterized by a sharp increase in the energy range from 65 to 70 meV, whereas that of our confined water gradually increases from 40 to 70 meV. This difference implies that water confined in MCM-41-S does not crystalize. From inspection of the spectra of confined water, one can tell that the G(E) at 180 K measured from the two different approaches slightly differs from the amorphous solid water at 10 K. Indeed, the density of states of amorphous ice and liquid water are not expected to be radically different.

Fig. 4.

The Q-dependent generalized librational density of states G(E) of H₂O are measured by FANS at NCNR. The G(E) of H₂O confined in MCM-41-S is measured twice at T = 180 K, P = 2,500 bars: one prepared from cooling (black), the other from warming (red). The G(E) of H₂O confined in MCM-41-S at T = 10 K, P = 2,500 bars is also measured after cooling from room temperature to 10 K at 2,500 bars (cyan). For comparison, the G(E) of bulk H₂O ice is measured at 30 K, 1 bar in the identical pressure cell (blue dashed line) to show the difference between crystalline and amorphous water.

After examining the possibility of a liquid–glass transition in confined heavy water, it is relevant to review the three major hypothesized scenarios for supercooled and glassy water (SF, LLCP, and CPF). The observed density hysteresis, although it is not a definitive proof, is consistent with the hypothesis of the coexistence of two liquid phases of confined heavy water with different densities, at pressures larger than 1,000 bars. The temperature of the maximum density difference at each pressure is overplotted on Fig. 1A. Above this locus, the confined heavy water has higher average density, implying a more HDL-like local structure, whereas below it, the confined heavy water has lower average density, implying a more LDL-like local structure. It has been shown theoretically that phase transitions in confined geometry are not sharply defined but rounded (47); hence the confinement poses additional difficulty to distinguish between SF and LLCP. Nevertheless, it may be possible in the future to determine whether the transition is truly first-order by varying the system sizes, because barriers separating phases of a first-order transition scale with system size. At this point, it is relevant to discuss the possibility of the existence of a liquid–liquid critical point in low temperature water. If such a critical point does exist as illustrated in Fig. 1, at low pressures along the extension of the coexistence line in the one phase region, a critical divergence of the response functions along with the correlation length should be observed (48). However, in confinement such as the quasi-1D pores of MCM-41-S, the correlation length is geometrically constrained by the walls of silica; hence it can grow only along the pore axis direction, making it even more challenging to identify whether there is a critical point. We did observe an increase of the maximum slope of the density profiles (proportional to the thermal expansion coefficient) from ambient pressure to 1000 bars, but the effect is very weak. Surprisingly, we observed an unexpected sudden change of slope in the density profiles (a “kink”) at the temperatures of the maximum slope at and below 1,000 bars. The kink might be related to the previously observed fragile-to-strong dynamic crossover of confined H₂O (45, 49, 50), whose origin is still under debate (48, 51–53). The temperature of the kink is rather close to that of the homogeneous nucleation of bulk water (despite the difference in isotopes), which is suppressed in confinement. This coincidence forces us to consider the possibility that the observed kink arises as a manifestation of the homogeneous nucleation in confinement. More experimental evidence and discussions regarding the kink will be provided in future publications.

Materials and Methods

Sample Preparation.

The MCM-41-S powder sample is made of micellar templated nanoporous silica matrices (54), consisting of grains of the order of micrometer size. In each grain, parallel cylindrical pores are arranged in a 2D hexagonal lattice with an interplane distance d = 30 ± 2 Å. The MCM-41-S is synthesized by reacting preformed β-zeolite seeds [composed by tetraethylammonium hydroxide (TEAOH, Acros), sodium hydroxide (NaOH), and fumed silica (Sigma)] with decyltrimethylammonium bromide solution (C₁₀TAB, Acros), then transferring the mixture into an autoclave at 120 °C for 2 d. After cooling down to room temperature, the mixture was adjusted to pH = 10. Then the mixture was sealed into autoclave at 100 °C for 2 d. Solid sample is collected by filtration, washed by water, dried at 60 °C in air overnight, and then calcined at 540 °C for 8 h. The molar ratios of the reactants are SiO₂∶NaOH∶TEAOH∶C₁₀TAB∶H₂O = 1∶0.075∶0.285∶0.204∶226.46. The pore diameter and pore volume are estimated to be 15 ± 2 Å and 0.50 cm³/g, respectively, with the Barret–Joyner–Halenda analysis. The pore diameter is also confirmed by fitting the elastic diffraction profile.

The dry MCM-41-S sample is then hydrated by exposing to water vapor in a closed container at room temperature. The achieved full hydration level for D₂O corresponds to a fractional mass gain of 0.5 (mass of absorbed water/mass of dry MCM-41-S). We performed an experiment of the surface functionalization of the Si-OH in MCM-41-S to determine the surface functional group Si-O-Si-(CH₃)₃ to the saturation monolayer level. The surface density of Si-OH is determined to be 1.16 groups/nm² through the chemical analysis of the carbon content. After the subtraction of the Si-OH on the external surface of the MCM-41-S grain (≈10%), we estimated H_silanol/H_water = 0.065. Because the Si-O-H bonds are very strong and are attached on rigid surfaces, the migration of silanol groups on the surface is not likely. Therefore, in the temperature range we worked on, we believe that the interaction between waters and surface Si-OH represent a contribution that is “constant” and water-like. That is, the hydrophilic silanol surface provides a small and constant perturbation to the confined water. It is known that near the hydrophilic surface such as silica, there is a layer of denser water, whereas in the center of the pores water distributes uniformly (32, 55–61). The behavior of water near a hydrophobic surface may be different because of the lack of compensating hydrogen bonds from the surface and therefore requires more careful investigations (10, 58–60, 62). In the pores of MCM-41-S, the long-range ice-like order cannot develop; thus, the homogeneous nucleation process is inhibited. Differential scanning calorimetry check was routinely performed to make sure of (i) no freezing of bulk water and (ii) no freezing of confined water occurs down to 130 K.

SPINS Experiment.

In this experiment, we attempt to measure the average density of D₂O confined in the pores of MCM-41-S. The measurement was carried out at the NCNR using the cold neutron triple-axis spectrometer SPINS, operated in an elastic scattering mode with incident neutron energy of 3.7 meV. The D₂O hydrated MCM-41-S sample was loaded in the NCNR pressure cell HW-02 with a sample volume of 1.5 cm³. D₂O has a considerably different coherent neutron scattering length density from that of the silica matrix, giving rise to a well-defined Bragg peak. Pressure was applied with helium gas (see SI Text). The sample temperature was controlled using a top-loading closed-cycle refrigerator. A small amount of helium was used to ensure thermal exchange between the sample and the wall of the refrigerator, whose temperature was controlled with accuracy better than 0.01 K. The density data are reported as a function of the sample temperature, which is recorded by a sensor located just above the pressure cell.

The diffraction pattern of our sample consists of three parts: (i) the low-Q scattering of the fractal packing of the grains, which follows a power law Q dependence; (ii) a Bragg peak at around 2π/d coming from the 2D hexagonal internal structure of the grains; and (iii) the Q-independent incoherent background. The elastic neutron diffraction was performed at the lowest and highest temperature at each pressure. Note that the only temperature dependence is the amplitude of the Bragg peak (at 0.21 Å^-1), which is directly related to the water density. Therefore, we sit at the peak position, measuring the scattering intensity I(Q = 0.21 Å^-1,T) as a function of temperature while ramping the temperature from 300 to 130 K at 0.2 K/ min. This ramping rate is slow enough to allow the sample to reach a uniform temperature.

Data Analysis.

In our experiment, we used long wavelength neutrons (λ = 4.7 Å) and focused on the small-angle region (Q from 0.15 Å^-1 to 0.35 Å^-1). In such a configuration, neutrons view the water and the silica matrix as continuous media and only the long-range (> 18 Å) order is probed. The short-range water–water, silica–silica, and water–silica correlation peaks are located at Q values larger than 1.5 Å^-1, which are beyond the Q range we studied and thus will not concern our measurements. In a small-angle diffraction experiment, the neutron scattering intensity distribution I(Q) is given by 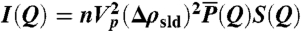, where n is the number of scattering units (water cylinders) per unit volume, V_p is the volume of the scattering unit, 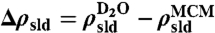is the difference of SLD between the scattering unit and the environment 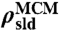, is the normalized particle structure factor (or form factor) of the scattering unit, and S(Q) is the intercylinder structure factor of a 2D hexagonal lattice (63). The SLD of the scattering unit 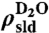is proportional to its mass density 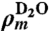as 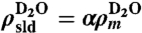, where 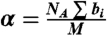, N_A is Avogadro’s number, M is the molecular weight of D₂O, and b_i is the coherent scattering length of the Ith atom in the scattering unit. The SLD of the silica material has been determined by a separate contrast matching experiment by hydrating the sample with a different ratio of D₂O and H₂O. When the molar ratio is [D₂O]∶[H₂O] = 0.66∶0.34, the Bragg peak is matched out. Compared to water, silica is a rather rigid material. Its thermal expansion coefficient is in the order of 10^-6/K compared to 10^-3/K of water. As shown in Fig. 2, the position and the width of the Bragg peaks do not change with temperature, indicating the structure change of the confining matrix is negligible in the measured temperature range. Therefore, based on the above relations, we find that all the variables in the expression for I(Q) are independent of temperature except for 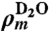. Hence we are able to determine the density of confined D₂O by measuring the temperature-dependent neutron scattering intensity I(Q) at the Bragg peak.

The form factor of a long (QL > 2π) cylinder is given by 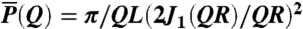, where L and R represent the length and the radius of the cylinder, respectively, and J₁(x) is the first-order Bessel function of the first kind. The structure factor S(Q) can be well approximated by a Lorentzian function. Therefore, the measured neutron scattering intensity is expressed as

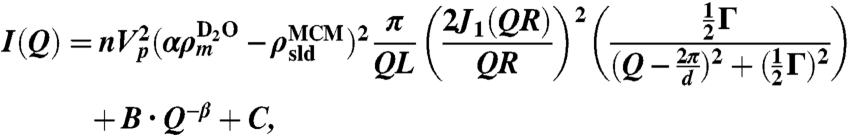[1]

and at the Bragg peak Q₀ = 2π/d,

[2]

where Γ is the FWHM, and C is the Q-independent incoherent background (8). The approximation of the Bragg peak by a Lorentzian function is purely empirical. The broadening of a diffraction peak comes from many factors, such as the imperfection of the lattice, the instrument resolution, etc. But the choice of the peak formula form will not affect the extraction of the density of water, which merely depends on the peak height.

By fitting the neutron scattering intensity with the above model at the highest and lowest temperature at each pressure, the parameters B, β, and C are obtained. We are thus able to subtract the “background” (the second and third term in the above equations) with confidence. We determine the last unknown temperature independent constant A by normalizing the density of the highest temperature at each pressure to that of the bulk D₂O taken from NIST Scientific and Technical Database (NIST Chemistry WebBook http://webbook.nist.gov/chemistry/fluid/).

Some of the authors have previously used a similar small-angle neutron scattering (SANS) to determine the density of D₂O in MCM-41-S at ambient pressure (8, 64). A similar method has also been used to measure the density of confined toluene (65) and benzene (66). Recently, the reliability of this method to determine the density of water confined in MCM-41-S has been criticized because of a possible layering effect of water in the pores (67). However, the scenario hypothesized in ref. 67 assumes the existence of voids in the hydrated pores; this possibility is not consistent with our measurement of a contrast matched sample ([D₂O]∶[H₂O] = 0.36∶0.34) in which the diffraction peak is almost completely masked and no evidence of the scattering from the voids can be recognized. The hypothesis of the existence of voids in the hydrated pores originates from a layering of density profiles suggested in ref. 67, which implies that water can penetrate into the wall of MCM-41-S. The problem of whether there is void (micropores) on the wall of MCM-41 has been investigated by the gas adsorption technique many times since 1993. The great majority concluded that MCM-41 materials do not have any microporosity. Recent experiments suggest that MCM-41 is exclusively mesoporous with no water penetration into the wall (68). On the basis of these results we believe that the layering density profiles suggested in ref. 67 is unrealistic and inconsistent with the scattering pattern of our measurements.

The effect related to a nonuniform distribution of water in the pore will be contained in the 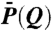term (see SI Text). It is generally believed that near the hydrophilic surface such as silica there is a 2- to 3-Å layer of water with about 10% higher density, whereas in the center of the pores water distributes uniformly (32, 55–61). When we compare the normalized particle structure factors of this core-shell cylinder and its average, we find that at around the Bragg peak position (Q = 0.2 Å^-1), the difference of the is about 5%. When compared to the observed 40% change of the SLD, one realizes that the change of density profile itself would not be enough to contribute to the overall change of the SANS intensities. The small fluctuations at the sub-Å scale do not provide further information for density, which is a macroscopic quantity. It should be emphasized that small-angle neutron scattering has a “low” spatial resolution and therefore the details of the SLD will have no appreciable effect on the collected data. Therefore, the nonuniform distribution of the water in the pores would account only for a minor correction to the change of the intensity of the Bragg peak, which is mainly influenced by the contrast between the average SLD in the pore and the silica matrix 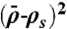. The small-angle scattering measurements allow us to determine the average density of fluids in the pores as previously performed by Alba-Simionesco and co-workers (65, 66).

FANS Experiment.

The inelastic neutron scattering (INS) experiment was performed using the FANS at the NCNR. The same MCM-41-S sample was hydrated with H₂O following the same procedure described previously with D₂O. Then the hydrated sample was loaded to the identical pressure cell used in the SPINS experiment. The temperature was controlled using a closed-cycle refrigerator with accuracy better than 0.1 K. The Cu(220) monochromator was used in order to access energy transfers between 30 and 250 meV. The measured INS spectra collected on FANS are representative, within certain approximations, of the generalized librational density of states G(E) of the water confined in MCM-41-S (69).