Abstract
In rapid frequency scan EPR with triangular scans, sufficient time must be allowed to insure that the magnetization in the x,y plane decays to baseline at the end of the scan, which typically is about 5 T2 after the spins are excited. To permit relaxation of signals excited toward the extremes of the scan the total scan time required may be much longer than 5 T2. However, with periodic, saw-tooth excitation, the slow-scan EPR spectrum can be recovered by Fourier deconvolution of data recorded with a total scan period of 5 T2, even if some spins are excited later in the scan. This scan time is similar to polyphase excitation methods. The peak power required for either polyphase excitation or rapid frequency scans is substantially smaller than for pulsed EPR. The use of an arbitrary waveform generator (AWG) and cross loop resonator facilitated implementation of the rapid frequency scan experiments reported here. The use of constant continuous low B1, periodic excitation waveform, and constant external magnetic field is similar to polyphase excitation, but could be implemented without the AWG that is required for polyphase excitation.
Keywords: digital detection, Fourier deconvolution, periodic excitation, polyphase excitation
1. Introduction
In continuous wave (CW) EPR the magnetic field is scanned slowly through resonance, and the field is modulated with an amplitude that is less than spectral line widths at a frequency such as 100 kHz. Phase sensitive detection at the modulation frequency gives the first derivative of the EPR absorption. However, when no field modulation is used, the magnetic field is scanned through resonance in a time that is short relative to relaxation times, and the spin response is detected at the carrier frequency with a mixer, the absorption signal (not its derivative) is detected and oscillations occur on the trailing edge as the spins relax. This experiment is called rapid scan EPR [1–7].
An alternative way of measuring rapid scan EPR signals is to scan the frequency at constant external magnetic field. Two methods of performing EPR frequency scans have been reported. (i) Hidemoto et al. simultaneously swept the source frequency and adjusted the frequency of an X-band resonator with a varactor diode to maintain a match with the source frequency [8,9]. The width of the scan was limited by the adjustment range of the resonator. Scan rates were in the slow-scan regime. (ii) At W-band a resonator quality factor, Q, of about 100 has a 3 dB bandwidth of 1 GHz, which permits relatively wide scans within the resonator bandwidth [10]. Scanning a V-band YIG source, which was up-mixed to generate 94 GHz, permitted scan widths up to 44 MHz in the slow and fast scan regime. Subtraction of off-resonance signals was used to correct for changes in power reflected from the resonator by the varying frequency.
In this paper we report rapid frequency scan EPR at 1 GHz using a cross-loop resonator (CLR), an arbitrary waveform generator (AWG) as a source, and direct detection at the carrier frequency. A novel experiment is based on spin excitation with a periodic waveform with period T equal to 5 to 6 T2. Since the spin response is periodic, the EPR slow scan spectrum can be restored from the rapid scan signal by deconvolution using Fourier series or discrete Fourier transform techniques. The experimental design was adapted from polyphase excitation experiments using the Frank sequence in NMR and EPR, in which the phase of the carrier frequency is varied and magnetic field is constant [11–13]. EPR spectra of lithium phthalocyanine (LiPc) obtained by frequency scan and continuous polyphase excitation are compared.
In section 2 the conceptual basis for rapid periodic frequency excitation is developed and the importance of monotonic (rather than triangular) excitation is explained. The rapid frequency scan experiment is compared with polyphase continuous excitation. Numerical solution of the Bloch equations is used to examine the behavior of a spin system undergoing rapid frequency scans with powers that are high enough that the response is non-linear. The simulations are compared with experimental data described in section 3.
2. Theoretical
2.1 Rapid Frequency Scan
Consider an EPR experiment in which the time-dependent excitation is described by Eq. (1).
| (1) |
where B1 is the amplitude of the oscillating magnetic field and ϕ(t) is the phase. Angular frequency is the derivative of phase with respect to time, so for a frequency scan in the rotating frame with constant rate b, ϕ (t) = bt2/2 and
| (2) |
For B1 small enough to avoid saturation, the spin system response y(t) to the excitation x(t) can be expressed as:
| (3) |
where h(t) is the impulse response of the spin system (the free induction decay), and the symbol * denotes the convolution operator. In the frequency domain convolution becomes multiplication:
| (4) |
where Y(ω), H(ω), and X(ω) are the Fourier transforms of y(t), h(t), and x(t), respectively. The EPR spectrum H(ω) can be calculated as Y(ω)/X(ω).
When the spin system is excited with a periodic waveform x(t), it takes about 5T1 for the system to come to dynamic equilibrium, and thereafter y(t) is periodic with period T. The periodic functions x(t) and y(t) can be represented by Fourier series:
| (5) |
| (6) |
The coefficients of the Fourier series, which are shown in Eq. (7) and (8),
| (7) |
| (8) |
are related as shown in Eq. (9)
| (9) |
The subscript k designates discrete angular frequencies, ωk. Thus for periodic excitation, the general expression in Eq. (4) becomes the discrete expression in Eq. (9). Division of Yk by Xk gives the spectrum, Hk, which is the Fourier transform of h(t).
| (10) |
The function h(t) becomes periodic because of the periodic excitation.
This Fourier series formulation points out an important characteristic of periodic excitation. If the spins that are excited somewhere in the scan do not relax before the end of a scan, they continue to relax in the beginning of the next scan as long as they are not excited again before they are essentially completely relaxed. The sawtooth frequency sweep ensures that the spins are excited only once for each scan, and periodically for each succeeding scan. Thus, no matter where the spins are excited in the scan, the entire period of the scan is available for those spins to relax nearly completely. The entire slow scan spectra can be recovered without the edge effects caused by the abrupt change in scan direction that occur in a triangular scan.
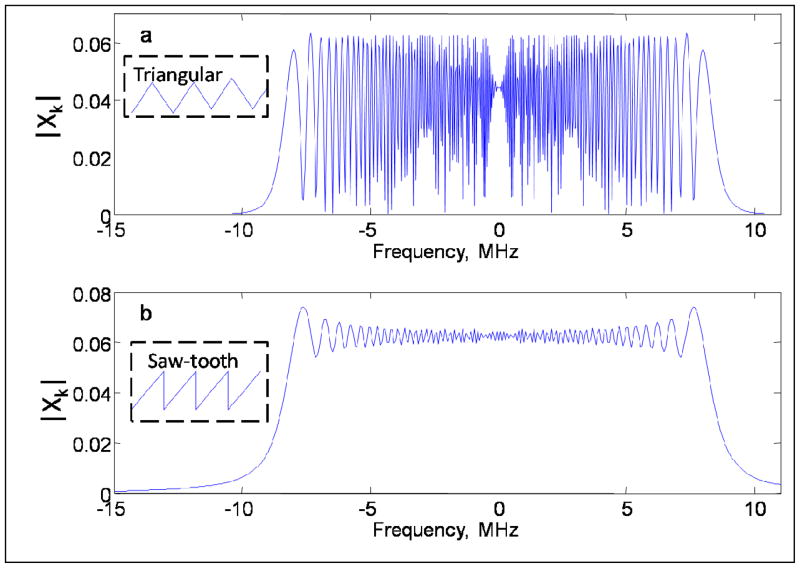
Equations (5–8) are valid for arbitrary periodic excitation of the spin system. Since experimental signals contain noise, small values in the divisor Xk of Eq. (10) are undesirable since this increases the noise. Either triangular or saw-tooth waveforms can be used to produce linear scans. Fig. 1 shows | Xk |for triangular (Fig.1a) and saw-tooth (Fig.1b) excitation. In the interval that corresponds to the frequency scan, both functions are oscillatory. However the variation, relative to the maximum value, is smaller for saw-tooth (Fig. 1b) than for triangular (Fig. 1a) excitation, which makes it preferable as the denominator in Eq. (10). The oscillations in Fig. 1a result from passing through the same frequency twice during the triangular scan, which results in the interference pattern in Fig1a. To be suitable for the Fourier analysis the periodic function must be monotonic and pass through each frequency only once per cycle. In the following discussion, saw-tooth excitation is discussed.
Fig. 1.
Comparison of | Xk |for triangular (a) and saw-tooth (b) excitation. The periods for the triangular and saw-tooth waveforms were 30 and 15 μs, respectively, and the scan ranges were ± 8.5 MHz.
An expression for Xk can be found by substitution of Eq. (2) for x(t) into Eq. (8):
| (11) |
where the scan is from −sw/2 to +sw/2. Integration of Eq. (11) gives Eq. (12)
| (12) |
where and erf(x) is the error function of a complex argument.
The analytical expression in Eq. (12) can be used to recover the absorption and dispersion components of the slow-scan EPR spectrum from | Yk | for the full period of the saw tooth scan, using Eq. (10).
2.2 Comparison of rapid frequency scans with polyphase continuous excitation
The proposed method for rapid frequency scan EPR is similar to polyphase continuous excitation with phases selected using the Frank sequence [13]. For periodic polyphase excitation ϕ(t) in Eq. (1) is given by Eq. (13)
| (13) |
where period T is divided into N intervals and function θ(t) is defined in Eq. (14):
| (14) |
Phases pn are elements of the Frank sequence with length N.
The formal definition of frequency is the time derivative of phase. For the polyphase experiment, frequency at any time in the experiment is formally either 0 or infinity because of the discontinuities in the phase. However, polyphase excitation produces phase wave packets that analogous to a frequency scan [11]. The abrupt phase alteration changes the position of the effective magnetic field in the rotating frame and the magnetization vector starts its precession around its new position. As a result, a frequency scan can be achieved either by smooth phase changes as in Eq. (2) or by a stepwise change as in Eq. (14). For the comparison the scan periods T for the two experiments were chosen to be equal. The scan rate was sw/T.
Substitution of Eq. (13) for periodic polyphase continuous excitation with period T into Eq. (1) gives xp(t)
| (15) |
The Fourier transform of Eq. (15) has been shown [13] to be
| (16) |
where
| (17) |
| (18) |
It follows from Eq. (17) and (18) that the excitation bandwidth is determined by the sinc function that would have been produced by a square pulse with duration ts. Thus the excitation bandwidth for the Frank sequence is the same as for a single pulse with duration ts [13].
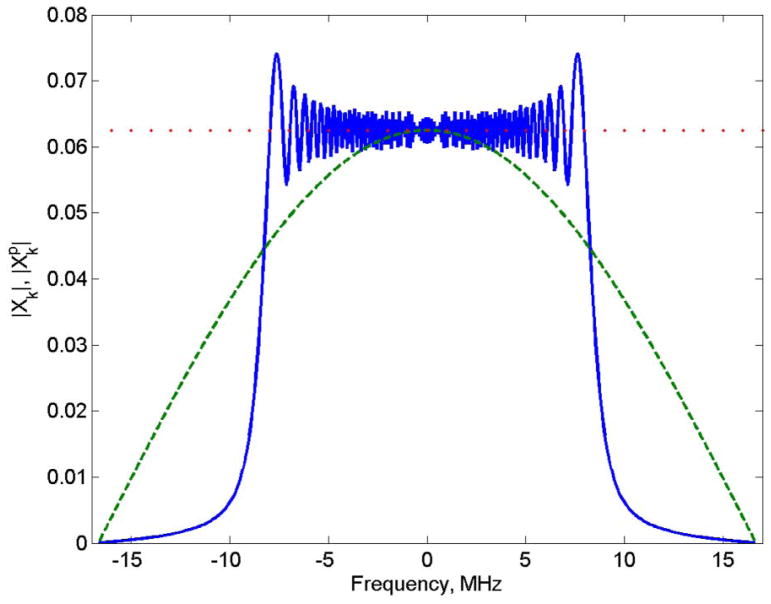
For comparison of the two methods the scan width for the fast frequency scan was set to 2πN/T for the polyphase experiment with N = 256 and T = 15 μs, which is −8.5 to 8.5 MHz. for polyphase excitation and | Xk | for rapid frequency scan are compared in Fig. 2. When used as the divisor in Eq. (10) the oscillations in | Xk | for rapid frequency scan can impact noise non-uniformly. Although for polyphase continuous excitation does not have oscillations, it is not flat across the scan width, which amplifies noise in the extremes of the frequency range. The maximum value is given in Eq. (19).
Fig. 2.
Comparison of for polyphase excitation (green dashed line) with N = 256, and | Xk |for rapid frequency scan (blue solid line) of ± 8.5 MHz. Calculations were done with B1=1 and T=15 μs. The y axis scales linearly with B1. The parameters were selected to correspond with experiment. The red dotted line is the limiting value for an infinitely wide scan. Resonator Q = 250 for the experiments corresponds to a 3 dB bandwidth of ±2.5 MHz which limits the bandwidth of frequencies that impact the spins. Since the signal bandwidth is much narrower than the bandwidth of the resonator, the impact of resonator Q on the excitation profile was not included in the calculation.
| (19) |
2.3 Comparison of periodic excitation with approximation of infinite scan widths
In the limit of infinite scan width the term [erf(p)-erf(q)] (Eq. (12)) becomes equal to two, and which is shown as the red dotted line in Fig. 2. In a triangular scan if Mx and My have returned to zero at the extremes of the scan, each half cycle of excitation can be approximated as an infinitely wide scan and Xk can be approximated by This approximation has been used in deconvolution of rapid NMR field and frequency scans [14,15] and EPR rapid magnetic field scans [2,5]. However, if the magnetization has not fully returned to zero at the extremes of the scans, the infinite scan approximation results in residual oscillations in the deconvolved spectra.
3. Experimental
3.1 Sample
LiPc prepared electrochemically following procedures in the literature [16,17] was provided by Prof. Harold M. Swartz, Dartmouth University. Multiple small crystals of LiPc were placed in a 3-mm OD tube. The tube was extensively evacuated and then flame sealed.
3.2 Spectroscopy
The CLR with resonant frequency of about 1 GHz is identical in construction, but with modified dimensions, to a previously described L-band resonator with resonant frequency about 1.9 GHz [18]. The CLR is key to the success of the experiment. When the incident frequency is offset from the resonator frequency, the reflected power increases. This makes it more difficult to detect the EPR signal, which is a change in the reflected power, with a conventional reflection resonator. A CLR has two orthogonal resonators, one for excitation and one for detection [18,19], so the power reflected from the excitation resonator does not get into the detection resonator. Both the excitation and detection resonators had Q ~250, and the isolation between the two resonators was about 60 dB.
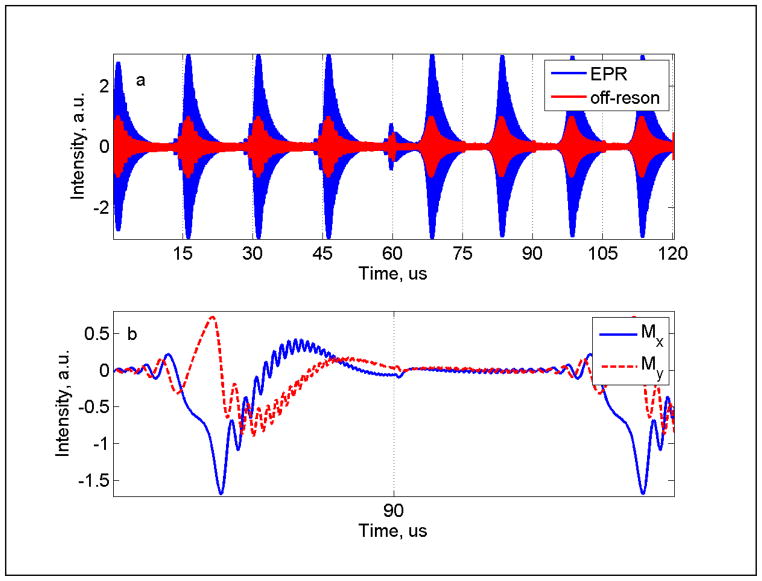
To compare spectra obtained with polyphase continuous excitation and rapid frequency scan a composite waveform consisting of four cycles of polyphase excitation xp(t) followed by four frequency scans x(t) was generated using a Matlab program. Each excitation had T=15 μs, so the total length of the waveform was 120 μs. The polyphase excitation had N = 256 rf phases. The waveform was downloaded to a Tektronix AWG7122C arbitrary waveform generator (AWG). The AWG, operating with a clock frequency ten times the resonance frequency, gave 10 points per rf cycle, which is 1.2×106 points in the waveform. The excitation waveform was amplified by 20 dB prior to the resonator and the signal was amplified by 30 dB prior to the digitizer. An Acqiris U1084A digitizer was used with a sampling rate of 4 GS/s. The spin response produced by this composite waveform was averaged during a time window of 120 μs. The signal obtained by subtraction of five off-resonance averages from five on-resonance averages is shown in Fig. 3a, along with the off-resonance average signal. Since signals were detected with a constant carrier frequency, the output from the digitizer was multiplied by e− jω carrier t in software to obtain y(t) in the rotating frame. A digital low-pass filter was used to select the base-band component. This processing in software is equivalent to hardware quadrature phase sensitive detection with a double balanced mixer and low-pass filter and produces perfectly orthogonal quadrature outputs.
Fig. 3.
Polyphase and fast frequency scan EPR signals for LiPc (a) digitized after amplification of the output of the detection resonator. There are 4 cycles of polyphase excitation (0–60 μs) and 4 cycles of the saw-tooth frequency scan (60–120 μs). The EPR signal (blue) was obtained by subtraction of the off-resonance background (red). (b) Mx and My components of the frequency-scan EPR signal y(t) obtained by digital phase-sensitive detection at the constant carrier (1.0378 GHz) for the time segment of the frequency scan from 80 to 100 μs
Data were collected for a series of B1 values to obtain lineshape information in the region where the response of the spin system is non-linear. Combinations of 3, 6, 10 or 12 db attenuators were used to change the AWG output voltage. Nutation frequency at resonance and the power required for a single pulse 90° FID were used to calibrate B1. The maximum B1 achieved in the CLR with 1Vpp AWG output and 20db amplifier gain was about 0.45 G.
3.3 Simulations
The Bloch equations were solved numerically for an EPR line on resonance at a series of B1 amplitudes using either frequency scan or polyphase continuous excitation. Calculated Mx and My components of the magnetization were combined to form a complex function y(t) that was Fourier transformed and then deconvolved using Eq. (10) to obtain the EPR spectrum. In the linear response regime h(t) decays exponentially to baseline within the time 5T2. However, in the nonlinear regime artifacts extend beyond 5T2. To minimize the impacts of the artifacts, an apodization filter with cutoff at 5T2 was applied to h(t). Multiplication by that function does not noticeably broaden the spectrum obtained by Fourier transformation, but reduces high frequency oscillations. Simulated spectra were fit with a Matlab non-linear least-squares fitting routine (lsqnonlin) to obtain amplitude and Lorentzian linewidth.
4. Results
Rapid frequency scan and polyphase excitation experiments were performed with a deoxygenated sample of LiPc, which had T2 = T1 = 2.32 μs. The lineshape is Lorentzian so this T2 corresponds to a full width at half height of 49 mG. The magnetic field was selected to position the resonance close to the center of the frequency scan. For polyphase excitation, resonance occurs at the beginning of a cycle. The signals obtained by rapid frequency scans and polyphase continuous excitation are shown in Fig. 3a. The directly digitized signal has a carrier frequency of 1.0378 GHz. Because of the relaxation times of the sample, the transverse magnetization did not returned to zero by the end of a cycle. For each experiment type more than one excitation cycle is required for the spins to come to a dynamic equilibrium, so the 3rd cycle was used for data processing. If a single type of excitation had been used, all subsequent cycles could have been co-added for data processing. The data processing window was 30 to 45 μs for polyphase excitation and 90 to 105 μs for frequency scans. For the data in Fig. 3a there is a discontinuity at 60 μs due to the transition from polyphase continuous excitation to frequency scan, which corresponds to an abrupt step off resonance.
Digital phase sensitive detection at the carrier frequency converts the signal shown in Fig. 3a to the rotating frame. A segment of the rapid frequency scan signal is shown in Fig. 3b, and demonstrates that Mx and My do not need to return to 0 at the end of a scan, which is at 90 μs. There is a sharp change in frequency between the end of one scan and the start of the next scan. Since the magnetization is not zero at the time of the transition, this causes a sudden change in the time dependence of magnetization, which appears at 90 μs in the example shown in Fig. 3b.
Full cycles of data were Fourier transformed to obtain Ykp or Yk for polyphase excitation or frequency scan, respectively. These results were then divided by Xkp or Xk to obtain the EPR spectrum, Hk (Eq. (10)).
4.1 Power saturation
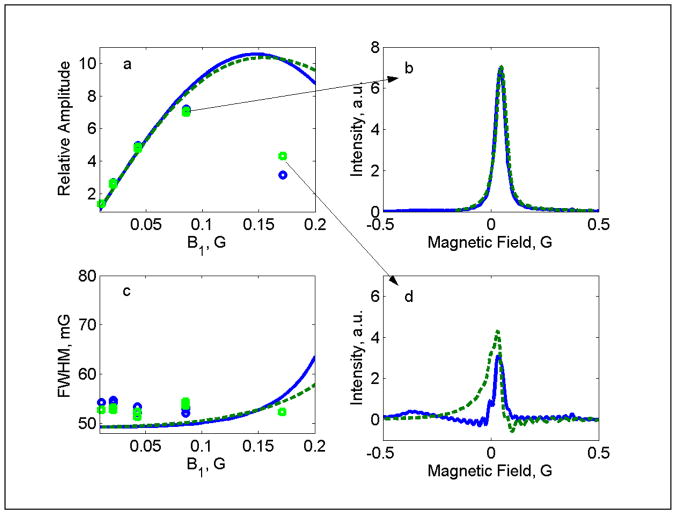
The dependence on microwave power of absorption signal amplitudes, line widths, and lineshapes is similar for fast frequency scans and polyphase continuous excitation (Fig. 4). For both experiments, signal amplitude increases approximately linearly with B1 up to about 0.05 G, which is in good agreement with simulations. Since the source amplitude is the same for both types of excitation, the input power and resultant B1 was essentially the same for polyphase and frequency sweep waveforms. The lineshapes obtained at B1 = 0.085 G (Fig. 4b) are Lorentzian and the widths agree with simulations based on the known T2. B1 = 0.17 G is well beyond the peak of the power saturation curve, and the lineshapes obtained by either method are substantially distorted (Fig. 4d).
Fig. 4.
Comparison of signals for LiPc obtained by rapid frequency scan (green points and dashed lines) and polyphase continuous excitation (blue points and solid lines). (a) Relative signal amplitudes as a function of B1, (b) lineshape obtained at B1 = 0.085 G, (c) FWHM line widths as a function of B1, and (d) lineshape obtained at B1 = 0.17 G. The simulated dependence of signal amplitude and linewidths on B1 is shown for polyphase excitation (solid blue line) and fast frequency scans (dashed green line).
5. Discussion
The experiments were performed with Q ~250 for both the excitation and detection resonators, which correspond to 3 dB bandwidths of about 4 MHz or 1.4 G. The frequency scans and polyphase continuous excitation (Fig. 3) were substantially wider than the bandwidth of the resonator. The signal of interest (Fig. 4) extended over a much narrower bandwidth, which fell well within the resonator bandwidth. To obtain wider spectra it would be necessary either to use lower resonator Q or correct for the impact of Q on the excitation profile.
The detected signals were processed by digital phase sensitive detection [20–24]. Direct detection at the carrier frequency followed by digital phase sensitive detection has two major advantages: (i) the noise is defined by the thermal noise and the first stage high frequency amplifier; (ii) the quadrature signals are perfectly orthogonal, which is important for analysis of the data.
5.1 Comparison of frequency scans with polyphase continuous excitation
The excitation profile for a frequency scan is more uniform than for polyphase excitation (Fig. 3). The polyphase excitation could be made more uniform over a frequency range of interest by using higher power. For example, to double the bandwidth and keep signal amplitude the same would require increasing N by a factor of 2, B1 by √2, and power by a factor of 2. Polyphase continuous excitation has been proposed as a low-power alternative to pulsed methods [11–13]. Even if the power is doubled to make the excitation profile more uniform, the peak power is still much lower than for pulsed experiments. If B1 is too large the signal is distorted as shown in Fig. 4d and discussed previously for polyphase continuous excitation [13].
The background signal (Fig. 3a) for both methods is the excitation attenuated by the isolation between the excitation and detection resonators. The amplitude of the leakage signal is proportional to B1. If it is too large, it may overwhelm the amplifier after the resonator or require a larger number of averages to compensate for insufficient dynamic range [13]. Although the time dependence of the background signals is different for the two excitation profiles, the amplitudes are similar. Even for these relatively strong signals, subtraction of the off-resonance response is required, which increases the noise in the spectrum.
Periodic frequency scans can be implemented without an AWG. The frequency scan waveform can also be generated by mixing a low-frequency scan function with a constant high frequency carrier. If an AWG is used the frequency scan waveform can be multiplied by a function that corrects for the Q effect of the excitation resonator.
5.2 Periodic excitation
The analysis of the frequency scans was based on the periodic saw-tooth excitation (Fig. 1b). Each frequency is traversed only once during the excitation period, which results in| Xk | with relatively shallow oscillations (Fig. 1b). By contrast, if a triangle waveform is used, each frequency is traversed twice during the excitation period and | Xk | has very deep oscillations, which amplifies noise in the deconvolved spectrum (Eq. (10)). If Mx and My have decayed to zero by the end of a half cycle of triangular excitation, then y(t) from each half cycle can be analyzed independently using the assumption that the scan is infinitely wide [5,14,15]. The excitation profile then becomes a straight line (Fig. 2). If the infinitely wide scan approximation is used to analyze data for which Mx and My have not decayed to zero by the end of the scan, oscillations are introduced into the spectra.
5.3 Advantages and disadvantages of rapid frequency and field scans
Rapid field scan experiments require magnetic field scan coils to produce homogeneous fields over the sample region and circuitry to drive the scans. This requires resonator designs that do not attenuate the rapidly changing fields and are not susceptible to generation of eddy currents that distort the waveform. The widths of the scans that can be produced are limited by the scan coils and driver circuitry. Since the field cannot be changed instantaneously, triangular scanning is used and the scan period must be sufficient for all lines in the spectra to relax to zero before the end of each half scan, typically 5 T2 after the last line for each half of the scan. The resonator Q limits the rate at which the field be scanned without damping signal oscillations. If Q is too high, the deconvolved spectrum is broadened. Background signals arise primarily from eddy currents induced in conducting components of the resonator and from microphonics. Background correction can be performed by subtraction of the off-resonance signal or by combining data obtained with an offset in center field [3].
Frequency can be scanned more rapidly than magnetic field and scanning frequency does not generate eddy currents [10], so it puts less restrictions on resonator design. However, the resonator Q limits the scan range. Since Q = υ/Δυ, this limitation is more severe at lower microwave frequency. If the scan width is too large, the relative intensities of signals vary with position in the scan and the background signal increases.
To increase the scan rate for a field scan, or increase the width of a frequency scan, resonator Q should be lowered. Since absolute signal intensity is proportional to Q, lowering Q to permit wider scans lowers signal amplitude.
5.4 Comparison with CW EPR
CW EPR spectra are measured by scanning the external magnetic field in the presence of an oscillating magnetic field. Magnetic field modulation is used to offset the EPR signal from the carrier frequency by the amount of the modulation frequency, which decreases noise. The modulation frequency normally does not exceed 100 kHz and the external magnetic field is swept slowly to avoid distortion of the spectrum. As a result, the CW EPR signal is narrow-banded and can be efficiently detected using a resonator with high Q, which improves signal intensity. However, lossy samples and living organisms reduce the resonator Q. As a result, the resonator bandwidth may be much larger than the CW signal bandwidth and the efficiency of the field-modulated EPR method is reduced. Rapid scan EPR can be the method of choice in this situation. The scan rate can be optimize to match a given resonator bandwidth, thus permitting a larger number of averages per unit time and optimization of the excitation power.
Research Highlights.
Rapid periodic saw-tooth frequency scans were produced with an arbitrary waveform generator.
Periodic excitation permits recovery of the slow scan EPR spectrum from the rapid scan signal by Fourier deconvolution.
A cross-loop resonator was used to isolate the excitation waveform from the detected signal.
Acknowledgments
Funding for this work from NIH NIBIB grant EB000557 (GRE and SSE) and NIH NIBIB P41 EB002034 (Howard J. Halpern, PI) is gratefully acknowledged. The loan of the AWG from Tektronix and the digitizer card from Agilent Acqiris is gratefully acknowledged.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Stoner JW, Szymanski D, Eaton SS, Quine RW, Rinard GA, Eaton GR. Direct-detected rapid-scan EPR at 250 MHz. J Magn Res. 2004;170:127–135. doi: 10.1016/j.jmr.2004.06.008. [DOI] [PubMed] [Google Scholar]
- 2.Tseitlin M, Rinard GA, Quine RW, Eaton SS, Eaton GR. Deconvolution of Sinusoidal Rapid EPR Scans. J Magn Reson. 2011;208:279–283. doi: 10.1016/j.jmr.2010.11.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Tseitlin M, Czechowski T, Quine RW, Eaton SS, Eaton GR. Background Removal Procedure for Rapid Scan EPR. J Magn Reson. 2009;196:48–53. doi: 10.1016/j.jmr.2008.10.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Tseitlin M, Dhami A, Quine RW, Rinard GA, Eaton SS, Eaton GR. Electron Spin T2 of a Nitroxyl Radical at 250 MHz Measured by Rapid Scan EPR. Appl Magn Reson. 2006;30:651–656. [Google Scholar]
- 5.Joshi JP, Ballard JR, Rinard GA, Quine RW, Eaton SS, Eaton GR. Rapid-Scan EPR with Triangular Scans and Fourier Deconvolution to Recover the Slow-Scan Spectrum. J Magn Reson. 2005;175:44–51. doi: 10.1016/j.jmr.2005.03.013. [DOI] [PubMed] [Google Scholar]
- 6.Joshi JP, Eaton GR, Eaton SS. Impact of Resonator on Direct-Detected Rapid-Scan EPR at 9.8 GHz. Appl Magn Reson. 2005;29:239–249. [Google Scholar]
- 7.Mitchell DG, Quine RW, Tseitlin M, Meyer V, Eaton SS, Eaton GR. Comparison of Continuous Wave, Spin Echo, and Rapid Scan EPR of Irradiated Fused Quartz. Radiation Measurements. 2011 doi: 10.1016/j.radmeas.2011.03.035. accepted for publication. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Hara H, Ikeya M, Nakajima T, Nishiwaki Y. Frequency Sweep ESR Spectrometer for Dosimetry and Dating. Radiat Prot Dosimetry. 1990;34:335–337. [Google Scholar]
- 9.Hara H, Ikeya M. Frequency-sweep ESR spectrometer for dosimetry and dating. Appl Radiat Isot. 1989;40:841–843. [Google Scholar]
- 10.Hyde JS, Strangeway RA, Camenisch TG, Ratke JJ, Froncisz W. W-Band Frequency-Swept EPR. J Magn Reson. 2010;205:93–101. doi: 10.1016/j.jmr.2010.04.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Blümich B, Gong Q, Byrne E, Greferath M. NMR with excitation by Frank sequences. J Magn Reson. 2009;199:18–24. doi: 10.1016/j.jmr.2009.03.009. [DOI] [PubMed] [Google Scholar]
- 12.Tseitlin M, Quine RW, Eaton SS, Eaton GR, Halpern HJ, Ardenkjaer-Larsen JH. Use of the Frank Sequence in Pulsed EPR. J Magn Reson. 2011;209:306–309. doi: 10.1016/j.jmr.2011.01.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Tseitlin M, Quine RW, Eaton SS, Eaton GR. Use of polyphase continuous excitation based on the Frank sequence for EPR and EPR Imaging. J Magn Reson. 2011;211:211–226. doi: 10.1016/j.jmr.2011.06.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gupta RK, Ferretti JA, Becker ED. Rapid scan Fourier transform NMR spectroscopy. J Magn Reson. 1974;13:275–290. [Google Scholar]
- 15.Dadok J, Sprecher RF. Correlation NMR spectroscopy. J Magn Reson. 1974;13:243–248. [Google Scholar]
- 16.Turek P, Andre JJ, Giraudeau A, Simon J. Preparation and study of a lithium phthalocyanine radical: optical and magnetic properties. Chem Phys Lett. 1987;134:471–476. [Google Scholar]
- 17.Grinberg VO, Smirnov AI, Grinberg OY, Grinberg SA, O’Hara JA, Swartz HM. Practical conditions and limitations for high spatial resolution of multi-site EPR oximetry. Appl Magn Reson. 2005;28:69–78. [Google Scholar]
- 18.Rinard GA, Quine RW, Eaton GR. An L-Band crossed-loop (bimodal) EPR resonator. J Magn Reson. 2000;144:85–88. doi: 10.1006/jmre.2000.2014. [DOI] [PubMed] [Google Scholar]
- 19.Rinard GA, Quine RW, Eaton GR, Eaton SS. 250 MHz crossed loop resonator for pulsed electron paramagnetic resonance. Magn Reson Engineer. 2002;15:37–46. [Google Scholar]
- 20.Tseitlin M, Eaton SS, Eaton GR. Reconstruction of the first derivative EPR spectrum from multiple harmonics of the field-modulated CW signal. J Magn Reson. 2011;209:277–281. doi: 10.1016/j.jmr.2011.01.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ahmad R, Som S, Kesselring E, Kuppusamy P, Zweier JL, Potter LC. Digital detection and processing of multiple quadrature harmonics for EPR spectroscopy. J Magn Reson. 2010;207:322–331. doi: 10.1016/j.jmr.2010.09.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Tseitlin MP, Tseitlin OA. Using of digital demodulation of multiharmonic overmodulated EPR signals to improve EPR oximetry reliability. Appl Magn Reson. 2009;36:25–34. [Google Scholar]
- 23.Hyde JS, Camenisch TG, Ratke JJ, Strangeway RA, Froncisz W. Digital detection by time-locked sampling in EPR. Biol Magn Reson. 2005;24:199–222. [Google Scholar]
- 24.Tseitlin M, Iyudin VS, Tseitlin OA. Advantages of Digital Phase-Sensitive Detection for Upgrading an Obsolete CW EPR Spectrometer. Appl Magn Reson. 2009;35:569–580. [Google Scholar]