Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2012 Aug 1.
Published in final edited form as: Evolution. 2011 Apr 7;65(8):2391–2398. doi: 10.1111/j.1558-5646.2011.01299.x

A slowly evolving host moves first in symbiotic interactions

James A Damore 1, Jeff Gore 1
PMCID: PMC3145917  NIHMSID: NIHMS287684  PMID: 21790584

Abstract

Symbiotic relationships, both parasitic and mutualistic, are ubiquitous in nature. Understanding how these symbioses evolve, from bacteria and their phages to humans and our gut microflora, is crucial in understanding how life operates. Often, symbioses consist of a slowly evolving host species with each host only interacting with its own sub-population of symbionts. The Red Queen hypothesis describes coevolutionary relationships as constant arms races with each species rushing to evolve an advantage over the other, suggesting that faster evolution is favored. Here, we use a simple game theoretic model of host-symbiont coevolution that includes population structure to show that if the symbionts evolve much faster than the host, the equilibrium distribution is the same as it would be if it were a sequential game where the host moves first against its symbionts. For the slowly evolving host, this will prove to be advantageous in mutualisms and a handicap in antagonisms. The result follows from rapid symbiont adaptation to its host and is robust to changes in the parameters, even generalizing to continuous and multiplayer games. Our findings provide insight into a wide range of symbiotic phenomena and help to unify the field of coevolutionary theory.

Symbioses play a vital role in nearly all ecosystems, but surprisingly little is known about how they evolve (Eberhard 1980; Neish 2002; Nechaev and Severinov 2008). Empirical and theoretical studies often restrict themselves to specific forms of interactions and complicated models that make it difficult to form powerful generalities (Herre et al. 1999; Edwards et al. 2006; Holland et al. 2004). However, in most symbiotic relationships, one partner evolves much faster than the other because of an asymmetry in generation time, mutation rate, or importance of the interaction (Van Valen 1973; Dawkins and Krebs 1979; Moran et al. 1995; Bergstrom and Lachmann 2003). Therefore, in an effort to better understand symbiotic interactions, many have employed the Red Queen hypothesis, which describes coevolutionary relationships as constant arms races to gain the upper hand, thus favoring rapid rates of evolution. This coevolutionary race can be clearly seen in interactions between bacteria and their phage where the bacteria struggle to gain resistance and the phages rush to overcome it. In fact, high evolutionary rates can be so highly favored that bacteria coevolving with phage develop mutation rates 10–100 fold higher than wild-type (Pal et al. 2007).

However, a recent theoretical study found an exception to the Red Queen hypothesis that they called the Red King effect: when two species fight over the benefits of a mutualism, the slower evolving species can actually have an advantage (Bergstrom and Lachmann 2003). In their basic model, the two species were assumed to be in a well-mixed environment, meaning that each member from both species interacted with every member of the other species. For some parameter regimes describing the interaction, the population reached the equilibrium that favored the slowly evolving species in a larger fraction of initial conditions, particularly those where both species start out being selfish. While being able to rapidly adapt may be advantageous in purely antagonistic relationships, sometimes being committed to a strategy can be beneficial. The authors liken this to “having one's hands tied” during a bargaining process, forcing the quickly evolving species to yield to rather than outrun its slowly evolving partner.

Introduction

In addition to hosts tending to evolve slower than their symbionts, each host also usually only interacts with the symbionts associated with it (Levin and Bull 1994; Lysenko et al. 2010). For example, an HIV-positive individual fights against the HIV infecting him or her, not all of the HIV strains in the world (McCutchan 2006). This hierarchical population structure also holds for many exosymbionts like watchman fish and protector ants (Pierce and Easteal 1986; Thompson 2004).

Here, we model a host-symbiont relationship as a game that each host plays in pairwise interactions with each of its symbionts. We combine the common asymmetry in evolutionary rate and population structure to allow for rapid adaptation of each symbiont population to its individual host. Thus, when the symbionts evolve much faster, only those adapted to their individual host will survive; the population of symbionts in a host will evolve to play the best response to their host's strategy. In turn, only the hosts that fare best when the symbionts respond optimally to the host's strategy will flourish.

The problem of predicting how the population evolves therefore becomes as simple as finding the optimal strategy for a sequential game where the host moves first and the symbiont moves second (Brams and Hessel 1984). For the slowly evolving host, moving first is beneficial in mutualisms, but is a disadvantage in antagonist interactions, consistent with the Red Queen and King hypotheses, but more prescriptive than both by specifying the final equilibrium. Importantly, our results are robust to changes in the parameters and also general enough to apply to multiplayer and continuous games.

Host-Symbiont Model

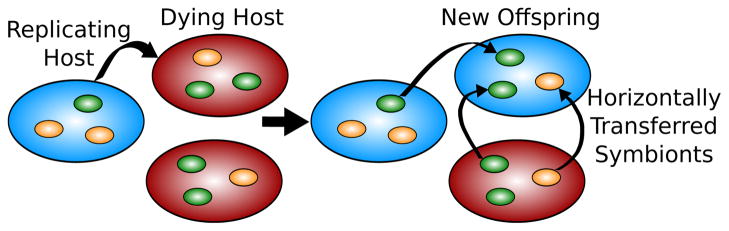
To model host-symbiont coevolution, we employed a common tool from evolutionary dynamics, the Moran process (Moran 1962; Nowak 2006; Nowak et al. 2010); each organism reproduces with probability proportional to its fitness, replacing a randomly chosen dying organism of the same species (Fig. 1). This fitness is the payout from pairwise interactions each host has with its own population of symbionts rather than the entire population of symbionts as done by Bergstrom and Lachmann (2003). The payout from these interactions is given by genetically predetermined strategies to a game played between the host and symbiont. We begin by assuming that whenever a symbiont reproduces, its offspring remains associated with the same host, and whenever a host reproduces, the new host offspring acquires its symbionts from other hosts (Fig. 1). The symbionts from every host, including the dying host, have an equal chance of being represented in the newly born host. The symbiont distribution in each new host is thus approximately the average over all symbiont populations. Also, to modulate the relative evolutionary rate (RER) of the symbionts, we varied their reproduction rate, allowing the symbionts to reproduce more often to imitate faster evolution; for instance, an RER of 5 means that the average symbiont will reproduce 5 times more often than the average host.

Figure 1.

Figure 1

Open in a new tab

Our model of host-symbiont coevolution. Each host plays a genetically determined strategy, represented by color, and reproduces with probability proportional to its fitness derived from pairwise interactions with each of its symbionts. The new host offspring receives horizontally transferred symbionts from the other hosts (including the dying host—not shown). Whenever a host or symbiont reproduces, its offspring plays the same strategy as its parent, unless it mutates with probability μ.

In our simulations, we used a population of 40 hosts and 40 symbionts associated with each host, for a total of 1600 symbionts. To maintain genetic diversity, each host and symbiont offspring can play a different strategy from its parent by mutating when born with probability μ = 0.01. However, as we will later see, the exact parameters of the model, including how new hosts acquire their symbionts and migration of symbionts between hosts, have very little effect on the results at high RER. In addition to simulations, we also analytically derived mean field approximations for the infinite and zero RER limit (see Supplemental Methods).

Results

Mutualisms

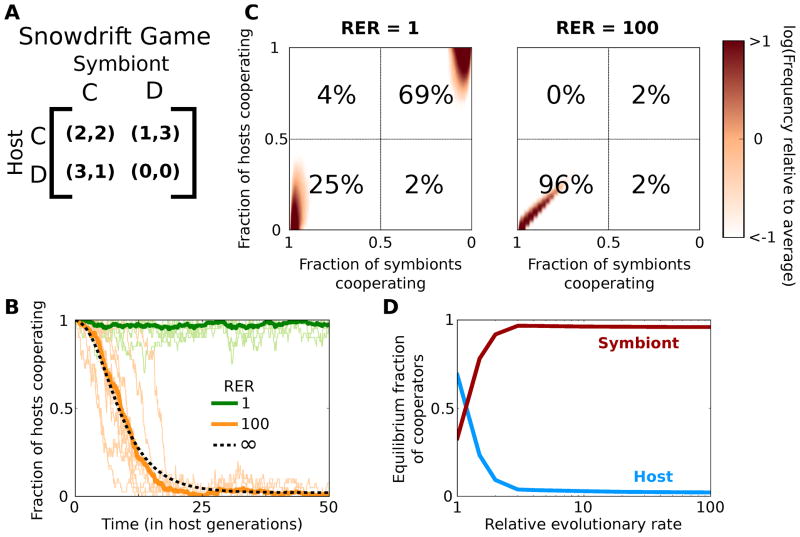
To examine the effect of a difference in evolutionary rate on the population dynamics, we first used a standard model for interspecies mutualisms, the snowdrift game (Fig. 2a), the most common example in symbiotic systems being nutrient production (Maynard Smith and Price 1973; Doebeli et al. 2004; Doebeli and Hauert 2005; Gore et al. 2009). The production of a certain essential nutrient (e.g. amino acid) is required for growth of both the host and symbiont, but neither species wants to be the one to carry the genomic and metabolic cost of producing it. If both players “cooperate” to produce the nutrient, then they share the benefits and costs equally, but either player has the incentive to “defect” and stop producing the nutrient to avoid paying the cost of production. However, if neither player produces the nutrient, both players starve. Two equilibria, where neither player can do better by changing its strategy, arise in this game: either the host cooperates and the symbionts defect or the host defects and the symbionts cooperate. However, in a sequential game, where one player moves before the other, there is only one equilibrium: the first player will defect because it forces the second player to “give in” and produce the nutrient.

Figure 2.

Figure 2

Open in a new tab

The population reaches the sequential game equilibrium as the relative evolutionary rate (RER) of the symbionts increases. (A) The payout matrix used for the snowdrift game played in pairwise interactions between each host and its symbionts. Each player can either Cooperate (C) or Defect (D). The host and symbiont receive a payout equal to the first and second number in each pair respectively. Each entry was given an offset of 1 to account for basal growth rate. (B) Ten simulation runs with RER of 1 and 100 are in light colors, with their average in darker, thick green and orange lines respectively, and the infinite RER limit is shown in the dashed line. The equilibrium of purely cooperating hosts and defecting symbionts is stable when RER = 1, but the sequential game equilibrium is the only stable state as RER increases. (C) Heat maps of the equilibrium probability distribution. The x-axis is reversed to mirror the payout matrix. The numbers in each quadrant are the percent of individual host-symbiont interactions that are in that corner. (C–D) The population goes from being bistable when RER is 1, to nearly all of the hosts defecting and the symbionts cooperating as RER increases.

The snowdrift game helps illustrate the difference between a well-mixed environment where every host interacts with every symbiont and our model where each host interacts with its own subpopulation of symbionts. As shown by Bergstrom and Lachmann (2003), in a well-mixed environment, the equilibrium of purely cooperating hosts and defecting symbionts is very stable, irrespective of the RER. While our model gives the same result when the symbionts reproduce at the same rate as the hosts (RER = 1), when the symbionts reproduce much faster (RER = 100), there is only one stable equilibrium: the sequential equilibrium with purely defecting hosts and cooperating symbionts (Fig. 2b).

To understand why only the sequential equilibrium is stable at high RER, imagine a new host that is the first to mutate to a defector in a population of cooperating hosts and defecting symbionts. When the symbionts evolve much faster than the hosts, the population of symbionts in this newly defecting host will quickly evolve to cooperate because that is the best strategy in their new environment. This host will soon have a payout close to 3 while the rest of the host population is still cooperating with their defecting symbionts and have a payout of about 1 (Fig. 2a). The new defecting host will therefore quickly take over the population. In contrast, when the symbionts reproduce at the same rate as their host, the symbiont populations do not evolve quickly enough and this newly defecting host will be stuck with defecting symbionts, giving it a payout closer to 0. Thus, both simultaneous move equilibria are stable when the evolutionary rates are equal. Of note, the symbionts reproducing 100 times as fast as the hosts, a reasonable rate for natural systems (Herre et al. 1999), is essentially equivalent to the symbionts always being in equilibrium with their host (Fig. 2b, dashed line).

Local, short term dynamics, however, paint an incomplete picture; often, the most evolutionarily relevant quantity is the equilibrium distribution reached after many generations (Fig. 2c). As one might expect, when the host and symbiont evolve at the same rate, the population becomes bistable, shifting periodically between the two equilibria; the population spends about 70% of the time with all of the hosts cooperating and symbionts defecting and the other 30% of the time with the hosts defecting and symbionts cooperating. However, as RER increases, the sequential game equilibrium with a purely defecting host population quickly becomes much more stable and the population spends nearly all of its time there. While increasing the number of hosts and symbionts stabilizes both equilibria at low RER, the sequential equilibrium remains the only stable point at high RER, independent of population size (Supplemental Fig. 1). Importantly, the snowdrift game is an example, contrary to our intuition, where evolving slowly is beneficial.

How high must RER be for the sequential game equilibrium to appear? This is a question of timescales; for a defecting host to spread in the population, the symbionts have to start cooperating in the defecting host before the host is replaced by the initially more fit cooperating hosts. For our parameters, it takes about three symbiont generations for cooperating symbionts to take over in a defecting host and about one host generation for an unfit host to be replaced (see Appendix). This corresponds to an RER of 3/1 = 3, which is exactly the point where the population settles into the sequential game equilibrium (Fig. 2d). A similar calculation shows that even if the difference in fitness between two competing strains of a virus is as low as 0.1%, then considerable in-host adaptation can occur, which is consistent with many parasitic phenomena and suggests that our findings are also applicable in the limit of weak selection (Levin and Bull 1994; Lysenko et al. 2010) (see Supplementary Text for details).

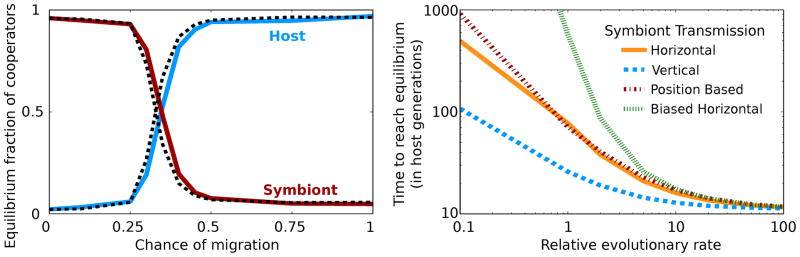
To test the stability of the sequential game equilibrium, we introduced the possibility of migration of symbionts between hosts: every time a symbiont reproduces, there is now a certain probability for its offspring to be born in a randomly chosen host rather than the same host as the reproducing symbiont (Fig. 3a). The final equilibrium, however, is unaffected until migration reaches the unrealistically high level of 30% (Nuismer et al. 1999). We also repeated our analysis using four different kinds of symbiont transmission: (i) horizontal transmission, our default where each new host receives its symbionts from the other hosts; (ii) vertical, the new offspring inherits its symbionts from its parent; (iii) position based, the new offspring acquires its symbionts from the dying host; and (iv) biased horizontal, each symbiont is horizontally transferred with probability proportional to its fitness. While horizontal may be the most generic, vertical transmission is common in endocellular symbionts and position based transmission often occurs for animal symbionts (Herre et al. 1999). At high RER, the equilibrium distribution is the same for all forms of symbiont transmission (Supplementary Fig. 1).

Figure 3.

Figure 3

Open in a new tab

The sequential game equilibrium is robust to symbiont migration between hosts. (A) The population becomes bistable for intermediate levels of migration and the equilibrium shifts at high levels. However, for realistic values of migration (<30%) the equilibrium remains unchanged for RER of 100 (solid lines) and infinity (dashed). (B) All forms of symbiont transmission are equivalent at high RER. The time to reach equilibrium is defined as the number of host generations it takes to reach a population of 90% defecting hosts in the snowdrift game from an initial purely cooperating host and defecting symbiont population. At high RER, this time is the same, independent of the form of symbiont transmission. At low RER, this time diverges.

While the final state does not depend on the form of symbiont transmission, the dynamics may be affected so we measured the time to reach equilibrium (which we define to be the number of host generations it takes to reach a population of 90% defecting hosts from an initial purely cooperating host and defecting symbiont population). The various forms of symbiont transmission have vastly different dynamics when the host and symbiont evolve at the same rate, but they are identical as RER increases (Fig. 3b). Importantly, our results are also robust to changes in the mutation rate, basal growth rate, and number of hosts and symbionts (Supplementary Fig. 1). It should also be noted that at low and moderate RER in our simulations, the host is highly favored when the symbionts are vertically transmitted which is consistent with the selection for benevolence found in host-parasite experimental evolution studies where vertical transmission is strictly maintained (Bull et al. 1991).

Returning to the nutrient production dispute between the host and its symbiont, our model predicts that the symbiont would produce the metabolite. This would explain why the endocellular bacterial symbiont of aphids, Buchenera sp. APS, commits nearly 10% of its genome to the production of glutamate and aspartate, two amino acids not produced by their aphid host (Shigenobu et al. 2000). This would also clarify why lytic phages infecting marine cyanobacteria Prochlorococcus dedicate much of their genome to photosynthesis and phosphate acquisition genes (Lindell et al. 2007). These and many other cases of apparent enslavements in symbiotic mutualisms can be understood by thinking of the relationship as a snowdrift game where the host moves first (or as an iterated prisoner's dilemma where the host is first to commit to a strategy (Axelrod and Hamilton 1981; Frean and Abraham 2004; Doebeli and Knowlton 1998), Supplementary Fig. 3).

Antagonistic Interactions

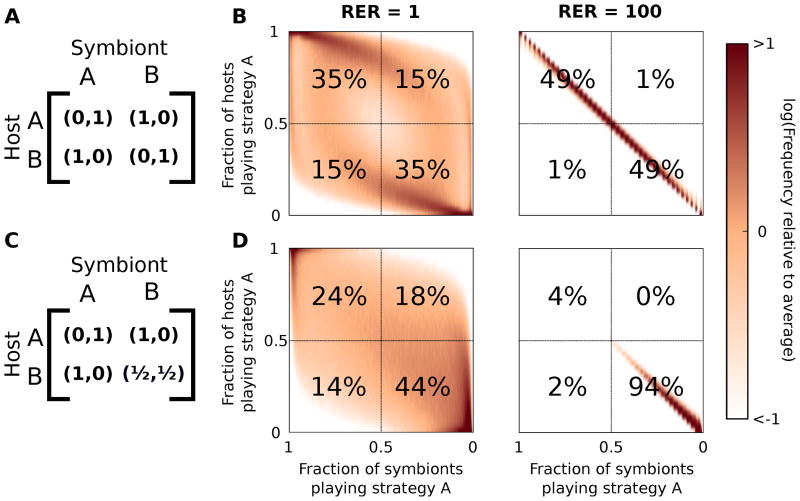
Most studies of symbiotic coevolution only concentrate on mutualistic or parasitic relationships, but our findings are generalizable to both types and help to unify the field. Perhaps the simplest and most relevant antagonistic game played between a host and a symbiont is immune system evasion (Kniskern and Rausher 2001). Imagine a situation where a host can either produce toxin A or toxin B to try to kill a parasite, which can, in turn, either be resistant to toxin A or B (Fig. 4a). When the host and parasite evolve at the same rate, we see periodic cycles with no clear winner (Fig. 4b). However, when the parasite evolves much faster than the host, the parasites definitively win this arms race (Fig. 4b). This is consistent with the Red Queen hypothesis because faster evolutionary rates are favored, but also note the end state is actually also the sequential game equilibrium because no matter which toxin the host uses, the parasites quickly evolve resistance.

Figure 4.

Figure 4

Open in a new tab

Antagonistic interactions also arrive at the sequential game equilibrium for high relative evolutionary rate (RER) of the symbiont. (A) The payout matrix of the cyclic fixed-sum game. The sum of the payouts is constant for each entry. (B) When the hosts and symbionts reproduce at the same rate, the population dynamics are cyclic with a slight bias towards the upper left and lower right quadrants. However, when the symbionts reproduce much faster, the host is highly disfavored. (C–D) If an asymmetry is added, similar dynamics result, but it becomes clear that rather than the host simply being disfavored, the sequential game equilibrium results at high RER. (To account for basal growth rate, an offset of 0.05 for (A–B) and 1 for (C–D) was added to each payout matrix)

To distinguish the sequential equilibrium, let us add an asymmetry to the payout matrix (Fig. 4c). Now rather than produce toxin B, the host has a more general defense that is good against both of the symbiont's strategies, but is still worse than producing toxin A when the symbiont is susceptible. When the evolutionary rates are equal, the population still cycles, now with a slight bias towards the general strategy by the host (Fig. 4d). As RER increases, however, the hosts abandon the specialist strategy and the population again reaches the sequential game equilibrium (Fig. 4d).

As we have shown, as RER increases, the population reaches the sequential game equilibrium where the host moves first for both mutualistic and antagonistic games (see also Supplementary Fig. 2). The Red Queen hypothesis is thus confirmed for antagonistic coevolution because moving first is always bad for fixed-sum games (Koller and Megiddo 1992). One of the most pertinent antagonistic interactions is the constant push to invent new antibiotics as bacteria rush to gain resistance; we as humans have artificially accelerated our evolution to stay ahead in this coevolutionary race.

Continuous Games

For the previous games we studied, each player could only choose one of two strategies; we now relax that constraint and consider a game where each player can play any of a continuum of strategies. A biological example of a continuous game is when two organisms fight over how much of a resource to use, when the production costs are shared. For simplicity, we can model this scenario by assuming that the benefit per use of the resource is constant and the shared cost per use increases linearly with the total amount used:

Payout(Host)=(Benefit−Cost∗(QH+QS))∗QH

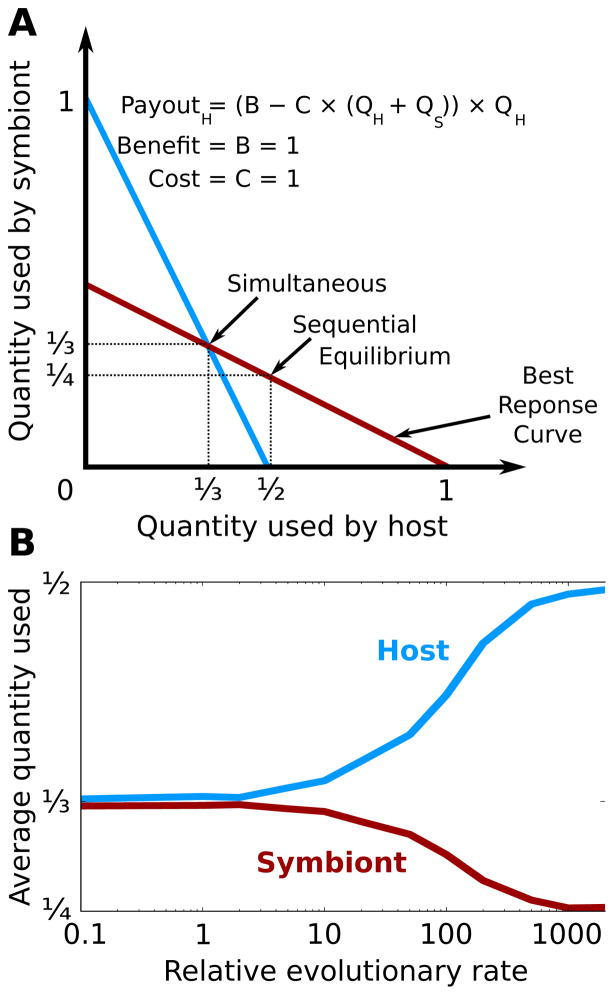
where QH and QS are the quantity used by the host and symbiont, respectively. If we set the benefit and cost per use to 1, then the simultaneous move equilibrium for both players is ⅓ (Fig. 5a). If, however, we let one player move before the other, the first player can take more than its share and because the resource becomes more expensive as more is used, the second player will use a lesser amount. In fact, because of the linearity of the cost and benefit, the first player's best move is the same as if the other player was not there, and the second player's best move is half of the first's: (½, ¼). This game is actually equivalent to the famous Cournot duopoly competition, where two firms choose a quantity of a product to make and the price that the product sells for is a function of the sum of the quantities.

Figure 5.

Figure 5

Open in a new tab

The sequential game equilibrium remains for continuous games such as the famous Cournot duopoly game. (A) Our model of interspecies conflict over how much of a resource with shared production costs to use. From the payout function, one can derive best response curves for the host and symbiont. If the two players move simultaneously, the equilibrium is where the best response curves intersect, but if the players move sequentially, the first player can do better by using more resources. Because of the linearity of the costs and benefits, the first player's optimal move is the monopolist's best move. (B) As RER increases, the population shifts from the simultaneous to the sequential equilibrium, with the host moving first. For model details, see Supplemental Methods.

Given the continuous nature of this game, we allowed the quantities used by each player to be any positive value. Also, each time an offspring is mutated, it uses a quantity equal to its parent's plus a random value taken from a normal distribution with mean 0 and standard deviation 0.1. As expected, the simultaneous equilibrium is achieved when the host and symbiont evolve at the same rate (Fig. 5b). However, as RER increases, the population amazingly finds its way to the sequential equilibrium. Similar to the snowdrift game, the slowly evolving host moves first to claim the majority of the benefits in this mutualism. Importantly, the sequential equilibrium is maintained even in continuous games.

The uneven distribution of benefits can provide a possible explanation for the extreme GC:AT ratios seen in endocellular symbionts. In the cell, the DNA bases guanine and cytosine (G and C) are more expensive to make than their alternatives adenine and thymine (A and T) (Rocha and Danchin 2002). Each organism, however, has an optimal GC:AT ratio for codon usage, DNA motifs, and DNA bending, creating a tension between organisms that share resources (Geggier and Vologodskii 2010). For examples, obligate parasitic and intracellular bacteria have a genomic GC frequency of 38% on average versus the 49% used by their free-living counterparts. Also, insertion sequences, plasmids, and phages have an AT enrichment of on average 1%, 2.7%, and 4% relative to their hosts—a trend that follows their reproductive rate (Rocha and Danchin 2002). This correlation remains even when the comparison is restricted to homologous genes, suggesting that the AT bias is not because of the different kinds of genes present in the symbionts. While alternative explanations exist for the AT bias in endosymbionts (Wernegreen and Funk 2004), this example is just one possible application of our findings in continuous games which are often a more realistic view of biology (Nowak and Sigmund. 2004; Foster and Wenseleers 2006; Leigh 2010).

Discussion

Here, we have demonstrated that when the symbionts evolve much faster than their host, rapid symbiont adaptation leads to the population converging to the sequential game equilibrium. However, when the host and symbiont evolve at the same rate, the dynamics are dominated by the Nash equilibria, which are any equilibria where each player is playing the best response to the other player's move. The snowdrift game has two Nash equilibria: one player cooperates while the other defects and vice versa. This causes the bistability seen when the evolutionary rates are equal. Also, the antagonistic games studied have no pure strategy Nash equilibria because the host always wants to play the opposite strategy as the symbionts and the symbionts always want to play the same strategy as the host. This lack of a Nash equilibrium is what causes the cyclic dynamics seen at RER = 1. In addition, the Cournot game is particularly interesting because it has both a Nash and a sequential equilibrium, but they are different. In this case, we saw that again the population moved from the Nash to the sequential equilibrium as RER increases. Intriguingly, once the symbionts are playing the sequential equilibrium, each host has the incentive to use less resources because they are not in a Nash equilibrium. However, any host that does mutate to use less will be punished when its symbionts evolve the best response to their host and use more resources (Fig. 5a). This rapid adaption of symbionts to their host is what maintains the sequential game equilibrium in the population despite the individual incentive of each host to cheat.

By using a very general and intuitive model, we have presented a novel and unifying theory of symbiotic coevolution. Our findings are more prescriptive than the Red Queen and King hypotheses by specifying the final equilibrium and applying to any game a host and symbiont might play. In fact, our results are general enough to apply to systems with more than two species, such as human, bacteria, and phage systems where we find that the slowly evolving host still moves first, the bacteria second, and the rapidly adapting phage last (Supplementary Fig. 4). Our results can also be applied to the study of the maintenance of symbioses by including host sanctions and the option of the symbiont being free living as an additional strategy. No matter how complicated the game is, if the symbiont evolves much faster than the host, then the equilibrium distribution is the same as it would be if the host and symbiont were instead playing a sequential game with the host moving first.

Our results can be best understood by remembering a famous anecdote from the game of chicken, where two players drive head on towards each other—the first person to swerve is forever deemed a “chicken,” but if neither driver swerves, the cars crash and everyone loses. The humorous, but not altogether joking, solution to the game is to throw your steering wheel out of the car, showing your opponent that you have committed yourself to driving your car straight and giving him no other option but to swerve. In our model, the host “throws the steering wheel out of the car” by evolving very slowly relative to its symbionts, committing itself to a certain strategy. Sometimes this is favorable, like in the snowdrift and Cournot duopoly game, but other times committing to a strategy can be harmful, in the case of antagonistic games. This is particularly relevant to us; as slowly evolving hosts to trillions of symbionts we often can do nothing but wait to see our symbionts' second move.

Supplementary Material

Supp Figure S1-S4

Acknowledgments

We would like to thank S. Serene, A. Velenich, H. X. Chao, H. Celiker and the rest of the laboratory for thoughtful discussions and/or aid with simulations. We also thank the two anonymous reviewers for their helpful comments. The laboratory acknowledges financial support through an NIH K99 Pathways to Independence Award.

Appendix

In general, the time it takes for a beneficial mutant to spread in a population is approximately the time for the mutation to arrive and survive stochastic extinction plus the time it takes for that mutant to fix in the population:

Timeformutanttofix=(1+r−1)/(1+r−N)∗1/mN+ln(N)/(r−1)

where N is the population size, μ the mutation rate, and r the relative growth rate of the mutant (Nowak 2006). The time for a mutation to arrive is 1/(μN) and (1 + r −1)/(1 + r −N) is the probability that the mutation will fix in the population. In turn, ln(N)/(r − 1) is the time it takes for the mutant to take over the population. Now, let us find these values for the snowdrift example in the text. The relative growth rate, r, of a cooperating symbiont in a defecting host is:

r=Payout(Cooperator)/Payout(Defector)=(1+offset)/(0+offset)=(1+1)/(0+1)=2

The symbiont population size, N, is 40 and the mutation rate, μ, is 0.01. This would tell us that the time for a cooperator to fix in the population is about 8.7 symbiont generations, but this is assuming that the symbiont population is initially all defectors which is not the case on average. Because of mutation and horizontal transmission, a new host starts on average with about 2 cooperating symbionts, so we no longer have to wait for a mutant to arrive. The equation reduces to:

Timeformutanttofix=ln(N/2)/(2−1)=ln(20)≈3SymbiontGenerations

which is the value cited in the main text.

Contributor Information

James A. Damore, Email: damore@mit.edu.

Jeff Gore, Email: gore@mit.edu.

References

  1. Axelrod R, Hamilton WD. The evolution of cooperation. Science. 1981;211:1390–1396. doi: 10.1126/science.7466396. [DOI] [PubMed] [Google Scholar]
  2. Bergstrom CT, Lachmann M. The Red King effect: when the slowest runner wins the coevolutionary race. Proc Natl Acad Sci USA. 2003;100:593–598. doi: 10.1073/pnas.0134966100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Brams SJ, Hessel MP. Threat Power in sequential games. Int Stud Quart. 1984;28:23–44. [Google Scholar]
  4. Bull JJ, Rice WR. Distinguishing mechanisms for the evolution of co-operation. J Theor Biol. 1991;149:63–74. doi: 10.1016/s0022-5193(05)80072-4. [DOI] [PubMed] [Google Scholar]
  5. Dawkins R, Krebs JR. Arms races between and within species. Proc R Soc Lond B. 1979;205:489–511. doi: 10.1098/rspb.1979.0081. [DOI] [PubMed] [Google Scholar]
  6. Doebeli M, Knowlton N. The evolution of interspecific mutualisms. Proc Natl Acad Sci USA. 1998;95:8676–8680. doi: 10.1073/pnas.95.15.8676. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Doebeli M, Hauert C, Killingback T. The evolutionary origin of cooperators and defectors. Science. 2004;306:859–861. doi: 10.1126/science.1101456. [DOI] [PubMed] [Google Scholar]
  8. Doebeli M, Hauert C. Models of cooperation based on the Prisoner's Dilemma and the Snowdrift game. Ecol Lett. 2005;8:748–766. [Google Scholar]
  9. Edwards DP, Hassall M, Sutherland WJ, Yu DW. Selection for protection in an ant—plant mutualism: host sanctions, host modularity, and the principal--agent game. Proc R Soc B. 2006;273:595–602. doi: 10.1098/rspb.2005.3273. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Foster KR, Wenseleers T. A general model for the evolution of mutualisms. J Evol Biol. 2006;14:1283–1293. doi: 10.1111/j.1420-9101.2005.01073.x. [DOI] [PubMed] [Google Scholar]
  11. Frean MR, Abraham ER. Adaptation and enslavement in endosymbiont-host associations. Phys Rev E. 2004;69:51913-1–6. doi: 10.1103/PhysRevE.69.051913. [DOI] [PubMed] [Google Scholar]
  12. Geggier S, Vologodskii A. Sequence dependence of DNA bending rigidity. Proc Natl Acad Sci USA. 2010;107:15421–15426. doi: 10.1073/pnas.1004809107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Gore J, Youk H, van Oudenaarden A. Snowdrift game dynamics and facultative cheating in yeast. Nature. 2009;459:253–256. doi: 10.1038/nature07921. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Herre EA, Knowlton N, Mueller UG, Rehner SA. The evolution of mutualisms: exploring the paths between conflict and cooperation. Trends Ecol Evol. 1999;14:49–53. doi: 10.1016/s0169-5347(98)01529-8. [DOI] [PubMed] [Google Scholar]
  15. Holland JN, DeAngelis DL, Schultz ST. Evolutionary stability of mutualism: interspecific population regulation as an evolutionarily stable strategy. Proc R Soc B. 2004;271:1807–1814. doi: 10.1098/rspb.2004.2789. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Koller D, Megiddo N. The complexity of two-person zero-sum games in extensive form. Game Econ Behav. 1992;4:528–552. [Google Scholar]
  17. Kniskern J, Rausher MD. Two modes of host-enemy coevolution. Popul Ecol. 2001;43:3–14. [Google Scholar]
  18. Leigh JG., Jr The evolution of mutualism. J Evol Biol. 2010;23:2507–2528. doi: 10.1111/j.1420-9101.2010.02114.x. [DOI] [PubMed] [Google Scholar]
  19. Levin BR, Bull JJ. Short-sighted evolution and the virulence of pathogenic microorganisms. Trends Microbiol. 1994;2:76–81. doi: 10.1016/0966-842x(94)90538-x. [DOI] [PubMed] [Google Scholar]
  20. Lindell D, et al. Genome-wide expression dynamics of a marine virus and host reveal features of co-evolution. Nature. 2007;449:83–86. doi: 10.1038/nature06130. [DOI] [PubMed] [Google Scholar]
  21. Lysenko ES, Lijek RS, Brown SP, Weiser JN. Within-Host Competition Drives Selection for the Capsule Virulence Determinant of Streptococcus pneumoniae. Curr Biol. 2010;20:1222–1226. doi: 10.1016/j.cub.2010.05.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Maynard Smith J, Price GR. The logic of animal conflict. Nature. 1973;246:15–18. [Google Scholar]
  23. McCutchan FE. Global epidemiology of HIV. J Medical Vir. 2006;78:S7–S12. doi: 10.1002/jmv.20599. [DOI] [PubMed] [Google Scholar]
  24. Moran NA, Dohlen CD, Baumann P. Faster evolutionary rates in endosymbiotic bacteria than in cospeciating insect hosts. J Mol Evol. 1995;41:727–731. [Google Scholar]
  25. Moran PAP. The statistical processes of evolutionary theory. Clarendon Press; Oxford, U.K: 1962. [Google Scholar]
  26. Nechaev S, Severinov K. The elusive object of desire--Interactions of bacteriophages and their hosts. Curr Opin Microbiol. 2008;11:186–193. doi: 10.1016/j.mib.2008.02.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Neish AS. The gut microflora and intestinal epithelial cells: a continuing dialogue. Microbes Infect. 2002;4:309–317. doi: 10.1016/s1286-4579(02)01543-5. [DOI] [PubMed] [Google Scholar]
  28. Nowak MA, Sigmund K. Evolutionary dynamics of biological games. Science. 2004;303:793–799. doi: 10.1126/science.1093411. [DOI] [PubMed] [Google Scholar]
  29. Nowak MA. Evolutionary Dynamics: Exploring the Equations of Life. Harvard University Press; Cambridge, MA: 2006. [Google Scholar]
  30. Nowak MA, Tarnita CE, Antal T. Evolutionary dynamics in structured populations. Phil Trans Soc B. 2010;365:19–30. doi: 10.1098/rstb.2009.0215. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Nuismer SL, Thompson JN, Gomulkiewicz R. Gene flow and geographically structured coevolution. Proc R Soc Lond B. 1999;266:605–609. [Google Scholar]
  32. Pal C, Macia MD, Oliver A, Schachar I, Buckling A. Coevolution with viruses drives the evolution of bacterial mutation rates. Nature. 2007;450:1079–1081. doi: 10.1038/nature06350. [DOI] [PubMed] [Google Scholar]
  33. Pierce NE, Easteal S. The selective advantage of attendant ants for the larvae of a lycaenid butterfly. J Anim Ecol. 1986;55:451–462. [Google Scholar]
  34. Rocha EPS, Danchin A. Base composition bias might result from competition for metabolic resources. Trends Genet. 2002;18:291–294. doi: 10.1016/S0168-9525(02)02690-2. [DOI] [PubMed] [Google Scholar]
  35. Shigenobu S, Watanabe H, Hattori M, Sakaki Y, Ishikawa H. Genome sequences of the endocellular bacterial symbiont of aphids Buchenera sp. APS Nature. 2000;407:81–86. doi: 10.1038/35024074. [DOI] [PubMed] [Google Scholar]
  36. Thompson AR. Habitat and mutualism affect the distribution and abundance of a shrimp-associated goby. Mar Freshwater Res. 2004;55:105–113. [Google Scholar]
  37. Van Valen L. A new evolutionary law. Evol Theor. 1973;1:1–30. [Google Scholar]
  38. Wernegreen JJ, Funk DJ. Mutation exposed: a neutral explanation for extreme base composition of an endosymbiont genome. J Mol Evol. 2004;59:849–858. doi: 10.1007/s00239-003-0192-z. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supp Figure S1-S4
NIHMS287684-supplement-Supp_Figure_S1-S4.pdf (2.2MB, pdf)

RESOURCES