Skip to main content
PMC home page
The Journal of Physiology logoLink to The Journal of Physiology
. 2011 May 3;589(Pt 13):3371–3381. doi: 10.1113/jphysiol.2011.209874

Force decline during fatigue is due to both a decrease in the force per individual cross-bridge and the number of cross-bridges

Marta Nocella 1, Barbara Colombini 1, Giulia Benelli 1, Giovanni Cecchi 1, M Angela Bagni 1, Joseph Bruton 2
PMCID: PMC3145945  PMID: 21540343

Non-technical summary

Prolonged muscle activity leads to a reduction of mechanical power and force output which is commonly indicated as muscular fatigue. The development of fatigue during repetitive stimulation of a skeletal muscle consists of an initial phase during which force decreases by 10–15%. This is followed by a second phase where force remains almost constant and finally a phase during which force drops precipitously to low levels. We show here that the initial fall in force is due to a reduction of the force generated by the individual molecular force generator, the cross-bridge, whereas in subsequent phases the force decrease is caused by a reduction in the number of molecular force generators. These results increase our understanding of muscular fatigue mechanisms.

Abstract

Abstract

Fatigue occurring during exercise can be defined as the inability to maintain the initial force or power output. As fatigue becomes pronounced, force and maximum velocity of shortening are greatly reduced and force relaxation is prolonged. In principle, force loss during fatigue can result from a decrease in the number of cross-bridges generating force or a decrease of the individual cross-bridge force or to both mechanisms. The present experiments were made to investigate this point in single fibres or small fibre bundles isolated from flexor digitorum brevis (FDB) of C57BL/6 mice at 22–24°C. During a series of 105 tetanic contractions, we measured force and fibre stiffness by applying small sinusoidal length oscillations at 2.5 or 4 kHz frequency to the activated preparation and measuring the resulting force changes. Stiffness data were corrected for the influence of compliance in series with the cross-bridge ensemble. The results show that the force decline during the first 20 tetani is due to the reduction of force developed by the individual cross-bridges and thereafter as fatigue becomes more severe, the number of cross-bridges decreases. In spite of the force reduction in the early phase of fatigue, there was an increased rate of tetanic force development and relaxation. In the latter stages of fatigue, the rate of force development and relaxation became slower. Thus, the start of fatigue is characterised by decreased cross-bridge force development and as fatigue becomes more marked, the number of cross-bridges decreases. These findings are discussed in the context of the current hypotheses about fatigue mechanisms.

Introduction

During periods of intense exercise, fatigue develops as an individual becomes unable to maintain the initial force or power output. Similar patterns of fatigue development are seen in exercising individuals and in isolated skeletal muscle preparations that are repeatedly stimulated to contract with tetanic contractions at 1–4 s intervals. Tetanic force decreases by up to 15% during the first minute and this is then followed by a phase of variable duration during which force remains stable or declines slowly until finally force declines rapidly (e.g. see Fig. 1 in Allen et al. 2008). At this time, the rate of shortening is reduced and muscle relaxation is prolonged. The causes and the mechanisms underlying the development of fatigue described above are incompletely understood. Much attention has focused on the possible intracellular changes that could underlie the loss of force-generating capacity. Several hypotheses have received much attention including a decrease in tetanic [Ca2+]i, acidosis, phosphate accumulation and reactive oxygen species (Allen et al. 2008; Lamb & Westerblad, 2011).

Figure 1. Both y0 and phase shift between length and force decrease with oscillation frequency up to 2 kHz.

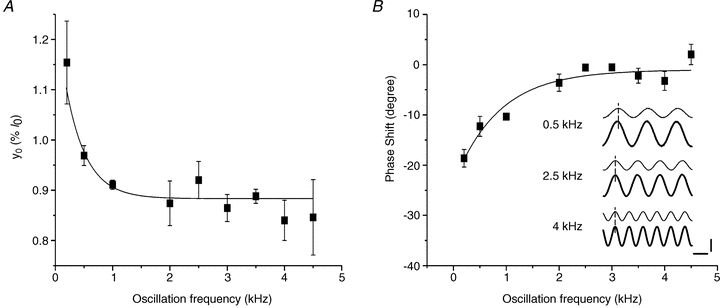
Figure 1

Open in a new tab

A, the line fitted on the experimental y0 data was the best fitting (R = 0.81) with the following single exponential decay equation: y0 = 0.39 ± 0.13 exp (–frequency/358 ± 87) + 0.88 ± 0.01. B, phase shift between length and force as function of oscillation frequency. Force leads length at frequency below 2 kHz, but it is in phase at higher frequencies. Mean ± SEM from experiments on 3 fibre bundles. Inset in B, typical records of force (thick traces) and length (thin traces) sinusoidal oscillations at 0.5 kHz (upper traces), 2.5 kHz (intermediate traces) and 4 kHz (lower traces) at tetanus plateau. Dashed line is drawn at the peak of length. Note that the phase shift (13 deg) present at 0.5 kHz disappears at frequencies above 2 kHz. Horizontal calibration, 250 μs; vertical calibration, 0.2%l0 or 10%P0. Phase shift in all our records at and above 2.5 kHz, even at forces down to 0.3 P0, was never greater than 5 deg.

In spite of repeated suggestions that cross-bridge function probably changes during the development of fatigue, relatively few experiments have examined if the number of cross-bridges and/or the mean force produced per cross-bridge change during the development of fatigue in intact mammalian muscles (Allen et al. 2008; Fitts, 2008). The aim of the present study was to clarify this point in intact mammalian muscle fibres.

Methods

Animals, fibre preparation and measurements

Single intact fibres or small bundles of up to 10 fibres were dissected from the flexor digitorum brevis (FDB) muscles of male C57BL/6 mice as described previously (Colombini et al. 2009). Animals were housed at controlled temperature (21–24°C) with a 12–12 h light–dark cycle. Food and water were provided ad libitum. Mice (3–6 months old) were killed by rapid cervical dislocation, according to the procedure suggested by the Ethical Committee for Animal Experiments of the University of Florence and the EEC guidelines for animal care of the European Community Council (Directive 86/609/EEC). The number of animals used was minimized by using more than one preparation from each FDB muscle. The dissection was performed manually under a stereo-microscope with a fine pair of scissors and needles, taking care to avoid stretching and to obtain preparations clean of debris from dead fibres. Small aluminium clips were attached to tendons as close as possible to the fibre ends and were used to mount the fibres horizontally in an experimental chamber (capacity 0.38 ml) between the lever arms of a capacitance force transducer (resonance frequency, 16–20 kHz) and of an electromagnetic motor used to change fibre length. Fibres were superfused continuously by means of a peristaltic pump at a rate of about 0.35 ml min−1 with a Tyrode solution of the following composition (mm): NaCl, 121; KCl, 5; CaCl2, 1.8; MgCl2, 0.5; NaH2PO4, 0.4; NaHCO3, 24; glucose, 5.5; EDTA, 0.1 and bubbled with 5% CO2– 95% O2 which gave a pH of 7.4. Fetal calf serum (0.2%) was routinely added to the solution.

The experiments were performed at room temperature (22–24°C). Bipolar stimuli (0.5 ms duration and 1.5 times threshold strength) were applied across the fibre by means of two platinum-plate electrodes mounted parallel to the fibre. Preparations were stretched to the length at which tetanic force was maximal, corresponding to a mean sarcomere length of 2.70 ± 0.02 μm (n = 10). Resting fibre(s) length, fibre largest and smallest diameters and resting sarcomere length (ls) were measured under ordinary light illumination using a microscope fitted with a 20× eyepieces and a 5× or 40× dry objective in the experimental chamber and checked later on digital images acquired by a video camera (Infinity Camera, Lumenera Corp., Canada) using image processing software. Mean preparation length (l0, clip to clip) was 1082 ± 46 μm (n = 10) of which 680 ± 36 μm were due to the fibre length and the remaining 402 μm to tendon attachment. Cross-sectional area of the single fibres or bundles was calculated as a * b*π/4 where a and b are the average values of the width and the vertical height (measured with fine focusing) of the preparation, respectively, measured at two to three different points along the preparation. Minimum and maximum cross-sectional areas were 790 μm2 (single fibre) and 9040 μm2 (bundle), respectively. Sarcomere length was measured by counting 10 sarcomeres on a calibrated scale on the acquired images. Stimuli and preparation length changes were controlled by custom-written software (LabView, National Instruments USA) which was also used to record force and length at sampling speed of up to 200 kHz.

Control tetanic contractions (400–800 ms duration, 70 Hz frequency) were obtained at 1 min or greater intervals. Plateau tetanic force (P0) was usually stable for up to 6 h but if P0 decreased by >10% over the period of the experiment, the data were discarded. A total of two single fibres and eight fibre bundles satisfied these criteria. Fatigue was induced using isometric contractions (400 ms, 70 Hz) evoked every 1.5 s and the protocol was stopped after 105 tetani or if force fell below 50% of the starting value. In all experiments, tetanic force recovered to more than 90% of its pre-fatigue value 2 h after the end of the fatiguing stimulation.

Analysis of mechanical properties of the preparation and stiffness measurements

To estimate the number of attached cross-bridges we measured fibre stiffness (Ford et al. 1977; Cecchi et al. 1982, 1986) by applying small 2.5 or 4 kHz sinusoidal length changes (dl) to one end of the activated preparation and by measuring the resulting force oscillations (dP) at the other end. Stiffness was then calculated as the ratio (dP/P0)/(dl/l0). Mean dl peak-to-peak amplitude was 1.78 ± 0.06 μm whereas dP mean amplitude was 20.31 ± 0.44%P0. Stiffness data presented here refer to the relative changes of this ratio during tetanus rise and during fatigue with respect to that measured at plateau before fatigue.

Stiffness needs to be measured with fast length changes to avoid truncation of the force response by the quick force recovery (Ford et al. 1977) but at the same time avoiding significant effects from fibre inertia. We investigated the effect of different length oscillation frequency in the range 0.2–4.5 kHz on stiffness measurements. Figure 1A shows that y0 (a measure of the relative preparation compliance, the reciprocal of stiffness) corresponding to the amount of instantaneous shortening which would just bring the isometric tension to zero (Ford et al. 1977), decreased from 1.10%l0 at 200 Hz to 0.89%l0 at 2 kHz and then remained approximately constant, up to 4.5 kHz.

This indicates that the quick recovery of force in this range had a negligible effect on stiffness. Consistent with this result, phase shift expected from the quick recovery (force leading length) was 19 deg at 200 Hz but was essentially zero at 2.5 kHz and higher frequencies (Fig. 1B) even when stiffness was measured at various tensions/times during the tetanus rise. None of the records used to measure stiffness in this paper, even at smaller forces (down to 0.3 P0), showed a phase shift between force and length greater than 5 deg.

The inertial forces, calculated as described in appendices D and E of Ford et al. (1977) even assuming a tendon compliance of twice the real value, were negligible for all our preparations (<0.2% of P0) even at 4.5 kHz. This is not surprising considering the very small length (∼1.1 mm) of the preparation and knowing that effects of inertia and surrounding fluid are both proportional to the square of fibre length. The calculated frequency of longitudinal oscillations was higher than 140 kHz, which is markedly higher than the value of 19 kHz calculated in frog fibres 5.6 mm long (Ford et al. 1977).

Thus, these results indicate that fibre stiffness measured with 2.5 kHz sinusoidal length oscillations is not significantly affected by quick force recovery or fibre inertia, representing a reliable measure of the instantaneous elasticity of the fibre.

Fatigue and tendon properties

Tendon properties were obtained from the experiments on the tetanus rise as shown in Results; however, it was necessary to test whether or not these properties are affected by the fatiguing protocol. To this end trimmed pieces of tendon from FDB muscles (mean length, 390 ± 60 μm; mean diameter, 153 ± 7 μm; n = 3) were mounted in the experimental chamber between the stretcher and force transducer, by means of aluminium clips, and were subjected to a series of 105 ramp-shaped stretches applied every 1.5 s. Each stretch increased the passive tension of the tendons up to a value similar to tetanic tension with a rise time of about 100 ms so as to mimic tetanic contractions during the fatiguing protocol. Sinusoidal length oscillations at 2.5 kHz were superimposed on the stretches to measure stiffness. Their amplitude was adjusted to give a maximum peak-to-peak sinusoidal tension of about 20% of the maximum tension. Stiffness was measured continuously throughout the whole tension rise with the following procedure. The force trace was high-pass filtered at 500 Hz using a fast Fourier transform (FFT filter) so as to obtain the oscillations on a zero line, then we obtained the absolute value of the signal which was successively low-pass filtered at 500 Hz to recover force modulation. Since length changes were strictly constant, force modulation corresponds to stiffness changes.

Results

Force and stiffness during fatigue

Figure 2 shows typical tetanic contractions and force responses to length oscillations in the same FDB fibre bundle during the first (control tetanus; A), the 24th tetanus (B) and the 105th tetanus (C) of a fatigue run.

Figure 2. Both force and stiffness are reduced in fatigue.

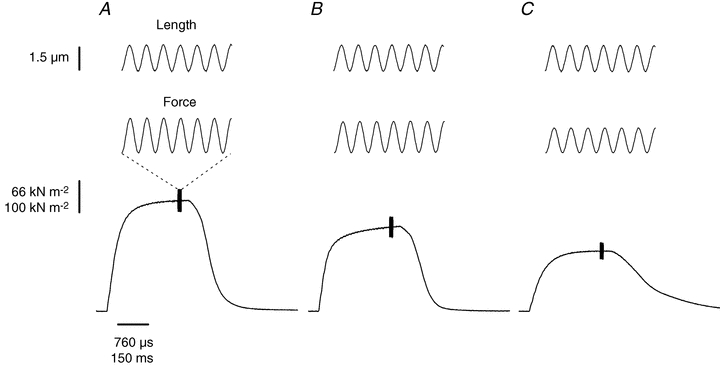
Figure 2

Open in a new tab

Typical records of the sinusoidal length change (top), the resultant force (middle) and tetanic force (bottom) during the first (A), 24th (B) and 105th (C) tetani of a series of tetanic contractions of the fatigue run. Dashed lines are used to indicate that top and middle traces are magnified to show that sinusoidal length changes (top) and force changes (middle) are in phase indicating a purely elastic behaviour of the fibre. Oscillations amplitude, 1.5 μm peak to peak corresponding to 0.15%l0; oscillation frequency, 2.5 kHz.

Tetanic force decreased by 24% in the 24th tetanus and by 45% during the 105th tetanus. Corresponding decreases in fibre stiffness, measured by the amplitude of force oscillations, were 10% in the 24th tetanus and 28% during the 105th and last tetanus. The mean tetanic force and stiffness changes occurring during fatigue in 10 preparations are shown in Fig. 3.

Figure 3. Tetanic force and fibre stiffness decrease at different rates during the induction of fatigue.

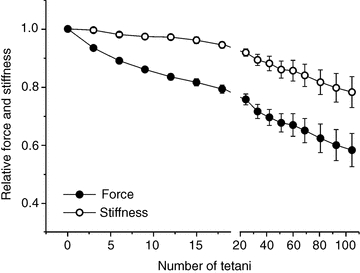
Figure 3

Open in a new tab

Tetanic force (filled circles) and fibre stiffness (open circles). The relatively high dispersion of data during the late period of fatigue is due to the variability of the extent of force depression in different fibres during this phase. This dispersion greatly decreases when stiffness data are plotted as a function of force as in Fig. 6. Data are expressed as a fraction of the values recorded during the first tetanus and are mean ± SEM; n = 10 (2 single fibres and 8 bundles).

It is obvious that over the first 12 tetani, force and stiffness do not decrease at the same rate: tetanic force falls by 17% whereas stiffness falls by only 3%. Thereafter the rate of decline in tetanic force and stiffness become similar. Similar qualitative changes in stiffness and tetanic force were also observed in two experiments on FDB fibres performed at 30°C (not shown here).

Stiffness correction for myofilament and tendon compliance

Stiffness results above refer to the whole preparation stiffness and they need to be corrected for tendon and myofilament contribution to extract the cross-bridge stiffness from which we can estimate the cross-bridge number.

To our knowledge, there are no data in the literature regarding the contribution of myofilaments to fibre compliance of mouse FDB muscle. Thus, for our calculation, we assumed the value of ∼38% found in mammalian fibres by Linari et al. (2004) with the striation follower and the remaining ∼62% was attributed to cross-bridge ensemble. Similar values were also reported for frog muscle (Colombini et al. 2010). We also assumed that cross-bridge and myofilament compliances are linear.

In principle, tendon compliance could be calculated from the difference between length changes applied to the preparation and those measured at sarcomere level. However, our FDB preparations were too short (∼1.1 mm) and the oscillations applied too small (1.78 μm peak to peak) to allow the use of a striation follower to measure sarcomere length change. Therefore, tendon compliance was calculated as the difference between y0 of our preparations, which includes tendons, and fibre y0 estimated from data reported in the literature. y0 of our preparations was 0.84 ± 0.02%l0 (n = 10), corresponding to an absolute length change of 1080 × 0.0084 = 9 μm. y0 of mammalian fast fibres at 12°C, taken from the same paper above by Linari et al. (2004), was ∼0.5% of fibre length. Knowing that when temperature is raised from 12°C to 22–24°C, tetanic tension increases by ∼50% (Stienen et al. 1996; Ranatunga, 2010) and that y0 increases by the same amount (Griffiths et al. 2002; Piazzesi et al. 2003; Colombini et al. 2008), we calculated that y0 of our fibres was ∼0.75% of fibre length, corresponding to 680 × 0.0075 = 5.1 μm. The difference between y0 of the preparation and that of the fibre, 9–5.1 = 3.9 μm, represents the length change of the tendon. Hence, at the tetanus plateau, tendon compliance is 3.9/9 or 43% of the preparation compliance whereas the remaining 57% is due to fibre compliance. Taking into account the above considerations regarding myofilament compliance, the total compliance of our preparation at tetanus plateau is as follows: 43% from tendon, 35% from the cross-bridges and 22% from myofilaments.

The contribution of tendon of 43% is valid only at plateau since tendon stiffness is non-linear (Cecchi et al. 1987). Thus, to correct preparation stiffness during fatigue it is necessary to know tendon contribution at each tension. This was obtained by measuring the stiffness of the preparations during the tetanus rise, a condition in which force and cross-bridge stiffness (and cross-bridge number) are linearly correlated (Bagni et al. 2005; Brunello et al. 2006). Figure 4A shows the results for our preparations. The force–stiffness relation is curved downward. The deviation from the linearity expected from cross-bridge stiffness is due to the contribution of tendon and myofilament to the stiffness of the preparation.

Figure 4. Tendon stiffness can be derived from stiffness data on the tetanus rise.

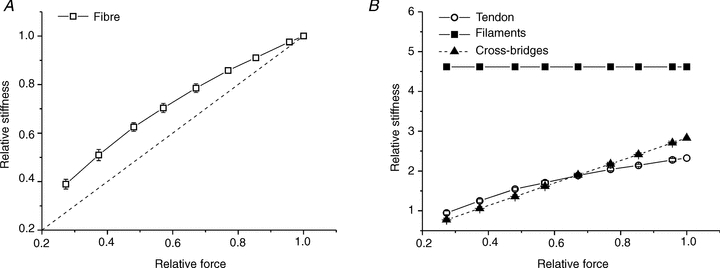
Figure 4

Open in a new tab

A, fibre stiffness is measured as a function of force during the tetanus rise. The downward curvature is due to the myofilament and tendon stiffness which contribute to fibre stiffness. The dashed line represents the direct proportionality between force and stiffness. B, stiffness of all the elastic components of the preparation during the rise of an isometric tetanus calculated for each of the experimental points in Fig. 3A with eqn (2). Symbols are: myofilaments (filled squares), tendon (open circles) and cross-bridges (filled triangles). Stiffness values are expressed relative to preparation stiffness at tetanus plateau. Values are mean ± SEM; n = 10 (2 single fibres and 8 bundles).

Given the series disposition of cross-bridges, myofilament and tendon compliances (Colombini et al. 2010), we can write the preparation stiffness (1/Ctr) as:

graphic file with name tjp0589-3371-m1.jpg (1)

where Ctr is the total compliance of the preparation, Cb is the cross-bridge compliance at tetanus plateau, on the tetanus rise Cf is the filament compliance (assumed Hookean), Cte is the tendon compliance at tetanus plateau and P/P0 is the relative force at which the measure is made. Hence, tendon compliance at each force is:

graphic file with name tjp0589-3371-m2.jpg (2)

The results of this calculation are shown in Fig. 4B where tendon stiffness is plotted as function of force, together with myofilament and cross-bridge stiffness. As expected, tendon stiffness increases with force indicating non-Hookean behaviour.

Effect of fatigue on tendon properties

The tendon data of Fig. 4B can be used to correct the preparation stiffness measured during fatigue shown in Fig. 3, providing that tendon properties are not affected by the fatiguing protocol. This possibility was investigated by subjecting trimmed pieces of tendon from FDB muscles, of length and diameter similar to the tendon attachment of our active preparations, to a series of 105 ramp-shaped stretches applied every 1.5 s. Stretches increased tendon passive tension up to a value similar to tetanic tension so as to simulate the fatiguing protocol. Stiffness was measured with superimposed 2.5 kHz length oscillations similarly to active preparations.

The results plotted in Fig. 5 show that: (1) tendon behaviour at 2.5 kHz oscillations frequency was purely elastic as length and force sinusoids were in phase, (2) tendon stiffness was non-linear as expected, and (3) it did not change appreciably during the series of stretches. This last point is very important as it shows that tendon properties do not change during the fatiguing protocol. Thus, tendon stiffness calculated on the tetanus rise can be used to correct the stiffness measurements during fatigue to extract cross-bridge stiffness.

Figure 5. Tendon properties do not change during fatiguing protocol.

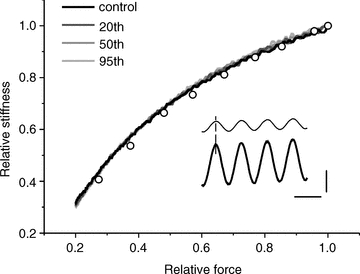
Figure 5

Open in a new tab

Typical tension–stiffness relations of a tendon preparation during the first, 20th, 50th and 95th stretches of a series of 105 stretches applied to simulate the effects of fatigue. All the 105 traces are almost perfectly superimposed with negligible difference between them; only 4 are plotted for clarity. The same results were obtained in all three experiments made. Tension and stiffness are expressed relative to the values at tension peak which was similar to the tetanic tension developed by our active preparation. The procedure to calculate stiffness continuously during the whole tension rise is described in the Methods section. Open circles show the calculated tendon stiffness from the data taken on the tetanus rise of Fig. 4B, normalized to 1. Note the very good similarity with data measured on tendon preparation. Inset, length (thin trace) and force (thick trace) sinusoids at 2.5 kHz are in phase. Records taken at tension of 62% of maximum. Vertical calibration, 8% of maximum tension or 0.7% of preparation length (440 μm); horizontal calibration, 400 μs.

Comparison of stiffness during tetanus rise and fatigue

When the data taken during fatigue of Fig. 3 are plotted in the form of a stiffness–force relation and compared with data of Fig. 4A, it is clear that at any force, the stiffness of the preparation is higher during fatigue than during the tetanus rise (Fig. 6). If myofilament stiffness is not affected by fatigue, as shown here for tendon stiffness, this difference can only be explained by an increased cross-bridge stiffness. This can be calculated by subtracting myofilament and tendon compliance from the total fibre compliance and taking the reciprocal.

Figure 6. Relative fibre stiffness is higher during fatigue than during the tetanus rise in non-fatigued fibres.

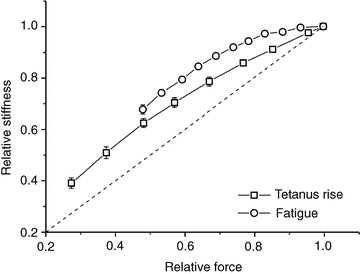
Figure 6

Open in a new tab

Relative stiffness data in non-fatigued preparations (open squares) taken from Fig. 4A and during fatigue (open circles) taken from Fig. 3. At any force, stiffness is greater during fatigue than during the tetanus rise, indicating a greater degree of cross-bridge stiffness. Measurements on the tetanus rise and fatigue were made on the same preparations, therefore the absolute fibre stiffness at plateau was the same in both cases.

Hence at any force, cross-bridge stiffness (1/Cb) is:

graphic file with name tjp0589-3371-m3.jpg (3)

where Ctf is the total fibre compliance during fatigue. Tendon and filament compliance were taken from the data on the tetanus rise. The results are shown in Fig. 7A. Cross-bridge stiffness (and thus cross-bridge number) is nearly constant during the initial 15 tetani of the fatigue run in spite of a simultaneous tension drop of ∼20%. Thereafter cross-bridge stiffness decreases steadily but always remaining higher than force.

Figure 7. Cross-bridge stiffness is essentially constant during early fatigue.

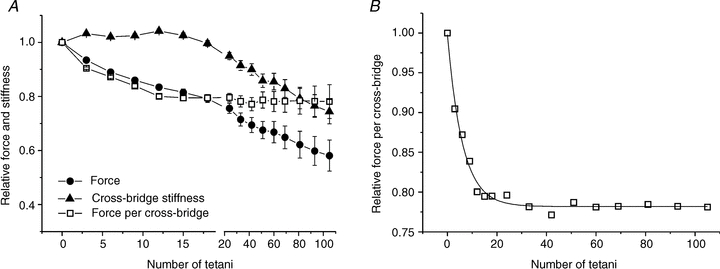
Figure 7

Open in a new tab

A, cross-bridge stiffness (filled triangles), force (filled circles) and force per cross-bridge (open squares) during fatigue. Cross-bridge stiffness remains nearly constant up to the 15th tetanus; thereafter it decreases in parallel with force. B, expansion of the time course of the individual cross-bridge force during fatigue shown in A. The continuous line is the best fit of the experimental data (R2 = 0.986) with the following equation: Force = 0.22 ± 0.01 exp (–number of tetani/6.08 ± 0.39)+ 0.780 ± 0.01. Error bars are omitted in B for clarity. Values are mean ± SEM; n = 10 (2 single fibres and 8 bundles).

Thus, the tension drop during early fatigue must be due to a reduction in the mean force developed per cross-bridge. This can be expressed by the ratio between force (proportional to force-generating cross-bridges) and cross-bridge stiffness (proportional to all cross-bridges) plotted in Fig. 7B. It can be seen that the relative force per cross-bridge decreases exponentially from the start of the fatigue run and attains a steady value of 0.78 after ∼20 tetani that is maintained throughout the remainder of the experiment.

Since in principle we could not exclude changes of the quick recovery speed during fatigue that could affect stiffness with respect to control, in a few experiments we measured stiffness using both 2.5 and 4 kHz frequency on the same preparation. The results are shown in Fig. 8. It is clear that force and stiffness changes are similar at both frequencies. There was no phase shift between force and length oscillations at any force at 2.5 and 4 kHz. Thus, stiffness changes during fatigue reflect changes in the elastic properties of cross-bridges.

Figure 8. Changes in force and stiffness measured with 2.5 kHz and 4 kHz length oscillations during the induction of fatigue do not differ significantly.

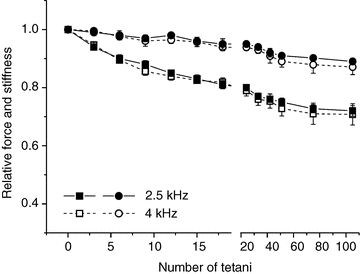
Figure 8

Open in a new tab

Filled symbols, 2.5 kHz, open symbols 4 kHz; squares, force; circles, stiffness. Values are mean ± SEM from 3 experiments on fibre bundles.

Rise and relaxation time during fatigue

Fatigue has been generally associated with a reduced rate of tetanic force development and a reduced rate of relaxation. For this reason we also investigated the effects of fatigue on the half-time of tetanus rise and relaxation. During the first 20 tetani, there was a marked (more than 20%) decrease of the tetanus rise half-time (Fig. 9A), from the rest value of 42.6 ± 2.4 ms to a minimum of 33.2 ± 0.5 ms, i.e. force development was faster. The rate of force development then recovered to its original level after 80 tetani and thereafter did not change further. Broadly similar changes were observed in the relaxation time (Fig. 9B): it was 100 ± 8 ms in the first tetanus, decreased during the first 10 tetani by about 20% and thereafter increased again so that at the end of the 105 tetani, it was about 30% greater than the initial control value.

Figure 9. Early in the induction of fatigue, both the rate of force development (A) and the rate of force relaxation (B) are increased compared to the control.

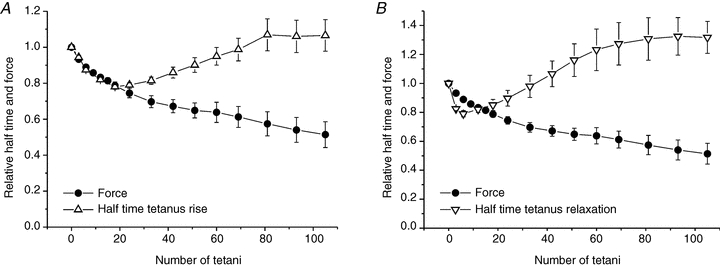
Figure 9

Open in a new tab

A, data points (upward open triangles) represent mean time required for force to develop to 50% of its mean plateau value. B, data points (downward open triangles) represent mean time required for force to decline to 50% of its mean plateau value. Data were obtained for the whole relaxation phase without distinguishing between the initial linear phase and the subsequent exponential decay. In both A and B, the filled circles represent the mean tetanic force (taken from Fig. 6) and is shown for reference. Values are expressed relative to those recorded during the first tetanus and are mean ± SEM; A, n = 7 (2 single fibres and 5 bundles) and B, n = 4 (bundles).

Discussion

There are two main novel findings in this study. First, the force decline during the initial phase of fatigue is due to a reduced force production by each individual cross-bridge. Second, when fatigue becomes more marked and tetanic force is reduced by up to 50%, this further decline in force is due to a decrease in the number of force-generating cross-bridges.

The pattern of force decline during the development of fatigue described here is similar to that described in earlier studies (Westerblad & Allen, 1991; Westerblad & Lännergren, 1991; reviewed in Allen et al. 2008), showing a relatively fast force decline during the first 15–20 tetani and a slower further fall of force during the subsequent 85–90 tetani. Our data show that the initial decline of force of about 20% is accompanied by a much smaller reduction of preparation stiffness (Fig. 3). Correction for the contribution from myofilaments and tendons allowed us to establish that cross-bridge stiffness remained nearly constant during this period, indicating that the associated force decline is caused by a reduction of the individual cross-bridge force (Fig. 7). The above correction was made by comparing our results with data in the literature assuming that y0 of our fibres was the same as that found in human muscle, and that cross-bridges and myofilament contribute to fibre compliance in the proportions of 62% and 38%, respectively (Linari et al 2004). While these values are subject to a degree of uncertainty, our analyses show that calculation of cross-bridge stiffness is relatively insensitive to changes in myofilament, cross-bridge and tendon compliances. For example, changing the ratio between cross-bridges and myofilament compliances or changing tendon compliance by ±20% affects the calculated cross-bridge stiffness during the early fatigue by less than 2%. Thus, it is clear that these uncertainties do not alter the main point of this paper i.e. the fall in force during early fatigue is produced by a reduction in the individual mean cross-bridge force. As shown in Fig. 7, the force per cross-bridge reaches its minimum of ∼0.78 after 20 tetani and thereafter changes little. Thus, this mechanism exerts its force depressing effect throughout the whole fatiguing period.

Measurements of tetanic [Ca2+]i have shown that it is not reduced but rather increased during the initial force decline. Indeed it is only when force begins to fall markedly (i.e. below 50% of initial force) that a significant decrease in [Ca2+]i can be demonstrated (Westerblad & Allen, 1991; Bruton et al. 2003). Thus, a lack of Ca2+ is not the underlying cause of the early cross-bridge force loss. A change in intracellular pH is also unlikely to explain the early decline in tetanic force during the first 10 tetani as intracellular pH shows little change (alkalinization of 0.02 pH units, Westerblad & Allen, 1992; Bruton et al. 1998). Previous studies examining changes in energy-rich phosphates using NMR have demonstrated that during a bout of contractile activity similar to that used in the present study, there is little change in [ATP] while both [Pi] and [ADP] more than double (Cady et al. 1989a,b; Jones et al. 2009). Increased [ADP] appears to play little role in modulating cross-bridge function (Cooke & Pate, 1985; Cooke, 2007). However, there is a large body of data which points to the depressant effect of increased [Pi] on force development in skinned fibres (Cooke & Pate, 1985; Coupland et al. 2001; Caremani et al. 2008). The precise mechanism by which Pi inhibits force production is unclear. Simple kinetic schemes suggest that elevated [Pi] can press the cross-bridges into a low force-generating state (scheme 1 in Ranatunga, 2010) or even cause actin and myosin to dissociate (Fig. 4 in Takagi et al. 2004). In accordance with the phosphate hypothesis, our data, showing a smaller individual cross-bridge force during the early fatigue, suggest that increased [Pi] pushes the cross-bridges into a low or no force-generating state with no detachment.

During the late stages of fatigue development there is little further change in the force developed by individual cross-bridges but rather the number of force-generating cross-bridges is reduced (Fig. 7). There are at least two likely factors that contribute to this. First, [Pi] will have increased to more than 30 mm (Cady et al. 1989b; Mizuno et al. 1994; Jones et al. 2009). The depressant effect of the further elevated [Pi] on tetanic force would now probably be accompanied by reduced cross-bridge recruitment due to a decrease in tetanic [Ca2+]i as Pi enters the SR and precipitates with Ca2+ thus reducing the releasable Ca2+ (Fryer et al. 1995). Second, intracellular pH will have fallen by 0.3 to 0.6 pH units (Sahlin et al. 1976; Cady et al. 1989a,b; Bruton et al. 1998); a fall of this magnitude will reduce tetanic force by about 15% as was demonstrated by Lännergren & Westerblad (1991). Finally, it is likely that the Ca2+ sensitivity of the contractile proteins was reduced by the combination of the reduced pH, increased [Pi] and the increased reactive oxygen species that are by-products of the increased metabolic demands of repeated contractions as suggested previously (Allen et al. 2008; Lamb & Westerblad, 2011). However, at this point in time, the target protein(s) for the reduction in Ca2+ sensitivity have not yet been identified.

A further interesting result of this study is the decrease in the half-times of force development and relaxation during the early stages of fatigue development. As shown in Fig. 9A, the half-time of tension rise decreases with the same time course of tension decay reaching a minimum value after about 20 tetani then increased again towards the resting level or slightly above. These observations are in agreement with the hypothesis that the decline in force in early fatigue is due to increased intracellular [Pi]. Increased rates of force rise and fall are in fact expected on a kinetic basis when intracellular [Pi] increases and these effects of elevated [Pi] have been previously demonstrated in skinned fibres and in small myofibril bundles (Hibberd et al. 1985; Millar & Homsher, 1990; Tesi et al. 2000; Takagi et al. 2004; Ranatunga, 2010). Accelerated changes in force are predicted by all of the simple kinetic schemes that seek to explain the effects of increased [Pi] on force which requires that (i) Pi release occurs in one or more reversible steps and (ii) cross-bridge force generation precedes Pi release (Millar & Homsher, 1990; Dantzig et al., 1992; Tesi et al. 2000; Takagi et al. 2004; Ranatunga, 2010). The increased half-time of force development that occurs during the late phase of fatigue indicates that additional mechanisms influence this parameter. Similar qualitative conclusions apply to the increased rate of force relaxation during early fatigue. It should be noted that this description refers to the whole relaxation period without distinguishing between the initial linear phase decay and the successive almost exponential decay.

Whereas there are no reports in the literature regarding the acceleration of relaxation during the early phase of fatigue, slowing of relaxation has been shown to occur either during intracellular acidification or the late stages of fatigue (Westerblad & Lännergren, 1991; Westerblad et al. 1997; Bruton et al. 1998). This slowed relaxation during fatigue has been reported in frog muscle (Dawson et al. 1980; Edman & Lou, 1990), in mouse muscle with and without a decline in intracellular pH (Edwards et al. 1975; Westerblad & Lännergren, 1991) and in human subjects with or without a decline in intracellular pH (Cady et al. 1989a). The accumulated data from these studies showing that (a) the rate of force relaxation continuously declined during the induction of fatigue and (b) the slowing of force relaxation by reduced intracellular pH was constant, suggested that some additional factor is involved in the slowing. Involvement of increased [Pi] in this slowing is complex given that both accelerated relaxation (e.g. Takagi et al. 2004) and slowed relaxation (e.g. Mulligan et al. 1999) have been demonstrated. The slowing of force relaxation might result from ADP accumulation or slowed Ca2+ handling (e.g. altered Ca2+ dissociation from buffers or Ca2+ re-uptake into the SR, see Allen et al. 2008). However, further experiments are required to resolve all the mechanisms involved in the slowing of tetanic force relaxation.

Lastly, it is interesting to point out that tendon properties, purely elastic at 2.5 kHz, are not significantly altered during the development of muscular fatigue in agreement with previous findings for human tendons in situ (Mademli et al. 2006).

Summary and perspective

In summary, the current experiments show that during fatigue, it is possible to independently alter the force per cross-bridge and the number of force-generating cross-bridges in an intact fibre. This study indicates that it is feasible and potentially worthwhile to devise training protocols or pharmacological phosphate ‘mops’ that limit the early rise in [Pi] and permit maximal force production for longer periods of time during strenuous activity.

Acknowledgments

This research was supported by the Ministero dell'Università e della Ricerca (PRIN 2006058094, 2007ABK385-002), Università di Firenze, Italy and funds at Karolinska Institute.

Author contributions

Experiments were carried out at Dipartimento di Scienze Fisiologiche, Università degli Studi di Firenze. The authors contributed to the paper as follows: performing the experiments: G.B., J.B., B.C. and M.N. Data analysis: M.A.B., G.C., B.C. and M.N. Design of the research: J.B. and G.C. Writing of the manuscript and revising it for intellectual content: M.A.B., J.B., G.C., B.C. and M.N. All authors read and approved the final version of the manuscript.

References

  1. Allen DG, Lamb GD, Westerblad H. Skeletal muscle fatigue: cellular mechanisms. Physiol Rev. 2008;88:287–332. doi: 10.1152/physrev.00015.2007. [DOI] [PubMed] [Google Scholar]
  2. Bagni MA, Cecchi G, Colombini B. Crossbridge properties investigated by fast ramp stretching of activated frog muscle fibres. J Physiol. 2005;565:261–268. doi: 10.1113/jphysiol.2005.085209. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Brunello E, Bianco P, Piazzesi G, Linari M, Reconditi M, Panine P, Narayanan T, Helsby WI, Irving M, Lombardi V. Structural changes in the myosin filament and cross-bridges during active force development in single intact frog muscle fibres: stiffness and X-ray diffraction measurements. J Physiol. 2006;577:971–984. doi: 10.1113/jphysiol.2006.115394. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Bruton J, Tavi P, Aydin J, Westerblad H, Lännergren J. Mitochondrial and myoplasmic [Ca2+] in single fibres from mouse limb muscles during repeated tetanic contractions. J Physiol. 2003;551:179–190. doi: 10.1113/jphysiol.2003.043927. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Bruton JD, Lännergren J, Westerblad H. Effects of CO2-induced acidification on the fatigue resistance of single mouse muscle fibers at 28°C. J Appl Physiol. 1998;85:478–483. doi: 10.1152/jappl.1998.85.2.478. [DOI] [PubMed] [Google Scholar]
  6. Cady EB, Elshove H, Jones DA, Moll A. The metabolic causes of slow relaxation in fatigued human skeletal muscle. J Physiol. 1989a;418:327–337. doi: 10.1113/jphysiol.1989.sp017843. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Cady EB, Jones DA, Lynn J, Newham DJ. Changes in force and intracellular metabolites during fatigue of human skeletal muscle. J Physiol. 1989b;418:311–325. doi: 10.1113/jphysiol.1989.sp017842. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Caremani M, Dantzig J, Goldman YE, Lombardi V, Linari M. Effect of inorganic phosphate on the force and number of myosin cross-bridges during the isometric contraction of permeabilized muscle fibers from rabbit psoas. Biophys J. 2008;95:5798–5808. doi: 10.1529/biophysj.108.130435. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Cecchi G, Colomo F, Lombardi V, Piazzesi G. Stiffness of frog muscle fibres during rise of tension and relaxation in fixed-end or length-clamped tetani. Pflügers Arch. 1987;409:39–46. doi: 10.1007/BF00584747. [DOI] [PubMed] [Google Scholar]
  10. Cecchi G, Griffiths PJ, Taylor S. Muscular contraction: kinetics of crossbridge attachment studied by high-frequency stiffness measurements. Science. 1982;217:70–72. doi: 10.1126/science.6979780. [DOI] [PubMed] [Google Scholar]
  11. Cecchi G, Griffiths PJ, Taylor S. Stiffness and force in activated frog skeletal muscle fibers. Biophys J. 1986;49:437–451. doi: 10.1016/S0006-3495(86)83653-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Colombini B, Benelli G, Nocella M, Musarò A, Cecchi G, Bagni MA. Mechanical properties of intact single fibres from wild-type and MLC/mIgf-1 transgenic mouse muscle. J Muscle Res Cell Motil. 2009;30:199–207. doi: 10.1007/s10974-009-9187-8. [DOI] [PubMed] [Google Scholar]
  13. Colombini B, Nocella M, Bagni MA, Griffiths PJ, Cecchi G. Is the cross-bridge stiffness proportional to tension during muscle fiber activation? Biophys J. 2010;98:2582–2590. doi: 10.1016/j.bpj.2010.02.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Colombini B, Nocella M, Benelli G, Cecchi, Bagni MA. Effect of temperature on cross-bridge properties in intact frog muscle fibers. Am J Physiol Cell Physiol. 2008;294:C1113–C1117. doi: 10.1152/ajpcell.00063.2008. [DOI] [PubMed] [Google Scholar]
  15. Cooke R. Modulation of the actomyosin interaction during fatigue of skeletal muscle. Muscle Nerve. 2007;36:756–777. doi: 10.1002/mus.20891. [DOI] [PubMed] [Google Scholar]
  16. Cooke R, Pate E. The effects of ADP and phosphate on the contraction of muscle fibers. Biophys J. 1985;48:789–798. doi: 10.1016/S0006-3495(85)83837-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Coupland ME, Puchert E, Ranatunga KW. Temperature dependence of active tension in mammalian (rabbit psoas) muscle fibres: effect of inorganic phosphate. J Physiol. 2001;536:879–891. doi: 10.1111/j.1469-7793.2001.00879.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Dantzig JA, Goldman YE, Millar NC, Lacktis J, Homsher E. Reversal of the cross-bridge force-generating transition by photogeneration of phosphate in rabbit psoas muscle fibres. J Physiol. 1992;451:247–278. doi: 10.1113/jphysiol.1992.sp019163. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Dawson MJ, Gadian DG, Wilkie DR. Mechanical relaxation rate and metabolism studied in fatiguing muscle by phosphorus nuclear magnetic resonance. J Physiol. 1980;299:465–484. doi: 10.1113/jphysiol.1980.sp013137. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Edman KA, Lou F. Changes in force and stiffness induced by fatigue and intracellular acidification in frog muscle fibres. J Physiol. 1990;424:133–149. doi: 10.1113/jphysiol.1990.sp018059. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Edwards RH, Hill DK, Jones DA. Metabolic changes associated with the slowing of relaxation in fatigued mouse muscle. J Physiol. 1975;251:287–301. doi: 10.1113/jphysiol.1975.sp011093. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Fitts RH. The cross-bridge cycle and skeletal muscle fatigue. J Appl Physiol. 2008;104:551–558. doi: 10.1152/japplphysiol.01200.2007. [DOI] [PubMed] [Google Scholar]
  23. Ford LE, Huxley AF, Simmons RM. Tension responses to sudden length change in stimulated frog muscle fibres near slack length. J Physiol. 1977;269:441–515. doi: 10.1113/jphysiol.1977.sp011911. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Fryer MW, Owen VJ, Lamb GD, Stephenson DG. Effects of creatine phosphate and Pi on Ca2+ movements and tension development in rat skinned skeletal muscle fibres. J Physiol. 1995;482:123–140. doi: 10.1113/jphysiol.1995.sp020504. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Griffiths PJ, Bagni MA, Colombini B, Amenitsch H, Bernstorff S, Ashley CC, Cecchi G. Changes in myosin S1 orientation and force induced by a temperature increase. Proc Natl Acad Sci U S A. 2002;99:5384–5389. doi: 10.1073/pnas.082482599. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Hibberd MG, Dantzig JA, Trentham DR, Goldman YE. Phosphate release and force generation in skeletal muscle fibers. Science. 1985;228:1317–1319. doi: 10.1126/science.3159090. [DOI] [PubMed] [Google Scholar]
  27. Jones DA, Turner DL, McIntyre DB, Newham DJ. Energy turnover in relation to slowing of contractile properties during fatiguing contractions of the human anterior tibialis muscle. J Physiol. 2009;587:4329–4338. doi: 10.1113/jphysiol.2009.175265. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Lamb GD, Westerblad H. Acute effects of reactive oxygen and nitrogen species on the contractile function of skeletal muscle. J Physiol. 2011;589:2119–2127. doi: 10.1113/jphysiol.2010.199059. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Lännergren J, Westerblad H. Force decline due to fatigue and intracellular acidification in isolated fibres from mouse skeletal muscle. J Physiol. 1991;434:307–322. doi: 10.1113/jphysiol.1991.sp018471. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Linari M, Bottinelli R, Pellegrino MA, Reconditi M, Reggiani C, Lombardi V. The mechanism of the force response to stretch in human skinned muscle fibres with different myosin isoforms. J Physiol. 2004;554:335–352. doi: 10.1113/jphysiol.2003.051748. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Mademli L, Arampatzisa A, Walsh M. Effect of muscle fatigue on the compliance of the gastrocnemius medialis tendon and aponeurosis. J Biomech. 2006;39:426–434. doi: 10.1016/j.jbiomech.2004.12.016. [DOI] [PubMed] [Google Scholar]
  32. Millar NC, Homsher E. The effect of phosphate and calcium on force generation in glycerinated rabbit skeletal muscle fibers. J Biol Chem. 1990;265:20234–20240. [PubMed] [Google Scholar]
  33. Mizuno T, Takanashi Y, Yoshizaki K, Kondo M. Fatigue and recovery of phosphorus metabolites and pH during stimulation of rat skeletal muscle: an evoked electromyography and in vivo31P-nuclear magnetic resonance spectroscopy study. Eur J Appl Physiol Occup Physiol. 1994;69:102–109. doi: 10.1007/BF00609401. [DOI] [PubMed] [Google Scholar]
  34. Mulligan IP, Palmer RE, Lipscomb S, Hoskins B, Ashley CC. The effect of phosphate on the relaxation of frog skeletal muscle. Pflügers Arch. 1999;437:393–399. doi: 10.1007/s004240050793. [DOI] [PubMed] [Google Scholar]
  35. Piazzesi G, Reconditi M, Koubassova N, Decostre V, Linari M, Lucii L, Lombardi V. Temperature dependence of the force-generating process in single fibres from frog skeletal muscle. J Physiol. 2003;549:93–106. doi: 10.1113/jphysiol.2002.038703. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Ranatunga KW. Force and power generating mechanism(s) in active muscle as revealed from temperature perturbation studies. J Physiol. 2010;588:3657–3670. doi: 10.1113/jphysiol.2010.194001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Sahlin K, Harris RC, Nylind B, Hultman E. Lactate content and pH in muscle obtained after dynamic exercise. Pflügers Arch. 1976;367:143–149. doi: 10.1007/BF00585150. [DOI] [PubMed] [Google Scholar]
  38. Stienen GJ, Kiers JL, Bottinelli R, Reggiani C. Myofibrillar ATPase activity in skinned human skeletal muscle fibres: fibre type and temperature dependence. J Physiol. 1996;493:299–307. doi: 10.1113/jphysiol.1996.sp021384. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Takagi Y, Shuman H, Goldman YE. Coupling between phosphate release and force generation in muscle actomyosin. Philos Trans R Soc Lond B Biol Sci. 2004;359:1913–1920. doi: 10.1098/rstb.2004.1561. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Tesi C, Colomo F, Nencini S, Piroddi N, Poggesi C. The effect of inorganic phosphate on force generation in single myofibrils from rabbit skeletal muscle. Biophys J. 2000;78:3081–3092. doi: 10.1016/S0006-3495(00)76845-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Westerblad H, Allen DG. Changes of myoplasmic calcium concentration during fatigue in single mouse muscle fibers. J Gen Physiol. 1991;98:615–635. doi: 10.1085/jgp.98.3.615. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Westerblad H, Allen DG. Changes of intracellular pH due to repetitive stimulation of single fibres from mouse skeletal muscle. J Physiol. 1992;449:49–71. doi: 10.1113/jphysiol.1992.sp019074. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Westerblad H, Bruton JD, Lännergren J. The effect of intracellular pH on contractile function of intact, single fibres of mouse muscle declines with increasing temperature. J Physiol. 1997;500:193–204. doi: 10.1113/jphysiol.1997.sp022009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Westerblad H, Lännergren J. Slowing of relaxation during fatigue in single mouse muscle fibres. J Physiol. 1991;434:323–336. doi: 10.1113/jphysiol.1991.sp018472. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from The Journal of Physiology are provided here courtesy of The Physiological Society

RESOURCES