Is an Intuitive Convergence Definition of Molecular Dynamics Simulations Solely Based on the Root Mean Square Deviation Possible?

Abstract

Molecular dynamics is a commonly used technique in computational biology. One key issue of each molecular dynamics simulation is: When does this simulation reach equilibrium state? A widely used way to determine this is the visual and intuitive inspection of root mean square deviation (RMSD) plots of the simulation. Although this technique has been criticized several times, it is still often used. Therefore, we present a study proving that this method is not reliable at all. We conducted a survey with participants from the field in which we illustrated different RMSD plots to scientists in the field of molecular dynamics. These plots were randomized and repeated, using a statistical model and different variants of the plots. We show that there is no mutual consent about the point of equilibrium. The decisions are severely biased by different parameters. Therefore, we conclude that scientists should not discuss the equilibration of a molecular dynamics simulation on the basis of a RMSD plot.

Introduction

Molecular dynamics (MD) is an “in silico” method to solve Newton's equations of motions for a given system of atoms. The applications of MD are manifold (Hansson et al., 2002) in areas such as protein sciences (Yaneva et al., 2009; Wan et al., 2008; Omasits et al., 2008; Karplus and Kuriyan, 2005), investigations of protein/membrane complexes (Wan et al., 2008), and nucleic acids (Luo and Bruice, 1998). Usually, MD simulations require a huge amount of computational power to take all interactions of all single atoms into account. Due to this runtime complexity, several solutions exist, for example, CHARMM (Brooks et al., 1983), AMBER (Case et al., 2005), NAMD (Phillips et al., 2005), GROMOS (Scott et al., 1999), and GROMACS (Hess et al., 2008). All of them have their advantages and drawbacks (see their respective manuals for details).

When scientists employ MD simulations to investigate a given system of atoms, they often conduct this experiment to see the influence of alterations in the system on the remaining system, for example, the binding of an altered peptide ligand (APL) to a receptor such as the major histocompatibility complex (MHC) (Knapp et al., 2009, 2010). Since these simulations usually start from an x-ray crystallography model, the system is required to adjust to the new ligand and to pass over to a new spatial arrangement. Based on this, one of the major questions arising is: When is the transition phase between the initial and new state completed, and when is the new spatial arrangement reached and maintained in a stable way? This stable state of the system is determined as its convergence (or equilibrium).

Several techniques for the definition of this equilibrium of a system exist and have been discussed in the literature (Grossfield and Zuckerman, 2009). They range from intra-molecular interaction energy, number of hydrogen bonds, root mean square fluctuations (RMSF), and torsion angle transitions to cluster counting (Smith et al., 2002). Also, structural histograms of clusters (Lyman and Zuckerman, 2006) and principal component analysis (Hess, 2002; Hess, 2000) were reported for this issue. However, a very common technique is the root mean square deviation (RMSD). The RMSD is defined as the spatial difference between two static structures:

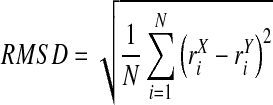(1)

Here, N denotes the number of atoms, i the current atom, r^X the target structure, and r^Y the reference structure. The RMSD is calculated between a defined starting point of the simulation and all succeeding frames. The target and reference structure may be aligned before RMSD calculation to minimize the total deviation. Subsequently, these RMSD values are depicted as a line-style plot where the authors determine the convergence and stability of a simulation based on their professional experience and intuition as various examples in the current literature show (Yaneva et al., 2009; Garzon et al., 2009; Sharma et al., 2009; Wells et al., 2009; Bismuto et al., 2009). In most cases, the authors determine a plateau of RMSD values as the equilibrium.

This technique has been criticized several times for its methodology, since, first, it does not provide information about which parts of the transition-states ensemble of the simulation were already sampled and, second, the position of the plateau specific for the respective simulation is unknown (Grossfield and Zuckerman, 2009). Highly dynamic RMSD plots may be treated as negative results (“no equilibrium”); however, equalized RMSD plots may not be indicative for equilibrium.

Although these drawbacks of the RMSD method are known, this relatively simple method is still often used in MD research (Lyman and Zuckerman, 2006). If scientists decide to apply the RMSD technique to determine the convergence of a simulation, irrespective of the general concerns mentioned above, they assume that their decision for the point of convergence is impartial, uninfluenced, and repeatable.

Thus, in this study, we present a survey with participants at different scientific qualification levels, different scaling of plots, and different color schemes, which illustrates that this assumption is not valid.

Methods

We implemented an online survey to interview scientists from the field in an easy, comfortable, and anonymous way. We showed 80 RMSD plots to each participant where each participant had to decide for each of the plots when the equilibrium/convergence of the simulation is reached. The detailed methods are described in the subsequent sections.

Underlying data

For this survey, we randomly selected 50 different RMSD data sets from previous MD projects of our group. To obtain an identical length of the MD trajectories, each data set was restricted to RMSD values based on the evaluation of the first 10 ns of the MD trajectories. From here on, one of these RMSD data sets is referred to as the prototype, while the plot created from the prototype using certain settings is referred to as the RMSD plot.

Variants in presentation of data

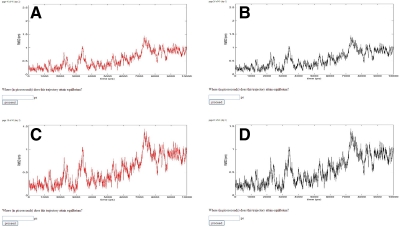
We illustrated the prototypes to the participants in different graphical styles varying in color and scaling. We utilized the colors black and red since (1) they are frequently used in the literature, and (2) intuitively, red appears active while black appears passive. For the size of the y-axis of the plot, we used 1.53 nm since the maximum RMSD values are at around 1.5 nm, and in the second variant we used 2.63 nm since this value is approximately 1 nm above. We refer to a y-axis size of 1.53 nm as fine scaled and a y-axis size of 2.63 nm as coarse scaled. These variations led to the following combinations (Fig. 1):

• 1) color of the plot, red; x-axis size, 10000 ps; y-axis coarse scaled

• 2) color of the plot, black; x-axis size, 10000 ps; y-axis coarse scaled

• 3) color of the plot, red; x-axis size, 10000 ps; y-axis fine scaled

• 4) color of the plot, black; x-axis size, 10000 ps; y-axis fine scaled

FIG. 1.

Different optical variants of the root mean square deviation (RMSD) plots. (A) Color of the plot, red; y-axis coarse scaled. (B) Color of the plot, black; y-axis coarse scaled. (C) Color of the plot, red; y-axis fine scaled. (D) Color of the plot, black; y-axis fine scaled.

In all four cases, we maintained the x-axis constant at 10000 ps. All four variants are based on the same RMSD data. Likewise, the remaining interface is identical in all variants.

Participants

We encouraged 10 different scientists from five different countries to participate in the survey. Seven participants were male and three female. At the time of the survey, two of them were Master's students, four were Ph.D. students, one was a postdoctoral fellow, and three were professors. This leads to an average qualification level between a Ph.D. student and a postdoctoral fellow, nicely representing a standard research group. Due to the setup of the study, a total number of 800 plots were evaluated by the participants, leading to enough repetitions per plot to obtain statistically significant results.

Selection of the illustrated data per participant

To consider the possible influence of different day, different scale, and different color on the evaluation of the 50 RMSD prototypes of the participants, we randomized the prototypes for these factors. Varying color and/or scale for the 50 prototypes yielded 200 different plots. We illustrated 40 plots on a first day and another 40 on a subsequent day to each participant. In order to aggravate identification of individual prototypes by the participants, these 80 plots consisted of 35 different RMSD prototypes that were randomized for each participant out of the overall sample of 50 prototypes. On the first day, we showed 15 of the 35 prototypes twice, using different scale and/or different color. Ten other of the 35 prototypes were shown only once. We randomized color and scale for these prototypes. On the second day, we showed the 15 prototypes from the first day again. To hamper identification of the prototypes, we changed scale and color in such a way that for each participant none of the plots was identical (same prototype with same color and same scale). The remaining 10 of the 35 prototypes were additionally illustrated on the second day. For these 10 prototypes, we randomized color and scale again. In total, we presented 800 (40 × 2 × 10) RMSD plots to the participants.

Restrictions for the participants

After each RMSD plot was shown, the participant had to decide at which time point (measured in pico seconds) the equilibrium is reached. The decisions were final (i.e., even if the participant used the back button of the browser and re-entered a new value, we took only the first decision into account). Additionally, the participants also had the opportunity to determine that the trajectory does not reach equilibrium state at all. However, the skipping of a RMSD plot was not possible. The participants had to determine a value of 0–10000 or “no equilibrium” at the first sight of each plot.

Technical implementation of the survey

We implemented the survey in PHP 5 using the Apache/2.0.61 web-server of the Medical University of Vienna. Furthermore, we utilized Matlab 7.9 to create the plots based on the RMSD data calculated by Gromacs 4 (Hess et al., 2008).

Statistical analysis

We calculated descriptive results (mean, median, minimum and maximum, frequencies). Additionally, we calculated a linear mixed-effects model fitted by restricted maximum likelihood with random factor plot to see the influence of participant, day, scale, and color on the time point of equilibrium. For the influence factor “participant,” we used effect coding. Furthermore, for this analysis, we used only those measurements that were assumed by the participants to actually have equilibrium in the observed time period. Additionally, we checked the distribution of residuals by visual inspection. To detect influences of the mentioned factors on the existence of equilibrium as a binary outcome variable, we performed a generalized linear mixed-model fitted by the Laplace approximation with random factor plot. We performed the analysis using R 2.8.0. In this context, we applied the functions lmer and glmer from the package lme4. We considered all p-values of <0.05 as statistically significant.

Results

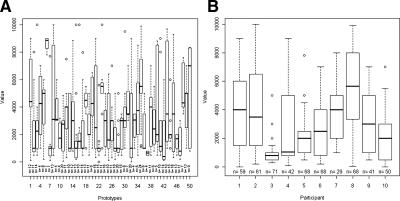
Out of the 800 plots, 396 (50%) were fine scaled and 393 (49%) were black. In 557 (70%) of the 800 plots of the 50 different RMSD prototypes, the participants indicated an equilibrium in the observed time period. In 289 (52%) of the plots on the first day, the participants specified equilibria, as compared to 268 (48%) of the 400 plots at the second day. In the 396 fine-scaled plots, equilibria were found in 252 (64%) plots, compared to 305 (76%) equilibria in the 404 coarse-scaled plots. A total of 274 (70%) of the 393 black plots were indicated to have equilibria, compared to 283 (70%) of the 407 red plots. Figure 2A shows the distribution of time points for each of the 50 different RMSD prototypes. Here, n is the number of plots of the according prototype with an indicated equilibrium in the observed time period. The crude median over all 557 plots was 2500 (min 0 to max 10000), while the median of the medians of the prototypes was 2875 (400–8850).

FIG. 2.

(A) Boxplots illustrating the results grouped by prototypes. (B) Boxplots illustrating the results grouped by participants.

Figure 2B shows the distribution of time points of indicated equilibria for each participant, where n gives the number of plots (out of the 80 plots of each participant) where the participant indicated equilibrium in the observed time period.

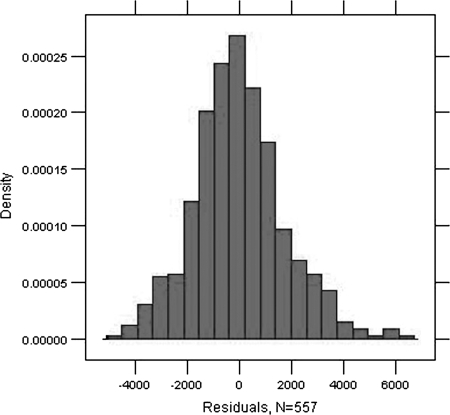
The time point of equilibrium chosen by the participants (including only those measurements where equilibrium is actually detected in the observed time period) was statistically significantly influenced by participant and scale. While participants 2, 7, and 8 valuated the plots significantly higher (p < 0.0001, p = 0.0016, p < 0.0001) than the mean assessment, participants 3, 5, 6, and 10 valuated the plots significantly lower (p < 0.0001, p < 0.0001, p = 0.0052, p = 0.0047). These p-values indicate substantial systematic deviations between participants even if Bonferroni threshold of p < 0.005 is applied. Participants 1, 4, and 9 show no significant deviation from the mean assessment. Coarse scaling causes statistically lower indicated time points of equilibrium (p = 0.0197). Day and color show no significant influence. Detailed information can be found in Table 1. Figure 3 shows the distribution of the residuals, which does not indicate any noticeable deviation from the assumption of a centered normal distribution.

Table 1.

Linear Mixed-Effects Model

	Estimate	SE	t-value	p-value
(Intercept)	3536.56	242.9813	14.55	<0.0001
Participant1	394.027	241.1775	1.634	0.1029
Participant2	1556.128	238.1697	6.534	<0.0001
Participant3	−2316.602	231.9044	−9.989	<0.0001
Participant4	−225.018	283.7134	−0.793	0.4281
Participant5	−1236.368	230.4955	−5.364	<0.0001
Participant6	−641.247	228.5019	−2.806	0.0052
Participant7	1117.612	352.6406	3.169	0.0016
Participant8	1915.835	240.8253	7.955	<0.0001
Participant9	180.307	288.6123	0.625	0.5324
Participant10	−744.674	262.4760	−2.837	0.0047
Day	−50.464	159.0235	−0.317	0.7511
Scale	−376.058	160.7773	−2.339	0.0197
Color	−62.215	159.4636	−0.39	0.6966

SE, standard error.

FIG. 3.

Distribution of the residuals.

Looking at the existence of equilibrium in the observed time period, participants 3, 5, 6, and 8 declared “no equilibrium” significantly more often (p < 0.0001, p < 0.0019, p = 0.0095, p = 0.0017) than the mean frequency. Also, coarse scaling is an indicator for the declaration of “no equilibrium” (p < 0.0001). Participants 4, 7, and 9 declared significantly less often (p = 0.0026, p < 0.0001, p < 0.0001) that “no equilibrium” occurs in the observed time period, whereas participants 1, 2, and 10 showed no significant difference from the mean frequency of specifying equilibrium. Also day and color has no statistically significant influence on the existence of equilibrium. Further information can be seen in Table 2.

Table 2.

Generalized Linear Mixed-Effect Model

	Estimate	SE	z-value	p-value
(Intercept)	−1.20337	0.28525	−4.219	<0.0001
Participant1	−0.08604	0.28525	−0.302	0.76
Participant2	−0.0619	0.29526	−0.21	0.83
Participant3	−1.62649	0.36917	−4.406	<0.0001
Participant4	0.77573	0.25763	3.011	0.0026
Participant5	−1.0853	0.35016	−3.099	0.0019
Participant6	−0.88525	0.3411	−2.595	0.0095
Participant7	2.29172	0.30586	7.493	<0.0001
Participant8	−1.03859	0.33071	−3.14	0.0017
Participant9	1.23615	0.27196	4.545	<0.0001
Participant10	0.47997	0.2683	1.789	0.074
Day	0.32448	0.19029	1.705	0.088
Scale	−0.8467	0.19381	−4.369	<0.0001
Color	0.16736	0.19093	0.877	0.38

SE, standard error.

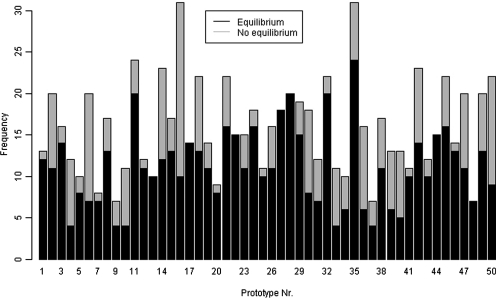
The median number of how often a prototype has been judged by the participants was 15.5 (7–31). For every of the 50 different prototypes, at least one participant determined that the simulation reached equilibrium in at least one color and scale. On the other hand, for 43 of the 50 prototypes at least one participant defined that the simulation does not reach equilibrium at all (Fig. 4).

FIG. 4.

Frequency of equilibrium and no equilibrium definitions per prototype.

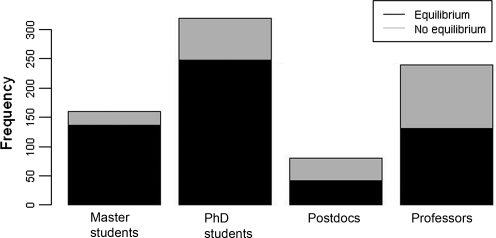
The training level had a severe influence on the decision as to whether simulations are determined as converged or not. Professorial and postdoctoral decisions are most cautious and critical: They determined 45.4% and 47.5% of all plots as not converged. On the other hand, Ph.D. students and Master's students were less critical: 22.5% and 15.0%, respectively. In Figure 5, we illustrate in detail how often participants of a certain qualification level determined RMSD plots as converged.

FIG. 5.

Frequency of equilibrium and no equilibrium definitions per training level.

Discussion

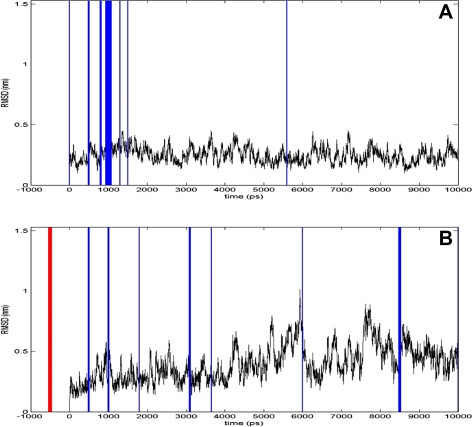
We present a survey investigating the intuitive definition of equilibrium reached by MD simulations based on the RMSD. In the title of this study, we ask the question if this intuitive definition is possible. Based on the results illustrated in this study, it is not conceivable that a scientist can determine the point of equilibrium of a MD simulation solely on his intuition and experience. Although in some cases the scientists agree on the time-point of equilibrium (Fig. 6A), in most cases their opinions diverge strongly (Fig. 6B). The scaling of the plots, especially, turned out to be crucial for the human decisions that equilibrium exists. By increasing the y-axis by about 1 nm, the results change significantly. Humans seem to be highly susceptible to the visual impression of a changed axis size. On the other hand, it is noteworthy that the color of the plot had no influence; a red plot is not seen as more active than a black one. Additionally, the day of participation has no significant influence on the results; the decisions are mainly consistent across the first and subsequent day. In contrast, the disagreements between opinions of the different scientists are severe, and in many cases, the chosen point of equilibrium seems to be almost randomly distributed over the 10 ns (Fig. 6B). For the far majority of all prototypes, no mutual consent over the different scientists can be drawn. Other scientists even argue that none of these simulations converged. Based on this disagreement, we argue that an intuitive equilibrium determination of MD simulations based on the RMSD is not possible. A possible reason for this disagreement is the lack of standards for the interpretation of RMSD plots that might aggravate the reproducibility. However, the construction of standards seems to be difficult, since the “true state of nature” with regard to equilibrium is unknown and gold standard methods to estimate equilibrium are missing. Therefore, the construction of material to be used in appropriate training procedures for assessment of “no equilibrium” for the individual interpretation of RMSD plots seems to be hampered by this dilemma of missing standards.

FIG. 6.

Two exemplary results. The blue vertical lines indicate where different participants defined the point of equilibrium. A thicker line describes that more participants choose the same time point. The red vertical line in the negative x-axis range depicts that the participants defined the simulations as never reaching the equilibrium. Both plots were created using the fine-scaled y-axis and the color black, although the points of equilibrium were extracted from all four color/scale combinations of the prototype. (A) An example for a very good agreement. With one exception all points of equilibrium were defined at around 1000 ps. (B) An example for no mutual consent. The points of equilibrium are distributed all over the 10,000 ps. The vast majority of all results is similar to (B) and shows no common mutual consent.

Furthermore, the RMSD was already criticized objectively several times for its methodology in principle; however, as mentioned before, there is currently no technique to describe a simulation as absolutely converged (Grossfield and Zuckerman, 2009). Therefore, this study adds to our knowledge that it is not (intuitively) possible to define the equilibrium of a MD simulation based on the RMSD since, even if the RMSD would contain sufficient information, researchers would not be able to draw a common conclusion from the same plot data. These results may even have implications for similar line-style-based techniques such as intramolecular interaction energy over time, number of clusters over time, or number of hydrogen bonds over time. All these techniques, irrespective of their methodological background, might suffer from the same biased human judgment as the RMSD.

We conclude that scientists should avoid determining the equilibrium of a MD simulation based on visual impression of RMSD values as is frequently done in current research.

Acknowledgments

This study was supported by the Austrian Science Fund (FWF P22258-B12).

Disclosure Statement

No competing financial interests exist.