A Robust Method for comparing Two Treatments in a Confirmatory Clinical Trial via Multivariate Time-to-event Methods that jointly incorporate Information from Longitudinal and Time-to-event Data

SUMMARY

We consider regulatory clinical trials that required a pre-specified method for the comparison of two treatments for chronic diseases (e.g. Chronic Obstructive Pulmonary Disease) in which patients suffer deterioration in a longitudinal process until death occurs. We define a composite endpoint structure that encompasses both the longitudinal data for deterioration and the time-to-event data for death, and use multivariate time-to-event methods to assess treatment differences on both data structures simultaneously, without a need for parametric assumptions or modeling. Our method is straightforward to implement, and simulations show the method has robust power in situations in which incomplete data could lead to lower than expected power for either the longitudinal or survival data. We illustrate the method on data from a study of chronic lung disease.

1. Introduction

Many clinical trials evaluate treatment differences for both correlated longitudinal and time-to-event data. For example, a confirmatory randomized clinical trial was conducted to compare a test treatment versus control in patients with Chronic Obstructive Pulmonary Disease (COPD). COPD is characterized by airflow limitation that is generally permanent and progressive. Although treatments can slow the progression, the disease is considered non-reversible. COPD often develops in long-time smokers and is typically diagnosed by spirometry, a procedure that measures the amount of air entering and leaving the lungs. For this COPD study, the investigators recorded the time to death within 3 years of randomization, as well as repeated measurements at 6 month intervals for respiratory lung function through ${\text{FEV}}_1^{*}$, with this being the percentage of FEV₁ (postbronchodilator forced expiratory volume at 1 second) to the predicted lung function [1]. Lung function is expected to deteriorate over time with death ultimately occurring, causing deterioration of lung function and survival to be highly correlated. There are well-established methods for analyzing the longitudinal and survival data separately, including the linear mixed model for longitudinal data [2] and the Cox proportional hazards model for survival data [3]. However, separate analysis of the longitudinal and survival data may be inefficient or biased when the longitudinal variable is correlated with the survival data [4], especially when incomplete data for patients could lead to lower than expected power for either the longitudinal or time-to-event data structure.

We focus on chronic diseases in which patients will experience deterioration in health regardless of treatment, as is the case with COPD, Alzheimer’s Disease, Parkinson’s Disease, and other such chronic disorders. In this context, the longitudinal data structure has a quantitative measure of deterioration or function, such as a direct measure of respiratory function (COPD) or cognitive function (Alzheimer’s Disease), and provides a relevant endpoint in its own right as opposed to a surrogate endpoint. We identify clinically-relevant thresholds in the longitudinal process and define multiple composite endpoints as the times to reach these thresholds or death, whichever comes first. Multivariate semiparametric and nonparametric methods are used to evaluate treatment differences on these composite time-to-event endpoints. Our method is straightforward to implement using standard software (SAS) and makes minimal or no assumptions regarding underlying distributions. Simulations show that the proposed method can have robust power in situations in which incomplete data for patients could lead to lower than expected power for either the longitudinal or time-to-event data structures. Our method is primarily of interest for clinical trials in a regulatory environment in which the primary comparison between two treatments must have a priori specification.

Many methods exist for jointly modeling distributions of correlated longitudinal and time-to-event data [4–12]. Although joint models may be conceptually appealing, they can be computationally demanding, difficult to implement, and may require specialized software [13]. Many of these methods make strong parametric assumptions regarding the longitudinal and time-to-event processes [14, 15] which may not be obvious and can be difficult to validate. Nonparametric methods have been proposed for correlated longitudinal and time-to-event data (e.g. [16, 17]), but these methods typically require a ranking of the importance of the outcomes, such as first comparing patients for time-to-event, and then comparing patients on the longitudinal measure if the comparison for time-to-event is not possible. For more complete reviews of joint modeling methods, see Hogan and Laird [13], Tsiatis and Davidian [14], Yu [15], and Ibrahim [18]. In contrast to these joint modeling methods, this manuscript focuses on a robust method for the comparison between treatments in regulatory clinical trials by jointly incorporating information from the longitudinal and time-to-event data. We recognize that joint modeling methods may additionally be of interest in regulatory settings to gain a complete understanding of the data, but such methods may be better suited as key secondary analyses and their discussion is beyond the scope of this paper.

The manuscript is organized as follows. In Section 2, we introduce the multivariate composite endpoint methods used in our approach. In Section 3, we present simulation studies that assess the type I error and power of our method relative to other methods. In Section 4, we apply our method to a clinical trial involving chronic lung disease, and we conclude with a discussion in Section 5.

2. Application of Multivariate Time-to-Event Methods

2.1. Wei-Lin-Weissfeld Method

Suppose there are M time-to-event endpoints. To apply the method of Wei et al. [19] (referred to as the WLW method), one fits a marginal Cox proportional hazards model for each of the M events

$${\lambda }_{\mathit{\text{mi}}}(t)={\lambda }_{m0}(t)\text{exp}\{{\mathit{x}}_i^{\prime }{\mathit{\beta }}_m\},$$ (1)

in which β_m = (β_m1,…, β_mp)′ is the vector of parameters for the mth marginal model, ${\mathit{x}}_i^{\prime }$ is a vector of baseline predictors, and λ_mi(t) is the hazard for subject i proportional to the baseline hazard λ_m0(t). Let $\mathit{\beta }=({\mathit{\beta }}_1^{\prime },\dots ,{\mathit{\beta }}_M^{\prime })\prime$ be the vector of all parameters and $\widehat{\mathit{\beta }}=({\widehat{\mathit{\beta }}}_1^{\prime },\dots ,{\widehat{\mathit{\beta }}}_M^{\prime })\prime$ be the maximum partial likelihood estimates from all M models. Wei et al. [19] showed that the asymptotic distribution of β̂ is normal with mean β and variance V; a consistent estimator V̂ of the variance is a function of the score residuals and information matrix (see Appendix). Given the asymptotic normal distribution of β̂ and variance estimate V̂, it is straightforward to construct a model-averaged log hazards ratio to summarize the treatment effect. Let β_e = (β_1e,…, β_Me)′ represent the vector of parameters for the marginal treatment effect (e indexes the experimental or treatment effect). Wei et al. [19] suggested estimating a model-averaged log hazards ratio using the estimate

$$\widehat{\theta }=\mathit{C}\prime {\widehat{\mathit{\beta }}}_e,$$ (2)

with C as ${\mathit{C}}_{\text{WLW}}={({\mathbf{1}}_M^{\prime }{\widehat{\mathit{V}}}_e^{-1}{\mathbf{1}}_M)}^{-1}{\widehat{\mathit{V}}}_e^{-1}{\mathbf{1}}_M$ and V̂_e equal to the estimated covariance matrix of β̂_e (constructed from the appropriate elements of V̂). This estimator was proposed as the optimal estimator because it has the smallest asymptotic variance among all linear estimators from β̂_e. Alternatively, C_equ = 1_M/M would invoke equal weights, which can be of interest for reasons given in Sections 3 and 5. A test statistic for comparing the average log hazards ratio to 0 can be constructed as

$$Z^2=\frac{{(\mathit{C}\prime {\widehat{\mathit{\beta }}}_e)}^2}{\mathit{C}\prime {\widehat{\mathit{V}}}_e\mathit{C}},$$ (3)

which has an asymptotic chi-square distribution with one degree of freedom. In SAS version 9.1 one can obtain this test statistic directly using the procedure PROC PHREG (see SAS documentation) or by fitting the marginal models and constructing the appropriate covariance matrix using residuals (see Appendix).

2.2. Nonparametric ANCOVA

Logrank scores are quantities which are used in nonparametric testing procedures for comparing the survival times of two or more groups with possible censoring [20, 21]. These scores are centered about zero starting with 1 and decreasing as endpoints lengthen (see Appendix). For M time-to-event endpoints, logrank scores can be computed for each of the M events separately to obtain M vectors of logrank scores. One can then use multivariate nonparametric ANCOVA to evaluate a treatment effect on all outcomes simultaneously adjusting for relevant covariables by weighted least squares methods that produce an estimated treatment effect β̂ and corresponding variance estimate V̂_β̂ [35, 22]; here β̂ is the estimated mean difference in logrank scores between the treatment groups (see Appendix). This method restricts the vector(s) of differences between means for the covariates to zeros on the basis of randomization. One can use (2) with C_equ to obtain an average difference in logrank scores between treatments (averaged across the M events) and its corresponding test statistic as given by (3). SAS macros are available to compute the logrank scores (please contact authors) and to perform multivariate nonparametric ANCOVA for comparing two treatment groups [23].

2.3. Defining the Multivariate Outcomes

We define M clinically relevant cutpoints or thresholds in the longitudinal data structure and use these cutpoints to construct (M + 1) “threshold endpoints”. We define the first M threshold endpoints as the time to the mth cutpoint or terminating event (e.g. death), whichever comes first, with the final threshold endpoint defined as the time to the terminating event. Subjects who do not experience a threshold event in the study are considered censored. Consider the study of COPD with ${\text{FEV}}_1^{*}$ threshold events at ≤ 50% or death (whichever comes first), ≤ 30% or death (whichever comes first), and death. Suppose three subjects have ${\text{FEV}}_1^{*}$ values and time of death as given in Table I. For subject A, the first threshold event is observed at 18 months, the second at 24 months, and the third at 26 months. For subject B, all three threshold events are censored at 36 months. For subject C, the first threshold event is observed at 6 months, and threshold events 2 and 3 are observed at 11 months. For subject D, the first threshold event is observed at 18 months, the second at 36 months, and the third is censored.

Table I.

Individual ${\text{FEV}}_1^{*}$ measurements

	Observation time in months
Subject	6	12	18	24	30	36	Time of death
A	70	60	40	25	-	-	26
B	75	70	60	65	60	55	-
C	40	-	-	-	-	-	11
D	70	60	40	55	35	25	-

Table gives ${\text{FEV}}_1^{*}$ values at each observation time and time of death $({\text{FEV}}_1^{*}=\text{Percent predicted}{\text{FEV}}_1)$

Various definitions of the thresholds are possible depending on the clinical relevance (e.g. requiring a longitudinal cutpoint to be sustained for two or more observations). The definition of these thresholds should be tailored toward the clinical application such that the interpretations of the threshold endpoints are clinically relevant. Because our method is meant for regulatory environments that require prespecified analyses, these thresholds should be defined a priori. In most relevant degenerative diseases, there are well established cutpoints in the longitudinal data structure representing clinical diagnosis of the various stages of the disease. In the absence of clinically based thresholds, one may choose thresholds based on the expected range of the longitudinal data, thereby resulting in a range of the number of events for each threshold event.

We implicitly make assumptions in both the WLW and logrank approaches. For the WLW approach, we assume that the observed time to reach a given threshold event has an underlying continuous nature and that the hazards ratio for reaching an event is constant across time for treatment and each covariate in the model. We also assume that there is a log-linear relationship between the explanatory variables and the underlying hazard function. For the logrank approach, essentially the only assumption is that the patients are randomized to their respective treatment groups. The logrank approach makes no modeling assumptions and does not require a continuous failure time.

For a clinical trial in a regulatory environment, it is often not clear how to work with correlated longitudinal and time-to-event data, nor is it clear as to whether the primary hypothesis should be based on the longitudinal or time-to-event data. The power of a time-to-event analysis would increase with a larger number of events, but this would also be associated with increasing (informative) dropout and decreasing power for a longitudinal analysis. Conversely, one has increasing power in a longitudinal analysis as missing data due to terminating events decreases, implying fewer events and decreasing power in a time-to-event analysis. Even in cases in which the amount of missing data is predictable, it may be unknown which process is likely to have greater sensitivity to treatment differences. Our method is attractive in such situations, as one can incorporate the composite endpoint structure from our multivariate approach in the study protocol with the understanding that it can lead to increased sensitivity to treatment differences compared to the standard longitudinal and time-to-event approaches and at worst should lead to a “second best” approach, as shown in simulation studies in Section 3. By specifying the multivariate composite endpoint approach as the primary analysis a priori, one can reduce the risk of selecting the data structure with poorer sensitivity to treatment differences and have a reasonably good chance of selecting an approach with better sensitivity to treatment differences, as shown in simulation studies in Section 3.

3. Simulation Studies

We conducted two simulations to evaluate the performance of our multivariate composite endpoint approach (using the WLW or logrank strategy) relative to standard methods using either of the longitudinal or survival data structures separately and to the joint model of Henderson et al. [6]. Our proposed approach is most useful in settings with a small to moderate treatment effect on both the longitudinal and survival data structures and fairly large samples sizes (e.g. ≥ 300 per group). If the treatment effect were known to be large in one or both of these processes a priori, there would be little need for our method. We first simulated the longitudinal data with a trend over time for the mean and a random intercept inducing an exchangeable correlation structure. We then generated terminating events using a piecewise exponential model at fixed time points. The hazard function depended on treatment, baseline covariates, and the population mean of the longitudinal variable for a given interval. In the second simulation, we simulated the longitudinal data in the same format as the first simulation, but we simulated deaths based upon subjects reaching a pre-determined threshold for the longitudinal variable. When subjects reach this threshold, the probability of death was set to 0.6 for each observed Y_ij below the threshold. We compare the methods based on power and type I error.

3.1. Comparing Methods

Let Y_ij be the longitudinal response of subject i at observation j, for i = 1,…,n and j = 1,…,n_i. Additionally, let y_i0 be the baseline value of the observed response (the longitudinal response at randomization) and x_i be the treatment indicator. Let T_i denote the time to death of the ith subject, and Z_i = min(T_i,U_i), in which U_i is a censoring time for survival of patient i. In both simulation setups we compare the following methods:

• WLW₁: The standard WLW approach using the optimal estimator of Wei et al. [19], i.e. ${\mathit{C}}_{\text{WLW}}={({\mathbf{1}}_4^{\prime }{\widehat{\mathit{V}}}_e^{-1}{\mathbf{1}}_4)}^{-1}{\widehat{\mathit{V}}}_e^{-1}{\mathbf{1}}_4$, which weights the marginal estimates by the inverse of the covariance matrix. Using threshold events, one will observe a greater number of events for earlier cutpoints; hence the optimal estimator places more weight on estimates from the earlier cutpoints compared to those from later cutpoints.

• WLW₂: A modified WLW approach using C_equ = (0.25, 0.25, 0.25, 0.25)′ that weights the marginal estimates equally, and is clinically justified by equal interest in all thresholds.

• LR: The multivariate logrank analysis using nonparametric ANCOVA based on the test statistic with equal weights, i.e. C_equ = (0.25, 0.25, 0.25, 0.25)′.

• Cox: A Cox proportional hazards model of the form

  $${\lambda }_i(t)={\lambda }_0(t)\text{exp}({\gamma }_1{x}_i+{\gamma }_2{y}_{i0}),$$ (4)

  in which λ_i(t) is the hazard of subject i at time t, λ₀(t) is an unspecified baseline hazard function at time t, and γ₁ and γ₂ are parameters indicating treatment and baseline measurement effects, respectively. To account for tied event times, we use both the approximation of Efron [24] and the discrete logistic likelihood.
• LM₁: A linear mixed model (with missing data due to failure) evaluating the treatment main effect,

  $$Y_{\mathit{\text{ij}}}={\beta }_0+b_{i0}+{\beta }_1{t}_{\mathit{\text{ij}}}+{\beta }_2{x}_i+{\beta }_3{y}_{i0}+{\epsilon }_{\mathit{\text{ij}}},$$ (5)

  in which t_ij is the observation time for subject i and observation j, β₀ is a model intercept, b_i0 is a random subject intercept, and ε_ij is the residual error. We assume ε_ij ~N(0, σ²) independent of b_i0 ~N(0, ψ).

• LM₂: A linear mixed model with time as a class variable (i.e. using indicator variables for each time point) and a time by treatment interaction. The treatment effect is evaluated at the last time point in which at least 50% of the subjects have an observed response. Observations are discarded for the later time points with fewer than 5% observed data, as this would not allow for precise estimates of the time effect and treatment by time interaction at these time points.

• Hen: A joint model based on the method of Henderson et al. [6] using SAS code from Guo and Carlin [4]. The longitudinal process takes the form of (5), and the time to event T_i follows an exponential distribution with hazard function

  $${\lambda }_i=\text{exp}\{{\gamma }_0+{\gamma }_1{x}_i+{\gamma }_2{y}_{i0}+{\gamma }_3{b}_{i0}\},$$ (6)

  in which γ₀ determines the baseline hazard function and γ₁, γ₂, and γ₃ indicate the effect of the treatment, baseline measurement, and random coefficient, respectively. The longitudinal and survival processes are linked through the random coefficient b_i0. A joint test H₀ : β₂ = γ₁ = 0 will test for a treatment effect in both the longitudinal and survival processes simultaneously. This joint model assumes a constant hazard over time.

3.2. Simulation One

To generate the longitudinal data, we set n = 600 and sampled ε ~ N(0, 1), b_i0 ~ N(0, 1), and calculated

$$Y_{\mathit{\text{ij}}}=b_{i0}+{\beta }_1{t}_{\mathit{\text{ij}}}+{\beta }_2{t}_{\mathit{\text{ij}}}{x}_i+{\epsilon }_{\mathit{\text{ij}}},$$ (7)

in which β₁ = (0, −0.2, −0.5) and β₂ = (0, .01, .02, .03, .04, .05) in different settings, with x_i ~Bernoulli(0.5) and t_ij = j for j = (1,…,10). We calculated a baseline value y_i0 = b_i0 + ε_ij to be used as a predictor for the various methods. We then generated the time-to-event data using a piecewise exponential model with hazard function

$${\lambda }_{\mathit{\text{ij}}}=\text{exp}({\gamma }_0+{\gamma }_{1}E(Y_{\mathit{\text{ij}}})+{\gamma }_2{x}_i)$$ (8)

for the interval (j − 1, j], in which E(Y_ij) is the expected value of the longitudinal outcome, γ₀ = −2, γ₁ = −0.5, and γ₂ = (0, −.05, −.10, −.15) over the simulations. For subject i with death in the interval (j − 1, j], we set Y_ij and all subsequent Y_ij to missing. We generated 5,000 datasets and calculate type I error rates and power at the α = 0.05 significance level. The threshold endpoints for both simulations were defined as time to the 1st, 2nd, and 3rd quartiles of the individual minimum longitudinal values or time to death, whichever comes first. To determine these thresholds, one obtains a minimum longitudinal value for each subject and then uses the quartiles of these values across all subjects as the threshold cutpoints. Although we recommend clinically relevant thresholds in practice, this default approach used in the simulation allows one to choose cutpoints that encompass the range of longitudinal values. This ensures a reasonable range in the number of events for each of the threshold events and thereby extracts useful information from the longitudinal process.

With the exception of Henderson’s joint model, which was overly conservative, all methods consistently preserved the type I error rate at 0.05. In general, the WLW approach had slightly greater power than the logrank approach. With minimal sensitivity to treatment differences in the longitudinal process (β₂ = 0, 0.01), the Cox model had the greatest power, followed by the multivariate composite endpoint methods and then the linear mixed models. For cases with no direct treatment effect on survival (i.e. γ₂ = 0, although treatment indirectly impacts survival through γ₁), the linear mixed model LM generally had the greatest power, followed by the multivariate composite endpoint methods and then the Cox model. Generally, for cases in which the longitudinal and time-to-event processes displayed somewhat equal sensitivity to treatment differences, the multivariate composite endpoint methods had greater power for detecting a treatment effect than either the Cox or linear mixed models. Also, the modified (weighted) WLW approach (WLW₂) had greater power than WLW₁. The performance of Henderson’s joint model varied over the simulations. It generally had less power than the multivariate composite endpoint approaches for β₁ = (−0.2, −0.5) (more longitudinal dropouts induced by failure), and greater power for β₁ = 0 (fewer longitudinal dropouts).

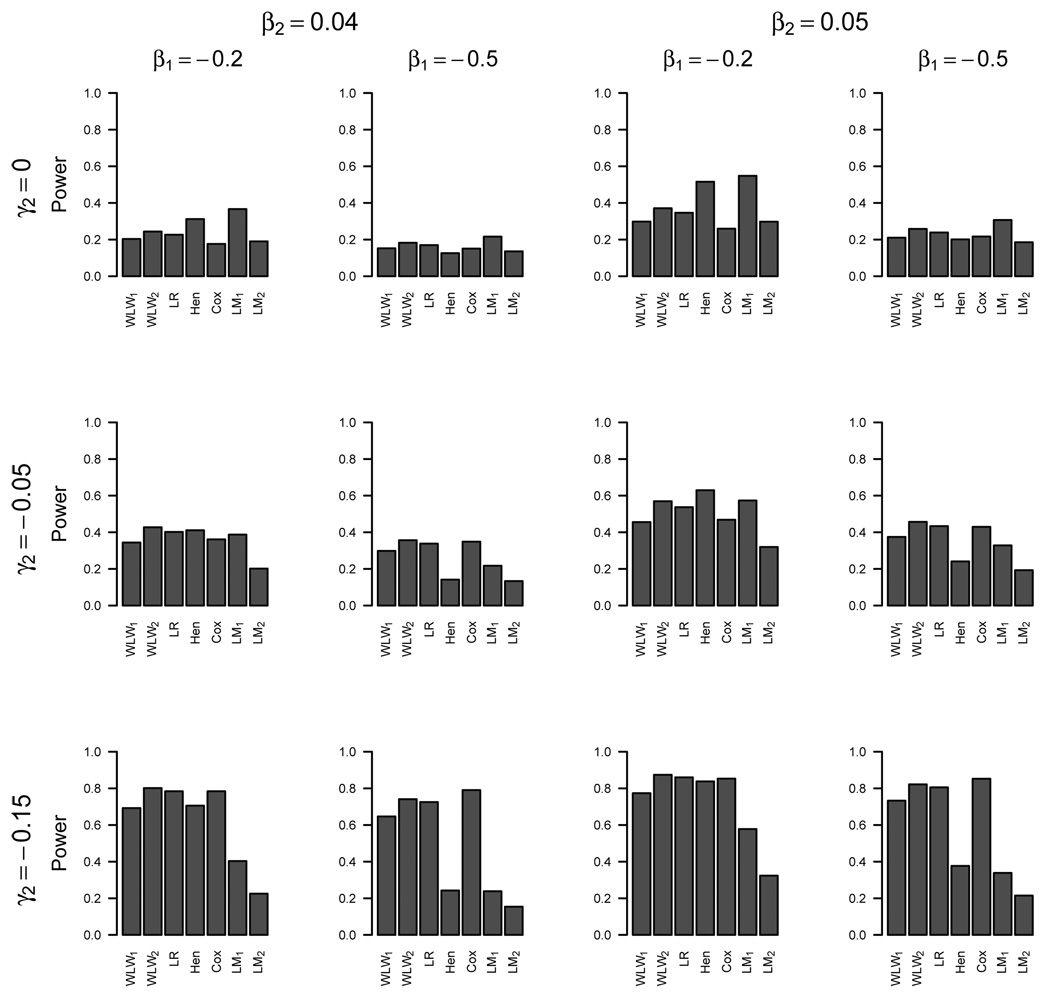
Figure 1 displays the power of the various methods for detecting a treatment effect for β₁ = (−0.2, −0.5), β₂ = (0.04, 0.05), and γ₂ = (0, −0.05, −0.15). These parameters were selected for the graphical display to show different situations for which different methods performed best relative to the others. For cases in which treatment does not directly impact survival (γ₂ = 0), the linear mixed models LM₁ and LM₂ have the greatest power, followed by the multivariate composite endpoint approaches, and then the Cox model. For datasets with greater sensitivity to treatment differences in the time-to-event process (γ₂ = −0.15), the multivariate composite endpoint approach and Cox model have about equal power, while the linear mixed models LM₁ and LM₂ have the least power. Henderson’s joint model is very competitive compared to the other methods in the case of little missing data (β₁ = 0) but has fairly low power with increased missing data (β₁ = −0.5) in the longitudinal process due to death.

Figure 1.

Simulation One: Power

We conducted three-way comparisons of WLW₂, Cox, and LM₁, as well as the logrank, Cox and LM₁, by ranking each method as best, 2nd best, or 3rd best of the three methods with respect to power (excluding parameter settings with null treatment differences). The WLW₂ and logrank methods performed best in 39% and 30% of the simulations (respectively), performed 2nd best in 61% and 70% of the simulations (respectively), and never performed the worst (0%).

3.3. Simulation Two

The second simulation generated the longitudinal data in the same manner but simulated deaths based on an increased probability of death upon reaching a pre-determined threshold for the longitudinal data rather than assuming the piecewise exponential model. We set the probability of death equal to 0.6 at all time points with Y_ij < −2.5. For subject i with death event at time j, we set Y_ij and all subsequent Y_ij to missing (and manage the patient as death at time j). Note in this setup, a subject may have technically died in the interval (j − 1, j] but may not have an observed death until time j. We sampled 5,000 datasets and calculated type I error rates and power at the α = 0.05 significance level. We used the same parameter values as simulation one, except β₂ = (0, .02, .03, .04, .06, .08) and β₁ = (−0.05, −0.15, −0.20, −0.25, −0.30, −0.40, −0.50, −0.70, −0.90, −1.4). One could view the failure times for the terminating event as interval-censored because deaths can only occur at j = (1,…,J). Hence we used the discrete logistic likelihood for the Cox survival model.

With the exception of Henderson’s joint model, which again was overly conservative, all methods consistently preserved the type I error rate at 0.05. In general, the logrank approach had slightly greater power than the WLW method, but the difference was minimal. For data sets with small amounts of missing data in the longitudinal outcome due to failure, i.e. < 20% (β₁ ≤ −0.15), the linear mixed models performed best, followed by the multivariate composite endpoint methods and then the Cox model. For data sets with 20% to 50% missing data due to failure (−0.15 ≤ β₁ ≤ −0.5), the multivariate composite endpoint approaches performed best, followed by the Cox model and then the linear mixed models. For data sets with 50% to 70% missing data (−0.70 ≤ β₁ ≤ −0.90), the multivariate composite endpoint approaches again performed best, followed by LM₁, the Cox model, and then LM₂. For data sets with greater than 70% missing data (β₁ = −1.4), LM₁ performs best followed by the multivariate composite endpoint methods, LM₂, and the Cox model. The modified WLW approach (WLW₂) again had greater power than WLW₁. Henderson’s model had less power than the multivariate composite endpoint approaches for all simulations except β₁ ≤ −0.15 (little missing data), with particularly low power (and below nominal type I error) when there was a large amount of missing data due to failure.

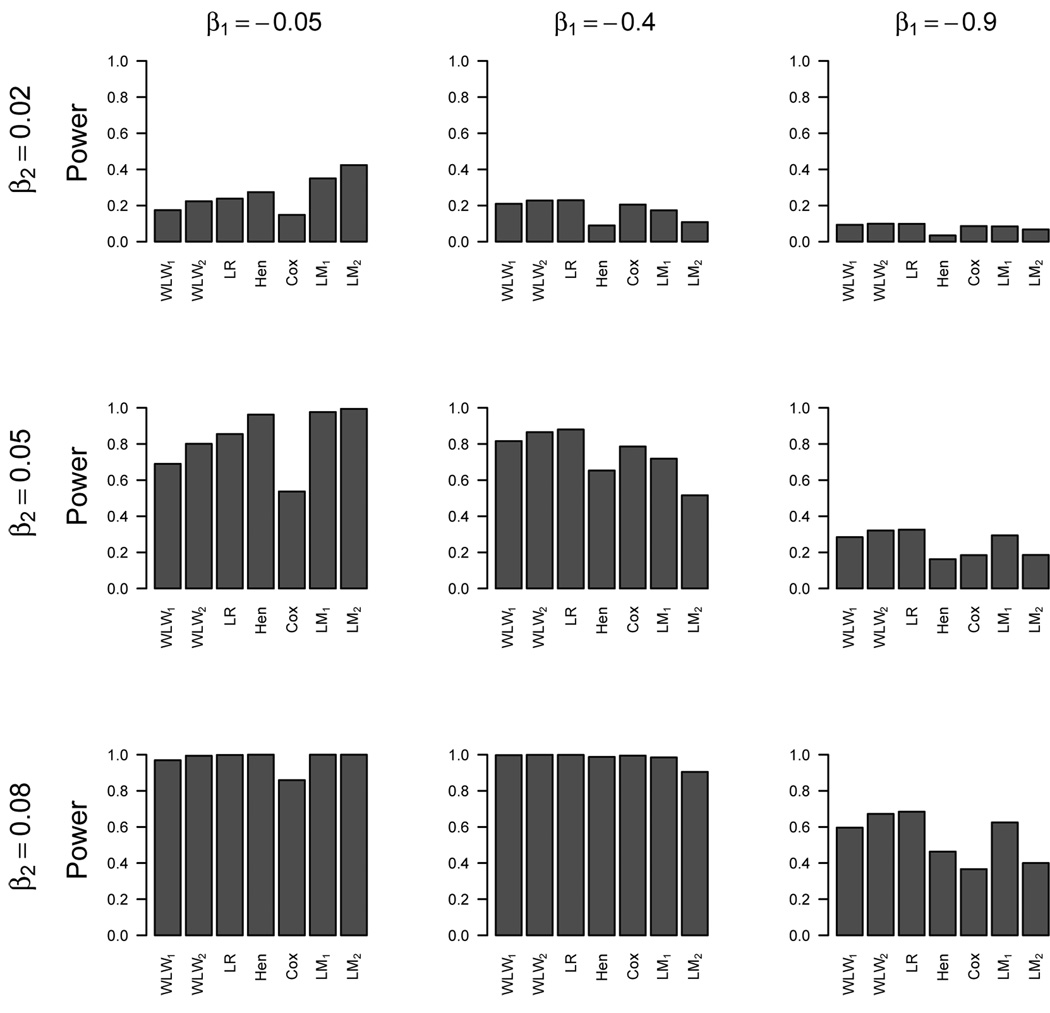
Figure 2 displays the power of the respective methods of detecting a treatment effect for β₂ = (0.02, 0.05, 0.08) and β₁ = (−0.05, −0.4, −0.9). For datasets with substantially greater sensitivity to treatment differences in the longitudinal process compared to the survival process (β₂ = 0.05, β₁ = −0.05), the linear mixed models have better power than the other methods, followed by Henderson’s joint model, the multivariate composite endpoint methods, and then the Cox model. For datasets with about equal sensitivity to treatment differences in the survival and longitudinal processes, the multivariate composite endpoint methods generally have better power than the Cox model, linear mixed models, and Henderson’s joint model. For the three-way comparisons of the WLW₂/logrank to the Cox and LM₁, the WLW₂ and logrank methods performed best in 73% and 78% of the simulations (respectively), performed 2nd best in 27% and 22% of the simulations (respectively), and never performed the worst (0%).

Figure 2.

Simulation Two: Power

4. Application

We illustrate our method for a clinical trial for 2,000 patients with COPD. Due to reasons of confidentiality, these patients (1,000 test treatment and 1,000 control) correspond to a random sample from the true study population, in which patients were randomized to either test treatment or control in permuted blocks with stratification by country and smoking status. Based on the GOLD criteria [25], the disease can be classified as mild $({\text{FEV}}_1^{*}\ge 80\%)$, moderate $(50\%\le {\text{FEV}}_1^{*}<80\%)$, severe $(30\%\le {\text{FEV}}_1^{*}<50\%)$, and very severe $({\text{FEV}}_1^{*}<30\%)$, with all criteria requiring the ratio of FEV₁ to FVC (forced vital capacity) to be less than 0.70.

We first evaluated the treatment effect on time to death within 3 years (the primary endpoint from the original study) using a Cox proportional hazards model with the following explanatory variables: treatment, baseline ${\text{FEV}}_1^{*}$, current smoking status (yes, no), age categories (< 55, 55–64, 65–74, ≥ 75), gender, body mass index categories (< 20, 20–25, 25–29, ≥ 29), race (white, other), and geographical region (USA, Asia-Pacific, Eastern Europe, Western Europe, other). Of the 2,000 patients, there were 139 deaths (13.9%) for patients on the test treatment and 153 deaths (15.3%) for patients on control. The estimated hazard ratio for test treatment versus control after adjustment for the covariates is 0.82 (p-value = 0.09) with a 95% confidence interval of (0.65,1.03), which is not statistically significant at α = 0.05.

We analyzed the longitudinal data for ${\text{FEV}}_1^{*}$ with a linear mixed model (LM₂) with the same explanatory variables as the Cox model, but also including time categories (6, 12, 18, 24, 20, and 36 months) and a treatment by time interaction. The observation time was regarded as a class variable through indicator variables for each observation time, and a random intercept was used to account for the intra-subject correlation. A total of 8,372 observations from 1,703 subjects were available for this longitudinal analysis. 68% of these 1,703 patients had observed ${\text{FEV}}_1^{*}$ measurements at the 3 year mark, and 18% of the observations were missing across all possible (1703 × 6) measurements, mostly due to death. We evaluated the treatment difference at the last observation time (3 years), resulting in an estimated difference of 1.94 percentage points (p-value ≤ 0.0001) with a 95% confidence interval of (1.0%, 2.9%) in favor of subjects on test treatment versus control.

We implemented the composite endpoint structure from the multivariate approaches to evaluate both data structures simultaneously, adjusting for baseline ${\text{FEV}}_1^{*}$, current smoking status, age, gender, body mass index, race, and region. We defined the threshold events as time to ${\text{FEV}}_1^{*}$ < 50% or death, time to ${\text{FEV}}_1^{*}$ < 30% or death, and time to death, in which the cutpoints were based on the GOLD criteria [25] corresponding to severe and very severe COPD (99% of the subjects entered the study with at least moderate COPD). For subjects with no ${\text{FEV}}_1^{*}$ measurements and death (or censored) times greater than 130 days, we censored the first two threshold events at 130 days, the earliest time at which an ${\text{FEV}}_1^{*}$ measurement was recorded.

The estimated differences in mean logrank scores are −0.074, −0.015, −0.024 for the three threshold events, respectively. The average difference in logrank scores for test treatment versus control using multivariate nonparametric ANCOVA is −0.04 (p-value = 0.005), indicating extended survival times for reaching a threshold event for treatment compared to control. The goodness of fit test (p-value = 0.41) supports compatibility with the expected balance for covariates from randomization between treatments. The respective marginal hazards ratios for the WLW approach are 0.86, 0.88, and 0.82. Using the optimal estimator, the WLW₁ hazards ratio is 0.86 (p-value≤0.0001) with a 95% CI of (0.81,0.92). The modified estimator WLW₂ has a hazards ratio of 0.86 (p-value=0.008) with a 95% confidence interval of (0.77, 0.96), indicating lower hazards of reaching a threshold event for treatment compared to control

In these data, the sensitivity to treatment differences is much smaller in the time-to-event process (p-value = 0.09) than the longitudinal process (p-value ≤ 0.0001). Because the multivariate composite approaches incorporate information from both processes, the sensitivity to treatment differences of the logrank and WLW approaches is somewhere between that of the longitudinal and time-to-event approaches, resulting in statistically significant differences between treatment and control (in favor of the treatment). The investigators of this study had prior evidence of a strong treatment effect on FEV₁ and conducted this study specifically to evaluate the treatment effect on mortality. However, had the investigators been equally interested in both longitudinal and survival endpoints a priori, a better approach may have been to specify a composite endpoint structure with either the logrank or WLW approach as the primary analysis, which can have more robust sensitivity to treatment differences. Also, to the extent to which the thresholds for the longitudinal data are clinically meaningful, such an analysis could be more clinically interpretable than an analysis based on the difference in means in the longitudinal process.

5. Discussion

Our simulation studies show two examples in which the proposed composite endpoint approach consistently performs better than at least one of the standard longitudinal or time-to-event approaches. This finding makes our method very attractive in regulatory settings that require prespecified analyses, because many investigators would rather be guaranteed their method does not have the worst power, and are satisfied with a method that performs better than either one or both of the Cox and linear models. Our method was also shown to have better overall performance (with respect to power and type I error), easier computation, and less restrictive assumptions than the joint model approach of Henderson et al. [6].

In our simulations, the use of equal weights (WLW₂) provided better performance than the “optimal” weights (WLW₁) in both simulations. We investigated several alternatives for the weights in both multivariate composite endpoint approaches and found that our methods are not overly sensitive to the specification of weights (excluding the weighted inverse matrix C_WLW) and one can use a smaller number of cutpoints in the longitudinal process (M = 1, 2 resulting in 2 or 3 threshold endpoints) to achieve a similar result. In practice, there is typically greater clinical interest in the more severe thresholds, but these thresholds also contain less information than the less severe thresholds due to a smaller number of events. The use of equal weights is an attempt to balance the precision obtained from the less severe thresholds with the clinical relevance of the more severe thresholds. Additionally, if one takes the view that the hazards ratios across the thresholds are similar, then an average of the hazards ratios is a justifiable summary measure. Similar weighting issues arise in clinical trials with multiple endpoints, in which Pocock [26] and Pocock et. al. [27] recommend equal weights for the global test statistic of comparing two treatment groups with k correlated endpoints. Other weighting schemes based on the inverse of the covariance matrix exist [28], but these “optimal” weights can lead to undesirable and counterintuitive weighting structures (e.g. negative weights) [26, 29]. Hence we recommend the use of equal weights for most applications.

The WLW and logrank approaches had very similar performance in our simulations with respect to power and type I error. The logrank approach makes fewer assumptions than the WLW approach but does not provide an interpretable point estimate or confidence interval to describe the magnitude of the treatment effect. In contrast, the WLW method provides an interpretable estimate (hazards ratio) and corresponding confidence interval, and can easily accommodate extensions to address treatment by covariable interactions. If there are concerns about the correctness of the proportional hazards model, we recommend specifying the logrank approach as the primary evaluation of the treatment effect and using the WLW method as a supportive analysis, which agrees with the approach of Koch et al. [30] for incorporating both non-parametric and hazard ratio estimation procedures in an analysis plan. One could also incorporate joint modeling methods [4–12] as key secondary analyses to gain a better understanding of the data.

The WLW approach assumes that failure time (e.g. time to a threshold event) is continuous. However, because longitudinal measurements are usually taken at fixed time points, there is some ambiguity as to whether the continuous time assumption is satisfied for the threshold endpoints in our applications. Extensions of the WLW approach for grouped failure time and interval censored data are available in the literature [31, 32, 33], but these methods are not easily implemented in standard statistical software packages and are not current practical alternatives. Despite this concern, our simulations did not show adversity for type I error.

We note that it is possible for subjects to have intermittent periods of recovery in the longitudinal process after reaching a certain stage of deterioration (e.g. they may reach a threshold event, experience recovery, and then reach the same threshold event again). For example, see Table I, in which subject D experiences a threshold 1 event at 18 months, has some recovery, and crosses threshold 1 again at 30 months. Although our method does not account for the second occurrence of a threshold event, the intermittent recovery naturally delays the time at which the next more severe threshold event is observed (when compared to subject A). Hence our method indirectly takes into account the intermittent recoveries by assessing more than one threshold. If the times to first occurrences of the respective threshold events are longer for treatment compared to control, then the treatment has produced a benefit to the patients, regardless of whether intermittent recoveries caused some threshold events to be observed more than once. We recognize that joint modeling methods [4–12] may more completely describe the longitudinal trajectory, and hence may be useful as key secondary analyses.

Our method is primarily intended for comparing two treatments in regulatory environments in which the primary analysis must be specified a priori. Extensions for comparing three or more treatments are possible but are beyond the scope of this paper. Our method is useful when treatment is expected to affect both longitudinal and time-to-event data, and it provides a composite endpoint structure with control of type I error for addressing the null hypothesis of no treatment difference. It has some analogy to more common composite endpoints, such as cardiovascular studies in which both the time to the first of myocardial infarction or death and time to death are of interest as primary outcomes. Typically, the design of a trial incorporating our method would involve having adequate power for both the longitudinal endpoint and the time-to-event endpoint, such that each of the separate analyses could have secondary roles for better understanding of the treatment effect (even if our method was used as the primary method). One could also base the power for the analysis on either of separate endpoints but use our method as the primary analysis, which will provide assurance that the study does not have severe loss of power due to deaths, dropout, or under-estimation of the true effect size.

The example in this article is based on a random sample from a true clinical trial that was conducted to compare three test treatments with placebo for patients with COPD. The background, design, results, and interpretation of this trial are reported by Calverley [34].

Appendix

A.1. The Wei-Lin-Weissfeld Method

Wei et al. [19] showed that

$$\widehat{\mathit{\beta }}\dot{~}N(\mathit{\beta },\mathit{V}),$$ (A.1)

in which V is estimated by

$$\widehat{\mathit{V}}=\left[\begin{array}{cccc}\hfill {\widehat{\mathit{V}}}_{11}\hfill & \hfill {\widehat{\mathit{V}}}_{12}\hfill & \hfill \dots \hfill & \hfill {\widehat{\mathit{V}}}_{1M}\hfill \\ \hfill {\widehat{\mathit{V}}}_{21}\hfill & \hfill {\widehat{\mathit{V}}}_{22}\hfill & \hfill \dots \hfill & \hfill {\widehat{\mathit{V}}}_{2M}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill {\widehat{\mathit{V}}}_{M1}\hfill & \hfill {\widehat{\mathit{V}}}_{M2}\hfill & \hfill \dots \hfill & \hfill {\widehat{\mathit{V}}}_{\mathit{\text{MM}}}\hfill \end{array}\right].$$ (A.2)

The estimated covariance matrix V̂ is composed of the sub-matrices V̂_mm′ = (R_m Â_m)′(R_m′ Â_m′), in which Â_m is the inverse of the information matrix and R_m is the matrix of score residuals for event outcome m. Conveniently, the quantity R_m Â_m is common output in most software packages and is known as the matrix of “dfbeta” residuals. The “dfbeta” residuals represent the approximate change in a parameter estimate when the ith observation is omitted. It follows that the asymptotic covariance matrix of β̂ can be obtained as a function of the “dfbeta” residuals.

A.2. Nonparametric Analysis of Covariance with Logrank Scores

Let n_j be the number of observations at risk at the beginning of the jth interval,

$$n_j=\{\begin{array}{c}N,j=1\hfill \\ N-{\displaystyle {\sum }_k(n_{k0}+n_{k1}),k=1,\dots ,(j-1)\text{and}j>1,}\hfill \end{array}$$ (A.3)

in which N is the sample size, n_k0 is the number of censored observations in the kth interval, and n_k1 is the number of observed endpoints in the kth interval. Then the logrank scores for the jth interval are

$$C_{\mathit{\text{jd}}}=d-{\displaystyle \sum _k(n_{k1}/n_k),k=1,\dots ,j,}$$ (A.4)

in which d = 1 for observed endpoints and d = 0 for censored endpoints.

Suppose we are interested in comparing two treatments for logrank scores for M outcomes, adjusting for p covariates. Let treatment i have sample size n_i, mean response ȳ_i of dimension (M × 1) for logrank scores and a mean of covariates x̄_i of dimension (p × 1). Let d = (ȳ₁ − ȳ₂) and u = (x̄₁ − x̄₂). We fit the model

$$E[\mathit{f}]=E\left[\begin{array}{c}\hfill \mathit{d}\hfill \\ \hfill \mathit{u}\hfill \end{array}\right]\stackrel{\wedge}{=}\left[\begin{array}{c}\hfill {\mathit{I}}_M\hfill \\ \hfill {\mathbf{0}}_{(p\times M)}\hfill \end{array}\right]\widehat{\mathit{\beta }}=\mathit{X}\widehat{\mathit{\beta }}$$ (A.5)

using weighted least squares with weights based on the covariance matrix V₀. Under H₀,

$${\mathit{V}}_0=\frac{n_1+n_2}{n_1{n}_2(n_1+n_2-1)}\left\{{\displaystyle \sum _{i=1}^2{\displaystyle \sum _{k=1}^{n_i}[\begin{array}{cc}\hfill ({\mathit{y}}_{\mathit{\text{ik}}}-\overline{\mathit{y}})({\mathit{y}}_{\mathit{\text{ik}}}-\overline{\mathit{y}})\prime \hfill & \hfill ({\mathit{y}}_{\mathit{\text{ik}}}-\overline{\mathit{y}})({\mathit{x}}_{\mathit{\text{ik}}}-\overline{\mathit{x}})\prime \hfill \\ \hfill ({\mathit{x}}_{\mathit{\text{ik}}}-\overline{\mathit{x}})({\mathit{y}}_{\mathit{\text{ik}}}-\overline{\mathit{y}})\prime \hfill & \hfill ({\mathit{x}}_{\mathit{\text{ik}}}-\overline{\mathit{x}})({\mathit{x}}_{\mathit{\text{ik}}}-\overline{\mathit{x}})\prime \hfill \end{array}}}\right]\}$$ (A.6)

in which ȳ and x̄ are means for all patients with treatments ignored [35, 22]. The weighted least squares estimator β̂ is obtained from

$$\widehat{\mathit{\beta }}={(\mathit{X}\prime {\mathit{V}}_0^{-1}\mathit{X})}^{-1}\mathit{X}\prime {\mathit{V}}_0^{-1}\mathit{f}$$ (A.7)

and its estimated covariance matrix is given by

$${\widehat{V}}_{\widehat{\mathit{\beta }}}={(\mathit{X}\prime {\mathit{V}}_0^{-1}\mathit{X})}^{-1}.$$ (A.8)

A criterion for departures from (A.5) in terms of random imbalances takes the form

$$Q=(\mathit{f}-\widehat{\mathit{f}})\prime {\mathit{V}}_0^{-1}(\mathit{f}-\widehat{\mathit{f}})$$ (A.9)

in which f̂ = Xβ̂. The statistic Q approximately has a chi-square distribution with p degrees of freedom and addresses the amount of random imbalance in the covariates at randomization.