Abstract
Background
Traditional vaccine trial methods have an underlying assumption that the effect of a vaccine is the same throughout the trial area. There are, however, many spatial and behavioral factors that alter the rates of contact among infectious and susceptible individuals and result in different efficacies across a population. We reanalyzed data from a field trial in Bangladesh to ascertain whether there is evidence of indirect protection from cholera vaccines when vaccination rates are high in an individual's social network.
Methods
We analyzed the first year of surveillance data from a placebo-controlled trial of B subunit-killed whole-cell and killed whole-cell-only oral cholera vaccines in children and adult women in Bangladesh. We calculated whether there was an inverse trend for the relation between the level of vaccine coverage in an individual's social network and the incidence of cholera in individual vaccine recipients or placebo recipients after controlling for potential confounding variables.
Results
Using bari-level social network ties, we found incidence rates of cholera among placebo recipients were inversely related to levels of vaccine coverage (5.28 cases per 1000 in the lowest quintile vs 3.27 cases per 1000 in the highest quintile; p = 0.037 for trend). Receipt of vaccine by an individual and the level of vaccine coverage of the individual's social network were independently related to a reduced risk of cholera.
Conclusions
Findings indicate that progressively higher levels of vaccine coverage in bari-level social networks can lead to increasing levels of indirect protection of non-vaccinated individuals and could also lead to progressively higher levels of total protection of vaccine recipients.
Introduction
Epidemiological theory is founded on the assumption of “homogeneous mixing,” with susceptible and infectious individuals mixing uniformly, without regard to age, location or other factors [1], [2]. However, a number of spatial and behavioral factors alter the rates of contact among infectious and susceptible individuals, which has implications for vaccination strategies and the evaluation of vaccination campaigns [2]. If susceptible individuals come in contact more often with immunized individuals than with non-immunized (possibly infected) individuals, they are less likely to contract the disease. Thus, a person's contact network is an important determinant of disease transmission as is the level of vaccination within that contact network [3]–[5]. Traditional vaccine trial methods typically evaluate the effectiveness of a vaccine by examining population-level morbidity and mortality, essentially ignoring possible heterogeneity due to differences in exposure among individual contact networks. To address this limitation, several new methods for evaluating vaccine efficacy have been developed. Ecological vaccine trials incorporate geographic information so that analysis of vaccine effectiveness can be conducted on geographic subpopulations [6], [7]. The premise behind a geographic analysis is that individuals are more likely to interact with others who are closer to them in space than those located further away [8]. Thus, disease and vaccination rates within a specific geographic area (often referred to as a “neighborhood”) represent exposure from an individual's contact network. Contact network epidemiology and social network analysis provide new methods for modeling the patterns of interactions among individuals that can lead to the transmission of an infectious disease [9]–[11]. These methods assume that individuals who are socially connected through kinship, friendship or work interact more often than those who are not [9]. Social network analysis is used to measure relationships between social entities [12], [13] and is particularly useful for measuring social relationships that influence disease outcomes or health interventions [9]. The probability of becoming infected is therefore conditioned by the number of infected and vaccinated individuals within a social (or contact) network.
In previous research, we used ecological vaccine trial methods to examine the geographic variation in the efficacy of a cholera vaccine. Analyses were conducted using results from a community-based individually randomized oral cholera vaccine trial conducted in Matlab, Bangladesh in 1985. Initial results suggested a protective efficacy (PE) of only ∼50% [14]. Our reanalysis of trial data found significant spatial heterogeneity in PE and suggested this spatial variation was due to ecological differences and/or spatial variation of vaccinated individuals in the study area [15]. Results also illustrated that variation is inversely related to vaccine coverage (i.e.,% of people vaccinated in an area) after adjusting for several ecological factors [7]. Higher levels of neighborhood vaccine coverage were linked to lower risk of cholera among residents, both in placebo recipients, for whom a strong inverse relationship was observed, and in vaccinees, for whom a suggestive relationship is evident [16]. These findings are consistent with the concept of herd immunity, which occurs when vaccination of a group of individuals in proximity to one another reduces the intensity of transmission of the infection among all members of the group regardless of immunization status [6]. The cholera vaccine conveyed a certain amount of “direct” protection, which is the protection conferred to a vaccinated individual because of biological immunity. But, progressively higher levels of vaccine coverage also appeared to convey higher levels of indirect protection of non-vaccinees in addition to the direct protection of vaccines [7], [16].
While our prior research used spatially-defined neighborhoods to model potential fecal-oral contact and the effect of the cholera vaccine, we hypothesize that social connectedness is also likely to influence disease transmission because contact networks are often determined by social interactions. This study adapts techniques from the social network and contact network epidemiology literature; we use kinship-based social networks to better model individual exposure to vaccinated individuals and potentially contaminated food and water. The V. cholerae pathogen is spread through the fecal-oral route but can also survive naturally in seas, ponds, and other aquatic environments [17], [18]. Thus, two modes of transmission based on these reservoirs have been identified. Primary transmission occurs via the local estuarine environments where V. cholerae is able to survive, spreading to the individual through some form of contact with water or, alternatively, consumption of shellfish or aquatic plants contaminated in their local habitat. Secondary transmission, in turn, refers to the diffusion of cholera from an infected individual to susceptibles in the population through fecal contamination. Secondary transmission occurs through person-to-person contact that is driven by human interaction and social contact, which leads to contamination of shared water sources [19]–[22]. The occurrence of direct person-to-person transmission is considered rare by some and supported by others [23]–[25]. In this study, we focus on the role of secondary transmission. If social contact is an important factor in the transmission of cholera and the efficacy of the vaccine, we would expect to see lower overall cholera rates and lower placebo group incidence among individuals with a high level of vaccination in their social network.
Past vaccine trials have not stratified placebo incidence or efficacy by social network connectivity because the studies did not collect information on social connections. This paper further analyzes this vaccine trial by exploring the effect of kinship-based social networks on protective efficacy and cholera risk. We hypothesize that protective efficacy and placebo group incidence are influenced by social networks because herd immunity is affected by the level of vaccination within an individual's social (or contact) network. Thus, unvaccinated people who are socially connected to people who have been vaccinated will be at lower risk for cholera due to social interactions that lead to less contaminated food and shared water environments (e.g., ponds, latrines) and because they are less likely to be exposed to the disease. By taking a social network approach, this research contributes to the discussion of how to plan, conduct and evaluate vaccine trials and will also provide insight into cholera transmission dynamics.
Methods
Study Area
The cholera vaccine trial was conducted in Matlab, Bangladesh, the research site of ICDDR,B. Matlab is located approximately 50 km south-east of Dhaka at the confluence of the Meghna and Ganges Rivers. Cholera is endemic in this region of Bangladesh. Rural Bangladeshis live in baris, which are groups of patrilineally-related households. Baris are located on raised plots of land, which typically resist flooding during monsoon season, and are surrounded by agricultural fields. An average of six distinct households constitute a bari and the different households in a bari are typically comprised of related individuals.
Data
This study uses two datasets including the original cholera vaccine trial database and a longitudinal demographic database from which the vaccine trial participants were selected.
Cholera Vaccine Trial Data
Details of the vaccine trial and database are documented comprehensively elsewhere [14], [16]. Briefly, a community based individually randomized oral cholera vaccine trial was conducted in Matlab in 1985. This double-blind trial measured the efficacy of two vaccines, the B subunit-killed whole cell (BS-WC) and the killed whole cell (WC) only vaccines. The control agent was E. coli K12 strain. Females aged 15 years and older and children aged 2–14 were the target groups of the trial. Three vaccine doses were given at 6 week intervals to 62 285 people in the target group. Identification of cholera cases took place at one hospital in Matlab and two community-based treatment centers in the study area. During 5 years of follow up, the cumulative protective efficacy was 49% in the BS-WC group (p<0.001) and 47% in the WC group (p<0.001) [26]. Protection by each vaccine was evident only during the first three years of follow-up and was lower in children who were vaccinated at 2–5 years then in older persons [26]. Because the two types of the cholera vaccines were identical in composition, apart from the inclusion of the B subunit, and because they conferred similar levels of protective efficacy [16], we grouped recipients of these vaccines together for analysis. The efficacy calculations are based on cholera cases that occurred between 14 and 365 days after a second dose of the placebo or vaccine. Because population migration progressively changed the composition of households and baris after dosing and because our aim was to investigate cholera incidence within stable social networks, which were developed using migration data, we chose to restrict our analyses to the first year of follow up after dosing. Such a short interval allowed us to assume the household populations and social networks were stable.
Longitudinal Demographic Data
Vaccine trial data were linked to the Matlab Health and Demographic Surveillance Systems (MHDSS) using a person-specific unique ID. The MHDSS is the most comprehensive longitudinal demographic database of a large population in the developing world and has recorded all vital demographic events and internal migrations of the study area population since 1966. In addition, people are visited monthly by community health workers and if they have severe diarrhea are treated at a hospital run by ICDDR,B. The MHDSS was used to associate known risk factors, such as age, sex, and religion, with individuals in the vaccine trial database and to construct the kinship-based social networks.
Kinship networks were created two different ways: using household-level and bari-level kinship connections. Household-level connections offer more specificity about kinship social ties while bari-level connections may capture a larger social network that includes non-related individuals that live nearby. The HDSS maintains all kinship ties among the Matlab residents and the exact dates each person resided in a household over time. Therefore, an individual can be traced from household to household over the course of his or her life (as long as he or she resides in the Matlab study area). Each individual in the HDSS has three identification (ID) numbers: a registration ID (RID), their current ID (CID) and a bari ID. When an individual is born or moves into the study area they are assigned a RID, which does not change during their lifetime. If a person moves into a new household, almost exclusively due to marriage, they are assigned a new CID and, if that household is located in a different bari, a new bari ID. This combination of ID numbers can be used to create networks of related individuals.
The kinship-based social networks we use in this study are based on individual-level migrations linking households or baris. We assume that when an individual moves to a new household, s/he maintains contact with the previous household or bari of residence. The mutual interaction between the old and new households forms a non-directional social connection. Each individual-level migration from household x to household y creates a social linkage between those two households and the baris in which they are located. Each linkage of this type is called a dyad. A complete list of all dyads, or an edgelist, can be represented as an n x n matrix, where n equals the number of households.
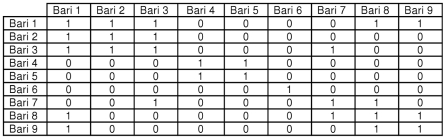
A network matrix is a rectangular arrangement of a set of elements represented as cells that are organized within rows and columns. These matrices allow mathematical and computational tools to summarize and find patterns [12], [13]. Figure 1 shows a hypothetical matrix of kinship relationships between baris 1 through 9. In a social adjacency matrix, 1 represents the presence of a single, non-directional social connection between two baris and 0 represents no social connection. In Figure 1, a value of 1 is given if there is a kinship relationship, while a value of 0 denotes that there is no relationship. Note that individuals in a bari can have kinship ties with other individuals in the same bari, which is shown in the table by a value of 1 given to the relationship between a bari and itself.
Figure 1. Matrix network example of bari-level kinship social connections.
GREY circles indicate baris while RED lines indicate a kinship-based social connection between the two linked baris.
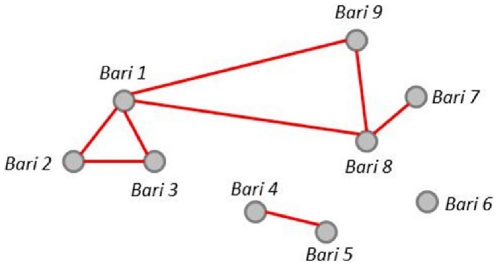
We can also represent kinship relationships as graphs, which is another form of visualizing networks. Figure 2 is the graph representation of the matrix shown in Figure 1. The nine baris included in Figure 2 show the kinship ties between all baris. Individuals in bari 6 have no external kinship ties (though individuals within the bari are tied to each other). Individuals in baris 1, 2, and 3 are related, and individuals in bari 1 have kinship ties to two additional baris (9 and 8). Individuals in bari 8 are related to bari 9 and 7, as are individuals in baris 4 and 5. Both the network matrix and graph can be built for kinship ties based on baris (as shown here) and households.
Figure 2. Graph network example of bari-level kinship social connections.
A “0” indicates no social connection between two baris while a “1” indicates a kinship-based social connection exists.
Statistical Methods
PE and vaccination coverage levels were measured by social network. We calculated where there was in inverse, monotonic trend for the relation between the level of vaccine coverage in a social network and the incidence of disease in individuals (vaccinees or placebo recipients) by calculating Spearman's correlation coefficients for quintiles of baris and households ordered according to the level of vaccine coverage. Only baris and households with at least one vaccinee or placebo recipient were ordered into quintiles (some inequalities in the number of individuals in the different quintiles occurred because baris or households, rather than individuals, were grouped). Separate analyses were conducted for household-based and bari-based kinship networks in order to compare cholera risk and protective efficacy calculated using the two different definitions of social network. Thus, the actual level of vaccine coverage differs for the quintiles based on household-level vaccine coverage vs. bari-level coverage. We assessed vaccine protective efficacy as [(1-relative risk of cholera in vaccinees vs. placebo recipients) x 100%] and calculated p values with the Χ 2 test and 95% CIs with test-based methods.
To estimate the variation in risk of a cholera event associated with the level of vaccine coverage in an individual's social network, odds ratios (ORs) and 95% confidence intervals (CIs) were calculated using generalized estimating equations (GEE) with a logit link function. These models are built using independent and exchangeable within-network correlation matrices to control for the correlation that may exist between individuals in the same social network. Several additional variables known to be associated with the risk of cholera were included to control for potential confounding effects: age, sex, religion, distance from the bari of residence to the nearest river and treatment center, occurrence of dysentery during follow-up and receipt of vaccine vs. placebo. We assessed effect modification between receipt of vaccine versus placebo and level of cholera vaccine coverage in an individual's social network as predictors of the risk of cholera as a two-way interaction between these variables in models that contained these variables as main effect terms. Two sets of models were estimated; one which included the level of vaccine coverage calculated using bari-level social networks and one which included vaccine coverage calculated using household-level social networks.
Results
49,336 vaccine recipients and 24,667 placebo recipients were included in our analysis. Within social networks developed using bari links, vaccine coverage ranged from 0 to 100% with a mean of 39% and a standard deviation of 15%. Vaccine coverage within social networks developed using household links was similar, ranging from 0 to 100% with a mean of 40% and a standard deviation of 28%. Within a year of vaccination, 204 cholera cases were detected, 96 (47%) of whom had been vaccinated.
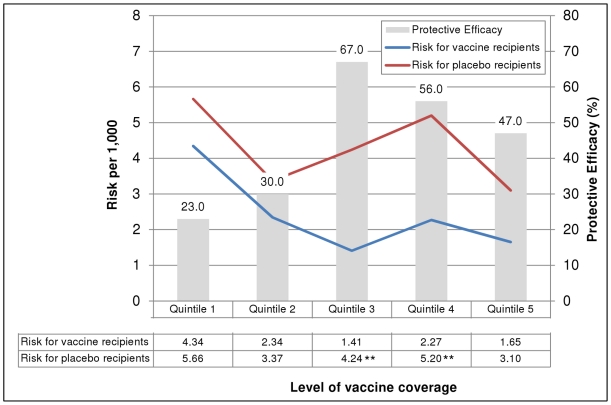
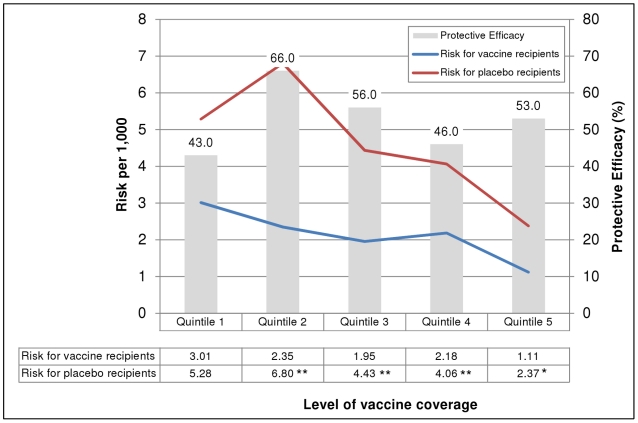
The risk of cholera in recipients of two or more doses of either vaccine or placebo was inversely related to the level of vaccine coverage of the household-level social network (figure 3), though this trend was not significant in placebo recipients (Spearman's correlation coefficient −0.6, p = 0.285) or vaccine recipients (Spearman's correlation coefficient −0.7, p = 0.188). The risk of cholera was also inversely related to the level of vaccine coverage of the bari-level social networks (figure 4). This trend was significant for both the vaccine and placebo recipients (Spearman's correlation coefficient −0.9, p = 0.037 for both). In addition, the risk of cholera was significantly lower among vaccinees in the second through fifth quintile of vaccine coverage but this difference was only observed with social networks developed using the bari-level connections.
Figure 3. Risk of cholera and protective efficacy of killed oral cholera vaccines, by level of vaccine coverage in household-level social networks.
** p<0.01 for the difference in risk between vaccinees and placebo recipients. Note: Quintile values are as follows: <27.2%, 27.2-40.0%, 40.1-50.0%, 50.1-62.5%, >62.5%. GREY bars show vaccine protective efficacy by quintile of vaccine coverage within social networks developed using household-level kinship connections. The number shown above each bar is the calculated protective efficacy. The RED line indicates the risk of cholera for placebo recipients while the BLUE line indicates the risk of cholera for vaccine recipients by quintile of vaccine coverage within social networks. The numbers contained in the table below the graph indicate the calculated cholera risk for each group. An asterisk (**) indicate that the cholera risk per 1,000 was significantly different between the placebo and vaccine groups (e.g., the confidence intervals for the two calculated rates did not overlap). Quintiles show the proportion of a person's social network that was vaccinated (e.g., for quintile 1, <27.2% of people in an individual's social network were administered the cholera vaccine).
Figure 4. Risk of cholera and protective efficacy of killed oral cholera vaccines, by level of vaccine coverage in bari-level social networks.
**p<0.01 for the difference in risk between vaccinees and placebo recipients; * p<0.05 for the difference in risk between vaccinees and placebo recipients. Note: Quintile values are as follows: <28.7, 28.7-37.9%, 38.0-44.9%, 45.0-51.8%, >51.8%. GREY bars show vaccine protective efficacy by quintile of vaccine coverage within social networks developed using bari-level kinship connections. The number shown above each bar is the calculated protective efficacy. The RED line indicates the risk of cholera for placebo recipients while the BLUE line indicates the risk of cholera for vaccine recipients by quintile of vaccine coverage within social networks. The numbers contained in the table below the graph indicate the calculated cholera risk for each group. An asterisk (**) indicate that the cholera risk per 1,000 was significantly different between the placebo and vaccine groups (e.g., the confidence intervals for the two calculated rates did not overlap). Quintiles show the proportion of a person's social network that was vaccinated (e.g., for quintile 1, <28.7% of people in an individual's social network were administered the cholera vaccine).
Tables 1 and 2 show the relationship between vaccine coverage of the household-level and bari-level social networks in models that used GEEs with the logit link function that controlled for potential confounding demographic variables known to be associated with risk for cholera in Matlab. Table 1 presents the models that used level of vaccine coverage developed using the household-level social networks. In the model examining both vaccine and placebo recipients (model 1), vaccination of the individual and the level of vaccine coverage of the individual's social network were shown to have independent protective effects on an individual's risk of cholera. The inverse relationship between the level of vaccine coverage of the social network and an individual's risk of cholera remained significant in the model that examined only vaccine recipients (model 2: p = 0.006) but not in the model that assessed only placebo recipients (model 3: p = 0.151).
Table 1. Predictors of cholera risk in recipients of vaccine or placebo, household-level social networks.
| Model 1: All recipients of > = 2 doses (n = 74,003) | Model 2: Recipients of > = 2 doses of vaccine (n = 49,336) | Model 3: Recipients of > = 2 doses of placebo (n = 24,667) | |||||||
| OR* | 95% CI | p | OR* | 95% CI | p | OR* | 95% CI | p | |
| Age | 0.98 | 0.96-0.99 | 0.0007 | 0.95 | 0.92-0.98 | 0.003 | 0.99 | 0.98-1.01 | 0.181 |
| Sex | 1.14 | 0.84-1.55 | 0.390 | 1.18 | 0.78-1.79 | 0.421 | 1.05 | 0.69-1.61 | 0.817 |
| Religion | 1.15 | 0.72-1.81 | 0.563 | 1.19 | 0.62-2.29 | 0.602 | 1.10 | 0.60-1.99 | 0.766 |
| Distance to nearest river | 0.86 | 0.76-0.98 | 0.025 | 0.83 | 0.69-1.00 | 0.051 | 0.89 | 0.75-1.06 | 0.198 |
| Distance to nearest treatment center | 1.11 | 1.03-1.20 | 0.005 | 1.13 | 1.03-1.25 | 0.014 | 1.09 | 0.99-1.21 | 0.089 |
| Experienced dysentery | 4.30 | 1.19-15.5 | 0.026 | 5.97 | 1.40-25.44 | 0.016 | 3.15 | 0.47-21.07 | 0.236 |
| Received > = 2 doses (vaccine vs. placebo)† | 0.52 | 0.39-0.70 | <0.0001 | ||||||
| Level of vaccine coverage in network (%) | 0.99 | 0.98-0.99 | 0.003 | 0.99 | 0.97-0.99 | 0.006 | 0.99 | 0.98-1.00 | 0.151 |
*Multivariate odds ratio for the cited variable, adjusted for all other variables in the table.
†Variable was not considered in models 2 and 3 since all individuals were either vaccinated or not in these models.
Table 2. Predictors of cholera risk in recipients of vaccine or placebo, bari-level social networks.
| Model 1: All recipients of > = 2 doses (n = 74,003) | Model 2: Recipients of > = 2 doses of vaccine (n = 49,336) | Model 3: Recipients of > = 2 doses of placebo (n = 24,667) | |||||||
| OR* | 95% CI | p | OR* | 95% CI | p | OR* | 95% CI | p | |
| Age | 0.98 | 0.97-0.99 | 0.001 | 0.95 | 0.92-0.98 | 0.003 | 0.99 | 0.98-1.00 | 0.202 |
| Sex | 1.14 | 0.83-1.56 | 0.426 | 1.18 | 0.77-1.80 | 0.443 | 1.05 | 0.68-1.62 | 0.813 |
| Religion | 1.11 | 0.70-1.74 | 0.664 | 1.19 | 0.62-2.29 | 0.597 | 1.06 | 0.58-1.93 | 0.858 |
| Distance to nearest river | 0.88 | 0.76-1.01 | 0.004 | 0.86 | 0.71-1.03 | 0.104 | 0.91 | 0.75-1.10 | 0.324 |
| Distance to nearest treatment center | 1.12 | 1.04-1.21 | 0.065 | 1.14 | 1.03-1.26 | 0.009 | 1.11 | 0.99-1.24 | 0.068 |
| Experienced dysentery | 4.63 | 1.41-15.14 | 0.011 | 6.12 | 1.51-24.85 | 0.011 | 3.17 | 0.46-21.87 | 0.242 |
| Received > = 2 doses (vaccine vs. placebo)† | 0.46 | 0.35-0.60 | <0.0001 | ||||||
| Level of vaccine coverage in network (%) | 0.98 | 0.97-0.99 | 0.0002 | 0.97 | 0.96-0.99 | 0.003 | 0.98 | 0.97-0.99 | 0.008 |
*Multivariate odds ratio for the cited variable, adjusted for all other variables in the table.
†Variable was not considered in models 2 and 3 since all individuals were either vaccinated or not in these models.
Table 2 presents the models that used level of vaccine coverage developed using the bari-level social networks. In the model examining both vaccine and placebo recipients (model 1), vaccination of the individual showed a significant protective effect on cholera risk (p<0.0001) as did level of vaccine coverage in the social network (p = 0.0002). The inverse relationship between the level of vaccine coverage of the bari-level social network and an individual's risk of cholera remained significant in the model that examined only vaccine recipients (model 2: p = 0.003) and in the model that examined placebo recipients (model 3: p = 0.008).
We did not find evidence of effect modification between receipt of vaccine versus placebo and level of cholera vaccine coverage in an individual's social network. Interaction terms between these two variables were not found to be significant in multivariate models (p = 0.33 for household-level network models and p = 0.65 for bari-level network models).
Discussion
When social networks were built using household-level kinship ties, high levels of cholera vaccine coverage in the social network were linked with a reduced risk of cholera in individuals who received the vaccine, but not for individuals who received a placebo. This shows a direct effect of the vaccine in preventing cholera. However, when social networks were built using bari-level kinship ties, high levels of vaccine coverage were linked with reduced cholera risk in both vaccinees and placebo recipients. Why the difference between the two social networks? The kinship networks developed using household-level connections represent interactions between households with one or more related individuals. There are, however, households in a bari that have no kinship ties. In addition, household with a kinship tie to a household in a different bari are only tied to that one household, not to any of the other households in that different bari. Thus, household-level social networks do not capture the additional social interactions that occur among individuals from unrelated households located in the same bari or unrelated households located in a different bari that may be visited while visiting relatives. The bari-level kinship networks represent a much larger social network. As long as some kinship tie between two households exists (in the same or a different bari) all individuals in the bari, regardless or household, are included in the social network. This represents a larger body of social interactions that may include neighbors and friends of related household members. Our findings suggest that including neighbors as well as kinship ties more accurately models cholera transmission dynamics. This is more than likely due to the integral role the environment plays in fecal-oral disease transmission and indicates that shared water and sanitation environments are more important for transmission dynamics than social contacts.
Our results may also be biased due to the fact that social networks were defined only through kinship linkages, which is a limitation of the study. Due to limitations with the dataset, additional network linkages based on non-kinship relationships were not explored. Friends and neighbors were only included in an individual's social network in as a result of being in a bari identified by a kinship linkage. Social interaction in Matlab occurs within or outside the household and with acquaintances and neighbors. However, contact with family members and kin is more common, many of which reside within the same household or in a location nearby. The basic social structure of rural Bangladeshi society is anchored in a system of kinship relations [27] and family remains an important institution despite increasing modernization. Activities in daily life, such as labor and meals, often take place in the presence of related individuals [28], [29]. Rural areas also more likely adhere to traditions such as purdah, the confinement of women to the home, limiting female social contact to family members [30]. Most secondary transmission of cholera in Matlab likely occurs with food and water acting as vehicles of transmission [31], [32]. If cholera is spread via consumption of water or food contaminated by others, there is a significant chance that the transmission is within the family. Recent research in Matlab suggests that siblings and parents of cholera patients have a higher risk of cholera and that household specific factors (socioeconomic status and hygiene practices) are important determinants of cholera risk [33]. Due to these important social and cultural factors, we hypothesized that kinship-based networks would accurately capture a majority of social interactions that might lead to secondary transmission and contamination of shared water and food. Our findings, however, do not support this hypothesis. Instead we found evidence that cholera transmission was lower, and herd immunity greater, for networks that also included neighboring baris.
Further evidence to support our findings regarding transmission dynamics emerged from our previous analyses of the Bangladesh trial that showed that higher levels of vaccine coverage within a 2km spatial neighborhood reduced cholera incidence within the placebo group as well as the vaccine group [7]. This paper employed ecological vaccine trial methods and used a 2 km spatial neighborhood to capture interactions within kinship-based social networks as well as neighbors that may share same water resources. The current analysis adds to previous findings by separating the effects of the social network (included in the 2 km spatial neighborhood and the household-level social network) from the added effects of the local environment (only included in the 2 km spatial neighborhood). The bari-level kinship network represents the “in between” case as it captures kinship social networks and some (though not all) neighbors who may share same water resources.
Given this, when the bari-level social network is used, findings indicate that progressively higher levels of vaccine coverage in a social network can lead to increasing levels of indirect protection of non-vaccinated individuals and could also lead to progressively higher levels of total (indirect plus direct) protection of vaccine recipients. This finding is similar to previous analyses that used the 2 km spatial neighborhood. When household-level social networks were used, higher levels of vaccine coverage did not lead to high levels of indirect protection of non-vaccinated individuals. This suggests that the local environment plays a more important role in the herd immunity effect observed in prior studies and the network based on purely social ties does not capture the role of the environment. The population-based social network does not perform as well as the distance-based social network for the transmission of cholera; therefore models indicate no reduction of the cholera risk with the increase of the coverage among social contacts. Both social ties and the local environment are important for understanding vaccine efficacy and the risk for contracting cholera.
While there is a small but well-regarded body of prior literature examining the influence of social networks on diseases that have a behavioral component such as STIs and obesity [34]–[37], few studies have examined the effect of social ties on infectious disease transmission. Giebultowicz, et al [38] found that the rate of cholera in an individual's social network was an important factor in determining cholera risk, but that the neighborhood environment was of greater importance in predicting higher rates of disease. Their paper provided important information on cholera transmission dynamics but did not investigate the impact of vaccination within a social network on disease rates. In Ecuador, Bates et al. [39] found that high levels of social connectedness and centrality were risk factors for diarrheal disease, though disease incidence among those connections was not considered in the analysis. We are not aware of any studies that examine the role of social networks in vaccine efficacy. In contrast to sexually transmitted infections, the study of enteric disease transmission requires an understanding of all social connections (not just sexual contacts) and accurate characterization of the shared water environment. The protective efficacy of a vaccine may, therefore, be dependent on the level of vaccine coverage within an individual's social network as well as among individuals in the surrounding neighborhood. Our data suggests that the environment and social interactions within that environment are important in cholera disease transmission. In addition, substantial levels of indirect vaccine protection, in addition to direct protection, could be attained if vaccine levels are high within an individual's social network and among neighbors sharing water resources.
Footnotes
Competing Interests: The authors have declared that no competing interests exist.
Funding: This work was supported by the National Science Foundation (BCS-0924479) (www.nsf.org). It was also supported by the ICDDR,B and its donors which provide unrestricted support to ICDDR,B for its operations and research. Current donors providing unrestricted support include: Government of the People's Republic of Bangladesh (GoB); Canadian International Development Agency (CIDA), Embassy of the Kingdom of the Netherlands (EKN), Swedish International Development Cooperative Agency (SIDA), and the Department for International Development, UK (DFID). We gratefully acknowledge these donors for their support and commitment to ICDDR,B's research efforts. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Bailey N. New York: Macmillan; 1975. The Mathematical Theory of Infectious Diseases.413 [Google Scholar]
- 2.May R, Anderson R. Spatial Heterogeneity and the Design of Immunization Programs. Mathematical Biosciences. 1984;72:83–111. [Google Scholar]
- 3.McCallum H, Barlow N, Hone J. How should pathogen transmission be modelled? Trends in Ecology & Evolution. 2001;16:295–300. doi: 10.1016/s0169-5347(01)02144-9. [DOI] [PubMed] [Google Scholar]
- 4.Meyers L, Pourbohloul B, Newman M, Skowronski D, Brunham R. Network theory and SARS: predicting outbreak diversity. Journal of Theoretical Biology. 2005;232:71–81. doi: 10.1016/j.jtbi.2004.07.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Anderson R, May R. Immunization and herd-immunity. Lancet. 1990;335:641–645. doi: 10.1016/0140-6736(90)90420-a. [DOI] [PubMed] [Google Scholar]
- 6.Ali M, Clemens J. Ecological aspects in vaccine trials. Expert Review of Vaccines. 2008;7:279–281. doi: 10.1586/14760584.7.3.279. [DOI] [PubMed] [Google Scholar]
- 7.Emch M, Ali M, Park JK, Yunus M, Sack DA, et al. Relationship between neighbourhood-level killed oral cholera vaccine coverage and protective efficacy: evidence for herd immunity. Int J Epidemiol. 2006;35:1044. doi: 10.1093/ije/dyl100. [DOI] [PubMed] [Google Scholar]
- 8.McPherson M, Smith-Lovin L, Cook J. Birds of a feather: Homophily in social networks. Annual Review of Sociology. 2001. pp. 415–444.
- 9.Morris M. Oxford: Oxford University Press; 2004. Network Epidemiology: A Handbook for Survey Design and Data Collection.252 [Google Scholar]
- 10.Meyers L, Newman M, Martin M, Schrag S. Applying network theory to epidemics: Control measures for Mycoplasma pneumoniae outbreaks. Emerging Infectious Diseases. 2003;9:204–210. doi: 10.3201/eid0902.020188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Meyers L. Contact network epidemiology: Bond percolation applied to infectious disease prediction and control. Bulletin of the American Mathematical Society. 2007;44:63–86. [Google Scholar]
- 12.Wasserman S, Faust K. Cambridge: Cambridge University Press; 1994. Social network analysis: Methods and applications.857 [Google Scholar]
- 13.Hanneman R. Riverside, California: Department of Sociology, University of California at Riverside; 2001. Introduction to social network methods. [Google Scholar]
- 14.Clemens JD, Sack DA, Harris JR, Van Loon F, Chakraborty J, et al. Field trial of oral cholera vaccines in Bangladesh: results from three-year follow-up. Lancet. 1990;335:270–273. doi: 10.1016/0140-6736(90)90080-o. [DOI] [PubMed] [Google Scholar]
- 15.Emch M, Ali M, Acosta C, Yunus M, Sack DA, et al. Efficacy calculation in randomized trials: global or local measures? Health Place. 2007;13:238–248. doi: 10.1016/j.healthplace.2006.01.005. [DOI] [PubMed] [Google Scholar]
- 16.Ali M, Emch M, von Seidlein L, Yunus M, Sack DA, et al. Herd immunity conferred by killed oral cholera vaccines in Bangladesh: a reanalysis. Lancet. 2005;366:44–49. doi: 10.1016/S0140-6736(05)66550-6. [DOI] [PubMed] [Google Scholar]
- 17.Colwell R, Kaper J, Joseph W. Vibrio cholerae, Vibrio parahaemolyticus, and other vibrios: occurrence and distribution in Chesapeake Bay. Science. 1977;198:394–396. [PubMed] [Google Scholar]
- 18.Colwell R, Huq A. Environmental reservoir of Vibrio cholerae: the causative agent of Cholera. Disease in Evolution. 1994;740:44–54. doi: 10.1111/j.1749-6632.1994.tb19852.x. [DOI] [PubMed] [Google Scholar]
- 19.Acosta CJ, Galindo CM, Kimario J, Senkoro K, Urassa H, et al. Cholera outbreak in southern Tanzania: risk factors and patterns of transmission. Emerg Infect Dis. 2001;7:583–587. doi: 10.3201/eid0707.010741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Birmingham ME, Lee LA, Ndayimirije N, Nkurikiye S, Hersh BS, et al. Epidemic cholera in Burundi: patterns of transmission in the Great Rift Valley Lake region. Lancet. 1997;349:981–985. doi: 10.1016/S0140-6736(96)08478-4. [DOI] [PubMed] [Google Scholar]
- 21.Spira WM, Khan MU, Saeed YA, Sattar MA. Microbiological surveillance of intra-neighbourhood E1 Tor cholera transmission in rural Bangladesh. Bull World Health Organ. 1980;58:731–740. [PMC free article] [PubMed] [Google Scholar]
- 22.Shapiro RL, Otieno MR, Adcock PM, Phillips-Howard PA, Hawley WA, et al. Transmission of epidemic Vibrio cholerae O1 in rural western Kenya associated with drinking water from Lake Victoria: an environmental reservoir for cholera? Am J Trop Med Hyg. 1999;60:271–276. doi: 10.4269/ajtmh.1999.60.271. [DOI] [PubMed] [Google Scholar]
- 23.Pollitzer R. Cholera. World Health Organization: Monograph Series. 1959;43:846. [PubMed] [Google Scholar]
- 24.Swerdlow D, Isaacson M. The epidemiology of cholera in Africa. In: Swerdlow D, Isaacson M, editors. Vibrio Cholera and Cholera: Molecular to Global Perspectives. Washington, DC: ASM Press; 1994. pp. 297–307. [Google Scholar]
- 25.Koelle K, Pascual M. Disentangling extrinsic from intrinsic factors in disease dynamics: A nonlinear time series approach with an application to cholera. American Naturalist. 2004;163:910–913. doi: 10.1086/420798. [DOI] [PubMed] [Google Scholar]
- 26.van Loon FP, Clemens JD, Chakraborty J, Rao MR, Kay BA, et al. Field trial of inactivated oral cholera vaccines in Bangladesh: results from 5 years of follow-up. Vaccine. 1996;14:162–166. doi: 10.1016/0264-410x(95)00122-h. [DOI] [PubMed] [Google Scholar]
- 27.Aziz KMA. Dhaka, Bangladesh: International Centre for Diarrhoeal Disease Research, Bangladesh; 1979. Kinship in Bangladesh.228 [Google Scholar]
- 28.Amin S. Family structure and change in rural Bangladesh. Population Studies-a Journal of Demography. 1998;52:201–213. [Google Scholar]
- 29.White S. Men, masculinities, and the politics of development. Gender and Development. 1997;5:14–22. doi: 10.1080/741922357. [DOI] [PubMed] [Google Scholar]
- 30.Amin S. The poverty-purdah trap in rural Bangladesh: Implications for women's roles in the family. Development and Change. 1997;28:213–233. [Google Scholar]
- 31.Quick RE, Thompson BL, Zuniga A, Dominguez G, De Brizuela EL, et al. Epidemic cholera in rural El Salvador: risk factors in a region covered by a cholera prevention campaign. Epidemiol Infect. 1995;114:249–255. doi: 10.1017/s0950268800057915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Gunn RA, Kimball AM, Mathew PP, Dutta SR, Rifaat AH. Cholera in Bahrain: epidemiological characteristics of an outbreak. Bull World Health Organ. 1981;59:61–66. [PMC free article] [PubMed] [Google Scholar]
- 33.Rahman KM, Duggal P, Harris JB, Saha SK, Streatfield PK, et al. Familial Aggregation of Vibrio cholerae-associated Infection in Matlab, Bangladesh. Journal of Health Population and Nutrition. 2009;27:733–738. doi: 10.3329/jhpn.v27i6.4324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Christakis N, Fowler J. The spread of obesity in a large social network over 32 years. New England Journal of Medicine. 2007. pp. 370–379. [DOI] [PubMed]
- 35.Rothenberg R, Muth SQ, Malone S, Potterat JJ, Woodhouse DE. Social and geographic distance in HIV risk. Sex Transm Dis. 2005;32:506–512. doi: 10.1097/01.olq.0000161191.12026.ca. [DOI] [PubMed] [Google Scholar]
- 36.Jolly AM, Wylie JL. Gonorrhoea and chlamydia core groups and sexual networks in Manitoba. Sex Transm Infect. 2002;78(Suppl 1):i145–151. doi: 10.1136/sti.78.suppl_1.i145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Wylie JL, Cabral T, Jolly AM. Identification of networks of sexually transmitted infection: a molecular, geographic, and social network analysis. J Infect Dis. 2005;191:899–906. doi: 10.1086/427661. [DOI] [PubMed] [Google Scholar]
- 38.Giebultowicz S, Ali M, Yunus M, Emch M. A comparison of spatial and social clustering of cholera in Matlab, Bangladesh. Health Place. 2010;17:490–497. doi: 10.1016/j.healthplace.2010.12.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Bates SJ, Trostle J, Cevallos WT, Hubbard A, Eisenberg JN. Relating diarrheal disease to social networks and the geographic configuration of communities in rural Ecuador. Am J Epidemiol. 2007;166:1088–1095. doi: 10.1093/aje/kwm184. [DOI] [PMC free article] [PubMed] [Google Scholar]