Limitation of Time-of-Flight Resolution in the Ultra High Mass Range

Abstract

In this work, we have examined the reason for the deterioration of resolution and mass accuracy of time-of-flight mass analyzers with increasing mass after the expansion induced kinetic energy has been eliminated by collisional cooling in an ion guide. Theoretically, removing the expansion–induced kinetic energy by collisional cooling permits the ions to travel along the ion guide axes without significant deviation so that they can be injected into the analyzer in a well-collimated ion beam with well-defined kinetic energy. If the ions can be injected into an orthogonal acceleration time-of-flight mass analyzer (oa-TOF) in this manner, high resolution mass analysis can be obtained regardless of mass or m/z. Unfortunately, high resolution did not result. It is our contention that the effusive expansion out of the first ion guide yields dispersive axial ejection that reduces TOF resolving power with increasing mass not m/z.

In this work, we have examined the reasons for the deterioration of resolution and mass accuracy of time-of-flight mass analyzers with increasing mass. Here we consider the work of Chernushevich and Thomson ¹ who were able to mass analyze proteasome 20S with a molecular weight of 692,000 Da by increasing the first ion guide pressure. This methodology permitted improved translational cooling that enhanced ion transmission into the mass analyzer. While we applaud their achievement of ESI mass analysis of such large ions, we were also struck by the resolution that they achieved under these conditions. Theoretically, removing the expansion –induced kinetic energy by collisional cooling permits the ions to travel along the ion guide axes without significant deviation so that they can be injected into the TOF analyzer in a well-collimated ion beam with well-defined kinetic energy. If the ions can be injected into an orthogonal acceleration time-of-flight mass analyzer (oa-TOF) in this manner, high resolution mass analysis can be obtained regardless of mass or m/z.

We estimated a resolving power (m/Δm) of approximately 215 was obtained for the +25 ion at m/z=25,395. This value is typical for ultra-high mass ions (>m/z 20,000) where care has been taken to eliminate the expansion-induced kinetic energy before mass analysis. We point out that the resolution achieved is quite respectable in comparison to the literature and they may be considered the current state-of-the-art in the ultra-high mass range. However, we keep coming back to the following question: “If the expansion-induced kinetic energy of the ions is eliminated so that the ions travel along the central axis of the guides and the ion kinetic energies are defined by the applied potentials as they are orthogonally injected into the acceleration region of the TOF analyzer, why does the resolution still deteriorate so rapidly with increasing mass?”

The answer to this question is crucial if we want to formulate strategies for obtaining high resolution analysis in the ultra-high mass range. The resulting benefits of obtaining resolved mass analysis in the ultra-high mass range will be far-reaching. It will permit large molecules and clusters to be identified, characterized and even quantified in the same manner as small molecules because they will fit within the working range of the mass analyzer. The rates of discovery in the areas of bioscience and nanotechnology will increase because the greatest leaps forward for any science occur through quantitation of the processes that are being studied. Before this advance can be made, the reason for the loss of resolution with increasing m/z when the ion kinetic energy into the TOF analyzer is being controlled must be precisely understood and defined.

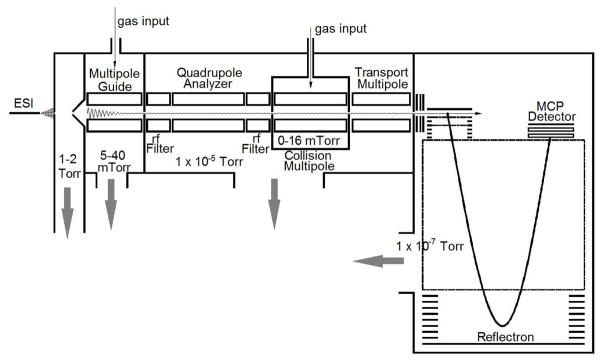
The state of the art for mass analysis in the ultra-high mass range by time of flight is accomplished with a Q-TOF that has been modified to apply increased pressure in the first ion guide. The frequency of the guides and analyzers are also reduced to accommodate larger mass-to-charge ratios (m/z). A schematic representation of the typical Q-TOF mass analyzer used for these purposes is shown in Figure 1. This configuration depicts an electrospray ion source. The ions enter the mass spectrometer through an orifice and pass through a differentially pumped region with an operating pressure of 1–2 Torr. The expanding particulate ions quickly become entrained in the gas flow because the stopping distance ^{2, 3} is less than a few millimeters at these pressures for molecular masses below 1 MDa. Consequently, the motion of the analyte in this region is defined by the flow of the carrier gas and only a small portion of the expanded gas and particles pass through the skimmer into the first ion guide chamber. The rest is lost through the pumping port.

Figure 1.

A schematic diagram of a typical Q-TOF that has been modified to perform time-of-flight mass analysis in the ultra-high mass range.

The expansion of the gas through the skimmer defines the velocity distribution of ions as they enter the ion guide. The velocity distribution of particles coming out of a 2 Torr expansion has been measured by Liu et al. during the development of aerodynamics lens-based inlet systems.⁴ Their velocity distribution can be used to approximate the behavior of the ions entering the quadrupole and validates Chernushevich and Thomson’s ¹ assumption that the velocity of all the ions with molecular masses below 1 MDa enter the first quadrupole at a constant velocity of approximately 400 m/s. This imparts expansion-induced kinetic energies that roughly increase linearly with mass up to approximately 800 eV at 1 MDa.

Energetic ion injection into the first ion guide yields large radial oscillations (depicted in Figure 1) for the ions that are captured by the fields of the guide. Ideally, collisions with the buffer gas will “stop” the ions within the guide. This means that the radial oscillations and forward motion induced by the expansion into the guide chamber have been eliminated inside the guide. Stopping the ions enables them to travel along the central axis of the ion guides. Because the field along this axis is zero, travel along the axis is mass independent. Any deviation from travel along the central axis will yield radial oscillations. Those oscillations can be exacerbated by passage through the fringe fields that occur at the ends of the guide by interaction of the rods with the end caps electrodes. Oscillations that exist after the first guide will continue to exist unless the ions are collisionally cooled with a buffer gas. The pressure of the analyzing quadrupole and the transport multipole (after the collision cell, see Figure 1) are in the 1 ×10⁻⁵ Torr range. Transmission through these devices is essentially collisionless. Chernushevich and Thomson ¹ did not use any buffer gas in the collision cell when measuring their high mass spectra. If there is no buffer gas in the collision cell, then the kinetic energy and dispersion of the ions injected into the TOF are defined by the ion trajectories out of the first ion guide.

Chernushevich and Thomson ¹ showed that when the radial oscillations and the forward motion induced by the expansion are still significant, the signal observed by the TOF was negligible. They also showed that increasing the ion guide pressure “stops” the ions in the guide and permit them to be observed by the TOF with excellent intensity. Unfortunately, the resolving power they observed for the large (> 600 kDa) noncovalently bound biomolecular ion complexes was less than stellar (m/Δm ≈ 200) measured at values of m/z > 20,000.

Close examination of Chernushevich and Thomson’s data (specifically Figure 11b in reference ¹) reveals that the resolving power is actually increasing with m/z from roughly 151 at m/z 15,774 and 215 at m/z 25,395. Since resolving power is known to decrease with increasing mass, this observation may seem unexpected. Review of the oa-TOFMS tutorials ^{5, 6} reveals that the largest loss of resolution results from dispersive injection of the ions into the acceleration region. Given the loss of resolving power relative to that observed in the low mass region suggests that dispersive ion injection into the TOF is the root cause. We need to now understand how the dispersion into the TOF can decrease with increasing m/z in Chernushevich and Thomson’s experiments ¹.

We noted the molecular masses at each of the observed values of m/z in Figure 11b of reference ¹ were roughly the same as were their cross sections and particle densities. We began with the hypothesis that these ions exit the first quadrupole with roughly the same dispersion. The pseudo-potential well depth defined as D=q_xyV/8 where q_xy is the Mathieu parameter and V is the voltage of the waveform measured 0 to peak. q_xy is inversely proportional to m/z; therefore, the well depth decreases with m/z. The well depth is important for defining the dispersion out of the guide for two reasons. First, it limits the range of angles that are captured by the fields of the guide—the lower the well depth the smaller the range of angles of injection that are caught by the fields and consequently the narrower the dispersion out of the device. Second, the well depth is a measure of the strength of interaction of the fields with the ions when they deviate from traveling along the central axis. In a collisionless guide, if the dispersion and kinetic energy distribution into the device is the same then the dispersion out of the device will decrease with increasing m/z.

Alternatively, it is well known that the resolving power decreases with mass in general. This suggests the dispersion into the TOF increases with increasing mass, but for a given value of the mass the dispersion into the TOF decreases with decreasing charge z. Our hypothesis suggests the cause of the dispersion into the TOF is a function of mass not m/z. If so, the dispersion is based on aerodynamics not electrodynamics. Additionally, the aerodynamic process that causes the dispersion has to occur after the ions are stopped. The only possibility is the expansion out of the first guide. This explains why the observed resolving power is significantly better for (CsI)_n⁺ clusters because aerodynamic induced dispersion should decrease with increasing particle density.⁷

The only aerodynamic force available coming out of the first guide is the gas expansion. The expansion out of Chernushevich and Thomson’s quadrupole is roughly effusive. An expansion is considered to be effusive if the mean free path of the carrier gas is greater than or equal to the diameter of the expansion orifice. The mean free path is equal to ~2-mm at approximately 25 mTorr in air. An effusive expansion means that the carrier gas undergoes few collisions as they pass through the orifice. The trajectories of ions are not supposed to be affected by effusive expansions. The rate of gas transmission through the orifice can be calculated from the wall collision rate, Z_w, times the area of the orifice, A: This is Graham’s Law of Effusion.

$$C_{\mathit{trans}}={AZ}_w=\frac{pA}{\sqrt{2\pi \mathit{mkT}}}$$ (1)

Here p is the pressure, m is the mass of the buffer gas, k is Boltzmann’s constant and T is the absolute temperature.

The particles in the middle of the first ion guide experience isotropic collisions. However, there is essentially no gas flow from outside the exit orifice into the first guide chamber. As the particles approach the exit orifice, the collisions become anisotropic until the buffer gas only collides with the half of the particle surface that faces the inside of the guide chamber. The gas-particle collision rate can be defined by equation (1) where A is the cross sectional area of the particle. Kauffman ⁸ has show that the cross sectional area of biomolecules can be reasonably approximated by assuming they are all spherical particles with a density of 0.8 g/cm³. We used equation 1 and Kaufman’s results between the molecular weight and the cross section to determine the particle collision rate at the orifice at a pressure of 30 mTorr as a function of particle molecular weight in Figure 2. This calculation assumes that the particles are not moving relative to the motion of the carrier gas. The accuracy of this assumption will increase with mass as the velocity of the particles decrease. At 30 mTorr, particles in the ultra high mass range experience a rate of more than a million carrier gas collisions per second at the orifice.

Figure 2.

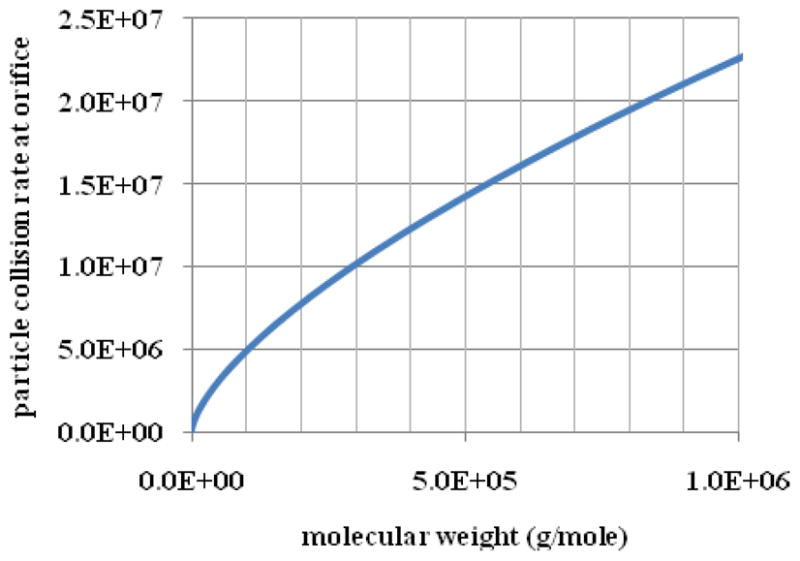
The particle-buffer gas collision rate at 30 mTorr at the exit orifice into vacuum calculated from equation (1) with the assumption that the particle is stationary relative to the gas velocity.

Next, the length of time that the particle/ion is being anisotropically bombarded by the carrier gas in the vicinity of the exit orifice is needed. In the middle of the guide, after the particles have been “stopped”, their velocity is defined by isothermal diffusion and the net flow of the gas through the device. Both of these contributions to the particle velocity are negligible in comparison to the velocity imparted by the potential drop applied between the guide axis and the exit end cap. We have calculated the ion velocity as a function of m/z in a collisionless environment for a 2 V potential drop. This calculation sets the upper limit of the ion velocity because it is accelerating through the buffer gas. The collisionless particle velocity of singly-charged 2 kDa ions is 437 m/s. A 2 kDa ion would traverse 1 –cm in approximately 23 μs. A 2 kDa ion would experience on the order of 10 collisions during its transit through the expansion if it is stationary relative to the carrier. The thermal velocity of N₂ is 475 m/s. Because the small ion velocities are in the same range as the thermal velocity of the buffer gas, any collisions that are experienced during the effusive expansion if any would not effectively alter the trajectories because of the small difference in the velocities.

The field induced velocity drops precipitously because of the 1/m^1/2 dependence. Large ions with m/z values greater than 20,000 have significantly smaller velocities than the carrier gas and larger cross sections. The maximum velocity of the 650 kDa ion is less than 35 m/s. This amounts to a velocity difference of 440 m/s. Assuming the anisotropic interaction distance is roughly 1 cm, the ion is in this zone for more than 29 ms and undergoes on the order 10⁴ high velocity collisions from the carrier gas. Because the ion velocity is decreasing as the cross section increases, the ions are undergoing more collisions that are increasingly effective because the velocity difference increases as the ion mass increases. This is the most likely cause of the mass dependent dispersion that results in the oa-TOF measurements after the ions are stopped by increasing the gas pressure in the first ion guide. Now that this effect has been defined, strategies may be formulated to mitigate this effect on TOF resolving power and mass accuracy.