Random-Effects Model Aimed at Discovering Associations in Meta-Analysis of Genome-wide Association Studies

Abstract

Meta-analysis is an increasingly popular tool for combining multiple different genome-wide association studies (GWASs) in a single aggregate analysis in order to identify associations with very small effect sizes. Because the data of a meta-analysis can be heterogeneous, referring to the differences in effect sizes between the collected studies, what is often done in the literature is to apply both the fixed-effects model (FE) under an assumption of the same effect size between studies and the random-effects model (RE) under an assumption of varying effect size between studies. However, surprisingly, RE gives less significant p values than FE at variants that actually show varying effect sizes between studies. This is ironic because RE is designed specifically for the case in which there is heterogeneity. As a result, usually, RE does not discover any associations that FE did not discover. In this paper, we show that the underlying reason for this phenomenon is that RE implicitly assumes a markedly conservative null-hypothesis model, and we present a new random-effects model that relaxes the conservative assumption. Unlike the traditional RE, the new method is shown to achieve higher statistical power than FE when there is heterogeneity, indicating that the new method has practical utility for discovering associations in the meta-analysis of GWASs.

Introduction

Genome-wide association studies (GWASs) are an effective means of detecting associations between a genetic variant and traits.¹ Although GWASs have identified many loci associated with diseases, those identified loci account for only a small fraction of the genetic contribution to the disease.² The remaining contribution can be accounted for by loci with very small effect sizes, so small that tens of thousands of samples are needed if they are to be identified.³ One can design and conduct a single study collecting such a large sample, but it will be very costly. A practical alternative is to combine numerous studies that have already been performed or that are being performed in a single aggregate analysis called a meta-analysis.^4–6 Recently, several large-scale meta-analyses have been performed for diseases including type 1 diabetes,⁷ type 2 diabetes,^8–10 bipolar disorder,¹¹ Crohn disease,¹² and rheumatoid arthritis¹³ and have identified associations not revealed in the single studies.

An intrinsic difficulty in conducting a meta-analysis is choosing which studies to include. Ideally, one would collect as many studies as possible to increase the sample size. However, the decision is not always simple because sometimes the studies differ enough that one would suspect that the effect size of the association would not be the same between studies. For example, if the populations or the environmental factors are substantially different between studies, there is a possibility that the strength of the association is affected by those factors.^14,15 If the effect size of the association varies between studies, we refer to this phenomenon as between-study heterogeneity or heterogeneity.^16–19

The way in which one optimally designs and analyzes a meta-analytic study is critically dependent on the between-study heterogeneity. If one decides to limit the heterogeneity in the data as much as possible, one will only collect studies that are highly similar to each other. Therefore, the sample size might not be maximized, but the heterogeneity in the data will be minimized. The commonly applied method of analyzing a collection of studies for which the effect sizes are expected to be similar is the fixed-effects model (FE) under an assumption of the same effect size between studies.^4,20,21 Instead, if one decides to allow some heterogeneity in the data, one can collect a greater number of studies to maximize the sample size. The commonly applied method of analyzing a collection of studies for which the effect sizes are expected to vary is the random-effects model (RE), explicitly modeling the heterogeneity.^16,18,22,23 In practice, researchers often apply both FE and RE.^24,25 This way, they can discover the maximum number of associations and compare the results of the two methods; such a comparison might help in the interpretation of the results.

A surprising phenomenon that caught our attention with regard to meta-analysis is that when one applies both FE and RE to detect associations in the dataset, RE gives substantially less significant p values than FE at variants that actually show varying effect sizes between studies. This is ironic because RE is designed specifically for the case in which there is heterogeneity. Because RE gives the same p value as FE at markers showing no heterogeneity, RE rarely, if at all, gives a more significant p value than FE at any marker. Therefore, all associations identified by RE are usually already identified by FE. We verify this phenomenon through simulations. Because FE is not optimized for the situation in which heterogeneity exists and because RE finds no additional associations, the causal variants showing high between-study heterogeneity might not be discovered by either method.

In this paper, we show that the underlying reason for this phenomenon is that RE implicitly assumes a markedly conservative null-hypothesis model. The analysis in RE is a two-step procedure extending the traditional estimation of effect size to hypothesis testing. First, one estimates the effect size and its confidence interval by taking heterogeneity into account.^16,17,26,27 Second, the effect size is normalized into a z score, which is translated into the p value. We show that this second step is equivalent to assuming heterogeneity under the null hypothesis. However, there should not be heterogeneity under the null hypothesis of no associations because the effect sizes are all exactly zero. We find that this implicit assumption of the method makes the p values overly conservative.

We propose a random-effects model that relaxes the conservative assumption in hypothesis testing. Our approach estimates the effect size and its confidence interval in the same way that the traditional RE approach does. However, instead of calculating a z score as is done in traditional RE, we apply a likelihood-ratio test and assume no heterogeneity under the null hypothesis. In essence, we are separating the hypothesis testing from the effect size estimation by informing the method that the existence of the heterogeneity is dependent on the hypothesis. By taking advantage of this information, the new method, unlike traditional RE, achieves higher statistical significance than FE if there is heterogeneity. Our simulations show that the new approach effectively acquires high statistical power under various types of heterogeneity, including when the linkage disequilbrium structures are different between studies.^28,29 Applying the method to the real datasets of type 2 diabetes⁹ and Crohn disease¹² shows that the method can have practical utility for finding additional associations in the current meta-analyses of GWASs.

The new method has several interesting characteristics. First, the new method is closely related to existing approaches in the meta-analysis. The statistic consists of a part corresponding to the average effect size, equivalent to FE, and a part corresponding to heterogeneity, asymptotically equivalent to Cochran's Q.¹⁶ This shows that heterogeneity as well as effect size contributes to the discovery of associations in our method. Second, the statistic asymptotically follows a mixture of χ² distributions,³⁰ and therefore the p value can be efficiently calculated. Third, although the new method is more sensitive to confounding than previous methods, a simple procedure similar to genomic control³¹ can reduce the effect of confounding.

Material and Methods

Heterogeneity

If there exists actual genetic effect but the effect size level varies between studies, we refer to this phenomenon as heterogeneity.¹⁶ A simple example of heterogeneity is when the populations are different between studies and the population-specific variation affects the pathways of disease and thus results in different effect sizes.^14,15 However, heterogeneity can also occur when the effect size is the same but the linkage disequilibrium structures are different between studies.^28,29 In this case, the virtual or observed effect sizes can vary at the markers as described below.

Because we define the heterogeneity as the difference in effect sizes, under the null hypothesis of no associations, there should be no heterogeneity. If there exists no genetic effect but we observe unexpected variation in the observed effect size, as can be the case for population structure, we will call it confounding and treat it separately.^31,32

LD Can Cause Heterogeneity

Assume N/2 cases and N/2 controls. Let p be the frequency of the causal variant having odds ratio γ. If we assume a small disease prevalence, the expected frequency in controls and cases is

$$p^{-}\approx p$$ (1)

$$p^{+}\approx \frac{\gamma p}{\left(\gamma -1\right)p+1}.$$ (2)

If γ is relative risk, Equation 2 is an exact equality. The usual z score statistic is

$$S=\frac{{\hat{p}}^{+}-{\hat{p}}^{-}}{\sqrt{2{\hat{p}}^{\pm }\left(1-{\widehat{p}}^{\pm }\right)/N}}$$

where $p^{\pm }=\left(p^{+}+p^{-}\right)/2$ and the hats (∧) denote observed values. S follows $\mathcal{N}\left(\lambda \sqrt{N},1\right)$ where

$$\lambda \sqrt{N}=\frac{p^{+}-p^{-}}{\sqrt{2p^{\pm }\left(1-p^{\pm }\right)/N}}$$

is the noncentrality parameter.³³

Now, assume that we instead collect a marker whose frequency is similar to that of the causal variant, with which it has a correlation coefficient r. Pritchard and Przeworski³⁴ show that the noncentrality parameter at the marker (${\lambda }_m\sqrt{N}$) is approximately $r\lambda \sqrt{N}$. The subscript m denotes that the values are for the marker.

Thus, we can solve the equation

$$\frac{p_m^{+}-p_m^{-}}{\sqrt{2p_m^{\pm }\left(1-p_m^{\pm }\right)/N}}=r\frac{p^{+}-p^{-}}{\sqrt{2p^{\pm }\left(1-p^{\pm }\right)/N}}$$

to obtain the virtual odds ratio γ_m at the marker. By further assuming that

$$p^{\pm }\left(1-p^{\pm }\right)\approx p_m^{\pm }\left(1-p_m^{\pm }\right),$$

we find that γ_m is approximately

$${\gamma }_m\approx \frac{\left(\left(\gamma -1\right)p-\gamma +1\right)r+\left(1-\gamma \right)p-1}{\left(\gamma -1\right)pr+\left(1-\gamma \right)p-1}.$$

Table 1 describes the pattern by which γ_m varies depending on γ and r. Note that if $\log \gamma =0$ (no genetic effect), $\log {\gamma }_m$ is also 0. In other words, there is no heterogeneity under the null hypothesis.

Table 1.

Pattern of Virtual-Effect Size under Various LD Conditions

Effect at Causal SNP	LD between Causal SNP and Marker	Virtual Effect at Marker SNP
β = 0 (no effect)	–	βm = 0 (no effect)
β > 0	r = 1.0 (perfect LD)	βm = β (same effect)
β > 0	r < 1.0 (imperfect LD)	βm < β (smaller effect)
β > 0	r = 0 (no LD)	βm = 0 (no effect)
β > 0	r < 0 (negative LD)	βm < 0 (effect in opposite direction)

β is the effect size at the causal SNP, and β_m is the virtual effect size observed at the marker. The LD measure is r, the Pearson correlation coefficient.

Traditional FE and RE Approaches

FE Approach

FE assumes that the magnitude of the effect size is the same, or fixed, across the studies.^20,21 The two widely used statistics are the inverse-variance-weighted effect-size estimate³⁵ and the weighted sum of z-scores.⁴ Let $X_1,\text{…},X_C$ be the effect-size estimates, such as the log odds ratios or regression coefficients, in C independent studies. Usually, $X_1,\text{…},X_C$ follow normal distributions if the sample sizes in each study are sufficiently large. Let $SE\left(X_i\right)$ be the standard error of X_i and $V_i=SE{\left(X_i\right)}^2$. Although V_i is estimated from the data, it is a common practice to consider it as a true value in the analysis. Let $W_i=V_i^{-1}$ be the inverse variance. The inverse-variance-weighted effect-size estimator is

$$\overline{X}=\frac{\sum W_i{X}_i}{\sum W_i}.$$ (3)

It follows that the standard error of $\overline{X}$ is $SE\left(\overline{X}\right)={\sqrt{\sum W_i}}^{-1}$. Because $\overline{X}$ will also follow a normal distribution, we can construct a statistic

$$Z_{FE}=\frac{\overline{X}}{SE\left(\overline{X}\right)}=\frac{\sum W_i{X}_i}{\sqrt{\sum W_i}},$$

which follows $\mathcal{N}\left(0,1\right)$ under the null hypothesis of no associations. The p value of the association if we assume a two-sided test will then be

$$p_{FE}=2\Phi \left(-\left|Z_{FE}\right|\right),$$

where Φ is the cumulative density function of the standard normal distribution.

The p value can also be obtained with z scores. Let $Z_1,\text{…},Z_C$ be the z scores. A weighted sum of z scores is

$$Z_{WS}=\frac{\sum {\sqrt{N_i{p}_i\left(1-p_i\right)}}_i{Z}_i}{\sqrt{\sum N_i{p}_i\left(1-p_i\right)}}.$$

N_i is the so-called effective sample size of study i and can be approximated to $2N_i^{+}{N}_i^{-}/\left(N_i^{+}+N_i^{-}\right)$ when $N_i^{+}/2$ cases and $N_i^{-}/2$ controls are in study i. p_i is the minor allele frequency of the marker in study i. The p value is then

$$p_{WS}=2\Phi \left(-\left|Z_{WS}\right|\right).$$

$p_{FE}$ and $p_{WS}$ are usually very similar.^36,37

Usually, the weights of only $\sqrt{N_i}$ instead of $\sqrt{N_i{p}_i\left(1-p_i\right)}$ are used under the assumption that the frequencies are similar.⁴ However, in general, explicitly employing frequency information in the weights can be the most powerful. One can easily demonstrate this in the case of binary alleles and binary traits by showing the following three things: (1) the Mantel-Haenszel test²¹ is the uniformly most powerful unbiased test, as shown by Birch,³⁸ (2) the inverse-variance weighted odds ratio is approximately equivalent to the Mantel-Haenszel, and (3) the weighted sum of z scores is approximately equivalent to the inverse-variance weighted log odds ratio only when the weights include the frequency information.

RE Approach

On the other hand, the RE approach assumes that the true value of the effect size of each study is sampled from a probability distribution having variance τ².¹⁶ The between-study variance τ² is estimated by various approaches,^{26,27,39–41} such as the method of moments,¹⁶ the method of maximum likelihood,⁴² and the method of restricted maximum likelihood.¹⁷ Given the estimated between-study variance ${\widehat{\tau }}^2$, the effect size estimate is calculated similarly to Equation 3 but with the additional variance term accounted for, as follows:

$${\overline{X}}^{\ast }=\frac{\sum {\left(W_i^{-1}+{\widehat{\tau }}^2\right)}^{-1}{X}_i}{\sum {\left(W_i^{-1}+{\widehat{\tau }}^2\right)}^{-1}}.$$

It follows that $SE\left({\overline{X}}^{\ast }\right)={\sqrt{\sum {\left(W_i^{-1}+{\widehat{\tau }}^2\right)}^{-1}}}^{-1}$. The test statistic can be similarly constructed as

$$Z_{RE}=\frac{{\overline{X}}^{\ast }}{SE\left({\overline{X}}^{\ast }\right)},$$ (4)

and the p value is

$$p_{RE}=2\Phi \left(-\left|Z_{RE}\right|\right).$$

Note that if the frequency and sample size are equal between studies ($W_1=\text{…}=W_C$), then ${\overline{X}}^{\ast }=\overline{X}$. However, because $SE\left({\overline{X}}^{\ast }\right)\ge SE\left(\overline{X}\right)$, we obtain $p_{RE}\ge p_{FE}$. That is, it is easily shown analytically that RE never gives a more significant p value than FE if the sample size is equal.

RE Assumes Heterogeneity under the Null Hypothesis

To show that RE implicitly assumes heterogeneity under the null hypothesis, we describe FE and RE as likelihood ratio tests. In a typical meta-analysis, the analysis is a two-step procedure: (1) the result of each study is summarized in a statistic (e.g., effect-size estimate), and (2) the statistics of the multiple studies are combined. Thus, each statistic can be considered as a single observation. Here we consider the likelihood of these observations rather than of the raw data. We make an assumption that each statistic follows a normal distribution; such an assumption is usually acceptable in GWASs because of the large sample size.

Let $X_1,\text{…},X_C$ be the effect-size estimates of C studies. Let V_i and W_i be the variance and inverse variance of X_i. Consider the likelihood ratio test under the fixed-effects model. Let L₀ and L₁ be the likelihood under the null and alternative hypotheses, respectively. Then,

$$L_0=\prod _i\frac{1}{\sqrt{2\pi V_i}}\exp \left(-\frac{X_i^2}{2V_i}\right)$$

$$L_1=\prod _i\frac{1}{\sqrt{2\pi V_i}}\exp \left(-\frac{{\left(X_i-\mu \right)}^2}{2V_i}\right),$$

where μ is the unknown true mean effect size. The test is whether $\mu \ne 0$. Solving $\partial L_1/\partial \mu =0$ shows that the maximum likelihood estimate of μ is

$$\widehat{\mu }=\overline{X}=\frac{\sum W_i{X}_i}{\sum W_i}.$$

Thus, the likelihood ratio test statistic for the composite hypothesis is

$$\begin{array}{c}-2\log \left(\lambda \right)=-2\log \left(\frac{\sup L_0}{\sup L_1}\right)\\ =\sum _i\frac{X_i^2}{V_i}-\sum _i\frac{{\left(X_i-\widehat{\mu }\right)}^2}{V_i}\\ =\sum _i\frac{2X_i\overline{X}-{\overline{X}}^2}{V_i}\\ =2\overline{X}\sum W_i{X}_i-{\overline{X}}^2\sum W_i\\ =\overline{X}\sum W_i{X}_i\\ =Z_{FE}^2,\end{array}$$ (5)

showing that this likelihood ratio test is equivalent to FE.

Similarly, RE can be described as a likelihood ratio test. The current RE framework estimates the between-study variance τ² first and subsequently uses the value in the statistical test. Let ${\widehat{\tau }}^2$ be the between-study variance as estimated by any method. Consider a likelihood ratio test assuming the same ${\widehat{\tau }}^2$ as a constant under both the null and the alternative hypotheses. The likelihoods are

$$L_0=\prod _i\frac{1}{\sqrt{2\pi \left(V_i+{\widehat{\tau }}^2\right)}}\exp \left(-\frac{X_i^2}{2\left(V_i+{\widehat{\tau }}^2\right)}\right)$$

$$L_1=\prod _i\frac{1}{\sqrt{2\pi \left(V_i+{\widehat{\tau }}^2\right)}}\exp \left(-\frac{{\left(X_i-\mu \right)}^2}{2\left(V_i+{\widehat{\tau }}^2\right)}\right).$$

The maximum likelihood estimate of μ is

$$\widehat{\mu }={\overline{X}}^{\ast }=\frac{\sum {\left(W_i^{-1}+{\widehat{\tau }}^2\right)}^{-1}{X}_i}{\sum {\left(W_i^{-1}+{\widehat{\tau }}^2\right)}^{-1}}.$$

Thus, the likelihood ratio test statistic is

$$-2\log \left(\lambda \right)=\sum _i\frac{2X_i{\overline{X}}^{\ast }-{\overline{X}}^{\ast 2}}{V_i+{\widehat{\tau }}^2}=Z_{RE}^2,$$

showing that this likelihood ratio test is equivalent to RE.

This conversely shows that the current RE calculates heterogeneity under the alternative hypothesis and then implicitly assumes the same heterogeneity under the null hypothesis, which we find to be the cause of the conservative nature of the method.

New RE Approach

We propose a new RE that assumes there is no heterogeneity under the null hypothesis. We employ the same likelihood ratio framework that considers each statistic as a single observation. Because we assume there is no heterogeneity under the null hypothesis, $\mu =0$ and ${\tau }^2=0$ under the null hypothesis. The likelihoods are then

$$\begin{array}{l}{L}_0=\prod _i\frac{1}{\sqrt{2\pi V_i}}\exp \left(-\frac{X_i^2}{2V_i}\right)\\ L_1=\prod _i\frac{1}{\sqrt{2\pi \left(V_i+{\tau }^2\right)}}\exp \left(-\frac{{\left(X_i-\mu \right)}^2}{2\left(V_i+{\tau }^2\right)}\right)\end{array}$$

The maximum likelihood estimates $\widehat{\mu }$ and ${\widehat{\tau }}^2$ can be found by an iterative procedure suggested by Hardy and Thompson.⁴² Specifically, given the current estimate ${\widehat{\mu }}_{\left(n\right)}$ and ${\widehat{\tau }}_{\left(n\right)}^2$, the next estimates are obtained by the formula

$${\widehat{\mu }}_{\left(n+1\right)}=\frac{\sum \frac{X_i}{V_i+{\widehat{\tau }}_{\left(n\right)}^2}}{\sum \frac{1}{V_i+{\widehat{\tau }}_{\left(n\right)}^2}}$$

$${\widehat{\tau }}_{\left(n+1\right)}^2=\frac{\sum \frac{{\left(X_i-{\widehat{\mu }}_{\left(n+1\right)}\right)}^2-V_i}{{\left(V_i+{\widehat{\tau }}_{\left(n\right)}^2\right)}^2}}{\sum \frac{1}{{\left(V_i+{\widehat{\tau }}_{\left(n\right)}^2\right)}^2}}.$$

Once we find the maximum likelihood estimates $\widehat{\mu }$ and ${\widehat{\tau }}^2$, the likelihood ratio test statistic can be built as follows:

$$S_{New}=-2\log \left(\lambda \right)=\sum \log \left(\frac{V_i}{V_i+{\widehat{\tau }}^2}\right)+\sum \frac{X_i^2}{V_i}-\sum \frac{{\left(X_i-\widehat{\mu }\right)}^2}{V_i+{\widehat{\tau }}^2}.$$ (6)

The statistical significance of this statistic can be assessed in various ways. The naive way is to permute the data within each study to obtain the null distribution. A more efficient approach is to sample X_i from $\mathcal{N}\left(0,V_i\right)$ on the basis of the normality assumption. However, for highly significant p values, sampling approaches can be inefficient. An even more efficient approach is to use asymptotic distribution. Because μ is unrestricted and τ² is restricted to be non-negative in the parameter space, μ corresponds to a normal distribution and τ² corresponds to a half of normal distribution in the orthonormal-transformed space. Therefore, the statistic asymptotically follows an equal mixture of 1 degree of freedom (df) χ² distribution and 2 df χ² distribution. See Self and Liang³⁰ for more details. However, the asymptotic result only holds when the number of studies is large. Given only a few studies, the asymptotic p value is overly conservative because of the tail of asymptotic distribution is thicker than that of the true distribution at the genome-wide threshold. This phenomenon is similar to that observed by Han et al.³³ in the context of correcting p values for multiple hypotheses.

Instead, we provide tabulated values. For each possible number of studies from 2 to 50, we generate 10¹⁰ null statistics to construct the p value tables that provide p values with reasonable accuracy up to ${10}^{-8}$. For p values more significant than ${10}^{-8}$, we use the asymptotic p value corrected by the ratio between the asymptotic p value and the true p value estimated at ${10}^{-8}$. Because the ratio keeps decreasing with significance level, using the ratio estimated at ${10}^{-8}$ will make the resulting p value slightly conservative but not anti-conservative. The tabulated values are built on an assumption of equal sample size between studies. Because the discrepancy between the asymptotic p value and the true p value is usually greater for unequal sample size than for equal sample size, using our tabulated values for unequal sample size case will make the resulting p value slightly conservative but not anti-conservative.

Relationship to FE and Cochran's Q Statistic

Our new method has the following relationship to previous methods. The statistic in Equation 4 can be decomposed into two parts,

$$\begin{array}{c}{S}_{New}=\sum \log \left(\frac{V_i}{V_i+{\widehat{\tau }}^2}\right)+\sum \frac{X_i^2}{V_i}-\sum \frac{{\left(X_i-\widehat{\mu }\right)}^2}{V_i+{\widehat{\tau }}^2}\\ =\left\{\sum \frac{X_i^2}{V_i}-\sum \frac{{\left(X_i-{\widehat{\mu }}^{\prime }\right)}^2}{V_i}\right\}+\left\{\sum \log \left(\frac{V_i}{V_i+{\widehat{\tau }}^2}\right)+\sum \frac{{\left(X_i-{\widehat{\mu }}^{\prime }\right)}^2}{V_i}-\sum \frac{{\left(X_i-\widehat{\mu }\right)}^2}{V_i+{\widehat{\tau }}^2}\right\}\\ =S_{\text{FE}}+S_{\text{Het}}\end{array}$$

where ${\widehat{\mu }}^{\prime }$ is the maximum likelihood estimate of μ under the restriction ${\tau }^2=0$, which may be different from $\widehat{\mu }$.

The first part of the statistic, $S_{FE}$, is equal to the FE statistic $Z_{FE}^2$ shown in Equation 5. This is the contribution of the mean effect. The second part of the statistic, $S_{Het}$, is equal to the statistic that we would obtain if we test ${\tau }^2\ne 0$. That is, this is the test statistic testing for heterogeneity. This shows that heterogeneity can actually help to find associations in our method. $S_{FE}$ asymptotically follows a 1 df χ² distribution, and $S_{Het}$ asymptotically follows an equal mixture of zero and 1 df χ².³⁰

$S_{Het}$ tests the same hypothesis as the Cochran's Q statistic.¹⁶ In the usual case, Q should be preferred because $S_{Het}$ requires a large number of studies for an asymptotic result. However, asymptotically they should give the same results.

This decomposability of the statistic can help interpretation because we can assess what proportion of the statistic is due to the mean effect and what proportion is due to the heterogeneity.

Correcting for Confounding

An advantage of the decomposability of the statistic is that one can apply a simple procedure similar to genomic control³¹ to each part to correct for confounding. Because the first part, $S_{FE}$, is exactly $Z_{FE}^2$, applying genomic control is straightforward. For the second part, $S_{Het}$, one can apply genomic control by assessing the median value under the restriction $S_{Het}>0$ and then comparing it to the expected value under the null hypothesis. We also provide the tabulated null median values of $S_{Het}$ for various numbers of studies.

Given the inflation factors ${\lambda }_{FE}$ and ${\lambda }_{Het}$ calculated for the first and the second parts separately, the corrected statistic will be

$$S_{New}^{\prime }=S_{FE}/{\lambda }_{FE}+S_{Het}/{\lambda }_{Het}.$$

Interpretation and Prioritization

In the usual meta-analysis where one collects similar studies and expects the common effect of the variant, the results found by FE should be the top priority, but the results found by our method can also suggest interesting regions. As suggested by previous studies,^18,22 an association showing large heterogeneity requires careful investigation of the cause of heterogeneity. If the heterogeneity is caused by the between-study difference in the underlying pathways of disease, a correct identification of the cause of heterogeneity might help researchers to understand the disease.

Note that the effect-size estimate and its confidence interval in our new RE remain the same as those in the current RE. This is because we changed the assumption only under the null hypothesis, whereas estimating effect size and its confidence interval can be thought of as happening under the alternative hypothesis. Note that an extremely wide confidence interval might not always correspond to a statistically nonsignificant result in our framework.

Simulation Framework

In the Results, we use the following simulation approach. Under the assumption of a minor allele frequency, an odds ratio, and the number of individuals of $N^{+}/2$ cases and $N^{-}/2$ controls, a straightforward simulation approach is to sample $N^{+}$ alleles for cases and $N^{-}$ alleles for controls according to the probabilities given in Equations 1 and 2. However, because we perform extensive simulations in which we assume thousands of individuals, we use an approximation approach that samples the minor-allele count from a normal distribution and rounds it to the nearest integer.

Results

Motivating Observation: RE Never Achieves Higher Statistical Significance than FE in Practice

We first describe our motivating observation that the current RE approach never achieves higher statistical significance than the FE approach in practice. In the Material and Methods, we have already analytically shown that if the sample size is equal between studies, the p value of RE ($p_{RE}$) cannot be more significant than the p value of FE ($p_{FE}$). Therefore, our interest is in the situation in which the sample size is unequal.

We assume five independent studies with unequal sample sizes of 400, 800, 1200, 1600, and 2000. Through all experiments, the sample size refers to the combined number of cases and controls in a balanced case-control study, and a population minor-allele frequency of 0.3 is assumed. Note that the specific values of the parameters are not the major factor affecting the results. For example, if we increase the sample size and decrease the minor-allele frequency or the assumed effect size, we will have the similar results (data not shown).

Our goal is to simulate every possible situation with a large number of random simulations to examine in which situation RE gives more significant results than FE. Because FE is optimal if there is no heterogeneity, we assume heterogeneity and randomly sample odds ratios of the studies from a probability distribution. We assume a mean odds ratio of $\gamma =1.1$ and sample the log odds ratio of each study from $\mathcal{N}\left(\log \left(\gamma \right),\log {\left(\gamma \right)}^2\right)$. This is large heterogeneity; with a high chance of $\Phi \left(-1.0\right)\approx 15.9$, the direction of the effect will even change.

On the basis of the sampled odds ratios, we sample the cases and controls for each study. Then we calculate $p_{FE}$ and $p_{RE}$ by using the inverse-variance weighted-effect-size approach. In calculating $p_{RE}$, we estimate ${\widehat{\tau }}^2$ by the method of moments of DerSimonian and Laird.¹⁶ If at least one of $p_{FE}$ and $p_{RE}$ is significant ($p\le 0.05$), we accept the study. Otherwise, we repeat the procedure. We construct one million sets of meta-analyses.

Figure 1 shows that our one million trials cover a variety of situations. Figure 1A shows that the p values ($p_{FE}$) are distributed in a wide range of significance levels covering the level above the genome-wide threshold. Figure 1B shows the distribution of the I² statistic, which is a metric of the amount of heterogeneity.¹⁷ Except for the peak at the zero, I² is distributed evenly from low to high. Figure 1C shows the distribution of the correlation between the sample size and the observed effect size. Because RE assigns a greater weight to smaller studies, it will be favorable to RE if smaller studies show larger effect sizes.⁵ Figure 1C shows that in half of the simulations, the correlation is negative, and therefore the situation is favorable to RE.

Figure 1.

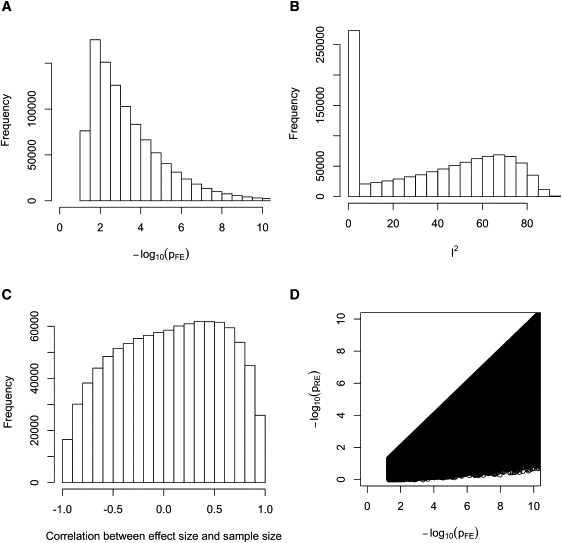
Our One Million Trial Simulations Comparing p Values of FE and RE

We assume five studies of sample sizes of 400, 800, 1200, 1600, and 2000. (A), (B), and (C) show that our simulations cover a wide range of p values ($p_{FE}$), heterogeneity (I²), and correlations between the effect size and sample size, respectively. (D) shows that RE never gives a more significant p value than FE in our simulations.

Table 2 shows that RE gives a more conservative p value than FE in 75% of trials and that it gives an equally significant p value in 25% of trials. However, surprisingly, in none of the trials does RE give a more significant p value than FE (Figure 1D). That is, we observe an extreme phenomenon that RE never achieves higher statistical significance than FE in our extensive random simulations.

Table 2.

Comparison of p Values of FE and RE in One Million Random Simulations

${\mathbf{p}}_{\mathbf{F}\mathbf{E}}\mathbf{<}{\mathbf{p}}_{\mathbf{R}\mathbf{E}}$	${\mathbf{p}}_{\mathbf{F}\mathbf{E}}\mathbf{=}{\mathbf{p}}_{\mathbf{R}\mathbf{E}}$	${\mathbf{p}}_{\mathbf{F}\mathbf{E}}\mathbf{>}{\mathbf{p}}_{\mathbf{R}\mathbf{E}}$
747,443	252,557	0

Our simulations are designed to explore many different situations, such as differing p value levels or heterogeneity levels. We assume five studies of sample sizes of 400, 800, 1200, 1600, and 2000.

We can explain this phenomenon at the statistics level. In order to obtain $p_{RE}<p_{FE}$, smaller studies must show larger effect sizes so that RE can re-weight the studies. For the weights to drastically change in such a way, the estimated between-study variance ${\widehat{\tau }}^2$ has to be large. However, if ${\widehat{\tau }}^2$ is large, the denominator of $Z_{RE}$ in Equation 4 also increases, diminishing the statistical significance. It seems that the significance-decreasing effect of the additional variance (${\widehat{\tau }}^2$) is always greater than the significance-increasing effect of re-weighting in practice.

This result suggests that the current RE might not be suitable for discovering candidate associations in GWAS meta-analysis, indicating the need for a new method.

False-Positive Rate

At threshold $\alpha =0.05$

We examine the false-positive rate of FE, RE, and the new RE method (new RE). We assume the null hypothesis of no associations and assume that there is no confounding. Because the effect sizes are all exactly zero, there is no heterogeneity. We construct five studies with an equal sample size of 1,000 and calculate the meta-analysis p value. We repeat this 100,000 times and estimate the false-positive rate as the proportion of the repeats whose p value is $\le 0.05$. We also differ the number of studies to 3, 10, and 20 studies. When we assume unequal sample sizes, we use evenly spaced values from 0 to 2000, such as 100, 200, …, 2000 for 20 studies. For new RE, we use the tabulated values to assess p values.

Table 3 shows that the false-positive rate of FE is constantly accurate regardless of the number of studies. RE is conservative and has a false-positive rate smaller than 0.05. This is because the between-study variance ${\widehat{\tau }}^2$ is often estimated as non-zero because of the stochastic nature of the sampling. As the number of studies increases, the conservative nature is reduced because more studies provide accurate information that the true τ² is zero. New RE shows accurate false-positive rates. New RE is slightly conservative when the sample size is unequal because, as explained in the Material and Methods, the tabulated values are constructed under an assumption of equal sample size. However, the false-positive rate is very close to the desired value even in that case.

Table 3.

False-Positive Rate of FE, RE, and the New RE at Threshold α = 0.05

# Studies	Sample Size	FE	RE	New RE
3	equal	0.0506	0.0381	0.0501
3	unequal	0.0504	0.0368	0.0488
5	equal	0.0493	0.0370	0.0496
5	unequal	0.0495	0.0364	0.0490
10	equal	0.0504	0.0394	0.0503
10	unequal	0.0495	0.0375	0.0484
20	equal	0.0499	0.0406	0.0497
20	unequal	0.0496	0.0395	0.0485

A sample size of 1000 is assumed when sample sizes are equal. For unequal sample sizes, we use evenly spaced values such as 100, 200, …, 2000 for 20 studies.

At More Stringent Thresholds

It is often of interest to examine the false-positive rate at a more stringent threshold close to the genome-wide threshold. Assuming the same settings for five studies, we simulate 100 million meta-analyses under the null hypothesis. With this large number of simulations, we can estimate the false-positive rate with reasonable accuracy for up to a threshold of approximately ${10}^{-6}$.

Table 4 shows that, at all thresholds that we tested, the false-positive rates of both FE and new RE are accurately controlled. On the other hand, RE becomes more conservative as the threshold becomes more significant.

Table 4.

False-Positive Rate of FE, RE, and the New RE at Thresholds of Increasing Significance

Threshold α	FE	RE	New RE
0.05	4.98 × 10−2 (1.00)	3.75 × 10−2 (0.75)	4.98 × 10−2 (1.00)
1 × 10−2	9.94 × 10−3 (0.99)	7.03 × 10−3 (0.70)	9.93 × 10−3 (0.99)
1 × 10−3	9.90 × 10−4 (0.99)	6.67 × 10−4 (0.67)	9.88 × 10−4 (0.99)
1 × 10−4	9.78 × 10−5 (0.98)	6.36 × 10−5 (0.64)	9.80 × 10−5 (0.98)
1 × 10−5	1.03 × 10−5 (1.03)	6.65 × 10−6 (0.67)	1.02 × 10−5 (1.02)
1 × 10−6	9.20 × 10−7 (0.92)	5.70 × 10−7 (0.57)	8.90 × 10−7 (0.89)

The ratio between the false-positive rate and the threshold α is shown in the parentheses. The estimates are obtained from 100 million null panels. Five studies of equal sample size 1000 are assumed.

Genome-wide Simulations

In this genome-wide simulation, we examined whether each of the meta-analysis methods shows a noninflated QQ plot under the null hypothesis. We simulated a GWAS meta-analysis of seven studies by using the Wellcome Trust Case Control Consortium (WTCCC) data.⁴³ We used the seven case groups of seven diseases as our cases of seven studies. Then we evenly divided the two groups of controls, 58C and NBS, one group at a time, into seven subgroups and used them as our controls. We removed all SNPs that are significant ($p<5\text{×}{10}^{-7}$) either in the original WTCCC study or in our simulated studies. Thus, most of the remaining SNPs should have been null. We also removed the SNPs with no rsIDs, SNPs filtered by WTCCC QC, and the chromosome 6 SNPs that include the major histocompatibility complex region. This resulted in 364,035 SNPs, which is still large enough to allow an examination of the characteristics of the methods.

The WTCCC results⁴³ and previous studies³² show that there can be a small amount of cryptic relatedness in the data of WTCCC. The genomic control factor of WTCCC is slightly more than 1.0, and the QQ plot of each disease shows a slight inflation at the tail. We were interested in whether this small confounding affects each method and by how much.

Figure 2 shows the QQ plots and the genomic control factors. The QQ plot of FE (Figure 2B) is very similar to the QQ plot of the single study (Figure 2A), showing that FE is not sensitive to the confounding. The QQ plot of RE (Figure 2C) looks completely null. The genomic control factor (0.86) is below 1.0, showing that RE is conservative. The QQ plot of new RE (Figure 2D) is more inflated than that of the single study or other methods. This shows that our method is more sensitive to the small confounding in the dataset. To correct for this, we calculate the genomic control factors for the mean-effect part of the statistic ($S_{FE}$) and the heterogeneity part of the statistic ($S_{Het}$) separately; these values are 1.04 and 1.11, respectively. After we correct the calculations with these factors, the inflation is reduced (Figure 2E). However, our method is still more inflated than other methods, suggesting that a more sophisticated method can be developed for a further correction.

Figure 2.

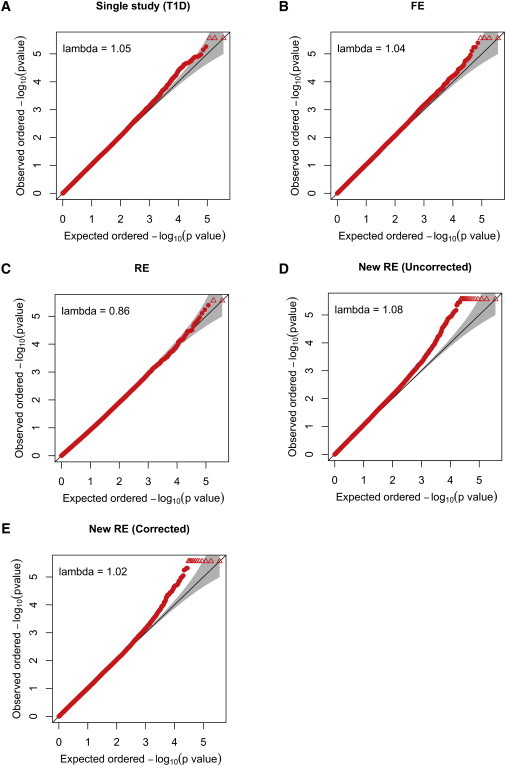
QQ Plot of Various Methods in the Simulated GWAS Meta-Analysis Involving the WTCCC Data

Lambda denotes the genomic control³¹ inflation factor.

Power

We compared the power of FE, RE, and new RE. We used the similar simulation settings of the five studies of equal sample size of 1,000. We constructed 10,000 sets to estimate the power as the proportion of the sets whose p value exceeds a genome-wide threshold ${10}^{-7}$.

We first assumed that the variability in effect size induced by between-study heterogeneity follows a normal distribution.^26,41 Starting from no heterogeneity, we gradually increased the between-study variance and examined how power changes. Specifically, given the mean odds ratio γ, we set the standard deviation of the effect size to be $k\log \left(\gamma \right)$, where we change k from 0 to 1. We used $\gamma =1.3$. We also simulated different settings. We assumed unequal sample sizes and assumed ten studies with an odds ratio of 1.2. When assuming unequal sample sizes, we used the sample size of 400, 800, …, 2000 for five studies and 200, 400, …, 2000 for ten studies.

Figure 3 shows that, when there is no between-study heterogeneity, FE is the most powerful. As the between-study heterogeneity increases, the power of FE drops. The power of RE is always the lowest among the three methods and drops with the amount of heterogeneity. The power of new RE is slightly lower than FE when no heterogeneity exists. As the between-study heterogeneity increases, new RE becomes the most powerful. New RE starts to outperform FE at a level of moderate heterogeneity, between $k=0.3$ and $k=0.4$. The relative performance between methods is the same for all four settings.

Figure 3.

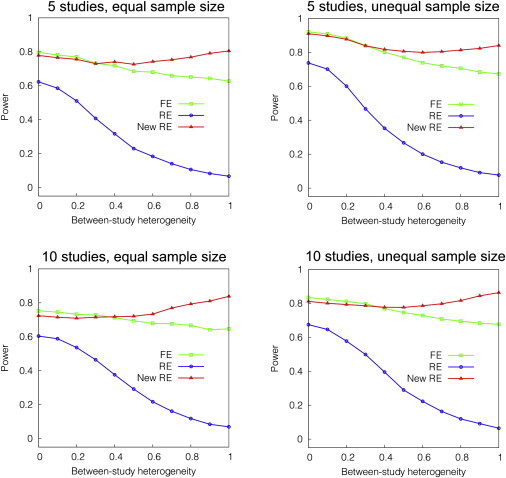
Power of FE, RE, and Our New RE Method in a Simulation Varying Between-Study Heterogeneity

We simulate various settings of the number of studies and sample size. The x axis denotes heterogeneity k, where we simulate the standard deviation of the effect size (log odds ratio) to be k times the effect size. We assume the mean odds ratio of 1.3 for five studies and 1.2 for ten studies. When we assume equal sample sizes, we use the sample size of 1000. When we assume unequal sample sizes, we use the sample sizes of 400, 800, …, 2000 for five studies and 200, 400, …, 2000 for ten studies.

Different LD

Although it is usual in the meta-analysis literature to assume the normal variability in the effect size, as in the previous experiment,^26,41 there can be other situations. Here we assume that the actual effect size is the same between studies but that different LD structures induce different virtual effect sizes at the marker. Assuming five studies of equal sample size of 1,000, we varied the correlation coefficient between the causal variant and the marker by the three patterns (cases 1, 2, and 3 in Table 5). We assumed an odds ratio γ = 1.3, 1.5, and 1.7 for cases 1, 2, and 3, respectively.

Table 5.

Correlation Coefficient r between the Causal Variant and the Marker in Three Different Scenarios Simulating Different LD Structures between Studies

	Study 1	Study 2	Study 3	Study 4	Study 5	Note
Case 1	1.0	1.0	1.0	1.0	1.0	no heterogeneity by LD
Case 2	1.0	0.8	0.6	0.4	0.2	heterogeneity by LD
Case 3	1.0	0.8	0.6	−0.2	−0.6	larger heterogeneity by LD

Figure 4 shows that, in case 1 under an assumption of no heterogeneity by LD, FE is the most powerful. In case 2 under an assumption of heterogeneity by LD, our new RE is the most powerful. In case 3, we assumed larger heterogeneity by LD and that the direction of the correlation is opposite in some studies. This situation should be rare, but it is certainly possible. In this case, FE and RE have low power, whereas our new RE has high power.

Figure 4.

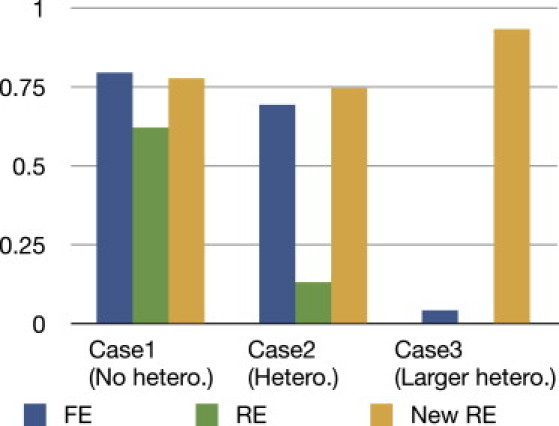
Power of FE, RE, and Our New RE Method when the LD Structures Are Different between Studies

The LD patterns that we assume for each case are described in Table 5. We assume an odds ratio of 1.3, 1.5, and 1.7 for cases 1, 2, and 3, respectively. We assume equal sample sizes of 1000 for five studies.

When Effects Exist in the Subset of Studies

Here we simulate another situation, in which the genetic effect of the variant only exists in a subset of the studies. This can happen when the populations are different between studies and the effect is dependent on the population.^14,15 Assuming five studies of equal sample size of 1,000, we decreased the number of studies having effect, C_E, from 5 to 2. We use an odds ratio γ = 1.3, 1.37, 1.45, and 1.6 for C_E = 5, 4, 3, and 2, respectively. Figure 5 shows that as the number of studies having an effect decreases, the power of FE and RE drops. By contrast, our new RE method achieves high power.

Figure 5.

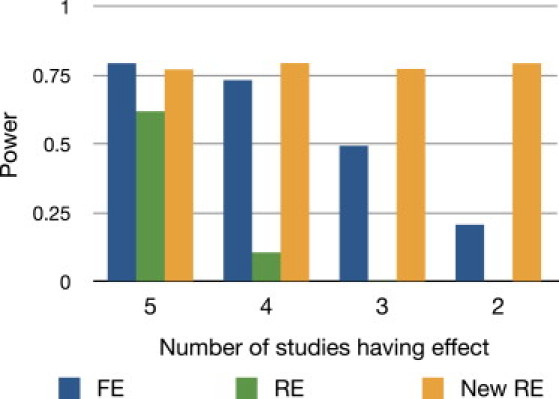
Power of FE, RE, and Our New RE when the Number of Studies Having an Effect Varies

We assume five studies and gradually decrease the number of studies having an effect from five to two. We assume equal sample sizes of 1000. We increase the odds ratio as the number of studies decreases to show the relative performance between methods.

The reason that we increase the odds ratio as the heterogeneity increases in this and previous experiments is to easily compare the power of methods at a moderate power level. Figure S1 shows a different setting where we assume a fixed odds ratio of 1.3, which shows decreasing power as C_E decreases, as it should, for each method.

Application to the Type 2 Diabetes Data

We applied our method to the real data of the meta-analysis of type 2 diabetes by Scott et al.⁹ The meta-analysis consists of three different GWASs, the Finland-United States Investigation on NIDDM Genetics (FUSION),⁹ the Diabetes Genetics Initiative,¹⁰ and the WTCCC.^8,43 Although a more recent meta-analysis of type 2 diabetes exists,^44,45 we used these data because Ioannidis et al.¹⁸ re-analyzed the data to compared FE and RE. In their analysis, Ioannidis et al. emphasize that the results of FE and RE can be critically different when heterogeneity exists, and results showing high heterogeneity should always be further investigated. However, the phenomenon whereby RE never gives more significant p value than FE also persists in their analysis.

Table 6 shows that at two SNPs (rs9300039 and rs8050136) out of ten associated SNPs, our new RE method achieves the highest statistical significance among all three methods. In Figure 6, we sort the SNPs by heterogeneity (I²) and plot the relative gain in statistical significance for both the traditional RE and our new RE compared to FE. This shows that FE achieves the highest statistical significance at low heterogeneity but that, as the heterogeneity increases, our new method achieves higher statistical significance. In contrast, the traditional RE gives the same p value as FE when there is no observed heterogeneity and becomes substantially conservative with heterogeneity. As a result, the traditional RE does not give a more significant p value than FE at any SNPs.

Table 6.

Application of the Three Methods to the Type 2 Diabetes Meta-Analysis Results of Scott et al.⁹

SNP	I2	FE p Value	RE p Value	New RE p Value
rs8050136	76.80	1.30 × 10−12	1.48 × 10−2	6.60 × 10−13
rs9300039	74.95	4.33 × 10−7	1.53 × 10−2	1.83 × 10−7
rs1801282	47.42	1.72 × 10−6	3.41 × 10−4	2.16 × 10−6
rs7754840	46.44	4.09 × 10−11	3.17 × 10−6	5.69 × 10−11
rs13266634	31.60	5.34 × 10−8	8.68 × 10−6	7.23 × 10−8
rs4402960	24.67	8.57 × 10−16	6.48 × 10−12	1.61 × 10−15
rs10811661	0.00	7.76 × 10−15	7.76 × 10−15	1.41 × 10−14
rs1111875	0.00	5.74 × 10−10	5.74 × 10−10	8.63 × 10−10
rs7903146	0.00	1.03 × 10−48	1.03 × 10−48	3.39 × 10−48
rs521911	0.00	6.68 × 10−11	6.68 × 10−11	1.05 × 10−10

The boldface denotes the top p value among three methods.

Figure 6.

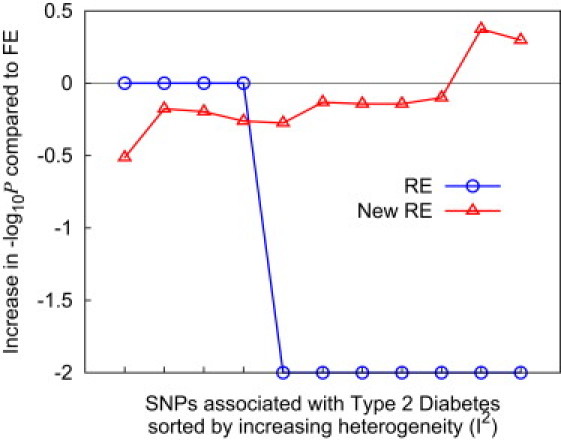
The Performance of RE and Our New RE in the Real Dataset of Type 2 Diabetes

The relative gain in statistical significance relative to FE is plotted for each method. We use the meta-analysis data of Scott et al.⁹

Both of the SNPs at which our new method achieves the highest statistical significance show high heterogeneity. Ioannidis et al.¹⁸ suggest that the heterogeneity at rs9300039 might reflect in part the different tag polymorphisms used in the other two GWASs, suggesting that the virtual effect size varies at the marker because of the use of different markers between studies. Ioannidis et al. also provide an insightful suggestion that rs8050136 (in FTO) might be caused by an unaccounted-for effect of obesity given that it is not significant in the Diabetes Genetics Initiative study, where the body-mass index is matched between cases and controls.¹⁰ This shows that our new RE method can be sensitive to unaccounted-for factors, including confounding.

Note that because in this analysis we used Scott et al.'s report⁹ that provides the odds ratios up to two digits after the decimal point, the actual results will be different from our results. However, our results suffice to show the relative performance between methods.

Application to the Crohn Disease Data

We also apply our method to the data of the recent meta-analysis of Crohn disease of Franke et al.¹² This meta-analysis consists of six different GWASs comprising 6,333 cases and 15,056 controls and even more samples in the replication stage. In this study, 39 associated loci are newly identified, increasing the number of associated loci to 71. We apply our method to 69 loci, excluding rs694739 and rs736289, for which detailed allele counts are missing in that study's Table S3. We use the data of six GWASs but exclude the replication samples.

Table 7 shows that at six loci out of 69, our new method achieves the highest statistical significance among three methods. See Table S1 for the results for all 69 loci. Again, the results show that our new RE can achieve higher statistical significance than FE, whereas the traditional RE does not provide a more significant p value than FE at any SNPs.

Table 7.

Application of the Three Methods to the Crohn Disease Meta-Analysis Results of Franke et al.¹²

SNP	Chromosome	Position	FE p Value	RE p Value	New RE p Value	I2
rs4656940	1	159,096,892	1.05 × 10−6	6.89 × 10−4	6.91 × 10−7	57.01
rs3024505	1	205,006,527	7.03 × 10−9	5.29 × 10−5	5.49 × 10−9	46.49
rs780093	2	27,596,107	1.12 × 10−4	5.95 × 10−2	2.78 × 10−5	61.85
rs17309827	6	3,378,317	5.62 × 10−6	1.00 × 10−4	4.98 × 10−6	22.98
rs17293632	15	65,229,650	6.17 × 10−13	2.11 × 10−6	3.41 × 10−13	52.11
rs151181	16	28,398,018	3.32 × 10−10	3.80 × 10−6	3.08 × 10−10	35.22

The boldface denotes the top p value among three methods. Only the six SNPs at which new RE achieves the top p value are shown in the table. See Table S1 for all 69 SNPs tested.

Discussion

We propose a new RE meta-analysis method that achieves high power when there is heterogeneity. We observe that the phenomenon whereby the traditional RE gives less significant p values than FE under heterogeneity occurs because of its markedly conservative null-hypothesis model, and we relax the conservative assumption. Application to the simulations and real datasets shows that our new method can have utility for discovering associations in GWAS meta-analysis.

In essence, the new method is an attempt to separate hypothesis testing from effect-size estimation. Hypothesis testing and point estimation are both important but distinct subjects in statistics.⁴⁶ The difference is that, in point estimation, the null hypothesis is not considered, and therefore it is conceptually equivalent to considering only the alternative hypothesis. Many of the traditional meta-analytic studies primarily focus on accurate estimation of the effect size, confidence interval, and heterogeneity (τ²), which is the point estimation.^16,35,42,47 The traditional RE approach is a naive extension of this framework to hypothesis testing, but this approach turns out to be conservative in association studies where assuming no heterogeneity is natural under the null hypothsesis.

Our method assumes no heterogeneity under the null hypothesis and assumes heterogeneity under the alternative hypothesis. Higgins et al.³⁹ describe many possible null and alternative hypotheses that are appropriate in various situations in meta-analysis, and our method is one specific combination of a null and an alternative hypothesis among those. Lebrec et al.⁴⁸ considered a similar combination, but our method differs from theirs in several ways. First, our formulation allows correcting for population structure, which is crucial in these studies because the effect of confounding is exaggerated in the new formulation. Second, we use a more accurate approximation of the statistical significance. Our simulation shows that one might lose power by using the asymptotically calculated p values, which can be conservative in comparison to this more accurate approximation (Figure S2).

In the application to the real datasets of type 2 diabetes⁹ and Crohn disease,¹² our method achieves higher statistical significance than FE at some SNPs, whereas the traditional RE does not. However, this occurred only at a relatively small number of SNPs, two SNPs out of ten for type 2 diabetes data and six SNPs out of 69 for Crohn disease data. The main reason for this small number should be the low heterogeneity in the overall data, but one reason might be that we applied our method only to the FE-uncovered associations that were readily available in the literature. The causal SNPs with high heterogeneity might not be discovered by FE and therefore might not be included in our analysis, which can be revealed by an application of our method to the whole-genome data.

In our experiments of both simulated and real datasets, FE always performs better than our method when there is no heterogeneity. However, Figures 3, 4, and 5 show that the relative power gain of FE is not very dramatic. This is in some sense surprising because our method assumes higher degrees of freedom than FE. Figure S2 shows that the performance gap is greater if we use the asymptotic p values. Thus, it seems that our estimation procedure aimed at obtaining more accurate p values is helping our method to have comparable power to FE in this situation.

In this paper, we explored many different scenarios of heterogeneity, including the case in which the effect size actually varies between studies as well as the case in which the observed effect size varies because of the different LD structures. Another scenario in which the observed effect size can vary in spite of unvarying effect size is that involving the “winner's curse,”⁴⁹ which might inflate the observed effect size in the initial stage in the multi-stage design. If the effect of this phenomenon is huge, our method can be useful for detecting such variants, although the interpretation should distinguish such phenomenon from the actual heterogeneity of varying effect sizes.

One important challenge in applying our method is the interpretation. Given the associations with high heterogeneity, a follow-up will always be essential for understanding the cause of heterogeneity and verifying the results. The ability to account for the heterogeneity and carefully investigate the results might allow us to expand the subject of meta-analysis to a broader area. The application of our method can extend beyond the analysis of a single disease to that of multiple diseases with similar etiology,⁴³ analysis of eQTL data independently collected from multiple tissues, or analysis of mixed samples with similar phenotypes but multiple causal pathways, as in the case of mental diseases.⁵⁰

Web Resources

The URL for data presented herein is as follows:

• METASOFT, http://genetics.cs.ucla.edu/meta