Image Correlation Microscopy for Uniform Illumination

Abstract

Image cross-correlation microscopy (ICM) is a technique that quantifies the motion of fluorescent features in an image by measuring the temporal autocorrelation function decay in a time-lapse image sequence. ICM has traditionally employed laser-scanning microscopes because the technique emerged as an extension of laser-based fluorescence correlation spectroscopy (FCS). In this work, we show that image correlation can also be used to measure fluorescence dynamics in uniform illumination or wide-field imaging systems and we call our new approach uniform illumination image correlation microscopy (UI-ICM). Wide-field microscopy is not only a simpler, less expensive imaging modality, but it offers the capability of greater temporal resolution over laser-scanning systems. In traditional laser-scanning ICM, lateral mobility is calculated from the temporal de-correlation of an image, where the characteristic length is the illuminating laser beam width. In wide-field microscopy, the diffusion length is defined by the feature size using the spatial autocorrelation function (SACF). Correlation function decay in time occurs as an object diffuses from its original position. We show that theoretical and simulated comparisons between Gaussian and uniform features indicate the temporal autocorrelation function (TACF) depends strongly on particle size and not particle shape. In this report, we establish the relationships between the SACF feature size, TACF characteristic time and the diffusion coefficient for UI-ICM using analytical, Monte-Carlo and experimental validation with particle tracking algorithms. Additionally, we demonstrate UI-ICM analysis of adhesion molecule domain aggregation and diffusion on the surface of human neutrophils.

INTRODUCTION

Over thirty years ago, fluorescence correlation spectroscopy (FCS) was developed to measure the mobility of fluorescent molecules in solution (Magde et al., 1974). With this technique, fluctuations of a fluorescent signal from a laser beam focus are detected on a photomultiplier tube. These fluctuations provide insight into the dynamics of fluorescent particles in solution. The change in signal is due to temporal variations in the number of fluorescent particles residing within the focal volume. The correlation of these fluctuations in time can be used to calculate diffusion coefficients as well as reaction kinetics (Elson & Magde, 1974, Magde et al., 1974). FCS was later extended to scanning systems where the sample was translated across the beam in either a line or circle (Petersen, 1986). Later yet, a laser scanning confocal microscope was used to create an image analog of FCS (Petersen et al., 1993). This technique, called image correlation spectroscopy (ICS), quantitatively characterized the distribution, density and aggregation of fluorescent domains or features in an image using spatial autocorrelation functions. ICS was further extended to study slow mobility of fluorescent domains in images by analyzing the temporal decay of the correlation function. This analysis was initially called image cross correlation spectroscopy (ICCS), but has recently been referred to as temporal image correlation spectroscopy (TICS) (Kolin & Wiseman, 2007) and is used to study receptor domain diffusion in cell membranes (Srivastava & Petersen, 1998).

The extension of FCS to ICS and TICS enabled study of whole image dynamics using the mathematical foundations of the single laser focus developed for FCS. By continuing to use a Gaussian illumination source, the fundamental characteristic length (e⁻² radius) to calculate the diffusion coefficient in FCS is preserved. Additional extensions and variations have been added to this suite of tools that we will refer to collectively as image correlation microscopy (ICM): notably, spatial image cross-correlation spectroscopy (ICCS) (Petersen et al., 1998) to measure transport and co-localization of two differently labeled molecules, applications in two-photon microscopy (Wiseman et al., 2000), and spatiotemporal image correlation spectroscopy (STICS) (Hebert et al., 2005) to measure both diffusion coefficients and vector velocities of fluorescent domains in cell membranes. All of these tools build on the mathematical foundation of FCS to create an array of options for the biophysical researcher.

To date, the applications of ICM techniques have been primarily limited to laser-scanning microscopes because of its evolution from laser-based FCS. However, there is a recent report that used ICM techniques with brightfield microscopy by blurring images with a Gaussian filter to prepare them for the traditional laser-scanning based ICM analysis (Immerstrand et al., 2007). Additionally, pixel-by-pixel analysis of total internal reflection fluorescence (TIRF) using ICM methods was used to create color maps of receptor dynamics on cell surfaces (Digman et al., 2008), Furthermore, another report investigated ICM using spinning disk confocal microscopy (Sisan et al., 2006). The authors developed a correction factor for low spatial resolution systems where the pixel size is more than two times greater than the effective illumination radius. These publications continue to extend ICM techniques beyond laser-scanning systems, but do not yet include a framework for determining molecular diffusion coefficients.

In this report, we set out to expand ICM to high-resolution uniform illumination or wide-field microscopy with a mathematical framework that does not require image manipulation. Uniform illumination fluorescence microscopy is more common than laser-scanning microscopy because of its simplicity, reduced cost and potential for greater temporal resolution. Application to uniform illumination systems is useful because it provides broader access to ICM analysis. Historically, ICM has been limited to laser-scanning systems primarily for two reasons. First, the observation volume, and thus the characteristic diffusion distance is defined and controlled by the focus of the excitation laser beam. Second, if the beam has a Gaussian profile, there exists a concise closed form solution of the spatial and temporal autocorrelation functions. Here we build on the original correlation spectroscopy literature to extend the mathematical framework of ICM to uniform illumination ICM (UI-ICM). Specifically, we show that the characteristic diffusion distance is weakly dependent on the beam profile in the original FCS analysis. We establish that in the absence of a laser in UI-ICM, the characteristic diffusion length is defined by the size of the feature itself, which can be estimated from the spatial autocorrelation function. We demonstrate these principles with simulated diffusion of both uniform disks and Gaussian particles and thus establish that particle shape is not an important consideration.

Finally, we confirm UI-ICM diffusion measurements of fluorescent beads in thin chambers using particle tracking as an alternative method. As an example application we study the motion and size of receptor domains on the surface of spherical resting human neutrophils. We find that diffusion measurements of L-selectin domains on the cell surface using UI-ICM are nearly identical to values previously obtained using fluorescence recovery after photobleaching (FRAP) (Gaborski et al., 2008).

Another report using spinning disk confocal microscopy investigated the limits of using low spatial resolution and developed a correction factor for when the pixel size is more than two times greater than the effective illumination radius. In our work presented here, the pixel size is just a fraction of the effective illumination radius or characteristic length.

THEORY

Traditional ICM theory has been derived in detail previously (Petersen et al., 1993, Srivastava & Petersen, 1998, Wiseman et al., 2000). Here we present a summary of the results. The spatial intensity fluctuation is defined as the difference between the fluorescence intensity at pixel location (x, y) in the image sampled at time t_o,i(x, y, t_o) and the mean image intensity, 〈i(x,y,t_o)〉.

$${\partial i(x,y,t)|}_{t_0}=i(x,y,t_o)-\langle i(x,y,t_0)\rangle$$ (1)

The corresponding spatiotemporal intensity fluctuation correlation function is

$$r(\xi ,\eta ,\tau )=\frac{\langle \partial i(x,y,t)\rangle \langle \partial i(x+\xi ,y+\eta ,t+\tau )\rangle }{\langle i(x,y,t)\rangle \langle i(x,y,t+\tau )\rangle }$$ (2)

where ξ, η and τ are all lag variables and the angular brackets denote spatial, and not temporal averaging. The spatial autocorrelation function (SACF) of an image recorded at time τ_o is given by

$${r(\xi ,\eta ,\tau )|}_{t_0}=\frac{\langle \partial i(x,y,t_0)\partial i(x+\xi ,y+\eta ,t_0)\rangle }{{\langle i(x,y,t_0)\rangle }^2}$$ (3)

Temporal autocorrelation (TACF) as a function of time lag τ is given by

$$r(0,0,\tau )=\frac{\langle \partial i(x,y,t)\partial i(x,y,t+\tau )\rangle }{\langle i(x,y,t)\rangle \langle i(x,y,t+\tau )\rangle }$$ (4)

where the resulting values between pairs of images with the same time lag τ separating them are averaged.

Gaussian beam subcase

When the imaging is performed with a scanning laser with a Gaussian profile, the SACF is approximated by (Wiseman et al., 2000)

$${r(\xi ,\eta ,0)|}_{t_0}=C_0{e}^{-\frac{{\xi }^2+{\eta }^2}{{\omega }_0^2}}+C_{\mathrm{\infty }}$$ (5)

and the TACF for a sample undergoing two-dimensional diffusion is (Wiseman et al., 2000)

$$r(0,0,\tau )=\frac{C_0}{(1+\frac{\tau }{{\tau }_d})}+C_{\mathrm{\infty }}$$ (6)

where τ_d is is the characteristic diffusion time. Samples undergoing different processes, such as flow, in general have different TACFs. The amplitude and DC offset of the fit to the SACF can be used in many applications such as extracting particle densities (Petersen et al., 1993). The ω_o parameter is the illuminating Gaussian laser's e⁻² radius. In diffusion experiments, this is the characteristic diffusion distance and is related to the characteristic diffusion time and the diffusion coefficient by

$$D=\frac{{\langle {\omega }_0\rangle }^2}{4{\tau }_d}$$ (7)

where the brackets indicate averaging of the ω_o obtained from each image in a time series.

Uniform beam subcase

Different correlation functions can be derived for illumination profiles other than Gaussian, but have increased complexity. An expression for the TACF using a uniform incident beam was derived in the original FCS papers (Elson & Magde, 1974, Magde et al., 1974) and is given by Eq. 4. Elson illustrated that overall behavior of the temporal decay does not strongly depend on the shape of the beam profile ((Elson & Magde, 1974); Figure 3.3).

$$r(0,0,\tau )=\frac{{\tau }_d}{\tau }{e}^{-\frac{2{\tau }_d}{\tau }}\left[I_0\right(2\frac{{\tau }_d}{\tau })+I_2(2\frac{{\tau }_d}{\tau }\left)\right]+2{\displaystyle \sum _{k=0}^{\mathrm{\infty }}}\frac{{(-1)}^k(2+2k)!(k+1)!(b^{k+2})}{{[(2+k)!]}^2{(k!)}^2}$$ (8)

Here, I_n is a modified Bessel function of the n^th order.

In Results and Discussion we explore the difference between the cases of Gaussian and uniform illumination and its effect on the TACF. Considering that in practice the point spread function creates Gaussian-like features, even in uniform illumination, we conclude that the weak dependence on beam shape allows us to overcome the limitation of not using Gaussian illumination. Therefore, the image feature size, which can be estimated from the SACF, is used to relate the characteristic time and diffusion coefficient (Eq. 7).

METHODS

Monte Carlo simulations

Monte Carlo simulations of particle diffusion were developed and run in MATLAB (MathWorks, Natick, MA) using the Optimization and Image Processing toolboxes. The image matrix size was either 200 × 200 pixels. For the studies involving many combinations of particle density and size distribution, the image matrix was set to 64 × 64 so that simulations could be completed within a reasonable amount of time. Simulations used either two-dimensional Gaussian particles or uniform intensity disks. Particle size within a simulation was uniform except when intentionally varied to study the effects of different distributions. The stated size of Gaussian particles refers to the e⁻² radius. Seeding densities was varied between 25 and 500 particles per field and initial particle positions were random.

Fluorescence microscopy

Uniform illumination fluorescence microscopy was performed at room temperature on an inverted Zeiss Axiovert 200m microscope equipped with a 100x 1.4 NA oil objective (Zeiss, Thornwood, NY). Wide field epi-illumination utilized a 100W mercury arc lamp attenuated with a 90% neutral density filter and the appropriate green and red fluorescence filter cubes. Images were recorded on a SensiCam EM cooled CCD camera (Cooke, Romulus, MI). Due to the low excitation power and robust fluorophores used in the neutrophil experiments, photobleaching resulted in just 5–10% reduction in mean and peak fluorescence values during imaging. An attempt to mathematically correct for this photobleaching is performed with a simple exponential function by fitting to the fluorescence decay over time (Song et al., 1995, Kolin et al., 2006). All microscope control, image acquisition and processing were performed with custom MATLAB algorithms.

Particle diffusion experiments

To validate the UI-ICM analysis experimentally, we fabricated thin chambers to measure the lateral mobility of small fluorescent beads. Glass slides and coverslips were prepared by washing with methanol. Glass surfaces were then treated with 1x phosphate buffered saline (PBS) solutions plus 5% fetal bovine serum (FBS). This protein treatment pacified the surface and reduced the likelihood of bead adsorption during experimentation. On the glass slide, two thin parallel tracks of vacuum grease from a syringe were drawn. 10 uL of 1:1000 dilution of 0.93 micron fluorescent beads (Bangs, Fishers, IN) in 1x PBS plus 5% FBS was placed between the two grease tracks. The coverslip was firmly pressed on the grease tracks resulting in a reproducible chamber thickness of approximately 10 um. The two openings were sealed with VALAP (1:1:1 mixture of Vasoline, lanolin and parafin). Wide-field epi-fluorescence time-lapse images were collected every 100ms for 25 seconds using Zeiss Camware software. Images were exported as a TIFF stack for analysis.

Particle tracking algorithms

Individual particle trajectories were extracted and analyzed using a custom built MATLAB routines described elsewhere (Ehrenberg & McGrath, 2005). Briefly, this routine sequentially extracts each particle from the whole image and determines its center position using a two-dimensional Gaussian fit (Cheezum et al., 2001) to an accuracy better than 4 nm. Mean square displacements are then calculated from the trajectories and the slope of a linear fit determines the diffusion coefficient in two dimensions from the equation 〈∂(r)²〉 = 4Dt.

Neutrophil preparation

Two microliters of whole blood obtained via finger stick was diluted into 80 uL Hank's Balanced Salt Solution (HBSS) without Ca²⁺ or Mg²⁺ plus 10 mM HEPES. To visualize adhesion molecules localized to the cell surface, cells were labeled with 3uL (1ug) fluorescent monoclonal antibodies (mAb). Antibodies were labeled with the AlexaFluor 546 monoclonal antibody labeling kit (Molecular Probes, Eugene, OR). LFA-1 was visualized with mouse monoclonal anti-CD11a (HI111, eBioscience, San Diego, CA) and L-selectin with anti-CD62L (DREG-56, eBioscience, San Diego, CA). Cells were labeled at room temperature for fifteen minutes and washed three times for 5 minutes at 170g. Prior to adding the cells to the microscope viewing chamber, cells were re-suspended in HBSS plus 10mM HEPES and 4% fetal bovine serum (FBS) to prevent cell adhesion to the glass cover slip. Experiments were performed with 60 minutes of antibody labeling to minimize receptor internalization during imaging. 100 Images were captured every 250 ms for 25 seconds. Cells were resting on the glass surface, but were free to move as a result of diffusion or convection in the chamber. To account for cell movement, cell position was tracked by using the Gaussian fit to the SACF of each image. The sequence of 50 consecutive images with the smallest cell trajectory was analyzed. If the mean translation per image was more than 50 nm, the data was not further analyzed due to movement artifacts. For control studies of immobile domains, some cells were fixed after fluorescent labeling. These cells were treated with 3.7% paraformaldehyde in HBSS with 10mM HEPES for 15 minutes at room temperature after which they were mixed with a 4% solution of FBS to prevent cross-linking of the cells to the substrate. A subset of these control cells where adhered to the FBS coated coverslip with 1% fresh paraformaldehyde.

RESULTS AND DISCUSSION

Particle simulations

One challenge in extending ICM to uniform illumination from laser-scanning microscopy (LSM) is determining the characteristic length that a particle must diffuse for significant decay of the temporal autocorrelation function (TACF). In LSM, the characteristic length used to calculate the diffusion coefficient is the 1/e² width of the focused laser beam (Eq. 5). For uniform illumination, there is no laser focus and thus the characteristic length is a function of the particle size. As shown previously in the original FCS literature (Elson & Magde, 1974), there is a concise close form solution of the TACF for Gaussian illumination of point particles. The TACF for a uniform intensity beam (Eq. 8), while more complex, was shown to be not significantly different (Elson & Magde, 1974). We reproduced Figure 3.3 from Elson and Magde using Eq. 6 and Eq. 8 to represent the TACF for Gaussian and uniform intensity beam illumination of point particles (Figure 1A).

Figure 1.

Decay in the temporal autocorrelation function (TACF) is not significantly impacted by particle shape. (A) The correlation decay for random diffusion of Gaussian intensity particles given by Eq. 6 (solid line) shows strong agreement with the random diffusion of uniform intensity disks given by Eq. 8 (circles). (B) Simulated random diffusion of particles displayed as either Gaussian (left) or uniform (right) intensity. 50 particles with a radius of 10 pixels were seeded over a 200 × 200 image matrix. (C) Correlation decay for simulated diffusing points represented as Gaussian particles (solid line) is very similar to to the same points represented as uniform disks (circles). (D) Diffusion length scales calculated from characteristic correlation decay correspond to the appropriate particle size for both Gaussian and uniform intensity. Three simulations were run for each type of particle at each particle size.

To test the similarity of the TACF for Gaussian particles and uniform disks, we created a random distribution of particles in a MATLAB simulation (Figure 1B). We represented the particle positions with either a 10 pixel 1/e² Gaussian radius or a 10-pixel uniform intensity radius. For each particle shape, we simulated random walks and calculated the TACF. As shown in Figure 1c, the TACF is nearly indistinguishable for the two types of shapes. Furthermore, the TACF decay is well approximated by Eq. 6. Consequently, we will use Eq. 6 to calculate time for the TACF decay. We further checked this approach by simulating images populated by particles of various sizes. Using Eq. 6 to calculate the decay time for the TACF, we could calculate the characteristic length using Eq. 7 and the known diffusion coefficient in the simulations. For both Gaussian and uniform particles, this procedure produced the known particle size as the characteristic length (Figure 1D). Any slight deviation was due to overlapping of two or more particles during the simulated random walk or particles on the edge of the image matrix. In practice, objects in a wide-field microscope are subject to blurring by the optical point spread function, making them well approximated by a Gaussian. These results confirm that the characteristic time of the TACF in UI-ICM is a function of the object diffusing a distance equivalent to its size.

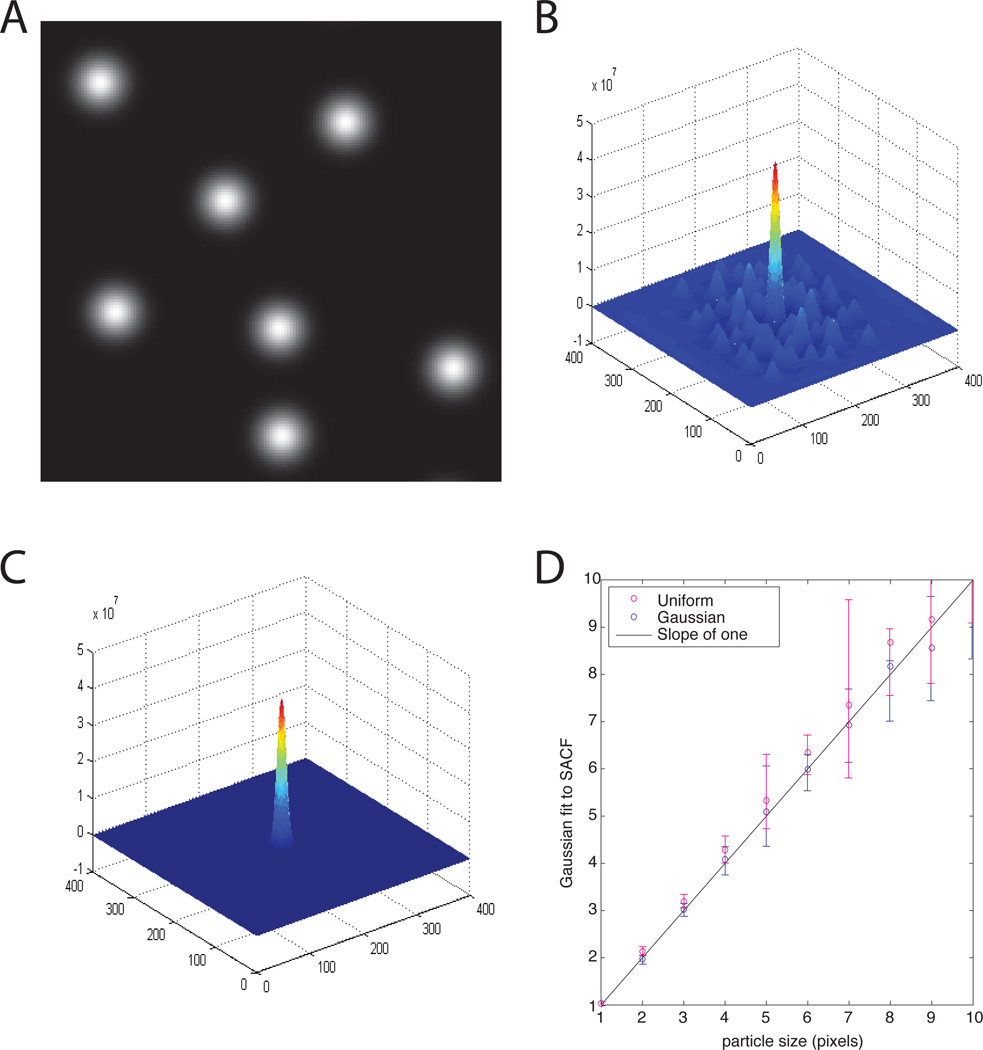
Because the size of diffusion particles is generally not known a priori, we questioned if estimating the size can be done using the SACF. To test this approach we created a random arrangement of particles in an image matrix using MATLAB (Figure 2A). We then calculated the spatial autocorrelation function (SACF) of each image and used a two-dimensional Gaussian fit to extract the 1/e² radius giving the characteristic size in the image (Figures 2B and 2C). Images were created with particles ranging in radius from 1 to 10 pixels of either Gaussian or uniform illumination (three images of each). We found an exact correspondence between seeded particle size and the size extracted from the SACF (Figure 2D). This confirms that the SACF can be used to calculate the characteristic diffusion length for uniform illumination applications of ICM, when the image feature size is not known a priori. The procedure for UI-ICM is now clear: 1) measure size from the SACF, 2) measure the TACF, and 3) determine the diffusion coefficient with Eq. 7. In the following we apply this procedure to more complex simulations as well as bead and cellular studies.

Figure 2.

Characteristic diffusion length is calculated from the Spatial Autocorrelation Function (SACF). (A) Gaussian illumination particles are randomly positioned on a 200 × 200 image matrix in MATLAB. (B) SACF is calculated for the simulated particles from (A). (C) Gaussian fit to the SACF. (D) Both simulated Gaussian and uniform intensity particles of various sizes are accurately measured with the Gaussian fit to SACF. Any deviation from the straight line was due to random positioning of particles, in which case some overlapped or were on the edge of the image matrix. Three simulations were run for each type of particle at each pixel size.

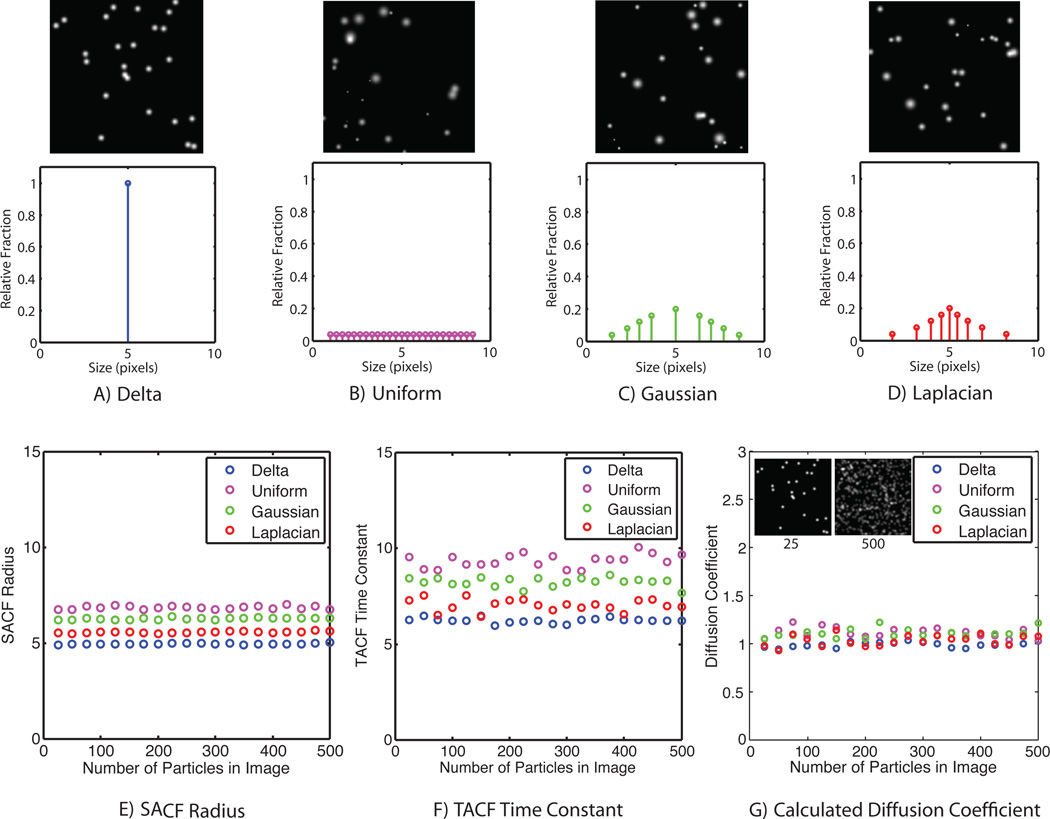
To test the robustness of UI-ICM to more complex particle distributions, we created simulations that had four distributions of Gaussian particles with a mean radius of 5 pixels: monodisperse (Figure 3A), uniform from 1–10 pixels (Figure 3B), Gaussian (Figure 3C), and Laplacian (Figure 3D). Regardless of particle size, each particle was given the same step size in the random walk, 1 pixel per unit time. Because larger particles occupy a greater fraction of an image, they tend to bias size extraction using the SACF; this is most evident for the uniform particle distribution (Figure 3E). Similarly larger particles, while moving the same step size as smaller particles per iteration, are slower to move out of their original positions and thus bias the population’s TACF toward a longer characteristic diffusion time (Figure 3F). Despite the effects of non-uniform size distribution, the diffusion coefficient calculated from population SACF’s and TACF’s were accurate for each particle distribution (Figure 3G). Additionally, to test for anomalous effects of particle density, where particles in the image may overlap, these simulations were run with between 25 and 500 particles on a 64 × 64 image matrix. This resulted in a crowded and overlapping picture at higher particle densities. Overlapping particles were treated additively without thresholding. We found there was no effect of particle density on the length and time extractions.

Figure 3.

Diffusion coefficients can be accurately predicted by UI-ICM even for complex particle size distributions. Diffusion was simulated for all particles as a two-dimensional random walk of one pixel per unit time on a 64 × 64 pixel image matrix. Simulations were run with four different distributions of Gaussian particle sizes, each with a 5 pixel mean radius: (A) Monodisperse particle size, (B) Uniform distribution, (C) Gaussian distribution, and (D) Laplacian distribution. Representative images show 50 particles randomly distributed. (E) SACF was calculated for each distribution with between 25 and 500 Gaussian particles randomly positioned across the image matrix. The maximum density resulted in many overlapping particles. Overlapping particle intensity was additive and was not thresholded; still, increasing the density of particles did not change the SACF radius. Although all distributions had the same mean radius, SACF radius is weighted more heavily by larger particles in the field (F) TACF was calculated for each distribution with between 25 and 500 Gaussian particles. Like the SACF, the TACF time constant was independent of particle density for each distribution, but biased toward larger particles. (G) Diffusion coefficients were calculated for each distribution at varying particle densities based on Eq. 8. The calculated diffusion coefficient for all distributions converged to 1 pixel per unit time for all densities and distributions, matching the simulation input. Insets show representative samples of 25 and 500 Gaussian particles of uniform size distribution.

Fluorescent bead experiments

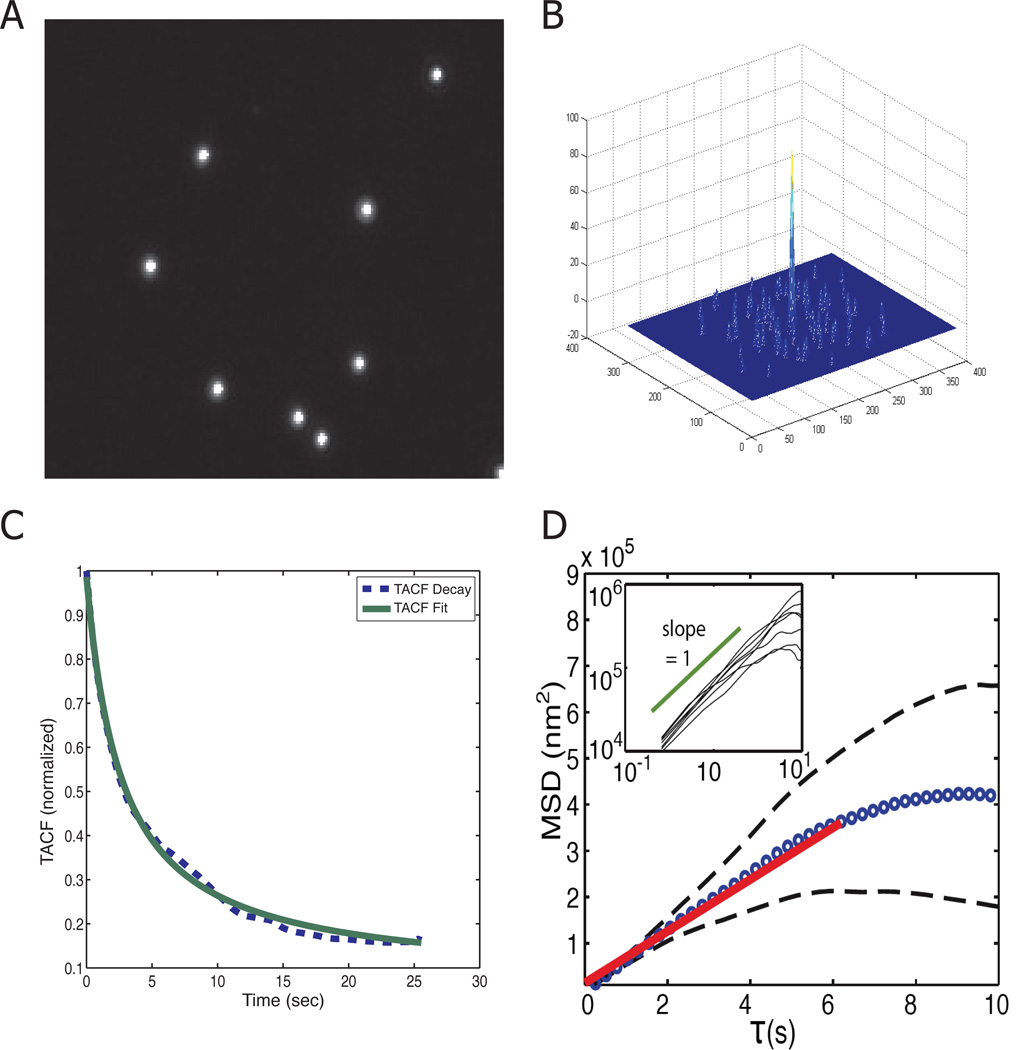
After conducting proof of principle experiments with MATLAB simulations of particle diffusion, we validated UI-ICM with diffusion measurements of fluorescent beads in solution. We imaged 0.93 micron fluorescent beads in 10 micron thick glass chambers every 100 ms for 25 seconds (Figure 4A). Although the physical bead size was provided by the manufacturer, we used the SACF to extract the characteristic diffusion length in the images (Figure 4B). We measured the SACF for each image in the time-lapse sequence and then averaged the results to determine a mean characteristic length for analysis. We then determined the TACF and fit the decay to Eq. 6 to extract the characteristic diffusion time (Figure 4C). Using Eq. 7, we calculated the mean diffusion coefficient of two experiments to be 1.2 × 10⁻¹⁰ cm²/sec. The fluorescent bead trajectories in these two movies were then monitored using an established particle tracking method (Ehrenberg & McGrath, 2005). In this method, the individual trajectories of each of 41 particles were tracked and used to calculate mean squared displacements. The mean squared displacement (MSD) at different times was calculated and is plotted as blue circles in Figure 4D. A linear fit to the early data produces a diffusion coefficient of 1.4 × 10⁻¹⁰ cm²/sec. The inset in the figure shows that the individual trajectories have a slope of 1 on a log-log plot, signifying random diffusion. The similarity in measurement of the diffusion coefficient using an entirely different approach validates UI-ICM as a method for determining particle diffusion coefficients.

Figure 4.

Fluorescent bead diffusion measurement with UI-ICM and validation with a particle tracking algorithm. 0.93 um fluorescent beads in 1x PBS were assembled into a 10 um thick chamber and observed at room temperature in an inverted fluorescence microscope. Images were taken every 100 ms for 25 seconds. (A) A characteristic static image of fluorescent beads in a 10 µm thick chamber. (B) SACF for the fluorescent beads. (C) TACF is plotted over 25 seconds. The data (blue dashed line) is well fit by Eq. 6 (green solid line). Using the characteristic time from the TACF decay and the size from SACF, the diffusion coefficient is calculated as 1.2 × 10⁻¹⁰ cm²/sec using UI-ICM. (D) The same fluorescent beads were tracked with a particle tracking algorithm and the average mean squared displacement (MSD) for 41 particles in two time-lapse movies are shown in blue circles. Black dashed curves indicate one standard deviation above and below the mean. A linear fit to the early time data shown in bold red yields D = 1.4 × 10⁻¹⁰ cm²/sec. The inset shows a log-log plot of a random sub-sample of the data compared to the ideal diffusive slope of 1.

Application to human neutrophils

An interesting and important application of ICM is the measurement of cellular receptor mobility. Outside of the correlation spectroscopy literature, mobility measurements are often performed with fluorescence recovery after photobleaching (FRAP) and single particle tracking (SPT) providing population and individual receptor mobility measurements, respectively. UI-ICM is similar to SPT in that is measures mobility of features on a cell surface, but is simpler in that it measures an ensemble average of fluorescent domain mobility in an image. Leukocytes are a particularly interesting application because there exists mobility data based both on FRAP and SPT measurements (Gaborski et al., 2008, Kucik et al., 1996, Cairo et al., 2006). Additionally, our recent observation of receptor organization into dynamic domains on the surface makes UI-ICM analysis well suited for this task (Gaborski et al., 2008).

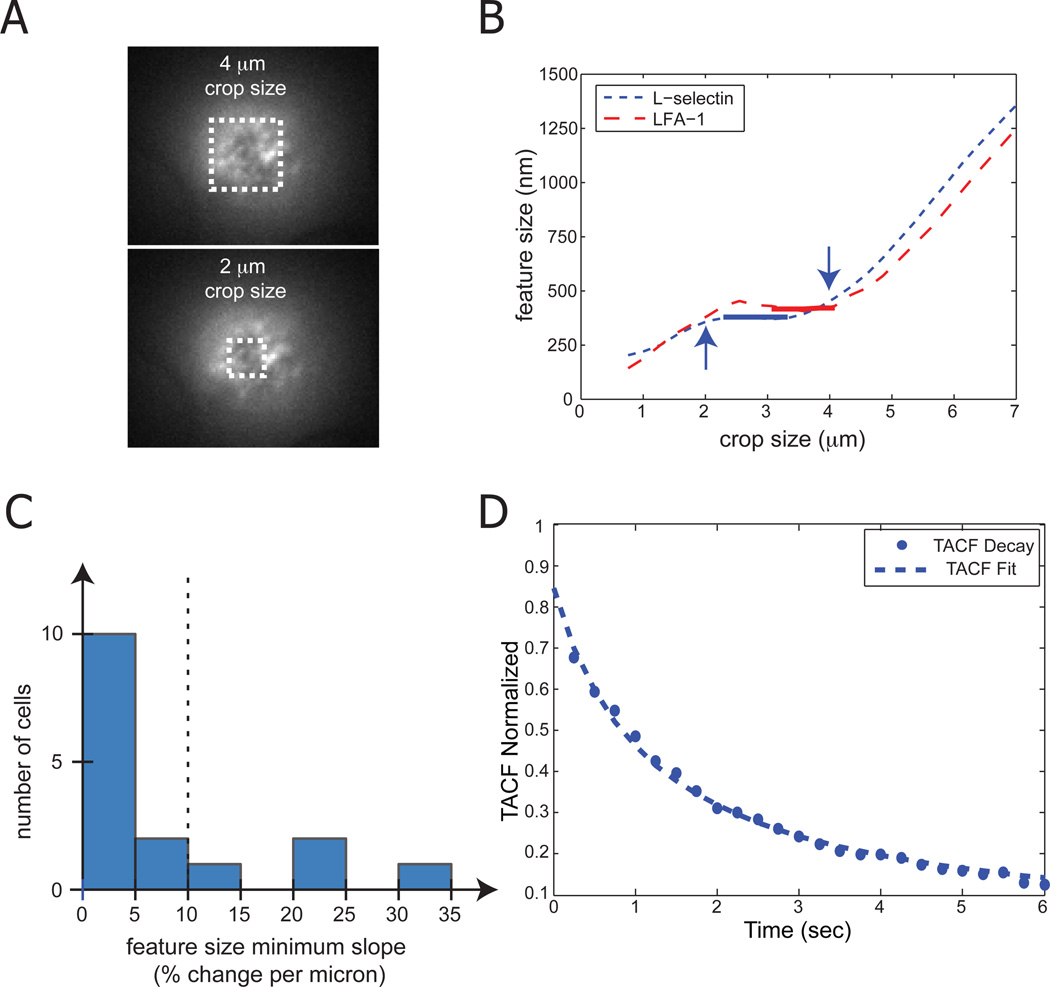
The application of UI-ICM to cell types that grow on planar surfaces is straight forward. Spherical cells, however, create a challenge in that their membranes are not planar. With wide-field epi-fluorescence, we typically find the focal thickness to be two or more microns with a 63× or 100× objective (Gaborski et al., 2008), capturing a significant slice of the bottom of a spherical cell. Here we labeled human neutrophils with fluorescent monoclonal antibodies for either L-selectin or LFA-1. Both of these molecules are important for adhesion to endothelium during inflammation, and appear as lightly punctate domains when labeled with fluorescent antibodies. We prepared coverslips with fetal bovine serum to reduce cell interactions with the coverglass and imaged cells by focusing just above the coverglass to capture the bottom quarter of the cell. We first show that it is important to select an appropriate region of interest by cropping the image (Figure 5A). When the crop size is too small, size extraction from the SACF is dominated by noise. As the crop size grows, the fluorescent features or domains in the cell membrane appropriately dominate the SACF, however as the crop size becomes too large, the cell itself becomes the primary feature in the SACF. Ideally, there is a range of crop sizes where the size extraction is not sensitive to the specific crop size (thick lines; Figure 5B). For neutrophils with a diameter of 8–9 microns, we generally find this crop range to be a 2 to 4 micron square. To select a single value for the SACF and TACF, we found a one-micron range with the minimum slope for each cell and used the mean value over this range. If the slope was more than 10% everywhere, then the cell was not further analyzed (Figure 5C). Of 24 cells samples, 18 met the criterion for inclusion. The excluded cells were either activating, changing shape, or moving in the cell chamber. Using the mean crop value, the TACF decay was measured and fit with Eq. 6 for each cell (Figure 5D). Using the characteristic time decay from Eq. 6 and the characteristic length from the SACF, a diffusion coefficient can be calculated.

Figure 5.

UI-ICM application to a spherical cell. To analyze receptor domain dynamics on the surface of human neutrophils (8–9 um diameter), it is necessary to analyze only the dynamic region of the image. Cells resting on the coverslip have a ‘footprint’ diameter of approximately 4 um using our non-confocal epi-fluorescence microscope. (A) Gaussian fit to the SACF defines the centroid of the cell. Crop sizes centered around the centroid are varied to determine the ideal region of interest (ROI). Black dash boxes show the size of a 2 and 4 um crop size (B) Feature size extraction from the SACF for two cells labeled for L-selectin or LFA-1 adhesion molecules is dependent on the crop size. Feature sizes from small crop sizes (< 2 um) are primarily a function of noise in the image. In most cells, there is a plateau region (2–4 um) where the feature size in not dependent on crop size. At larger crop sizes (> 4 um), the cell itself is the primary feature and significantly affects feature size extraction. For each cell, the minimum slope (thick line) over a one micron crop size is found. The mean SACF width in this region is used to determine the feature size. (C) Histogram of minimum slopes. Cells that do not have a plateau with a minimum slope less than 10% are not further analyzed. (D) The TACF for a representative neutrophil is measured over six seconds. The data (circles) is well fit by Eq. 6 (dashed line).

To measure the diffusion coefficients of neutrophil adhesion molecules, we prepared glass cover slips with FBS so that neutrophils did not adhere to the surface to minimize receptor interactions with the glass (Supplemental Movie S1). Cell wobble and movement during imaging contributes to TACF decay and apparent diffusion. To measure the degree of this baseline TACF decay, it was necessary to measure the TACF of immobile domains on the neutrophil surface. After fluorescently labeling cells, some were fixed with 3.7% paraformaldehyde and then washed to lock receptors and domains in place on the cell surface. This procedure enabled cell wobble above the cover slip, without domain or receptor diffusion (Supplemental Movie S2). We also tracked the movement of the cell centroid using the SACF Gaussian fit. We found that on average, most fixed cells translated less than 50 nm per image (250 ms) and had a consistent TACF decay that correlated to an apparent diffusion coefficient of 0.4 × 10⁻¹⁰ cm²/sec (n=8). Unfixed cells labeled for LFA-1 typically had measured diffusion coefficients at least four times greater than fixed cells with immobile domains. Since the two diffusive processes (cell wobble and domain movement) are independent, they are additive and the cell wobble component can be subtracted from the total measurement to obtain domain mobility. To test for any experimental system dynamics, we further adhered some of the fixed cells to the glass surface with 1% fresh paraformaldehyde and measured a diffusion coefficient more than one order of magnitude lower (Supplemental Movie S3). This confirmed that mobility measurements are attributable entirely to cell dynamics and not the experimental system. After correcting for inherent cell wobble, we find the diffusion coefficient of LFA-1 domains on human neutrophils to be 1.2 × 10⁻¹⁰ cm²/sec (n=16) when labeled with monoclonal antibodies and measured at room temperature. We recently reported that the diffusion coefficient of LFA-1 when measured with FRAP under the same conditions to be 1.3 × 10⁻¹⁰ cm²/sec (n=16) (Gaborski et al., 2008). In many cases, FRAP measurements are a composition of rapid molecular recovery as well as slower domain movement into the bleach band. ICM, unlike FCS and FRAP, cannot measure rapid molecular diffusion and is more suited towards measuring the movement of slower protein aggregates and domains within cell membranes (Srivastava & Petersen, 1998, Bates et al., 2006). For human neutrophils the agreement between FRAP and ICM suggests domain diffusion is a significant component of the FRAP measurement and adhesion molecule mobility outside of slow moving domains may be limited.

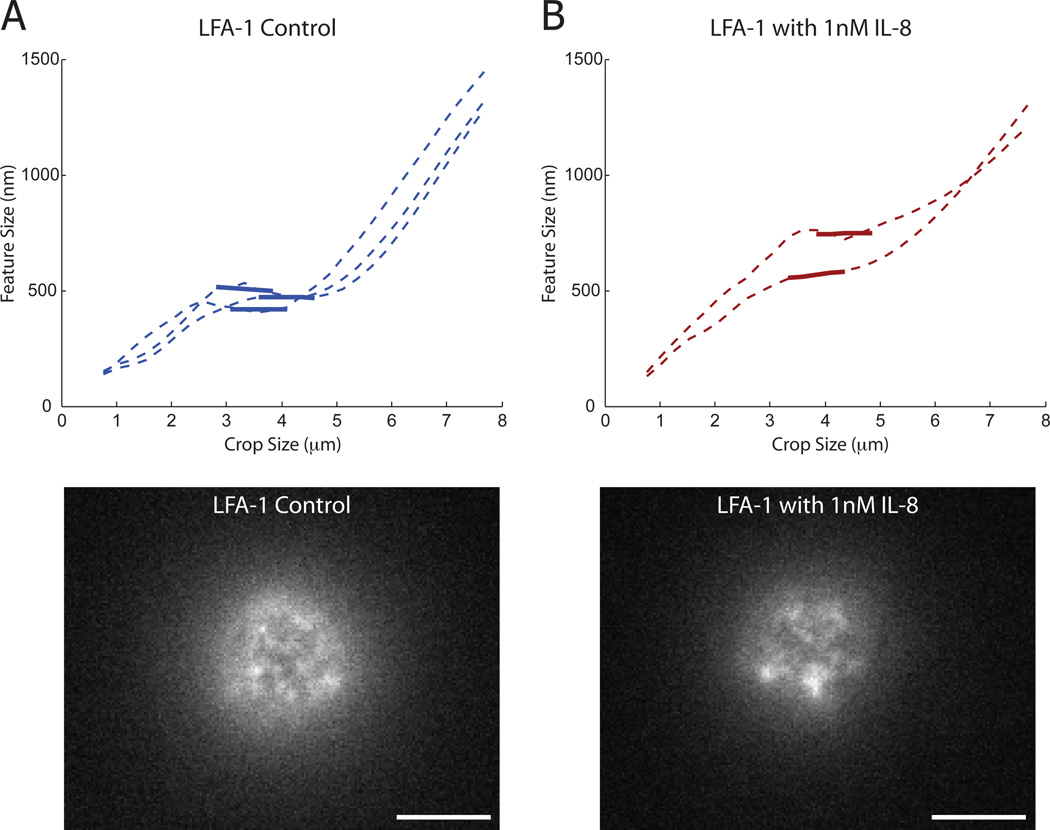
Resting neutrophils are known to be activated by IL-8, which changes the conformation of LFA-1 adhesion molecules and can lead to receptor clustering (Seo et al., 2001). Using the above cropping criterion, we performed preliminary studies on spherical human neutrophils to quantitatively measure the feature size of LFA-1 domains before and after activation with 1 nM IL-8 (Figure 6). We confirmed that activated neutrophils with a clustered integrin appearance had quantitatively larger feature sizes than untreated cells (640 nm versus 490 nm). This result is consistent with previous reports of neutrophil adhesion molecule clustering upon cell activation (van Kooyk & Figdor, 2000). As neutrophils become activated, their morphology transitions from spherical to a flattened and motile cell. Morphological changes complicate analysis, therefore our measurements were made at the earliest stages of activation before significant shape change. This type of shape change is also problematic for traditional techniques such as FRAP due to dynamic boundary conditions and SPT due to cell movement dominating particle motion. However, once the morphological transition is complete, existing ICM techniques such as STICS can be used for dynamic cell analysis (Hebert et al., 2005).

Figure 6.

Adhesion molecule cluster formation upon neutrophil stimulation with IL-8. Human neutrophils were labeled for LFA-1 with fluorescent monoclonal antibody. (A) Control cells had a feature size of 490 nm using the method described in Figure 5. Three plots are shown. A characteristic image of an untreated cell is shown below. (B) Cells were then activated with 1 nM IL-8 for 15 minutes and imaged. Two cells that maintained a spherical morphology where analyzed. The feature size increased to 640 nm. A characteristic image shows a clear increase in receptor domain size. White scale bar is 5 microns.

CONCLUSIONS

Here we have shown that ICM can be extended to uniform illumination or wide-field fluorescence microscopy. The previously limiting feature of laser beam width defining the characteristic diffusion length is overcome by using the SACF to calculate feature size. We also demonstrate that UI-ICM methods are not limited to sparse fluorescent features, but can accurately measure lateral mobility of densely crowded features in a time-lapse sequence. The extension of ICM to uniform illumination microscopy will significantly increase its potential use by scientists who do not regularly use laser-scanning microscopes out of practicality or expense. Lastly, we explore the use of UI-ICM on spherical human neutrophils, which are difficult to analyze with confocal systems. We show that lateral mobility measurements of LFA-1 domains are similar to LFA-1 lateral mobility measured with FRAP.

Supplementary Material

Supplemental Movie S1

Supplemental Movie S1. Non-adherent resting human neutrophil fluorescently labeled for CD62L. Time-lapse wide-field fluorescence imaging recorded every 250 ms for 12.5 seconds. Focal plane is at the bottom of the neutrophil, just above the bottom coverslip.

Supplemental Movie S2

Supplemental Movie S2. Non-adherent fixed human neutrophil fluorescently labeled for CD62L. CD62L adhesion molecules are fixed in place on the neutrophil surface. Time-lapse wide-field fluorescence imaging recorded every 250 ms for 12.5 seconds. Focal plane is at the bottom of the neutrophil, just above the bottom coverslip.

Supplemental Movie S3

Supplemental Movie S3. Adherent fixed human neutrophil fluorescently labeled for CD62L. CD62L adhesion molecules are fixed in place on the neutrophil surface, which is fixed to the bottom coverslip. Time-lapse wide-field fluorescence imaging recorded every 250 ms for 12.5 seconds. Focal plane is at the bottom of the neutrophil at the coverslip.