A proposed method of bias adjustment for meta-analyses of published observational studies

Abstract

Objective Interpretation of meta-analyses of published observational studies is problematic because of numerous sources of bias. We develop bias assessment, elicitation and adjustment methods, and apply them to a systematic review of longitudinal observational studies of the relationship between objectively measured physical activity and subsequent change in adiposity in children.

Methods We separated internal biases that reflect study quality from external biases that reflect generalizability to a target setting. Since published results were presented in different formats, these were all converted to correlation coefficients. Biases were considered as additive or proportional on the correlation scale. Opinions about the extent of each bias in each study, together with its uncertainty, were elicited in a formal process from quantitatively trained assessors for the internal biases and subject-matter specialists for the external biases. Bias-adjusted results for each study were combined across assessors using median pooling, and results combined across studies by random-effects meta-analysis.

Results Before adjusting for bias, the pooled correlation is difficult to interpret because the studies varied substantially in quality and design, and there was considerable heterogeneity. After adjusting for both the internal and external biases, the pooled correlation provides a meaningful quantitative summary of all available evidence, and the confidence interval incorporates the elicited uncertainties about the extent of the biases. In the adjusted meta-analysis, there was no apparent heterogeneity.

Conclusion This approach provides a viable method of bias adjustment for meta-analyses of observational studies, allowing the quantitative synthesis of evidence from otherwise incompatible studies. From the meta-analysis of longitudinal observational studies, we conclude that there is no evidence that physical activity is associated with gain in body fat.

Introduction

Many issues of public health importance cannot be investigated in intervention studies or randomized trials, for either ethical or practical reasons.^1,2 Observational studies then provide the only source, or a large component, of relevant evidence. Such studies are notoriously prone to biases, caused for example through selection of participants, confounding and loss to follow-up. Especially when only published information is available, the potential impact of biases on the reported results and their interpretation is often unclear.³

This issue comes to the fore when undertaking a systematic review,⁴ for then the objective is to collate and synthesize all the available evidence in a rigorous way. Systematic reviews have in the main focused on intervention studies, and especially randomized trials.⁵ In these situations, although potential biases still have to be considered, there is an appreciation of their major sources and potential impact.⁶ Reviews of observational studies commonly reach rather qualitative conclusions, for example based on a tabulation of study-specific results together with a commentary on their idiosyncrasies and potential biases. An overall quantitative conclusion using meta-analysis is often avoided because of the intangible nature of some of the biases, the incompatibility of methods of presenting results in different articles,⁷ and the fact that relevant information is often missing in publications. Alternatively, a rather arbitrary dichotomy is introduced to separate the ‘better’ from the ‘poorer’ quality studies, and a quantitative meta-analysis of the former presented. This simplistic approach essentially disregards any biases in the ‘better’ studies, and assumes that the ‘worse’ studies are totally non-informative. Similarly, simple scoring of studies according to some measure of quality does not directly address their biases.⁸

In the context of systematic reviews of intervention studies, both randomized and non-randomized, work has recently been developed to quantify the potential biases using subjective opinion elicited from experts so that meta-analysis can be undertaken.⁹ Using elicited opinion is necessary, because there is rarely sufficient empirical evidence about the potential size of particular biases relevant to an individual study.¹⁰ The magnitude of biases always of course remains uncertain, and quantifying this uncertainty is part of the elicitation process. Here, we extend this work on intervention studies to the more problematic context of observational studies.

Methods

Our aim is to make a quantitative conclusion, on the basis of observational studies, about a particular association of public health importance. As an example, we consider the relationship between physical activity and subsequent change in adiposity in children. Relevant studies were undertaken in different contexts (populations, methods, lengths of follow-up), but we aim to make a conclusion relevant to a specific target setting. The studies then suffer from two forms of bias: internal bias (or lack of rigour) and external bias (or lack of relevance to the target setting). In the following explanation of our proposed approach, the focus is on the methods; more details of the example and its interpretation are provided elsewhere.¹¹

Physical activity and obesity example

Obesity is a major global health issue,¹² and the increase in obesity of children is of particular concern.¹³ It is proposed that increasing physical activity, which raises energy expenditure, may protect against excess weight gain. But the evidence underpinning this assertion is incomplete. Most cross-sectional studies of physical activity and body weight indeed show an inverse association.¹⁴ However, their interpretation is problematic, because the direction of any causal link is unclear (does physical activity lead to lower weight, or does obesity lead to lower levels of physical activity?). In addition, studies not using objective measures may be distorted by reporting biases for physical activity.¹⁵ Thus we focus on longitudinal observational studies in children, which relate objective measures of baseline physical activity to objective measures of subsequent change in adiposity, found in a thorough literature search from January 2000 to September 2008.^11,16

Six studies fulfilling the eligibility criteria were found.^17–22 They are characterized by heterogeneity in populations studied, age and gender groups recruited, follow-up times, measures of physical activity level and body composition and which confounders are adjusted for. One of the studies is summarized in Table 1, and will provide a running example in this article. Most studies measured percentage of total weight as body fat (%BF) at baseline and follow-up, and regressed change in %BF on baseline physical activity level and confounders. Results from these regression analyses were presented in various ways, for example either a partial regression or a partial correlation coefficient with a P-value, and often without a direct measure of uncertainty such as a standard error or confidence interval (CI).

Table 1.

Characteristics of one example longitudinal study¹⁸ of physical activity level and subsequent change in adiposity, and data extracted

Sample	47 normal-weight girls aged 5–9 years from Alabama, USA
Exposure	PAEE during 24 h in a calorimetric chamber
Outcome	Percentage BF by dual-energy X-ray absorptiometry
Time period	Baseline and after an average of 1.6 years (SD 0.4 years)
Analysis	Stepwise regression of change in %BF on predictors including PAEE
Sample size for longitudinal analysis n	39
Reported P-value	0.04
Fisher-transformed correlation z (SE)	–0.34 (0.17)
Correlation r calculated from z (95% CI)	–0.33 (–0.59 to –0.01)

Target setting and categories of bias

The overall approach to identify and quantify the biases of original studies in relation to a target setting is depicted in Figure 1. For each original study undertaken, an idealized version is described that is not subject to any internal biases. This separates the internal biases from the external biases, which are themselves broken down into components so that they can be more easily assimilated and opinions about their magnitude elicited.

Figure 1.

Overview of bias adjustment method: separating internal and external biases

The key components of a well-defined target setting in our example were considered to be the population, the measure of physical activity, the measure of change in adiposity and the duration of follow-up. The specific target setting chosen is shown in Table 2, in order to address the most relevant public health question in the UK. Although some aspects (for example, the choice of change in %BF as the outcome measure) were well represented within the studies undertaken, others were not (all the studies were conducted in the USA but the target population was the UK). Also shown in Table 2 is the idealized version of the example study from Table 1. The idealized study uses the same design, population, measures and context as the original study, but is not subject to any internal biases (for example, no loss to follow-up, proper control of confounding). There is no subjectivity involved in defining the idealized study; it does not have to be practicable but is merely a mechanism to enable internal and external biases to be separated. The differences between the original and idealized study represent internal biases, and differences between the idealized study and the target setting (Table 2) represent potential external biases.

Table 2.

Target setting for meta-analysis, and the idealized version of one example study¹⁸

	Target setting	Idealized version of one example study18
Population	General population of children aged 4–11 years in the UK	Normal-weight girls aged 5–9 years from Alabama, USA
Exposure	Free-living PAEE objectively measured at baseline	PAEE measured by whole-room indirect calorimetry (laboratory conditions)
Outcome	Subsequent change in %BF, objectively measured at baseline and follow-up	Subsequent change in %BF measured at baseline and follow-up by dual-energy X-ray absorptiometry
Time interval	Outcome assessed over a 2-year period	Follow-up at 1.6 years

The sources of internal bias were put into six categories (Figure 1): selection bias (whether the sample recruited was representative of the intended population), control of confounding (whether essential confounders have been adjusted for), exposure measure (problems in assessing physical activity), attrition (loss to follow-up), outcome measure (problems in measuring change in adiposity) and any other biases (e.g. when the statistical analysis used was thought to have introduced bias). These six categories of bias were generally mutually exclusive, so that each potential bias in each study could be placed in one category, and considered to operate independently of each other. The external biases were in four categories (population, exposure measure, outcome measure and follow-up time) that relate to the definition of the target setting. To help itemize the specific biases for each study, a checklist was developed (Figure 2) based on previous work^3,9,23 and this was completed for each study.

Figure 2.

Checklists used for longitudinal studies of physical activity and obesity: internal and external biases

The choice of appropriate confounders to adjust for is a difficult issue. Rather than attempt to say whether the choice of a particular set of confounders was ‘correct’, we judged the bias from the adjustment presented in relation to using a standard set of confounders (namely age, gender, ethnic group, sexual maturity, baseline fat mass and baseline lean mass). Moreover, we did not consider the effects of within-subject variation over time in the assessment of physical activity. Thus the target parameter to be estimated in the meta-analysis is that for the association between change in %BF and observed baseline physical activity energy expenditure (PAEE) adjusted for a specific set of confounders.

Extracting results

The principal quantitative result extracted from each study, which would form the basis for the meta-analysis, was chosen to be as close as possible to an estimate of the target parameter. Then the extent to which biases would have to be assessed was minimized. For example, adjusted associations were chosen if available, and reported associations with PAEE were preferred over associations with total energy expenditure. Since the exposure and outcome variables were on different scales in different studies, and because results were presented in different formats, it was necessary to convert all extracted results to a common scale. Moreover, standard errors were not always provided. Our solution was to transform all associations into correlation coefficients using, if nothing else were available, the sample size and the P-value to derive these.

We use the result that the Fisher-transformation of a correlation coefficient r, namely , has an approximate normal distribution with standard error where n is the sample size.²⁴ Thus, the relevant (two-sided) P-value reported in the article is first converted into a standard normal score S taking due regard of the sign of the association in the article, the Fisher-transformed correlation derived as , and the correlation as . Where papers presented both a correlation coefficient and a P-value, our derived correlation agreed well with the published value.

Bias assessments

The process of eliciting biases was as follows, for each study in turn. The same subject-matter specialist and one statistician reviewed each study’s publication, defined the idealized version of the study and completed the checklist in Figure 2 by qualitatively describing each potential source of bias. The internal biases were then assessed by a group of six quantitatively trained assessors (primarily statisticians) and the external biases by a group of five subject-matter specialists (primarily physical activity epidemiologists). Having read the paper and checklist, the group agreed any modifications to be made to the checklist, but avoided discussing the seriousness or magnitude of potential biases. Each bias was classified by the group as operating either additively or proportionally on a correlation scale. An additive bias could introduce a correlation where none was in truth present; examples included inadequate control of confounding or biases caused through missing data or loss to follow-up. A proportional bias would change the magnitude but not the sign of the correlation, thus exaggerating or attenuating a true effect; examples included differences between populations, and biases caused by undertaking stepwise regression and retaining only statistically significant predictors.

After the group discussion, each assessor individually considered biases in each category (Figure 1). A first qualitative stage was to consider whether the bias was potentially large, medium, small or negligible, and in what direction. They then indicated their view about the magnitude of an additive bias, and their uncertainty about this, on the upper scale in Figure 3. This required marking an interval on the untransformed correlation scale such that they believed there was a two-thirds chance that the bias lay inside this interval, and a one-third chance that it lay outside. To help guide these judgements, Figure 4 shows the impact of different biases on the magnitude of the CI for the correlation according to sample size. From this, a guideline was suggested that additive biases of magnitude >0.2 were large, those between 0.1 and 0.2 were moderate and those <0.1 were small. If an assessor had no opinion about the direction of the bias, then the interval would be placed symmetrically about zero. If an assessor thought that the bias would tend to favour a negative correlation, the centre of the interval would be on the left-hand side of the upper scale in Figure 3, and vice-versa for a bias favouring a positive correlation. If there was thought to be no or negligible bias, the ‘interval’ became a point at zero on the scale. Biases considered proportional by the group were indicated on the lower scale in Figure 3 in a similar way, indicating exaggeration or attenuation of effect.

Figure 3.

Elicitation scales for additive and proportional biases

Figure 4.

Effect of ranges for an additive bias on the width of the 95% CI for the bias-adjusted correlation coefficient

Meta-analysis

We performed meta-analysis of correlation coefficients on the Fisher-transformed scale because the distribution of z is more symmetric than that of r. We incorporated assessments of the biases elicited on the correlation scale but transformed onto the z scale. Since the range of z is from minus to plus infinity, this has the theoretical advantage that additive biases cannot produce impossible values of the underlying correlation. However, in our context where correlations are modest in magnitude, this is of limited practical importance because the values of z and r are numerically close in the range –0.3 to +0.3.

The calculations for including the bias assessments in the meta-analysis follow published methods,⁹ and Stata code is available.²⁵ In brief, a bias assessment interval marked on the scales in Figure 3 is considered to be an estimated bias ± one standard deviation (SD), since this corresponds to a two-thirds (67%) interval for a normal probability distribution. For each study and assessor, the total internal additive bias is calculated by adding the individual bias estimates and summing their variances (squared SDs). The total internal proportional bias and estimated variance for each study and assessor are also calculated.⁹ These two quantities are combined to give a total internal bias and variance. This total bias for each assessor and study is subtracted from the observed study result, and the total variance of the bias added to the study result variance, to give an internal bias-adjusted estimate and variance for each study and each assessor. The external biases are then incorporated using a similar procedure. These adjusted estimates for each study are then averaged across assessors by median pooling,²⁶ taking the median of the bias-adjusted estimates and the median of the variances; this corresponds to a ‘typical’ assessor.

Random-effects meta-analysis across studies was undertaken on the Fisher-transformed correlation scale. The impact of heterogeneity was summarized by the I² statistic,²⁷ which estimates the percentage of variation between study results explained by true heterogeneity rather than chance. Values of I² close to 0% represent little heterogeneity beyond that compatible with chance. Summary estimates and intervals were converted back to the correlation scale for presentation.

Results

To explain the process, we first consider the biases, elicitations and adjustments performed for the one example study¹⁸ summarized in Table 1. The study result extracted was based on a sample size of 39 and a reported P-value of 0.04 from a multiple regression for the association of baseline PAEE and other covariates with change in %BF, yielding a calculated (partial) correlation of –0.33 (95% CI –0.59 to –0.01).

The internal biases reflect differences between the study undertaken and the idealized version of the study (Table 2); the elicited internal biases are shown in Figure 5 (top). Since there was little information about recruitment, it is possible that the girls in the example study were not representative of the population intended. The resulting selection bias was considered an additive bias; the assessors generally had no opinion about the direction of the bias but some were more uncertain about its impact than others. The reported result included adjustment for age and baseline fat-free mass but not ethnic group or baseline fat mass; the assessors generally thought that the resulting bias was quite modest (compared with the standard specified set of confounders), with no strong opinion about its direction. There were no differences in implementation of the exposure and outcome measures between the actual study and the idealized study, so no biases were recorded for these items. Only 39 out of the original 47 study entrants had the requisite follow-up data, and there was no comment in the published study about whether the girls omitted were similar to those included in the analysis. The assessors again did not have an opinion about the direction of the resulting bias. Finally, the study reported results from a stepwise regression, where non-significant effects had been excluded. The assessors regarded this as a proportional bias, generally likely to exaggerate the size of the reported association between PAEE and change in %BF.

Figure 5.

Bias elicitations (67% intervals) for one study¹⁸ by six internal bias assessors and five external bias assessors; correlation scale. Blank sub-figures indicate the absence of that bias

For the external biases, the idealized version of the study is compared with the target setting (Table 2); the elicited external biases, which were all considered as proportional, are shown in Figure 5 (bottom). Since %BF was the outcome in both the idealized study and target setting, there is no bias for this component. The potential biases relate to differences in population (age range, gender and country), PAEE being measured under laboratory rather than free-living conditions, and a slight difference in follow-up interval. The assessors generally thought that the PAEE measurement used in the study might diminish the association as compared with the target setting, but the other biases were generally thought to be small (proportional bias near 1).

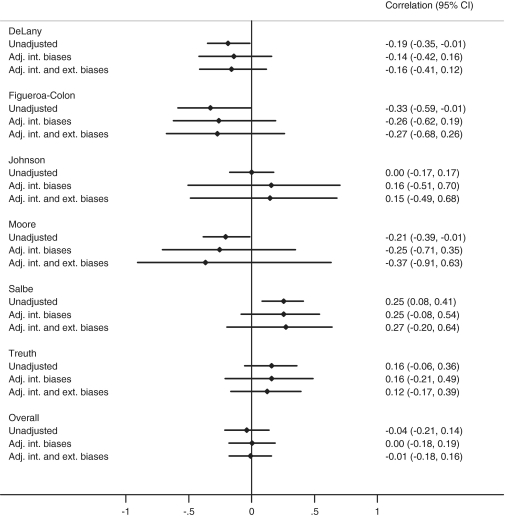
The effect of adjusting for these biases, pooled over assessors, is shown in Table 3. The anticipated direction of the internal biases overall brings the correlation slightly nearer zero, and the CI width increases to reflect the uncertainty in the biases. The effect of the external biases is to further increase the CI width, but the correlation estimate remains almost the same. These results are also shown in Figure 6 (second study).

Table 3.

Unadjusted and bias-adjusted correlations between baseline physical activity level and change in %BF for one example study¹⁸, and meta-analysis of unadjusted and bias-adjusted correlations (95% CI)

	Correlation for one example study18	Meta-analysis of correlations in all six studies; I2 for heterogeneity
Unadjusted	−0.33 (−0.59 to –0.01)	−0.04 (−0.21 to 0.14); I2 = 78%
Adjusted for internal biases (corresponds to idealized versions of each study)	−0.26 (−0.62 to 0.19)	0.00 (−0.18 to 0.19); I2 = 15%
Adjusted for internal and external biases (corresponds to target setting, Table 2)	−0.27 (−0.68 to 0.26)	−0.01 (−0.18 to 0.16); I2 = 0%

Figure 6.

Meta-analysis of six studies^17–22 for the association between physical activity and subsequent change in adiposity on the correlation scale. Results are shown unadjusted for any biases, adjusted for internal biases and adjusted for both internal and external biases

A similar exercise was undertaken for each of the six studies in our example, leading to bias-adjusted results for each study and corresponding meta-analyses (Figure 6, Table 3). The meta-analysis of unadjusted correlations gave a summary estimate of −0.04 (95% CI –0.21 to 0.14), but with substantial heterogeneity (I²= 78%). This heterogeneity reflects both the different study designs and measures used, but also the effect of biases. Adjusting for the internal biases reduced the heterogeneity (I²= 15%). After also taking into account the external biases, there was no apparent heterogeneity (I²= 0%) and the pooled correlation was –0.01 (95% CI –0.18 to 0.16). The overall conclusion from the bias-adjusted meta-analysis, now consistently expressed in terms of the correlation between PAEE and subsequent change in %BF, is that there is little or no association. To help interpretation, the pooled correlation can be converted to a regression coefficient; using published standard deviations of PAEE and change in %BF,¹⁷ the estimated bias-adjusted regression coefficient was –0.05 (95% CI –1.00 to 0.91) change in %BF per 1 MJ/day (239 kcal/day) increase in PAEE.

After adjustment for the biases, the relative weights the different studies receive in the meta-analysis change. For example, the fourth study²⁰ in Figure 6 received 17% of the weight in the unadjusted meta-analysis but only 2% in the fully adjusted meta-analysis. This in part reflects the uncertainty in the external biases for this study, since accelerometer counts were used as a measure of physical activity rather than a direct measure of PAEE, and skin-fold thickness as a measure of body composition rather than %BF.

To investigate the consistency across assessors, we repeated the bias adjustments for each of the internal bias assessors separately, and then for each of the five external bias assessors. The results from the meta-analysis (Figure 7) show consistency across assessors, and do not change the overall conclusion based on a ‘typical’ assessor (Figure 6 and Table 3).

Figure 7.

Meta-analysis of six studies^17–22 for the association between physical activity and subsequent change in adiposity on the correlation scale. Results are shown using the internal bias adjustments from each of six internal bias assessors (IA1–IA6) separately, the overall internal bias-adjusted result, and adjusted for internal and external biases using the external biases from each of five external bias assessors (EA1–EA5) separately, and the overall result adjusted for both internal and external bias

Discussion

We have presented a method of obtaining an overall quantitative summary in a systematic review of observational studies, where numerous potential biases may operate. This is in contrast to the common approach where a vague and non-committal qualitative conclusion is drawn, because of the poor quality, reporting or relevance of the component studies. This apparently daunting task has been achieved by breaking it down into small manageable steps as follows: (i) define a target question, (ii) describe an idealized version of each study, (iii) separate internal from external biases, (iv) separate categories of these biases, (v) compile a checklist of the possible biases in each study, (vi) agree this checklist within a group of assessors, (vii) elicit the biases and their uncertainty from assessors independently for each category of bias for each study and (viii) perform a bias-adjusted meta-analysis. Although this is a time-consuming process, there are no obvious alternatives, since empirical evidence on the size and uncertainty of all the biases is not available.

Other methods of adjusting for biases in meta-analysis have previously been proposed. Some have adjusted for certain biases by specifying a model with parameters that together determine the bias in the target effect.²⁸ These methods have been developed, for example employing external empirical data, to address misclassification of exposure or outcome²⁹ and uncontrolled confounding,³⁰ using a full or approximate likelihood approach. Others have used distributions to represent directly the overall internal and external biases in the effect of interest in each study.³¹ Like the former more complex methods,^28–30 we model biases due to individual sources, but like the latter simpler method,³¹ we assume a direct form for the bias in the target effect. Our aim has been to present generic methods that can be used in a routine setting. Specifically, we have extended a previous approach for intervention studies where the outcome scale was relative risk,⁹ tailored to the context of observational studies where the outcome scale is correlation. In contrast, simple methods based on weighting by quality scores are known to be inadequate.³²

For the example considered, we conclude that there is little or no relationship between physical activity and subsequent change in %BF in children, since the estimated pooled correlation is almost zero with tight confidence limits. Although physical activity is no doubt important for various aspects of health, a policy focusing on increasing physical activity alone, without changing dietary habits, is unlikely to be effective in reducing obesity in children.¹¹ Before biases are considered, the results of the different studies were severely heterogeneous, which makes a pooled result very difficult to interpret. After adjusting for internal biases, the results are less heterogeneous across studies, but the pooled result still refers to the associations between the measures of physical activity and change in adiposity used in the different studies. After also adjusting for external biases, the correlation refers to that between PAEE and change in %BF, as in the target setting, and so is directly interpretable. The lack of heterogeneity between studies at this stage is what one would expect if the bias adjustment process was working as intended. The CI for the pooled correlation now incorporates the uncertainty about the magnitudes of the biases, rather than the heterogeneity between studies as in the unadjusted analysis.

In the example presented, the pooled estimate and CI are quite similar between the unadjusted and bias-adjusted meta-analyses. In other examples we have undertaken, the bias-adjusted pooled estimate or its precision were rather different from the unadjusted values. In a meta-analysis of intervention studies of the effect of routine antenatal anti-D prophylaxis on maternal sensitization, bias adjustments led to a similar overall odds ratio but a substantially wider CI.⁹ In a meta-analysis of observational studies of the relationship between dietary energy density and subsequent changes in adiposity in children, bias adjustments made the correlation both more positive and more imprecise, suggesting that the near-null rather precise unadjusted association might be misleading.³³

There are of course limitations to the approach we have adopted which add uncertainty around the final conclusions. First, the elicited biases are subjective. Assessors may not agree with each other, and different assessors might have reached different judgements, including for example whether a particular bias is best represented as additive or proportional. Assessors might also not be consistent in how they judge the same bias on different occasions. We have minimized these problems by involving assessors who are experienced in the biases being judged (either methodological or subject-matter specialists), by using independent judgements from a group of assessors, and basing results on median pooling (which corresponds to a ‘typical’ assessor and eliminates extreme judgements). Moreover, in general, the judgements of the different assessors were quite similar (Figures 5 and 7), and using more assessors would not have reduced the uncertainty about the views of a typical assessor. The method would be improved if it were better informed by empirical evidence, for example from meta-epidemiological studies,¹⁰ or if authors themselves investigated the potential for bias in their studies.³⁴ Analyses of individual participant data, when these are available for at least one of the contributing studies, can help in the assessment of biases, for example in investigating the potential impact of missing data, of adjustment for different confounders or of categorizing a continuous exposure.³³

A second issue relates to the limits necessarily placed on the process. We consider results in terms of correlations, since these can always be derived from just the sample size and reported P-value. Any approximations in extracting results from a published paper (for example, rounded P-values, uncertain sample sizes or unclear analytical methods) can be considered as an additional internal bias. Although meta-analysis of correlations or regression coefficients is an established method^35,36 and has been used before in the field of nutrition and energy expenditure,³⁷ it is conceptually a somewhat difficult scale on which to elicit biases. Hence we provided some guidance, derived from Figure 4, on what might be considered small or large additive biases. Our process assesses confounding bias relative to a pre-specified set of confounders, and considers only the published studies available and so does not address publication or dissemination biases.³⁸ It also does not adjust for biases resulting from within-person variability over time, in either the exposure or confounders, since these ‘multivariate measurement error’ effects are very hard to judge. This is an example where parametric modelling of individual biases using empirical evidence^29,30 would be more reliable. For these reasons, one needs to be somewhat cautious in making a causal interpretation from the summarized results.

The work we have presented could be further developed, and it would be beneficial if our methods were applied to other examples by independent investigators in the future. Web-based software could be developed to aid the elicitation process and subsequent analysis. Ideally, our approach needs validation, either against empirical evidence or for example in the context of a systematic review that pre-dates a planned large definitive study, where the design of the latter provides the relevant target setting. Most fundamentally, experience with the method needs to be gained in terms of real policy decision-making, for example in national public health intervention assessments.³⁹ It is exactly in this kind of context where quantitative summaries, acknowledging the uncertainties from methodologically limited studies, are required.

Funding

UK Medical Research Council Population Health Sciences Research Network (grant number PHSRN27).