New Predictive Models of Heart Failure Mortality Using Time-Series Measurements and Ensemble Models

Abstract

Background

Morbidity and mortality associated with heart failure remains high. A wide variety of demographic and clinical factors, as well as biomarkers are associated with increased mortality. Despite this, most multivariate predictive models for heart failure mortality have predictive accuracies characterized by a C-statistic (area under the receiver operating curve) of around 0.74.

Methods and Results

We analyzed data on 963 patients enrolled in the Vesnarinone Evaluation of Survival Trial (VEST), including circulating levels of two cytokines (TNF and IL-6) and their receptors sampled at baseline, and at 8, 16 and 24 weeks. We built multivariate logistic regression models using standard clinical variables and time-series of cytokine and cytokine receptor levels, using independent components analysis to handle collinearity among cytokine measurements, and L2-penalized stepwise regression for variable selection. We also built ensemble models with these data using gentle boosting. Our multivariate logistic regression model using time-series cytokine measurements predicts one-year mortality significantly better (p=0.001) than the baseline model, with a C-statistic of 0.81±0.03. Without the cytokines, the baseline model has a C-statistic of 0.73±0.03, and with only baseline cytokine and cytokine receptor levels added, the model has a C-statistic of 0.74±0.04. An ensemble model of 100 decision stumps with serial cytokine measurements has a significantly better (p=0.04) C-statistic of 0.84±0.02. An ensemble model with baseline cytokine data and without the serial measurements has a C-statistic of 0.74±0.04.

Conclusions

Significant gains in accuracy of one year mortality prediction in chronic heart failure can be obtained by using logistic regression models that incorporate serial measurements of biomarkers such as cytokine and cytokine receptor levels. Ensemble models capture inherent variability in large patient populations, and boost predictive accuracy through the use of time-series measurements.

Introduction

Morbidity and mortality associated with heart failure (HF) remain high [1,2]. Expensive management strategies for the treatment of advanced HF such as left ventricular assist devices and heart transplantation have improved both survival and quality of life for patients with HF [3]. This has led to the need to accurately predict both short and long term survival not only for physicians to time such interventions, but also to discuss prognosis with patients and to help with end of life decisions.

A wide variety of factors has been associated with increased mortality in HF including demographic factors (e.g., gender), clinical factors (e.g., renal dysfunction), co-morbidities (e.g., diabetes), cardiac imaging markers (e.g., cardio-thoracic ratio and ejection fraction) and serum biomarkers (e.g., brain natriuretic peptide (BNP) and C-reactive protein (CRP)). Some of the well known mortality prediction models are from the Enhanced Feedback for Effective Cardiology Treatment (EFFECT) study [4], the Acute Decompensated Heart Failure National Registry (ADHERE) [5] for 30 day mortality prediction for hospitalized patients, the Candesartan in Heart Failure: Assessment of Reduction in Mortality and Morbidity (CHARM) trial [6], and the Seattle Heart Failure Model (SHFM) [7] for 1, 2 and 5 year mortality prediction for ambulatory patients. The predictive power of these multivariate models, as measured by the C-statistic, or the area under the receiver operating curve, varies from 0.68–0.73 for short-term to 0.73–0.79 for long-term survival. Of these, the SHFM has been extensively validated [8] on many data sets. Despite the intuitive appeal of these models, the less than optimal accuracy has limited the routine use of these models in clinical practice. Improved estimation of the risk of mortality might significantly impact the ability of physicians to formulate more appropriate treatment plans.

Various biomarkers including inflammatory biomarkers such as cytokines and cytokine receptors [9] have been shown to be prognostically important. Statistical machine learning [10] offers principled approaches to incorporating data on such markers into current risk estimation models. The aim of the present study was to develop an improved model for predicting survival in patients with HF, using statistical machine learning algorithms to integrate time-series measurements of cytokine and cytokine receptor levels with the standard clinical variables used in prognostic modeling. Here, we also evaluate whether an “ensemble” of models can estimate one-year survival better than a single model system.

Methods

Study sample

In our analysis, we used data from the first 1200 participants in the Vesnarinone Evaluation of Survival Trial (VEST) [11] for whom measurements of the levels of plasma tumor necrosis factor (TNF) interleukin-6 (IL-6) and their receptors: soluble TNF receptors (sTNFR1 and sTNFR2), and soluble IL-6 receptor (sIL6R), were gathered at baseline, 8, 16, 24, and 48 weeks. No serial measurements other than the cytokines are available for this cohort of patients. The study protocol for measuring all the predictor variables, except for the cytokines, has been previously published in [9]. Detailed description of the assays for measuring cytokines as well as their coefficients of variation has been presented previously [12 (data supp.),13].

Thirty one patients were excluded from the analysis (18 patients with NYHA class II and 13 patients with incorrect baseline measurements). From the remaining 1169 patients with NYHA functional class III and IV, we eliminated 206 patients for whom various baseline variables were missing, following the methodology previously used [12,13]. Baseline information on each patient includes age, gender, weight, NYHA class, ischemic or non-ischemic etiology, cardiothoracic ratio, left ventricular ejection fraction (LVEF), blood urea nitrogen (BUN), hepatic enzymes: alanine aminotranferease (ALT) and aspartate aminotransferase (AST), serum sodium and potassium, creatinine, as well as creatinine clearance, percentage of lymphocytes and quality of life as measured by the Minnesota Living with Heart Failure questionnaire [14]. We also include vesnarinone dose (placebo, 30 milligrams, 60 milligrams) for each patient.

Incorporating time series measurements into logistic regression models

The above data from the cytokine database of the VEST trial was subject to a binary classification analysis, where patients who survived beyond 52 weeks after entry into the trial were assigned to one class (class 0), and patients who died before 52 weeks were assigned to the other class (class 1). Here we were interested in modeling survival as a dichotomous outcome variable (alive or dead) at a defined point in time, namely 52 weeks after baseline randomization visit. The rationale for this approach was based on the premise that if a clinician recognized that there is a high probability of mortality within one year, it would prompt the recommendation of more aggressive life-saving therapies (e.g., circulatory assist device, or a cardiac transplant). Conversely, knowing that there is a low probability of mortality within a year, a clinician might not seek to pursue aggressive strategies because of concern about the inherent morbidity and mortality of these therapies. The standard modeling methodology for problems with dichotomous outcome variables is logistic regression [10].

In order to determine the utility of time series measurements, we built three logistic regression models to predict survival beyond 52 weeks after entry into the trial. The first model uses standard baseline measurements as predictor variables. It allows us to compare our results with existing work in the literature. The second model adds baseline cytokine measurements to the predictor variables of the first model. It measures the incremental value of adding baseline cytokines to the standard model. The third model includes cytokine measurements up to week 24 to the second set of predictor variables. In constructing this model, we treat cytokine levels for patients who die before 24 weeks as missing data. This model provides an assessment of the utility of serial follow-up measurements to predict survival. Clearly, the third model uses more recent information than the first two models; however it is not a priori obvious that follow-up cytokine levels (baseline or recent relative to the 52 week horizon) have predictive value for one-year survival. Additional details of the statistical modeling including the handling of collinearity in time series measurements, model selection and cross-validation for model assessment are presented in Supplemental Methods.

Evaluation of ensemble models

Traditional logistic regression produces linear models. In order to handle non-linear effects within the framework of logistic regression, the statistical model has to explicitly include interaction terms in the analysis. Given that there are an exponential number of possible interaction terms to consider, it becomes computationally prohibitive to exhaustively enumerate and evaluate each interaction, particularly when there a number of predictive variables built into the model. An alternative approach is to use the well-established method termed “ensemble modeling” derived from statistical machine learning [10]. Ensemble models achieve high classification accuracy by combining the results of multiple statistical models. Instead of learning a single global model over the entire data, ensemble learning produces a set of models. Given data for a new patient, each component model in the ensemble classifies the patient as a survivor or non-survivor for the 52 week horizon. The final classification for the patient is the category that is predicted by a majority of the component models of the ensemble. Ensemble classifiers are automatically learned using boosting, a special family of machine learning techniques [10]. Additional details of ensemble modeling are presented in Supplemental Methods.

Results

Descriptive statistics on the 963 patients in our study are summarized in Table 1. Univariate analysis using the t-test reveals that LVEF, cardio-thoracic ratio, BUN, serum sodium, creatinine and creatinine clearance, percentage lymphocytes and the quality of life scores are significantly different between the cohort that survives past one year from entry into the trial, and the cohort that did not survive. The non-survivors were more likely to be male, NYHA class IV and have an ischemic etiology of HF. The cytokine levels at baseline and at 24 weeks were significantly different, with soluble TNF-receptor 1, soluble TNF-receptor 2, and IL-6 being the most important cytokines, as we have described previously [9]. Similar differences hold for cytokine levels at 8, and 16 weeks.

Table 1.

Patient Demographics

	Survivors (n=791)	Deaths (n=172)	p-value
Age, y	61.3 ± 12.2	62.1 ± 11.6	0.004
Male, %	76.4	82.6	0.09
NYHA class (III ), %	90	81	0.004
Ischemic etiology, %	56.6	61.5	0.004
Weight, kg	82.6 ± 20.1	81.3 ± 18.9	0.4103
Ejection Fraction, %	21.1 ± 6.0	18.4 ± 5.1	0.001
Cardio-thoracic ratio	0.55 ± 0.07	0.58 ± 0.07	0.001
Blood urea nitrogen	23.7 ± 12.4	33.7 ± 17.9	0.001
ALT, u/L	22.2 ± 12.4	23.7 ± 26.6	0.4863
AST, u/L	21.7 ± 14.7	21.4 ± 24.3	0.88
Serum sodium, mg/L	138.7 ± 3.4	137.6 ± 4.1	0.001
Potassium, mg/L	4.4 ± 0.49	4.4 ± 0.53	0.55
Digoxin dose, mcg/kg	2.6 ± 1.0	2.4 ± 1.0	0.02
Creatinine, mg/dL	1.42 ± 0.37	1.61 ± 0.44	0.001
Creatinine clearance, ml/min	68.8 ± 29.9	58.5 ± 29.1	0.001
Lymphocytes, %	23.8 ± 7.9	20.4 ± 8.2	0.001
Vesnarinone dose (0/30/60 mg)	256/271/326	54/56/62	0.5088
MLWHF score	51.7 ± 23.1	56.3 ± 23.5	0.02
log TNF-α at baseline	1.67 ± 0.54	1.77 ± 0.6	0.05
log sTNFR1 at baseline	7.4 ± 0.4	7.6 ± 0.5	0.001
log sTNFR2 at baseline	8.3 ± 0.4	8.5 ± 0.4	0.001
log IL-6 at baseline	1.4 ± 0.7	1.8 ± 0.8	0.001
log sIL6R at baseline	3.6 ± 0.3	3.7 ± 0.2	0.004
log TNF-α at 24 weeks	1.7 ± 0.5	1.9 ± 0.6	0.003
log sTNFR1 at 24 weeks	7.4 ± 0.45	7.7 ± 0.48	0.001
log sTNFR2 at 24 weeks	8.3 ± 0.4	8.6 ± 0.4	0.001
log IL-6 at 24 weeks	1.4 ± 0.7	1.95 ± 0.9	0.001
log sIL6R at 24 weeks	3.6 ± 0.26	3.7 ± 0.26	0.03

Incorporating time-series measurements into logistic regression models

There are 18 predictor variables comprising the standard baseline measurements which were used to build the first logistic regression model, shown in Table 2. We used ten-fold cross-validation to assess the predictive accuracy of the model. The C-statistic of this baseline model was 0.73 ± 0.03. The variables BUN, LVEF, cardio-thoracic ratio and percentage lymphocytes account for almost all of the variability in the outcome variable.

Table 2.

Logistic regression model for predicting 52 week mortality using standard baseline measurements

Variable	Coefficient	Std. error	p-value
intercept	−2.12	0.89	0.017
BUN	0.036	0.006	0.00001
ejection fraction	−0.066	0.016	0.00002
lymphocytes	−0.042	0.012	0.0007
cardio-thoracic ratio	3.163	1.263	0.012

C-statistic with ten-fold cross-validation = 0.73 ± 0.03

P(non-survival) = −2.12 + 0.036 * BUN −0.066 * EF −0.042 * lymph + 3.163 * CT-ratio

P(survival) = 1 − P(non-survival)

We next added baseline cytokines, transformed by ICA (see Supplemental Methods), to the 18 standard predictors. The new model is shown in Table 3. As shown, BUN, LVEF, cardiothoracic ratio and percentage lymphocytes continue to be important. The estimated coefficients for these four predictors are very similar to the ones for the previous model. The independent component factor coefficients indicate that baseline levels of IL-6 and TNF add a modest increase to the C-statistic of the model, which was 0.74±0.04 in ten-fold cross-validation.

Table 3.

Logistic regression model for predicting 52 week mortality using standard baseline measurements and baseline cytokines

Variable	Coefficient	Std. error	p-value
intercept	−2.287	0.919	0.013
BUN	0.035	0.006	0.00001
ejection fraction	−0.068	0.016	0.00002
lymphocytes	−0.028	0.013	0.02
cardio-thoracic ratio	3.108	1.31	0.021
X2	0.212	0.09	0.018
X3	−0.238	0.09	0.009

C-statistic with ten-fold cross-validation = 0.74 ± 0.04

X2 = 0.2 log TNF + 0.11 log sTNFR1 + 0.09 log sTNFR2 + 0.71 log IL6 + 0.008 log sIL6R

X3 = 0.4 log TNF − 0.09 log sTNFR1 − 0.08 log sTNFR2 − 0.134 log IL6 + 0.015 log sIL6R

P(non-survival) = −2.287 + 0.035 * BUN −0.068 * EF − 0.028 * lymph + 3.108 * CT-ratio + 0.212 * X2 – 0.238 * X3

P(survival) = 1 − P(non-survival)

The final model that we constructed uses the 18 basic predictors and five major components of the ICA-transformed cytokine levels at baseline and for weeks 8, 16, 24. The estimated model parameters are shown in Table 4. The ten-fold cross-validated C-statistic for the full model was 0.81±0.03. BUN, cardio-thoracic ratio, LVEF, and percentage lymphocytes continued to be significant predictors as in the previous models. A study of the independent components factor coefficients shows that the new significant predictors were the TNF and TNF receptors at weeks 8, 16 and 24 (factor X2 and X3), IL-6 at baseline, week 8 and week 24 (factor X5), and IL-6 receptor levels at baseline, week 8 and week 24 (factor X2). Each independent factor emphasizes a different aspect of the underlying cytokine measurements. The importance of the baseline cytokine values in the model was reduced in the presence of serial follow-up measurements of cytokines. The model accounts for the variance in one-year survival significantly better, as demonstrated in the significant improvement of the ten-fold cross-validated C-statistic from 0.73 ± 0.03 to 0.81 ± 0.03 (p=0.001). Thus the use of a statistical model that incorporates a series of timed measurements of biomarkers (in this case, cytokines) is more accurate than a model that utilizes a single measurement of a biomarker obtained at baseline. Figure 1 shows the receiver operating characteristic curve for all three models and visually demonstrates that follow-up measurements of cytokine levels add significant predictive power.

Table 4.

Logistic regression model for predicting 52 week mortality with standard baseline measurements and cytokines at baseline, 8, 16 and 24 weeks.

Variable	Coefficient	Std. error	p-value
Intercept	−2.88	1.01	0.044
BUN	0.038	0.006	0.00001
ejection fraction	−0.055	0.018	0.003
lymphocytes	−0.026	0.014	0.0056
cardio-thoracic ratio	2.98	1.454	0.04
X2	−0.809	0.084	0.00001
X3	0.233	0.121	0.05
X5	−0.305	0.099	0.002

C-statistic for ten-fold cross-validation = 0.81 ± 0.03

P(non-survival) = −2.88 + 0.038 * BUN − 0.055 * EF − 0.026 * lymph + 2.98 * CT-ratio − 0.809 * X2 + 0.233 * X3 − 0.305 * X3

Factor X2 is determined by sTNFR1 and sTNFR2 at weeks 16 and 24.

Factor X3 is determined by sTNFR1 and sTNFR2 at week 8.

Factor X5 is determined by IL6 at baseline, week 8 and week 24, and sTNFR2 at week 16.

For full definitions of the factors, please consult Supplemental Tables.

Figure 1.

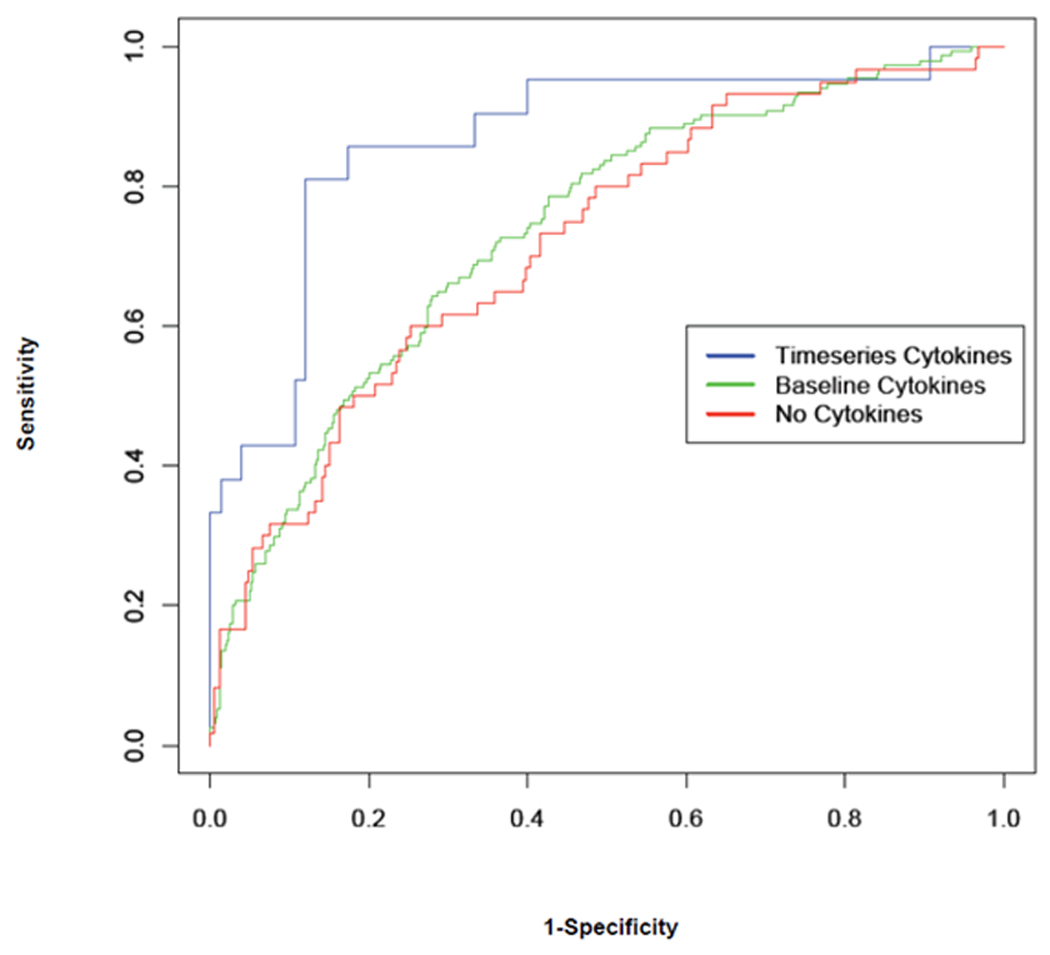
The receiver operating curves for the three logistic regression models for one-year mortality prediction in heart failure, developed in this paper. The three models use standard clinical variables only (no cytokines, C-statistic of 0.73), standard variables and baseline cytokines only (C-statistic of 0.74), and standard variables and serial cytokine measurements at baseline, 8, 16 and 24 weeks (C-statistic of 0.81).

The net reclassification improvement (NRI) is an alternative to the C-statistic for binary classification problems. For our analysis, there is a 1.1% improvement in NRI in moving from the logistic regression model built without cytokines to one with baseline cytokines alone. The improvement in NRI is about 8.7% when comparing the logistic regression model with cytokines up to 24 weeks, against the logistic regression model with baseline cytokines alone. Thus, the NRI measure is consistent with improvements observed in the C-statistic.

An important question that arises from this analysis is whether the improvement in accuracy in predicting mortality at 52 weeks from the time of randomization came from using data available at 24 weeks, as opposed to the data that were obtained at baseline. We did not use the entire complement of measurements at 24 weeks to make predictions of survival at the 52 week time point; rather, we only added the measurement of the cytokine and cytokine receptors up to week 24. The majority of the measurements used in the model were taken from baseline measurements. To make the comparison between the models fair, so that they both make predictions 52 weeks from the last used measurement, we re-ran the logistic regression model construction and evaluation procedure by advancing the prediction horizon to 76 weeks, i.e., 52 weeks after the 24 week cytokine measurement. The model with time series measurements had a C-statistic of 0.79±0.03, which is significantly better (p = 0.01) than the model with baseline cytokines alone, which had a C-statistic of 0.74±0.04. The model without any cytokine data had a C-statistic of 0.73±0.05. This demonstrates that the use of time series data improves prediction accuracy both for the problem of predicting survival at 52 weeks from baseline randomization, as well as between 24 and 76 weeks from baseline.

Ensemble Models

In order to determine whether the C-statistic of 0.81±0.03 represented a “ceiling” for predictive accuracy with respect to HF mortality, we also employed a well-established method in statistical machine learning termed ensemble modeling, which constructs a highly accurate classification model by combining models, instead of producing a single global model. Each model classifies a new data point (patient), and the overall classification is determined by taking a weighted vote of the individual model predictions. The ensemble model that we constructed used the standard predictors for heart failure mortality, and five major components of the ICA-transformed cytokines at baseline and for weeks 8, 16, and 24 weeks. Our model consisted of 100 decision stumps learned by gentle boosting with the logistic loss function. The C-statistic for the ensemble model with ten-fold cross validation was 0.84 ± 0.02, which was significantly better (p=0.04) than the logistic regression models derived before.

In contrast to logistic regression analysis, which can be represented by a single equation, ensemble models are difficult to present directly in the form of a single equation. The standard approach in the machine learning literature [10] is to visualize the model through an “averaged variable importance plot”. The importance of a variable in an ensemble of models is the reduction in prediction error that results from using that variable in a component model, which is then summed over all the components of the ensemble [10]. We average variable importance scores over ten cross-validation runs to produce the plot in Figure 2. This figure groups variables according to their relative importance. As shown, the 24 week cytokine levels, BUN and LVEF were among the top variables in the analysis. The cytokine levels at week 8 are more important than those for week 16. This sorting of the predictor variables allows us to gain insight into how the ensemble works. That is, classifications were based primarily on the cytokine levels at week 24 and week 8, as well as the BUN and LVEF, cardio-thoracic ratio and percentage lymphocytes at baseline. Of note, these baseline variables have been shown to have prognostic importance in other studies. Demographic variables like age, gender and weight and most baseline laboratory values, other than BUN and percentage lymphocytes were not as useful for predicting 52 week mortality.

Figure 2.

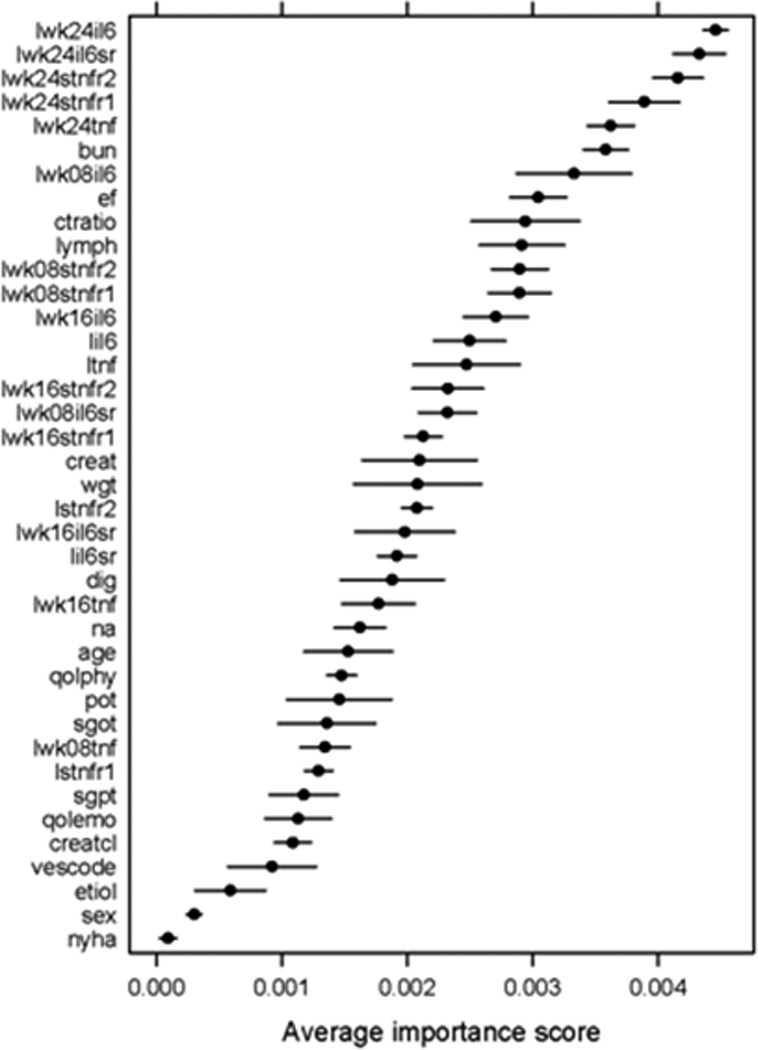
Average variable importance computed over ten cross-validation runs with gentle boosting on 100 decision stumps. The horizontal lines are confidence bars.

These results are consistent with what we observed with the logistic regression model in the previous section. The rise in predictive power comes from moving away from a global model with a single set of coefficients, to a model with 100 different sets of coefficients to capture the variability inherent in a large patient population. The decision regions defined by an ensemble classifier implicitly group patients into cohorts with similar characteristics and similar classifications. This is the essence of personalization as defined by Kohane [15].

A logical question that arises is whether it is possible to obtain similar performance benefits by using ensemble models with baseline measurements alone. To explore this possibility, we built an ensemble model of 100 decision stumps with gentle boosting on baseline data without any cytokines. This model has a C-statistic of 0.74±0.04, which is a modest increase over a single logistic regression model constructed from the same data. This result explains the origin of the significant increase in the C-statistic to 0.84 in the ensemble model that employed serial measurements of cytokines. The increase in the value of the C-statistic comes primarily from the improved accuracy of the constituent classifiers, which use the time series cytokine data, and secondarily from the error reduction effects of majority voting.

Discussion

There are two major new findings of this study. The first is that a multivariate logistic regression model of mortality that employs baseline and serial measurements of cytokine and cytokine receptors levels up to 24 weeks (when added to a standard set of prediction variables), predicts one-year mortality significantly better (C-statistic 0.81 versus 0.73; p =0.001) than does a logistic regression model of mortality without the serial measurements of cytokines and cytokine receptors. Importantly, the C-statistic for the logistic regression model of mortality without serial measurements of cytokines and cytokine receptors was similar to results that have been reported in the literature [7]. Moreover, adding baseline cytokines to the model only improved predictive accuracy from 0.73 to 0.74, which is consistent with a similar study done using the Seattle Heart Failure Model, in which the addition of baseline levels of the biomarker, BNP, did not yield significant changes in prediction accuracy to the overall model [8]. We also examined the accuracy of predicting survival to 76 weeks with each of these models, so that the prediction horizon was 52 weeks away from the 24 week measurement of cytokines. We find that the C-statistic for the model with the time series data was 0.79, which was significantly better (p = 0.01) than the model with baseline cytokines alone (0.74). The model without any cytokines had a C-statistic of 0.73. Thus, significant gains in accuracy of the prediction of one year mortality can be obtained in chronic heart failure by using serial measurements of biomarkers rather than baseline values alone.

The lack of widespread availability and costs of cytokine and cytokine receptor measurements is a potential clinical limitation of our study. Accordingly, this study should be viewed as a proof-of-concept study with respect to the potential advantage of time series measurements in predicting survival. Unfortunately, we were not able to obtain time-series measurements of different types of follow-up data from the VEST data base (including that for BUN, serum sodium, or blood pressure). However, it is likely that time series measurements of standard clinical biomarkers may offer a similar increase in predictive accuracy over multiple measurements obtained at a single point in time. To answer this latter question we will require additional studies.

The results of this study support the point of view that clinical models that predict mortality can be improved significantly by moving away from obtaining a large series of measurements at a single point in time, and focusing instead on a smaller set of relevant measurements (e.g. BUN, BNP, creatinine, troponin, systolic blood pressure) that can be readily obtained during regular follow-up visits. Our data support the point of view that the accurate assessment of patient prognosis is a dynamic, sequential process, rather a static snap shot process based on measurements taken at a single time point. Changes observed with serial measurements are more likely to lead to improved prognostic capability because they reflect both ongoing changes in the underlying disease process, as well as the individual response (i.e. responder or non-responder) of a patient to a given form of therapy. In particular, changes in time series measurements may be especially useful for intermediate risk patients in guiding clinical decisions about aggressive interventions.

It should be noted that while we used measurements at week 8, 16, and 24 from baseline in this study, we do not wish to imply that these are the optimal intervals for serial measurements. Indeed, the optimal timing of number of time series measurements is not known, and will likely vary with the predicted mortality risk and the disease severity of the patient cohort that one is following.

Our model can be easily implemented and adapted for routine clinical use with Web-based calculators, since it mirrors the way physicians themselves update survival estimates based on follow-up visits with their patients. This type of “real time” modeling of prognosis may be invaluable for adjusting medication dose, the timing of implantation of circulatory assist devices and/or cardiac transplantation. Indeed it extends the concept of using a single biomarker to guide HF therapy, insofar as it simultaneously incorporates a variety of different patient variables in the prognostic model.

A second major finding of this study is that an ensemble model learned by gentle boosting [16] performed significantly better (p=0.04) than the standard logistic regression model that employs time series data, and has a C-statistic of 0.84 in a ten-fold cross-validation. We postulate that the reason for this significant increase in predictive accuracy with ensemble modeling is that an ensemble of models adjusts better for the biological variability inherent in clinical studies that are derived from patient data. An ensemble model may thus be useful clinically in terms of predicting outcomes. Analysis of significant predictor variables in the ensemble via the variable importance plot in Figure 2 reveals an important role of cytokine levels in mortality prediction. As shown, the weights for the cytokines and cytokine receptors at weeks 16 and 24 had a greater impact than more traditional markers of poor outcome (e.g., creatinine clearance). These results suggest that ensemble models are likely to be more effective than single models learned from large patient cohorts, and appear promising for personalization of therapy for chronic HF. The inputs to such models will include a selected set of baseline measurements and small amounts of follow-up data. Ensemble models can also be easily adapted for routine clinical use.

As with any multivariate model for outcome prediction, overfitting of the model is an important issue to consider. To reduce the risk of overfitting, we use ten-fold cross-validation. Cross-validation allows various parameters of the model to be estimated and evaluated against multiple subsets of the data set, which reduces the possibility of overfitting. Secondly, the sample size of 963 is large relative to the number of parameters that we assess. Finally, we use regularized forms of the learning algorithms to control model complexity and to minimize risk of overfitting. Further, since our models are derived from the VEST trial and consist only of NYHA class III and IV patients in the VEST database, there is the possibility of selection bias in the model. However, the demographics of patients analyzed are precisely the ones for which accurate estimation of survival probabilities is critical in a regular clinical setting. Finally, the effects of Vesnarinone also need to be taken into account as the original trial showed that Vesnarione had a deleterious effect on mortality with a 4% increase in short term morality over placebo. Vesnarinone was not a significant parameter in our model and did not change the prediction ability even if included by default in the model used. The most likely explanation for this discrepancy would be the fact that our dataset of 963 patients in whom cytokine data was obtained, is a subset of the 3833 patients included in the VEST trial. The differences in mortality between Vesnarinone and placebo were modest and the dataset of 963 used in this paper is not adequately powered to show this difference. As the mortality prediction did not vary even if Vesnarinone was used as a default parameter in the model, we think that it is unlikely to change the generalizability of the model in predicting mortality in advanced HF.

In conclusion, we have developed a model for predicting mortality in patients with advanced HF using baseline standard clinical data and time series data of serum cytokine and cytokine receptor levels. Our results suggest that time series measurements of biomarkers predicts one-year mortality significantly better than does a traditional logistic regression model of mortality that does not incorporate any time series data. Moreover, our results suggest that the predictive accuracy of HF mortality is improved (C-statistic of 0.84) using an ensemble method, which was significantly better than either traditional logistic regression models and/or time series measurements. While the clinical utility of the approach with more readily available serial measurements remains to be assessed, we believe that these models can be easily incorporated into a web based calculator in the clinic in order to provide a “real time” assessment of patient prognosis that can be used to adjust therapeutic strategies while the patient is still in the clinic. Using time series data rather than baseline values alone appears to be the key in improving the accuracy of such prediction models. With that said, it bears emphasis that the results obtained with time series measurements in the VEST data base need to be validated in additional patient cohorts, as well as in prospective studies before they can be used clinically.

Summary.

We analyzed data on 963 patients enrolled in the Vesnarinone Evaluation of Survival Trial (VEST), including circulating levels of two cytokines (TNF and IL-6) and their receptors sampled at baseline, and at 8, 16 and 24 weeks. We built multivariate logistic regression models using standard clinical variables and time-series of cytokine and cytokine receptor levels, using independent components analysis to handle collinearity among cytokine measurements, and L2-penalized stepwise regression for variable selection. We also built ensemble models with these data using gentle boosting. Without the serial cytokines, our baseline model has a C-statistic of 0.73±0.03, while our ensemble model of 100 decision stumps with serial cytokine measurements has a significantly better C-statistic of 0.84±0.02.

The results of our study support the point of view that clinical models that predict mortality can be improved significantly by moving away from obtaining a large series of measurements at a single point in time, and focusing instead on a smaller set of relevant measurements (e.g. BUN, BNP, creatinine, troponin, systolic blood pressure) that can be readily obtained during regular follow-up visits. Changes observed with serial measurements are more likely to lead to improved prognostic capability because they reflect both ongoing changes in the underlying disease process, as well as the individual response (i.e. responder or non-responder) of a patient to a given form of therapy. In particular, changes in time series measurements may be especially useful for intermediate risk patients in guiding clinical decisions about aggressive interventions.