A simple model based on mutation and selection explains trends in codon and amino-acid usage and GC composition within and across genomes

Abstract

Background:

Correlations between genome composition (in terms of GC content) and usage of particular codons and amino acids have been widely reported, but poorly explained. We show here that a simple model of processes acting at the nucleotide level explains codon usage across a large sample of species (311 bacteria, 28 archaea and 257 eukaryotes). The model quantitatively predicts responses (slope and intercept of the regression line on genome GC content) of individual codons and amino acids to genome composition.

Results:

Codons respond to genome composition on the basis of their GC content relative to their synonyms (explaining 71-87% of the variance in response among the different codons, depending on measure). Amino-acid responses are determined by the mean GC content of their codons (explaining 71-79% of the variance). Similar trends hold for genes within a genome. Position-dependent selection for error minimization explains why individual bases respond differently to directional mutation pressure.

Conclusions:

Our model suggests that GC content drives codon usage (rather than the converse). It unifies a large body of empirical evidence concerning relationships between GC content and amino-acid or codon usage in disparate systems. The relationship between GC content and codon and amino-acid usage is ahistorical; it is replicated independently in the three domains of living organisms, reinforcing the idea that genes and genomes at mutation/selection equilibrium reproduce a unique relationship between nucleic acid and protein composition. Thus, the model may be useful in predicting amino-acid or nucleotide sequences in poorly characterized taxa.

Background

Different organisms have idiosyncratic, and sometimes extremely biased, preferences for one synonymous codon over another. Although differences in codon usage among genes and species have been widely studied, general principles have been difficult to find. Although it has been known for some time that the frequencies of some codons and amino acids correlate with genome GC content [1], the causality has remained unclear: correlations could exist because selection for a particular codon or amino-acid usage produces a particular genome GC content, or because mutation towards a particular GC content determines codon and amino-acid usage according to combinatorial principles. Here we show that codon and amino-acid usage is consistent with forces acting on nucleotides, rather than on codons or amino acids, although both mutation and selection play important roles.

Codon usage can be surprisingly biased in different species. For example, the amino acid lysine has two codons, AAA and AAG. Although some organisms, such as Lactobacillus acidophilus, use the two codons equally, others show extreme preferences: Streptomyces venezuelae uses AAA only 2.2% of the time, whereas Buchneria aphidicola uses it for 91% of lysine residues. Amino-acid usage also differs greatly among species: for instance, the amount of arginine varies almost ten-fold, from less than 1.5% of all amino-acid residues in species of Borrelia to 12.7% in Mycobacterium tuberculosis (data from [2]). Because of these extreme biases, knowing an organism's preferred codon usage is of direct practical relevance in minimizing degeneracy of PCR primers and in maximizing the effectiveness of in vivo genetic manipulation. Trends in codon usage across species could also influence molecular phylogenetic reconstruction, and clarify the relative roles of neutral evolution and natural selection in determining nucleotide sequences.

The evolutionary theory of synonymous codon usage began with two separate lines of research, both of which suggested that most substitutions were selectively neutral, but which explained different phenomena. The first line sought to explain interspecific variation in overall sequence composition, and noted correlations between GC content and amino acid content across different species. This suggested that genomes were at equilibrium with respect to mutation, and explained how directional mutation could affect the composition of coding sequences [1,3,4], although it does not explain why species with similar genome compositions have recognizably distinct sequences for individual genes. The second line sought to explain the origin and maintenance of sequence variation within populations, and the fixation of particular alleles between species. This relied on the concept of silent mutations and the relative power of selection and drift in small populations [5,6]. Different usage patterns of synonymous codons are invisible at the protein level: how can selection operate when the amino-acid meaning remains unchanged [7]? However, without directional mutation pressure, the fixation of silent mutants would not lead to the extreme biases in synonymous codon usage actually observed [4].

Subsequently, codon usage in a few species has been extensively characterized, and linked causally to a wide variety of both adaptive and nonadaptive factors including tRNA abundance [8,9,10,11,12,13,14], gene expression level [15,16,17,18,19,20,21,22,23], local compositional biases [24,25,26,27,28], rates and patterns of mutation [29,30,31,32], protein composition [33,34,35,36], protein structure [37,38,39], translation optimization [40,41,42] (but see [43]), gene length [44,45,46,47], and mRNA secondary structure [48,49,50,51,52].

In contrast, trends across species have received far less attention. The genome GC content has been shown to correlate with cross-species differences in frequencies of codons [53,54] and amino acids [29,33,34,55,56,57,58]. Genome composition may even influence the structure and chemistry of proteins [36,57,59]. Comparing different microbial genomes, codon usage in individual genes also correlates with estimated expression level [60,61] and tRNA copy number [62].

One important point is that these regressions are ahistorical: by predicting a relationship between gene and protein composition, these studies imply that the history of a gene or species is unimportant compared to its current state. This has important implications for species or genes that have uncertain phylogenetic relationships or differ greatly in composition from their close relatives. Although closely related organisms tend to have similar genome compositions, there are considerable exceptions (such as Mycoplasma pneumoniae versus M. genitalium). If distantly related species with similar GC contents have the same amino-acid or codon usages, we can conclude that phylogenetic constraints are relatively unimportant, and perhaps that genomes are at or near equilibrium with respect to mutation and selection (otherwise, different unrelated species would not attain the same amino-acid composition predicted from the nucleotide composition). Such ahistorical relationships are particularly useful in cases where the goal is prediction of the current state of a sequence (for example, for making PCR primers), rather than reconstruction of its history.

Although regression lines have been fitted to relationships between GC content and codon and amino-acid usage empirically, permitting qualitative inferences, quantitative theoretical predictions relating these responses to each other have thus far had limited success. This can be remedied by taking into account the differential effect of selection on the different positions within codons. Here we present a simple model, based solely on purifying selection and mutation at the nucleotide level, that quantitatively predicts both codon and amino-acid usage trends across archaea, bacteria and eukaryotes on the basis of the genome GC content.

The model also provides insights into the causality between genome composition and protein composition. Every nucleic acid sequence necessarily has an associated GC content, but there need be no similarities in codon usage between different species with the same GC content (for instance, any specified GC content could be obtained by mixing AAA and GGG codons in different ratios). If GC content were an artifact of selection for a particular codon or amino-acid usage, there would be many different ways of arranging the codon frequencies to get the same GC content. If, on the other hand, the codon and amino-acid usage is an artifact of mutation (or selection) towards a particular GC content, the responses of the three codon positions to directional nucleotide substitution predict a single codon or amino-acid usage for each GC content. Thus, if distantly related species fit the response curves predicted by the model, we can conclude either that forces at the nucleotide level drive codon and amino-acid usage, and there is nothing special about certain codons or amino acids, or that there is a unique spectrum of preferred codon and amino-acid usages that applies to all species, extends over a huge range of compositions, and happens to match the predictions of the model by chance.

Results and discussion

Empirical relationships between GC content and codon/amino-acid frequency

Graphs regressing codon and/or amino-acid frequency onto GC content for subsets of the 64 codons and 20 amino acids (GC response graphs) have been plotted previously, although typically for particular orthologs across up to 30 species [57,58] or for individual genes within a species [29,33,34]. The exception is an analysis of the influence of GC content on average amino-acid composition in 59 bacterial species [56]. Here we plot only the graph for two arginine codons, CGA and CGG (Figure 1a), and for two amino acids, arginine and threonine (Figure 1b), to illustrate that some codons and amino acids, such as CGC and arginine, show a clear relationship with genome GC content; others, such as CGA and threonine, show no relationship whatsoever. All amino acids differ in frequency by two- to ten-fold in different species, however, suggesting that most sites within proteins can tolerate amino-acid substitutions.

Figure 1.

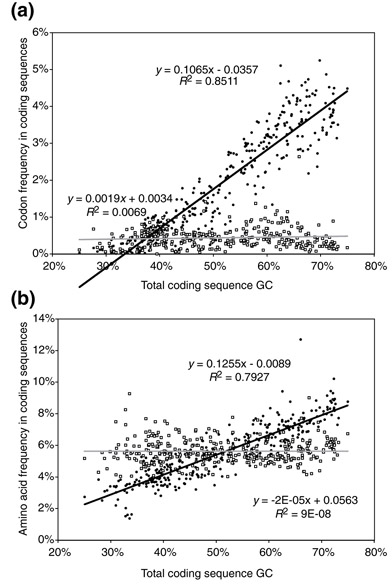
Only some codons and amino acids respond to GC content. (a) Plot of codon frequency within coding sequences versus total GC content, for the arginine codons CGA (white squares) and CGC (black circles) in bacteria and archaea. Linear regression lines are shown in black for CGC and gray for CGA. (b) A similar plot for the amino acids threonine (white squares) and arginine (black circles) in bacteria and archaea. The plots show that whereas CGC and arginine clearly correlate with GC content, CGA and threonine do not. The three relevant parameters for the response, slope, intercept and correlation coefficient, are all highly correlated with each other (see Table 1).

The following regression analyses assume a specific flow of causality: that GC content drives codon (and amino-acid) usage. We favor this direction because there are many ways to get a GC content from different codon usages, but only one way to predict a set of codon usages from GC content. Our interpretation follows Muto and Osawa's seminal demonstration of the high correlation between the GC content of noncoding, exon, intron, tRNA and rRNA sequences, which indicates that a common force influences the composition of all parts of the genome [53].

Three different properties of the regression line could be considered as measures of a codon's (or amino acid's) response to GC content: the slope (which describes the rate of response, or sensitivity, to GC content variation), the intercept (marking the lower boundary of GC content, at which the codon/amino acid is predicted to disappear), and the correlation coefficient (describing the degree of variation in codon/amino-acid usage that can be understood in terms of genome GC content). These three measures are in fact highly correlated with one another (Table 1). We use total GC content rather than third position GC content (GC3) for the regressions, as total GC is easily measured directly in the laboratory for otherwise uncharacterized organisms; to estimate GC3, at least some gene sequences are required. In principle, it is preferable to use GC3 where available, as total genome (or coding sequence) GC already contains the data used to measure the GC content at the other positions. Consequently, regressing GC1 or GC2 against total GC might introduce systematic biases, whereas regressing against GC3 better represents deviation from neutrality [4]. However, total GC and GC3 are so highly correlated (in part because GC3 changes much faster than GC1 and GC2) that for practical purposes it makes no difference.

Table 1.

Pairwise correlations between measures of response to genome GC content

	Amino acids (n = 21)				Codons (n = 64)
	Archaea/bacteria		Eukaryotes		Archaea/bacteria		Eukaryotes
	Slope	Intercept	Slope	Intercept	Slope	Intercept	Slope	Intercept
Slope	-	0.95	-	0.96	-	0.90	-	0.91
Correlation coefficient	0.92	0.96	0.96	0.98	0.90	0.97	0.94	0.94

All pairs of measures are highly correlated. Critical values: for amino acids (n = 21 including stop codons), r of 0.9 corresponds to P = 3 × 10 ^-8. For codons (n = 64), r of 0.9 corresponds to P = 5 × 10^-24. The x intercept is transformed as x' = 1/(50% - x) to minimize the effects of extreme values with large errors: this occurs for codons and amino acids with very flat slopes.

The factors determining the response of each codon and each amino acid to genome GC content turn out to be surprisingly simple. An amino acid's response (Figure 2a) is determined by the mean GC content of its codons (that is, the amino acids with particularly AT- or GC-rich codons are most sensitive to genome GC content), which explains 71-79% of the variance in response, depending on the measure used (slope is the poorest fit; correlation coefficient is the best). A codon's response (Figure 2b) is determined by the difference between its GC content and the mean GC content of its synonyms, explaining 71-87% of the variance. (In other words, genome GC content influences the presence or absence of codons with extreme GC content more than synonyms with intermediate GC content. This follows from the fact that the third codon position changes faster than the other two positions, and does not depend directly on the amino acid that each codon encodes.) This relationship applies to both eukaryotes and prokaryotes. Most of the diversity in GC content within eukaryotes, and hence most of the significance of the regressions, comes from unicellular and multinucleate organisms, including fungi and protists, rather than from the multicellular plants and metazoa. This is to be expected, because the relatively early-diverging protist lineages also account for most of the molecular diversity within the eukaryotes [63].

Figure 2.

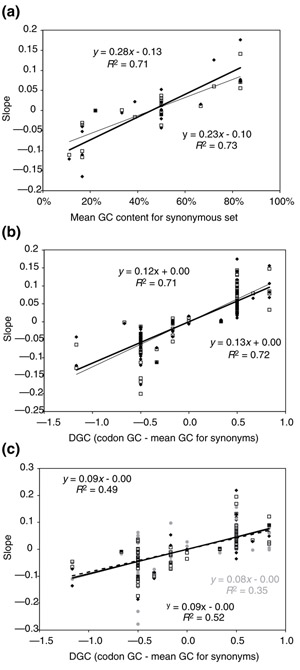
Codon and amino-acid responses are determined by their individual GC content. (a) Plot of response to GC content (here, the slope of the regression of absolute frequency in coding sequences on genome GC content) versus composition of the 21 codon sets (20 amino acids and termination) for archaea/bacteria (black symbols, thick lines) and eukaryotes (white symbols, thin lines). (b) A similar plot for the 64 codons. Note that, of the three measures of response, the slope is the least highly correlated with codon or amino-acid composition (see Table 2). For amino acids the composition is the mean GC content of their codons (a). For codons (b,c) the composition is the difference (ΔGC) between the codon's GC content and the mean GC content for all codons encoding the corresponding amino acid. (c) A response-composition plot of the 64 codons showing response within genomes rather than between them, for a bacterium (Synechocystis, black symbols, thick line), an archaean (Archaeoglobus, gray symbols, gray line), and a eukaryote (Drosophila, white symbols, dashed line). The gray line is almost coincident with the thick line; the points are clustered along the abscissa because the structure of the code restricts the possible GC content of the codon sets.

Although the figures reported above include termination codons, excluding these codons does not greatly affect the result (for instance, R² increases from 0.72-0.75 for slope in the codon graph for eukaryotes when the three termination codons are excluded). Similarly, excluding tryptophan and methionine, which have only one codon each and thus necessarily fall at the origin, makes no difference, as the best-fit line (for codons) passes through the origin anyway. Excluding stop codons, tryptophan and methionine increases R² by only 0.019 on average for the various measures of response. Excluding stop codons makes slightly more difference on the amino-acid graph (increasing R² by 0.031 on average, more influential than any single amino-acid point). When stop codons, tryptophan and methionine are all excluded, R² increases by only 0.046 on average.

Interestingly, the same sorts of relationships seem to hold within, as well as among genomes. Figure 2c examines the response of codons to GC content across individual genes within sample genomes representing all three domains of life: eukaryotes (Drosophila), bacteria (Synechocystis), and archaea (Archaeoglobus). The codon frequency in individual genes seems to be predictable on the basis of the overall GC content of the coding sequences: the relative GC content of individual codons explains about half the variance in response in their absolute frequencies within each coding sequence (that is, the presence or absence of a particular codon depends on the extent to which alternative synonyms of more 'suitable' GC content exist). This is despite the fact that codon usage in individual genes is known to be influenced by a long list of other factors, including the amino-acid sequence necessary for the gene's function (although the fraction of crucial residues may typically be small). The effect cannot be fully explained by synonymous substitutions, because codons with the same third-position base but different codon doublets respond differently.

Before proceeding, we note that these plots themselves emphasize the causality within the system. Our analysis shows that all amino acids and all codons behave in a predictable manner within each genome, indicating that the GC content within coding sequences determines the codon (and hence amino-acid) composition rather than being a passive reflection of a preferred codon or amino-acid usage. Hence, this uniform robustness supports the idea that there is little special about particular codons or amino acids. In all three domains of life, it appears that every codon and every amino acid follows a single trend determined by the overall compositional properties of genomes. Even within genomes, the overall composition of individual genes seems to explain up to half the variance in the responses of the individual codons and amino acids. This raises the question: what drives GC content?

A mutational model

The simple empirical relationship between the composition of codons and amino acids and their responses to changing genome composition suggests that these responses might be quantitatively predictable on theoretical grounds. We take as our starting points Sueoka's hypothesis that genome composition is largely determined by mutation bias, specifically the ratio of AT→GC to GC→AT mutations [3,29,32], and Muto and Osawa's demonstration that different types of sequence, and the three codon positions within exon sequences, vary in their response to genome GC content with the third position changing the fastest, which suggests that the different observed substitution rates might be explained by the differential effects of mutation [53].

We assume for simplicity that the genome is divided into two types of site - constant and variable; that all variable sites respond identically to mutational pressure; and that all third-position sites are variable (that is, that under this initial model there is no selective consequence to silent mutations). Accordingly, GC3 (the third-position GC content) reflects the ratio of AT→GC to GC→AT mutations. When plotted against GC3, the slope of the GC1 and GC2 graphs give the intensity of selection at those two positions relative to GC3 [4], whereas the values at GC3 = 0% and GC3 = 100% give the identity of the bases at the constant positions (Figure 3). In other words, when all the variable sites (as measured by GC3) are as biased as possible towards one state, we assume that any sites at position 1 or 2 that still have the opposite state are maintained by selection and cannot change. Thus, the frequency of each codon can be estimated as:

Figure 3.

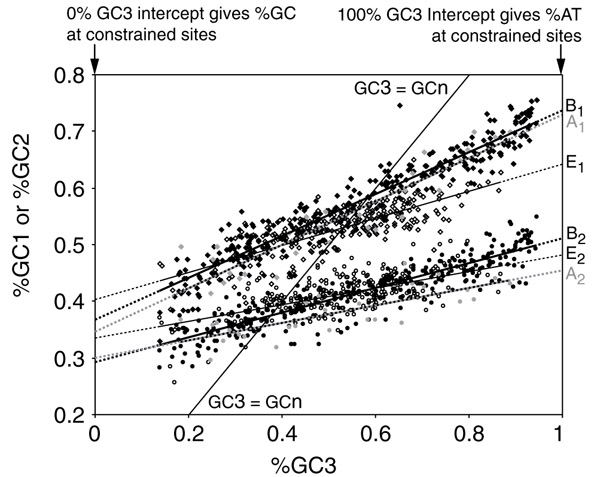
The codon responseto genome GC content varies with position. A re-plot of GC3 versus GC1, GC2 from [4], using the additional sequence data now available. Each point represents an organism, classified by domain: archaea, gray; bacteria, black; eukaryotes, white. GC1, diamonds; GC2, squares. Lines are model I least-squares regressions. Where GC3 = 0%, the remaining %GC in position 1 and position 2 is assumed to represent constant sites (that is, those fixed by selection to remain G or C). Similarly, where GC3 = 100%, the remaining %AT in position 1 and position 2 is assumed to represent constant sites where A or T have been fixed.

P[XYZ] = P[X₁]P[Y₂]P[Z₃]        (1)

where P[X₁], P[Y₂], and P[Z₃] denote the probability of getting base X at position 1, base Y at position 2, and base Z at position 3, respectively.

The probability of getting a particular base at a particular position is given by:

P[X_n] = P[X|c_n]P[c_n] + P[X|v]P[v_n]        (2)

where P[c_n] denotes the probability that a site is constant at position n, and P[v_n] denotes the probability that a site is variable at position n (that is, that it is not constant). These two probabilities sum to 1. P[X|c_n] denotes the conditional probability of getting base X at a constant site at position n, and P[X|v] denotes the conditional probability of getting base X at a variable site (assumed to be the same across all three positions).

Comparing the responses of GC1 and GC2 to GC3 (Figure 3, Tables 2 and 3), we can see that:

Table 2.

Correlations between composition and response to GC content

	Amino acids		Codons
Correlation	Archaea/	Eukaryotes	Archaea/	Eukaryotes
with:	bacteria		bacteria
Slope	0.842	0.853	0.840	0.849
Intercept	0.878	0.886	0.931	0.910
Correlation	0.886	0.887	0.934	0.922
coefficient

Amino acids: correlation of each measure of response with mean codon GC content. Codons: correlations with difference between GC content and mean GC content of synonymous codons. See also Figure 2.

Table 3.

Responses of GC1 and GC2 to changes in GC3, by domain

	n		R2	Slope ± SE	Y at GC3 = 0 ± SE	Y at GC3 = 100 ± SE
Bacteria	311	GC1	0.91	0.370 ± 0.007	0.367 ± 0.004	0.737 ± 0.003
		GC2	0.80	0.219 ± 0.006	0.291 ± 0.004	0.510 ± 0.003
Archaea	28	GC1	0.85	0.38 ± 0.03	0.35 ± 0.02	0.73 ± 0.02
		GC2	0.60	0.16 ± 0.03	0.30 ± 0.01	0.45 ± 0.01
Eukaryotes	257	GC1	0.57	0.24 ± 0.01	0.402 ± 0.008	0.643 ± 0.007
		GC2	0.38	0.15 ± 0.01	0.334 ± 0.007	0.482 ± 0.006

Because there is error in both axes, but there should be a definite causal relationship between GC3 and GC1 or GC2, we use model I regression to predict specific values of GC1 or GC2 from a set value of GC3, and thus to calculate the most likely proportion and GC content of constant sites [73].

1. The slopes for GC1 in bacteria and archaea are almost identical. However, the bacterial/archaeal slope differs significantly from the eukaryotic slope. Thus, first-position residues are less labile among the eukaryotes tested. (Note that the number of degrees of freedom is n1 + n2 - 4: the data are constrained by a sum and a regression mean-square).

2. The slopes for GC2 are not significantly different in the three domains.

3. The intercepts for archaea and bacteria do not differ, except for GC2 when GC3 is 100%. The intercepts for the pooled archaea/bacteria sample always differ from those of eukaryotes.

4. Archaea behave far more like bacteria than like eukaryotes. Using the Kolmogorov-Smirnov test in two dimensions as implemented in [64], N_A = 28, N_B = 311, N_E = 257: for GC1 versus GC3, D_AB = 0.19, P_AB = 0.33, D_AE = 0.30, P_AE = 0.03; for GC2 versus GC3, D_AB = 0.21, P_AB = 0.02; D_AE = 0.54, P_AE = 4 × 10^-6. Differences between eukaryotes and bacteria, or between eukaryotes and the combined archaeal/bacterial data set, were highly significant (P < 10^-6 that both represent samples drawn from the same population for each pairwise test).

5. The general patterns are replicated in the three domains. Thus, the relationship between the first-, second- and third-position GC content emerges independently in evolutionarily separate groups. Further subdividing each domain shows that many lineages have explored the same wide range of GC contents, reproducing the same relationships.

The major distinction is between eukaryotes and prokaryotes, which presumably has an ecological or structural rather than a phylogenetic explanation. The slopes may be different because of the great differences in genome size and generation time, or because the partitioning of genetic material into the specialized environment of the nucleus changes patterns of mutation. Eukaryotes also have far more noncoding DNA, which could potentially isolate coding regions from selection for genomic GC content if this were an important force: however, for this analysis we consider only the coding regions, which still differ greatly in composition among different eukaryotes (suggesting that selection has not acted to conserve the GC content of coding sequences). The intercepts may be different because the set of proteins in each domain differs, and so the distribution of nucleotides in critical sites need not be conserved. It is also possible that the selection of genes that have been studied differs between the groups, although the few organisms for which complete genomes are known are not outliers. To reflect the major differences separating the eukaryotes from the other domains, we pooled the archaeal and bacterial data and contrast this with the eukaryotic data, fitting slopes and intercepts to the model for the two groups separately.

Does the model accurately reflect codon usage?

The model outlined above requires four parameters (estimated GC1 and GC2 at GC3 = 0% and GC3 = 100%) defined from the data, and uses these to predict the slopes and intercepts of regressions on GC content of the 64 codons and 21 codon sets (20 amino acids and termination). As the model is deterministic, it is not useful for predicting the correlation coefficients. When composition is summed across all three codon positions (for example, CGA and GGT would be counted among the eight codons comprised of two G or C and one A or T, with the A/T at the third position), the model is remarkably accurate for both bacteria (Figure 4a-c) and eukaryotes (Figure 4d), though in each case, GC3 shows the greatest deviations from the model (perhaps indicating that the labile GC3 is 'fine tuned' by the other selective pressures linked to codon usage).

Figure 4.

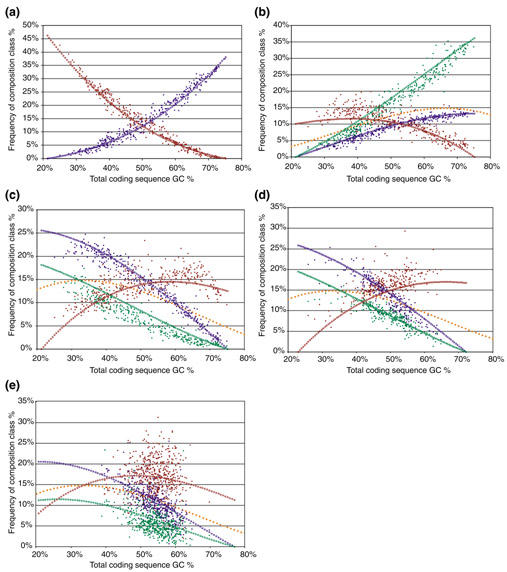
Predicted versus actual responses for sets of codons with identical composition. Each line is the sum of eight codons with the same GC content (by position). Each solid circle is a species. Lines of open circles are the theoretical predictions based on the four-parameter model. (a) All-GC (blue) and all-AT (red) codons in prokaryotes. (b) Codons with two G or C and one A or T, the minority base being at the first (blue), second (green), or third (red) position. Note that the third-position slope is actually of opposite sign to the first- and second-position slopes. The orange line is what would be expected if there were no position dependence (that is, P(GC)²P(AT) as in [56]). (c) As in (b), but for codons with two A or T and one G or C. In this case, the orange line is P(AT)²P(GC). (d) As in (c), but for eukaryotes. (e) As in (d), but now each point is a randomly chosen gene in Drosophila.

This model even performs moderately well when applied to a random sample of 500 genes from the Drosophila genome (Figure 4e): although the unexplained variance is much greater, the points clearly cluster around the three lines predicted by the position-dependent model rather than the single (orange) line that overall composition alone would predict (as in previous, simpler models). In each case, the white-centered lines are the theoretical predictions, and each dark point represents a species. The orange line is the frequency that would be expected from the GC content without taking into account the position-dependent composition biases, that is by (GC)ⁿ(1-GC)^3-n, where GC is the genome GC content and n is the number of G and C in the codon [56]. Taking the position dependence into account thus provides a much better fit to the data.

We compare the predicted and actual slopes for each of the 64 codons in Figure 5. The model explains 77% of the variance in slopes for the regression of codon frequency on GC content in eukaryotes, and 80% of the variance in prokaryotes. Additionally, the model is an unbiased estimator: the slopes are 1, and the intercepts are 0. The results are similar for the intercepts, and for amino-acid usages (Table 4).

Figure 5.

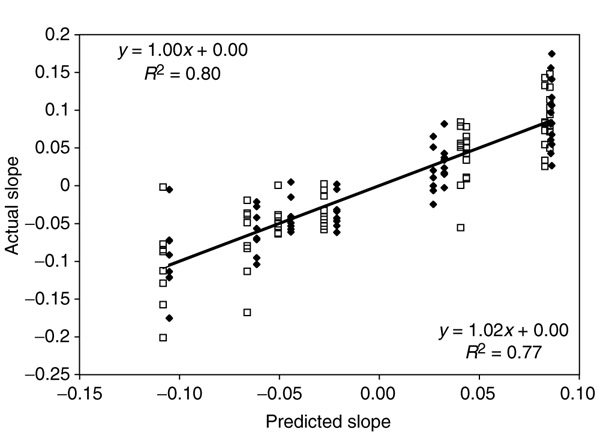
Comparison of predicted versus actual codon responses. Both bacteria/archaea (black) and eukaryotes (white) show a very good fit between the model and the data (in this case, predicted slopes along the x axis and actual slopes along the y axis). The slope is 1 and passes through the origin in both cases, indicating that the model is an unbiased predictor of codon usage trends. See Table 4 for other comparisons.

Table 4.

Concordance between predictions and data

		Archaea/bacteria			Eukaryotes
	Amino acids/codons	Observed	Four-parameter	24-parameter	Observed	Four-parameter	24-parameter
Observed	Slope	-	0.89	0.93	-	0.88	0.92
	Intercept	-	0.91	0.92	-	0.90	0.91
Four-parameter	Slope	0.83	-	0.95	0.80	-	0.96
	Intercept	0.82	-	0.99	0.80	-	0.98
24-parameter	Slope	0.90	0.94	-	0.85	0.95	-
	Intercept	0.86	0.96	-	0.80	0.95	-

Each entry is the correlation coefficient between the predicted and observed values for the 64 codons (above the diagonal) or 21 amino acid sets (below the diagonal) for archaea and bacteria (left) and eukaryotes (right). See Figure 5 for an example (the graph for the first entry on the second column: note that the graph shows R², not R).

Can selection account for the remaining variance?

The four-parameter model discussed above assumes, for the sake of simplicity, that A = T and C = G (Chargaff's rule). For double-stranded DNA molecules, this is necessarily true because of Watson-Crick base pairing. Less well known is the intra-strand Chargaff's rule, which states that the same relationship holds within large, single-stranded DNA molecules (in particular, the two strands of the Bacillus subtilis genome) [65,66]. The interpretation of this intra-strand rule is statistical rather than mechanical: if there are no biases in mutation and selection between the two strands, or if genes are distributed evenly between the two strands, a C→G mutation on one strand (for example) cannot be distinguished from a G→C mutation on the other. Thus, the twelve possible nucleotide-substitution rates reduce to just six and, at equilibrium, Chargaff's rule should hold even within the set of coding sequences in a genome [30]. As long as all nucleotide-substitution rates are positive, this equilibrium condition holds for all possible substitution matrices [67].

In actual genomes, however, the intra-strand Chargaff's rule is frequently violated because the leading and lagging strands have different substitution patterns and genes are not evenly distributed [31]. In respect of our model, not only the position of a base but also its identity affects how fast it responds to genome GC content (Table 5). Interestingly, the intra-strand Chargaff's rule is violated in a position-dependent manner. For both prokaryotes and eukaryotes, the third codon position is pyrimidine-rich (C3/G3 = 1.11 and 1.15 respectively; T3/A3 = 1.24 and 1.36), and the first codon position is purine-rich (C1/G1 = 0.58 and 0.62; T1/A1 = 0.63 and 0.65). The second codon position is mixed (C2/G2 = 1.34 and 1.32; T2/A2 = 0.97 and 0.87). Consequently, relaxing the assumption of the intra-strand Chargaff's rule should increase the accuracy of the model.

Table 5.

Violations of Chargaff's rule and rate constancy

	|slope A/B|	|slope E|	Error
T1	0.251	0.248	6.591
C1	0.421	0.382	4.640
A1	0.466	0.334	2.474
G1	0.296	0.201	3.930
T2	0.095	0.126	7.738
C2	0.221	0.217	5.256
A2	0.333	0.254	11.984
G2	0.207	0.163	7.487
T3	0.938	0.986	0.065
C3	1.108	1.212	0.065
A3	0.917	1.051	0.076
G3	0.746	0.825	0.082

|slope AB| is the absolute value of the change of a given nucleotide at a given position (relative to total coding sequence GC content) in archaea/bacteria; |slope E| is the corresponding slope in eukaryotes. Error is a measure of the average consequence of a change in a particular base at a particular codon position (for example, T1 is T at the first position, using a methodology based on [69]. See text for explanation.

These differences in composition could reflect coding constraints, if a functional proteome required a particular amino-acid composition. As we have seen, however, the frequency of particular amino acids varies greatly among different organisms, decreasing the likelihood that there is a unique, optimal composition. Additionally, the amino acids respond predictably with changing GC content, in a manner consistent with processes acting only at the level of single nucleotides.

If the bases do not change at the same rates, the assumption that the GC content at each position completely describes the nucleotide composition is unwarranted. The four-parameter model discussed above assumes that, for each of the three codon positions, each of the four bases changes equally rapidly with changing genome GC content. Interestingly, this is not actually the case. For example, G changes far more slowly than any other nucleotide when at the third codon position, but faster than T when at the first or second codon position. Furthermore, A at the second position changes nearly twice as fast as T at the second position (Table 5). This violates the assumption that all variable sites are equal.

Is there any rationale behind these seemingly arbitrary rates? Here, selection rather than mutation may provide an answer. Most mutations are deleterious; furthermore, the greater the effect of a particular change, the less likely it is to be advantageous [68]. We can estimate the average effect of changing each base at each position according to a method used previously to calculate the effects of errors in individual codons [69]. Briefly, for each mutation, the difference in 'polar requirement' [70,71] between amino acids encoded by the original and new codons is squared. The resulting error value is averaged for all applicable mutations, weighting transitions more heavily than transversions because they occur more frequently (in this case, by a factor of 4 as reported in [72] for comparison of human pseudogenes with their functional predecessors). This gives an a priori estimate of the impact of a given set of mutations based on the chemical properties of the amino acids and the configuration of the genetic code.

In fact, the mean-square error does an excellent job of accounting for the difference in slopes. The mean-square errors give a logarithmic fit to the rates of change, but because there is no reason to believe this functional relation to be the correct one we used a nonparametric test for correlation (Spearman's rank coefficient [73]). For eukaryotes, r_s = -0.83 (P = 8.3 × 10^-4); for prokaryotes, r_s = -0.86 (P = 3.3 × 10^-4); n = 12 in both cases. The rank order of the mean-square errors does not change when the modular power and/or the transition bias are varied over the range one to ten, so the correlations are robust across parameter space. In other words, because the rate of change of the different nucleotides depends on the magnitude of error introduced on average by altering them, we interpret the variable response of GC content at each position to be dependent on base identity as the result of selection against substitution of dissimilar amino acids.

Relaxing the constraints of the model

To take differential selection into account, we relax the assumption of the intra-strand Chargaff's rule as follows. The four-parameter model presented above requires two parameters each for two regression lines, relating the first- and second-position GC content to the third-position GC content. However, if the frequencies of the four nucleotides at each codon position can vary independently with GC content (subject to the constraint that the nucleotide frequencies at each position are constrained by a sum), it is necessary to characterize the regression lines of each base at each position to make predictions about the nucleotide composition of the set of constant bases at each position, and of the most likely states of variable bases for a given GC content.

Hence we constructed a 24-parameter model (4 bases × 3 positions × 2 parameters for each regression line) where, for each position, we plotted the percentage of each of the four bases against total GC content. For a given total GC content, the expected frequency of a particular base at a particular position is estimated directly from its regression line, which is based on two parameters (the slope and the intercept). This takes into account the fact that an organism at a given GC content will predictably violate the intra-strand Chargaff's rule in its coding sequences. This could be considered an extension of Takahata's analysis of rate heterogeneity among the four nucleotides [74], but extended for the reading-frame-dependent selection in coding sequences. The model actually has only 18 degrees of freedom (rather than 24), as the sums are constrained, but predicts a set of codon frequencies that potentially has 63 degrees of freedom.

This 24-parameter model explains somewhat more of the variance in both codon and amino-acid responses (slope and intercept), although the marginal benefit is greater in prokaryotes than in eukaryotes (Table 4). The improvement in R² can explain nearly 40% of the variance unexplained by the four-parameter model in some cases (amino-acid slopes in archaea/bacteria), although in other cases the 24-parameter model does not offer an improvement (for example, amino-acid intercepts in eukaryotes). One possible interpretation is that for our data set selection plays a greater role in the genome composition of prokaryotes. This is certainly plausible given the bias in eukaryotic sequences towards large species with small populations. More generally, we may infer that, on the scale of whole genomes, differential mutation and selection between the two strands play relatively little role in determining codon usage.

Conclusions

We have shown that the GC content of individual codons and amino acids is the primary determinant of their response to biases in sequence composition, both among and (to a lesser extent) within genomes. Although the literature contains many examples of correlations between GC content and the frequency of particular codons and amino acids, our model is able to recapture quantitatively the behavior of essentially all codons and amino acids by invoking forces that act only on the level of individual nucleotides. This is likely to be due to a combination of mutation and selection: mutation can act in parallel across an entire genome, changing many sites simultaneously; however, this process is limited by the consequences of error at each position.

The simplest hypothesis, that codon usage depends solely on codon GC content [56], fits the data poorly (compare orange lines with red, green and blue lines in Figure 4). One can, however, explain most of the variance in the response of both codons and amino acids by taking into account the fact that the three codon positions change at different rates, and that the four nucleotides are not evenly distributed among the sites that are functionally constrained. Additionally, accounting for the fact that the four nucleotides change at different rates allows some further improvement, which ranges from minimal to drastic depending on the exact circumstances. This supports the basic principle of neutral evolution, the idea that most change in nucleotide and protein sequences is driven by mutation and limited by purifying selection that varies for different sites and molecules (reviewed in [75]). Within this context, it supports the idea that most of this neutral change is driven by directional mutation, which thus explains differences in nucleotide composition among species [4].

Although the conclusion that amino acids with GC-rich codon doublets are more frequent in GC-rich genomes, and that those with AU-rich codon doublets are more frequent in AT-rich genomes, is neither new nor surprising [34], our model accurately and quantitatively predicts these responses for essentially all codons and amino acids by invoking forces acting on individual nucleotides. The genetic code constrains which codons and which amino acids can respond to biases in nucleotide composition, in part because mixed codons necessarily respond more slowly to forces acting on particular types of bases than do homogeneous codons. Thus, although GC content only explains the variance in usage of some codons and some amino acids, we can accurately predict which codons and amino acids will show clear responses and, for those that do show clear responses, accurately predict their frequencies in particular genomes (for example, Figure 1 shows an example of a codon for which 85% of the variance in usage is explained by genome GC content, and an amino acid for which 79% of the variance is explained). Thus, especially for species with few close relatives, variable sites may even be more useful for predicting PCR primer sequences than conserved sites, although this will depend on the particular sequence and genome composition.

We have focused on codon usage at the level of whole genomes (or samples of genes where whole genomes are not available), an area that has received relatively little attention. This large-scale view does not consider the selective factors influencing individual genes, and the fact that the model provides much better fit across genomes than within them may reflect local adaptation to factors such as expression level [11]. What remains surprising is that our simple model can explain so much of the variance in codon and amino-acid response to GC content in these different systems. Identifying deviations from the predictions based on nucleotide composition may identify genes that are under unusual selection pressures, whether for a particular amino-acid composition or for a specific pattern or degree of codon bias.

The fact that both amino-acid and codon usage are so closely entwined with genome composition has important practical implications. For phylogenetic analysis, the fact that some amino acids (such as arginine) change rapidly and predictably with GC content slightly undermines the idea that amino-acid sequences are more stable than nucleotide sequences: pairs of species with convergent GC contents might also evolve convergent protein sequences, especially at functionally unconstrained positions. For example, the frequencies of both lysine and arginine are highly (but oppositely) correlated with GC content, and lysine and arginine can easily substitute for one another in proteins. Each of the three domains of life has explored a wide range of genome GC contents, and organisms at the extremes of the range but with different evolutionary histories may share more convergent amino-acid substitutions than currently recognized.

For sequence analysis, the prospects are more promising: given very limited information about a species (the GC content), it may be possible to estimate the codon usage and therefore minimize the degeneracy of PCR primers, even if no closely related species have been characterized. Organisms with extreme genome compositions, or with genome compositions that differ markedly from their close relatives (such as Mycoplasma pneumoniae versus other mycoplasmas) should be particularly accessible. This should be especially useful in developmental genetics and in environmental applications where model systems are not available.

The fact that the model holds independently for different lineages of organisms (for example, bacteria and eukaryotes), and, to a lesser extent, for individual genes within species, strongly suggests that the trends are ahistorical. Given rates of change for each nucleotide at each codon position, determined jointly by selection, mutation, and the genetic code structure, we can predict the codon and amino-acid composition of a particular sequence from its overall compositional properties, without reference to related sequences. Interestingly, the history of a sequence seems relatively important in determining its codon and amino-acid usage. This fact is likely to be particularly important in cases where a species diverges greatly in GC content from its closest relatives: knowing its GC content will allow much better prediction of specific gene sequences than simple comparison with conserved sites in related sequences (which may in some cases be similar because of shared genome composition rather than functional constraint).

Finally, our model explains many of the details of individual codon and amino-acid responses over the wide range of genome compositions found in nature. Perhaps surprisingly, individual amino acids with specific structural or functional roles within proteins (such as and arginine) respond to GC content no differently than the rest, and their frequencies can be very sensitive to genome composition despite the effects this might have on the properties of the translated products. This ability of amino-acid frequencies to vary so widely implies that functional proteins may be less constrained by sequence (and therefore easier to evolve) than previously imagined.

Materials and methods

Species and gene codon usage totals were downloaded from CUTG (Codon Usage Tabulated from GenBank) [2,76], which is based on GenBank Release 117.0. Of 675 species with at least 20 protein-coding sequences tabulated from nuclear DNA, we excluded 53 eukaryotes and 17 bacteria on the grounds that they had alternative genetic codes (for example, Tetrahymena and Mycoplasma), or had introns accidentally tabulated in the database as part of the coding sequence (for example, Pongo and Homo). These were detected as an excess of termination codons greater than 1 per 20 coding sequences (that is, at least 5% more stop codons than genes). We excluded an additional nine eukaryotes for which a few genes had been tabulated repeatedly as independent sequences (for example, Naja atra), leaving a sample size of 311 bacteria, 28 archaea, and 257 eukaryotes with at least 20 distinct coding sequences tabulated in the database. The choice of 20 coding sequences was arbitrary, intended to ensure a sufficiently large sample size to estimate properties of entire genomes; raising the stringency to species with 50 or 100 coding sequences (288 and 176 species, respectively) reduced the size of our data set but gave almost identical results (data not shown). We made no attempt to separate the genes by chromosome (for eukaryotes), expression level, or location, except that organellar genes were not considered. Except where otherwise noted, 'total GC' refers to the total GC content of coding sequences, rather than of genomes. These values are sufficiently highly correlated that it makes no difference which is used.

We estimated nucleotide and amino-acid compositions for genomes from the species sum records from CUTG, which sum the codons for all nuclear coding sequences deposited in GenBank for each species. We did not make any effort to exclude short, truncated, duplicated or hypothetical genes, although comparison with a filtered data set based on an earlier release of GenBank revealed no significant differences (data not shown). Thus, genes made contributions proportional to their lengths.

Codon frequencies were calculated both including and excluding termination codons. Data reported here include termination codons. Because termination codons are rare, this does not significantly alter the results, except for allowing inferences about the relative usage of UAA, UAG and UGA as termination signals.