Detection of undistorted continuous wave (CW) electron paramagnetic resonance (EPR) spectra with non-adiabatic rapid sweep (NARS) of the magnetic field

Abstract

A continuous wave (CW) electron paramagnetic resonance (EPR) spectrum is typically displayed as the first harmonic response to the application of 100 kHz magnetic field modulation, which is used to enhance sensitivity by reducing the level of 1/f noise. However, magnetic field modulation of any amplitude causes spectral broadening and sacrifices EPR spectral intensity by at least a factor of two. In the work presented here, a CW rapid-scan spectroscopic technique that avoids these compromises and also provides a means of avoiding 1/f noise is developed. This technique, termed non-adiabatic rapid sweep (NARS) EPR, consists of repetitively sweeping the polarizing magnetic field in a linear manner over a spectral fragment with a small coil at a repetition rate that is sufficiently high that receiver noise, microwave phase noise, and environmental microphonics, each of which has 1/f characteristics, are overcome. Nevertheless, the rate of sweep is sufficiently slow that adiabatic responses are avoided and the spin system is always close to thermal equilibrium. The repetitively acquired spectra from the spectral fragment are averaged. Under these conditions, undistorted pure absorption spectra are obtained without broadening or loss of signal intensity. A digital filter such as a moving average is applied to remove high frequency noise, which is approximately equivalent in bandwidth to use of an integrating time constant in conventional field modulation with lock-in detection. Nitroxide spectra at L- and X-band are presented.

1. Introduction

In 1963, Klein and Barton formulated the basic principles of the signal-to-noise ratio (SNR) when using rapid scans and spectral averaging [1]. To paraphrase this work: if noise is white and two spectra are compared, the first acquired in a single scan in time T with an integrating time constant τ and the second acquired by summing n spectra, each acquired in time T/n with integrating time constant τ/n, the SNRs will be the same. However, if the noise has a 1/f character, the latter method will exhibit lower noise. These authors present data in which multiple EPR spectra using magnetic field modulation and lock-in detection were acquired and averaged. In the present paper, we extend the method of Klein and Barton by using direct detection and compare results with data obtained using the conventional 100 kHz magnetic field modulation method, which also overcomes 1/f noise. The applications are to spin labels, but the methodology and conclusions are widely applicable.

The method presented here utilizes non-adiabatic rapid-sweep (NARS) EPR. A small magnetic field sweep coil produces a triangular variation of the polarizing magnetic field over a spectral fragment at a repetition rate that is sufficiently high that 1/f noise arising from the receiver, the microwave source, and the environment is overcome. An analog-to-digital converter (ADC) with a high sampling rate converts the detected signal to a digital format, which is then averaged as the spectral fragment is repetitively swept. A series of spectral segments is collected across the spectrum and combined to arrive at a complete pure absorption spectrum. This spectrum will contain high frequency noise since it was acquired at high bandwidth. A digital filter is applied to remove this noise, which reduces the bandwidth in a manner that is analogous to use of an integrating time constant.

Bloch found two solutions to the phenomenological equations that bear his name, depending on whether or not the sweep of the magnetic field was adiabatic (i.e., so rapid that no thermal relaxation of excited spins occurs) or non-adiabatic such that the spin system remains in thermal equilibrium during sweep through the resonance condition [2]. The adiabatic condition is given in Eq. (1) in a form provided by Pake, where H₁ is the magnitude of the incident RF field, H_o is the static magnetic field, ω is the RF frequency, γ is the gyromagnetic ratio, and T₁ is the spin-lattice relaxation time [3].

$$H_1^{-1}|(d/dt)(H_0-\omega /\gamma )|\gg 1/T_1,\text{Adiabatic}$$ (1)

$$H_1^{-1}|(d/dt)(H_0-\omega /\gamma )|\ll 1/T_1,\text{Non-adiabatic}$$ (2)

The basic idea of NARS is to satisfy the condition for non-adiabatic sweep, Eq. (2), but at the same time to use a sufficiently rapid sweep repetition rate that 1/f noise is avoided. Whether or not these conditions can be satisfied depends on the spin-lattice relaxation time.

A loop-gap resonator (LGR) is advantageous for NARS EPR because it exhibits a lower quality factor, Q, and a higher filling factor, η, than a cavity resonator [4]. The power needed to achieve the same H₁ field at the sample is reduced, and the effects of phase noise and microphonics are diminished. The incorporation of a low-noise microwave amplifier (LNA) improves receiver performance. The amplifier is placed after the resonator, but before the signal mixer, to boost noise on the microwave carrier above the 1/f noise of the receiver. Improvement in the performance of ADCs permits sampling frequencies that are fast relative to the polarizing field sweep. In this manner, sensitivity is greatly improved, even though the rate of sweep of magnetic field through resonance is reduced in accordance with Eq. (2). In summary, following Klein and Barton, the SNR is improved by increase in the number of accumulations per second, which diminishes the impact of 1/f phase noise [1].

We turn to a consideration of magnetic field modulation, which consists of superimposing a sinusoidal field of the form H_m [sin (ω_mt)] onto the static magnetic field, where H_m is the modulation amplitude and ω_m is the modulation frequency. When resonance occurs, microwave sidebands arise ± nω_m away from the microwave carrier frequency. By offsetting the EPR microwave signal sidebands from the carrier and detecting them with a lock-in detector followed by an integrating time constant, microwave source phase noise is diminished, and if ω_m is sufficiently high, 1/f detector noise and microphonics are also reduced [5].

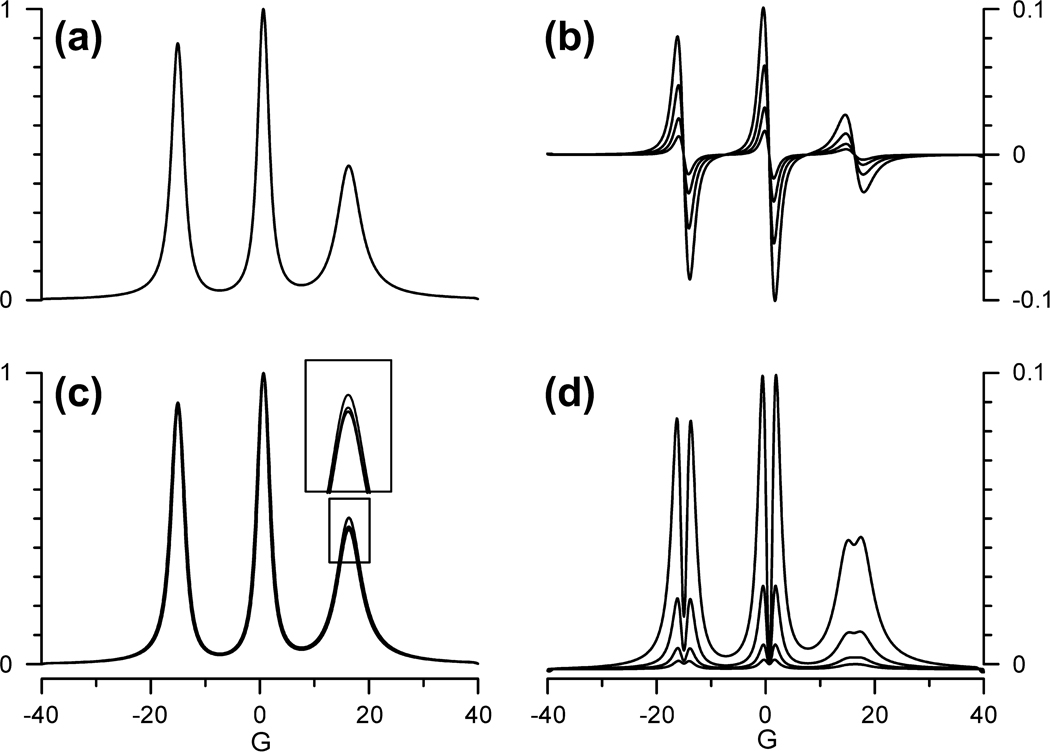
The noise in the system is ultimately determined by the integrating time constant, which establishes the receiver bandwidth. The digital filter in NARS detection and the use of the integrating time constant in the lock-in detection method are approximately equivalent. However, the lock-in method has a disadvantage because all magnetic field modulation causes spectral broadening and sacrifices EPR signal intensity. The extent of these effects is related to the modulation amplitude compared to the EPR linewidth. Figure 1 displays the effects of magnetic field modulation on a nitroxide undergoing intermediate motion using EasySpin, a MATLAB® (MathWorks™, Natick, MA) toolbox used to perform spectral simulations [6], and pseudomodulation, a method that convolves sinusoidal modulation of an independent parameter of an arbitrary function with that function. It accurately models that portion of the transfer function of an EPR spectrometer that is associated with magnetic field modulation [7]. This figure reveals that an increase in modulation amplitude leads not only to an increase in signal intensity, but also to an increase in spectral broadening. To measure lineshape parameters in a CW experiment, a compromise must be made to achieve sufficient signal intensity while maintaining spectral integrity. This lineshape-lineheight compromise is typically addressed by selecting a modulation amplitude that is approximately one-quarter of the narrowest linewidth. Spectral distortion is diminished under these conditions, but Fig. 1b shows that more than 80% of the pure absorption signal is also sacrificed. The methods of this paper are designed to overcome this loss of an estimated factor of five in signal height.

Fig. 1.

(a) Simulated absorption spectrum of a nitroxide at 9.5 GHz where g_x = 2.0085, g_y = 2.0061, g_z = 2.0023; A_x = 6.2 G, A_y = 4.3 G, A_z = 36.9 G; and τ_R = 8 × 10⁻¹⁰ s.

(b) Pseudomodulation of absorption spectrum with amplitudes of 0.25, 0.5, 1.0, and 2.0 G, resulting in progressively greater signal intensity. Note the change in vertical scale.

(c) Integration of the pseudomodulated spectra. Spectra have been normalized to one for comparison. Relative peak heights of the three lines are fairly well preserved. (d) Residual of the integrated pseudomodulated spectrum subtracted from the unmodulated spectrum in (a). Field modulation results in line-broadening under all conditions.

The effects of field modulation presented in Fig. 1 are well documented [8; 9], and methods of analysis have been developed [10]. Alternative detection schemes, such as direct current (DC) detection, are not sensitive enough to observe weak signals due to phase and receiver noise, while alternative techniques, such as microwave frequency swept EPR or rapid scan EPR spectroscopy, deal with responses of the spin system resulting from adiabatic rapid passage [11; 12]. Fedin et al. obtained absorption spectra using a multifrequency approach with a modulated longitudinal field [13]. These various methods have limitations. In the judgment of the authors, there remains a need to develop a practical and versatile method to collect the undistorted pure absorption CW EPR spectrum.

2. Methods

2.1. Sample preparation

For X-band experiments presented here, a 200 µM sample of deuterated (1-oxyl-2,2,5,5-tetramethylpyrroline-3-methyl) methanethiosulfonate (pdMTSL) (Toronto Research Chemicals, Toronto, ON, Canada) was prepared in sec-butylbenzene in a five-fold molar excess of nonparamagnetic analog (MMTS) to avoid potential dimerization and exchange broadening. To achieve narrow lines, the sample was degassed using the freeze-pump-thaw method in a 3-mm ID quartz EPR tube and sealed with a torch.

For L-band experiments, a 10 µM aqueous sample of 1-oxidanyl-2,2,6,6-tetramethlypiperidin-4-ol (TEMPOL) was prepared for use in a 3 mm ID quartz sample tube. It was not degassed.

2.2. X-band EPR spectroscopy

Both CW and NARS spectra were collected on a Varian E-9 spectrometer fitted with a modified Varian E-101 X-band microwave bridge, previously discussed by Hyde et al. [14], and equipped with a five-loop–four-gap MACOR silver-plated 5 mm ID resonator with a loaded Q of approximately 300 (Molecular Specialties Inc., Milwaukee, WI). A Miteq LNA (Hauppage, NY) model AMF-2S-8596-4 (NF = 2.5 dB, gain = 20 dB) was added to the bridge to lower the receiver noise figure (NF). The high gain of the LNA is the determining factor for the NF of the microwave bridge. For an analysis and discussion of the use of an LNA to improve the NF of an X-band bridge, the reader is referred to Hoentzsch et al. [15]. A Watkins-Johnson model WJ-M80C double-balanced mixer with a specified single-sideband conversion loss of 6 dB was used, followed by a wideband signal preamplifier (gain = 28 dB).

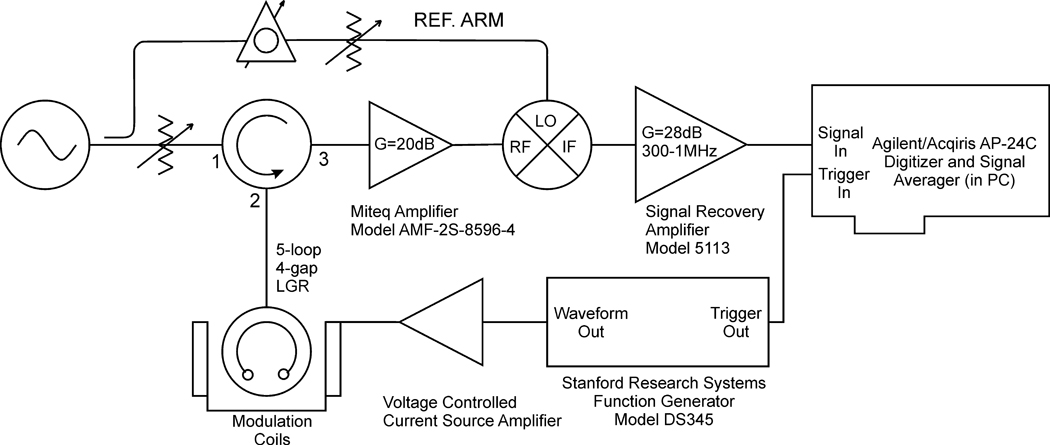
Figure 2 displays the instrumental setup used to perform the NARS experiment. A triangular waveform is produced by a Stanford Applied Research Systems model DS345 direct-to-digital synthesis function generator. The DS345 output waveform has a 12-bit vertical resolution and an output sampling frequency of 40 MHz. It also outputs a logic pulse for triggering during the data-acquisition process.

Fig. 2.

Instrumental setup utilized to perform the NARS experiment.

The DS345 Synthesized Function Generator provides the triangular-waveform input drive for the voltage-controlled current-source amplifier, which drives the sweep coil. The current-source amplifier is a forced-air cooled Apex Inc. PA-19 hybrid amplifier using a 60 V power supply. (The PA-19 is no longer available. Apex Inc. is now Cirrus Logic, Austin, TX.) Current through the coil is sensed through a precision 1-ohm resistor in series with the sweep coil. A maximum field excursion of 28.2 G peak-to-peak was obtained at 5.2 k triangular repetition rate. Quine et al. describe an amplifier design with greater current and voltage-compliance capabilities [16]. However, increase of the sweep amplitude may not be desirable in the experiment described here because of the non-adiabatic condition. For a given magnetic field sweep rate, the waveform repetition frequency can be increased to a level that is sufficient to overcome 1/f noise by decreasing the sweep amplitude, although collection of data in segments may be required to recover the entire absorption spectrum.

The sweep coil was designed specifically to minimize vibration that arises from Lorentz forces, which, consequently, minimizes acoustical noise. Each half of the sweep coil consists of 20 turns of 24-gauge enameled copper wire wound onto opposite sides of a 5.7-cm diameter, 2.5-mm thick fiberglass tube with several heavy layers of epoxy to minimize acoustical noise. The total inductance of the coils in series is 180 µH with a self-resonant frequency of 980 kHz. The fiberglass tube was mounted in a robust Delrin^® plastic housing and securely clamped against the magnet pole faces. This setup provides a resultant field of 4.7 G/A at the sample.

A Signal Recovery (Oakridge, TN) model 5113 preamplifier provides an additional 28 dB of gain external to the bridge preamplifier. The 5113 model is a selectable gain and bandwidth amplifier. For X-band experiments, the bandwidth was 300 Hz to 1 MHz. An Agilent/Acqiris model AP-240 ADC/Averager PCI card installed in a PC was used to digitize and average the signal following the 5113 amplifier. An in-house LabVIEW^® program was used to control various AP-240 parameters, including the sampling frequency, number of sample points per record, trigger delay time, and number of records to be averaged. Additionally, the program displays the results of the signal averaging of the previous 1,024 scans to observe real-time changes as well as the sum of all scans.

CW spectra were collected using conventional field modulation at 100 kHz and an in-house LabVIEW^® program for data acquisition. For X-band experiments, a single, 1-min, 100 G scan over 1024 points was performed for each spectrum, using a 0.25 G modulation amplitude and 128 ms time constant. Spectra were baseline-corrected using a linear fit and integrated for comparison with NARS spectra.

NARS and CW spectra were collected consecutively (within minutes of each other) without change in coupling or microwave power, which was 250 µW throughout. Temperature control was achieved with a modified Varian V6040 variable temperature control unit equipped with an Omega (Stamford, CT) microprocessor and gas exchange system.

2.3. L-band EPR spectroscopy

The goal of the L-band experiment presented here was to make a careful comparison of relative sensitivities of NARS and CW EPR spectra of the center line of 10 µM TEMPOL (1.7 G peak-to-peak width). Spectra were collected at room temperature using an L-band bridge of in-house design equipped with a one-loop–one-gap resonator at an operating frequency of 1.9 GHz. The NARS configuration for L-band was functionally identical to the X-band configuration presented in Fig. 2, although there are a few differences. The microwave bridge contained a solid-state cavity oscillator instead of klystron, a Miteq (Hauppage, NY) model ASF2-01000200-05-10P-6-GW LNA (NF = 0.5 dB, gain = 28 dB), and a wideband signal preamplifier (gain = 40 dB). The Signal Recovery 5113 amplifier bandwidth was 100 Hz–300 kHz with a gain of 40 dB.

The NARS spectrum was collected using a 5.2 kHz sweep rate with the voltage adjusted to obtain a 20 G sweep width as determined by Fremy’s salt in water. A conventional 100 kHz 20 G CW EPR spectrum was collected for 1 min using a 0.8 G modulation amplitude with a 0.50 s integrating time constant. Both spectra were collected using 250 µW input microwave power.

3. Results

3.1. Lineshape comparison at X-band

NARS spectra were collected using a variety of instrumental settings. The triangular repetition rate of the function generator and the applied voltage to the current-source amplifier were investigated most thoroughly. Because these are under the control of the investigator, the magnetic field sweep rate and width can be adjusted accordingly to accommodate the requirements of the experiment that are determined by the relaxation properties of the system under study.

Repetition rates between 1 and 12 kHz were studied over a range of applied voltages leading to magnetic field sweep rates that varied from 10 to 600 kG/s, all of which satisfy the non-adiabatic condition, Eq. (2). The data acquisition time was held constant throughout. Spectra obtained using lower repetition rates exhibited lower SNR compared to higher rates, establishing the presence of 1/f noise. The frequency and voltage limitations of the current-source amplifier restricted the maximum available sweep width at higher repetition. Considering these results, a compromise repetition rate was used in the studies presented here to obtain convenient and efficient signal averaging times for adequate signal-to-noise, while providing sufficient sweep amplitude to scan through a significant portion of the nitroxide spectrum.

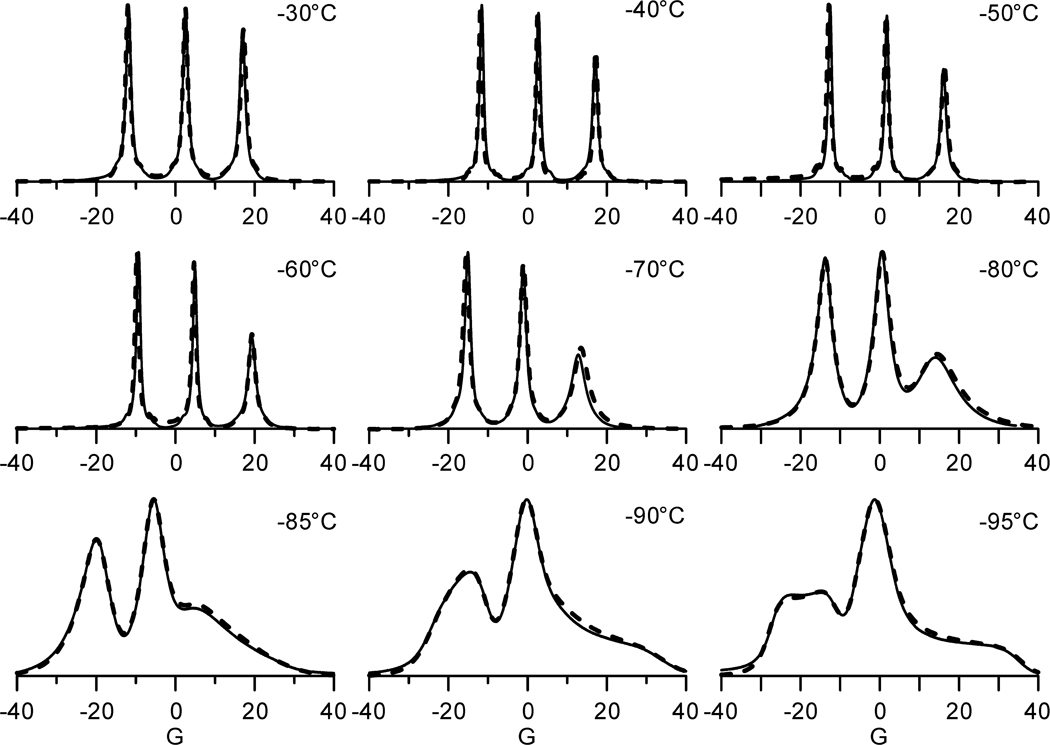
To validate the NARS technique and assess the differences between it and magnetic field modulation, EPR spectra of pdMTSL in degassed sec-butylbenzene were collected at nine different temperatures between −30°C and −95°C using both techniques. At these temperatures, the sample viscosity varies approximately 0.03 to 8.18 P, allowing observation of lineshapes over three orders of magnitude in rotational correlation time [17]. NARS was performed using a 5.2 kHz repletion rate and the maximum sweep amplitude that could be used without triangular waveform distortion. Under these conditions, a 28.2 G spectral width, as measured by the hyperfine splitting of Fremy’s salt in water, was achieved (300 kG/s). Because the width of the nitroxide spectrum exceeds the sweep width of the apparatus, the full spectrum was obtained in segments. The low-field portion of the spectrum was collected first. Then, the static field was increased by 10 G, and an additional spectral segment was collected. The process was repeated as necessary to record data from the complete spectrum. Because a background spectrum was collected for each segment and the nitroxide spectral width varied with rotational correlation time, the total acquisition times varied between 4 and 7 min. The segments were pieced together in the computational software MATLAB^® (MathWorks™, Natick, MA) using a least-squares fitting of the overlapped features.

Figure 3 shows the integrals of the first-harmonic spectra collected using 0.25 G magnetic field modulation (dashed line) overlaid on the assembled pure absorption spectra collected using the NARS technique (solid line). In absolute units for data acquired in the same time, the field modulation spectra are weaker than the NARS spectra because of the low field modulation amplitude that was used. Gains were adjusted in order to overlay NARS and CW spectra and compare lineshapes. The spectral shapes are in good agreement over all rotational correlation times.

Fig. 3.

EPR spectra of 200 µM pdMTSL in degassed sec-butylbenzene collected using magnetic field modulation (dashed line) and NARS (solid line).

The agreement seen in Fig. 3 is gratifying in two respects. Firstly, at small field modulation amplitude, the EPR spectral shapes are proportional to the first derivative of the pure absorption spectra, as expected, and integration results in spectra that have the shape of a pure absorption spectrum. Secondly, a triangular sweep rate was found that resulted in NARS spectra with minimal contamination from incipient free-induction decay effects associated with adiabatic rapid passage.

The NARS spectra exhibit much higher SNR in Fig. 3, which is not apparent because of the high sample concentration, high sample volume, and low dielectric loss of the solvent. Noise is not evident in the data of Fig. 3. Small discrepancies are seen in shape between the integrated first harmonic spectra and the NARS spectra that could arise from a variety of sources. Limitations in the use of large-field modulation amplitudes or the use of triangular field sweeps that are too rapid for NARS can be investigated using displays such as those of Fig. 3. These limitations can be expected to depend on the level of the incident microwave power and the frequency of sinusoidal magnetic field modulation.

3.2. Sensitivity comparison at L-band

Very low-frequency CW EPR often deals with narrow lines and observation of small linewidth changes. For example, in spin label oximetry, linewidths or features as small as 0.2–0.5 G occur. To observe changes in these features, field modulation amplitudes of 0.1 G or smaller are required, and poor SNR is expected based on Fig. 1. In addition, the SNR is further diminished by a loss of signal due to changes in the Boltzmann distribution as the microwave frequency is lowered. Sensitivity comparisons between field modulation and NARS experiments were performed at L-band where the improvements in SNR through the use of NARS are expected to be especially beneficial.

Noise aspects of the L-band spectrometer were carefully measured. Noise in an EPR spectrum is comprised of receiver noise, which is independent of bridge output power, and source noise, which is dependent on bridge output power. The receiver noise floor ideally is determined by the LNA, which ought to have sufficient gain that noise arising from subsequent units in the receiver chain (namely, the signal mixer, bridge preamplifier, and the Signal Recovery 5113 amplifier) is inconsequential. Source noise is mostly comprised of the phase noise output of the microwave source in the bridge. Both sources of noise tend to exhibit a 1/f dependence, rising in level as the measurement frequency is decreased. In field modulation experiments, the noise is filtered and lies in a narrow band centered at the field modulation frequency (typically, 100 kHz). The bandwidth is set by the lock-in time constant and is on the order of 0.1 to 10 Hz. As a result, low frequency noise tends to dominate the spectrum, while high frequency noise is mostly unobservable. In the NARS experiment, the receiver bandwidth is much higher, but low frequency noise is considerably diminished because of the short acquisition time of each scan, while high frequency noise becomes readily apparent. The SNR is improved by averaging a large number of scans. A digital filter is then applied, which is equivalent to use of an integrating time constant in the lock-in detector. The bandwidths of receivers for NARS detection and conventional lock-in detectors can, in principle, be identical.

The bridge noise output over a wide frequency range was measured. The spot-noise output of the receiver (with the reference arm on) was within 1 dB from 8 to 100 kHz. The receiver noise level rises by 2, 5, and 9 dB at 5, 2, and 1 kHz, respectively. NARS experiments reported here were performed with a 5 kHz triangular repetition rate and were presumably slightly degraded by receiver noise. The low receiver noise arises from the use of a microwave low noise amplifier. With an LNA in place, there is no longer a benefit to use of 100 kHz to overcome 1/f receiver noise. Source noise was measured with the bridge microwave phase-shifter adjusted for EPR absorption detection and the sample-containing resonator critically coupled. Source noise could only be seen at maximum bridge output power (approximately 23 mW) at 1 kHz. The noise output in this case was 2 dB above the receiver noise floor at 1 kHz. It is concluded that receiver noise dominates for powers below full power.

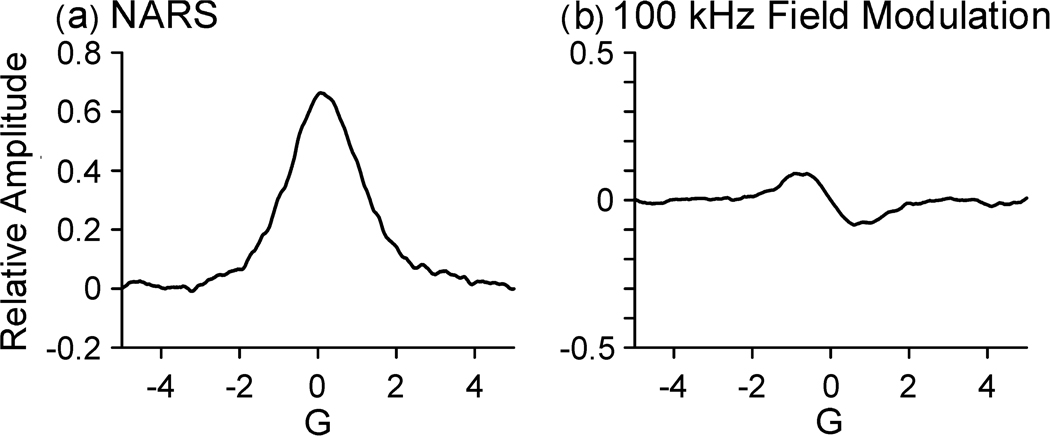
Figure 4 shows the first harmonic (0.8 G field modulation amplitude) and the filtered NARS spectrum of the center line of 10 µM TEMPOL in water, each collected during 1 min of data acquisition. The first harmonic was collected in a single 1 min scan, 0.5 s integrating time constant, while 625,000 averages were accumulated for NARS. A 21-point moving average was utilized as a digital filter to smooth the 4096-point NARS spectrum. The resulting noise character was similar to that of the field modulation experiment. Under these conditions, a factor of five in SNR improvement could be observed for NARS, which arises from decreased signal intensity because of the use of field modulation (see Fig. 1). The gain in Fig. 4 was adjusted so that the noise levels were about the same. Data (not shown) were acquired using 0.5 G field modulation, resulting in narrower lines, further loss of the spectral amplitude, and a greater factor of improvement for NARS.

Fig. 4.

Comparison of (a) NARS and (b) field modulation spectra of 10 µM TEMPOL in water at L-band. A factor of five improvement in SNR was observed with NARS detection. Data were acquired in the same acquisition time.

In an ideal spectrometer, the noise is determined by the most narrow bandwidth in the amplifier chain. Here, we compare a moving average with a two-pole integrating time constant, which were set to have about the same bandwidth, although not, of course, precisely the same source filter characteristics.

4. Discussion

The quality of information provided by CW EPR spectroscopy depends on the ability to determine the location, width, and shape of spectral components. Figure 1 shows that magnetic field modulation can affect the measurements of the latter two. Field modulation is a very robust technique that should be used if the signal intensity is sufficiently high that small modulation amplitudes can be used. For weak samples, detection of small lineshape changes, or for quantitative measurements of linewidth broadenings, NARS detection should be taken into consideration. For example, interspin distances can be determined with CW EPR spectroscopy by measuring the broadening of the central feature after a second spin is introduced to the system. Because dipolar broadening has a 1/r³ dependence, longer distances give rise to very small changes relative to the intrinsic linewidth and require the utmost sensitivity. Broadening resulting from the use of magnetic field modulation could produce considerable uncertainty in the estimation of r.

The most notable advantage of NARS is its factor of about five improvement in SNR. The simulations in Fig. 1b show how magnetic field modulation leads to the lineshape-lineheight compromise. By utilizing a direct detection scheme, NARS avoids this compromise while maintaining spectral integrity. We hypothesize that this improvement can open the L-band region (1–2 GHz) to practical usage, since it nearly compensates for the loss of signal intensity in comparison with X-band that arises from the frequency dependence of the Boltzmann factor. If NARS were used at X-band, the SNR would be expected to increase by a factor of five, and the difference between L- and X-band would again be determined by the Boltzmann factor.

The NARS experiment collects the undistorted pure absorption EPR spectrum, which contains all of the linear spectroscopic information. This is significant because magnetic field modulation causes spectral distortion and, therefore, cannot be used to recover the undistorted pure absorption spectrum. Should the first harmonic be desired in the NARS experiment, as might be the case when comparing results with previously published papers, the displays are readily calculated with the aid of pseudomodulation [7]. In fact, all of the higher harmonics can be recovered from the absorption spectrum. This sets NARS apart and gives it the potential to become a new general purpose tool in CW EPR spectroscopy.

The central problem in NARS spectroscopy lies in the fact that the triangular field sweep effectively replaces the sweep of the static magnetic field and, therefore, is required to be homogeneous in amplitude and phase over the sample. However, when a conductor, such as a microwave resonator, is placed in a time-varying electromagnetic field, eddy currents are induced on the surface. To reduce effects of eddy currents on the uniformity of this field at the sample, two schemes are generally employed: (1) wall plating thicknesses are chosen to be thin enough for modulation penetration but thick enough to support the microwave fields, and (2) slots are cut parallel to wall currents in order to avoid disrupting RF currents, while creating potentials for modulation penetration. In the current study, we used the former technique at X-band and the latter at L-band. At the current state of our technology, the parallel slot technique is inferior.

The Fourier transform of the triangular waveform used to sweep the field consists of a series of sinusoidal frequencies instead of the single frequency used in the magnetic field modulation experiment. There is a frequency dependence to eddy current formation, so each of these frequencies is individually affected by the microwave resonator in a different way. As a result, each frequency gives rise to a magnetic field with a different amplitude and phase at the sample. Presumably, the relative success of the five-loop–four-gap resonator used for the X-band experiment arose from the fact that it had been designed to be electrically thin at 100 kHz and, therefore, was very transparent to lower frequencies.

5. Conclusion

A new CW EPR technique, termed NARS, that uses a small coil to sweep the polarizing magnetic field repetitively at a rate that approaches, but does not satisfy, the adiabatic condition (Eq. (2)) has been developed at two microwave frequencies. Under these circumstances, a direct detection scheme was practical and the lineshape-lineheight compromise required when using sinusoidal magnetic field modulation with lock-in detection was overcome. Nitroxide lineshapes obtained using old and new techniques were in good agreement at X-band across a range of correlation times when field modulation amplitudes were chosen to be sufficiently small. A factor of five gain in signal intensity was measured at L-band, and similar gains are expected at other microwave frequencies. This factor will increase if a more conservative choice of field modulation amplitude is made. Enabling hardware included a low-noise microwave amplifier, which greatly reduced 1/f receiver noise, and a loop-gap resonator, which greatly reduced the effects of phase noise from the microwave source. Acquisition of spectra in segments, as demonstrated at X-band, makes NARS a general purpose EPR spectroscopic method. 100 kHz field modulation is no longer required in EPR to overcome these sources of 1/f noise.