Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2011 Aug 1.
Published in final edited form as: J Phys Chem Lett. 2010;1(15):2264–2268. doi: 10.1021/jz100663e

Real-Time Infrared Overtone Laser Control of Temperature in Picoliter H2O Samples: “Nanobathtubs” for Single Molecule Microscopy

Erik D Holmstrom 1, David J Nesbitt 1,*
PMCID: PMC3148086  NIHMSID: NIHMS308474  PMID: 21814589

Abstract

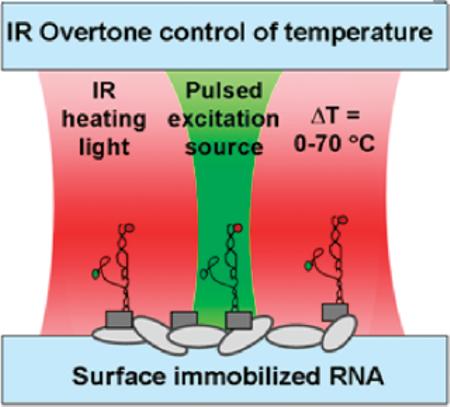
graphic file with name nihms-308474-f0001.jpg

An approach for high spatiotemporal control of aqueous sample temperatures in confocal microscopy is reported. This technique exploits near-IR diode-laser illumination to locally heat picoliter volumes of water via first-overtone excitation in the OH-stretch manifold. A thin water cell after the objective resonantly removes any residual IR light from the detection system, allowing for continuous observation of single-molecule fluorescence throughout the heating event. This technique is tested quantitatively by reproducing single-molecule RNA folding results obtained from “bulk” stage heating measurements. Calibration of sample temperatures is obtained from time-correlated single-photon counting studies of Rhodamine B fluorescence decay. We obtain an upper limit to the heating response time (τheat < 20 ms) consistent with even faster estimates (τheat ≈ 0.25 ms) based on laser spot size, H2O heat capacit,y and absorption cross section. This combination of fast, noncontact heating of picoliter volumes provides new opportunities for real-time thermodynamic/kinetic studies at the single-molecule level.

Temperature arguably represents the most critical experimental variable for detailed thermodynamic/kinetic study of chemical and biological processes. Of particular interest, temperature control at the focus of a confocal microscope objective offers significant potential for kinetic exploration of nanoparticle1,2 and biological3–5 systems at the single molecule level. Such temperature control can, in principle, be achieved from “bulk” methods by heating the entire sample, stage, and objective with an enclosed stage-heater and heated objective collar. Although quite powerful, there are several important physical limitations to such a bulk heating approach. First of all, the time constants for heating/cooling of the stage and objective can be unacceptably long, requiring multiple minutes to achieve steady-state temperatures necessary for single-molecule fluorescence detection. Second, the speed of such bulk stage heating approaches preclude use of powerful temperature jump methods to activate a specific process of interest, such as denaturation/renaturation of proteins, melting of nucleotide interactions, annealing of nanomaterials, etc. Furthermore, elevated objective temperatures (>50 °C) can soften optical cement and thereby destroy the precise lens alignment crucial to high numerical aperture photon collection. Finally, prolonged exposure to elevated temperatures may facilitate unwanted degradation of the entire sample, which can decrease the length of observation times and increase background fluorescence.

Despite these challenges, there have been attempts to alleviate/overcome some of the shortcomings associated with bulk sample-heating, particularly with biological systems. Resistive joule-heating in microfluidic systems has been used to increase sample temperatures to > 90 °C and thereby induce polymerase chain reaction;6–8 however, constraining the heating to within a small subvolume of the sample is difficult. Others have used the absorbance of water in the near-IR region to directly heat the surrounding medium.9–15 The use of IR light provides optical control of the heated volume, as well as large, programmable temperature changes over short periods of time. As a result, IR laser overtone heating is well poised to remedy a number of shortcomings associated with traditional stage-heating methods. Specifically, the use of resonant near-IR laser excitation of H2O permits optically controlled, uniform heating of picoliter volumes in a well-defined confocal geometry. Furthermore, any residual transmitted IR laser intensity can be selectively blocked with high specificity by attenuation with a thin bulk-absorbing H2O filter. Consequently, the combination of (i) uniform sample heating and (ii) exponential rejection of residual light permits temperature-dependent studies of kinetics/thermodynamics while maintaining the continuous, high-fluorescence sensitivity necessary for single-molecule studies.

The thrust of the present work describes an IR-absorption-based heating approach coupled with single-molecule fluorescence resonance energy transfer (smFRET) microscopy to simultaneously heat and observe folding of single RNA molecules. To accomplish thermal control of RNA samples, IR light is used to vibrationally excite the first overtone band (νOH = 2←0 @ 1445 nm) of the OH-stretch in water (Figure 1). This noncontact heating method makes it possible to systematically control the temperature of small volumes of aqueous solution. The result is a confocal fluorescence microscopy apparatus capable of broad temperature control (T = 20–90 °C), high accuracy (±0.5 °C), and heating rates in excess of 104 °C/s, which offers enormous potential for thermodynamic/kinetic studies of conformational dynamics of biomolecules at the single-molecule level. The reliability and accuracy of this technique are tested by using IR-absorption-based heating to reproduce thermodynamic folding studies of the GAAA tetraloop–receptor from the Tetrahymena ribozyme.16

Figure 1.

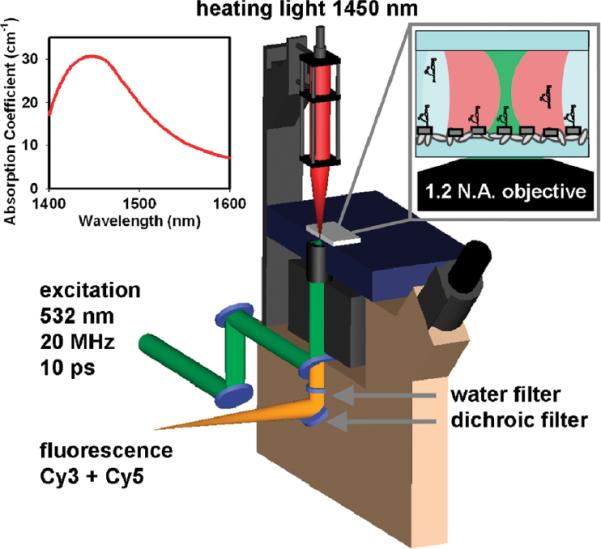
Figure 1

Open in a new tab

Cutaway diagram of IR absorption based heating apparatus. Inset shows the absorption coefficient (α) of water in the νOH =2←0 overtone band region near 1.45 μm.

To achieve IR-absorption-based temperature control of aqueous solutions, a fiber-coupled 1445 nm continuous-wave laser was incorporated into an inverted fluorescence microscope (Figure 1) with a 532 nm pulsed laser excitation source. This apparatus is capable of color, polarization, and time-resolved single-photon.16 In the studies described herein, an XYZ-translation stage-controlled optical cage is used to focus (f = 100 mm) IR light down to a 17 μm (full width at half-maximum) diameter spot in the focal plane of (and coaxial with) the microscope objective. The IR laser power (PIR) is controllable between 0 and 160 mW, with typical peak incident laser intensities of Io ≈ 47 kW/cm2. At λ = 1.445 μm, the absorption coefficient, α(λ), is equal to 30.3 cm−1.17 For an H2O sample depth of ~150 μm, this corresponds to a Beers Law absorbance of A ≈ 1.05 (base e) and nearly uniform local heating throughout the ~35 pL sample volume. For an aqueous sample dominated by the heat capacity of water (Cp(H2O) = 4.184 J/K/cm3), this model predicts a maximum heating rate ([dT/dt](t=0) = [α(λ) χ I°]/Cp) of 3.4 χ 105 °C/s.

A microscope objective collects the fluorescence from a donor/acceptor fluorophore-labeled RNA construct. The fluorescent photons are separated from the excitation source and directed toward the detection system using a dichroic mirror. Before detection, the fluorescent photons are spatially separated by color and polarity using various optical elements to accommodate FRET experiments (see Fiore et al.16). Detection of fluorescent photons is accomplished with single-photon avalanche photodiodes and a time-correlated single-photon counting (TCSPC) module.16 A thin 3 mm water filter located under the objective is used to prevent excess IR light not absorbed by the sample from reaching the detection system. Infrared light is attenuated with essentially complete efficiency (T ≈ 8 × 10−10), and yet with minimal loss of sample fluorescence (T ≈ 0.9).

An important associated challenge is accurate measurement of the sample temperature, which is accomplished using TCSPC methods to measure the temperature-dependent fluorescence lifetime (τfluor) of Rhodamine B.18 To establish reliable calibration over the full range of interest (20–90 °C), the Rhodamine B lifetimes are measured (i) in situ with TCSPC methods and (ii) benchmarked against studies in a temperature-controlled fluorimeter. The fluorescence decay curves in both regimes are least-squares fit to a convolution of single-exponential decay and a well-defined instrument response function to determine τfluor as a function of temperature.

Previous experiments exploiting this property of Rhodamine B have focused mainly on either τfluor or fluorescence intensity, with the resulting empirical calibration curves typically interpolated as a means of inferring the solution temperature.13,19–21 We can take this analysis one step further by considering a realistic Arrhenius kinetic model for the temperature-dependence of Rhodamine B. Specifically, it has been shown that the quantum yield (QY) of Rhodamine B approaches unity as the temperature decreases.18 Additionally, it is also known that the rate constant for the nonradiative relaxation from the excited state (knrad) is strongly temperature-dependent and vanishes at low temperature.18,22 On the basis of the relationship between decay rate constants and fluorescence quantum yield (QY = krad/[krad + knrad]), these observations suggest the temperature dependence of τfluor to arise from the nonradiative rate, i.e., knrad(T). This can be simply modeled as an activated process, with the temperature dependence of knrad(T) dictated by the well-known Arrhenius equation, i.e., knrad(T) = A exp(−Ea/kT).

Analysis and results from such an Arrhenius model are summarized in a standard Arrhenius plot of ln[knrad(T)] versus 1/T (Figure 2). Over the range of temperatures observed, ln[knrad(T)] decreases linearly with 1/T, which when fit to the Arrhenius equation yields an activation energy (Ea) for accessing the nonradiative decay channel of 7.2(1) kcal/mol. This is qualitatively consistent with previous Arrhenius analyses of nonradiative decay in methanol (Ea = 5.2(4) kcal/mol), ethanol (Ea = 5.0(4) kcal/mol) and 1-propanol (Ea = 4.1(5) kcal/mol), which is clearly indicative of a reduction of Ea with decreasing solvent polarity.23 Of particular relevance to the present work, this expression provides physically motivated calibration of τfluor as a function of solution temperature, and thereby a noninvasive measure of temperature for picoliter volumes of H2O.

Figure 2.

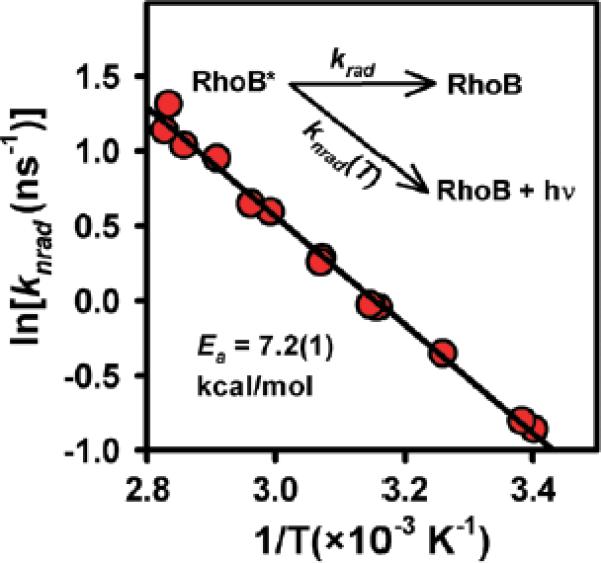
Figure 2

Open in a new tab

Arrhenius analysis of the nonradiative component knrad(T) for temperature-dependent Rhodamine B fluorescence rates. By explicitly measuring kfl = krad + knrad(T) and modeling knrad(T) as a thermally activated Arrhenius process, one can use TCSPC and the Arrhenius equation as a calibration curve for temperature.

As a quantitative demonstration of such an IR-absorption-based heating method, we have also investigated equilibrium thermodynamics for RNA folding at the single-molecule level.16 Specifically, a donor/acceptor-labeled RNA construct and smFRET are used to study the temperature-dependent folding/unfolding dynamics of the GAAA tetraloop–receptor tertiary interaction. Most importantly, this permits a direct comparison with previous single-molecule measurements of enthalpy and entropy based on bulk microscope stage-heating.

The equilibrium constant as well as the individual rate constants for folding/unfolding are determined using previously established methods.24 Figure 3 depicts a van't Hoff plot of R ln[Keq] versus 1/T obtained from both the present study (IR-absorption heating) as well as previous work (bulk stage heating). Results from this work (ΔH°=18(2) kcal/mol, ΔS° = 58(6) cal/mol/K) and bulk stage heating experiments (ΔH°=17(2) kcal/mol, ΔS°=56(5) cal/mol/K) are clearly in excellent agreement, with all thermodynamic quantities indistinguishable within experimental uncertainty. This represents strong confirmation that the present IR-laser absorption-based heating methods can be used to obtain high-quality kinetic/thermodynamic data on single-molecule samples.

Figure 3.

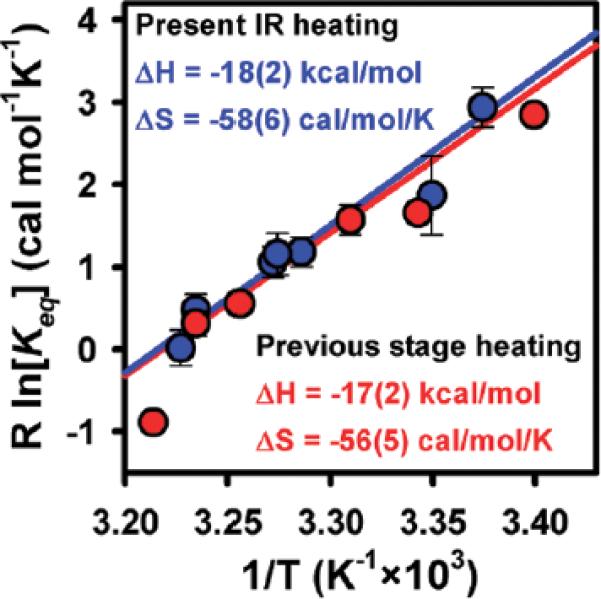
Figure 3

Open in a new tab

Van't Hoff plot of R ln[Keq] vs 1/T for smFRET studies of RNA folding providing ΔH° and ΔS° for the GAAA tetraloop–receptor tertiary interaction. Note the excellent agreement between the laser-overtone and stage-based heating techniques.

One critically important advantage of the IR laser heating method is the high temporal control of sample temperature, which we can address more quantitatively from the data. To determine a maximum rate and upper limit time-scale for heating, fluorescence from Rhodamine B is measured as a function of time during abrupt heating/cooling cycles (Figure 4). To obtain sufficient accuracy in the fluorescence lifetime information, τfluor at each time point is determined from a least-squares exponential decay fit to 2000 photons, which at maximum fluorescence rates corresponds to a minimum bin time of ~20 ms. The prompt decrease in τfluor reflects a correspondingly rapid increase in knrad(T), which from the Arrhenius expression translates into an IR laser-induced jump of ΔT = 23.2(5) °C. Interestingly, the characteristic rate for laser heating above ambient temperature is currently limited by the minimum bin time, with the data clearly establishing an upper limit for the heating process (τheat <20ms). It is also worth noting that the ability to monitor confocal fluorescence continuously throughout the temperature jump event high-lights a critical kinetic advantage of the present narrow band IR laser absorption heating technique over broad band IR-induced heating methods.12

Figure 4.

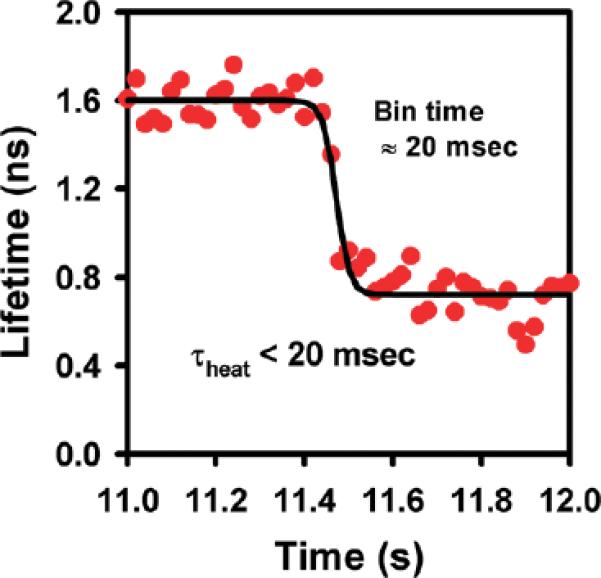
Figure 4

Open in a new tab

Time scale for IR-absorption-based heating. By monitoring Rhodamine B fluorescence lifetimes, one can directly measure characteristic times associated with laser heating of the sample. The characteristic heating time is currently limited by the time binning resolution of the data (<20 ms), which is slower than, but consistent with, predictions (see text for details).

This analysis can be explored further based simply on conservation of energy and Newton's Law of cooling. If we at first assume no heat flow into/out of the illuminated sample volume, conservation of energy relates the time-dependent deposition of thermal energy (d(ΔQ)/dt = α(λ) Io) to the time-dependent change in local temperature (d(ΔT)/dt = Cp(H2O) d(ΔQ)/dt). In this approximation, the temperature derivative is given by d(ΔT)/dt = (α(λ) × Io)/Cp(H2O), which for 50 mW of IR light focused to an area of A=π(17 μm)2/4 at 1445 nm (α(λ) = 30.3 cm−1) predicts a maximum initial rate of ~1.1 105 °C/s. It is worth noting that, because of the relatively small absorbance per unit length, and therefore uniform heating conditions, this prediction is rather insensitive to the sample depth.

Of course, this initial rate is not maintained indefinitely due to thermal conduction and loss of heat to the surrounding medium, resulting in a steady-state temperature increase. This temperature change can be analyzed via Newton's law of cooling, d(ΔT)/dt ∝ −ΔT, which can be integrated to yield a single-exponential rise/fall to an asymptotic steady-state temperature, i.e., ΔT(t) = ΔT∞ × [1 − exp(−t/τheat)]. This time constant (τheat) will be a function of thermal-conduction efficiency away from the laser heated volume. However, τheat can be simply re-expressed from the expression above to yield τheat = (ΔT∞)/[d(ΔT)/dt](t=0) in terms of (i) the maximum initial rate of temperature change ([d(ΔT)/dt](t=0)) and (ii) the asymptotic temperature rise (ΔT∞), which can be experimentally measured for a given PIR. Note that since both ΔT∞ and [d(ΔT)/dt](t=0) are approximately proportional to intensity, τheat will be largely insensitive to the incident PIR.

More quantitatively, for a 43 mW IR laser focused to a sample area of A = 235 μm2 in water, the asymptotic temperature rise is empirically found to be ΔT∞=23.2(5) °C. From the above expression, this predicts τheat ≈ 0.25 ms, which is substantially faster but nevertheless consistent with the experimentally determined upper limit. We are currently extending these studies to digitally switched laser outputs, faster fluorescence rates, and shorter bin times to constrain this limit further. However, we anticipate that some of this discrepancy may be a result of thermal gradients and heat flow. By way of evidence, the heating and cooling time constants from such a first-order model are predicted to be equal, whereas, experimentally, the cooling time is observed to be considerably longer (τcool ≈ 320(20) ms) and easily measurable with a 20 ms bin time. One interpretation is that, on the time scale of heating (>20 ms), the heated volume closely resembles the profile of the incident IR laser beam. However, over longer times, heat can diffuse radially away from the pseudocolumn of water giving rise to a broad volume of heated water. As such, this large volume of water will cool down more slowly than it takes the small volume of water to heat up. Unfortunately, this broad heated region will expose more surface tethered molecules to elevated temperatures and potentially contribute to unwanted sample degradation and background fluorescence, but is still significant improvement from bulk sample heating. Nevertheless, this simple first-order analysis of rapid temperature changes suggests intriguing prospects for temperature jump capabilities and single-molecule kinetics on the millisecond time scale. Specifically, this technique coupled with smFRET provides the ability to observe, in real-time, intermediate states in the melting pathway of large noncoding RNAs.

In summary, we have presented results from a confocal method with high spatial (30 μm) temporal (<20 ms) and thermal (±0.5 K) control of aqueous smFRET samples based on excitation of the OH-stretch overtone with 1445 nm laser light. The benefits of this noncontact method of resonant IR laser heating are (i) much larger dynamic temperature range compared to more traditional stage-heating methods, as well as (ii) the ability for continuous sensitive monitoring of fluorescence at the single molecule level throughout the heating event. These temperature increases can be accurately calibrated from the temperature-dependent fluorescence lifetimes of Rhodamine B, making it particularly useful for quantitative studies of temperature-dependent kinetics/thermodynamics in a variety of systems.

Indeed, such resonant IR-laser absorption-based heating techniques have very recently been adapted to wide-field microscopy experiment10,11 demonstrating the applicability of the technique to single-cell in vivo studies. This work has furthered the application of IR-absorption-based heating to the field of single-molecule microscopy. In particular, the prospects for temporal control of picoliter sample temperatures down to the millisecond time scale with resonant absorption of the residual IR flux offers access to temperature jump experiments performed at the single-molecule level and monitored in real time.

The three-piece donor/acceptor labeled GAAA tetraloop–receptor construct, as well as all solution preparations, annealing and tethering protocols are as described previously;16 only experimental modifications necessary for the current study are presented herein. Sample holders are created with standard glass slides and coverslips. Double-sided tape is placed across a clean glass slide creating two closely spaced parallel channels and sealed with a clean glass coverslip. In the first channel, fluorescence measurements of 500 nM Rhodamine B (in water) under constant power illumination are used to determine knrad(T) with <1% error, from which the sample temperature can be calculated from the Arrhenius expression calibration curve (Figure 2). FRET trajectories from a series of single RNAs immobilized in the second channel are then collected under identical constant power illumination, simply by translating the glass slide assembly. As a control, independent tests with Rhodamine B in both channels reveal no temperature difference within experimental uncertainty (±0.5 K) that could potentially arise from variations in the glass or sample-holder preparation. For all of the above experiments, the microscope stage is not temperature controlled and thus is confined to the ambient room temperature. As such, all temperature changes are a result of increases in laser power.

ACKNOWLEDGMENT

This work is funded in part by the National Science Foundation, the National Institute of Standards and Technology, and the W. M. Keck Foundation initiative in RNA sciences at the University of Colorado, Boulder. We would like to thank Drs. Arthur Pardi and Christopher D. Downey for their contributions to the RNA construct design. We would also like to thank Dr. David Rueda and Mr. Rui Zhao for technical discussions and encouragement.

REFERENCES

  • (1).Li S, Zhang K, Yang JM, Lin LW, Yang H. Single Quantum Dots As Local Temperature Markers. Nano Lett. 2007;7:3102–3105. doi: 10.1021/nl071606p. [DOI] [PubMed] [Google Scholar]
  • (2).Valerini D, Creti A, Lomascolo M, Manna L, Cingolani R, Anni M. Temperature Dependence of the Photoluminescence Properties of Colloidal CdSe/ZnS Core/Shell Quantum Dots Embedded in a Polystyrene Matrix. Phys. Rev. B. 2005;71:235409. [Google Scholar]
  • (3).Bartley LE, Zhuang XW, Das R, Chu S, Herschlag D. Exploration of the Transition State for Tertiary Structure Formation between an RNA Helix and a Large Structured RNA. J. Mol. Biol. 2003;328:1011–1026. doi: 10.1016/s0022-2836(03)00272-9. [DOI] [PubMed] [Google Scholar]
  • (4).Hohng S, Wilson TJ, Tan E, Clegg RM, Lilley DMJ, Ha TJ. Conformational Flexibility of Four-Way Junctions in RNA. J. Mol. Biol. 2004;336:69–79. doi: 10.1016/j.jmb.2003.12.014. [DOI] [PubMed] [Google Scholar]
  • (5).Kato H, Nishizaka T, Iga T, Kinosita K, Jr., Ishiwata S. Imaging of Thermal Activation of Actomyosin Motors. Proc. Natl. Acad. Sci. U.S.A. 1999;96:9602–9606. doi: 10.1073/pnas.96.17.9602. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • (6).de Mello AJ, Habgood M, Lancaster NL, Welton T, Wootton RCR. Precise Temperature Control in Microfluidic Devices Using Joule Heating of Ionic Liquids. Lab Chip. 2004;4:417. doi: 10.1039/b405760k. [DOI] [PubMed] [Google Scholar]
  • (7).Hu GQ, Xiang Q, Fu R, Xu B, Venditti R, Li DQ. Electrokinetically Controlled Real-Time Polymerase Chain Reaction in Microchannel Using Joule Heating Effect. Anal. Chim. Acta. 2006;557:146–151. [Google Scholar]
  • (8).Zhao QL, Huang QA, Lin YC. Design and Numerical Analysis of a Joule-Heating-Induced Continuous-Flow Polymerase Chain Reaction Microchip. J. Micro/Nanolithogr., MEMs, MOEMs. 2009;8:021101. [Google Scholar]
  • (9).Braun D, Libchaber A. Trapping of DNA by Thermophoretic Depletion and Convection. Phys. Rev. Lett. 2002;89:188103. doi: 10.1103/PhysRevLett.89.188103. [DOI] [PubMed] [Google Scholar]
  • (10).Ebbinghaus S, Dhar A, McDonald D, Gruebele M. Protein Folding Stability and Dynamics Imaged in a Living Cell. Nat. Methods. 2010;7:319. doi: 10.1038/nmeth.1435. [DOI] [PubMed] [Google Scholar]
  • (11).Schoen I, Krammer H, Braun D. Hybridization Kinetics Is Different Inside Cells. Proc. Natl. Acad. Sci. U.S.A. 2009;106:21649. doi: 10.1073/pnas.0901313106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • (12).Zhao R, Marshall M, Alemán EA, Lamichhane R, Feig A, Rueda D. Laser-Assisted Single-Molecule Refolding (LASR) Biophys. J. doi: 10.1016/j.bpj.2010.07.019. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • (13).Slyadnev MN, Tanaka Y, Tokeshi M, Kitamori T. Photo-thermal Temperature Control of a Chemical Reaction on a Microchip Using an Infrared Diode Laser. Anal. Chem. 2001;73:4037–4044. doi: 10.1021/ac010318p. [DOI] [PubMed] [Google Scholar]
  • (14).Mao HB, Arias-Gonzalez JR, Smith SB, Tinoco I, Bustamante C. Temperature Control Methods in a Laser Tweezers System. Biophys. J. 2005;89:1308–1316. doi: 10.1529/biophysj.104.054536. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • (15).Peterman EJG, Gittes F, Schmidt CF. Laser-Induced Heating in Optical Traps. Biophys. J. 2003;84:1308–1316. doi: 10.1016/S0006-3495(03)74946-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • (16).Fiore JL, Kraemer B, Koberling F, Erdmann R, Nesbitt DJ. Enthalpy-Driven RNA Folding: Single-Molecule Thermodynamics of Tetraloop–Receptor Tertiary Interaction. Biochemistry. 2009;48:2550–2558. doi: 10.1021/bi8019788. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • (17).Wieliczka DM, Weng SS, Querry MR. Wedge Shaped Cell for Highly Absorbent Liquids - Infrared Optical-Constants of Water. Appl. Opt. 1989;28:1714–1719. doi: 10.1364/AO.28.001714. [DOI] [PubMed] [Google Scholar]
  • (18).Karstens T, Kobs K. Rhodamine B and Rhodamine 101 as Reference Substances for Fluorescence Quantum Yield measurements. J. Phys. Chem. 1980;84:1871–1872. [Google Scholar]
  • (19).Muller CB, Weiss K, Loman A, Enderlein J, Richtering W. Remote Temperature Measurements in Femto-liter Volumes Using Dual-Focus-Fluorescence Correlation Spectroscopy. Lab Chip. 2009;9:1248. doi: 10.1039/b807910b. [DOI] [PubMed] [Google Scholar]
  • (20).Robinson T, Schaerli Y, Wootton R, Hollfelder F, Dunsby C, Baldwin G, Neil M, French P, Demello A. Removal of Background Signals from Fluorescence Thermometry Measurements in PDMS Microchannels Using Fluorescence Lifetime Imaging. Lab Chip. 2009;9:3437–3441. doi: 10.1039/b913293g. [DOI] [PubMed] [Google Scholar]
  • (21).Ross D, Gaitan M, Locascio LE. Temperature Measurement in Microfluidic Systems Using a Temperature-Dependent Fluorescent Dye. Anal. Chem. 2001;73:4117–4123. doi: 10.1021/ac010370l. [DOI] [PubMed] [Google Scholar]
  • (22).Arbeloa FL, Arbeloa TL, Estevez MJT, Arbeloa IL. Photophysics of Rhodamines - Molecular-Structure and Solvent Effects. J. Phys. Chem. 1991;95:2203–2208. [Google Scholar]
  • (23).Casey KG, Quitevis EL. Effect of Solvent Polarity on Nonradiative Processes in Xanthene Dyes: Rhodamine B in Normal Alcohols. J. Phys. Chem. 1988;92:6590. [Google Scholar]
  • (24).Downey CD, Fiore JL, Stoddard CD, Hodak JH, Nesbitt DJ, Pardi A. Metal Ion Dependence, Thermodynamics, and Kinetics for Intramolecular Docking of a GAAA Tetraloop and Receptor Connected by a Flexible Linker. Biochemistry. 2006;45:3664–3673. doi: 10.1021/bi0520941. [DOI] [PMC free article] [PubMed] [Google Scholar]

RESOURCES