Abstract
Large scale molecular interaction networks are being increasingly used to provide a system level view of cellular processes. Modeling communications between nodes in such huge networks as information flows is useful for dissecting dynamical dependences between individual network components. In the information flow model, individual nodes are assumed to communicate with each other by propagating the signals through intermediate nodes in the network. In this paper, we first provide an overview of the state of the art of research in the network analysis based on information flow models. In the second part, we describe our computational method underlying our recent work on discovering dys-regulated pathways in glioma. Motivated by applications to inferring information flow from genotype to phenotype in a very large human interaction network, we generalized previous approaches to compute information flows for a large number of instances and also provided a formal proof for the method.
1 Introduction
Recent advances in high-throughput experiments and computational methods made it possible to obtain molecular interaction networks for human and several model organisms [1–7]. Such large-scale interaction networks are found to be useful by providing a systems level view of complex biological processes. Numerous computational approaches have been proposed to analyze the networks and utilize them for various purposes such as understanding gene functions, identifying essential genes, and uncovering disease genes and dysregulated pathways.
Information flow based network analysis has been adopted in many studies where it is assumed that two distant nodes in the network may communicate (or interact) with each other by propagating the signals through intermediate nodes in the network. The nodes receiving or sending more flows are more likely to be crucial in the network and the pairs of nodes with a large amount of flow between them are likely to be functionally related. Different flow models have been used depending on the way the flow navigates through the network.
One popular approach to model the information propagation in the interaction network is the random walk model or its equivalent form of circuit networks [8–13]. In random walk approaches, the information from a subset of genes is propagated randomly through the interactions. Links may be weighted to indicate the reliability of the interactions or the correlation of gene expression levels. It has been shown that computing the probability that a random walker arrives at a particular node in the network can be translated into a problem of finding a current flow solution to a circuit network [14]. Other flow models such as minimum cost network flow or time-dependent network flow have been also suggested.
In the computational aspect, calculating information flows in a sophisticated model can be costly, especially given the enormous size of interaction networks. Therefore, designing algorithms for effective computation would have a significant impact on expediting the network analysis.
This manuscript consists of two parts. In the first part, we aim to provide an overview of the state of the art of research in network analysis based on information flow models. We focus on the studies that utilized random walks and circuit network approaches. However, several other flow methods are discussed as well. The second part includes a formal description and the mathematical proofs of our new computational methods underlying our recent work on inferring information flow from genotype to phenotype in a very large human interaction network.
2 Information Flow based Network Analysis
In general, a random walk on a graph is defined by the probabilities of moving from one node to another in each step. Given a graph and a starting node, a neighbor is selected at random based on the probabilities and the random walker moves to the selected neighbor. Then a neighbor of the current node is selected at random and the procedure repeated. It is well known that such random walks are closely related to electric circuit networks [14]. Namely, let us consider an electric circuit network G and let C(u, v) denote the conductance of a link (u, v). The corresponding random walk can be obtained by defining the transition probability p(u, v) from u to v to be C(u, v)/C(u) where C(u) is . Doyle and Snell [14] showed that given a unit amount of current entering into a source node s and leaving from a sink t in the circuit network, the amount of current passing through a node (resp., a link) is proportional to the expected number of times that the random walker visits a node (resp., a link). The current amount passing through each node can be computed by solving a system of linear equations based on Kirchhoff’s and Ohm’s laws.
In the following, we review recent studies that use information flow approaches to solve various biological problems ranging from uncovering causal genes and their associated pathways (Section 2.1), identifying disease genes (Section 2.2), and gene functions (Section 2.3) to network centrality analysis (Section 2.4). Most methods are primarily based on random walks and circuit flow networks but other closely flow models are also discussed.
2.1 Inferring Causal Genes and Dysregulated Pathways
In expression quantitative trait loci (eQTL) analysis, gene expression levels are assumed to be a quantitative phenotype and it is attempted to identify genetic loci controlling the phenotypic changes by determining the associations between the genotypic variations in genomic loci and gene expression levels. While the technique is being increasingly used in genome wide association studies, it has two major limitations. First, as associations are determined for a locus and more than one genes may reside near the associated locus due to the spacing of the markers thus a fine mapping is required to infer the causal gene responsible for the phenotypic changes. Furthermore, eQTL analysis cannot provide the underlying molecular mechanism through which the information on genetic alteration is propagated. To overcome these limitations, several studies proposed computational methods utilizing molecular interaction networks [12, 13, 15, 16].
Tu et al. [13] developed a computational method to infer causal genes and underlying causal paths explaining a given association and applied the method to the data obtained from yeast knock-out experiments. Their algorithm is based on a random walk through a molecular interaction network. Suppose that a target gene gt (i.e., a gene that is differentially expressed within the set of yeast strains considered in the experiment) has an association with an eQTL region reqtl. Let T(gt) = { t1, t2, … tn } be the set of transcription factors of the target gene gt and C(reqtl) = { c1, c2, … cm } be the candidate causal genes residing in the region reqtl. Assuming that the activities of genes on the pathway are correlated with the expression of the target gene, they assigned the weight w(g) of a gene g in the network to be the absolute value of the Pearson’s correlation coefficient between the expression values of g and gt. For each transcription factor ti, a random walker traverses genes in the network starting from ti and the probabilities of moving from a gene g to its neighbors Nei(g) = {g′1, g′2, …, g′k} are proportional to the weights of genes in Nei(g). To avoid cycles, in each step they eliminated genes that were already traversed from Nei(g) and revised the probabilities accordingly. The walk stops when the walker arrives at one of the candidate causal genes or a dead end. To estimate the probability that a random walker visits each candidate causal gene, the procedure is performed, for each transcription factor ti, a sufficiently large number of times, counting the number of times, N(ti, cj), that the walkers arrive at each causal gene cj when starting from the transcription factor ti. The likelihood L(cj) of a gene cj being a causal gene is estimated to be proportional to the weighted sum of N(ti, cj)’s, where w(gt,ti) indicates the causal effect of transcription factor ti on the target gene gt. Tu et al. also identified potential causal paths by starting from the causal gene with the largest L(cj) and traversing backwards the nodes with the largest number of visits.
Using the analogy between random walks and circuit networks, Suthram et al. [12] developed a method called eQED, which integrated eQTL analysis with molecular interaction information using the circuit network model. Since some links in molecular networks (e.g., TF-DNA interactions) are directed and the equivalence of random walks and electric networks is valid only when the links are undirected, they extended the model by formulating a linear programming problem. Specifically, let G(N, E) denote the molecular interaction network where N is a set of nodes and E represents a set of links. Suppose that there is a subset of directed links, D⊂E. Then we can obtain the amount of current for each link by solving the following linear programming formulation.
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
where I(u, v) represents the current sent through a link (u, v),V(v) denotes the voltage of a node v, and d(u,v) is a variable associated with a directed link used to enforce the correct direction of current flow. Constraints (2) and (3) correspond to Ohm’s law and Constraints (4) represent Kirchhoff’s current law. By minimizing the objective (1) while satisfying constraints (5) and (6), we can make sure that the links are used in the correct direction only.
Suthram et al. further extended their work considering multiple loci simultaneously. As there are typically more than one locus that have significant associations with the expression level of a target gene, they included all the associated loci in a single circuit and predicted causal genes. They validated their method with the results of a genome-wide eQTL study in yeast by Brem and Kruglyak [17].
Inspired by the previous work by Tu et al. [13] and Suthram et al. [12], we developed a circuit flow based method to identify causal genes and dysregulated pathways in Glioma, where we utilized a large human interaction networks [8, 9]. We describe the current flow algorithm that underlines this work in Section 3.
Yeger-Lotem et al. [15] used a different type of flow algorithm, called minimum cost network flow, to uncover cellular mechanisms for responses to the toxicity of alpha-synucleain, a protein implicated in neurodegenerative disorders including Parkinson’s disease. First, using genetic screening, they selected genetic “hits” - genes that modify α-syn toxicity when overexpressed. Separately, they identified genes differentially expressed following α-syn expression from mRNA profiling data. Observing that genetic hits are mostly enriched with response regulators while differentially expressed genes are biased toward metabolic processes, they devised a minimum cost flow based algorithm (called ResponseNet) to identify molecular interaction paths connecting the two sets of genes. In general, a minimum cost network flow in a network G=(N, E) sends flow from a source node s to a sink node t though network links [18]. Each link is associated with a cost per unit amount of flow passing through the link as well as a capacity limiting the amount of flow along the link. The goal is to minimize the total cost by sending flow without violating the capacity constraints. In the ResponseNet algorithm, flow passes from genetic hits (sources S) through intermediate interaction links to differentially expressed genes (sinks T). The cost, we, of a link e is assigned in such a way that interactions acting in a common cellular response pathways receive low costs. In addition, an artificial source s and sink t is created and links from s to genetic hits S and links from differentially expressed gene T to t are added. For links from s to genetic hits, a constant negative cost is assigned, thus sending more flow lowers the total cost. Capacities for links from differentially expressed genes to t were assigned based on their transcript levels while all other links have uniform capacity. Let E(i) denote all links that a node i is involved in. Aiming to find a subset of genetic hits mostly likely modulate the differentially expressed genes and identify intermediate nodes that are likely to be part of response pathways, they formulated a linear programming as follows.
| (8) |
| (9) |
| (10) |
| (11) |
Constraints (9) and (10) ensure the flow conservation while constraints (11) are for capacity constraints. Using the solution to the linear programming, they found a subnetwork connecting the genetic hits and the differentially expressed genes. The intermediate nodes in the subnetwork included genes that are potentially part of response pathways but were detected by neither genetic screen nor mRNA profiling. They also prioritized genes based on the amount of flow, in which genes receiving more flow are considered more important.
2.2 Prioritizing Disease Genes
Network flow approaches have also been used to identify disease genes [19, 20]. Starting from known genes associated with diseases, random walkers traverse the network, and potential disease genes are prioritized according to the probabilities with which the corresponding nodes are visited.
Kohler et al. [19] collected known disease genes for several cancer types and complex disorders, and developed a random walk based method to prioritize disease associated genes. They mapped the set of genes they want to prioritize along with other known disease genes in the network and used the known disease genes as the sources of random walks. They ranked the candidate genes according to the probabilities obtained from the random walk. To validate the method, they used the leave-one-out cross validation. In other words, the random walk started from all but one known disease gene and 100 genes located in the chromosome nearest to the left-out disease gene were chosen as candidate genes. They ranked the candidate genes according to the probabilities obtained from the random walk and measured how well the method identified the left-out gene. Consider a random walker starting from known disease genes and the initial probability vector P(0) is set so that all known disease genes have the same probability A transition matrix T is defined in such a way that the walker moves to a neighbor with uniform probability among neighbors. In addition, the walk can restart with probability r in each step. Then the probability vector P(t+1) whose i-th element is the probability of being at node i at time t+1 can be represented as follows.
| (12) |
Based on the equation (12), the steady-state probability vector P∞ is computed iteratively by running iterations until the L1 norm of the change vector is small enough. Candidate genes were prioritized according to the values in the steady-state probability vector P∞.
They also considered diffusion kernel method for prioritization, in which diffusion kernel is defined as
| (13) |
where D is a diagonal matrix where i-th diagonal element Dii is the degree di of node i and A is the adjacency matrix of a given network. The diffusion kernel method can be considered as a different type of random walk where a walker may be lazy and choose to stay at the node with a probability 1-diβ. Then the rank of each candidate gene j is determined according to . They obtained similar performance with two methods (random walk with restarts and diffusion kernel method) and reported that the two random walk based algorithms outperformed simple local search algorithms and sequence based ranking algorithm.
Vanunu et al. [20] further extended this approach in two ways. First, they assigned different weights to interactions based on confidence scores. In addition, they assumed that even the genes with no known relationship to a query disease may receive nonzero initial probabilities (that are also used for a restart of a random walk) if they are associated with similar diseases.
2.3 Identifying Functional Modules
Given the fact that a large portion of proteins, even in a well-studied organism, are little understood beyond their sequences, predicting protein functions is an important problem in the post-genomic era. Initial prediction methods have been largely based on sequence homology. With the emergence of large-scale interaction networks, alternative computational methods utilizing molecular interactions have been recently proposed.
Stojmirovic and Yu [21] used a random walk model and proposed a general framework to infer context-specific information propagation in molecular interaction networks. Suppose that a subset of nodes S are selected as either sources or sinks while T denotes the set of remaining nodes. The choice of sources and destinations provides the context of analysis and the method can be used, for example, to identify an Information Transduction Module (ITM) which is the nodes most affected by information flow in the given context. To achieve this goal, they start with an n × n transition matrix P, which is defined based on the adjacency matrix and represented as
| (14) |
where PAB denotes a submatrix for the transition probabilities from nodes in A to nodes in B. They considered two models – the absorbing model where S represents sinks and the emitting models where S defines sources. In the absorbing model, let Fij denote the probability that the information originating from i ∈ T is absorbed at j ∈ S in the long-term or equilibrium state. Then they proved that the following equation holds:
| (15) |
Similarly in the emitting models, Hij denotes the expected number of times that a transient node j in T is visited by a random walk that was emitted from source i, and they obtained
| (16) |
Note that the existence of solutions to the both equations depends on whether the matrix (I − PTT) is invertible. They showed that if any transient node t in T in the underlying graph is reachable from at least one node in S, then the matrix (I − PTT) is invertible and the inverse is the same as .
Stojmirovic and Yu extended the model in several ways to obtain biologically more realistic results. Specifically, dissipation coefficients are used to allow the information to dissipate both at S and T. By setting the coefficient > 1, the information can also be amplified. In addition, nodes can have their potentials, which direct the information flow either towards or away from selected nodes. By adjusting potential functions depending on the applications, interaction links can have different weights, which allows context-specific information diffusion analysis. In the emitting model, a subset of nodes in T may be selected as pseudosinks in which a certain fraction of information can be accumulated instead of leaving the nodes.
Finally, Information Transduction Modules are selected as sets of nodes from which sinks are reached with high probability (in the absorbing model) or nodes with large deposited information content (in emitting models). Using this approach they identified information transduction modules related to HATs (histone acetyltransferases) in yeast protein-protein interaction networks. The emitting model with pseudosinks was used to obtain possible interaction interfaces between Mcm1, a yeast transcription factor and the HATs.
Enright et al. applied Markov cluster (MCL) algorithm to identify protein families on a network constructed based on sequence similarity. MCL algorithm, originally developed for graph clustering, computes the probabilities of random walks through a given graph by repeatedly performing two operations: expansion and inflation. In expansion step, the square of a stochastic matrix is computed to obtain the probabilities of random walks for all pair of nodes with one node as source and the other as destination. Inflation step is performed by taking the power of each entry followed by scaling (to make the matrix stochastic again). More formally, the inflation operator Γr(M) with a parameter r for a stochastic matrix M is defined by
| (16) |
Initially they computed a stochastic matrix M where each entry Mij represents the sequence similarity between two proteins i and j. The two operators are then repeatedly applied to the matrix in alternating way until an equilibrium state is reached. Clusters are naturally obtained upon the termination of the algorithm as the network is partitioned into different segments in such a way that there cannot be any moves between two different segments. The inflation parameter r defines the granularity of the clustering: As the parameter r is increased, the “tightness” of the resulting clusters is also increased.
Nabieva et al. [22] studied a related problem of finding functional annotations for unannotated genes based on network topology and annotations of other genes in the network. Intuitively, they used the information flow from annotated nodes to predict the protein functions of unannotated nodes. Rather than using a circuit flow approach, they devised a heuristic algorithm called FunctionalFlow. In each round, the certain amount of flow is pushed from the nodes with known functional annotations and is forwarded to neighboring nodes. The amounts of flow forwarded into neighbors are proportional to the weights of the links, which are assigned based on experimental data. The algorithm runs for a finite number of steps and the total amount of flow entering a node defines functional scores, and as a result, nodes closer to the sources tend to receive higher scores.
2.4 Identifying central nodes in a network
The centrality analysis in a molecular interaction network helps to identify nodes playing crucial roles in biological processes. Measures such as node degrees or betweenness are used to estimate the centrality of a node in the network. However, node degrees consider only local connectivity ignoring the global structure of the networks. While betweenness may be better to predict network hubs, the measure only considers shortest paths and does not take into account other alternative paths.
Newman [11] proposed a centrality measure called random-walk betweenness. Intuitively, by counting flows over all possible paths, one can identify hub nodes through which a large amount of information is propagated. Suppose that f(s, t) (i) is the fraction of times that a random walker passes through node i while traversing from s to t. The betweenness B(i) can be obtained by averaging f(s, t) (i) over all s and t pairs. Utilizing the fact that the current flow in an electrical circuit is equivalent to a random walk, a matrix representation to solve the problem can be derived as follows: Let D be the diagonal matrix where Dii is the degree di of node i and let A be the adjacency matrix of a given network. Suppose that V(st) denotes the voltage vector for the circuit flow from s to t and the source vector T(st) is defined as Ti(st) = 1 if i is the source node s, −1 if i is the sink node t, and 0 otherwise. Then we have
| (17) |
The matrix (D-A), called Kirchhoff matrix1 is singular – the sum of all the rows or columns gives a zero vector. Thus we remove any arbitrary equation and also choose an arbitrary node v and set the voltage of v to be 0 (thus removing the column corresponding to v). Defining the resulting matrix to be (D-A)v, we obtain2
| (18) |
Matrix (D-A)v, is a reduced Kirchhoff matrix and by Kirchhoff matrix tree theorem, the determinant of this matrix is equal to the number of the spanning trees of the network [23]. Thus for any nontrivial graph this determinant is nonzero and the matrix is invertible.
Finally, the current passing through node i for source s and destination t is given as
| (19) |
Random walk betweenness is defined as the average number of visits of random walkers, which is the same as the average amount of current over all source and target pairs. Accordingly, it is given as
| (20) |
Note that one needs to compute the inverse matrix only once, which is computationally the most expensive part in the algorithm, and use it to obtain the voltages for any source and destination pair.
Missiuro et al. [10] extended the random walk centrality measure by considering interaction confidence. The conductance of an interaction in the circuit network is set to be proportional to its confidence score. They applied the method to find betweenness in two interaction networks – S. cerevisiae and C. elegans: for yeast, socio-affinity indices [4] are used as confidence scores while the method is tested with uniform confidence scores in the worm network. They showed that, in the networks considered in their study, the centrality measure they obtained correlates with essentiality and pleiotropy.
Zotenko et al. [24] studied the relation of several centrality measures, including random walk betweenness (which they call the current flow centrality), and gene essentiality in yeast interaction networks constructed using different approaches. In their study, a gene is considered essential if it is essential for growth in optimal laboratory conditions. They found that current flow centrality correlates with essentiality in all but Y2H networks. Interestingly, this correlation disappears after controlling for the dependence between vertex degree and essentiality. They also observed that for all the networks considered in the study, the current flow centrality is the best predictor of vulnerability to attack among all centrality measures that they considered. That is, removing nodes with high current centrality is more likely to disintegrate the network than removing the equivalent number of nodes that are central in other criteria. Such results suggest that while current flow centrality may not necessarily explain yeast gene essentiality, it correctly identifies communication hubs.
3 Inferring Information Flow from Multiple Sources to Sinks
Newman [11] showed how to use a matrix representation to obtain the flow solutions to a large number of source and sink pairs effectively and applied the method to compute random walk betweenness. Motivated by our application to uncover dys-regulated pathways in complex diseases, such as cancer, we generalized this technique by allowing each circuit flow instance to have multiple sources and multiple sinks. In addition, links in the network may be weighted considering confidence scores or gene expression levels and the weights are used to represent the resistance in the circuit. Since our application required solving the corresponding problem on a huge human interaction network (11,969 human proteins connected by 103,966 links [8, 9]), we utilized an idea based on blockwise matrix inversion to expedite the computation.
3.1 System of Linear Equations
Let G = (N, E) represent a molecular interaction network where N is a set of nodes and E is a set of molecular interactions. Two subsets of nodes S={s1, s2, … ss}, T={t1, t2, … tt} ⊂ N are defined as sources and destinations. Let s, t, n denote the size of set S, T, and N, respectively. Each edge e has conductance w(e), which can be defined differently depending on the applications. Let I(i, j) denote the amount of current passing through a link (i, j) ∈ E and V(i) denote the voltage of a node i∈V. Ohm’s law gives the following equation.
| (21) |
Let us assume that the amount of current entering each source is the same and the total amount is 1. For sinks, we create a pseudo-sink t′ and add links from all nodes in T to t′. Then Kirchhoff’s current law can be written as follows.
| (22) |
| (23) |
| (24) |
Finally, we set the voltage of all nodes in T to be 0 so that all current flows into one of the sinks and there is no current flow between them, which can be written as
| (25) |
Combining equation (22) with (23)–(25), we obtain
| (26) |
| (27) |
| (28) |
where W̃(i) = Σj∈Nei(i) w(i, j).
Let us define a vector V = [V(i) for i ∈ N] and a vector IT = [I(i, t′) for i ∈ T]. Then we can rewrite Equations (27)–(29) as a matrix form as follows.
| (29) |
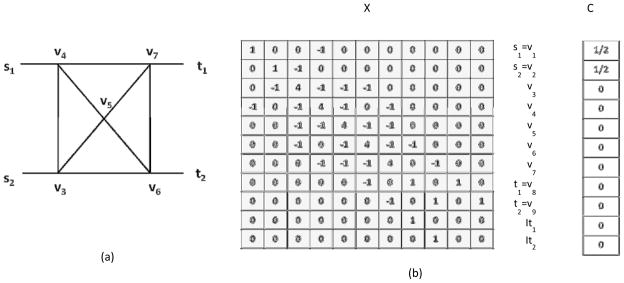
where W̃ is an n ×n diagonal matrix whose i-th diagonal element is W̃(i). An n ×n matrix W is defined as W(i, j) = w(i, j). A is an n×t matrix where A(i, j) = 1 if i=tj and 0 otherwise. B is a t×n matrix and is defined as B(i, j) = 1 if j=ti and 0 otherwise. Finally, C is a column vector of size n+t where C(i) = 1/s if i∈S and 0 otherwise. Let X denote the coefficient matrix. An example of a network and the corresponding matrix formulation is given in Figure 1.
Figure 1.
An example of a network (a) and its matrix representation (b) as in equation (30). The coefficient matrix X, the variable vector and vector C are shown in (b).
3.2 Computing the solution
The solution to the system of linear equations (30) can be obtained by simply computing the inverse of the matrix as follows.
| (30) |
Note that W̃−W remains the same regardless of source and sink sets when the same network and weights are used. When the solutions to a large number of source and destination sets need to be computed, it would be more efficient to precompute the inverse of the common submatrix and utilize blockwise inversion to obtain the inverse of the whole matrix [25] [26]. Since W̃−W is singular (this is a weighted Kirchhoff matrix and therefore the sum of all elements in each row/column is zero), we take the upper-left submatrix of size n-1 by n-1. Let P denote the reduced submatrix. The remaining submatrices are denoted as Q, R and S (See equation (32)). Utilizing the formula for the inverse of the block matrix [26] (below we will show the invertibility of the matrices) we obtain:
| (31) |
where
| (32) |
| (33) |
| (34) |
| (35) |
Given the voltages V of all nodes, the amount of current passing through each link and node is given as
| (36) |
| (37) |
We now show that all matrices for which we computed the inverse are non-singular. Since P is a reduced Kirchhoff matrix, it is generically non-singular [23]. Submatrix S − R · P−1 · Q is called Schur complement of P. Using block decomposition formula [26] we can decompose our original matrix, X, as follows:
| (38) |
The right side of the equation is block LU decomposition of matrix X.
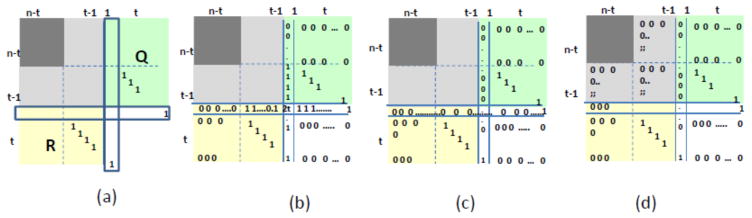
First we argue that X is generically invertible. Without loss of the generality, we can assume that the rows (columns) of X are ordered so that all non-sink nodes precede all sink nodes. Then the matrix representation using Q, R is shown in Figure 2(a).
Figure 2.
Matrix operations for the proof of invertibility of matrices. The gray area corresponds to P and the dark gray area corresponds to the submatrix spanned by nodes that are not sink nodes. The yellow and green areas are submatrices Q and R, respectively S is left blank. The n-th column/row are highlighted in Figure (a). (b) Matrix after summing up all rows/columns and putting the result in the n-th row/column. (c) Matrix after cleaning all, but the last element in the n-th row/column (d) Final matrix after removing all nonzero elements in the light gray area. The dark grey matrix remains non-zero.
Let us add all the rows and replace the n-th row with the summation of the rows. We do the same for the columns. The resulting matrix is shown in Figure 2(b). Using the last row/column we can eliminate all positive values in the n-th row/column except the last one, obtaining the matrix shown in Figure 2(c). Finally, using the vectors from yellow and green rows/columns we can clean all nonzero elements in the light gray area of matrix P. The absolute value of the determinant of the final matrix (Figure 2(d)) is equal to the absolute value of the determinant of the dark gray area. Note that this matrix corresponds exactly to the matrix for the network obtained from our original network by contracting all sink nodes to a dummy node and removing the row and column corresponding to this dummy node. Thus, this submatrix is a reduced Kirchhoff matrix and is, generically, non-singular.
Therefore the whole matrix X is, generically, non-singular (as long as the sinks are connected to the rest of the networks). By the LU decomposition in (39), we have
and therefore, the non-singularity of X and P implies the non-singularity of Schur complement S − R · P−1 · Q−1. This proves all matrices for which we compute the inverse are non-singular and therefore we can obtain the inverse of X using the blockwise inversion method described above.
It takes O(n3) time to compute the inverse of a matrix and (33)–(36) can be computed in time O(t·n2). Therefore, the solutions to multiple source and destination sets can be computed in time O(n3+m·t·n2) where m is the number of instances to be computed (i.e. the number of different pairs of source and destination sets).
3.3 Applications
As discussed in Section 2.1, the current flow algorithm is found to be useful to identify causal genes in associated eQTL regions and dys-regulated pathways. For a given target gene, an eQTL analysis may find multiple associated regions and each region can contain dozens of candidate causal genes. Among these candidate causal genes we would like to identify the ones whose alterations are most likely to cause the abnormal expression for the given target gene. For this purpose, we utilized a molecular interaction network and the circuit flow approach [8, 9]. Namely we attempted to identify the most likely causal genes based on the amount of current entering the genes when the current is pushed from the target gene through the molecular interaction network.
We applied the current flow algorithm described in Section 3.2 to identify potential causal genes in Glioma [8, 9]. The inputs to this problem are gene copy number variations in cancer tissues, gene expression profiles of the same set of patients, and gene expression profiles for a set of non-cancer cases. We first selected a set of differentially expressed genes in cancer patients compared to non-tumor cases as target genes. For each target gene, chromosomal regions where copy number variations correlated with the gene expression changes are identified. Recall that more than one genes may reside in the associated region due to the spacing of the markers and linkage disequilibrium. To identify potential causal genes, we used the current flow algorithm. More specifically, for each selected target gene g and an associated region R, we created a circuit network where the target gene g is a source of the current flow and the candidate genes residing in the region R are included in the sink set T. Assuming that the activities of genes on the affected sub-network are correlated with the expression of the target gene, we defined the conductance w(u, v) to be (|corr(u, g)|+|corr(v, g)|)/2 where corr(a, b) denotes Pearson’s correlation coefficient of the gene expression levels of gene a and b. We computed the amount of current going through nodes in the network and estimated an empirical p-value for each pair of a target and a causal gene, utilizing a permutation test: random networks were generated preserving node degrees, and assuming that each edge has a unit conductance, we ran the circuit flow algorithm in each random network for the same set of target and candidate genes. Empirical p-values were computed using a Z-test based on current values in the random networks.
Considering genes with significant p-values, we were able to identify putative causal genes as well as commonly dys-regulated pathways and hub nodes on such pathways. Among identified pathways we found several important players in Glioma or more generally in cancer such as EGFR and Insulin Receptor signaling pathways, and RAS signaling. Compared to simple genome-wide association studies which only identifies putative associations between causal loci and target genes, our method provides an increased power of predicting causal disease genes and uncovering dys-regulated pathways.
In our study, we found that for a given target gene, there might be up to more than a hundred of associated eQTL regions. Note that the current flow instances for the same target gene share the network structure and link conductance, and therefore, have the same submatrix P. Once the computation of P−1, which is the most expensive part in the algorithm, is done, the solutions for all instances can be obtained quickly.
In the above mentioned case, we had only one source node and multiple sink nodes in each circuit flow instance. However it is not difficult to envision applications where there are more than one source nodes. For example, we may perform clustering based on gene expression levels, and use a cluster of nodes as target genes (i.e., the sources of current flow). Another example is the prioritization of disease genes described in Section 2.2, in which multiple source nodes collected from known disease associations were used.
4. Conclusion
In this paper, we first provided an overview of recent research on information flow based network analysis. Information flow approaches have been used to solve various biological problems such as uncovering causal genes and pathways, identifying disease genes, predicting gene functions, and network centrality.
We also described an efficient algorithm to compute current flow solutions to a large number of instances when they share the same network structure, and showed how it can be applied to infer information flow from genotype to phenotype in a large human interaction network. While the calculation of information flows in such a large network is computationally expensive we showed that our method can significantly expedited the analysis.
Acknowledgments
YAK, SW and TMP are supported by the Intramural Research Program of the National Institutes of Health, National Library of Medicine. JHP was partially supported by the Polish Scientific Grant: Nr. N N201387034, the GWU REF grant, and the CCAS/UFF award.
Footnotes
It is also called Laplacian matrix or admittance matrix.
With a slight abuse of notations, we used V(st) and T(st) here to refer the vectors after removing the entries corresponding to node v
References
- 1.Ewing RM, et al. Large-scale mapping of human protein-protein interactions by mass spectrometry. Mol Syst Biol. 2007;3:89. doi: 10.1038/msb4100134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Rual JF, et al. Towards a proteome-scale map of the human protein-protein interaction network. Nature. 2005;437(7062):1173–8. doi: 10.1038/nature04209. [DOI] [PubMed] [Google Scholar]
- 3.Stelzl U, et al. A human protein-protein interaction network: a resource for annotating the proteome. Cell. 2005;122(6):957–68. doi: 10.1016/j.cell.2005.08.029. [DOI] [PubMed] [Google Scholar]
- 4.Gavin AC, et al. Proteome survey reveals modularity of the yeast cell machinery. Nature. 2006;440(7084):631–6. doi: 10.1038/nature04532. [DOI] [PubMed] [Google Scholar]
- 5.Giot L, et al. A protein interaction map of Drosophila melanogaster. Science. 2003;302(5651):1727–36. doi: 10.1126/science.1090289. [DOI] [PubMed] [Google Scholar]
- 6.Krogan NJ, et al. Global landscape of protein complexes in the yeast Saccharomyces cerevisiae. Nature. 2006;440(7084):637–43. doi: 10.1038/nature04670. [DOI] [PubMed] [Google Scholar]
- 7.Li S, et al. A map of the interactome network of the metazoan C. elegans. Science. 2004;303(5657):540–3. doi: 10.1126/science.1091403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Kim YA, Wuchty S, Przytycka TM. Identifying Causal Genes and Dysregulated Pathways in Complex Diseases. PLoS Comput Biol. doi: 10.1371/journal.pcbi.1001095. To appear. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kim YA, Wuchty S, Przytycka TM. Simultaneous Identification of Causal Genes and Dys-Regulated Pathways in Complex Diseases. Research in Computational Molecular Biology (RECOMB) 2010 [Google Scholar]
- 10.Missiuro PV, et al. Information flow analysis of interactome networks. PLoS Comput Biol. 2009;5(4):e1000350. doi: 10.1371/journal.pcbi.1000350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Newman M. A measure of betweenness centrality based on random walks. Social Networks. 2005;27(1):39–54. [Google Scholar]
- 12.Suthram S, et al. eQED: an efficient method for interpreting eQTL associations using protein networks. Mol Syst Biol. 2008;4:162. doi: 10.1038/msb.2008.4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Tu Z, et al. An integrative approach for causal gene identification and gene regulatory pathway inference. Bioinformatics. 2006;22(14):e489–96. doi: 10.1093/bioinformatics/btl234. [DOI] [PubMed] [Google Scholar]
- 14.Doyle PGSJ. Random walks and electric networks. 1984 [Google Scholar]
- 15.Yeger-Lotem E, et al. Bridging high-throughput genetic and transcriptional data reveals cellular responses to alpha-synuclein toxicity. Nat Genet. 2009;41(3):316–23. doi: 10.1038/ng.337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Lee E, et al. Analysis of AML genes in dysregulated molecular networks. BMC Bioinformatics. 2009;10(Suppl 9):S2. doi: 10.1186/1471-2105-10-S9-S2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Brem RB, Kruglyak L. The landscape of genetic complexity across 5,700 gene expression traits in yeast. Proc Natl Acad Sci U S A. 2005;102(5):1572–7. doi: 10.1073/pnas.0408709102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ravindra K, Ahuja TLM, Orlin James B. Network flows : theory, algorithms, and applications. Prentice Hall; 1993. [Google Scholar]
- 19.Kohler S, et al. Walking the interactome for prioritization of candidate disease genes. Am J Hum Genet. 2008;82(4):949–58. doi: 10.1016/j.ajhg.2008.02.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Vanunu O, Sharan R. A propagation-based algorithm for inferring gene-disease associations. German Conference on Bioinformatics. German Conference on Bioinformatics. 2008:LNI136. [Google Scholar]
- 21.Stojmirovic A, Yu YK. Information flow in interaction networks. J Comput Biol. 2007;14(8):1115–43. doi: 10.1089/cmb.2007.0069. [DOI] [PubMed] [Google Scholar]
- 22.Nabieva E, et al. Whole-proteome prediction of protein function via graph-theoretic analysis of interaction maps. Bioinformatics. 2005;21(Suppl 1):i302–10. doi: 10.1093/bioinformatics/bti1054. [DOI] [PubMed] [Google Scholar]
- 23.Tutte WT. Graph Theory. Cambridge University Press; 2001. [Google Scholar]
- 24.Zotenko E, et al. Why do hubs in the yeast protein interaction network tend to be essential: reexamining the connection between the network topology and essentiality. PLoS Comput Biol. 2008;4(8):e1000140. doi: 10.1371/journal.pcbi.1000140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Potokina E, et al. Gene expression quantitative trait locus analysis of 16 000 barley genes reveals a complex pattern of genome-wide transcriptional regulation. Plant J. 2008;53(1):90–101. doi: 10.1111/j.1365-313X.2007.03315.x. [DOI] [PubMed] [Google Scholar]
- 26.Carlson DH. What are Schur complements, anyway? Linear Alg Appl Reports. 1986;74:257–275. [Google Scholar]