Abstract
The p53 gene is crucial for effective tumor suppression in humans as supported by its universal inactivation in cancer cells either through mutations affecting the p53 locus directly or through aberration of its normal regulation. The p53 tumor repressor is regulated through a negative feedback loop involving its transcriptional target MDM2. MDMX is also an essential negative regulator of p53. Several computational models have been proposed to simulate the dynamics of the p53-MDM2 loop, but they do not include MDMX, only account for some basic interactions between p53 and MDM2 and cannot capture the intrinsic noise in the loop. In this article, we present a comprehensive model for the p53-MDM2/MDMX loop that accounts for most known interactions among p53, MDM2 and MDMX. Our model is characterized by a set of molecular reactions, which enables us to employ stochastic simulation to investigate the dynamics of the loop. In agreement with experiments, our results show that p53 and MDM2 undergo oscillations after DNA damage in the presence of noise, and the variation in oscillation amplitudes is much higher than that in oscillation periods. Our simulations predict that intrinsic noise contributes to 60%–70% of the total variation in oscillation amplitudes and periods. The protein levels of p53, MDM2, and MDMX after treatment with Nutlin in our simulations are also consistent with experimental results. Our simulation results further predict that p53 levels increase dramatically after MDM2 is knocked out, but increase with a much less amount after MDMX is knocked out. This may partially explain why MDM2-null and MDMX-null mouse embryos die in different developmental stages. Our stochastic model and simulation provide insights into the variability of the behavior of the p53 pathway and can be used to predict the dynamics of the pathway after certain interventions.
Key words: algorithms, gene chips, gene networks, genetics, machine learning
1. Introduction
The tumor suppressor p53 plays a central role in maintaining the integrity of the genome and is crucial for effective tumor suppression in humans (Hainuat and Wiman, 2005). Approximately 50% of all malignancies carry a p53 mutation, and of those tumors that do not have mutated p53, a large proportion have inactivated p53 function by another mechanism (Horn and Vousden, 2007). The p53 pathway is activated in response to cellular stresses such as DNA damage and oncogene activation, which leads to a variety of response including DNA repair, cell-cycle arrest, senescence, apoptosis (Toledo and Wahl, 2006; Vogelstein et al., 2000). While the p53 pathway is composed of hundreds of genes and their products, its core control involves three proteins: p53, MDM2 and MDMX (Toledo and Wahl, 2006; Levine et al., 2006). The MDM2 protein, that is positively regulated by p53 gene, acts on p53 protein as an E3-ubiquitin ligase and induces p53 ubiquitination and degradation. This negative feedback loop keeps p53 protein at low levels in the absence of stress signals, which allows normal cell proliferation. In addition to MDM2, MDMX is required to restrain p53 function in a nonredundant manner. More specifically, MDMX affects p53 abundance by modulating the levels and activity of MDM2; MDMX also binds to the transactivation domain of p53 and inhibits p53 transcriptional activity, which contributes to the overall inhibition of p53 (Toledo and Wahl, 2006; Marine et al., 2006).
Experimental studies have shown that p53 and MDM2 undergo oscillatory dynamics after ionizing radiation-induced DNA damage (Bar-Or et al., 2000; Lahav et al., 2004; Geva-Zatorsky et al., 2006). In individual cells, protein levels of p53 and MDM2 change out of phase with one another. The period of these oscillations and the peak levels of p53 and MDM2 protein have been observed in vivo to be variable from cell to cell. Several computational models have been proposed to explain the oscillations of p53 and MDM2 in cells (Bar-Or et al., 2000; Geva-Zatorsky et al., 2006; Ma et al., 2005; Wagner et al., 2005; Ciliberto et al., 2005; Monk, 2003; Tiana et al., 2002; Mihalas et al., 2000). However, all these models do not include MDMX and only account for some basic interactions between p53 and MDM2. Moreover, since these models all employ ordinary differential equations (ODE) to model the interactions between p53 and MDM2, they are essentially deterministic models. In order to simulate the variability in the oscillation period and amplitudes observed in single cells, stochasticity is added to certain parameters of the model (Geva-Zatorsky et al., 2006; Ma et al., 2005). Although this approach may reflect extrinsic noise, it does not capture the effect of the intrinsic noise inherent to the pathway (Kærn et al., 2005; Raser and O'Shea, 2005).
Since there is significant stochasticity in gene expression arising from fluctuations in transcription and translation (Kærn et al., 2005; Raser and O'Shea, 2005), a stochastic model for the p53-MDM2/MDMX loop is needed to correctly reflect the intrinsic noise inherent to gene expression and other chemical reactions. Given the important role that MDMX plays in the p53 pathway (Toledo and Wahl, 2006; Marine et al., 2006), it is highly desirable to incorporate MDMX into a computational model. Although relatively simple models can produce the oscillations of p53 and MDM2 after DNA damage (Bar-Or et al., 2000; Geva-Zatorsky et al., 2006; Ma et al., 2005; Wagner et al., 2005; Ciliberto et al., 2005; Monk, 2003; Tiana et al., 2002; Mihalas et al., 2000), one may gain more insights into the p53 pathway if a model can capture more detailed interactions among p53, MDM2 and MDMX that have been discovered in a number of studies. In this paper, we present a model for the p53-MDM2/MDMX loop that accounts for most known interactions among p53, MDM2 and MDMX based on experimental results reported in the literature. The model is characterized by 48 chemical reactions. Since stochastic simulation can correctly reflect the intrinsic noise in a chemically reacting system (Gillespie, 1977; McAdams and Arkin, 1997), we employ the exact stochastic simulation algorithm (SSA), that we recently developed for chemically reacting systems with delays (Cai, 2007), to simulate the dynamics of p53, MDM2 and MDMX based on the proposed model.
2. Methods
2.1. Model description
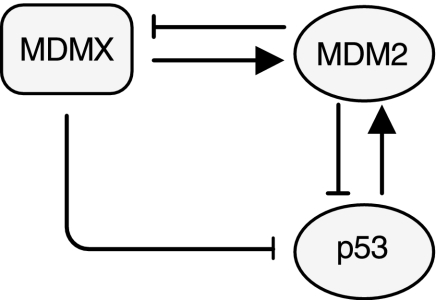
Figure 1 depicts a block diagram of the model for the p53-MDM2/MDMX loop (Toledo and Wahl, 2006; Marine et al., 2006). The transcription factor p53 positively regulates the expression of MDM2 gene. MDM2 in turn catalyzes p53 ubiquitination, thereby causing proteasomal degradation of p53. MDM2 also inhibits MDMX by inducing MDMX ubiquitination. MDMX forms a heterodimer with MDM2, which stabilizes MDM2. MDMX can bind to p53 and inhibit the transcriptional activity of p53. MDMX also stimulates MDM2-mediated ubiquitination and degradation of p53. The model is characterized by 48 reactions specified in Table 1 and by 21 molecular species described in Table 2. We next describe these reactions in detail.
Fig. 1.
p53-MDM2-MDMX loop.
Table 1.
Reactions and Parameters
| Reaction | Parameter (min−1) |
|---|---|
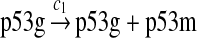 |
c1 = 0.113 |
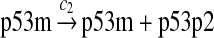 |
c2 = 0.8 |
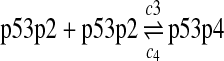 |
c3 = 0.004, c4 = 2160 |
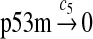 |
c5 = 1.16 × 10−3 |
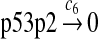 |
c6 = 2.78 × 10−3 |
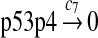 |
c7 = c6/2 |
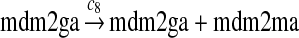 (delay1a) (delay1a) |
c8 = 1.456 |
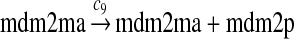 |
c9 = 0.92 |
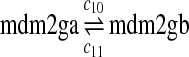 |
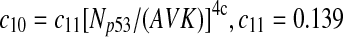 |
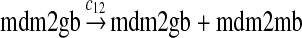 (delay2b) (delay2b) |
c12 = 6c8 |
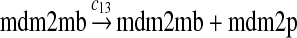 |
c13 = 14c9 |
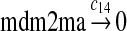 |
c14 = 0.01 |
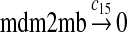 |
c15 = c14 |
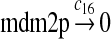 |
c16 = 3.3 × 10−2 |
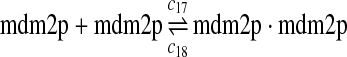 |
c17 = 0.004, c18 = 180 |
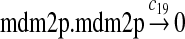 |
c19 = c16/2 |
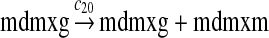 |
c20 = 1.775 |
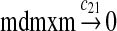 |
c21 = c14 |
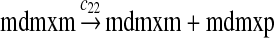 |
c22 = c9 |
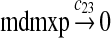 |
c23 = 3.85 × 10−3 |
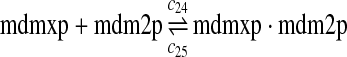 |
c24 = 0.002, c25 = 18 |
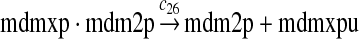 |
c26 = 0.98 |
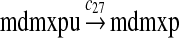 |
c27 = 1.96 |
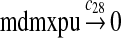 |
c28 = 1.16 × 10−2 |
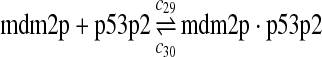 |
c29 = 1.84 × 10−3, c30 = 123.6 |
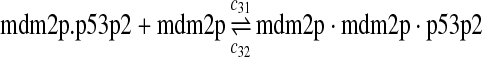 |
c31 = c29,c32 = c30 |
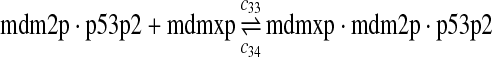 |
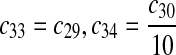 |
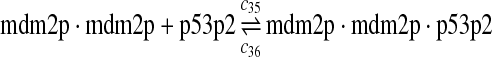 |
c35 = c29,c36 = c30 |
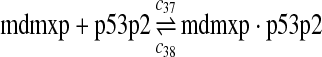 |
c37 = c29,c38 = c30 |
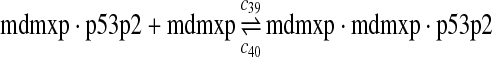 |
c39 = c29,c40 = c30 |
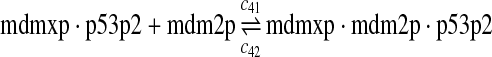 |
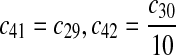 |
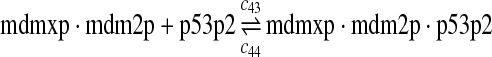 |
c43 = c29,c44 = c30 |
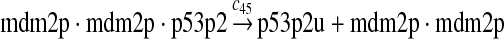 |
c45 = 0.98 |
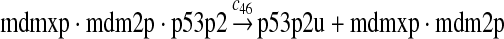 |
c46 = 3c45 |
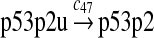 |
c47 = 2.45 |
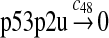 |
c48 = 0.139 |
Delay1 is uniformly distributed in the interval [30 min 50 min].
Delay2 is uniformly distributed in the interval [55 min 75 min].
See text for explanation.
Table 2.
Molecular Species
| Species | Description |
|---|---|
| p53g | p53 gene |
| p53m | p53 mRNA |
| p53p2 | p53 protein dimer |
| p53p4 | p53 protein tetramer |
| mdm2ga | MDM2 gene without p53 bound |
| mdm2ma | MDM2 mRNA transcribed from promoter 1 |
| mdm2p | MDM2 protein |
| mdm2gb | MDM2 gene with p53 bound |
| mdm2mb | MDM2 mRNA transcribed from promoter 2 |
| mdmxg | MDMX gene |
| mdmxm | MDMX mRNA |
| mdmxp | MDMX protein |
| mdmxpu | Ubiquitinated MDMX protein |
| mdmxp·mdm2p | MDMX and MDM2 protein dimer |
| mdm2p·p53p2 | Complex of MDM2 protein and p53 dimer |
| mdmxp·p53p2 | Complex of MDMX protein and p53 dimer |
| mdm2p·mdm2p | MDM2 protein dimer |
| mdm2p·mdm2p·p53p2 | Complex of MDM2 dimer and p53 dimer |
| mdmxp·mdm2p·p53p2 | Complex of MDM2/MDMX dimer and p53 dimer |
| mdmxp.mdmxp.p53p2 | Complex of MDM2 dimer and p53 dimer |
| p53p2u | Ubiquitinated p53 protein dimer |
p53 expression and tetramerization (reactions 1–7)
Since the amount of p53 protein in cells is determined mainly by its degradation rate (Vogelstein et al., 2000; Oren, 1999), we assume that p53 is transcribed constitutively as specified by reaction 1. In vitro study of biogenesis showed that p53 dimers are formed cotranslationally and tetramers are formed posttranslationally (Nicholls et al., 2002). Reaction 2 represents the translation of p53 mRNA that produces p53 dimers. It has been shown that p53 exists as dimers and tetramers in solution (Weinberg et al., 2004). Moreover, the p53 tetramer is assembled as a “dimer of dimer” (Clore et al., 1994; Lee et al., 1994). The tetramerization and disassociation of p53 dimers are described by reactions 3 and 4. Reaction 5 represents the degradation of p53 mRNA, and reactions 6 and 7 represent the constitute degradation of p53 protein before being uibiquitinated.
MDM2 expression and degradation (reactions 8–19)
The MDM2 gene has two promoters (Juven et al., 1993; Wu et al., 1993; Barak et al., 1994; Zauberman et al., 1995). The first promoter (P1) is located upstream of exon 1 and is constitutively active. The second promoter (P2) is near the 3′ end of intron 1; it contains a p53 binding site and is activated by p53. Reaction 8 represents the constitutive transcription of MDM2 from P1. The product of reaction 8 is delayed, which accounts for the time needed for transcription, splicing, translocation and translation. Reaction 9 represents translation of the MDM2 mRNA transcribed from P1. Reaction 10 models the event that p53 binds to the promoter of MDM2 as a tetramer, while reaction 11 models the disassociation of p53 with the MDM2 gene. Reaction 12 represents the transcription of MDM2 from P2 after p53 binds to its binding site. Like reaction 8, reaction 12 is delayed. We do not include a delay in other reactions such as reactions 1 and 20, since only delays in reactions 8 and 12 affect the oscillation of p53 and MDM2. Reaction 13 represents translation of the MDM2 mRNA transcribed from P2. Reactions 14 and 15 specify the degradation of MDM2 protein. Reaction 16 represents the degradation of MDM2 protein. Reactions 17 and 18 describe the dimerization and disassociation of MDM2 protein (Kawai et al., 2007; Tanimuraa et al., 1999). Reaction 19 represents the degradation of MDM2 dimer.
MDMX expression and ubiquitination (reactions 20–28)
MDMX lacks p53 binding sites in its promoter region and is not induced by p53 after DNA damage (Shvarts et al., 1996; Marinea and Jochemsen, 2005). Hence, we assume that MDMX is transcribed constitutively, as specified by reaction 20. Reaction 21 represents the degradation of MDMX mRNA. Reaction 22 represents the translation of MDMX mRNA. Reaction 23 describes constitutive degradation of MDMX protein without ubiquitination. MDMX and MDM2 form heterodimers (Kawai et al., 2007; Tanimuraa et al., 1999; Sharp et al., 1999; Stad et al., 2000), and reactions 24 and 25 represent dimerization and disassociation of MDMX and MDM2. Reaction 26 specifies the ubiquitination of MDMX catalyzed by MDM2 (de Graaf et al., 2003; Pan and Chen, 2003; Ma et al., 2006). It was shown that MDMX is deubiquitinated and stabilized by HAUSP (Meulmeester et al., 2005). Reaction 27 represents deubiquitination of MDMX. Reaction 28 represents the degradation of ubiquitinated MDMX.
p53, MDM2, and MDMX interactions (reactions 29–44)
Both MDM2 and MDMX can bind to the N-terminal transactivation domain of p53 via their N-terminal domains. It was observed that p53, MDM2 and MDMX can form a triple complex (Sharp et al., 1999; Stad et al., 2000). Reactions 29–44 represent the interactions among p53, MDM2 and MDMX.
p53 ubiquitination and degradation (reactions 45–48)
Reactions 45 and 46 represent ubiquitination of p53 catalyzed by MDM2. Note that reactions 45 and 46 are consistent with the observation that dimerization/oligomerizaton of p53 is necessary for p53 to be efficiently ubiquitinated (Kubbutat et al., 1998; Maki, 1999). Reaction 47 represents deubiquitination of ubiquitinated p53 by HAUSP (Li et al., 2004). Reaction 48 represents the degradation of ubiquitinated p53 by proteasome.
Model limitations
Like all existing computational models (Bar-Or et al., 2000; Geva-Zatorsky et al., 2006; Ma et al., 2005; Wagner et al., 2005; Ciliberto et al., 2005; Monk, 2003; Tiana et al., 2002; Mihalas et al., 2000), our model is a single-compartment model, because we do not differentiate between nuclear and cytosolic pools of p53, MDM2 and MDMX with appropriate translocation rates. MDMX is a cytoplasmic protein and depends on MDM2 to import into the nucleus. Low levels of MDM2 induce monoubiquitination and nuclear export of p53, whereas high levels promote its polyubiquitination and nuclear degradation (Li et al., 2003). Our current model does not include shuttling of p53 and MDMX between the nucleus and cytoplasm, but can be extended to a multi-compartment model when more experimental data become available.
2.2. Parameter estimation
Each reaction is associated with a reaction probability rate constant, c, which determines the probability that a specific reaction occurs in an infinitesimal time interval. The probability rate constant c of a specific reaction can be calculated from the conventional rate constant k as follows: c = k for a unimolecular reaction, c = k/(AV) for a bimolecular reaction with two different reactants and c = 2k/(AV) for a bimolecular reaction with one reactant (Gillespie, 2007), where A = 6.022 × 1023 is the Avogadro's number, and V is the system volume. We assume that the system is a sphere with a diameter of 10 μm which is the diameter of a typical mammalian cell nucleus (Dundr and Misteli, 2001). This results in a volume V = 5 × 10−13 L. Note that translation is modeled as a unimolecular reaction. Therefore, the system volume does not affect the calculation of probability rate constant of translation, although translation occurs in the cytoplasm. As we will describe next, most of the probability rate constants were calculated from the conventional rate constants reported in the literature, while several probability rate constants were determined in simulations.
The transcription rates of p53(c1), MDM2(c8), and MDMX(c20) are unknown. No experimental result on the deubiquitination rates of MDMX (c27) and p53 (c47) was reported in the literature. Therefore, we determined these rates in simulations as described in Model Calibration. In the following, we describe how the remaining probability rate constants were determined.
The rate c2 is estimated from the polysome profile of p53 mRNA (Del Prete et al., 2007). Comparing the polysome profile of p53 (Del Prete et al., 2007) with that of MDM2 (Brown et al., 1999), we estimated that the ribosome density of p53 is approximately 1.3 times of that of MDM2. Considering that the p53 protein has 393 amino acids, we estimated the translation rate of p53 to be 1.6 proteins per minute. See description of c9 for the method for calculating the translation rate from the ribosome density.
It has been shown that p53 exists as dimers and tetramers in solution with a equilibrium constant equal to kd,p53 = 3.2 μM (Weinberg et al., 2004). We chose the rate constant of reaction 3 as k3 = 107M−1sec−1, which is approximately one order of magnitude lower than the diffusion limit. The rate constant of reaction 4 was then k4 = kd,p53k3. The probability rate constants c3 and c4 were calculated from k3 and k4 using the method described earlier. Since determination of c3 was not based on any experimental results, we tested the sensitivity of simulation results to c3. Increasing or decreasing c3 ten times did not cause noticeable changes in simulation results (data not shown).
The half-life of p53 mRNA is about 10 hours in human RKO colorectal carcinoma cells (Mazan-Mamczarz et al., 2003), 22–23 hours in primary chicken embryo fibroblast (CEF) cells and murine embryo fibroblast (MEF) cells, and 2–3 hours in immortal CEF and MEF cells (Kim et al., 2001a,b). We used a half-life of 10 hours to calculate c5. Specifically, c5 = ln(2)/T1/2, where T1/2 is the half-life. Note that the median half-life of human mRNA was estimated to be about 10 hours (Yang et al., 2003).
The half-life of p53 protein was increased from about 20 minutes to 120–130 minutes after the cell was treated with doxorubicin (Ju et al., 2007) or Apigenin (McVean et al., 2000). Treatment with doxorubicin can damage DNA and causes cellular response to DNA damage such as post-translational modification of p53 (Toledo and Wahl, 2006) and reduced stability of MDM2 (Stommel and Wahl, 2004), which may significantly diminish the efficiency of p53 ubiquitination. It is not clear how Apigenin stabilizes p53, but it was speculated that Apitenin might activate protein kinases that phosphorylate p53 (McVean et al., 2000), which reduces the interaction between MDM2 and p53, thereby diminishing the ubiquitination of p53. Therefore, we interpreted that the half-life of unubiquitinated p53 is 120–130 minutes and calculated c6 and c7 from a half-life of 125 minutes.
Reaction 8 includes a delay which accounts for the time needed for transcription, splicing, translocation and translation. We assume that this delay is random and uniformly distributed in [30 min, 50 min] with a mean of 40 minutes (Ma et al., 2005).
The rate c9 is estimated from the polysome profile of MDM2 mRNA (Brown et al., 1999) as follows. The polysome loading curve is an exponential function: x = exp((y − b)/a) (Arava et al., 2003; MacKay et al., 2004), where x is the number of ribosome, y is the fraction number and a and b are two constants. From the MDM2 polysome experiment (Brown et al., 1999), we have two observed points: x1 = 1, y1 = 3, x2 = 5 and y2 = 5.4. In the polysome experiment (MacKay et al., 2004) which was done by the same group as the MDM2 polysome experiment (Brown et al., 1999), the number of ribosome at the maximum fraction number was estimated to be about 25. Based on this observation, we assumed another point: x3 = 12 and y3 = 19. Using these three points and the least square method, we found a = 3.0 and b = 2.24. It can be verified that the number of ribosome at the maximum fraction number is about 25. Using this polysome loading curve and the four polysome profiles of MDM2 (Brown et al., 1999), we estimated number of ribosomes per transcript to be 2.5. The speed of translation is approximately 2–5 amino acids per second for eukaryotic cells (Alberts et al., 2002; Mathews et al., 2007). We assumed that the speed of translation is 3 amino acids per second. Multiplying the number of ribosomes per transcript by the speed of translation, we got a translation rate of 450 amino acids per minute. Dividing the translation rate by the number of amino acids of a protein, which is 491 for MDM2, we got a translation rate of 0.92 protein per minute.
The half-life of p53-DNA complex was reported to be 25 minutes (McLure and Lee., 1998); however, it may be lower under physiologic condition (Weinberg et al., 2004, 2005). We used a half-life of 5 minutes to calculate c11 in Table 1. As we describe in the Results, we also ran simulations using a c11 calculated from a half-life of one minute and twenty five minutes. Taking into account cooperative binding of the p53 tetramer to DNA, we estimated c10 as follows. The probability that the MDM2 gene is bound by a p53 tetramer is assumed to follow the Hill equation: 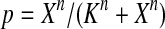 , where X is the concentration of free p53. If we denote the number of p53 dimers as Np53p2 and the number of p53 tetramer as Np53p4, we have
, where X is the concentration of free p53. If we denote the number of p53 dimers as Np53p2 and the number of p53 tetramer as Np53p4, we have 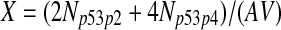 . The Hill coefficient n was chosen to be 4 (Weinberg et al., 2004). The parameter K was chosen to be 35 nM so that p is very close to zero in the absence of stress signals. From reactions 10 and 11, we can see that p is also equal to c10/(c10 + c11). Therefore, we have c10 = c11[X/(AV K)]4. Note that we assumed that free p53 could bind to its responsive elements and activate its target genes. However, Ma et al. (2005) assumed that p53 exists in either an inactive or an active state. Only after p53 is activated by ATM, it can bind to and activate its target genes. Our assumption that p53 does not have two distinct states and all free p53 are active is based on the following observations from cells treated with Nutlin. It has been demonstrated that treatment with Nutlin resulted in increased p53 levels and transcriptional activity (Vassilev et al., 2004), and that Nutlin does not induce DNA damage (Wade et al., 2006; Thompson et al., 2004). Therefore, it is unlikely that ATM is activated after treatment with Nutlin, and it in turn activates p53.
. The Hill coefficient n was chosen to be 4 (Weinberg et al., 2004). The parameter K was chosen to be 35 nM so that p is very close to zero in the absence of stress signals. From reactions 10 and 11, we can see that p is also equal to c10/(c10 + c11). Therefore, we have c10 = c11[X/(AV K)]4. Note that we assumed that free p53 could bind to its responsive elements and activate its target genes. However, Ma et al. (2005) assumed that p53 exists in either an inactive or an active state. Only after p53 is activated by ATM, it can bind to and activate its target genes. Our assumption that p53 does not have two distinct states and all free p53 are active is based on the following observations from cells treated with Nutlin. It has been demonstrated that treatment with Nutlin resulted in increased p53 levels and transcriptional activity (Vassilev et al., 2004), and that Nutlin does not induce DNA damage (Wade et al., 2006; Thompson et al., 2004). Therefore, it is unlikely that ATM is activated after treatment with Nutlin, and it in turn activates p53.
We chose c12 = 6c8 based on the experimental results (Mendrysa and Perry, 2000) as follows. After the cells were exposed with gamma irradiation, the mRNA transcribed from P2 could be increased up to 32-fold. The basal level of the mRNA transcribed from P2 was 10 to 30% of the level of mRNA transcribed from P2. If we assume that the 32-fold increase in mRNA was due to the fully-activated P2, then c12 is 3–10 times of c8. Taking the average of this range, we choose c12 = 6c8. In some situations, MDM2 transcription is induced later than that of other p53 target genes (Perry et al., 1993; Knippschild et al., 1995; Lu and Levine, 1995). Therefore, we assumed a longer delay for reaction 12 than for reaction 8, which was chosen to be uniformly distributed in [55 min, 75 min].
We chose c13 = 14c9, since experiments showed that the translation rate of the mRNA transcribed from P2 is 8–20 times of that of the mRNA transcribed from P1 (Brown et al., 1999; Landers et al., 1997). The half-life of MDM2 mRNA was reported to be 60–120 minutes (Hsing et al., 2000; Mendrysa et al., 2001), and thus, we used a half-life of 70 minutes to calculate c14 and c15. The half-life of MDM2 protein is 20–25 minutes under the normal condition without DNA damage (Stommel and Wahl, 2004; Capoulade et al., 1998; Olson et al., 1993). The rate c16 and c19 were calculated from a half-time of 21 minutes. The equilibrium constant of MDM2 dimerization, kd,mdm2, is much higher than that of MDM2 and MDMX dimerization, kd,mdm2x. We assumed that kd,mdm2 = 10kd,mdm2x. Since kd,mdm2x was estimated to be 30nM as described later, we have kd,mdm2 = 300 nM. Like k3, we chose the rate constant k17 = 107M−1sec−1 and then calculated k18 = kd,mdm2k17.
We assumed that MDMX mRNA has the same half-life as MDM2 mRNA, and thus, we took c21 = c14. We assumed that MDMX has the same translation rate as the MDM2 mRNA transcribed from P1, and chose c22 = c9. The half-life of MDMX was reported to be about 3 hours under normal condition without ionizing radiation (Kawai et al., 2003). We assumed that deubiquitination rate of MDMX under normal condition limits the amount of ubiquitinated MDMX and the half-life of unubiquitinated MDMX is 3 hours. We therefore calculated c23 from a half-life of 3 hours.
We estimated the equilibrium constant of reactions 24 and 25 to be kd,mdm2x = 30 nM as follows. It was reported that MDM2 and MDMX exist predominately as heterodimers and anti-MDM2 immunopreciptitation of MCF-7 cell lysates resulted in almost complete depletion of MDMX from the lysates (Kawai et al., 2007). Based on these observations, we assumed that 70% of MDM2 form heterodimers with MDMX. Using deterministic simulation that will be described later, we found that the equilibrium constant to be 30 nM, when 70% of MDM2 form heterodimers with MDMX. Like k3 and k17, we chose the rate constant k24 = 107M−1sec−1 and then calculate k25 = kd,mdm2xk24.
We assumed that MDM2 catalyzes the ubiquitination of MDMX and p53 with the same efficiency. Since it was reported that one mole of MDM2 transfers 0.98 moles of ubiquitin to p53 per minute (Ma et al., 2006), we chose c26 = 0.98. The half-life of MDMX after ionizing radiation was reported to be about 1 hour (Kawai et al., 2003). Since DNA damage significantly reduces the deubiquitination of MDMX by HAUSP, we interpreted that the half-life of ubiquitinated MDMX is 1 hour and calculated c28 accordingly.
The equilibrium constant of reaction 29 and 30, kd,mp53 was reported to be 60–700 nM (Schon et al., 2002; Laia et al., 200; Sakaguchi et al., 2000; Kussie et al., 1996). We used the following experimental results (Schon et al., 2002): kd,mp53 = 220 nM, k29 = 9.2 × 104 M−1s−1 and k30 = 2 s−1 (Schon et al., 2002), and calculated c30 and c31 accordingly. We assumed that reactions 31, 33, 35, 37, 39, 41, and 43 have the same rate as reaction 29: c31 = c33 = c35 = c37 = c39 = c41 = c44 = c29. The rates c32, c36, c38, c40, and c44 can be smaller than c30 possibly due to cooperative binding, but we assumed that they are equal to c30 because no any experimental result on these rates is available. Since the disassociate constant of MDM2 and MDMX heterodimer is very small, we assume that c34 and c42 are equal to c30/10.
It was reported that one mole of MDM2 transfers 0.98 moles of ubiquitin to p53 per minute (Ma et al., 2006). Therefore, we chose c45 = 0.98. It was reported that MDMX could stimulate ubiquitination of p53 by MDM2 (Linares et al., 2003; Gu et al., 2002). Specifically, it was observed that MDMX increased the ubiquitination rate 10 times when the amount of MDM2 was rate-limiting. It was also observed that expression of MDMX increased the half-life of MDM2 3 times. Therefore, we estimated that the net increase in the ubiquitination rate due to MDMX is 3 fold and chose c46 = 3c45. Since the smallest value for the half-life of p53 in the absence of stress signals was reported to be 5 minutes (Giaccia and Kastan, 1998), we calculated c48 from a half-life of 5 minutes for the ubiquitinated p53. Note that the actual half-life of p53 is greater than 5 minutes depending on the deubiquitination rate c47.
2.3. Stochastic simulation
Gillespie's SSA (Gillespie, 1977) is often employed to simulate the stochastic dynamics of genetic circuits (Kærn et al., 2005; McAdams and Arkin, 1997). However, Gillespie's SSA cannot deal with delays in certain reactions. Recently, we developed an exact SSA for chemically reacting systems with delays (Cai, 2007). We used this exact SSA to simulate the dynamics of the system described in Table 1.
2.4. Deterministic simulation
A set of ODEs for the number of molecules of each species in Table 2 can be easily derived based on the reactions in Table 1. The numerical solution to these ODEs roughly reflect the mean of the results of stochastic simulation. We used these ODEs to tune several unknown parameters.
2.5. Data analysis
Customized Matlab software (Mathworks Inc.) was written to analyze data generated from stochastic simulations, for example, to calculate the mean and standard error of protein levels, to identify the peaks of p53 and MDM2 during oscillation, and to calculate peak amplitudes and widths. Oscillation periods were calculated using the short-time Fourier transform (STFT) method (Vetterli and Kovacevic, 1995). Specifically, Fourier transform was applied to protein levels of p53 and MDM2 within a time window of 22 hours, after the mean level was subtracted. The largest peak at a non-zero frequency was identified as the oscillation frequency within the time window, and the period of the oscillation is the inverse of the oscillation frequency. Note that the maximum period that can be identified by the STFT is 11 hour since a time window of 22 hours was used.
3. Results and Discussion
3.1. Model calibration
We need to tune the parameters c1, c8, c20 so that the levels of p53, MDM2 and MDMX proteins match the experimental results (Wang et al., 2007), and adjust c27 and c47 so that the half-lives of MDMX and p53 are consistent with experimental results. It was reported that average p53, MDM2 and MDMX protein levels in MCF7 cells are approximately 104, 5.6 × 104, and 8.7 × 104 molecules per cell, respectively (Wang et al., 2007). We first chose an initial value for each of c1, c8, c20, c27 and c47. Then, using the initial condition that the number of p53, MDM2 and MDMX genes are 2 and the levels of all other molecular species are zero, we ran deterministic simulation for a sufficiently long time so that the system reaches the steady state. We compared the levels of p53, MDM2 and MDMX in the steady state with the experimental results, and then, adjusted c1, c8, c20 if necessary and ran deterministic simulation again. We estimated the half-life of p53, MDM2 and MDMX protein as follows. After the system reached the steady state, we stopped the translation process, i.e., set c2 = c9 = c13 = c22 = 0, and then ran deterministic simulation 400 minutes. Comparing the protein levels during this 400 minute period with the levels in the steady state, we calculated the half-life of p53, MDM2 and MDMX. If necessary, we adjusted c27 and c47 and ran simulation again. This process was iterated until the levels and half-life of p53, MDM2 and MDMX in the steady state match the experimental results. We then fine-tuned the parameters using stochastic simulation. Specifically, we used the values of the parameters obtained in deterministic simulation to run stochastic simulation 100 times and compared the average levels and the half-life of p53, MDM2 and MDMX with the experimental results. We adjusted the values of the parameters and reran stochastic simulations. This process was iterated until the average levels and the half-life of p53, MDM2 and MDMX match the experimental results.
Finally, we got the values of c1, c8, c20, c27 and c47 listed in Table 1. Our stochastic simulations using these values yielded the following results: the average levels of p53, MDM2 and MDMX and their standard errors in the steady state are 1.03 × 104 ± 1.27 × 103, 5.81 × 104 ± 1.98 × 104, and 8.70 × 104 ± 2.33 × 103 molecules per cell, respectively; the half-lives of p53, MDM2, and MDMX are 25.08 ± 0.12, 97.83 ± 0.15, and 181.53 ± 0.08 minutes, respectively. The average levels of p53 and MDMX are very close to the experimental results and their standard errors are small. The average levels of MDM2 are also close to the experimental result but their standard errors are relatively large. The half-life of p53 is within the range of 5–30 minutes reported experimentally. The half-life of MDMX is about 3 hours, which is almost the same as the experimental measurements (Kawai et al., 2003). The half-life of MDM2 seems not in the typical range around 25 minutes, but a similar half-life of MDM2 was also reported (Kawai et al., 2003). This is because, in the MCF7 cells considered here, the levels of MDMX is larger than the levels of MDM2, which stabilizes MDM2.
3.2. Oscillations of p53 and MDM2 after DNA damage
After DNA damage, the half-life of MDM2 reduces to about 5–10 minutes (Stommel and Wahl, 2004), possibly due to impaired deubiquitination of MDM2 by HAUSP (Li et al., 2004). HAUSP-mediated deubiquitination of MDMX is also compromised after DNA damage (Meulmeester et al., 2005). DNA damage leads to phosphorylation of p53 in the N-terminal transaction domain, and it was proposed that N-terminal phosphorylation reduces association of p53 with MDM2, thereby stabilizing p53 (Craig et al., 1999). However, in vivo studies showed that N-terminal phosphorylation only marginally alters p53 stability (Toledo and Wahl, 2006; Wahl et al., 2005). Therefore, we did not consider the effect of phosphorylation in our simulations. The mechanism of activating p53 after DNA damage by ataxia telangiectasia mutated (ATM) was modeled by Ma et al. (2005). It was shown that this model can capture the effect of radiation dose: the number of oscillation rather than the amplitude of p53 and MDM2 is dependent on radiation does. While it is possible to incorporate such mechanism into our model, we did not consider it in our simulations, but simply reduced the half-life of MDM2 to 8 minutes (c16 = 0.086) and the deubiquitination rate of MDMX to zero (c27 = 0) after DNA damage. Essentially, our stochastic simulations were concerned about the oscillatory behavior of p53 and MDM2 after the p53-MDM2 loop is activated, rather than the mechanism that activates the p53-MDM2 loop.
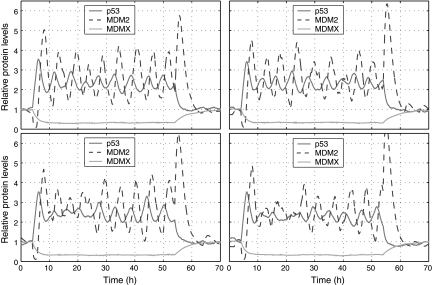
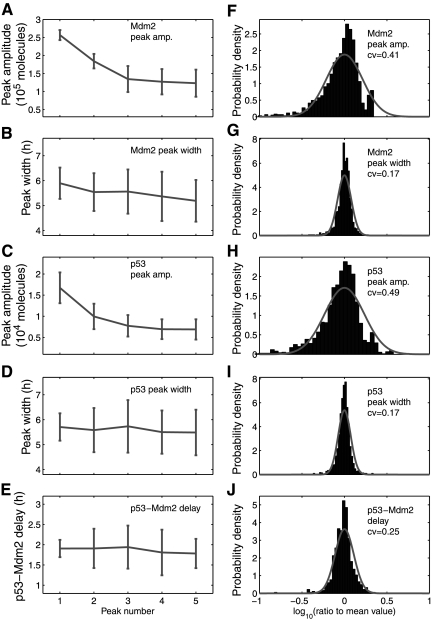
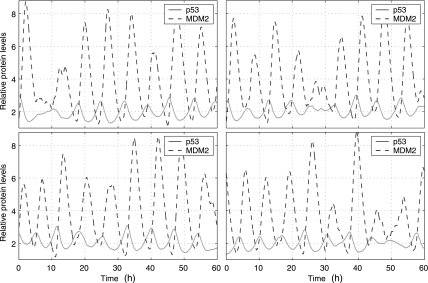
Our stochastic simulation started with the steady-state obtained from deterministic simulation as the initial state at t = 0. We ran simulation using the normal values of the parameters in Table 1 until t = 4 hours. We assumed that DNA damage started at t = 4 hours, and thus, we reduced c16 to 0.086 and c27 to 0 at t = 4 hours. We assumed that DNA damage was repaired at t = 54 hours and restored c16 and c27 to their normal values at t = 54 hours. Figure 2 shows trajectories of p53, MDM2, and MDMX levels in MCF7 cells from four simulation runs which correspond to four individual cells. It is seen that p53 and MDM2 start to oscillate after DNA damage and oscillations end shortly after the DNA damage is repaired. In contrast to deterministic simulation, stochastic simulations here clearly show that there are significant variations in the peak amplitude and width. MDMX does not oscillate along with p53 and MDM2, but quickly reduces to very low levels after DNA damage and returns to the normal level after DNA damage is repaired. The average peak-to-trough amplitude of oscillations does not appear to change considerably over time, except for the first two peaks whose amplitude is considerably higher than that of other peaks (Fig. 3A, C). This is due to the fact that we treat the effect of DNA damage like a switch, and change c16 and c27 with sharp discontinuity. If we allow c16 and c27 to reduce slowly over certain time after DNA damage, the average amplitude of first two peaks can be similar to that of other peaks (data not shown), as observed in experiments (Geva-Zatorsky et al., 2006). The mean peak width does not change considerably over time (Fig. 3B, D).
Fig. 2.
Relative levels of p53, MDM2 and MDMX protein in four individual MCF7 cells. The y-axis is the number of p53, MDM2 and MDMX protein molecules divided by their corresponding steady-state levels without DNA damage: 104 (p53), 5.6 × 104 (MDM2) and 8.7 × 104 (MDMX) molecules per cell (Wang et al., 2007). DNA damage starts at 4 hours and ends at 54 hours.
Fig. 3.
Average amplitude, width, and time delay of oscillation peaks and their variance, c11 = 0.139. (A–D) Average peak-to-trough amplitude and peak width of the first five p53 and MDM2 oscillation peaks and (E) average delay between P53 and MDM2 peaks in 100 cells shown with their standard errors. (F–J) The distribution of peak-to-trough amplitude, peak width, and delay divided by the mean value in logarithmic scale. Solid line: Log-normal probability density function with mean = 0 and standard deviation = 0.21(F), 0.08(G), 0.23(H), 0.07(I), 0.11(J).
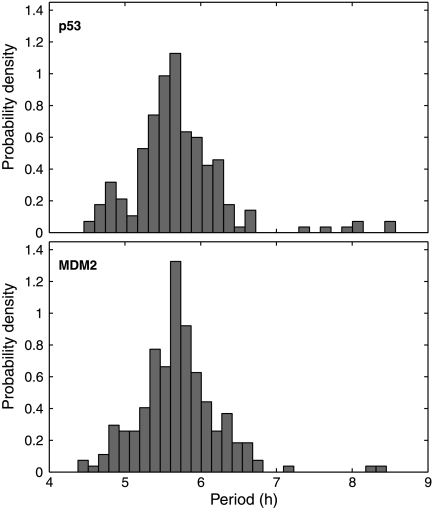
Distributions of oscillation periods are depicted in Figure 4. The mean and standard errors of the periods are 5.7 ± 0.6 h for p53 and 5.7 ± 0.5 h for MDM2. While the mean period is very close to the experimental result (5.5 h), the standard error is about one-third of that calculated from experimental measurements (Geva-Zatorsky et al., 2006). MDM2 peaks followed p53 peaks at a delay of 1.83 ± 0.45 h (Fig. 3E), which is similar to the experimental result (2 ± 0.5 h) (Geva-Zatorsky et al., 2006). We examined the variations in oscillation peaks. We found that the peak-to-through amplitudes of MDM2 and p53 varied with a coefficient of variance (CV; standard error divided by mean) of 0.41 and 0.49 (Fig. 3F, H), respectively, which are smaller than the experimental result (0.7) (Geva-Zatorsky et al., 2006). In contrast to the large variations in amplitude, the peak width and p53-MDM2 delay of individual peaks varied with a CV of 0.17 (Fig. 3G, I) and 0.25 (Fig. 3J), respectively, which are smaller than experimental results (CV = 0.3) (Geva-Zatorsky et al., 2006). The CV of oscillation periods is about 0.07, which is much smaller than that of peak amplitudes. Note that it is reasonable that the variations in our simulation results are smaller than experimental results, because experiment results include both intrinsic and extrinsic noise, whereas our simulations only account for intrinsic noise.
Fig. 4.
Distribution of p53 and MDM2 oscillation periods in MCF7 cells.
As described in earlier, c11 in Table 1 was calculated from a half-life of 5 minutes for the p53-MDM2 complex. The parameter c11 determines the rate that the MDM2 gene switches back and forth between the state that the gene is constitutively transcribed from promoter 1 and the state that the gene is activated by p53 and transcribed from promoter 2. This rate may significantly affect the stochasticity in the levels of p53 mRNA and protein (Kærn et al., 2005). We also ran simulations for two different values of c11: c11 = 0.693 that was calculated from a half-life of 25 minutes and c11 = 0.028 that was calculated from a half-life of 1 minute. No significant difference in the statistics of peak width and amplitude, as well as p53-MDM2 delay, was observed for three different values of c11 (data not shown).
From above comparison between simulation and experimental results, we have the following two main observations: (1) consistent with experimental results, our simulations showed that variations in peak width, period and p53-MDM2 delay are smaller than those in peak amplitudes, and (2) the intrinsic noise contributes to 60–70% of overall variations.
3.3. Effect of Nutlin
Small molecule Nutlin-3 can bind to MDM2 and inhibit its interaction with p53, resulting in increased p53 levels and transcriptional activity (Vassilev et al., 2004). However, Nutlin-3 does not disrupt MDMX-p53 interaction (Wade et al., 2006; Hu et al., 2006; Patton et al., 2006). Moreover, Nutlin-3 does not induce DNA damage (Wade et al., 2006; Thompson et al., 2004). Since transcription of MDM2 is positively regulated by p53, the increased p53 levels after treatment with Nutlin-3 cause significant increase in MDM2 levels (Wang et al., 2007). In spite of high MDM2 levels, MDMX levels after Nutlin-3 treatment are often slightly increased (Wang et al., 2007; Hu et al., 2006). No significant changes in MDMX mRNA levels and the half-life of MDMX protein were observed after Nutlin-3 treatment (Hu et al., 2006). It is not clear how Nutlin-3 affects ubiquitination and degradation of MDMX. In our model, the ubiquitination rate of MDMX is determined by reactions 24–26. Disrupting MDMX-MDM2 interaction (reaction 24 and 25) and/or directly decreasing the ubiquitination rate (reaction 26) will decrease degradation of MDMX.
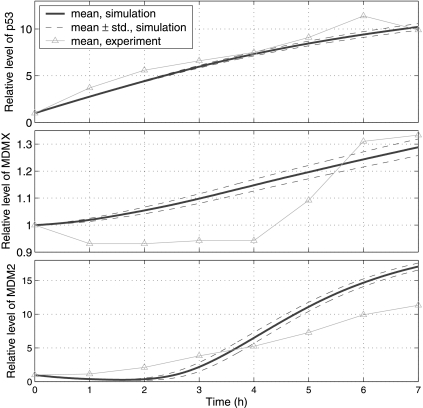
In order to simulate the effect of Nutlin, we decreased c29, c31, c33, c35, c41, and c42 N1 (N1 > 1) times to reflect the disruption of MDM2-p53 interaction. As we discussed earlier, we can reduce c24 and/or c26 to reflect the decreased efficiency of MDMX ubiquitination. In the first set of simulations, we decreased c24 N2 (N2 > 1) times while keeping c26 unchanged. Figure 5 depicts simulation results for N1 = N2 = 100, as well as experimental results (Wang et al., 2007). It is seen from Figure 5 that simulated p53 level matches the experimental result very well, and that simulated MDMX and MDM2 levels are qualitatively consistent with experimental results. However, the simulated MDM2 level at 7 hours after treatment with Nutlin is relatively higher compared to the experimental result. Hence, there may be other unknown mechanisms preventing MDM2 levels from increasing dramatically that are not included in our simulation. We ran simulations for different N1 and N2 and found that simulation results (data not shown) do not change much when N1 and N2 are in between 100 and 1000. In the second set of simulations, we reduced c26 while keeping c24 unchanged. When N1 = 100 and c26 was reduced from 0.98 to the range of 0.4–0.6, the MDMX levels were consistent with experimental results (data not shown). From these two sets of simulations, we see that our model can produce results that are consistent with experimental results after treatment with Nutlin.
Fig. 5.
Relative levels of p53, MDMX and MDM2 after treatment with Nutlin-3. Protein levels are normalized by their steady levels before the treatment:104 (p53), 5.6 × 104 (MDM2) and 8.7 × 104 (MDMX) molecules per cell (Wang et al., 2007). In simulations, effect of Nutlin-3 is modeled by decreasing c24, c29, c31, c33, c35, c41 and c42 100 times. Simulation results are compared with experimental results (Wang et al., 2007).
3.4. MDM2 or MDMX knockout
MDM2-null mouse embryos die very early in development due to increased apoptosis (Jones et al., 1995; Montes de Oca Luna et al., 1995), whereas MDMX-null mouse embryos die later probably because of cell proliferation arrest (Parant et al., 2001; Finch et al., 2002; Migliorini et al., 2002). It is interesting to see the levels of p53 protein in MDM2- or MDMX-null cells. To simulate protein levels in MDM2-null cells, we set the number of MDM2 genes (mdm2ga in reaction 8 and mdm2gb in reaction 12) to be zero. The mean and standard errors of p53 and MDMX levels were found to be 4.15 × 105 ± 231 (p53) and 3.14 × 105 ± 238 (MDMX) molecules per cell. Compared to the protein levels in cells with MDM2 (104 (p53) and 8.7 × 104 (MDMX) molecules per cell), the average levels of p53 and MDMX were increased 41.5 and 3.6 times, respectively.
To simulate protein levels in MDMX-null cells, we set the number of MDMX genes (mdmxg in reaction 20) to zero. Interestingly, p53 and MDM2 in MDMX-null cells undergo oscillation as shown in Figure 6. The mean and standard errors of oscillation period of p53 and MDM2 are 6.9 ± 0.5 h which is larger than the period of oscillations after DNA damage. Table 3 lists the peak amplitude and width, trough amplitude and period of p53 and MDM2 obtained from 100 simulation runs when MDMX is knocked out. The average peak (trough) amplitude of p53 is increased 2.7 (1.6) times compared to the p53 levels in cells with MDMX. The overall average level of p53 is increased about 2 times, which is much smaller than that in MDM2-null cells. This may partially explain why MDM2-null and MDMX-null mouse embryos die in different developmental stages.
Fig. 6.
Relative levels of p53 and MDM2 in four MDMX-null cells. Levels of p53 and MDM2 are normalized by their levels in cells with MDMX.
Table 3.
Relative Protein Levels and Oscillation Periods in MDMX-Null Cells
| Mean | Standard error | CV | |
|---|---|---|---|
| p53 peak amplitude | 2.70 | 0.25 | 0.09 |
| p53 trough amplitude | 1.62 | 0.17 | 0.10 |
| p53 peak width | 6.71(h) | 0.75(h) | 0.11 |
| p53 period | 6.89(h) | 0.49(h) | 0.07 |
| MDM2 peak amplitude | 7.01 | 1.49 | 0.21 |
| MDM2 trough amplitude | 1.64 | 0.38 | 0.23 |
| MDM2 peak width | 6.69(h) | 0.82(h) | 0.12 |
| MDM2 period | 6.88(h) | 0.52(h) | 0.08 |
Levels of p53 and MDM2 are normalized by the levels in cells with MDMX, 104 (p53) and 5.6 × 104 (MDM2) molecules per cell (Wang et al., 2007).
Acknowledgments
We thank Dr. Alan R. Fersht for helpful discussions on p53 and MDM2 interaction, Dr. David R. Morris for helpful discussions on estimating the translation rate of MDM2 from polysome profiles, and Zhouyi Xu for his help with running simulations. This work was supported by the National Science Foundation (NSF) (CAREER Award CCF-0746882 to X.C.) and the National Institutes of Health (NIH) (grant R01CA85679 to Z.M.Y).
Disclosure Statement
No competing financial interests exist.
References
- Alberts B. Johnson A. Lewis J., et al. Molecular Biology of the Cell. 4th. Garland Science; New York: 2002. [Google Scholar]
- Arava Y. Wang Y. Storey J.D., et al. Genome-wide analysis of mRNA translation profiles in Saccharomyces cerevisiae. Proc. Natl. Acad. Sci. USA. 2003;100:3889–3894. doi: 10.1073/pnas.0635171100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bar-Or R.L. Maya R. Segel L.A., et al. Generation of oscillations by the p53-Mdm2 feedback loop: a theoretical and experimental study. Proc. Natl. Acad. Sci. USA. 2000;97:11250–11255. doi: 10.1073/pnas.210171597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barak Y. Gottlieb E. Juven-Gershon T., et al. Regulation of mdm2 expression by p53: alternative promoters produce transcripts with nonidentical translation potential. Genes Dev. 1994;8:1739–1749. doi: 10.1101/gad.8.15.1739. [DOI] [PubMed] [Google Scholar]
- Brown C.Y. Mize G.J. Pineda M., et al. Role of two upstream open reading frames in the translational control of oncogene mdm2. Oncogene. 1999;18:5631–5637. doi: 10.1038/sj.onc.1202949. [DOI] [PubMed] [Google Scholar]
- Cai X. Exact stochastic simulation of coupled chemical reactions with delays. J. Chem. Phys. 2007;126 doi: 10.1063/1.2710253. article no. 124108. [DOI] [PubMed] [Google Scholar]
- Capoulade C. dePaillerets B.B. LefreAre I., et al. Overexpression of MDM2, due to enhanced translation, results in inactivation of wild-type p53 in Burkitt's lymphoma cells. Oncogene. 1998;16:1603–1610. doi: 10.1038/sj.onc.1201702. [DOI] [PubMed] [Google Scholar]
- Ciliberto A. Novak B. Tyson J.J., et al. Steady states and oscillations in the p53/Mdm2 network. Cell Cycle. 2005;4:488–493. doi: 10.4161/cc.4.3.1548. [DOI] [PubMed] [Google Scholar]
- Clore G.M. Omichinski J. G. Sakaguchi K., et al. High-resolution structure of the oligomerization domain of p53 by multidimensional NMR. Science. 1994;265:386–391. doi: 10.1126/science.8023159. [DOI] [PubMed] [Google Scholar]
- Craig A.L. Burch L. Vojtesek B., et al. Novel phosphorylation sites of human tumour suppressor protein p53 at ser20 and thr18 that disrupt the binding of mdm2 (mouse double minute 2) protein are modified in human cancers. Biochem. J. 1999;342:133141. [PMC free article] [PubMed] [Google Scholar]
- de Graaf P. Little N.A. Ramos Y.F.M., et al. Hdmx protein stability is regulated by the ubiquitin ligase activity of Mdm2. J. Biol. Chem. 2003;278:38315–38324. doi: 10.1074/jbc.M213034200. [DOI] [PubMed] [Google Scholar]
- Del Prete M.J. Vernal R. Dolznig H., et al. Isolation of polysome-bound mRNA from solid tissues amenable for RT-PCR and profiling experiments. RNA. 2007;13:414–421. doi: 10.1261/rna.79407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dundr M. Misteli T. Functional architecture in the cell nucleus. Biochem. J. 2001;356:297–310. doi: 10.1042/0264-6021:3560297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Finch R.A. Donoviel D.B. Potter D., et al. mdmx is a negative regulator of p53 activity in vivo. Cancer Res. 2002;62:3221–3225. [PubMed] [Google Scholar]
- Geva-Zatorsky N. Rosenfeld N. Itzkovitz S., et al. Oscillations and variability in the p53 system. Mol. Systems Biol. 2006;2 doi: 10.1038/msb4100068. 2006.0033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giaccia A.J. Kastan M.B. The complexity of p53 modulation: emerging patterns from divergent signals. Genes Dev. 1998;12:2973–2983. doi: 10.1101/gad.12.19.2973. [DOI] [PubMed] [Google Scholar]
- Gillespie D.T. Exact stochastic simulation of coupled chemical reaction. J. Phys. Chem. 1977;81:2340–2361. [Google Scholar]
- Gillespie D.T. Stochastic simulation of chemical kinetics. Annu. Rev. Phys. Chem. 2007;58:35–55. doi: 10.1146/annurev.physchem.58.032806.104637. [DOI] [PubMed] [Google Scholar]
- Gu J. Kawai H. Nie L., et al. Mutual dependence of MDM2 and MDMX in their functional inactivation of p53. J. Biol. Chem. 2002;277:19251–19254. doi: 10.1074/jbc.C200150200. [DOI] [PubMed] [Google Scholar]
- Hainuat P., editor; Wiman K.G., editor. 25 Years of P53 Research. Springer; New York: 2005. [Google Scholar]
- Horn H.F. Vousden K. Coping with stress: mutiple ways to activate p53. Oncogene. 2007;26:1306–1316. doi: 10.1038/sj.onc.1210263. [DOI] [PubMed] [Google Scholar]
- Hsing A. Faller D.V. Vaziri C., et al. DNA-damaging aryl hydrocarbons induce Mdm2 expression via p53-independent post-transcriptional mechanisms. J. Biol. Chem. 2000;275:26024–26031. doi: 10.1074/jbc.M002455200. [DOI] [PubMed] [Google Scholar]
- Hu B. Gilkes D.M. Farooqi B., et al. MDMX overexpression prevents p53 activation by the MDM2 inhibitor nutlin. J. Biol. Chem. 2006;281:33030–33035. doi: 10.1074/jbc.C600147200. [DOI] [PubMed] [Google Scholar]
- Jones S.N. Roe A.E. Bradley L.A., et al. Rescue of embryonic lethality in Mdm2-deficient mice by absence of p53. Nature. 1995;378:206–208. doi: 10.1038/378206a0. [DOI] [PubMed] [Google Scholar]
- Ju J. Schmitz J.C. Song B., et al. Regulation of p53 expression in response to 5-fluorouracil in human cancer RKO cells. Clin. Cancer Res. 2007;13:4245–4251. doi: 10.1158/1078-0432.CCR-06-2890. [DOI] [PubMed] [Google Scholar]
- Juven T. Barak Y. Zauberman A., et al. Wild type p53 can mediate sequence-specific transactivation of an internal promoter within the mdm2 gene. Oncogene. 1993;8:3411–3416. [PubMed] [Google Scholar]
- Kærn M. Elston T.C. Blake W.J., et al. Stochasticity in gene expression: from theories to phenotypes. Nat. Rev. Genet. 2005;6:451–464. doi: 10.1038/nrg1615. [DOI] [PubMed] [Google Scholar]
- Kawai H. Lopez-Pajares V. Kim M.M., et al. RING domain-mediated interaction is a requirement for MDM2's E3 ligase activity. Cancer Res. 2007;67:6026–6030. doi: 10.1158/0008-5472.CAN-07-1313. [DOI] [PubMed] [Google Scholar]
- Kawai H. Wiederschain D. Kitao H., et al. DNA damage-induced MDMX degradation is mediated by MDM2. J. Biol. Chem. 2003;278:45946–45953. doi: 10.1074/jbc.M308295200. [DOI] [PubMed] [Google Scholar]
- Kim H. You S. Farris J., et al. Post-transcriptional inactivation of p53 in immortalized murine embryo fibroblast cells. Oncogene. 2001a;20:3306–3310. doi: 10.1038/sj.onc.1204423. [DOI] [PubMed] [Google Scholar]
- Kim H. You S. Foster L.K., et al. The rapid destabilization of p53 mRNA in immortal chicken embryo fibroblast cells. Oncogene. 2001b;20:5118–5123. doi: 10.1038/sj.onc.1204664. [DOI] [PubMed] [Google Scholar]
- Knippschild U. Kolzau T. Deppert W., et al. Cell-specific transcriptional activation of the mdm2-gene by ectopically expressed wild-type form of a temperature-sensitive mutant p53. Oncogene. 1995;11:683–690. [PubMed] [Google Scholar]
- Kubbutat M. H.G. Ludwig R.L. Ashcroft M., et al. Regulation of mdm2-directed degradation by the c terminus of p53. Mol. Cell Biol. 1998;18:5690–5698. doi: 10.1128/mcb.18.10.5690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kussie P.H. Gorina S. Marechal V., et al. Structure of the MDM2 oncoprotein bound to the p53 tumor suppressor transactivation domain. Science. 1996;274:948–953. doi: 10.1126/science.274.5289.948. [DOI] [PubMed] [Google Scholar]
- Lahav G. Rosenfeld N. Sigal A., et al. Dynamics of the p53-Mdm2 feedback loop in individual cells. Nat. Genet. 2004;36:147–150. doi: 10.1038/ng1293. [DOI] [PubMed] [Google Scholar]
- Laia Z. Augerb K.R. Manubayb C.M., et al. Thermodynamics of p53 binding to hdm2(1126): effects of phosphorylation and p53 peptide length. Arch. Biochem. Biophys. 200;381:278–284. doi: 10.1006/abbi.2000.1998. [DOI] [PubMed] [Google Scholar]
- Landers J.E. Cassel S.L. George D.L., et al. Translational enhancement of mdm2 oncogene expression in human tumor cells containing a stabilized wild-type p53 protein. Cancer Res. 1997;57:3562–3568. [PubMed] [Google Scholar]
- Lee W. Harvey T.S. Yin Y., et al. Solution structure of the tetrameric minimum transforming domain of p53. Nat. Struct. Biol. 1994;1:877–890. doi: 10.1038/nsb1294-877. [DOI] [PubMed] [Google Scholar]
- Levine A.J. Hu W. Feng Z., et al. The p53 pathway: what questions remain to be explored? Cell Death Differ. 2006;13:1027–1036. doi: 10.1038/sj.cdd.4401910. [DOI] [PubMed] [Google Scholar]
- Li M. Brooks C.L. Kon N., et al. A dynamic role of HAUSP in the p53-mdm2 pathway. Mol. Cell. 2004;13:879–886. doi: 10.1016/s1097-2765(04)00157-1. [DOI] [PubMed] [Google Scholar]
- Li M. Brooks C.L. Wu-Baer F., et al. Mono- versus polyubiquitination: differential control of p53 fate by mdm2. Science. 2003;302:1972–1975. doi: 10.1126/science.1091362. [DOI] [PubMed] [Google Scholar]
- Linares L.K. Hengstermann A. Ciechanover A., et al. HdmX stimulates hdm2-mediated ubiquitination and degradation of p53. Proc. Natl. Acad. Sci. USA. 2003;100:12009–12014. doi: 10.1073/pnas.2030930100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu H. Levine A. J. Human TAFII31 protein is a transcriptional coactivator of the p53 protein. Proc. Natl. Acad. Sci. USA. 1995;92:5154–5158. doi: 10.1073/pnas.92.11.5154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma J. Martin J.D. Zhang H., et al. A second p53 binding site in the central domain of Mdm2 is essential for p53 ubiquitination. Biochemistry. 2006;45:9238–9245. doi: 10.1021/bi060661u. [DOI] [PubMed] [Google Scholar]
- Ma L. Wagner J. Rice J.J., et al. A plausible model for the digital response of p53 to DNA damage. Proc. Natl. Acad. Sci. USA. 2005;102:14266–14271. doi: 10.1073/pnas.0501352102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKay V.L. Li X. Flory M.R., et al. Gene expression analyzed by high-resolution state array analysis and quantitative proteomics. Mol. Cell. Proteomics. 2004;3:478–489. doi: 10.1074/mcp.M300129-MCP200. [DOI] [PubMed] [Google Scholar]
- Maki C.G. Oligomerization is required for p53 to be efficiently ubiquitinated by MDM2. J. Biol. Chem. 1999;274:16531–16535. doi: 10.1074/jbc.274.23.16531. [DOI] [PubMed] [Google Scholar]
- Marine J.-C. Francoz S. Wahl G., et al. Keeping p53 in check: essential and synergistic functions of Mdm2 and Mdm4. Cell Death Differ. 2006;13:927–934. doi: 10.1038/sj.cdd.4401912. [DOI] [PubMed] [Google Scholar]
- Marinea J.-C. Jochemsen A.G. Mdmx as an essential regulator of p53 activity. Biochem. Biophys. Res. Commun. 2005;331:750–760. doi: 10.1016/j.bbrc.2005.03.151. [DOI] [PubMed] [Google Scholar]
- Mathews M.B. Sonenberg N. Hershey J.W.B., et al. Origins and Principles of Translational Control. Cold Spring Harbor Laboratory Press; Cold Spring Harbor, NY: 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mazan-Mamczarz K. Galbn S. deSilanes I.L., et al. RNA-binding protein HuR enhances p53 translation in response to ultraviolet light irradiation. Proc. Natl. Acad. Sci. USA. 2003;100:8354–8359. doi: 10.1073/pnas.1432104100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McAdams H.H. Arkin A. Stochatic mechanisms in gene expression. Proc. Natl. Acad. Sci. USA. 1997;94:814–819. doi: 10.1073/pnas.94.3.814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McLure K.G. Lee P.W.K. How p53 binds DNA as a tetramer. EMBO J. 1998;17:3342–3350. doi: 10.1093/emboj/17.12.3342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McVean M. Xiao H. Isobe K., et al. Increase in wild-type p53 stability and transactivational activity by the chemopreventive agent apigenin in keratinocytes. Carcinogenesis. 2000;21:633–639. doi: 10.1093/carcin/21.4.633. [DOI] [PubMed] [Google Scholar]
- Mendrysa S.M. McElwee M.K. Perry M.E., et al. Characterization of the 5′ and 3′ untranslated regions in murine mdm2 mRNAs. Gene. 2001;264:139–146. doi: 10.1016/s0378-1119(00)00589-8. [DOI] [PubMed] [Google Scholar]
- Mendrysa S.M. Perry M.E. The p53 tumor suppressor protein does not regulate expression of its own inhibitor, MDM2, except under conditions of stress. Mol. Cell. Biol. 2000;20:2023–2030. doi: 10.1128/mcb.20.6.2023-2030.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meulmeester E. Maurice M.M. Boutell C., et al. Loss of HAUSP-mediated deubiquitination contributes to DNA damage-induced destabilization of Hdmx and Hdm2. Mol. Cell. 2005;18:565–576. doi: 10.1016/j.molcel.2005.04.024. [DOI] [PubMed] [Google Scholar]
- Migliorini D. Denchi E.L. Danovi D., et al. Mdm4 (Mdmx) regulates p53-induced growth arrest and neuronal cell death during early embryonic mouse development. Mol. Cell. Biol. 2002;22:5527–5538. doi: 10.1128/MCB.22.15.5527-5538.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mihalas G.I. Simon Z. Balea G., et al. Possible oscillatory behavior in p53Mdm2 interaction computer simulation. J. Biol. Syst. 2000;8:21–29. [Google Scholar]
- Monk N.A. Oscillatory expression of Hes1, p53, and NF-κB driven by transcriptional time delays. Curr. Biol. 2003;13:1409–1413. doi: 10.1016/s0960-9822(03)00494-9. [DOI] [PubMed] [Google Scholar]
- Montes de Oca Luna R. Wagner D.S. Lozano G., et al. Rescue of early embryonic lethality in mdm2-deficient mice by deletion of p53. Nature. 1995;378:203–206. doi: 10.1038/378203a0. [DOI] [PubMed] [Google Scholar]
- Nicholls C.D. McLure K.G. Shields M.A., et al. Biogenesis of p53 involves cotranslational dimerization of monomers and posttranslational dimerization of dimers. J. Biol. Chem. 2002;255:12937–12945. doi: 10.1074/jbc.M108815200. [DOI] [PubMed] [Google Scholar]
- Olson D.C. Marechal V. Momand J., et al. Identification and characterization of multiple mdm-2 proteins and mdm-2-p53 protein complexes. Oncogene. 1993;8:2353–2360. [PubMed] [Google Scholar]
- Oren M. Regulation of the p53 tumor suppressor protein. J. Biol. Chem. 1999;274:36031–36034. doi: 10.1074/jbc.274.51.36031. [DOI] [PubMed] [Google Scholar]
- Pan Y. Chen J. MDM2 promotes ubiquitination and degradation of MDMX. Mol. Cell. Biol. 2003;23:5113–5121. doi: 10.1128/MCB.23.15.5113-5121.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parant J. Chavez-Reyes A. Little N.A., et al. Rescue of embryonic lethality in Mdm4-null mice by loss of Trp53 suggests a nonoverlapping pathway with MDM2 to regulate p53. Nat. Genet. 2001;29:92–95. doi: 10.1038/ng714. [DOI] [PubMed] [Google Scholar]
- Patton J.T. Mayo L.D. Singhi A.D., et al. Levels of HdmX expression dictate the sensitivity of normal and transformed cells to Nutlin-3. Cancer Res. 2006;66:3169–3176. doi: 10.1158/0008-5472.CAN-05-3832. [DOI] [PubMed] [Google Scholar]
- Perry M.E. Piette J. Zawadzki J.A., et al. The mdm-2 gene is induced in response to uv light in a p53-dependent manner. Proc. Natl. Acad. Sci. USA. 1993;90:11623–11627. doi: 10.1073/pnas.90.24.11623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raser J.M. O'Shea E.K. Noise in gene expression: origins, consequences, and control. Science. 2005;309:2010–2013. doi: 10.1126/science.1105891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sakaguchi K. Saito S. Higashimoto Y., et al. Damage-mediated phosphorylation of human p53 threonine 18 through a cascade mediated by a casein 1-like kinase. effect on Mdm2 binding. J. Biol. Chem. 2000;275:9278–9283. doi: 10.1074/jbc.275.13.9278. [DOI] [PubMed] [Google Scholar]
- Schon O. Friedler A. Bycroft M., et al. Molecular mechanism of the interaction between MDM2 and p53. J. Mol. Biol. 2002;323:491–501. doi: 10.1016/s0022-2836(02)00852-5. [DOI] [PubMed] [Google Scholar]
- Sharp S.A. Kratowicz S.A. Sank M.J., et al. Stabilization of the MDM2 oncoprotein by interaction with the structurally related mdmx protein. J. Biol. Chem. 1999;274:38189–93816. doi: 10.1074/jbc.274.53.38189. [DOI] [PubMed] [Google Scholar]
- Shvarts A. Steegenga W.T. Riteco N., et al. MDMX: a novel p53-binding protein with some functional properties of MDM2. EMBO J. 1996;15:5349–5357. [PMC free article] [PubMed] [Google Scholar]
- Stad R. Ramos Y.F.M. Little N., et al. Hdmx stabilizes Mdm2 and p53. J. Biol. Chem. 2000;275:28039–28044. doi: 10.1074/jbc.M003496200. [DOI] [PubMed] [Google Scholar]
- Stommel J.M. Wahl G.M. Accelerated MDM2 auto-degradation induced by DNA-damage kinases is required for p53 activation. EMBO J. 2004;23:1547–1556. doi: 10.1038/sj.emboj.7600145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanimuraa S. Ohtsukaa S. Mitsuia K., et al. MDM2 interacts with MDMX through their RING finger domains. FEBS Lett. 1999;447:5–9. doi: 10.1016/s0014-5793(99)00254-9. [DOI] [PubMed] [Google Scholar]
- Thompson T. Tovar C. Yang H., et al. Phosphorylation of p53 on key serines is dispensable for transcriptional activation and apoptosis. J. Biol. Chem. 2004;279:53015–53022. doi: 10.1074/jbc.M410233200. [DOI] [PubMed] [Google Scholar]
- Tiana G. Jensen M.H. Sneppen K., et al. Time delay as a key to apoptosis induction in the p53 network. Eur. Phys. J. B. 2002;29:135–140. [Google Scholar]
- Toledo F. Wahl G.M. Regulating the p53 pathway: in vitro hypotheses, in vivo veritas. Nat. Rev. Cancer. 2006;6:909–923. doi: 10.1038/nrc2012. [DOI] [PubMed] [Google Scholar]
- Vassilev L.T. Vu B.T. Graves B., et al. In vivo activation of the p53 pathway by small-molecule antagonists of MDM2. Science. 2004;303:844–848. doi: 10.1126/science.1092472. [DOI] [PubMed] [Google Scholar]
- Vetterli M. Kovacevic J. Wavelets and Subband Coding. Prentice Hall; Englewood Cliffs, NJ: 1995. [Google Scholar]
- Vogelstein B. Lane D. Levine A.J., et al. Surfing the p53 network. Nature. 2000;408:307–310. doi: 10.1038/35042675. [DOI] [PubMed] [Google Scholar]
- Wade M. Wong E.T. Tang M., et al. Hdmx modulates the outcome of p53 activation in human tumor cells. J. Biol. Chem. 2006;281:33036–33044. doi: 10.1074/jbc.M605405200. [DOI] [PubMed] [Google Scholar]
- Wagner J. Ma L. Rice J.J., et al. p53-Mdm2 loop controlled by a balance of its feedback strength and effective dampening using ATM and delayed feedback. IEE Proc. Syst. Biol. 2005;152:109–118. doi: 10.1049/ip-syb:20050025. [DOI] [PubMed] [Google Scholar]
- Wahl G.M. Stommel J.M. Krummel K., et al. Gatekeepers of The Guardian: P53 Regulation by Post-Translational Modification, MDM2 and MDMX. Springer; New York: 2005. [Google Scholar]
- Wang Y.V. Wade M. Wong E., et al. Quantitative analyses reveal the importance of regulated Hdmx degradation for p53 activation. Proc. Natl. Acad. Sci. USA. 2007;104:12365–12370. doi: 10.1073/pnas.0701497104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weinberg R.L. Veprintsev D.B. Bycrott M., et al. Comparative binding of p53 to its promoter and DNA recognition elements. J. Mol. Biol. 2005;348:589–596. doi: 10.1016/j.jmb.2005.03.014. [DOI] [PubMed] [Google Scholar]
- Weinberg R.L. Veprintsev D.B. Fersht A.R., et al. Cooperative binding of tetrameric p53 to DNA. J. Mol. Biol. 2004;341:1145–1159. doi: 10.1016/j.jmb.2004.06.071. [DOI] [PubMed] [Google Scholar]
- Wu X. Bayle J.H. Olson D., et al. The p53-mdm-2 autoregulatory feedback loop. Genes Dev. 1993;7:1126–1132. doi: 10.1101/gad.7.7a.1126. [DOI] [PubMed] [Google Scholar]
- Yang E. van Nimwegen E. Zavolan M., et al. Decay rates of human mRNAs: Correlation with functional characteristics and sequence attributes. Genome Res. 2003;13:1863–1872. doi: 10.1101/gr.1272403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zauberman A. Flusberg D. Haupt Y., et al. A functional p53-responsive intronic promoter is contained within the human mdm2 gene. Nucleic Acids Res. 1995;23:2584–2592. doi: 10.1093/nar/23.14.2584. [DOI] [PMC free article] [PubMed] [Google Scholar]