Abstract
Cognitive process models, such as Ratcliff’s (1978) diffusion model, are useful tools for examining cost- or interference effects in event-based prospective memory (PM). The diffusion model includes several parameters that provide insight into how and why ongoing-task performance may be affected by a PM task and is ideally suited to analyze performance because both reaction time and accuracy are taken into account. Separate analyses of these measures can easily yield misleading interpretations in cases of speed-accuracy tradeoffs. The diffusion model allows us to measure possible criterion shifts and is thus an important methodological improvement over standard analyses. Performance in an ongoing lexical decision task (Smith, 2003) was analyzed with the diffusion model. The results suggest that criterion shifts play an important role when a PM task is added, but do not fully explain the cost effect on RT.
Keywords: Prospective Memory, Diffusion Model, Monitoring and Attentional Resources, Response Time Models
Event-based prospective memory (PM) tasks involve remembering to perform intended actions after a delay, when a specific target event occurs. Such tasks often occur in the midst of other activities that must be interrupted to perform the intended action. To capture this aspect of real world PM, the PM task is embedded in an ongoing task in the typical laboratory paradigm (Einstein & McDaniel, 1990). For instance, participants may be busily engaged in an ongoing lexical decision task, and at the same time must remember to interrupt their decisions to carry out another action (i.e., press a certain key on a computer keyboard) when a particular target occurs (e.g., the word tiger appears on the screen).
Much theoretical and experimental work on PM has focused on the processes involved in retrieving such intentions (e.g., Einstein & McDaniel, 1996; West, 2007; Smith, Hunt, McVay, & McConnell, 2007). Particularly, researchers have examined whether successful PM always requires resource-demanding preparatory attentional processes (Smith, 2003, 2008, 2010), or whether spontaneous retrieval of the intention occurs under specific circumstances (McDaniel & Einstein, 2000, 2007). The empirical approach towards addressing this question rests on the analysis of ongoing-task performance in the presence versus absence of a PM task. The cost- or interference effect of PM refers to the finding that reaction time (RT) on non-PM-target trials in the ongoing task can be increased by the need to remember the PM task, and can covary with PM performance (Smith, 2003). It is assumed that RT can increase as PM absorbs attentional resources that would otherwise be devoted to the ongoing task. In the last decade, numerous studies have examined cost effects (see Smith et al., 2007, for an overview) and their relationship with characteristics of the PM targets, such as salience and focality (Einstein et al., 2005), individuals’ resource allocation (Marsh, Hicks, & Cook, 2005), and potential boundary conditions to demonstrations of cost effects (Cohen, Jaudas, & Gollwitzer, 2008; but see Smith, 2010). However, to date surprisingly little is known about the specific processes that lead to the slowing when cost effects occur. Why and how does processing change in the ongoing task with an additional requirement to remember an intention?
In this article, we argue that cognitive process models, such as the diffusion model (e.g., Ratcliff, 1978), are useful tools for addressing these questions through the measurement of latent variables assumed to underlie performance in ongoing tasks. We will first describe the diffusion model in more detail and point out the importance of considering speed-accuracy tradeoffs in task performance. We will then present a model-based reanalysis of data from Smith (2003, Experiment 1) to demonstrate how additional insight into cost effects can be gained.
The Diffusion Model
In cognitive psychology, the diffusion model has been successfully applied to a variety of paradigms in which individuals make simple and fast two-choice decisions, with mean latencies not much over 1 to 1.5 s. Previous applications of the model have included, among others, lexical decisions (Ratcliff, Gomez, & McKoon, 2004; Wagenmakers, Ratcliff, Gomez, & McKoon, 2008), animacy categorization (Spaniol, Madden, & Voss, 2006), recognition memory (Criss, 2010; Ratcliff, 1978), practice effects (Dutilh, Vandekerckhove, Tuerlinckx, & Wagenmakers, 2009), and the identification of factors underlying age-related slowing (e.g., Ratcliff, Thapar, Gomez, & McKoon, 2004; Ratcliff, Thapar, & McKoon, 2006). See Ratcliff and McKoon (2008) and Wagenmakers (2009), for reviews of the model, Gardiner (2004) and Smith (2000) for mathematical foundations, and Ratcliff and Tuerlinckx (2002), and Voss and Voss (2008) for different methods of parameter estimation. In general, the diffusion model provided a close fit to the observed RT distributions and response accuracy in most applications. Many ongoing tasks routinely used in PM research could provide appropriate data; the current experiment used a lexical decision task, which has been studied in detail with the diffusion model (Ratcliff, Gomez, et al., 2004; Wagenmakers et al., 2008), and which is a frequently used ongoing task in PM research (e.g., Marsh et al., 2005).
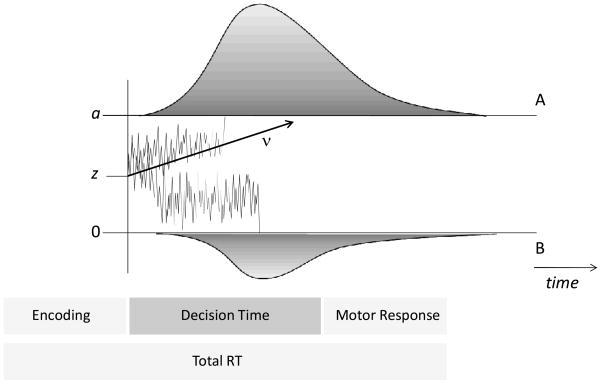
A basic assumption of Ratcliff’s diffusion model is that two-choice decisions are based on continuously accumulating information, starting from a value z on a decision-related strength-of-evidence axis (y-axis in Figure 1). A diffusion process moves from this starting point z over time (x-axis in Figure 1) until one of two thresholds, associated with a decision (“A” vs. “B”), is reached. The average speed of information uptake (i.e., the ratio of accumulated evidence per time unit) is a systematic influence (drift rate parameter v) that drives the process to one of the thresholds. A positive slope of v (as shown in Figure 1) indicates that relatively more evidence is collected for the upper (“A”) than the lower (“B”) threshold, whereas negative slopes of v imply the opposite. Drift rate determines processing efficiency in the actual decision phase, with high absolute values predicting both fast and accurate decisions. However, the accumulation process within a trial is also affected by random noise1, implying that trials with the same drift rate do not always terminate at the same time or threshold (thereby producing RT distributions and errors, respectively; see the different process tracks in Figure 1). Parameter a represents the distance between the two decision thresholds (the value of the lower threshold is set to 0) and quantifies the amount of evidence that is required until a decision is made. This parameter reflects the decision maker’s speed-accuracy criterion. Smaller values of parameter a predict faster RTs and more errors (a liberal speed-accuracy setting), whereas higher values predict slower RTs and fewer errors (a conservative speed-accuracy setting). The relation of the starting point z to the thresholds is an indicator of response bias. If a decision maker does not favor one response over the other, the starting point position is equidistant from both decision thresholds, z = a/2, which holds for many experiments (Wagenmakers, van der Maas, & Grasman, 2007). Values larger or smaller than a/2 indicate bias in favor of the upper or lower threshold, respectively. The diffusion model assumes that observed RT can be split into a decision phase (described above) and a nondecision component, Ter, which includes the processes before or after the actual decision (e.g., stimulus encoding and motor response execution), and which is added to the diffusion exit time.
Figure 1.
Illustration of the diffusion model. The vertical axis is the decision axis, and the horizontal axis is the time axis. Diffusion processes start at point z and move over time until the upper threshold (positioned at a) or the lower threshold (positioned at zero) is reached. Reaction time distributions for decisions associated with the upper and the lower thresholds are shown. The two sample process tracks illustrate that different thresholds can be reached with the same (positive) drift rate due to random influence. Total RT is the sum of the decision time and a nondecision component that represents the duration of processes such as perceptual encoding and motor response execution.
The complete version of the diffusion model allows for variation of parameters across trials of an experiment. Drift rate is assumed to vary normally around mean v with standard deviation η to capture trial-by-trial fluctuations in stimulus features or alertness. The starting point z and the nondecision component Ter are assumed to be uniformly distributed with width sz and st, respectively. With inter-trial variability of drift rate η, the model predicts slower RTs for error responses than for correct responses, and variability of the starting point (sz) predicts the reverse pattern (see Ratcliff & Rouder, 1998). All parameters of the diffusion model are summarized in Table 1 with a description.
Table 1.
Diffusion Model Parameters
| Parameter | Description | No-PM Condition | PM Condition | t(93)a |
|---|---|---|---|---|
| z | Mean starting point | a/2 | a/2 | -- |
| a | Threshold separation | 1.91 (0.08) | 2.22 (0.06) | 3.15 ** |
| v | Mean drift rate | 3.03 (0.20) | 2.36 (0.07) | −3.90 ** |
| Ter | Mean nondecision time | 0.41 (0.01) | 0.43 (0.01) | 0.94 |
| sz | Range of starting point | 0.73 (0.09) | 0.72 (0.04) | −0.12 |
| st | Range of nondecision time | 0.04 (0.01) | 0.04 (0.01) | −0.13 |
| η | Drift rate variability | 0.51 (0.13) | 0.50 (0.05) | −0.10 |
| KS-distanceb | 0.02 (0.001) | 0.02 (0.001) | −1.33 | |
| p-valuec | .90 (0.02) | .93 (0.02) | 0.80 |
Notes. Best-fitting parameter values are averaged across participants in the No-PM condition and in the PM condition. Standard errors are in parentheses. KS = Kolmogorov-Smirnov.
PM Condition versus No-PM Condition (independent-samples test).
KS-distance T between predicted and empirical cumulative distribution functions of response time.
Probability values of the KS-tests larger than .05 indicate no significant deviations of predicted from empirical distributions.
p < .01
Speed-Accuracy Tradeoffs
In research on PM, analyses of ongoing-task performance are typically conducted to assess the resource demands of PM (McDaniel & Einstein, 2007), and inference mainly concerns mean RT of correct responses or mean accuracy. It is well-known, however, that both measures are in a tradeoff relationship (e.g., Pachella, 1974; Schouten & Bekker, 1967). That is, participants can increase their accuracy at the expense of slower responding, or vice versa. Such speed-accuracy tradeoffs imply that RT can be slower not because a task is more difficult or more resource-demanding, but because participants adopt a different criterion when they weigh the importance of speed versus accuracy. Consider the example of ongoing-task performance in the upper half of Table 2 (cf. Wagenmakers et al., 2007). Participants are faster in Condition A than in Condition B, but they also commit more errors. It is thus possible that both conditions are equally difficult (or resource-demanding), but participants in Condition B sacrifice speed for higher accuracy. Of course, it is also possible that fewer processing resources are available in Condition B than in A, or vice versa. With observed mean RT and accuracy, we cannot disentangle these possibilities. Finally, a comparison of Conditions B and C reveals that participants in the latter respond more slowly, whereas accuracy is identical. Many researchers would assume that Condition C is more difficult (or resource-demanding) than Condition B, as speed-accuracy tradeoffs alone cannot provide an explanation. However, it is not trivial to go beyond ordinal conclusions and quantify which of the underlying processes are responsible for a slowing in Condition C.
Table 2.
Performance and Corresponding Parameter Values in Three Hypothetical Ongoing-Task Conditions
| Condition
|
|||
|---|---|---|---|
| A | B | C | |
| Mean Performance | |||
| RT | 591 | 690 | 740 |
| Proportion Correct | .881 | .953 | .953 |
| Diffusion Model Parameters | |||
| Drift Rate v | 2.0 | 2.0 | 2.0 |
| Threshold Distance a | 1.0 | 1.5 | 1.5 |
| Nondecision Time Ter | 0.4 | 0.35 | 0.4 |
Notes. The conditions differ in nondecision time and threshold distance, but not in the rate of information uptake (simulated data). For this example, z = a/2, and the variability parameters η, sz, st were fixed to 0. RT: Reaction time in ms.
Together, mean RT and accuracy provide important information about task performance, but they should not be considered in isolation; this problem is obviously relevant when PM researchers compare ongoing-task performance in the presence versus absence of PM, or when they compare the impact of different PM conditions (e.g., focal/nonfocal PM tasks, number of PM target cues, etc.). In most previous studies that examined the cost of PM, the dependent variable of interest was either RT or accuracy in the ongoing task; most of the variance in performance typically appeared in one of these measures, but not in both (e.g., in lexical decisions and many other ongoing tasks, differences in mean accuracy are uncommon if aggregated over participants; see Marsh et al., 2005, Exp. 3, or Smith & Bayen, 2006, Exp.1, for rare exceptions). In addition, analyses of RTs and accuracy were always performed separately, lacking a combined index of performance. It is therefore not surprising that speed-accuracy tradeoffs in the PM paradigm have not been considered thus far although they could play a role, indeed.
The diffusion model (e.g., Ratcliff, 1978) can address this issue, because it allows us to separate criterion shifts from other processing components involved in two-choice (ongoing) tasks (see Brown & Heathcote, 2008, or Usher & McClelland, 2001, for alternative models). Consider the bottom half of Table 2 with the corresponding diffusion model parameters for the above example. The assessment at the level of latent parameters is theoretically more informative and reveals that differences in nondecision time (Ter) and speed-accuracy criterion (a), but not in the rate of information uptake (v), explain the differences in observed performance. That is, participants are slower in Condition C than in Condition B, because they have a longer nondecision time (slower stimulus encoding or response execution), but their processing speed during the actual ongoing-task decisions is not affected. Meaningful psychological interpretations of this type could not be derived from standard analyses; we therefore argue that the diffusion model is a useful tool for the PM paradigm and provide an application in the following section (cf. Horn, Smith, Bayen, & Voss, 2008).
Experiment
Method
Design and Materials
We analyzed the data from an experiment by Smith (2003) with the diffusion model. The objective of this experiment was to examine the impact of PM on ongoing-task performance. Each participant studied six PM target words, which subsequently occurred twice in 504 trials of an ongoing lexical decision task. In the PM condition (n = 62), participants were told to remember to press the F1 key when they saw a target word during the experiment. In the No-PM condition (n = 33), participants received the same instructions, but were additionally told that they did not have to remember this intention until after the completion of the lexical decision phase (i.e., their intention was not linked to the context of this phase).
Stimuli presented during the lexical decision task were letter strings that included 126 medium-frequency words (Kučera & Francis, 1967; 6 targets, 120 filler words), and 126 nonwords, created by moving the first syllable of each word to the end. The strings appeared in random order and were repeated in a different random order in the second half of the experiment. See Smith (2003, Exp. 1) for further details concerning the procedure.
Results
The results are reported in two ways. In the first section, we reanalyzed the behavioral data of all non-PM-target trials (accuracy and trimmed RTs). Smith’s (2003) original study focused on a selected number of control items in the ongoing task, but we used more trials because a diffusion model analysis requires sufficient observations for robust parameter estimation. The subsequent sections include the corresponding modeling results.
For all analyses of ongoing-task data, we considered non-PM-target trials exclusively, and RTs smaller than 300 ms or greater than 3000 ms were eliminated (1.27 % of all nontarget trials), because they can lead to degenerate parameter estimates (e.g., Ratcliff & Tuerlinckx, 2002).2
Ongoing-task performance
Smith (2003, Exp. 1) reported a cost on ongoing-task performance as a consequence of the embedded PM task. The present analysis replicated this finding, indicating that participants’ RTs in the PM Condition (M = 925, SD = 163) were significantly slower than in the No-PM Condition (M = 747, SD = 111), t(93) = 6.26, p < .001 (unequal-variances test, ε = .94). The accuracy of lexical decisions did not differ between the PM condition (M = .972, SD = .019) and the No-PM condition (M = .977, SD = .015), t(93) = 1.12, p = .27. Aggregated over participants, accuracy was not far from ceiling, and most of the variance in ongoing-task performance between the conditions appeared in RT. However, we found indications for speed-accuracy tradeoffs at the interindividual level in the course of the present reanalysis. There was a positive relationship between participants’ speed and their accuracy in the ongoing lexical-decision task; this was the case for the PM condition, r(62) = .27, p = .032, and the No-PM condition, r(33) = .55, p < .001. Thus, slower individuals tended to be more accurate within both groups, and it is important to extract such effects with an explicit model before conclusions about actual performance are derived.
Prospective memory
PM performance (M = .69, SD = .20) was positively correlated with ongoing-task RT in the PM condition, r(62) = .34, p = .007. This finding has been interpreted as competition for limited resources devoted to lexical decisions versus the PM task (Smith, 2003). Furthermore, there was a positive relationship between ongoing-task accuracy and PM performance, r(62) = .59, p < .001.
Model fit
The present diffusion model analysis rests on the Kolmogorov-Smirnov statistic (KS; Kolmogorov, 1941) for parameter estimation. This approach provides a robust and fine-grained alternative to other estimation procedures (e.g., maximum likelihood, chi square; see Ratcliff & Tuerlinckx, 2002, for an overview), because the whole RT distributions are used as input, and binning into RT quantiles is not required. The test statistic T represents the maximum vertical distance between the predicted and the empirical cumulative distribution function of RT, and the parameter values are determined in such a way that T is minimized (cf. Voss & Voss, 2007, 2008).
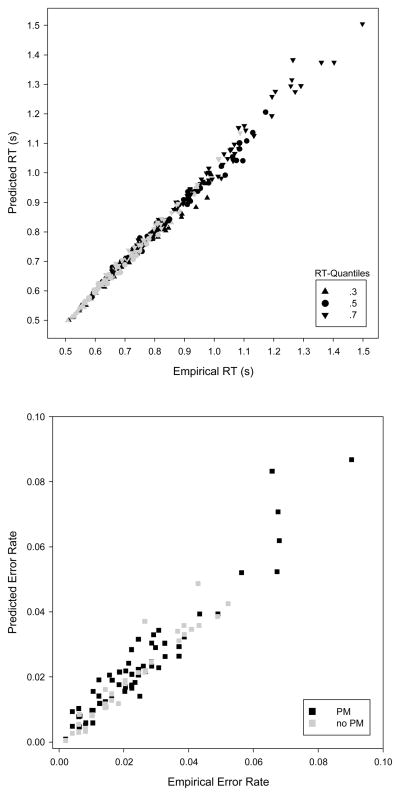
Goodness of fit was evaluated on the individual and on the aggregate level. First, we computed KS-tests for each model. None of 95 model tests detected significant deviations from empirical data (the averaged T statistics and p-values are in Table 1). To visualize individual model fit, empirical and predicted RT quantiles (.3, .5, and .7) of correct responses and the proportion of errors are plotted in Figure 2 for each participant. A diagonal line (with a slope of +1) would represent perfect correspondence between empirical and predicted values in each panel. As can be seen, the correspondence is generally high and the residuals do not indicate systematic biases in the model predictions. The diffusion model adequately reproduces the effects on individual RTs and accuracy in the PM paradigm.
Figure 2.
Individual fits of the diffusion model. The upper panel shows empirical (observed) and predicted RT quantiles (.3, .5, and .7) for each participant in the PM condition (black) and in the No-PM condition (grey). The lower panel shows the correspondence of the proportions of error responses. Diagonal lines with a slope of +1 would indicate perfect fit.
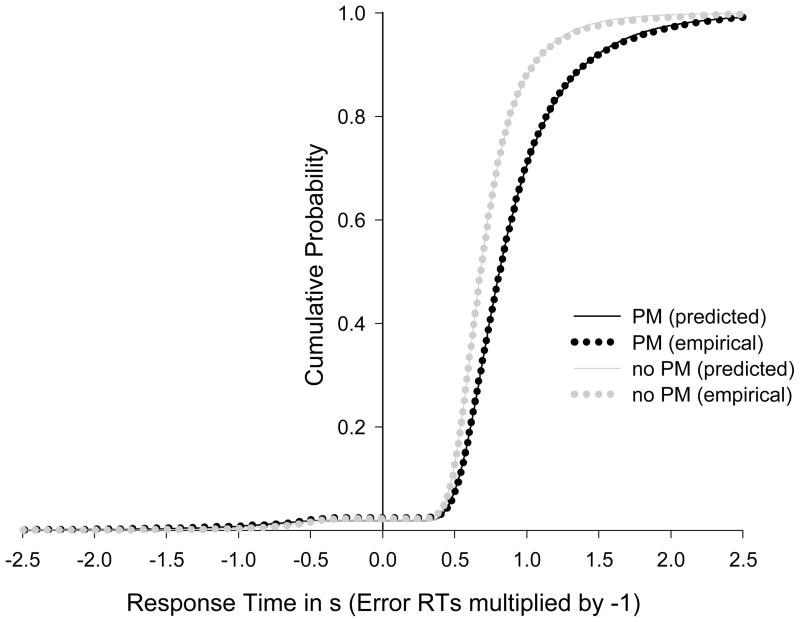
Second, the complete empirical and the complete predicted RT distributions can be visualized to assess model fit. In Figure 3, the RTs from all participants in a condition are combined in a single cumulative distribution function, including correct and error responses. For this purpose, error responses are multiplied by −1, and the corresponding distribution of error RTs is mirrored at the zero point of the time axis (Voss, Rothermund, & Voss, 2004). Thus, the portion of the distribution function on the negative side of the x-axis represents the error latencies and the portion on the positive side of the x-axis represents the latencies for correct responses. The distribution functions intercept the y-axis at the error rate.
Figure 3.
Distributions of response time. The graphs show the empirical (observed) and the model’s predicted cumulative distribution functions of response time, aggregated over individuals in the PM condition (black) and No-PM condition (grey), respectively. Negative values on the horizontal axis are latencies of error responses (multiplied by 1), and positive values are latencies of correct responses.
As seen in Figure 3, the error rates in the present lexical decision task are very low, and there is a marked difference in the whole RT distribution between the PM and the No-PM condition. In sum, Figure 3 indicates an excellent fit at the aggregate level, as there are almost no deviations between the predicted and empirical RT distributions.
Diffusion model analysis
We fit the diffusion model separately to the data from each participant. The resulting mean parameter estimates for the PM and for the No-PM condition are listed in Table 1. Because some participants made few errors in the lexical decision task and lexical variables were not the focus of the present analysis, we aggregated responses over stimulus types for the sake of robust parameter estimation.3 That is, responses were coded as correct (upper threshold) versus false (lower threshold) to obtain a single measure of drift rate, thereby aggregating over the two string types (words, nonwords). With this coding, the mean starting point z was fixed to a/2 (e.g., Ratcliff, 2002), because biases (e.g., a bias to respond “nonword”) cancel out if both string types occur equally often. That is, participants favor correct and false responses equally often and the expected value of the starting point across trials equals a/2. Biases can contribute to starting point variability sz, however (see Klauer, Voss, Schmitz, & Teige-Mocigemba, 2007, for this approach).
The statistical comparison of the diffusion model parameters that yielded the best model fit for participants in the PM and the No-PM conditions revealed a significantly higher threshold parameter a (speed-accuracy setting) when there was an additional PM task (see Table 1). On average, individuals in this group responded more cautiously and required relatively more information before they terminated the decision processes in the ongoing task. However, the model-based analyses also indicated that criterion shifts alone do not fully explain the cost effect of PM on RT. For the present ongoing task, the rate of information accumulation v (collapsed across words and nonwords) was lower for the condition with the embedded PM task. Holding an intention may have interfered with the efficiency of processing the letter strings, as captured by this parameter. Finally, nondecision time Ter and the variability parameters st, sz, and η had comparatively little effect on the cost of PM in this study. In general, the variability parameters have smaller impact on overall mean RT or accuracy, and are more important for the relative speed of correct and false responses, which was not the focus of this study.
Discussion
The diffusion model analysis demonstrates that the cost of PM on an ongoing task (as reported by Smith, 2003) can be split into separate processing components that are theoretically informative for PM researchers. More specifically, the addition of a PM task induces more cautious speed-accuracy settings, thereby increasing the latencies of the ongoing lexical decisions. It is typically assumed that such settings are stable across an experimental block, (e.g., Ratcliff, 1978; Wagenmakers et al., 2008; the diffusion model does not assume variability in threshold distance a), and are formed at the outset (e.g., when participants receive instructions at the beginning of an ongoing task). Differences in criterion settings may therefore reflect participants’ metacognitive beliefs about the upcoming task, which is perceived as more complex or more demanding with additional PM instructions. This is in line with research on strategic allocation policies and their impact on cost effects (Hicks, Marsh, & Cook, 2005; Marsh et al., 2005). The current results indicate that the model’s a parameter could be a useful candidate for quantifying the effects of metacognitive beliefs. Shifts of the boundaries are also consistent with Smith’s (2003, 2010) proposal that embedding a PM task in an ongoing task changes the fundamental nature of the ongoing-task context.
The demonstration of a criterion shift in the current study is an important first step in the application of the diffusion model for understanding the processes that contribute to cost effects. The present results also suggest that the speed of information uptake v is decreased in the PM condition, likely because PM absorbs resources that would otherwise be devoted to the ongoing task, thereby slowing processing efficiency (cf. Smith, 2008, 2010). This interference effect occurs during the actual decision process in the ongoing task, when information about the stimulus is accumulated. The current analysis provides a foundation for future research examining whether other components can contribute to cost effects – dependent on characteristics of the PM task – and how changes in the model parameters relate to PM performance. For instance, our continuing work with the diffusion model indicates that nondecision time (and not drift rates) can account for a slowing if participants adopt a more controlled strategy in PM tasks (e.g., “monitoring” for targets in nonfocal PM tasks or even more vigilance-like tasks; cf. Graf & Uttl, 2001). Such effects are expected from other studies, as individuals have been shown to sequentially check for the presence of targets before or after their actual ongoing-task decisions (Scullin, McDaniel, Shelton, & Lee, 2010), thereby producing a slowing. Moreover, motor response coordination and task-set switching, which would map onto nondecision time (cf. Klauer et al., 2007), may become more prominent in such situations.
The observed parameter differences between the conditions may be due to the retrospective component (remembering the intention content; i.e., the targets and associated actions), the prospective component (remembering that an intention needs to be realized), or both (cf. Einstein & McDaniel, 1990). In the present study, all participants initially learned the PM target words to criterion and recall in a posttest-questionnaire was similar in both groups and generally high (ca. 85%; cf. Smith, 2003). Thus, substantial RT-variance between the conditions is likely attributable to the impact of the prospective component, and not an effect of differences in retrospective-memory load. In light of similarities between PM- and dual-task paradigms, note that participants did not continuously respond to a frequently occurring secondary task and their PM performance was far from ceiling. These characteristics may support the view that part of the slowing reflects intention-retrieval processes, and not a load from any secondary task (see Graf & Uttl, 2001, for a conceptual framework that distinguishes “PM proper” from “vigilance” tasks).
In conclusion, criterion shifts (parameter a) play an important role when a PM task is added to an ongoing task, but they do not fully explain the increase in RT, as other processing components also contribute to the cost of PM. The model-based approach is more informative than standard cost analyses, because parameters quantify the processes that are of theoretical interest at the latent, individual level. This approach can therefore fruitfully contribute to the debate about what costs can or cannot reveal about PM retrieval (Einstein & McDaniel, 2010; Smith, 2010).
Acknowledgments
The research was supported in part by Grant AG034965 from the National Institute on Aging (RES).
Footnotes
Within-trial Gaussian noise with variance s2 is a scaling parameter in the model. This diffusion coefficient is set to 1 for all present model fits. Different values for s2 would simply rescale the absolute values of the other parameters, but would not change their relations.
As suggested by a reviewer, we systematically examined further cutoff-criteria for the lower tail (200, 225, 250, 325, 350 ms) and the upper tail (2000, 2250, 2750, 3250, 3500 ms) of the RT distributions and fit the diffusion models to the so-trimmed data. The pattern of significant and nonsignificant effects was consistently the same as that reported in the present results section.
To examine whether biases in favor of a stimulus type were present, we compared the relative speed of correct versus error responses (cf. Wagenmakers et al., 2007). An a priori bias for a particular stimulus type (e.g., nonwords) would imply faster correct than error responses for this stimulus type, and the reverse pattern of RT for the other type (e.g., words). To obtain reliable estimates of mean error-RT, participants with more than three errors on each stimulus type were included in these analyses. No significant disordinal interactions emerged in the 2 (response correctness) ×2 (stimulus type) ANOVAs, suggesting that biases in favor of a particular stimulus type were neither present in the PM nor the No-PM condition (largest F < 2.91, smallest p > .10).
Parts of this project were presented at the 29th International Congress of Psychology, Berlin, Germany, July 2008, and at the 3rd International Conference on Prospective Memory, Vancouver, Canada, July 2010.
Contributor Information
Sebastian S. Horn, Institut für Experimentelle Psychologie, Heinrich-Heine-Universität Düsseldorf
Ute J. Bayen, Institut für Experimentelle Psychologie, Heinrich-Heine-Universität Düsseldorf
Rebekah E. Smith, Department of Psychology, The University of Texas at San Antonio
References
- Brown SD, Heathcote A. The simplest complete model of choice response time: Linear ballistic accumulation. Cognitive Psychology. 2008;57:153–178. doi: 10.1016/j.cogpsych.2007.12.002. [DOI] [PubMed] [Google Scholar]
- Cohen AL, Jaudas A, Gollwitzer PM. Number of cues influence the cost of remembering to remember. Memory and Cognition. 2008;36:149–156. doi: 10.3758/mc.36.1.149. [DOI] [PubMed] [Google Scholar]
- Criss AH. Differentiation and Response Bias in Episodic Memory: Evidence From Reaction Time Distributions. Journal of Experimental Psychology: Learning Memory and Cognition. 2010;36:484–499. doi: 10.1037/a0018435. [DOI] [PubMed] [Google Scholar]
- Dutilh G, Vandekerckhove J, Tuerlinckx F, Wagenmakers EJ. A diffusion model decomposition of the practice effect. Psychonomic Bulletin & Review. 2009;16:1026–1036. doi: 10.3758/16.6.1026. [DOI] [PubMed] [Google Scholar]
- Einstein GO, McDaniel MA. Normal aging and prospective memory. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1990;16:717–726. doi: 10.1037//0278-7393.16.4.717. [DOI] [PubMed] [Google Scholar]
- Einstein GO, McDaniel MA. Retrieval processes in prospective memory: Theoretical approaches and some new empirical findings. In: Brandimonte M, Einstein GO, McDaniel MA, editors. Prospective memory: Theory and applications. Mahwah, NJ: Lawrence Erlbaum; 1996. pp. 115–141. [Google Scholar]
- Einstein GO, McDaniel MA. Prospective Memory and what costs do not reveal about retrieval processes: A commentary on Smith, Hunt, McVay, and McConnell (2007) Journal of Experimental Psychology: Learning Memory and Cognition. 2010;36:1082–1088. doi: 10.1037/a0019184. [DOI] [PubMed] [Google Scholar]
- Einstein GO, McDaniel MA, Thomas R, Mayfield S, Shank H, Morrisette N, et al. Multiple processes in prospective memory retrieval: Factors determining monitoring versus spontaneous retrieval. Journal of Experimental Psychology: General. 2005;134:327–342. doi: 10.1037/0096-3445.134.3.327. [DOI] [PubMed] [Google Scholar]
- Gardiner CW. Handbook of stochastic methods. Berlin, Germany: Springer; 2004. [Google Scholar]
- Graf P, Uttl B. Prospective memory: A new focus for research. Consciousness and Cognition. 2001;10:437–450. doi: 10.1006/ccog.2001.0504. [DOI] [PubMed] [Google Scholar]
- Hicks JL, Marsh RL, Cook GI. Task interference in time-based, event-based, and dual intention prospective memory conditions. Journal of Memory and Language. 2005;53:430–444. doi: 10.1016/j.jml.2005.04.001. [DOI] [Google Scholar]
- Horn SS, Smith RE, Bayen UJ, Voss A. Analyzing the cost of prospective memory with the diffusion model. International Journal of Psychology. 2008;43:787. [Google Scholar]
- Klauer KC, Voss A, Schmitz F, Teige-Mocigemba S. Process components of the implicit association test: A diffusion-model analysis. Journal of Personality and Social Psychology. 2007;93:353–368. doi: 10.1037/0022-3514.93.3.353. [DOI] [PubMed] [Google Scholar]
- Kolmogorov A. Confidence limits for an unknown distribution function. Annals of Mathematical Statistics. 1941;12:461–463. [Google Scholar]
- Kučera H, Francis W. Computational analysis of present-day American English. Providence, RI: Brown University Press; 1967. [Google Scholar]
- Marsh RL, Hicks JL, Cook GI. On the relationship between effort toward an ongoing task and cue detection in event-based prospective memory. Journal of Experimental Psychology: Learning Memory and Cognition. 2005;31:68–75. doi: 10.1037/0278-7393.31.1.68. [DOI] [PubMed] [Google Scholar]
- McDaniel MA, Einstein GO. Strategic and automatic processes in prospective memory retrieval: A multiprocess framework. Applied Cognitive Psychology. 2000;14:S127–S144. [Google Scholar]
- McDaniel MA, Einstein GO. Prospective memory: An overview and synthesis of an emerging field. Thousand Oaks, CA: Sage; 2007. [Google Scholar]
- Pachella RG. The interpretation of reaction time in information processing research. In: Kantowitz HB, editor. Human information processing: Tutorials in performance and cognition. Potomac, MD: Erlbaum; 1974. pp. 41–82. [Google Scholar]
- Ratcliff R. A theory of memory retrieval. Psychological Review. 1978;85:59–108. [Google Scholar]
- Ratcliff R. A diffusion model account of response time and accuracy in a brightness discrimination task: Fitting real data and failing to fit fake but plausible data. Psychonomic Bulletin & Review. 2002;9:278–291. doi: 10.3758/bf03196283. [DOI] [PubMed] [Google Scholar]
- Ratcliff R, Gomez P, McKoon G. A diffusion model account of the lexical decision task. Psychological Review. 2004;111:159–182. doi: 10.1037/0033-295X.111.1.159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, McKoon G. The diffusion decision model: Theory and data for two-choice decision tasks. Neural Computation. 2008;20:873–922. doi: 10.1162/neco.2008.12-06-420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Rouder JN. Modeling response times for two-choice decisions. Psychological Science. 1998;9:347–356. [Google Scholar]
- Ratcliff R, Thapar A, Gomez P, McKoon G. A diffusion model analysis of the effects of aging in the lexical-decision task. Psychology and Aging. 2004;19:278–289. doi: 10.1037/0882-7974.19.2.278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Thapar A, McKoon G. Aging and individual differences in rapid two-choice decisions. Psychonomic Bulletin & Review. 2006;13:626–635. doi: 10.3758/bf03193973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Tuerlinckx F. Estimating parameters of the diffusion model: Approaches to dealing with contaminant reaction times and parameter variability. Psychonomic Bulletin & Review. 2002;9:438–481. doi: 10.3758/bf03196302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schouten JF, Bekker JAM. Reaction time and accuracy. Acta Psychologica. 1967;27:143–153. doi: 10.1016/0001-6918(67)90054-6. [DOI] [PubMed] [Google Scholar]
- Scullin MK, McDaniel MA, Shelton JT, Lee JH. Focal/Nonfocal cue effects in prospective memory: Monitoring difficulty or different retrieval processes? Journal of Experimental Psychology: Learning Memory and Cognition. 2010;36:736–749. doi: 10.1037/a0018971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith PL. Stochastic dynamic models of response time and accuracy: A foundational primer. Journal of Mathematical Psychology. 2000;44:408–463. doi: 10.1006/jmps.1999.1260. [DOI] [PubMed] [Google Scholar]
- Smith RE. The cost of remembering to remember in event-based prospective memory: Investigating the capacity demands of delayed intention performance. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2003;29:347–361. doi: 10.1037/0278-7393.29.3.347. [DOI] [PubMed] [Google Scholar]
- Smith RE. Connecting the past and the future: Attention, memory, and delayed intentions. In: Kliegel M, McDaniel MA, Einstein GO, editors. Prospective memory: Cognitive, neuroscience, developmental, and applied perspectives. Mahwah, NJ: Erlbaum; 2008. pp. 27–50. [Google Scholar]
- Smith RE. What costs do reveal and moving beyond the cost debate: Reply to Einstein and McDaniel (2010) Journal of Experimental Psychology: Learning Memory and Cognition. 2010;36:1089–1095. doi: 10.1037/a0019183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith RE, Bayen UJ. The source of adult age differences in event-based prospective memory: A multinomial modeling approach. Journal of Experimental Psychology: Learning Memory and Cognition. 2006;32:623–635. doi: 10.1037/0278-7393.32.3.623. [DOI] [PubMed] [Google Scholar]
- Smith RE, Hunt RR, McVay JC, McConnell MD. The cost of event-based prospective memory: Salient target events. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2007;33:734–746. doi: 10.1037/0278-7393.33.4.734. [DOI] [PubMed] [Google Scholar]
- Spaniol J, Madden DJ, Voss A. A diffusion model analysis of adult age differences in episodic and semantic long-term memory retrieval. Journal of Experimental Psychology: Learning Memory and Cognition. 2006;32:101–117. doi: 10.1037/0278-7393.1.101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Usher M, McClelland JL. The time course of perceptual choice: The leaky, competing accumulator model. Psychological Review. 2001;108:550–592. doi: 10.1037//0033-295x.108.3.550. [DOI] [PubMed] [Google Scholar]
- Voss A, Rothermund K, Voss J. Interpreting the parameters of the diffusion model: An empirical validation. Memory & Cognition. 2004;32:1206–1220. doi: 10.3758/bf03196893. [DOI] [PubMed] [Google Scholar]
- Voss A, Voss J. Fast-dm: A free program for efficient diffusion model analysis. Behavior Research Methods. 2007;39:767–775. doi: 10.3758/bf03192967. [DOI] [PubMed] [Google Scholar]
- Voss A, Voss J. A fast numerical algorithm for the estimation of diffusion model parameters. Journal of Mathematical Psychology. 2008;52:1–9. doi: 10.1016/j.jmp.2007.09.005. [DOI] [Google Scholar]
- Wagenmakers EJ. Methodological and empirical developments for the Ratcliff diffusion model of response times and accuracy. European Journal of Cognitive Psychology. 2009;21:641–671. doi: 10.1080/09541440802205067. [DOI] [Google Scholar]
- Wagenmakers EJ, Ratcliff R, Gomez P, McKoon G. A diffusion model account of criterion shifts in the lexical decision task. Journal of Memory and Language. 2008;58:140–159. doi: 10.1016/j.jml.2007.04.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagenmakers EJ, van der Maas HLJ, Grasman R. An EZ-diffusion model for response time and accuracy. Psychonomic Bulletin & Review. 2007;14:3–22. doi: 10.3758/bf03194023. [DOI] [PubMed] [Google Scholar]
- West R. The influence of strategic monitoring on the neural correlates of prospective memory. Memory & Cognition. 2007;35:1034–1046. doi: 10.3758/bf03193476. [DOI] [PubMed] [Google Scholar]