Vasomotion becomes less random as diabetes progresses in monkeys

Abstract

Objective

Changes in vasomotion may precede other global indices of autonomic dysfunction that track the onset and progression of diabetes. Recently we showed that baseline spectral properties of vasomotion can discriminate among normoglycemic (N), prediabetic (PreDM), and diabetic (T2DM) nonhuman primates. In this study, our aims were 1. To determine the time-dependence and complexity of the spectral properties of vasomotion in three metabolic groups of monkeys; 2. To examine the effects of heat-provoked vasodilatation on the power spectrum; and 3. To compare the effects of exogenous insulin on the vasomotion.

Materials and Methods

Laser Doppler flow rates were measured from the foot in 9 N, 11 PreDM, and 7 T2DM monkeys. Baseline flow was measured at 34 °C, and under heat stimulation at 44 °C. Euglycemic, hyperinsulinemic clamps were performed to produce acute hyperinsulinemia. The Lempel-Ziv complexity, prediction error, and covariance complexity of 5-dimensional embeddings were calculated as measures of randomness.

Results and Conclusions

With progression of diabetes, measures of randomness of the vasomotion progressively decreased, suggesting a progressive loss of the homeostatic capacity of the peripheral circulation to respond to environmental changes. Power spectral density among T2DM animals resided mostly in the 0 – 1.45 Hz range, which excluded the cardiac component, suggesting that with progression of the disease, regulation of flow shifts toward local rather than central (autonomic) mechanisms. Heating increased all components of the spectral power in all groups. In N, insulin increased the vasomotion contributed by endothelial, neurogenic, vascular myogenic and respiratory processes but diminished that due to heart rate. By contrast, in T2DM, insulin failed to stimulate the vascular myogenic and respiratory activities, but increased the neural/endothelial and heart rate components. Interestingly, acute hyperinsulinemia resulted in no significant vasomotion changes in the chronically hyperinsulinemic PreDM, suggesting yet another form of “insulin resistance” during this stage of the disease.

Introduction

Derangement of vasomotion has been cited as a possible cause of diabetic neuropathy (13). It has also been suggested that changes in vasomotion precede other global indices of autonomic dysfunction that track the onset and progression of diabetes(25). In a recent work (38), we showed that spectral properties and measures of randomness of vasomotion can discriminate among normoglycemic, metabolic syndrome/prediabetic, and overtly diabetic nonhuman primates. Spectral measures were shown to be more effective than traditional physiological measures such as fasting plasma glucose (FPG), glycosylated hemoglobin level (HbA1c), and insulin level (IRI) in distinguishing normoglycemic from prediabetic subjects, suggesting that measures of vasomotion may be useful in discerning those likely to develop diabetes (in prediabetes) and in those with established diabetes, to discern those likely to develop diabetic neuropathy.

Heating is frequently used to study the available reserve of the skin microcirculation to undergo vasodilation. In this study we aimed to: (A) investigate the time dependence of some spectral properties and three measures of complexity in the course of the heat treatment, (B) examine at higher-resolution the heat-induced changes in low-frequency spectral peaks that have previously been reported to be associated with physiological mechanisms influencing vasomotion (27), and (C) examine the effects of hyperinuslinemia on the characteristics of the vasomotion, before and during heating.

The three measures of complexity used in this study, Lempel-Ziv complexity, Prediction Error, and Covariance Complexity, are among a new and powerful set of tools that have recently become available for the analysis of data from complex systems. They make possible the study of seemingly random time series that was not possible with prior traditional techniques. A loss of complexity of a physiologic time series is currently viewed as indicative of disease (40) while intrinsic variability of a physiological phenomenon reflects the adaptability of underlying control networks.

In this study, we found that in response to thermal stimulation, the spectral properties among the three metabolic risk groups varied significantly, and the character of the vasomotion became less random as the disease status progressed.

Using a small representative sample of monkeys undergoing transition from normoglycemia to spontaneous type 2 diabetes, we also looked at the effects of insulin on the heat response. Our results confirm earlier results on normoglycemic subjects studied without a heat stimulus. Furthermore, our results indicate that in the diabetic animal, all of the measures changed in the direction of normal values in the presence of exogenously administered insulin.

Materials and Methods

A. Animals

We analyzed vasomotion data from 27 rhesus macaques: 9 normoglycemic, 11 metabolic syndrome/prediabetic, and 7 overtly diabetic, taken from a larger colony of monkeys which has been maintained consistently for approximately 25 years for the study of aging, obesity and diabetes. The larger colony includes rhesus monkeys of both sexes aged 10–39 years, although longitudinal clinical data are available from age 5 in some monkeys. The characteristics of the colony have been described previously(12, 15–17, 34, 36, 37). The present study sample included adult rhesus monkeys (Macacamulatta), ranging in age from 9.9 – 29.9 years, and in body weight from 5.9 – 25 .3 kg. The monkeys were classified into the following 3 groups: (A) normoglycemic monkeys, (N) (fasting plasma glucose (FPG) < 80 mg/dl), (B) prediabetic monkeys (PreDM) (FPG: 80–125mg/dl and/or impaired glucose tolerant (IGT), defined as a glucose disappearance rate K_gluc<2.5 %/min by intravenous glucose tolerance test [IVGTT], and/or insulin resistant (IR), defined as an insulin-stimulated peripheral glucose uptake rate during a euglycemic-hyperinsulinemic clamp [M rate] of < 7.5 mg/kg fat-free mass [FFM] per minute, and/or hyperinsulinimic (IRI ≥ 100 μU/ml), and (C) monkeys with type 2 diabetes (T2DM, defined as having FPG ≥ 126 mg/dl.) Table 1 summarizes the mean values of key physiological variables for each group.

Table 1.

Metabolic characteristics of the three groups, expressed as means ± s.e.m.

Variable	N	PreDM/IR	DM
Age (yrs)	19.4 ± 2.0	18.5 ± 1.2	20.4 ± 2.5
Body Weight (kg)	14.0 ± 1.2	16.3 ± 1.1	12.2 ± 2.0
FPG(mg/dl)	69.7 ± 2.6	77.12±6.4	191.1±26.5*#
HbA1C (%)	4.55 ± 0.6	5.76± 0.56	8.73 ± 0.70*#
IRI (microU/ml)	51.0 ±9.3	117.4 ± 23.5*	50.0 ± 23.7
SBP (mm Hg)	123.4 ±10.2	137.2 ±6.1	136.5 ± 6.2
DBP (mm Hg)	63.9 ± 4.3	66.7 ± 2.5	64.6 ± 1.9
Triglycerides (mg/dl)	112.9 ± 15.1	295.9 ± 115.9	599.6 ± 148.9*
Kg (%/min)	3.34 ± 0.31	2.24 ± 0.20*	1.25 ± 0.11*#
M rate (mg/kg FFM/min)	8.06 ± 1.36	5.21 ± 0.65*	3.47 ± 0.98*

In the table shown,

^*significant difference from the control group;

^#significant difference from the prediabetic group.

B. Spectra and measures of randomness

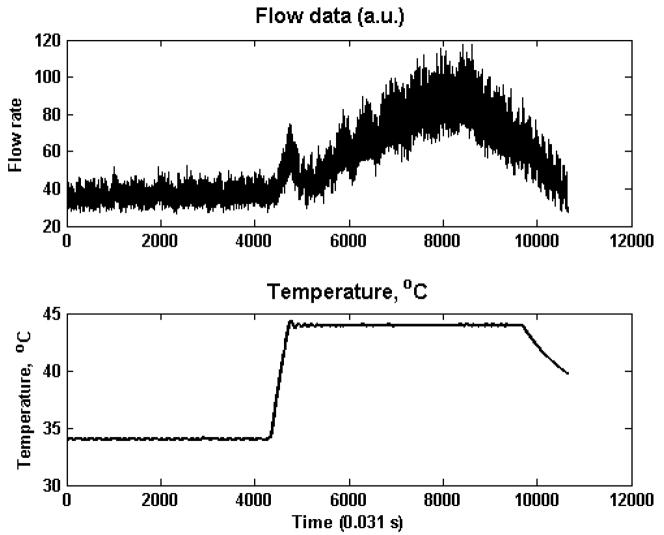
Laser Doppler flow rates were measured using a PerimedPeriflux 5000 System with a pre-set sampling time of 0.031 s from the dorsum of the foot of the anesthetized monkeys after an overnight fast. For the “heat treatment,” using the built-in heating element of the Laser Doppler probe, the skin area of each monkey was first acclimatized to 34 °C after which flow rates were measured for ~ 60 seconds. Flow rate measurements continued as the local skin temperature was increased linearly to 44°C, and then maintained at 44°C for 2 minutes. Figure 1 shows a sample recording of the heat treatment data.

Fig. 1.

Sample heat treatment data for a normoglycemic subject. Top: Flow rate, Bottom: temperature (°C)

C. Time dependence

There was some variability in the data file lengths before and after the onset of heating. Thus, to study time dependence using data files that included the same number of points before and after heating onset, each data file was truncated, as necessary, to include 521 points (16.15 s) before the start of the heat ramp and 4855 points (150.50 s) after initiation of heating. These numbers were dictated by the shortest available data file lengths before and after heating onset.

The truncated data files were subdivided into non-overlapping 400-point (12.4 s) epochs and for each of these epochs we made four calculations: (i) The percentage of spectral power in the frequency bands 0.00 – 1.45 Hz (the “1-Hz band”) and 1.53–2.98 Hz(the “2-Hz band”), (ii) the Lempel-Ziv complexity, (iii) the prediction error, and (iv) the covariance complexity of 5-dimensional embeddings. The sequences of values so obtained provide time-dependent characterizations of the data and are further defined as follows:

i. Spectral power

To estimate spectral power, the mean and the linear trend of each epoch were removed and the resulting sequence was subjected to a Hanning window before calculating its Fast Fourier Transform (FFT). The resulting frequency resolution was Δf = 0.081 Hz (39). Comparisons of the spectra of raw data with those of data that have been lowpass-filtered with cutoffs at 32 Hz and 16 Hz show that there are negligible contributions to the data from components with frequencies exceeding 16 Hz.

ii. Complexity

The algorithmic complexity of a symbol sequence is the length of the shortest instruction set needed to reconstruct it. For a series of a given length, a random sequence has the highest complexity because there are no rules that would reproduce it. An ordered sequence is less complex than a random one – the more ordered, the less complex. There are many ways of estimating complexity (28). Regardless of how it is estimated, it provides a measure of how much the structure of the time series differs from that of a random sequence with the same distribution of symbols (38, 39).

In this analysis, we applied a definition of complexity described by Lempel and Ziv (22). To calculate the Lempel-Ziv complexity, the time series is first reduced to a sequence of zeros and ones. That is, if an element of the time series exceeds the median, it is replaced by 1, otherwise, it is replaced by 0. Then, the resulting sequence is expressed as a unique set of shorter sequences of zeros and ones (2, 39). The Lempel-Ziv complexity is equal to the number of these sub-sequences.

iii. Prediction error

Future values of a random sequence cannot be predicted from its past. For ordered sequences, there exists some possibility of prediction – the more ordered, the more predictable. A commonly used algorithm to measure predictability makes use of a procedure similar to one that was previously popular in weather forecasting. To predict tomorrow’s weather, look for a day in the past when the conditions were closest to today’s, and then predict that tomorrow’s weather will be like the day that followed that day in the past.

For a sequence of values, x ={x₁, x₂, …, x_N}, to predict the k ^th element, we look for that past value of x (call it x_Q) which is closest to the previous element, x_k−1. Our prediction is the element of the sequence that follows x_Q: (x_k)_pred= x_Q+1 [see, e.g., ref.2 (2)for details and caveats]. The quality of a set of predictions is assessed by the prediction error,

$$\mathit{err}=\frac{\frac{1}{n_p}{\displaystyle \sum _{k=1}^{n_p}}\left|x_k-{(x_k)}_{\mathit{pred}}\right|}{{\sigma }_x},$$

where n_p is the number of predictions made and σ_x is the standard deviation of the x’s.

iv. Covariance complexity

A sequence of measurements of a single variable, x ={x₁, x₂, …, x_N}, can be expressed as a sequence m-dimensional vectors, X₁= (x₁, x_2, …, x_m), X₂= (x₂, x_3, …, x_m+1), …, X₃= (x₃, x_4, …, x_m+2), etc. Under certain conditions, this is called an m-dimensional embedding (see e.g., ref.1)(1). These vectors are points in an m-dimensional mathematical space. If x is a random sequence, then the points would be distributed uniformly in the space. Otherwise, their distribution would show some structure. The covariance complexity, C, is a measure of that structure (see, e.g., ref. 2(2)) and ranges from C = 0 for a very structured distribution to C =1 for a random sequence.

D. Higher resolution

Low-frequency peaks in the human vasomotion spectrum have been associated with specific physiological processes: heart beat (spectral peaks at ~ 0.6–2 Hz), respiration (~ 0.15–0.6 Hz), myogenic activity in the vessel wall (~0.05–0.15 Hz), sympathetic activity ~ 0.02–0.05 Hz), and endothelial activity (~ 0.008–0.02 Hz) (19). These intervals were described by Rossi in human subjects (30) as heart activity (~0.6–1.6 Hz), respiratory (~0.2–0.6 Hz), vascular myogenic (~.06–0.2Hz), sympathetic (~0.02 – 0.06 Hz) and endothelial (~0.009–.02 Hz). In monkeys, these intervals may be slightly different as heart rate frequencies are in the range from 1.5 – 3.0 Hz and respiratory rates usually range from 0.33–1.0 Hz. Significant changes in some of these peaks have been noted in connection with insulin administration (27). Investigation of these peaks required using longer epochs both before and during the heat treatment, resulting in slightly smaller sample sizes: 8 normal, 10 prediabetic, and 5 diabetic- subjects. For each of the remaining subjects, we calculated the power spectral densities (PSD’s) of 1067-point (33.1-s) epochs before the start of the temperature ramp and again at the start of the temperature plateau. This greater epoch length resulted in a spectral resolution of 0.030 Hz which resolved all but the neurogenic (sympathetic) and endothelial components. It is the sum of the contributions of these latter two that are reported below.

E. Euglycemic, hyperinsulinemic clamp to produce acute maximalhyperinsulinemia

After baseline flow and heat- provoked changes in flow were measured, monkeys underwent a, euglycemichyperinsulinemic clamp to measure insulin-mediated glucose uptake while holding circulating glucose levels steady at normal levels. For the clamp, 2 contralateral cannulas were placed, one for administration of glucose (20%), the other for insulin. Insulin was initiated at a priming dose followed by a continuous infusion of insulin. At t= 4 minutes, glucose infusion was initiated and blood samples obtained every 5 minutes with glucose infusion rate adjusted after each determination in order to maintain steady-state plasma glucose values of ~ 4.7 mmol/L (85 mg/dl). The procedure has been previously described as a method to assess whole body insulin sensitivity (5). Whole body glucose disposal rate (M-rate) was estimated from the average of the exogenous gluocose infusion rate during steady state at maximal insulin stimulation, and calculated for the metabolically active fat-free mass. Steady-state insulin levels were > 3000 μU/ml), which based on prior studies, were sufficient to completely suppress endogenous hepatic glucose production. The insulin-induced peripheral glucose disposal rate (M rate) was calculated during the last 30 minutes of the clamp period. Flow rates were measured before the clamp procedure (no insulin), before and during heating (heat-stimulated response), and every ten minutes during the clamp (insulin and insulin + heating response). Glucose tolerance was measured during a separate intravenous glucose tolerance procedure and is expressed as K_gluc, or the log glucose disappearance rate between 5 and 20 minutes following the glucose bolus.

Results

A. Time dependence

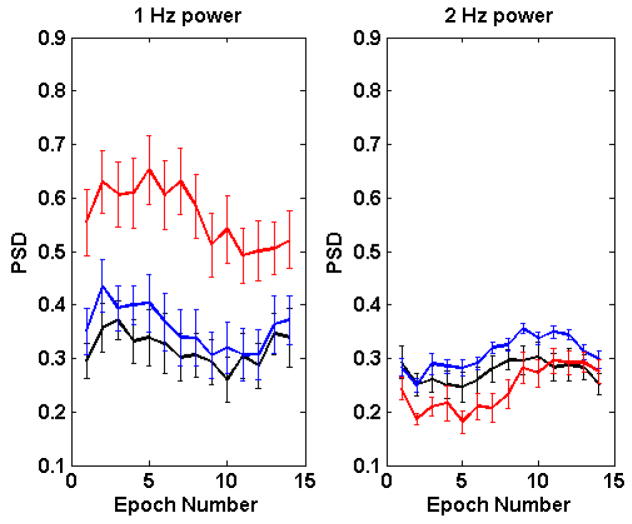
Fig. 2 shows the time dependence of spectral power in the 1-Hz and 2-Hz bands. The values for each of the metabolic states (normal, prediabetic, diabetic) are averages for all subjects in that state. The error bars are standard errors of the mean.

Fig. 2.

Time dependence of the fraction of spectral power in the 1-Hz band (left panel) and in the 2-Hz band (right panel). Epochs are separated by 12.4 s. Heat treatment starts in epoch 2. In both panels, normal = black, prediabetic = blue, diabetic = red.

Fig. 2 shows that for both frequency bands, values for the diabetic group are dramatically different from those of the other two (10⁻²≥ t-test p≥10⁻¹⁰). Spectral power in the 1-Hz band is significantly greater among the diabetic group than among the other two metabolic risk groups. Power in the 2-Hz band, however is less in the diabetic group.

At baseline, the PSD of the normal animals in the 2-Hz band did not differ significantly from the PreDM group; however, with introduction of heat, the PSD became significantly greater in the prediabetic monkeys (t-test p = 0.0015); similarly, while the power in the 1-Hz band did not differ significantly between the two groups at baseline (t-test p = 0.11), following introduction of heat (from epochs 2–8), the spectral power of the N and PreDM groups in the 1-Hz band became significantly different, with the PreDM group demonstrating a much greater response to heat than the N group. This is consistent with our previously reported findings that in response to thermogenic stimulation, prediabetic monkeys exhibit an augmented response when compared to the normal group (35)

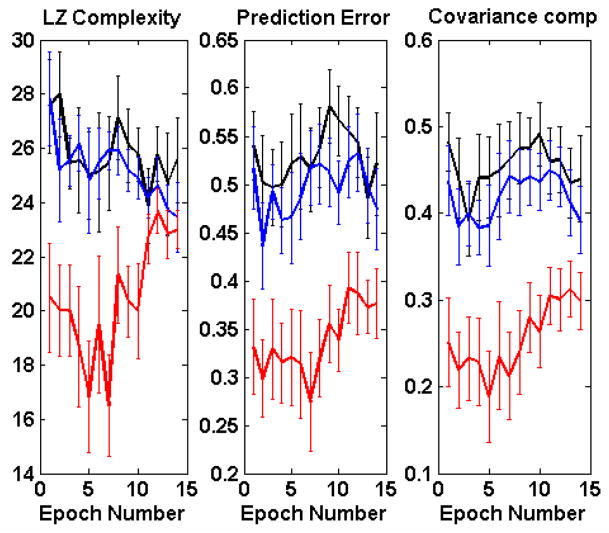
Fig. 3 shows three measures of randomness: the Lempel-Ziv complexity, prediction error, and covariance complexity of 5-dimensional embeddings. For all of these measures, lower values correspond to lower complexity or less randomness. Fig. 3 shows that based on the values of the indices, the vasomotion time series of the diabetic monkeys were significantly less random (more ordered) than those of the normal and prediabetic monkeys. The Lempel-Ziv complexities of normal and prediabetic groups were indistinguishable (t-test p = 0.72), but their prediction errors were distinguishable (p = 0.052); the covariance complexities separated the two groups even more distinctly (p = 0.023).

Fig. 3.

Changes in complexity with progression of diabetes. Left: Lempel-Ziv complexity, Center: Prediction error, Right: Covariance complexity. In all panels, normal = black, prediabetic = blue, diabetic = red.

It appears that as the disease progresses from normal to prediabetic and further to the diabetic states, the complexity became less. Fig. 3 shows that at the onset of heating (epoch 2), the vasomotion of all groups, as assessed by the LZ complexity, prediction error and covariance complexity, became less random. For the diabetic group, the randomness remained below baseline until epoch 7 at which time it became increasingly more random. It approaches, but at no time does it attain, the randomness of the normal and prediabetic cases.

B. Higher resolution spectra and response to heat

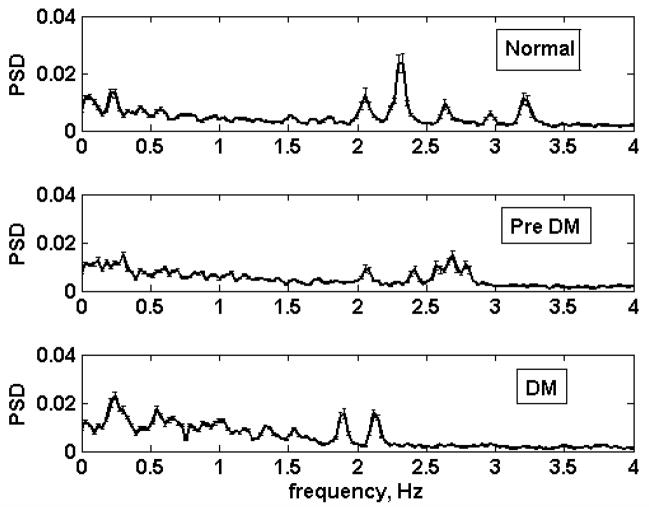
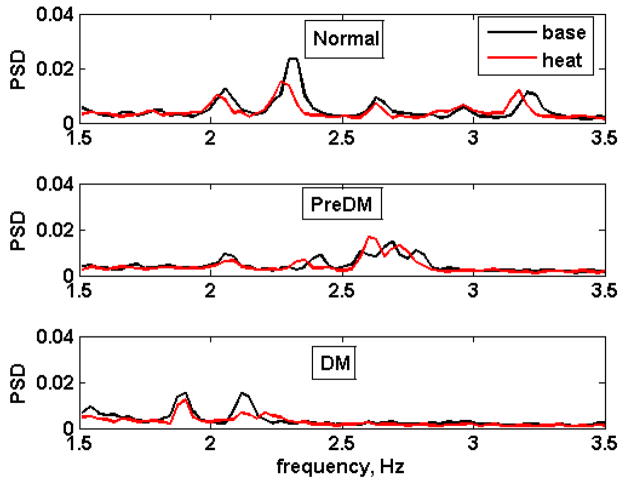
Fig. 4 shows the average baseline (pre heat-treatment) spectra of the three metabolic groups. Among the normal animals, there are prominent peaks at frequencies as high as 3.3 Hz which were absent among the prediabetic and diabetic monkeys. The peaks in the 1.5 – 3.3 Hz range are most likely associated with the heart rate since monkey heart rates fall within this range.

Fig. 4.

Average baseline spectra (pre- heating) of normal (top), prediabetic (middle) and diabetic (bottom) animals. Error bars are standard errors of the mean.

(1) The 1-Hz band

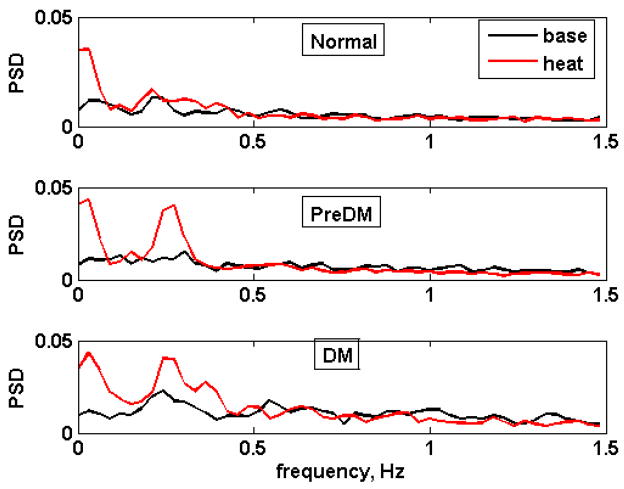
Fig. 5 shows responses to heat treatment of the three metabolic risk groups in the 1-Hz band. Heating induces substantial increases in the frequency bands associated with endothelial/neuronal (0.00–0.0605 Hz) and possibly myogenic (0.181–0.574 Hz) processes.

Fig. 5.

Average vasomotion spectra in the 0.00 – 1.48 Hz range for the three metabolic groups. Top: normal, middle: prediabetic, bottom: diabetic. Black: baseline, red: heat treatment. The spectra were calculated using 1067 points (33.1 s), averaged over 8 normoglycemic subjects, 10 prediabetic, and 5 diabetic.

Table 2 shows the behavior of the peaks in the 0.000 – 3.356 Hz range as the disease progresses, for baseline and in response to heat treatment. Since our resolution was 0.031 Hz, endothelial and neuronal signals were combined together.

Table 2.

Fraction of spectral energy in the low-frequency range. In each cell, the figures are mean ± s.e.m., respectively.

		Baseline			Heat treatment
Frequency range (Hz)		Norm	Pre DM	DM	Norm	Pre DM	DM
0.00–0.0605*	Endothelial, neurogenic	0.031 ±0.007	0.045 ±0.011	0.031 ±0.007	0.088◆±0.029	0.090 ±0.025	0.125◆±0.047
0.091–0. 574	Myogenic	0.127 ±0.021	0.167 ±0.024	0.259* ±0.034	0.152 ±0.022	0.203◆±0.036	0.413◆*# ±0.048
0.605–1.481	Respiratory	0.122 ±0.019	0.156 ±0.025	0.323*# ±0.050	0.110 ±0.010	0.117◆±0.016	0.237*# ±0.041
1.512–3.356	Heartbeat	0.315 ±0.021	0.269 ±0.012	0.219* ±0.031	0.269◆±0.022	0.258 ±0.015	0.150◆*# ±0.018

^◆significant difference from the preheat value in the SAME group;

^*significant difference from N;

^#significant difference from PreDM.

Endothelial, neurogenic (0.00 Hz <f≤ 0.065 Hz): The mean values for the three metabolic classes were indistinguishable both at baseline and during heat treatment. There were significant heat-induced increases, at the ~ 95% confidence level, in the normal (p=.034) and diabetic (p=.031) groups, and a tendency to increase in the PreDM (p= 0.057)

Myogenic (0.091 Hz ≤f≤ 0.574 Hz): At baseline, the mean value for the diabetic group was the highest, being significantly greater than that of the normal group (F = 5.38, p = 0.0134). During heat treatment, this component was still highest among the diabetic animals, being significantly greater than the mean value of the N and PreDM groups (F = 11.94, p = .000387). While there were no heat-induced changes observed in the N group in this frequency range, the power in this spectral component increased significantly in both the prediabetic and diabetic animals in response to heat (p= 0.032 and p = 0.037 in the PreDM and DM respectively).

Respiratory (0.605 Hz ≤f≤ 1.481 Hz): At baseline, the mean value for the diabetic group was again the highest, being significantly greater than those of the normal and the prediabetic monkeys (F= 10.68, p < 0.001). The same was true during heat treatment when the mean value of the power spectral density was significantly higher in the DM(0.24 ± 0.02) than in the N (0.11±.025) or the PreDM (0.12 ± .02) groups, with F =9.53, p = 0.001237. In the PreDM group the contribution of this fraction significantly declined, whereas no significant heat-induced changes in the N and the DM were observed.

Heartbeat (1.512 Hz ≤f≤ 3.356 Hz): At baseline, the mean value for the diabetic group was the least, differing significantly from that of the normal (F= 5.12, p = 0.016). After heating, the diabetic group still had the lowest value of the power density in this range, being significantly less than that of the PreDM and N groups (F= 9.32, p= 0.00137). Heating reduced the contribution of this fraction significantly in the normal (p=0.01) and DM (p= 0.03) groups, but had no effect in the PreDM group.

In summary, heating induced an increase in the endothelial/neurogenic (0.00 – 0.065Hz) component of the spectral energy in all three groups. For the frequency range from 0.091 to 0.574 Hz (which we have labeled “myogenic”), heating appeared to increase the contribution of this fraction, especially in the PreDM and DM groups. This component of the spectral energy was significantly greater in the diabetic animals than in the normal group, both at baseline and following heat treatment. The diabetic animals demonstrated the highest values for the respiratory component, whereas the normal animals had the highest values for the heart rate component, both before and during heating. However in both the N and DM animals, heating decreased the mean power density in the heart rate range.

(2) The 2-Hz band

Fig. 6. shows the baseline and heat responses of the three risk groups for a slightly expanded 2-Hz band (1.512 – 3.356 Hz). The multiple peaks in the normal (top) and prediabetic (middle) spectra reflect different locations of the ~ 2 Hz peaks of the individual subjects, rather than multiple peaks in each subject. As the disease progresses, these peaks, located at various frequencies in the normal animals converged at a common value among the diabetic subjects, while variability in the PreDM was less than N but more than DM. Heating did not appear to significantly increase the power density contribution of this frequency range in any of the groups.

Fig. 6.

Effect of heat treatment on the 2-Hz spectral band (1.51–3.56 Hz). Top: normal, middle: prediabetic, bottom: diabetic. Black: baseline, red: heat treatment.

B. Effects of insulin perfusion

Time dependence

The following analyses were performed on three representative monkeys, one from each metabolic group, which were studied during a euglycemic, hyperinsulinemic clamp procedure to measure insulin sensitivity. This provides some initial information concerning the effects of insulin on the heat response of the vasomotion properties of subjects from the different metabolic groups.

The three subjects showed very different responses to insulin as can be seen in Table 3.

Table 3.

Changes in the fraction of spectral energy in low-frequency peaks due to insulin infusion. These values are from single subjects in each category. In each cell, the upper number is the energy fraction before insulin administration, the lower is in the presence of insulin.

		Baseline			Heat treatment
Frequency range (Hz)		Norm	Pre DM	DM	Norm	Pre DM	DM
0.00–0.0605*	Endothelial, neurogenic	0.042 0.127	0.033 0.018	0.017 0.085	0.272 0.257	0.034 0.040	0.178 0.223
0.091–0.574	Myogenic	0.186 0.436	0.135 0.084	0.308 0.316	0.250 0.362	0.153 0.643	0.466 0.290
0.605–1.481	Respiratory	0.165 0.192	0.217 0.205	0.329 0.163	0.135 0.160	0.180 0.091	0.153 0.153
1.512–3.356	Heartbeat	0.402 0.159	0.257 0.275	0.200 0.288	0.226 0.142	0.280 0.315	0.133 0.223

Normal

During the first seven epochs (~87 s) insulin infusion increased the power in the 1-Hz band and decreased that in the 2-Hz band, most dramatically before the start of the heat treatment. Insulin increased the spectral energy contribution of the endothelial/neurogenic, myogenic and respiratory components prior to heating, but reduced that due to heart rate. The combination of heating and insulin increased the myogenic contribution above that of heating alone. In that same period, all the measures of randomness decreased in the presence of insulin.

Prediabetic

Insulin reduced the endothelial/neurogenic, myogenic and respiratory components of the power spectrum at baseline (prior to heating) but slightly increased the contribution of the heart rate. However the combination of heat and insulin resulted in a profound elevation of the myogenic component in the prediabetic animal, when compared to preheat baseline, insulin only and heat only values. After administration of insulin, all the indices of complexity increased relative to baseline in the prediabetic animal.

Diabetic

Insulin increased the contribution of the endothelial/neurogenic frequency range, had virtually no effect on the myogenic contribution compared to baseline, reduced the respiratory component of the spectrum while increasing the contribution of the heart rate. The 2-Hz peak shifted toward a higher frequency and the power density increased almost 2-fold. Hence, insulin perfusion in the diabetic animal caused all of the measures to change in the direction of the average normal values so that the values approached those in the normal subject.

Discussion

Vasomotion is believed to be a mechanism which enables fine-tuning of perfusion by adjusting the volume and distribution of the local flow to the needs of the tissue, thus making flow more homogenous in the microcirculation (13, 30, 41). These cyclic variations in constriction and dilatation of arterioles are in turn evoked by a variety of stimuli, such as pressure, heat, neurogenic input, metabolic environment as well as central (autonomic) controls. The cutaneous microcirculation plays an important role in thermoregulation. Regulation of flow of the cutaneous microcirculation may be mediated in part by endothelial or local neurogenic (axon flare) mechanisms. Khan, et al (18) have noted that endothelium-mediated increases in flow induced by metacholine infusion were not significantly different between normal and diabetic patients. Lefrandt, et al, (21) on the other hand, reported a reduction in sympathetically-mediated vasomotion in the skin, which was attributed to a decrease in the power of the low frequency components (0.02 to 0.40Hz) of the power density spectrum.

In this study, we noted that for the frequency ranges below 0.0605 Hz, baseline values of this component of the spectral power appeared to be similar among the three metabolic groups corroborating Khan’s observations that baseline values showed no significant differences. Following heat-provocation, an increase in the contribution of the endothelial-neurogenic component (frequencies < .0605 Hz) of the spectral power was observed in all three groups when compared to baseline (pre-heat) values, implying that the endothelial- local neurogenic processes remained intact even in diabetes.

In addition to neurogenic and enodothelial regulation of peripheral flow, distribution and redistribution of flow through capillary units can also be regulated by oscillations in vascular smooth muscle tone in response to other stimuli in the local environment. For the ranges from 0.09 to 0.57 Hz, the diabetic group had the largest values of the power at baseline and after heating, as compared with the control group. If the frequency range between 0.09 and 0.57Hz does in fact represent vascular myogenic mechanisms, these appeared to be enhanced in the diabetic subjects both at baseline and in response to heat. Addition of insulin without heat, however, while enhancing this “myogenic” component in the normal monkey, resulted in no significant change in the diabetic monkey, and a reduction in power in the prediabeticmoneky, suggesting a form of insulin resistance in the non-normal groups.

This frequency range includes the frequency range ~0.1Hz which has been described by others to be influenced in part by sympathetic activity (25, 33). Schmiedel reports that oscillations induced by alpha-adrenergic agonists which he associated with the 0.1 Hz range were significantly reduced in patients with peripheral or autonomic neuropathy, compared to diabetic patients without neuropathy, or non-diabetic controls(31). Stanberry’s original description of impaired vasomotion in human diabetic subjects referred to a decrease in area under the curve of the Fast Fourier Transform (power fraction, in our case) for frequencies less than 6 cpm (~0.1 Hz). Since this range was derived from human data, it is unclear which frequency range this would correspond to in monkeys. In this study, mean values of the spectral power in the range from 0–0.09 Hz (combined contributions of endothelial, neural and myogenic mechanisms) did not vary among the three groups at baseline.

The highest mean values of the fraction of the spectral energy associated with the respiratory component of the vasomotion (0.605 <f< 1.481) was observed among the diabetic animals both at baseline and with heating. We speculate that respiratory oscillations probably occur with greatest frequency in this group because of ventilatory adjustments which attempt to correct the metabolic acidosis associated with diabetes. In contrast, the component of the vasomotion associated with heart rate was highest among the normal animals. Therefore, while a “decrease in vasomotion” was seen among the diabetic animals in the range associated with cardiac oscillations, oscillations in the frequency range of the respiratory component were highest in the diabetic group, both at baseline and during heating. Furthermore, the “myogenic” component (frequency between 0.091 and 0.574 Hz) of the vasomotion was highest in the diabetic group both at baseline and during heating. These may indicate that with diabetes, microvascular flow is regulated to a greater extent by local mechanisms (endothelium/neural/myogenic) in response to existing conditions in the immediate local environment (e.g. heat, pressure, pH, oxygenation, metabolites) with a proportional loss of central or autonomic mechanisms as reflected by heart rate.

In this study we observed that all measures of vasomotion randomness, including Lempel-Ziv complexity, prediction error, and covariance complexity, dramatically decreased among diabetic animals compared to normoglycemic subjects. The loss of randomness parallels the natural history of the disease. In prediabetes, two out of the 4 measures of complexity (prediction error and covariance complexity) were significantly different from the normal group. The decrease in the randomness of the vasomotion time series is reminiscent of previous studies of another system, the human heart (14), which showed that the heartbeat tends to become less chaotic and more periodic as disease progresses -- i.e., as sudden cardiac death becomes more imminent. While we did not study specific measures of chaos, our findings indicate that, consistent with these earlier findings, with progression of diabetes, the power of the lower frequencies of the vasomotion signal increased, that of the higher frequencies decreased, suggesting greater periodicity and the signal’s apparent decrease in randomness.

Similarly, examination of the 2-Hz band in the three metabolic groups revealed that while several peaks were prominent among the normal monkeys, likely representing different heart rhythms, the values converged on a single lower frequency in the diabetic group, again indicative of diminishing complexity with progression of the disease. This reduction in randomness in heart rate variability among the diabetic animals is likely associated with the increasing severity of autonomic dysfunction that is characteristic of diabetes. Similar to our previous observations, we found that the spectral power in the 2 Hz band was highest in prediabetic animals and was significantly greater than that of the normal group. The chronic hyperinsulinemia of the prediabetic/metabolic syndrome monkeys and the known effect of insulin to stimulate the sympathetic nervous system may account for the average heart rate frequencies of the prediabetic animals (Fig. 6) shifting towards the higher values.

The role of insulin-induced capillary recruitment in insulin-mediated glucose uptake is unclear. Barrett suggested that insulin-mediated glucose transport could be attributed to insulin’s ability to relax resistance vessels, thus increasing its own transendothelial transport into muscle (4). A suggested mechanism by which insulin regulates perfusion is by its effects on vasomotion (6–11, 29, 30, 32). Newman suggested that insulin increased microvascular flow by increasing vasomotion and that this process is impaired in acute insulin resistance (27). Serne (32) reported that in healthy individuals, systemic hyperinsulinemia increases leg blood flow, number of perfused capillaries, both endothelium-dependent and independent vasodilation, and enhanced contributions of the 0.01–0.02 Hz and the 0.4–1.6 Hz components. Local introduction of insulin to the skin microcirculation via iontophoresis also induced an increase in flow, independent of systemic effects of insulin. Similar findings were reported by de Jongh, et al (10) in healthy individuals undergoing hyperinsulinemic clamp procedures. More recently they noted that while local administration of insulin induced skin microvascular vasodilatation in lean women, this was not the case for obese women (11) where the contribution of the endothelial (0.01 to 0.02) and neurogenic (0.02–0.06) processes to the total power spectrum were less, suggesting impaired vasomotion among the obese subjects.

Whether it is true that microvascular dysfunction exacerbates insulin resistance and consequent metabolic derangement remains controversial (8, 9). While insulin is vasodilatory by stimulating endothelial production of nitric oxide (NO) (24), compensatory hyperinsulinemia (or insulin resistance) is associated with decreased endothelium- dependent vasodilation (3). Apart from NO, insulin can also stimulate secretion of endothelin-1 from endothelium through the MAP kinase pathway, thus favoring vasoconstriction (24, 26). In diabetes, the dysregulation of both parasympathetic and sympathetic nervous systems may result in loss of reflex vasoconstriction and heart rate variability (23).

Apart from its effects on the endothelium and the autonomic nervous system, insulin may also exert effects on vascular smooth muscle. In the skin microcirculation of healthy subjects Rossi, et al, (30) reported that iontophoretic administration of insulin resulted in a significant increase in cutaneous perfusion compared to saline, which based on spectral analysis, was likely due to the significant increase in the contribution of the myogenic component. Indeed, in the present study we also found that the response of the “myogenic” frequency interval to insulin was also particularly large in the normal animal. In contrast, the diabetic animal responded to hyperinsulinemia with an increase in power in the endothelial/neurogenic frequencies, but with no significant change in the myogenic range. If this is a typical response, then it would appear that diabetic animals are refractory to the increase in myogenic vasomotion induced by insulin, while still capable of responding by increasing vasomotion due to the endothelium/neurogenic processes. Noteworthy are the decline in the contribution of the respiratory component and the concomitant increase in the heart-rate induced vasomotion in the diabetic monkey, probably a result of exogenous insulin correcting some of the metabolic abnormalities present in diabetes. The prediabetic monkey, which had chronic hyperinsulinemia before the clamp, demonstrated a decrease in vasomotion due to endothelial, neural, myogenic and respiratory mechanisms. Such a response may represent a loss of vasomotor tone of the chronically dilated microcirculation brought about by the plethora of insulin, in lieu of a “healthy” oscillatory state where the microvessels could respond to the external environment with the appropriate vasomotor mechanism. The only noted insulin-induced increase in the prediabetic animal was in the heart rate component, a finding similar to the increase in heart rate variability observed in the insulin-resistant offspring of type 2 diabetic probands (20).

Our data suggest that in the normal animal, insulin tends to increase the vasomotion contributed by endothelial, neurogenic, vascular myogenic processes and respiratory processes, while the contribution of cardiac rhythms is diminished. In contrast, the diabetic animal failed to show any significant increase in vasomotion attributable to an increase in vascular myogenic activity after insulin infusion; respiration-induced vasomotion decreased, but the heart rate component showed a dramatic increase. Administration of exogenous insulin to the insulin-deficient diabetic animal appeared to change the characteristics of the power spectrum so that it approached the values of the normal animal.

Most importantly, our study showed that in parallel with the progression of diabetes as represented by the three metabolic groups, measures of randomness of the vasomotion progressively decreased. This suggests a progressive loss of homeostatic capacity of the peripheral circulation, and a reduction in the ability of the system to respond to complex and local changes in the environment through variation of the vasomotion.