In Brief: Standard Deviation and Standard Error

I know of scarcely anything so apt to impress the imagination as the wonderful form of cosmic order expressed by the ``Law of Frequency of Error’’. … Whenever a large sample of chaotic elements are taken in hands and marshalled in the order of their magnitude, an unsuspected and most beautiful form of regularity proves to have been latent all along. The tops of the marshalled row form a flowing curve of invariable proportion; and each element, as it is sorted in place, finds, as it were, a pre-ordained niche, accurately adapted to fit it.

Sir Francis Galton (Natural Inheritance, 1889:66).

Background

Physicians often confuse the standard deviation and the standard error [6], possibly because the names are similar, or because the standard deviation is used in the calculation of the standard error. However, they are not quite the same, and it is important that readers (and researchers) know the difference between the two so as to use them appropriately and report them correctly.

Question

What are the differences between the standard deviation and standard error?

Discussion

The standard deviation is a measure of the dispersion, or scatter, of the data [3]. For instance, if a surgeon collects data for 20 patients with soft tissue sarcoma and the average tumor size in the sample is 7.4 cm, the average does not provide a good idea of the individual sizes in the sample. It could be that the sizes in the sample are similar and lie between 7 and 9 cm or that the sizes are dissimilar with some tumors being very small and others very large. In the former case, size likely will play little role in the differences in outcome between patients, whereas in the latter case tumor size could be an important factor (confounding variable) explaining differences in outcome between patients or relating to other variables such as surgical margins. Further, having an estimate of the scatter of the data is useful when comparing different studies, as even with similar averages, samples may differ greatly. It therefore is important to report the variability in the sample and this is done with the standard deviation of the sample,

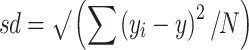1

with y_i the size of an individual observation, y the average size in the sample, and N the number of observations in the sample. In this case, sd = 2.56 cm. If data are normally distributed, approximately 95% of the tumors in the sample have a size that falls within 1.96 standard deviations on each side of the average. Therefore, in the current sample, most patients have a tumor size between 2.4 and 12.4 cm. Histograms, in which the number or frequency of observations is plotted for different values or group of values, are a good way to illustrate the scatter of the data; scatter diagrams, in which the values of one continuous variable are plotted against those of another, may help readers see the relation between two variables and the dispersion of one against the other.

In contrast, the standard error provides an estimate of the precision of a parameter (such as a mean, proportion, odds ratio, survival probability, etc) and is used when one wants to make inferences about data from a sample (eg, the sort of sample in a given study) to some relevant population [4]. When the standard error relates to a mean it is called the standard error of the mean; otherwise only the term standard error is used. For instance, in the previous example we know that average size of the tumor in the sample is 7.4 cm, but what we really would like to know is the average size of the tumor in the entire population of interest (ie, all patients with such tumors, not just those in the study). We can take the sample mean as our best estimate of what is true in that relevant population but we know that if we collect data on another sample, the mean will vary according to what is called the “sampling distribution.” Ideally we would like to have a measure of the uncertainty surrounding our estimate. However, with only one sample, how can we obtain an idea of how precise our sample mean is regarding the population true mean? Assume the parameter (say tumor size) in the population has mean μ and standard deviation σ. We know that if we draw samples of similar sizes, say N as in the sample of interest above, from the population many times (eg, n times), we will obtain a great number of means (m₁, m₂, … m_n) scattered around the true population mean μ (Fig. 1). Given a statistical property known as the central limit theorem [5], we know that, regardless the distribution of the parameter in the population, the distribution of these means, referred as the sampling distribution, approaches a normal distribution with mean and standard deviation

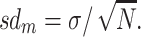2

Since we know that in a normal distribution approximately 95% of the observations (in the present case, the observations are the means of each sample drawn from the population) fall within 1.96 standard deviations on each side of the mean (in the present case, this refers to the mean of the means), we can safely assume that 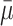 ± 1.96 × sd_m will contain 95% of the means drawn from the population. The problem is that when conducting a study we have one sample (with multiple observations), eg, s₁ with mean m₁ and standard deviation sd₁, but we do not have 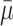or sd_m. However, it happens that m₁ is an unbiased estimate of μ and what is called the standard error,

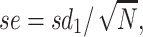3

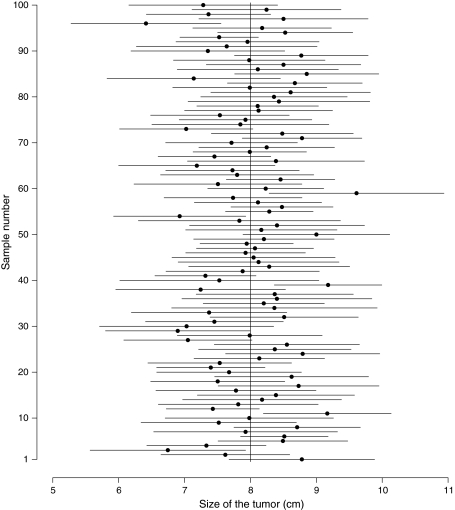
is our best estimate of sd_m (the standard error is in essence the standard deviation of the sampling distribution of a random variable [4]). So the range determined by m₁ ± 1.96 × se (in lieu of 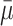 ± 1.96 × sd_m) provides the range of values that includes the true value of the population with a 95% probability: this is the 95% confidence interval. The value 1.96 is the standard normal random deviate for the probability of 1-α/2 with α = 5%. For instance, in the previous example (where m₁ = 7.4, sd₁ = 2.56, and se₁ = 0.57), we can be confident that there is a 95% probability that the mean size of the tumor in the population lies between 6.43 and 8.5 cm. In the example of 100 samples of tumor size, seven samples (3, 11, 29, 39, 54, 59, and 96) have a confidence interval that does not include the true population mean (Fig. 1). Figure 2 shows the relation between the population mean, the sampling distribution of the means, and the mean and standard error of the parameter in the sample.

Fig. 1.

One hundred samples drawn from a population with mean μ = 8 (solid line) and standard deviation σ = 2.5 (dashed lines) are shown. Seven samples (3, 11, 29, 39, 54, 59, and 96) have a 95% confidence interval that does not include the population mean.

Fig. 2.

The cascade from the distribution of the parameter in the population, to the sampling distribution of the means, and to a single sample is shown. We can see how we work our way back from the mean and standard error of the mean in the sample (m₁ = 7.4, and se = 0.57), to construct an interval (m₁ ± 1.96 × se), closely resembling the interval 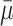 ± 1.96 × sd_m, that has a 95% probability to include the true population mean (μ = 8).

Myths and Misconceptions

First, if the distribution in the sample is nonnormal, then it is preferable to describe the scatter with other measures such as numerically with percentiles (first and third quartiles) or graphically with a histogram [2] rather than a standard deviation.

Second, when computing the standard deviation, one may see formulas where the ∑(y_i– y)² is divided by N or by N − 1 (Bessel’s correction [1]). The former gives the standard deviation of the data in the sample and the latter gives a better estimation of the true value of the standard deviation in the population. Although there is little difference between the two, the former underestimates the true standard deviation in the population when the sample is small and the latter usually is preferred.

Third, when inferring from a sample to a larger theoretical population, the sample must be representative of the population. It is only then that we may make inferences from the sample to that population.

Finally, physicians should always clarify when writing a report whether they refer to the standard deviation or the standard error. Statements, such as average 3.4 cm (±1.2), are ambiguous and should not be used. To decide whether to report the standard deviation or the standard error depends on the objective. If one wishes to provide a description of the sample, then the standard deviations of the relevant parameters are of interest. For instance we would provide the mean age of the patients and standard deviation, the mean size of tumors and standard deviation, etc. If, on the other hand, one wishes to have the precision of the sample value as it relates to that of the true value in the population, then it is the standard error that should be reported. For instance, when reporting the survival probability of a sample we should provide the standard error together with this estimated probability. However, because the confidence interval is more useful and readable than the standard error, it can be provided instead as it avoids having the readers do the math. If a researcher is interested in estimating the mean tumor size in the population, then he or she would have to provide the mean and standard deviation of tumor size to describe the sample observed and the standard error or confidence interval to infer to the population.

Conclusion

Physicians should understand that the standard deviation and standard error are quite different. The standard deviation is a purely descriptive statistic, almost exclusively used as a measure of the dispersion of a characteristic in a sample. However, the standard error is an inferential statistic used to estimate a population characteristic.