A Double-Layered Mixture Model for the Joint Analysis of DNA Copy Number and Gene Expression Data

Abstract

Copy number aberration is a common form of genomic instability in cancer. Gene expression is closely tied to cytogenetic events by the central dogma of molecular biology, and serves as a mediator of copy number changes in disease phenotypes. Accordingly, it is of interest to develop proper statistical methods for jointly analyzing copy number and gene expression data. This work describes a novel Bayesian inferential approach for a double-layered mixture model (DLMM) which directly models the stochastic nature of copy number data and identifies abnormally expressed genes due to aberrant copy number. Simulation studies were conducted to illustrate the robustness of DLMM under various settings of copy number aberration frequency, confounding effects, and signal-to-noise ratio in gene expression data. Analysis of a real breast cancer data shows that DLMM is able to identify expression changes specifically attributable to copy number aberration in tumors and that a sample-specific index built based on the selected genes is correlated with relevant clinical information.

1. Introduction

Genomic alterations, including copy number variants (CNV), inversions, and tandem repeats, have been implicated in phenotypic variation in recent studies (Freeman et al., 2006; Redon, 2006). Copy number aberration refers to cytogenetic events in which the DNA replication process is disturbed and abnormal number of DNA is copied in newly generated cells, leading to local chromosomal variation. These events are larger than genetic variants such as single nucleotide polymorphisms but smaller than chromosome-wide events such as aneuploidy, rearrangements, and fragile sites (Feuk et al., 2006). Copy number aberration is localized on each chromosome and manifested in varying lengths, and thus the definition applies to a wide variety of cytogenetic events. Since gene expression has long been used as a proxy for phenotypic variation in human populations and copy number changes are directly related to transcription, it is therefore of great interest to study the association between the two levels of data (Stranger et al., 2007).

Although copy number aberration has been characterized as genetic variants in large-scale studies (Redon, 2006), it is challenging to identify copy number-associated gene expression in these studies because copy number aberration is a low-frequency event in large populations. Delineating the association between the two data may be more promising in cancer studies because copy number aberration is more prevalent in cancer populations due to genomic instability in tumor cells, and thus the role of copy number in altering gene expression is supposed to be more pronounced in cancer studies. Paired data are already available for a variety of common cancer types under case-control design, often generated using array-based comparative hybridization (Pinkel et al., 1998), or array CGH, and gene expression microarrays. Pollack et al. (2002) was one of the earliest to investigate the association between the two data in breast cancer cell lines and tissue samples. Hyman et al. (2002) found that nearly half the amplification events in breast cancer cell lines were associated with elevated gene expression and replicated similar results in tumor tissue samples. The association between the two types of data has also been reported in other types of cancer (Tonon et al., 2005). These genome-wide surveys of tumor samples generally suggest that changes in expression levels can be ascribed to copy number aberration in some genes, but also demonstrate that the association might not be so strong as to explain the variability in gene expression solely based on copy number changes.

Statistical analysis of these two data sets is challenging mainly because copy number data show dynamic stochastic behavior due to genomic alterations of varying length, often manifested in segmental patterns. Thus, the measurement of each gene cannot be considered statistically independent as in the analysis of gene expression data, and accordingly, a de-noising procedure accounting for local homogeneity should be incorporated into the joint analysis. Copy number segmentation has been a subject of various statistical methods. Popular algorithms include circular binary segmentation (Olshen et al., 2004), hidden Markov models (Fridlyand et al., 2004; Marioni et al., 2006; Stjernqvist et al., 2007; Rueda and Diaz-Uriarter, 2007), hierarchical clustering-based algorithms (Wang et al., 2005), information criteria-based change point model (Zhang and Siegmund, 2007), and a mixture model-based dynamic programming algorithm (Picard et al., 2007). Comparison of some of these algorithms has been provided in recent reviews (Willenbrock and Fridlyand, 2005; Lai et al., 2005; Chari et al., 2006). Segmentation algorithms are not only useful for identifying sites of common chromosomal aberration in cancer but are also helpful for joint analysis. This is because copy number-associated expression changes can be searched within the segments of aberrant copy number only, saving the effort to interrogate the entire genome. Tonon et al. (2005) and Kim et al. (2007), for example, performed linear correlation analysis and differential expression hypothesis testing respectively, after identifying candidate regions by applying segmentation algorithms.

To date, few systematic approaches are available for the joint analysis of copy number and gene expression data. Lipson et al. (2004) developed a regional analysis called genomic continuous submatrix (GCSM), which scans the genome with a moving window of linear correlation coefficients to screen for locally consistent correlations between the two data. GCSM uses the raw copy number data for linear correlation analysis and hence segmental patterns are captured by appropriate widths of the scanning windows. However, the association between the two data is likely nonlinear in the sense that copy number aberration is a sample specific event and thus raw measurements are not comparable across different samples as in gene expression data. van Wieringen and van de Viel (2008) proposed a nonparametric hypothesis testing framework (vWvV tests) for finding changes in the gene expression distribution that incorporates the probability of copy number gain or loss. Even though vWvV tests utilize the probability of copy number aberration in the testing procedure, the hypothesis testing framework may not be an optimal way to identify copy number-associated expression because aberrant copy numbers are low frequency events even in cancer tissue samples and widely vary by gene, and many hypotheses may be untestable due to lack of data for genes with aberrant copy number.

The concept of copy number-associated expression is gene-centric but specific to individual samples at the same time. Hence, it is important to be able to quantify the evidence for impact of copy number aberration on gene expression for every gene in every sample. In this work, a novel Bayesian inference and sampling algorithms for a double-layered mixture model (DLMM) is proposed. DLMM directly models segmental patterns in the copy number data to produce copy number aberration profile in probability scale, and simultaneously scores the association between paired copy number and gene expression data using related latent variables in the two data sets. The method assigns high scores to elevated or reduced expression measurements only if the expression changes are observed consistently across samples with copy number aberration. Since DLMM simultaneously computes the probability of copy number amplification and deletion and the probability of copy number-associated expression conditional on the former, DLMM ensures high specificity of the copy number influence on gene expression and removes the burden of separate analysis for the two data.

2. Methods

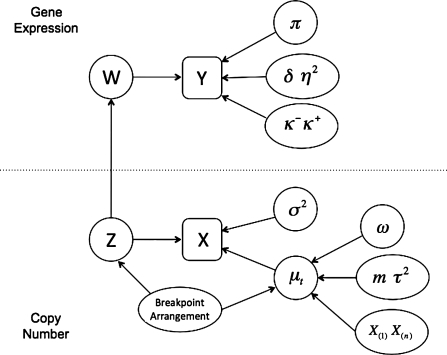
DLMM is composed of two main parts, one for copy number data and the other for gene expression data respectively. A graphical representation is provided to show the conditional independence structure of the model parameters in Figure 1. For simplicity, tumor-only analysis is discussed throughout this work, but the methodology can easily be extended to two-group comparisons such as tumor versus normal tissue.

FIG. 1.

Graphical representation of the double-layered mixture model. X and Y denote the observed copy number and expression data, respectively. Z and W are the calls of aberrant copy number and differential gene expression associated with aberrant copy number. X₍₁₎ and X_(n) denote minimum and maximum copy numbers in the sample, respectively. Note that the mixture model in the copy number data is sample-specific, while that in the gene expression data is gene-specific. Given these parameters, the two data sets are independent.

2.1. Model for copy number data

Let N denote the number of tumor samples. Suppose that copy number data X = {x_gs} are observed for genes 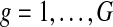in samples 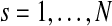. The copy number data in sample s (e.g., log-scaled intensity ratios of array CGH data) are modeled as a series of Gaussian random variables with mean parameters forming a stochastic process on the chromosome, represented in a piecewise constant function. Each chromosome of sample s is divided into T_s segments, with T_s being a Poisson random variable with mean λ_s. The parameter λ_s is assumed to follow Gamma distribution 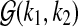for all 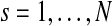. The Poisson-Gamma mixture leads to negative binomial prior for T_s, which can be considered as a flexible prior accounting for over-dispersion. In this setting, there are (T_s − 1) boundary points between adjacent segments and two fixed points on the start and end positions of the chromosome, to give (T_s + 1) points in total. These breakpoints are denoted by (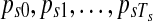) with subscript s to indicate that the position of these points varies by sample. Every segment 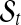defined by (p_{s(t − 1)}, p_st) is required to contain at least one gene, and the copy number data in sample s in the segment is modeled as independent observations from Gaussian distribution with mean μ_ts and variance .

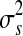Formally, the model for copy number data can be written as follows. For each sample s with segment configuration ,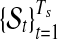

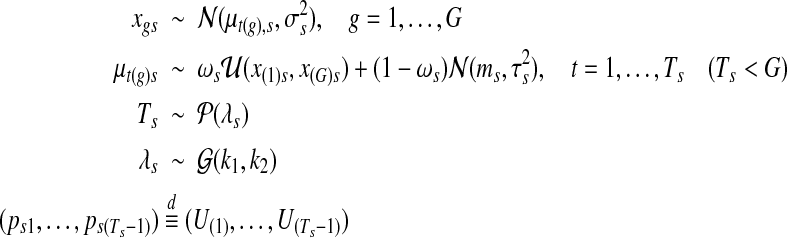where t(g) indexes the segment containing gene g, and U_(i) denote the i-th order statistic of (T_s − 1) Uniform random variables on an open interval (0, L). The mean process, 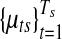, follows a Uniform-Gaussian mixture prior distribution, and (x_(1)s, x_(G)s) are the minimum and maximum copy number data in sample s, respectively. In the mixture distribution of 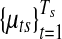, latent variables are introduced for the sampling procedure. Define latent variables 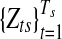as follows. In each segment ,

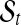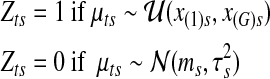In the above, m_s, the genome-wide mean copy number, is assumed to follow 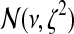prior distribution. The variance components in the likelihood and the prior are assumed to follow inverse Gamma distributions 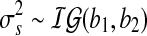and 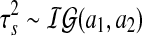, respectively, and the mixing proportion ω_s is assumed to have Uniform 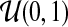prior distribution.

2.2. Model for gene expression data

Suppose that gene expression is measured for some of the G genes, which is denoted by Y = {y_gs} with parallel indexing of gene IDs in the copy number data. For example, if gene g has both the copy number and the expression data, 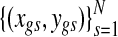denotes the paired data across the N samples. To keep the notation tractable, it is assumed that every gene has both copy number and gene expression measurements, i.e., t(g) = g for all g. Extending to the case where copy number data has denser coverage than expression data is trivial, as is incorporating multiple chromosomes. The 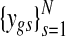are modeled as observations from Uniform-Gaussian mixture distribution, where the Uniform component corresponds to the expression distribution in samples with aberrant copy number and the Gaussian component corresponds to the expression distribution in samples with normal copy number. If the data contain non-tumor samples, all measurements from those samples will belong to the Gaussian component, guiding the estimation of the mixture in a semi-supervised way. The mixture formulation attempts to quantify the enrichment of copy number-associated expression levels in the tail of the expression distribution of each gene.

More specifically, a hierarchical Uniform-Gaussian mixture model is fitted to the gene expression data:

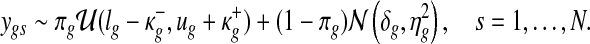Note that this mixture model is specified for each gene; by contrast the corresponding mixture model in the copy number data is specified for each sample. The gene expression model specification has been previously used in gene expression modeling of Parmigiani et al. (2002). A set of latent variables 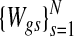are defined for each gene g,

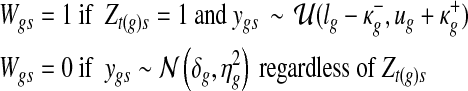respectively, where (l_g, u_g) denote the minimum and the maximum expression values of gene g across the samples, and (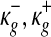) are the extended tail parameters for the Uniform component representing under- and over-expression of gene g. Priors for the Gaussian component are given as 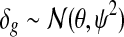and 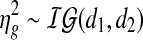. Priors for the Uniform component are the following: 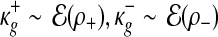and .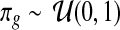

In the definition of the latent variables in the two data sets, note that Z_t(g),s = 0 implies W_gs = 0, meaning that the definition of over- or under-expression is relative to the expression distribution in samples with no aberrant copy numbers. Thus, even if a gene is highly expressed in many samples, this gene will not be considered as over-expressed so long as this is not related to the concordant amplification. In terms of model parameters, this implies that δ_g can be far from zero, requiring appropriate elicitation of prior. This definition of W therefore highlights the gene and the sample with expression changes specifically associated with copy number changes.

2.3. Probabilistic scoring and criterion-based gene selection

DLMM reports two sets of probability scores: the copy number probability P(Z_t(g)s = 1), and the probability of copy number-associated expression changes P(W_gs = 1). Note that these two probabilities always satisfy

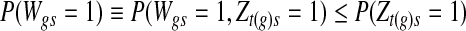so that over- and under-expression is scored conditional on aberrant copy number only.

Since the event {W_gs = 1} may represent either over- or under-expression, the direction of changes should be matched with concurrent changes in the copy number data so that copy number gain is associated with over-expression, and copy number loss is associated with under-expression. This is equivalent to calculating an over-expression score 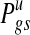and an under-expression score 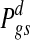separately, where

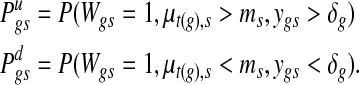The event {Z_t(g),s = 1} is omitted in each expression because it is a necessary condition for {W_gs = 1}. One can summarize the two-dimensional score into a signed score 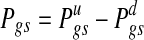or report the two scores separately. In this work, the score difference P_gs is followed. This calculation results in signed probability for a gene in a specific sample, and a positive or negative score of large magnitude indicates strong evidence for copy number-associated expression of the given gene in the sample.

Since this probability score is the joint probability of aberrant copy number and gene expression, this number can range from a very small number to a value close to 1, depending on multiple factors such as the sample size, the prevalence of copy number changes, and the separation of copy number-associated expression from expression distribution in samples with normal copy numbers. Since the range of joint probability may vary by data sets, it is important to establish a unified criterion to select genes based on estimated model parameters and model fit. The L-measure introduced by Ibrahim et al. (2002) is well-suited for the purpose. L-measure is a goodness-of-fit criterion combining posterior variance and squared bias. Its computation at a probability threshold p* is achieved by taking the average of the following quantity over the posterior samples used for the inference:

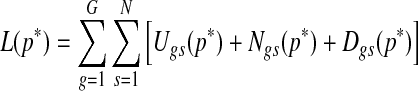where

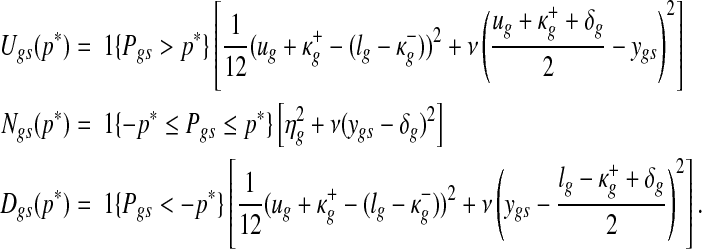The weighting constant ν of the squared bias relative to the predictive variance was set to 0.5, following the theoretical justification of Ibrahim et al. (2001). Copy number associated expression was selected using the threshold yielding the minimal L-measure.

2.4. Inference

Bayesian inference was performed by Markov chain Monte Carlo (MCMC). Due to the segmentation in the copy number data, a part of the posterior sampling involves transdimensional moves guided by reversible jump MCMC. Samples are drawn from the appropriate posterior distributions in the following order: [Copy Number Parameters] → [Copy Number Segment Arrangement] → [Gene Expression Parameters].

2.4.1. Gibbs sampler for copy number parameters

In a fixed segmentation arrangement (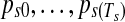), the segmental mean μ_ts in of sample s is drawn from

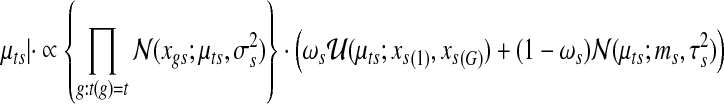by Metropolis-Hastings sampling. Next, the latent variables Z_ts are drawn by sampling from Bernoulli random variable with success probability

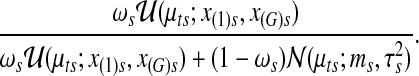The rest of the parameters are updated through Gibbs sampling from the appropriate closed-form conditional distributions. The variance component for segmental means has the following distribution:

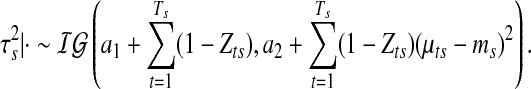The variance of raw data is drawn from

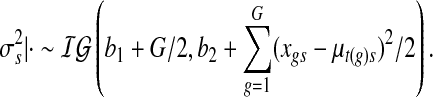Finally, the mixing proportion is drawn from

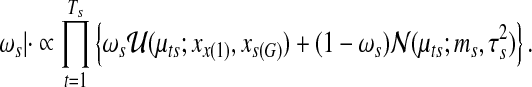2.4.2. Gibbs update for expression parameters

The mean and variance of the Gaussian component are updated from

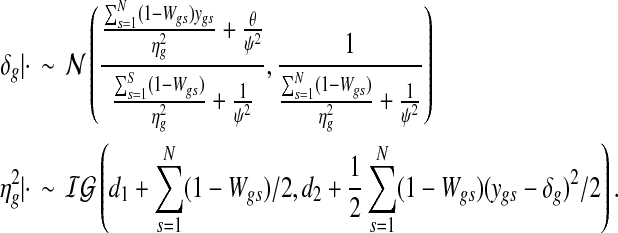The extended tail parameters in the Uniform component is updated as follows:

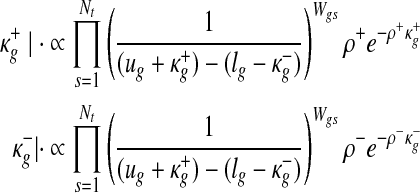and the mixing proportion is drawn from

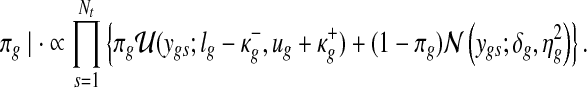Finally, the latent variables {W_gs} are updated from Bernoulli distribution with success probability

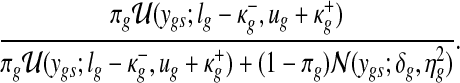2.4.3. Breakpoint arrangement update by reversible jump MCMC

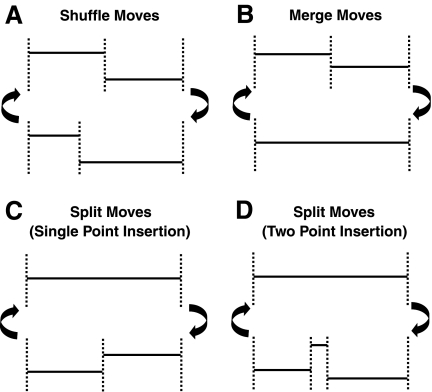
The most challenging part of the sampling steps is altering the segment arrangement in the copy number data because it involves taking transdimensional moves. Four types of arrangement changes are suggested: (A) shuffling of existing breakpoints, (B) merging of two adjacent segments, (C) spliting of an existing segment by single point insertion, and (D) spliting of an existing segment by two-point insertion. These moves will be attempted at randomly chosen locations with corresponding probability of (0.1, 0.4, 0.1, 0.4). The choice of these probabilities was made in a way that the sampler attempts proposals for transdimensional moves more often, increasing the acceptance rates in the sampling. In our test runs, it was found that the two-point insertion move is able to capture short length segments spanning five or less genes better than the single point insertion. This move resembles the operation of circular binary segmentation algorithm (Olshen et al., 2004) where an arc is chosen from a circular band, i.e., chromosome with both ends tied to one another, for testing of differential copy number changes.

One can move an existing boundary point left or right, altering membership of the genes on the borderline into either side of the two adjacent segments. This move will solely change the likelihood without changing the dimension of the parameter space, since it retains the same number of breakpoints (Fig. 2A). For this update, an existing boundary point is randomly selected, and a new location is proposed by randomly shifting the current location. The acceptance criterion is simply the likelihood ratio of the two adjacent segments (Metropolis-Hastings).

FIG. 2.

Four types of breakpoint arrangement changes. Types B–D involve trans-dimensional moves.

The more challenging updates are adding and removing boundary points. These moves are called split and merge moves (Fig. 2B–D). Since merge moves work exactly the opposite way split moves operate, only the split moves will be elaborated. There are two types of split moves, one in which a single boundary point is added inside a randomly chosen segment, and another in which two-points are added so that resulting range flanked by the two new points form a new segment, giving three daughter segments for the chosen segment. Single point insertions will add one additional mean parameter and one additional breakpoint, increasing the model parameter dimension by two, while two-point insertions will add twice as many parameters, adding the dimension by four.

The single point insertion is discussed first. Updates are attempted at randomly chosen locations within each sample. A new point p* is poposed so that p_{s(t − 1)} < p* < p_st for some 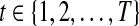. This additional point divides an existing segment with mean copy number μ_ts into two distinct daughter segment means, requiring the specification of two new mean copy number 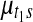and 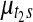in place of μ_ts. As there is an increment of dimension by one parameter in each sample, the two new mean values are proposed so as to satisfy

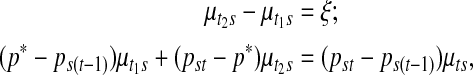where 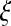is a random number generated from a Gaussian proposal 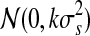for dimension matching purposes, where the constant k is adjusted in a way that will retain a sufficient rate of acceptance. This update complies with the detailed balance condition of the reversible jump MCMC (Green, 1995). This proposal is equivalent to specifying the mean values for the two daughter segments:

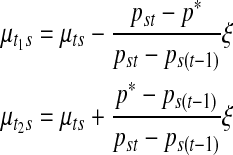This inverse relationship is used for the opposite move for merging. Notice that this transdimensional move has a unit Jacobian since the transformation 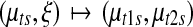is orthonormal. Then the Metropolis-Hastings ratio for the acceptance of the new proposal becomes

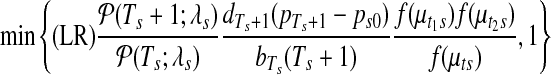where LR denotes likelihood ratio and f (·) refers to the Uniform-Gaussian prior distribution for the segmental means.

The second type of split move proceeds by randomly selecting a segment and proposes two middle points 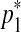and 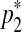in a way that every one of the three resulting segments (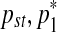), (), 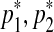and (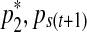) contains at least one probe. This split move creates three segments, hence a single mean parameter needs to be divided into three daughter means, namely, 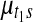, , 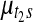and 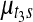, such that

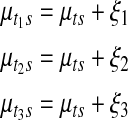subject to

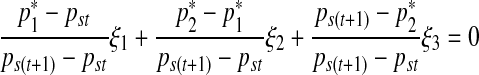As in the previous case, this relationship can be inversely translated into

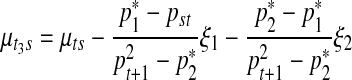Unlike in the single point insertion case, this parametrization comes with a non-unit Jacobian 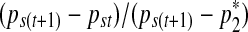. With proposal of (ξ₁, ξ₂) from Gaussian kernel, the Metropolis-Hastings ratio for the acceptance of new proposal becomes

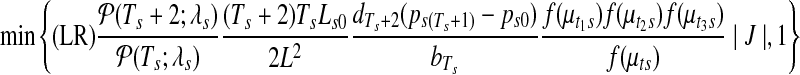where f (·) again refers to the Uniform-Gaussian prior distribution for the segmental means, and (L_s0, L) are the lengths of the chosen segment in sample s and the whole chromosome, respectively, and |J| is the Jacobian.

3. Results

3.1. Simulation study

Simulation studies were conducted to assess the performance of DLMM under varying circumstances. The major sources of variability affecting the detection of copy number-associated expression are the frequency of copy number aberration, factors affecting gene expression other than copy number (confounding hereafter), and signal-to-noise ratio in the gene expression data. Although the signal-to-noise ratio in the copy number data is also an important determinant in the success of DLMM, this parameter was set to 5 in known locations in order to reduce the complexity of simulation setting. Copy number data were generated for two sample sizes (15 and 30) and 1,000 genes, and gene expression data were generated for 100 genes equally spaced out on the hypothetical chromosome. This was repeated 20 times for each combination of the three factors and the sample size. DLMM was run for each set and the performance of DLMM was summarized by the average area under the curve (AUC) over the repeats. AUC was chosen as a comparable measure since the optimal cutoff based on the L-measure may differ across different datasets.

Background copy number data were first generated from Gaussian distribution with mean 0 and standard deviation 0.2. This setting assumes that the copy number data is transformed into log2 ratio of intensity values in the case of array CGH data. Copy number aberration was planted in windows of 20 genes in each sample at twenty known locations, with the cross-sample frequency ranging from 10% to 30%. If a gene was included in this event in a specific sample, the corresponding gene expression measurement was generated from Gaussian distribution with mean equal to standard deviation 0.2 multiplied by a chosen signal-to-noise ratio (1, 2, or 3), otherwise drawn from Gaussian distribution with mean 0 and standard deviation 0.2. The choice of mean and variance parameters had little impact on the final simulation results. In order to add gene expression changes due to confounding, expression values for the genes with normal copy numbers were altered in randomly selected samples with the same effect size with the copy number-associated expression. This confounding effect was inserted with frequency ranging from 10% to 40%.

Table 1 summarizes the results under the variety of situations considered in the simulation. Generally, AUC of the ROCs tended to be higher in the data sets of the larger sample size (30) than those of the smaller sample size (15), and the same trend was observed for stronger signal-to-noise ratio in the gene expression data. Also, it is obvious that the increasing frequency of copy number aberration results in greater AUC of the ROC curve, i.e. improved detection of copy number-associated expression, when the signal-to-noise ratio and the confounding effect are fixed. Similarly, when the signal-to-noise ratio and the frequency of copy number aberration are fixed, more confounding effect led to reduced ROC for detecting the events. Overall, the simulation study shows that signals as low as 10% can be recovered in the presence of a wide range of confounding effect with a fairly good chance (AUC of the ROCs ranging from 0.7 to 0.8), but it also warns that both the confounding and the frequency of copy number aberration are important factors to be considered in the practical application.

Table 1.

Area Under the Curve (AUC) of Receiver Operating Characteristic (ROC) in the Simulation Data Sets

	N = 15	Confounding				N = 30	Confounding
CNA	S/N = 1	10%	20%	30%	40%	S/N = 1	10%	20%	30%	40%
	10%	0.826	0.791	0.756	0.736	10%	0.840	0.817	0.789	0.775
	20%	0.835	0.807	0.784	0.747	20%	0.844	0.824	0.789	0.771
	30%	0.848	0.815	0.792	0.779	30%	0.861	0.826	0.783	0.745

CNA	S/N = 2	10%	20%	30%	40%	S/N = 2	10%	20%	30%	40%
	10%	0.886	0.864	0.833	0.800	10%	0.914	0.900	0.878	0.828
	20%	0.899	0.865	0.840	0.828	20%	0.910	0.903	0.881	0.839
	30%	0.916	0.902	0.880	0.868	30%	0.926	0.907	0.877	0.860

CNA	S/N = 3	10%	20%	30%	40%	S/N = 3	10%	20%	30%	40%
	10%	0.923	0.909	0.869	0.848	10%	0.921	0.905	0.871	0.859
	20%	0.931	0.908	0.873	0.848	20%	0.916	0.915	0.880	0.866
	30%	0.928	0.916	0.891	0.868	30%	0.915	0.911	0.885	0.870

For each case with 15 or 30 samples, simulation data were generated 20 times for 1,000 genes with varying signal-to-noise ratio, frequency of copy number aberration, and confounding effect of expression change not related to copy number aberration.

3.2. Breast cancer cDNA microarray data

The proposed method was applied to the breast cancer data in Pollack et al. (2002). 5581 genes were selected from 6095 genes in the original data, meeting the requirement that every gene in the filtered data has missing values in 30% or less of the 37 samples in both copy number and gene expression data. This is a slightly more stringent filtering compared to the procedure in van Wieringen and van de Viel (2008). Median centering was applied to both copy number and gene expression data. Standard deviation of each sample was adjusted to the median standard deviation (SD) across the 37 tumor samples in the copy number data (SD = 0.27).

Using Pollack data has several advantages. First, the data was generated using the same cDNA microarray platform of ∼8,000 clones (300–500 bp long on average) for both copy number and gene expression data. Second, the clones in this array platform represent Unigene clusters and their homologue EST sequences, with average inter-clone distance of 0.5 million bp, providing genome-wide coverage despite the modest resolution. Interestingly, nearly half the known oncogenes reported in cancer gene census of Futreal et al. (2004) are included in this set, and thus the impact of copy number on expression changes can be directly assessed in this data. Third, previously proposed methodologies including GCSM and vWvW have been tested on this data set, and therefore it serves as a good benchmark data set to compare the performance.

3.2.1. Prior elicitation and convergence of MCMC

Noninformative priors were specified wherever possible. To be precise, priors for the variance parameters in the copy number data were set at b₁ = b₂ = a₁ = a₂ = 0.01. Prior parameters for the genome-wide mean copy number parameter m_s for all samples were set at ν = 0 and ζ = 1. This prior can be considered as noninformative considering the fact that all copy number profiles have been equally scaled with standard deviation 0.27. Priors in the parameters for gene expression were set at θ = 0 and ψ² = 100 for the mean parameters 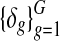in order to allow δ_g deviate from zero as explained earlier. d₁ = d₂ = 0.01 were set for the variance parameters 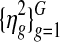, ρ+ and ρ− were set equal to the standard deviation of each gene for the tail of the Uniform component. All priors can be considered noninformative since the variability of prior has been set wider than the estimates from the raw data.

The mean number of copy number segments λ_s requires a more elaborate elicitation of prior. When noninformative prior was given (e.g., k₁ = 0.01 and k₂ = 0.01), segmentation results varied widely across the samples, and the need for elaborate prior elicitation was noted. A relatively large value was preferred for λ₀ in the Pollack data because each clone in this cDNA microarray is positioned every 500K bp, and thus the changes in a small number of clones may easily represent a segmental change. For this reason, k₁ = G/100 and k₂ = 0.1 were specified, where G is the number of genes on a chromosome. In general, (k₁, k₂) should be adjusted in different data sets. In a high-resolution data set such as high-throughput SNP array data, one can set moderate priors for λ_s, which also saves computation time because the number of parameter updates is proportional to the number of segments.

Samples were drawn from the posterior distribution using Markov chain Monte Carlo. 10,000 iterations were run with 1,000 initial period of burn-in. For the Pollack dataset with 5581 genes, the entire algorithm takes around 30 minutes. One can reduce the computation time even further if some of the nuisance parameters are integrated out or MLE estimates are plugged in using the EM algorithm (e.g., variance parameters whose posterior distribution has a closed form solution), but this was not pursued in this work. Convergence of Markov chain was visually monitored for randomly selected 50 copy number and gene expression parameters, namely (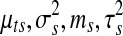) and (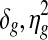). In five repeated runs, all selected parameters showed quick convergence to reasonable range of values within 200 initial burn-in period (not shown).

3.2.2. Regions with aberrant copy number

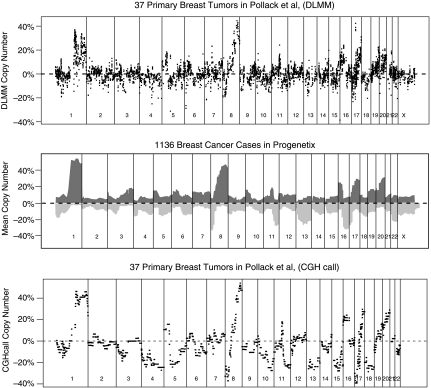
The estimated copy number probabilities of DLMM were validated by benchmarking its cross-sample average copy number probabilities against the average copy number profile of 1136 breast cancer cases stored in Progenetix CGH database (Baudis and Cleary, 2001). The latter can be regarded as a well-established copy number profile of breast cancer cases since the data consists of 40 independent studies of varying sample sizes. Figure 3 shows a graphical comparison between the two profiles. The DLMM copy number profile shown in the top panel has 937 clones (16.7% of 5581 genes) with aberrant copy number probabilities (0.2 in absolute value) concentrated in cytobands 1p32-p34, 1q, 8p21, 8q21-24, 16p11-12, 17q11 and 17q21-25, and 20q11-13. Copy number aberration in these regions have also been reported in more than 20% of the samples across studies in Progenetix as illustrated in the middle panel.

FIG. 3.

Average copy number probabilities of double-layered mixture model (DLMM) of the Pollack data, Progenetix data of 1136 breast cancer cases, and mean copy number calls by CGHcall.

The copy number probabilities of DLMM have also been compared to those computed by CGHcall (van de Wiel et al., 2007), which calculates similar posterior probability of amplification or deletion events using raw measurements and pre-existing segmentation results. The bottom panel of Figure 3 shows the average copy number probabilities computed from CGHcall. Although the average profiles in DLMM and CGHcall overlapped in most chromosomes, some of the calls for deletion events in CGHcalls were not found in DLMM (e.g., chromosomes 4, 5, 10, 15, and 18). However, no pronounced deletion events were found in all five chromosomes in the Progenetix data. By contrast, a Progenetix record of 20% deletion event in chromsome 13 was recovered more clearly by CGHcall than DLMM. Unless the benchmark set represents the general breast cancer population poorly, the overall comparison shows that DLMM and CGHcall make similar copy number calls with a caveat that the latter method can be more prone to false positive calls for the Pollack data.

3.2.3. Copy number-associated gene expression changes

Using the probability scores and the criterion-based gene selection, genes were selected if the score was 0.04 and above in absolute value in each sample separately. The threshold score 0.04 was chosen based on the minimal L-measure across multiple candidate cutoff points shown in Table 2. Following this step, 203 genes with copy number-associated over- or under-expression in near 10% frequency (3 out of 37 samples) were selected. The set of selected genes will be called DLMM signature from here on.

Table 2.

L-Measure Values with ν = 0.5 in Selecting Copy Number-Associated Gene Expression Changes

Threshold	0.01	0.02	0.03	0.04	0.05	0.10	0.20	0.50
L-Measure	121587	119772	119384	119350	119385	119496	119686	119857

Decimal points were rounded off.

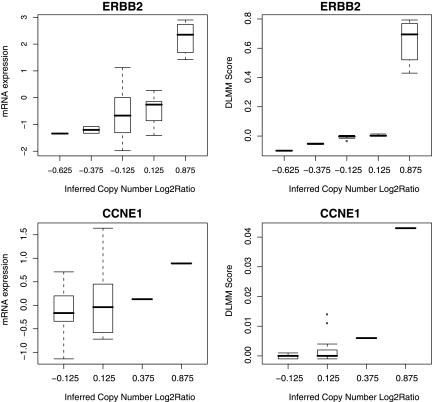
Congruent with the results using GCSM (Lipson et al., 2004) and vWvV tests (van Wieringen and van de Viel, 2008), many selected genes were found on the amplified regions on chromosomes 1, 8, and 17. Eight genes from the cancer gene census were included in the list: APC, FGFR1, EXT1, MYC, FANCA, MLLT6, ERBB2, and CLTC. As a clear demonstration of how the scoring works in DLMM, Figure 4 shows the case of ERBB2 located in the cytoband 17q11, where 8 samples (22% of 37) shows amplification events. All these samples were assigned the joint probability score 0.4 and above as shown in the top right panel of the figure. The other seven genes all show similar patterns (data not shown). Even though the proportion of actual oncogenes is low in the DLMM signature, it is interesting to observe that 152 genes (75%) are located within 500K bp distance from at least one oncogene, indicating a high degree of proximity of DLMM signature to the oncogenes. The observation that the expression of oncogenes themselves is not largely influenced by the copy number changes should not be surprising since the oncogenes are targets of more direct regulation controlled by other oncogenes and tumor suppressors than cytogenetic events.

FIG. 4.

Observed gene expression and double-layered mixture model (DLMM) score against copy number probabilities in ERBB2 and CYCLINE (CCNE1) genes. ERBB2 was selected by DLMM, genomic continuous submatrix (GCSM), and nonparametric tests as top candidate, while CYCLINE was selected only by the nonparametric tests. Other rank-based tests did not pick up CYCLINE either. However, copy number probabilities in CCNE1 is significantly high in only one out of 37 tumor samples.

In order to strengthen the biological interpretation of the DLMM signature, DAVID (Dennis et al., 2003) was used to examine the enrichment of Gene Ontology (GO) biological processes in the DLMM signatures. Table 3 lists the GO terms with the highest statistical significance. As expected, the genes related to the regulatory activities regarding cell death and cell cycle are deemed to be the main targets of copy number-associated expression changes. Despite its small number of hits, it is interesting to observe the term “positive regulation of epithelial cell proliferation,” as primary breast epithelial cells are the major targets for carcinogenesis. It is noted that this biological interpretation is quite different from that of the analysis of van Wieringen and van de Viel (2008), where a significantly greater number of genes (1225) were selected based on their hypothesis testing framework.

Table 3.

Gene Ontology Biological Process Terms Enriched in the DLMM Signature

Function	Counts	p-value	FDR
Apoptosis	22	8.8e-05	0.2%
Cell death	22	2.1e-04	0.4%
Regulation of apoptosis	16	6.4e-04	1.1%
Regulation of progression through cell cycle	14	4.2e-03	7.2%
Negative regulation of progression through cell cycle	8	7.2e-03	12.1%
Integrin-mediated signaling pathway	5	7.4e-03	12.3%
Positive regulation of epithelial cell proliferation	3	2.1e-02	31.3%
Negative regulation of apoptosis	7	3.7e-02	49.0%
Cell morphogenesis	11	4.2e-02	53.1%

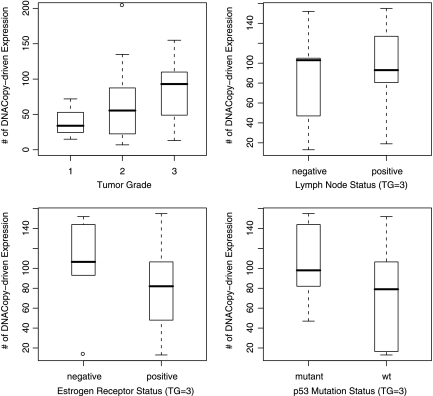
In addition to the GO term analysis, the DLMM signature is highly correlated with the clinical indicators of breast cancer provided in Pollack et al. (2002). To see this, the frequency of having a score above the threshold was calculated in each sample, i.e., 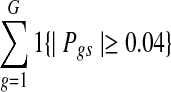, resulting in a sample-specific enrichment index of copy number-associated gene expression changes. This index was compared with the tumor grade, as well as lymph node status, estrogen receptor (ER) status, and p53 gene mutation status. The latter three were compared only for tumor grade 3 samples because almost all lymph node negative (and thus ER negative) samples were at lower tumor grade. Figure 5 shows the result. The top left panel illustrates that the samples in higher tumor grade have increased enrichment of the genes with copy number-associated expression. The top right panel shows that lymph node positive samples tend to have more copy number-associated gene expression changes, while the bottom left panel shows a similar trend for ER negative samples relative to ER positive ones. Also, the bottom right panel indicates that the mutation status of p53 gene is also positively correlated with the number of copy number-associated expression changes.

FIG. 5.

Sample-specific enrichment index of copy number associated gene expression is correlated with tumor grade and other clinico-pathological information related to breast cancer. The index was compared against lymph node status, estrogen receptor status, and p53 mutation information for the tumors in grade 3 only due to biased sampling of low-grade tumors with respect to the distribution of lymph node and estrogen receptor status.

3.2.4. Comparison

The DLMM signature was compared to the genes selected by using the GCSM and the vWvV tests.

GCSM searches for genes whose expression levels are linearly correlated with raw copy number levels in the local neighborhood of each gene. Using this method, Lipson et al. (2004) reported 174 genes with the GCSM score above 40, and this list includes five oncogenes in the cancer gene census (PRCC, SET, MLLT6, ERBB2, MYH9). Comparing the signatures, 53 genes (26% of DLMM) overlap with the DLMM signature, implying that there is a significant discrepancy between the two gene selection criteria. This is expected since the analysis in DLMM is one-to-one correspondence between the two data without regional analysis.

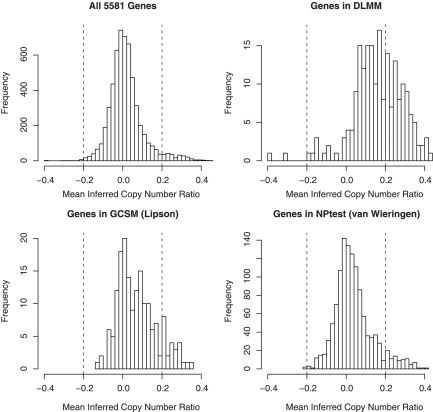
It was found that many genes unique to the GCSM signature are from regions where probabilistic copy number profiles show little aberrant behavior in probability, which means that high linear correlations can still be observed in regions with few significantly aberrant copy number changes. Figure 6 clearly shows this result. The top left panel shows the distribution of average copy number probabilities in all 5581 genes, and the top right and the bottom left panels show those in DLMM and GCSM signatures, respectively. These figures illustrate that the DLMM signature is enriched in regions with higher prevalence of significant copy number changes than GCSM in probability scale, enhancing the specificity of copy number-associated expression changes in the former. However, it should also be noted that the regional analysis feature of GCSM has recovered three new oncogenes (PRCC, SET, MYH9) that were not recovered by DLMM, indicating that there are target genes that DLMM have missed but the regional analysis of GCSM identified.

FIG. 6.

Comparison of the double-layered mixture model (DLMM) signature with the genomic continuous submatrix (GCSM) signature and the van Wieringen and van de Viel (vWvV) signature in terms of average copy number profiles. Many selected genes in the latter two sets are not enriched in regions with aberrant copy numbers.

The vWvV tests consists of a modified Cramér-Von Mises test and another test based on weighted Mann-Whitney statistic. These statistics are used to test the equality of gene expression distribution between samples with and without copy number gain or loss. Significance of the test statistics is computed based null distributions generated from permutations and probability computed by CGHcall are used as weighting factors in this process. vWvV tests have reported a total of 1225 genes (22% of 5581 genes) with FDR less than or equal to 10%. These include 37 genes from the cancer gene census, which accounts for 3% of the total. DLMM signature shares 125 (61% of DLMM) genes with this set, which is more than double the overlap with the GCSM signature. All eight oncogenes in the DLMM signature are in the common signature as well.

Despite the close overlap, the two gene signatures are vastly different in terms of size. A histogram of the mean copy numbers of all 1225 genes was drawn in the bottom right panel of Figure 6. The plot shows that the distribution of average copy number probabilities in 1225 genes is almost identical to the entire set of 5581 genes, without significant enrichment in aberrant copy number levels (e.g., 0.2 and above in absolute value).

To investigate this more closely, the estimated copy number probabilities were plotted against raw gene expression DLMM scores for 10 genes used for the power study in van Wieringen and van de Viel (2008). These genes were included in the vWvV signature and they were selected for the power study because these genes are candidates known to be associated with the development of breast cancer in the literature. Thus, the assumption made in their work is that these genes serve as the gold standard where copy number associated expression changes are supposed to be observed. Surprisingly, DLMM selected the ERBB2 gene only (a few genes were filtered out in the missing data filter). However, when the copy number profiles were revisited for the remaining nine genes inferred from both CGHcall method and DLMM, it was observed that either the proportion of samples with high copy number probability calls was low, or the expression distribution was not clearly separable between samples with and without aberrant copy number changes in probability (readers are referred to the supplemental information of van Wieringen and van de Viel [2008]).

This also corroborates with the previous observation in the DLMM analysis that the majority of oncogenes reported in cancer gene census were not directly associated with copy number-associated expression changes in DLMM analysis. See the example of CYCLINE gene (CCNE1) shown in the bottom panels of Figure 4. Although the pattern exhibits positive correlation between the two data, only two samples have copy number probability above 0.2. Not only such a small proportion is insufficient to represent the group of samples with aberrant copy number, but also the gene expression of those samples are not clearly separated from the other genes.

4. Discussion

In this work, a model-based method DLMM has been proposed for identifying coherent signals in the paired profiles of copy number and gene expression. DLMM consists of copy number probability estimation and copy number-associated differential expression analysis. The method achieves the goal by computing the joint probability of aberrant copy number and concordant differential gene expression between samples with and without copy number changes, and thus accounts for uncertainty in both data simultaneously. The analysis of the breast cancer data has shown that the copy number probabilities estimated by DLMM are largely congruent with a large-scale repository of breast cancer cases, and the selected signature of genes showing evidence of copy number associated expression are located in the vicinity of known oncogenes while many oncogenes were not directly under the influence themselves. The sample-specific index constructed from the selected genes was also correlated with the clinico-pathological information, highlighting the potential of this gene signature as a diagnostic or prognostic measure in cancer.

Joint inference for these two data sets is challenging, particularly because copy number data should be analyzed within each sample while gene expression data analysis is a comparison across samples. The reason the copy number data analysis is specific to individual samples is that, unlike properly normalized gene expression data, experimental copy number of a gene is not directly comparable across samples for two main reasons. First, every tumor biopsy results in a mixture of tumor and normal cells and the ratio of this mixture varies by sample. Thus with a common reference sample used in competitive hybridization, the copy number levels in each sample are affected by the proportion of tumor cells in the specimen, especially for genes with aberrant copy number. Hence, approaches that take the raw copy number data as measurements comparable across the samples (e.g., GCSM) (Lipson et al., 2004) may be subject to unexpected errors, and this was shown in the analysis of Pollack data. Second, relative copy number levels can be inferred more accurately if one considers the segmental patterns present in the copy number data, particularly because the signal-to-noise ratio is not often very high and thus local data may help identify signals that are weak but consistent in the neighborhood of each gene. For example, the median sample standard deviation in local windows of 100 clones was around 0.12, while the copy number ratio in the regions most frequently reported as amplified (1q, 8q) was as small as 0.35 in relevant samples. Therefore, those methods using sample-specific copy number probability calls such as DLMM and vWvV tests seem to be more relevant than linear correlation analysis.

Despite the differences in inferential techniques between DLMM and vWvV tests, the two methods share a common principle of distinguishing gene expression distributions between samples with and without aberrant copy numbers. vWvV tests adopt a nonparametric hypothesis testing framework for the hypothesis that the expression distributions are equal in the two groups of samples by incorporating uncertainty of copy number calls in each sample with a tuning algorithm for unbalanced grouping. However, it was shown that, through the examples of the oncogenes in the Pollack data, the method selects genes whose copy number calls are high in few samples only even after applying the tuning algorithm proposed in their work. DLMM takes a different approach, where the scores of copy number associated expression levels are computed for individual genes in each sample and the frequency that the score is above a chosen threshold across the samples is used for final selection of relevant events. This approach seems more relevant than both vWvV and GCSM in the joint analysis because copy number associated gene expression changes is a relatively rare event compared to direct gene regulation.

DLMM can easily be extended to tumor-normal comparisons or comparisons between different types of tumors by changing the way the final joint probability is calculated from the latent variables Z and W. In tumor-normal case, one can perform a semi-supervised estimation by making the normal samples contribute to the estimation of parameters in the mixture component for samples without aberrant copy number levels, i.e., (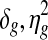) with 100% chance by fixing W = 0 since normal cells are supposed to have little copy number aberration. In tumor-tumor comparisons, one should keep track of copy number changes in the two groups separately, and select genes whose copy number-associated expression changes are unique in either group. DLMM can also be used for the data where more than a single copy number probe or clone can be mapped to a gene in the expression data. The segmentation applies to high-resolution arrays exactly the same way the Pollack data was analyzed in this work, and one can still score the coherent signal in the two data by defining multiple W variables for each pair of copy number probe and gene expression probe.

Acknowledgments

We thank Wessel van Wieringen and Mark van de Viel for sharing their data. H. Choi is grateful to Dr. Alexey Nesvizhskii for his support of this research. D. Ghosh would like to acknowledge the support of the Huck Institute for Life Sciences and R01 GM72007.

Disclosure Statement

No competing financial interests exist.