Abstract
Identifying genes (biomarkers) and predicting the clinical outcomes with censored survival times are important for cancer prognosis and pathogenesis. In this article, we propose a novel method with L1 penalized global AUC summary maximization (L1GAUCS). The L1GAUCS method is developed for simultaneous gene (feature) selection and survival prediction. L1 penalty shrinks coefficients and produces some coefficients that are exactly zero, and therefore selects a small subset of genes (features). It is a well-known fact that many genes are highly correlated in gene expression data and the highly correlated genes may function together. We, therefore, define a correlation measure to identify those genes such that their expression level may be low but they are highly correlated with the downstream highly expressed genes selected with L1GAUCS. Partial pathways associated with the correlated genes are identified with DAVID (http://david.abcc.ncifcrf.gov/). Experimental results with chemotherapy and gene expression data demonstrate that the proposed procedures can be used for identifying important genes and pathways that are related to time to death due to cancer and for building a parsimonious model for predicting the survival of future patients. Software is available upon request from the first author.
Key words: biology, cancer genomics, combinatorial optimization, DNA arrays, functional genomics, gene clusters, gene expression, HMM, statistics
1. Introduction
Because of the differences at molecular levels, patients may respond very differently to the same treatment. It is, therefore, very important to identify a small group of genes and pathways associated with survival. Gene selections with survival data in the statistical literature are mainly within the penalized Cox or additive risk regression framework (Tibshirani, 1996, 1998; Gui and Li, 2005; Van Houwelingen et al., 2006; Segal, 2006; Ma and Huang, 2007; Liu, 2007). The L1 and Lp (p < 1) penalized Cox regressions do simultaneous gene (feature) selection and survival prediction, and have been extensively studied in the bioinformatics literature. Cox proportional hazards model is a semi-parametric model in which the baseline hazard is estimated nonparametrically, while the covariate (gene) effect is estimated by partial log likelihood maximization. The performance of the survival model is evaluated by the global area under the ROC curve summary (GAUCS) (Heagerty and Zheng, 2005).
The receiver operating characteristic (ROC) curve was originally proposed for evaluating the performance of binary classification (Bradley, 1997). An ROC curve provides complete information on the set of all possible combinations of true-positive and false-positive rates, but is also more generally useful as a graphic characterization of the magnitude of separation between the case and control distributions. AUC is known to measure the probability that the marker value (score) for a randomly selected case exceeds the marker value for a randomly selected control and is directly related to the Mann-Whitney U-statistic (Pepe, 2003, 2005). For survival data, a survival time can be viewed as a time-varying binary outcome. Given a fixed time t, the instances that ti = t are regarded as cases and samples with ti > t are controls. The global AUC summary is then defined as GAUCS = P(Mj > Mk|tj < tk), which indicates that the subject who died earlier has a larger value with the score, where M is a score function. Heagerty and Zheng (2005) have shown that GAUCS is a weighted average of the area under time-specific ROC curves. When the survival model is measured with the global AUC summary (GAUCS), it is reasonable to build a model with direct GAUCS maximization. Due to the very high-dimensional space of the covariates (genes), L1 penalized global AUC summary (L1GAUCS) maximization is proposed for simultaneous gene selection and survival prediction.
It is a known fact that genes are highly correlated in gene expression data. However, standard statistical learning methods can only select a small subset of highly differentiated genes that lead to either the highest prediction accuracy or the smallest p-values, while most biologists recognize that the magnitude of differential expression does not necessarily indicate biological significance. From the biological prospective, even a very small change in expression of particular gene may have dramatic physiological consequences if the protein encoded by this gene plays a catalytic role in a specific cell function. Many other downstream genes may amplify the signal produced by this truly interesting gene, thereby increasing their chance to be selected by current gene selection methods. For a regulatory gene, however, the chance of being selected by current methods may diminish as these methods can only select downstream genes with bigger changes in expression. The characteristic of the regulatory genes is that their gene expression changes may be low, but they are highly correlated with the downstream highly expressed genes. We will catch those genes with our newly defined correlation measure.
This goal of the current study is to develop a computationally affordable and well-behaved estimating approach, which can effectively identify the genes for right censored survival data with L1 penalized GAUCS (L1GAUCS) maximization. In Section 2, we formulate the penalized GAUCS model and propose an efficient algorithm for simultaneous feature selection and survival prediction. The correlation measure for catching the upstream regularized genes is also introduced. The proposed approach is demonstrated with chemotherapy and gene expression examples in Section 3. Concluding remarks are discussed in Section 4.
2. L1 Penalized Global Auc Summary Maximization
Consider we have a set of n independent observations 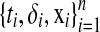 , where δi is the censoring indicator and ti is the survival time (event time) if δi = 1 or censoring time if δi = 0, and
, where δi is the censoring indicator and ti is the survival time (event time) if δi = 1 or censoring time if δi = 0, and 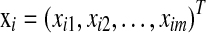 is the m-dimensional input vector of ith sample. Let
is the m-dimensional input vector of ith sample. Let 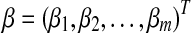 be a vector of regression coefficients, and we define
be a vector of regression coefficients, and we define 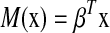 to be the risk score function, also denoting
to be the risk score function, also denoting 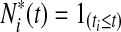 and the corresponding increment
and the corresponding increment 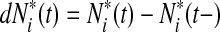 . The time-dependent sensitivity and specificity are defined by sensitivity
. The time-dependent sensitivity and specificity are defined by sensitivity 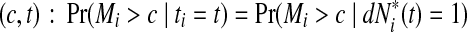 and specificity
and specificity 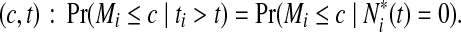 Here sensitivity measures the expected fraction of subjects with a marker greater than c among the subpopulation of individuals who die (cases) at time t, while specificity measures the fraction of subjects with a marker less than or equal to c among those who survive (controls) beyond time t. With this definition, a subject can play the role of a control for an early time, t < ti, but then play the role of case when t = ti (Heagerty and Zheng, 2005). Then, ROC curves are defined as
Here sensitivity measures the expected fraction of subjects with a marker greater than c among the subpopulation of individuals who die (cases) at time t, while specificity measures the fraction of subjects with a marker less than or equal to c among those who survive (controls) beyond time t. With this definition, a subject can play the role of a control for an early time, t < ti, but then play the role of case when t = ti (Heagerty and Zheng, 2005). Then, ROC curves are defined as 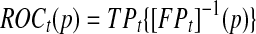 for
for 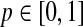 , and the area under the ROC curve for time t is
, and the area under the ROC curve for time t is 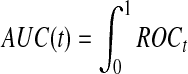
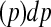 , where TPt and FPt are the true and false positive rate at time t respectively, and
, where TPt and FPt are the true and false positive rate at time t respectively, and 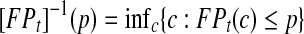 . ROC methods can be used to characterize the ability of a marker to distinguish cases at time t from controls at time t, However, in many applications there is identified no prior time t, thus a global accuracy summary is defined by averaging over t:
. ROC methods can be used to characterize the ability of a marker to distinguish cases at time t from controls at time t, However, in many applications there is identified no prior time t, thus a global accuracy summary is defined by averaging over t:
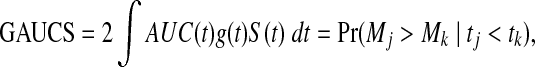 |
which indicates the probability that the subject who died (cases) at the early time has a larger value of the marker, where S(t) and g(t) are the survival and corresponding density functions, respectively.
We can define the optimization problem
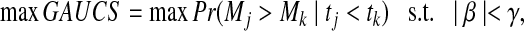 |
(1) |
where 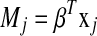 and
and 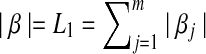 . The ideal situation is that
. The ideal situation is that 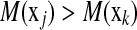 or
or 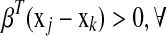 couple
couple 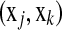 with corresponding times tj < tk (or j < k) and δj = 1. If we allow margins between couples
with corresponding times tj < tk (or j < k) and δj = 1. If we allow margins between couples 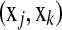 for all j < k and take a quadratic loss function, the optimization problem can be defined as
for all j < k and take a quadratic loss function, the optimization problem can be defined as
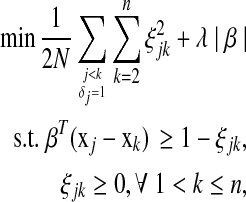 |
(2) |
where 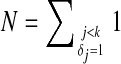 is the number of items with j < k and δj = 1. When ties in the event times are presented, variables associated with each tied time appear in the constraints independently. Solving equation (2) is equivalent to solving the following problem:
is the number of items with j < k and δj = 1. When ties in the event times are presented, variables associated with each tied time appear in the constraints independently. Solving equation (2) is equivalent to solving the following problem:
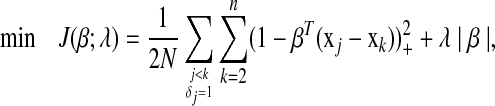 |
(3) |
where Z+ is Z if Z > 0, and 0 otherwise. Note that |β| is not differentiated at 0, we therefore introduce the subdifferential concept (Hiriart-Urruty and Lemaréchal, 2001) for the derivatives. The subdifferential of a convex function 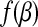 is defined as
is defined as
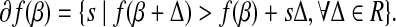 |
(4) |
In other words, a subdifferential is a range of slopes s such that the line through 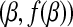 with slope s contains the graph of f in its upper half space. This is a set-valued generalization of the normal derivative and reduce to the normal derivative
with slope s contains the graph of f in its upper half space. This is a set-valued generalization of the normal derivative and reduce to the normal derivative 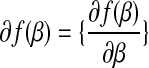 .
. 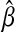 is a global minimizer of a convex function
is a global minimizer of a convex function 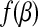 if and only if
if and only if 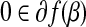 .
.
To find the optimal solution of β, we first rewrite the first part 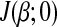 of equation (3) as a function of the i-th parameter βi and treat remaining parameters
of equation (3) as a function of the i-th parameter βi and treat remaining parameters 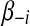 as fixed constants. Let
as fixed constants. Let 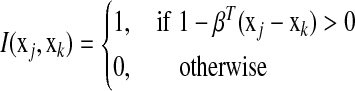 , we have
, we have
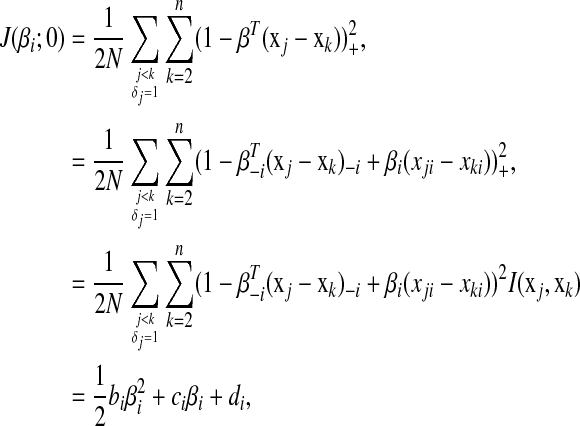 |
(5) |
where
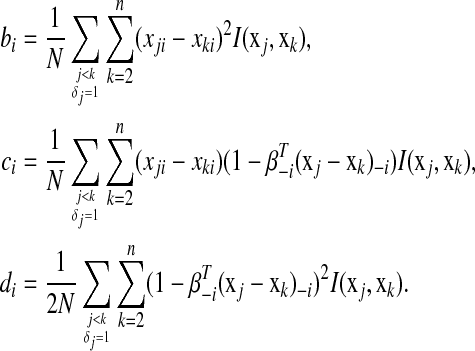 |
Equation (5) is a quadratic function of βi, the first order derivative w.r.t. βi is
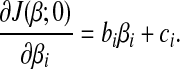 |
Then the subdifferential of 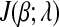 w.r.t. βi is
w.r.t. βi is
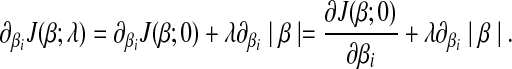 |
(6) |
According to equation (4), the subdifferential of the L1 penalty is
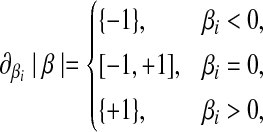 |
We have
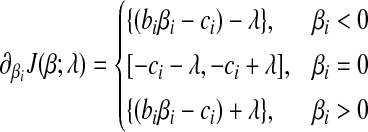 |
(7) |
The subdifferential 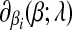 is a piece-wise monotonically increasing linear function with the slope bi > 0. To find the global minimum, we set
is a piece-wise monotonically increasing linear function with the slope bi > 0. To find the global minimum, we set 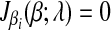 . The value of ci (relative to λ) controls which part of
. The value of ci (relative to λ) controls which part of 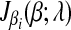 is set to zero. (1) if ci < −λ, then −ci − λ > 0, so that βi < 0 for the zero-intercept. Solving biβi − (ci + λ) = 0, we have
is set to zero. (1) if ci < −λ, then −ci − λ > 0, so that βi < 0 for the zero-intercept. Solving biβi − (ci + λ) = 0, we have 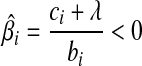 . (2) if
. (2) if 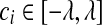 , then
, then 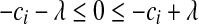 , or
, or 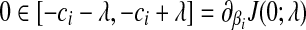 . Hence, the global minimum occurs at
. Hence, the global minimum occurs at 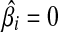 . (3) if ci > λ, then −ci + λ < 0, so that the zero intercept is greater than zero, we set biβi − ci + λ = 0, for the global minimum. we have
. (3) if ci > λ, then −ci + λ < 0, so that the zero intercept is greater than zero, we set biβi − ci + λ = 0, for the global minimum. we have 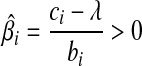 . Putting these results together, the optimal solution
. Putting these results together, the optimal solution 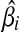 is a piece-wise linear, monotonically increasing function of ci:
is a piece-wise linear, monotonically increasing function of ci:
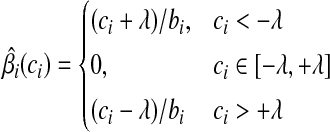 |
(8) |
Therefore, we can update the coefficient of each input with fixed left coefficients. The coordinator-wised algorithm is very easy to implement and converges in 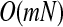 .
.
In gene expression analysis, after we select a small subset of downstream genes with bigger change in expression, we will identify those regularized genes that may have low expression but are highly correlated with each of the highly expressed genes using a newly defined correlation measure (R). 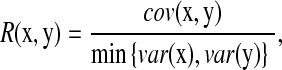 where
where 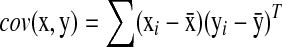 is the standard covariance and
is the standard covariance and 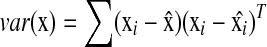 is the variance. Based on this definition, we have
is the variance. Based on this definition, we have 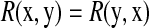 , and R = 0 when x and y are independent. This R is different from the standard correlation coefficient
, and R = 0 when x and y are independent. This R is different from the standard correlation coefficient 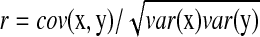 in its denominator. It can catch the genes that have very small change in expression but are highly correlated with significant expressed (downstream) genes. For instance, given
in its denominator. It can catch the genes that have very small change in expression but are highly correlated with significant expressed (downstream) genes. For instance, given 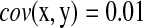 ,
, 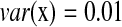 , and
, and 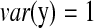 , we have R = 1 but r = 0.1. Therefore, we can identify several highly correlated gene clusters with R and find the related partial pathways associated with these gene clusters using DAVID (http://david.abcc.ncifcrf.gov/).
, we have R = 1 but r = 0.1. Therefore, we can identify several highly correlated gene clusters with R and find the related partial pathways associated with these gene clusters using DAVID (http://david.abcc.ncifcrf.gov/).
3. Computational Results
3.1. Breast cancer prognosis and chemotherapy data
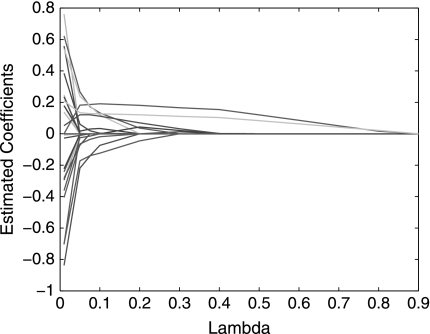
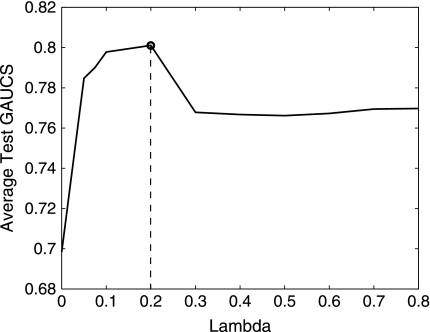
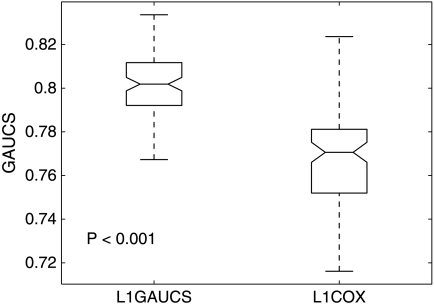
Our first example is a publicly available data with 253 breast cancer patients (Wolberg et al., 1999). The data set contains patients' 32 nuclear features, survival time, and chemotherapy information. The 32 features include the mean, standard deviation, and maximum (worst) values of ten cytological nuclear measurement of size, shape, and texture taken from the patient's breast by a non-surgical fine needle aspirate procedure, together with the tumor size excised from the patient's breast during surgery and lymph node metastasis. We want to identify a subsect of features that can predict the survival of the patients. Ten-fold cross-validations are used to evaluate the performance of the proposed method. To prevent the bias coming from a specific partition, we divide the data into ten-folds 100 times and overall performance of the model is evaluated. The optimal path of the coefficient estimate and the average test GAUCS with different λ are given in Figures 1 and 2, respectively. Figures 1 and 2 show that the proposed method reaches maximal global AUC summary at λ* = 0.2 and all βi's are zero, when λ = 0.9. The selected features with λ* = 0.2 and the comparison of the proposed methods and penalized Cox regression L1COX (Gui and Li, 2005) are given in Table 1. Table 1 shows that lymph node status, tumor size, and the largest perimeter are strongly associated with death. The larger those three variables, the later the breast cancer stage and, therefore, the less the survival time. This is consistent with common sense. Other nuclear features selected with L1GAUCS and L1COX methods are not totally consistent, but most of them are either the same or related. The performance comparison with 100 partitions is given in Figure 3. L1GAUCS performs statistically significant better than L1Cox methods with two more features. The optimal λ* = 0.2 and average test GAUCS = 0.8 with L1GAUCS, and the optimal λ* = 4.5 and the average test GAUCS = 0.77 with L 1COX method.
FIG. 1.
Optimal path of the coefficients.
FIG. 2.
Average test GAUCS with different lambda values.
Table 1.
Selected Features with Different Survival Model
| L1GAUCS |
L1COX |
||
|---|---|---|---|
| Features | Estimators | Features | Estimators |
| Texture | −0.191 | Perimeter | 0.472 |
| Concave point | −0.079 | Symmetry | −0.42 |
| SD compactness | 0.083 | Fractal dimension | −0.55 |
| Largest perimeter | 0.316 | SD radius | 0.78 |
| Tumor size | 0.168 | Tumor size | 0.188 |
| Lymph node status | 0.134 | Lymph node status | 0.301 |
| Worst smoothness | 0.759 | ||
| Worst concavity | 0.788 | ||
| λ* = 0.2 | GAUCS = 0.80 | λ* = 4.5 | GAUCS = 0.774 |
FIG. 3.
Test GAUCS with different methods.
3.2. MCL microarry data
A survival study for mantle cell lymphoma (MCL) patients with gene expression data was reported by Rosenwald et al. (2003). The primary goal of this study was to discover genes that have good power to predict the patients' survival risk. Among 101 untreated patients with no history of previous lymphoma included in this study, 92 were classified as having MCL based on established morphologic and immunophenotypic criteria. Survival times of 64 patients were available, and the other 28 patients were censored. The median survival time was 2.8 years (range, 0.02–14.05 years). Lymphochip DNA microarrays were used to quantify mRNA expressions in the lymphoma samples from the 92 patients. The gene expression data contains expression values of 8810 genes. Utilizing a two-step approach, we first built marginal L1GAUCS models with the expression levels for each gene as a one-dimensional input. All genes with marginal p-values less than 0.1 are then included in the second step L1GAUCS survival model. Similar approach has been extensively used in previous studies (Ma and Huang, 2007). Out of 8810 genes, 1721 are identified to be marginally significant at the 0.1 level. We then build a L1GAUCS model with the 1721 genes. L1GAUCS includes a regularization parameter, controlling the complexity of the model and the sparsity of the model parameters, which must be chosen by the user or alternatively optimized in an additional model selection stage. However, we cannot use the same cross-validation estimate for both model selection and performance evaluation, as this would introduce a strong selection bias in favor of the existing L1GAUCS model. A nested cross-validation procedure is therefore used instead. Ten-fold cross-validation is used for performance evaluation in the “outer loop” of the procedure, in each iteration of which model selection is performed individually for each classifier based on a separate leave-one-out cross-validation procedure using the training data only. Because of the small sample size and high-dimensional genes, leave-one-out cross-validation in the “inner loop” is likely to provide a reliable performance measure for model selection. Even though this nested cross-validation is computationally expensive, it provides an almost unbiased assessment of generalization performance as well as a sensible automatic method of setting the value of the regularization parameter. The optimal regularized parameter is λ = 0.3, and the average test GAUCS = 0.84 with only six genes with nonzero estimates. Genes selected with the L1GAUCS survival prediction method are listed in Table 2.
Table 2.
Selected Genes with Nonzero Estimates
| UniGene ID | Genes |
|---|---|
| Hs.497741 | Centromere protein F, 350/400 ka (mitosin) |
| Hs.156346 | Topoisomerase (DNA) II alpha 170 kDa |
| Hs.532755 | Likely ortholog of mouse gene trap locus 3 |
| Hs.241517 | Polymerase (DNA directed), theta |
| Hs.142442 | HP1-BP74 |
| Hs.521101 | Similar to Williams-Beuren syndrome critical region protein 19 |
The description of the six genes can be found at the NCBI website (www.ncbi.nlm.nih.gov). Gene Hs.497741 (CENPF) encodes a protein associated with the centromere-kinetochore complex, 3210 amino acids (aa), 367594 Da, containing internal repeats, coiled-coil (potential) and NLS (potential). Over-expression of CENPF mRNA was associated with larger tumor size as well as estrogen receptor (ER)–negative, high-grade tumors. CENPF mRNA expression correlated significantly with worse overall survival and a decreased probability of remaining metastasis-free, which may indicate that CENPF itself is a good candidate for biomarker for MCL. Studies show that gene Hs.156346 (TOP2A) is a proliferation marker, an indicator of drug sensitivity, and a prognostic factor in mantle cell lymphoma. This gene encodes a DNA topoisomerase, an enzyme that controls and alters the topologic states of DNA during transcription. The gene encoding this enzyme functions as the target for several anticancer agents, and a variety of mutations in this gene have been associated with the development of drug resistance. Reduced activity of this enzyme may also play a role in ataxia-telangiectasia. Gene Hs.241517 (DNA Pol theta) has a specialized function in lymphocytes and in tumor progression. Three other genes (Hs.532755, Hs.142442, and Hs.521101) are also either directly associated with lymphoma or important in tumor proliferation.
We then identify the highly correlated genes with |R| > 0.9 for each of the six selected genes and find the associated partial pathways for the highly correlated genes with DAVID. The associated pathways are given in Table 3. Pathways identified in Table 3 play a crucial role in regulating the growth and survival of MCL. For instance, TGF-beta signaling pathway is involved in many cellular processes in both the adult organism and the developing embryo including cell growth, cell differentiation, apoptosis, cellular homeostasis, and other cellular functions. Studies (Moller et al., 2007) showed that upregulation of the TGFbeta signaling pathway has implications for hemopoietic cell growth and chronic myeloid leukemia. P53 signaling is another well-known cancer-related pathway. The tumor-suppressor protein p53 exhibits sequence-specific DNA-binding, directly interacts with various cellular and viral proteins, and induces cell cycle arrest in response to DNA damage. The p53-dependent pathways help to maintain genomic stability by eliminating damaged cells either by arresting them permanently or through apoptosis. p53, therefore, is frequently targeted by genetic alterations in MCL patients. Most other survival-related pathways identified are also related to either the cell cycle machinery and senescence, DNA damage response pathways, or cell survival signals. In this article, we discuss cell cycle and MCL in more detail.
Table 3.
Survival-Related Pathways for Correlated Genes
| UniGene ID | Associated KEGG pathways |
|---|---|
| Hs.497741(314) | Cell cycle (13) |
| TGF-beta signaling pathway (6) | |
| Ubiquitin mediated proteolysis (7) | |
| p53 signaling pathway (5) | |
| One carbon pool by folate (3) | |
| Hs.156346 (228) | Wnt signaling pathway (12) |
| Purine metabolism (11) | |
| MAPK signaling pathway (15) | |
| Apoptosis (8) | |
| Insulin signaling pathway (10) | |
| Cell cycle (14) | |
| Hs.532755 (270) | Cell cycle (12) |
| TGF-beta signaling pathway (6) | |
| p53 signaling pathway (5) | |
| Adherens junction (5) | |
| Tight junction (5) | |
| Hs.241517 (89) | Cell cycle (5) |
| p53 signaling pathway (3) | |
| Hs.142442 (34) | Pathogenic Escherichia coli infection—EPEC (2) |
| Pathogenic Escherichia coli infection—EHEC (2) | |
| Hs.521101 (1) | None |
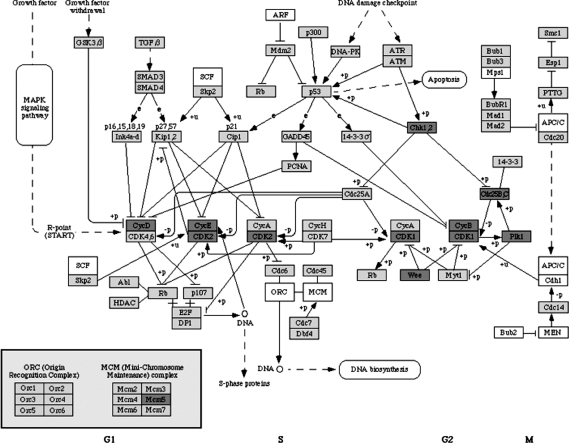
KEGG cell cycle regulatory pathway and associated correlated genes are given in Figure 4 and Table 4, respectively. Regulation of the cell cycle involves steps crucial to the cell, including detecting and repairing genetic damage, and provision of various checks to prevent uncontrolled cell division. Thirteen genes identified on the pathway are over-expressed for patients with less survival time. All 13 genes are important in cell cycle regulation in MCL. Both Cyclin D1 (CCND1) and cyclin b1 are the key regulators of the cell cycle and are overexpressed in patients with a shorter survival time. Elevated levels of CCND1 expression in MCL cells may accelerate G1/S-phase transition of the cell and therefore tumor cell proliferation. Many studies suggest that CCND1 deregulation plays an important role in pathogenesis of MCL, and the level CCND1 expression appears to be directly correlated with the tumor cell proliferation rate in MCL. Both CDK1 (CDC2) and CDK2 are overexpressed in patients with a shorter survival time. They are the members of a large family of protein kinases that initiate the principal transitions of the eukaryotic cell cycle. Mutations in the CDKs and/or their inhibitors is associated with several forms of cancer. CDKs perform a common biochemical reaction, called “phosphorylation,” that activates or inactivates target proteins to orchestrate coordinated entry into the next phase of the cell cycle. The interaction of cyclins (b1, d1) and CDKs determines is a cell's progress through the cell cycle. Polo-like kinases (Plks) are important regulators of cell cycle progression during M-phase. Plks are involved in the assembly and dynamics of the mitotic spindle apparatus and in the activation and inactivation of CDK/cyclin complexes. Plk1 has a role in the regulation of tyrosine dephosphorylation of CDKs through phosphorylation and activation of Cdc25C. Other genes identified also play very importance roles in cell cycle. Many pharmacologic strategies targeting cell-cycle regulatory pathways have been proposed. Cyclin D1, CDKs, Plks, and other genes are all potential cancer drug targets.
FIG. 4.
KEGG pathway: cell cycle.
Table 4.
Correlated Genes on the Pathway
| Gene symbols | Gene names |
|---|---|
| CCND1 (cycD) | cyclin d1 |
| ccnb1 (cycB) | cyclin b1 |
| Plk1 | polo-like kinase 1 (drosophila) |
| CDK2 | cyclin-dependent kinase 2 |
| CDC25C | cell division cycle 25c |
| ywhaq | tyrosine 3-monooxygenase/tryptophan 5-monooxygenase activation protein, theta polypeptide |
| CDC2 (CDK1) | cell division cycle 2, g1 to s and g2 to m |
| WEE1 | wee1 homolog (s. pombe) |
| Ccne1 | cyclin e1 |
| RBX1 | ring-box 1 |
| MCM5 | mcm5 minichromosome maintenance deficient 5, cell division cycle 46 (s. cerevisiae) |
| CHEK1 | chk1 checkpoint homolog (s. pombe) |
| MCM2 | mcm2 minichromosome maintenance deficient 2, mitotin |
4. Conclusion
It is of great interest to develop sound computational techniques that are capable of both identifying disease-associated genes and related pathways, and predicting survival risks based on the selected genes. In this article, we have developed L1 penalized global AUC summary (L1GAUCS) maximization methods for gene (feature) selection, pathway identification, and survival prediction with right censored survival data and high-dimensional gene expression profiles. This is the first attempt to use the penalized global AUC maximization for survival analysis. We analyze the chemotherapy and MCL microarray data using the proposed approach. Empirical studies have showed that the proposed approach is able to identify the small subset of genes (features) with nice prediction performance.
Furthermore, it is well known that many genes are highly correlated in gene expression data. The standard supervised learning methods can only identify a small subset of independent genes with the highest prediction power. We have defined a novel correlation measure to identify those highly correlated genes. Most pathways and related genes we find have been shown to be associated with MCL in other studies.
We have found hundreds (or tens) of genes associated with each gene identified with L1GAUCS. Only a small number of genes are appeared on the partially known pathway. Other genes are left unexplored. We will explore the gene-gene interaction and causal relation among the correlated genes in a separate study.
Acknowledgments
We thank the associate editors and the anonymous referees for their constructive comments which helped improve the manuscript. Z. Liu was partially supported by grant 1R03CA128102-02 from the National Institute of Health. X. Chen was partly supported by NSF-0644366 CAREER award.
Disclosure Statement
No competing financial interests exist.
References
- Bradley A.P. The use of the area under the ROC curve in the evaluation of machine learning algorithms. Pattern Recog. 1997;30:1145–1159. [Google Scholar]
- Gui J. Li H. Penalized Cox regression analysis in the high-dimensional and low-sample size settings, with applications to microarray gene expression data. Bioinformatics. 2005;21:3001–3008. doi: 10.1093/bioinformatics/bti422. [DOI] [PubMed] [Google Scholar]
- Heagerty P.J. Zheng Y. Survival model predictive accuracy and ROC curves. Biometrics. 2005;61:92–105. doi: 10.1111/j.0006-341X.2005.030814.x. [DOI] [PubMed] [Google Scholar]
- Hiriart-Urruty J.B. Lemaréchal C. Fundamentals of Convex Analysis. Springer Verlag; Heidelberg: 2001. [Google Scholar]
- Liu Z. Cox's proportional hazards model with Lp penalty for biomarker identification and survival prediction. Proc. 6th Int. Conf. Machine Learn. Appl. 2007:624–628. [Google Scholar]
- Ma S. Huang J. Additive risk survival model with microarray data. BMC Bioinform. 2007;8:192. doi: 10.1186/1471-2105-8-192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moller G.M. Frost V. Melo J.V., et al. Upregulation of the TGFbeta signalling pathway by Bcr-Abl: implications for haemopoietic cell growth and chronic myeloid leukaemia. FEBS Lett. 2007;581:1329–1334. doi: 10.1016/j.febslet.2007.02.048. [DOI] [PubMed] [Google Scholar]
- Pepe M.S. The Statistical Evaluation of Medical Tests for Classification and Prediction. Oxford University Press; New York: 2003. [Google Scholar]
- Pepe M.S. Evaluating technologies for classification and prediction in medicine. Statist. Med. 2005;24:3687–3696. doi: 10.1002/sim.2431. [DOI] [PubMed] [Google Scholar]
- Rosenwald A. Wright G. Wiestner A., et al. The proliferation gene expression signature is a quantitative integrator of oncogenic events that predicts survival in mantle cell lymphoma. Cancer Cell. 2003;3:185–197. doi: 10.1016/s1535-6108(03)00028-x. [DOI] [PubMed] [Google Scholar]
- Segal M.R. Microarray gene expression data with linked survival phenotypes: diffuse large-B-cell lymphoma revisited. Biostatistics. 2006;7:268–285. doi: 10.1093/biostatistics/kxj006. [DOI] [PubMed] [Google Scholar]
- Tibshirani R. Regression shrinkage and selection via the lasso. J. R. Statist. Soc. B. 1996;58:267–288. [Google Scholar]
- Tibshirani R. The lasso method for variable selection in the Cox model. Statist. Med. 1997;16:385–395. doi: 10.1002/(sici)1097-0258(19970228)16:4<385::aid-sim380>3.0.co;2-3. [DOI] [PubMed] [Google Scholar]
- Van Houwelingen H.C. Bruinsma T. Hart A.A., et al. Cross-validated Cox regression on microarray gene expression data. Statist. Med. 2006;25:3201–3216. doi: 10.1002/sim.2353. [DOI] [PubMed] [Google Scholar]
- Wolberg W.H. Street W.N. Mangasarian O.L. Importance of nuclear morphology in breast cancer prognosis. Clin. Cancer Res. 1999;5:3542–3548. [PubMed] [Google Scholar]