Abstract
Purpose
The present study had two purposes: provide an illustration of use of the National Longitudinal Survey of Youth 1979 Children’s (CNLSY; U.S. Department of Labor, 2009) database and use the database to seek convergent evidence regarding the magnitude and significance of genetic effects influencing low and typical performers on measures of language, reading, and mathematics.
Methods
A kinship algorithm that assigned a degree of genetic relatedness to all available pairings was applied to the 1994 wave of the CNLSY sample. Four cognitive achievement outcomes related to language, reading, and mathematics were analyzed across the general sample as well as for children selected below the lowest 20th percentile.
Results
The tests of receptive vocabulary, decoding, reading comprehension, and mathematics all suggested estimates of group heritability and full sample heritability of moderate effect sizes, and all estimates were statistically significant. Furthermore, all estimates were within confidence intervals of previously reported estimates from twin and adoption studies.
Conclusion
The present study provides additional support for significant genetic effects across low and wide ranges of specific achievement. Moreover, this study supports that genetic influences on reading, language, and mathematics are generalizable beyond twin and adoption studies.
Keywords: NLSY, genetics, language
The National Longitudinal Survey of Youth 1979 (NLSY79) is a large-scale, nationally representative multipurpose panel survey of 12,686 men and women who were between the ages of 14 and 22 years of age on December 31, 1978 (Baker, Keck, Mott, & Quinlan, 1993). Annual interviews were conducted on the original sample from 1979 until 1994, after which biannual interviews were performed. The collection of this survey was initiated and sponsored by the U.S. Department of Labor to ascertain information about this cohort’s employment, education, training, and family experiences. More specifically, each survey round contained a core set of questions concerning the following topics: labor market experience, training investment, schooling, family income, health conditions, geographic residence and environmental characteristics, household composition, and marital and fertility histories (Center for Human Resource Research, 2006).
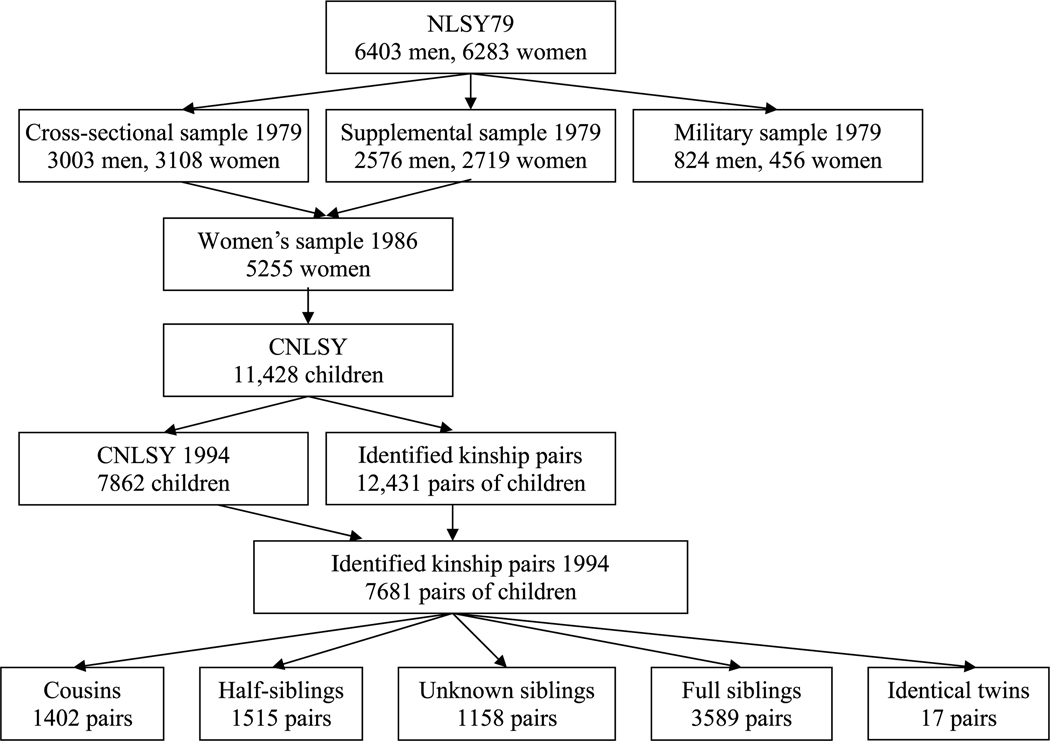
The sampling design of the original NLSY79 cohort was composed of three subsamples (see Figure 1): (a) a “cross-sectional sample” of 6,111 respondents who were representative of the non-institutionalized civilian segment of young people living in the United States in 1979 who were between the ages of 14 and 22; (b) a “supplemental sample” of 5,295 respondents of oversampled civilian Hispanic or Latino, Black, and economically disadvantaged White youth living in the United States in 1979 between the ages of 14 and 22; and (c) a “military sample” of 1,280 respondents who were enlisted in any branch of the military as of September 30, 1978, between the ages of 17 and 22 (Center for Human Resource Research, 2006). Funding limitations resulted in the second and third (other than 201 randomly selected individuals) subsamples being dropped from the survey after 2000 and 1984, respectively.
Figure 1.
Flow of data from the total National Longitudinal Survey of Youth 1979 (NLSY79) sample to the sample used in the present analysis.
To date, there are 21 rounds of publicly available data from the NLSY79 cohort. Retention is calculated by dividing the total number of respondents by the number of respondents who are eligible for interview. Retention rates from rounds 1 through 16 were all around or above 90%. After round 16 (1994), retention rates have lessened to an extent, falling to a low of 76.9% in the most recent year available, 2004 (Center for Human Resource Research, 2006).
The Children of the NLSY79 Database
Beginning in 1986, children of the 5,255 women in the NLSY79 cohort have been interviewed every 2 years (see Figure 1). It should be noted that because the military sample was dropped from data collection before 1986, none of their potential children is included. This sample of the children of the NLSY79 women (CNLSY) is supported by the National Institute of Child Health and Development (NICHD). As of the last available collection point (2004), a total of 11,428 children have been identified as born to the women of NLSY79 (see Figure 1). On average, it has been calculated that the NLSY79 women have 1.9 children identified in the children’s sample, representing a predicted 90% of their total childbearing. In general, the CNLSY sample represents all children who were born to women between the ages of 14 and 22 in 1979.
However, there is a selection bias within the CNLSY that must be recognized. Given that the sampling design is to measure all children of the original cohort of women once they are born, there is an intrinsic prejudice toward which women are having children at any given time of data collection. More specifically, the women who already had children in the first few measurement points had their children young, as either teenage mothers or young adults. This group of women is more likely to be less educated and from one of the minority groups (Chase-Lansdale, Mott, Brooks-Gunn,&Phillips, 1991). Therefore, the older children present in the CNLSY database also tend to have lower education attainment and come from a lower socioeconomic status (Chase-Lansdale et al., 1991). Given this trend, there is a complementary bias toward the younger children present in the CNLSY sample in that they were born from older mothers, making them more likely to be at a higher socioeconomic status and to be of non-minority status (Center for Human Resource Research, 2004).
Data collection across survey dates focused on assessments of cognitive ability, temperament, motor and social development, behavior problems, self-competence, and the quality of the home environment (Center for Human Resource Research, 2004). Further, beginning in 1988, children older than 10 years of age were assessed via personal interviews on school, family, peer relations, and general attitudes and behaviors. As of 1994, all children of the CNLSY who were 15 years old or older for that year (termed “young adults”) were given a different protocol than those younger than 15 (termed “younger children”), who continued to receive the same assessment and interview battery as previously conducted. Specifically, the young adults were given personal interviews that were akin to the interviews that were given to their mothers when they were adolescents and young adults.
Until 1992, all data collection was conducted by trained field testers using a pencil-and-paper method. Beginning in 1994, collection moved to a computer-assisted personal interview (CAPI), with all instruments fully computerized by the year 2000. The CAPI involves the testers going into the field with laptop computers that are programmed to automatically select the appropriate next question based on skip patterns. After the split to young adult or younger children subsamples in 1994, all younger children interviews were conducted in person. All young adult interviews were conducted in person from 1996 until 1998, after which data collection moved to telephone rather than in-home visits. Completion rates for the CNLSY cohort are calculated by taking the number of all children who are interviewed and dividing that by the number of children who are eligible for collection based on their mother being interviewed. Younger children must be living in the home of their mother, but young adults need not be to be eligible. Therefore, before the age split, child completion rates were relatively stable at around 97%. After the split, the completion rates for younger children stayed around 90%, and for young adults, around 83%.
Interviews for the CNLSY involve multiple modes conducted in the mother of the respondent’s home by experienced trained field staff. These modes include mother reports, child reports, interviewer observations, and interviewer-administered assessments (Center for Human Resource Research, 2004). The mother report includes, at the family level, questions about the home environment, employment, family education and competence, household composition, and father presence and contact. Mothers of the children also report on child-specific questions such as temperament, behavior problems, motor and social development, family (e.g., parent monitoring, religiosity, feelings toward child), school (e.g., overall success, quality of school, total number of school attended), and health. The child report contains questions concerning family interactions and parenting, attitudes, behaviors, moods, classroom activities, teacher practices, homework, after-school and summer activities, computer use, friends, dating, TV viewing practices, work for pay, community service and volunteering, alcohol and drug use, peer pressure, risky behavior, neighborhood safety, and religion. The interviewer report is an evaluation on the attitude of the child toward the testing paradigm, the child’s physical condition, and whether anything occurred that interfered with the testing session. Also, the interviewer comments on the home environment. Finally, the interviewer-administered assessment includes general questions about the child’s age, height, and weight, as well as a measure of self-perceived adequacy and competence, and psychometric batteries of ability. The measures of ability include a test of short-term memory, mathematics, word recognition and reading comprehension, and receptive vocabulary.
User guides are available online for both the original NLSY79 sample (Center for Human Resource Research, 2004) as well as the CNLSY sample (Center for Human Resource Research, 2006). All available data for both samples are available in one publicly available Web site (U.S. Department of Labor, 2007). A free user account is required to pull the data, which are easily available by variable name or topic area.
Genetic Influences on Language, Reading, and Mathematics Skills
Quantitative genetics methodology allows for individual differences in measured abilities to be decomposed into genetic and environmental contributions (Plomin, DeFries, McClearn, & McGuffin, 2008). Both twin and adoption studies have been employed to study the etiology of language, reading, and mathematics performance. These are described in terms of additive genetic (effects that are due to the summation of genetic influences across many genes; h2), shared environmental (environmental influences that make family members more similar; c2), and nonshared environmental (environmental influences that make family members distinct; e2) effects. Twin studies achieve this by comparing differences in the amount of similarity between a set of twins based on the extent to which they share genes (i.e., monozygotic twins share 100% of their genes, and dizygotic twins theoretically share 50% of their genes on average). Adoption studies compare the extent to which nonrelated children in a family are similar to each other and to their adoptive and/or biological parents. These two types of studies, and their extensions, have informed the literature as to genetic etiology of the components of language, reading, and mathematics skill in an unselected population, as well as within populations of individuals with disabilities (Plomin et al., 2008).
In general, within most domains of language, reading, and mathematics, genetic effects are substantial and significant (see Plomin & Kovas, 2005, for review). For example, vocabulary skills in young children show significant genetic estimates (h2 = .32–.46; Byrne et al., 2006; DeThorne et al., 2008). Mathematics performance has shown significant genetic influences across a broad base of studies as well (h2 = .44–.67; Hart, Petrill, Thompson, & Plomin, 2009; Knopik & DeFries, 1999; Oliver et al., 2004). Likewise, word recognition has shown consistent and significant estimates of genetic effects across both twin (h2 = .42–.49; Light, DeFries, & Olson, 1998; Petrill, Deater-Deckard, Thompson, DeThorne, & Schatschneider, 2006) and adoption studies (h2 = .45; Brooks, Fulker & DeFries, 1990). However, other measures of reading, such as decoding fluency, phonological decoding, and reading recognition, have suggested higher point estimates for heritability across both twin (h2 = .65–.80; Gayan &Olson, 2003; Harlaar, Dale, & Plomin, 2007) and adoption studies (h2 = .57; Wadsworth, Corley, Hewitt, & DeFries, 2001). However, these more recent higher point estimates are within the range of confidence intervals of the more moderate estimates.
The above studies have provided estimates of genetic heritability for the full spectrum of performance in language, reading, and mathematics; other studies have focused specifically on heritability of disabilities in both twin and adoption studies (Plomin & Kovas, 2005). For example, several projects have examined the genetic influences for reading impairment (hg2 = .52–.73; Castles, Bates, Coltheart, Luciano, & Martin, 2006; Harlaar, Hayiou-Thomas, & Plomin, 2005; Hawke, Wadsworth, Olson, & DeFries, 2007; Light & DeFries, 1995) and for impairment in mathematics performance (hg2 = .38–.65; Alarcón, DeFries, Light, & Pennington, 1997; Oliver et al., 2004). More specifically for language impairment, significant genetic influences have been suggested for composites of widely varying language aspects (e.g., vocabulary, syntax, phonology, and articulation, hg2 = .38; Viding et al., 2004), as well as for individual components (e.g., nonword repetition, hg2 = .38; Bishop et al., 1999). Moreover, research has suggested that in general, the magnitude of genetic effects that influence the lower end of performance (i.e., impairment) is similar to that influencing the wide range of performance (see Plomin & Kovas, 2005, for review). This has led to a general conclusion across the field toward a “quantitative trait locus (QTL) hypothesis,” which assumes that multiple genes influence a disorder such as dyslexia, forming a continuum of vulnerability (Plomin & McGuffin, 2003). Therefore, these genes influence not just the disability, but the entire spectrum of ability.
The results from twin and adoption studies have been persuasive within the field of quantitative genetics, but there are also some important possible limitations regarding the use of twin and adoption studies to provide estimates of genetic effects. That is, given the seemingly special nature of families of both twins and adoptees, there has been debate as to whether genetic influences are inflated in these samples (see Plomin et al., 2008, for review) and whether results showing moderate and significant genetic effects are generalizable to nontwin and nonadoptive samples of children (e.g., Stoolmiller, 1999). For example, one methodological assumption of a twin design is the “equal environments assumption.” Specifically, this assumption states that the influences of the environment that makes siblings more similar are roughly equal for both monozygotic and dizygotic twins in the same family (Plomin et al., 2008). If this assumption were violated by identical twins being treated more similarly solely by virtue of their status as identical twins (e.g., due to looking more like) than fraternal twins, then estimates of genetic influences would be artificially inflated. Similarly, given that parents self-select into the adoptive process and are on average more affluent and provide a high-quality home environment, they may have a more restricted range of influence than the typical family (Baumrind, 1993; Stoolmiller, 1999). This restriction of family environment would also serve to artificially inflate the estimates of genetic influences while undermining the importance of the shared environment (Stoolmiller, 1998, 1999). Taken together, the possible violation of the equal environments assumption in twin designs (e.g., Eaves, Foley, & Silberg, 2003), along with the potentially restricted range of family environment in adoption designs (e.g., Stoolmiller, 1999), may serve to limit the generalizability of these methodologies.
However, there is evidence to the contrary. First, the theoretical limitations in twin and adoption studies have shown negligible influence on the magnitude and significance of genetic estimates (e.g., Evans & Martin, 2000). Furthermore, despite the limitations to both twin and adoption studies separately, results are highly concordant across both types of designs, as well as for combined designs (Plomin et al., 2008; Plomin & Kovas, 2005). That said, although there is much support for the twin and adoption studies in the field, these samples cannot address the question of genetic influences in nontwin samples (Eaves et al., 2003). There has yet to be much research to support the conclusion that genetics play a moderate and significant role within cognitive domains outside of the typical twin and adoption studies.
The NLSY79 study is a publicly available data set that is nationally representative of women ages 14 to 22 in 1979. Moreover, data are available in the children’s data set on all of the children these women have had (CNLSY; Baker et al., 1993). Importantly, the CNLSY was in part designed to examine early development and is also genetically sensitive in design. As part of the study design of measuring all available children in the women’s households, it is possible to analyze the naturally occurring kinship pairs within the sample. Furthermore, by using information on the genetic relatedness from these kinships, estimates of genetic influences on achievement outcomes can be calculated (Rodgers & Rowe, 1987; Rodgers, Rowe, & Li, 1994). By using a large, representative sample such as the CNLSY, issues of generalizability of results such as those raised against twin and adoption studies are less meaningful. Therefore, any consistency in results across study designs would serve to strengthen the results of hallmark quantitative genetic designs.
As mentioned previously, the CNLSY administers psychometric batteries of school achievement tests that incorporate language, reading, and mathematics to thousands of children (Center for Human Resource Research, 2004). Given the potential power of such a large sample size, it is possible to examine not only the genetic point estimates of the total “unselected” sample (e.g., Rodgers, Rowe & May, 1994), but also whether that same magnitude of effects influences the low end of the performance spectrum. Moreover, these results can be compared to previously reported estimates from the twin and adoption study literature. For example, Rodgers, Rowe, and May used the CNLSY to examine genetic influences on broad-based intelligence, resulting in estimates of heritability in the total unselected sample (h2 = .50) similar to those found across numerous twin and adoption studies (see Plomin & Rende, 1991, for review). This same study (Rodgers, Rowe, & May, 1994) also examined genetic influences on the individual measures of language, reading, and mathematics within the unselected sample and found similar results in terms of magnitude and significance as research reported previously (h2 = .48–.74; e.g., Plomin & Kovas, 2005). The present study will build on the Rodgers, Rowe, and May (1994) analysis in numerous ways. First, Rodgers, Rowe, and May examined the genetic and environmental estimates of the full sample only and did not apply any selection to the sample, such as low performers only. Second, the present sample will be more inclusive of the entire CNLSY sample, as the linking algorithm has since been applied to all individuals in the CNLSY, something that was not available to Rodgers, Rowe, and May. More specifically, the Rodgers, Rowe, and May sample only included 1,044 pairs of children, whereas the present sample includes 7,681 pairs. Finally, the present analyses include psychometric batteries measured at a later survey year (i.e., 1994) than Rodgers, Rowe, and May, which included 1986 and 1988. This is important because beginning in 1994, a more accurate testing paradigm, CAPI, was introduced.
ANALYSIS IN THE CNLSY: ILLUSTRATIVE RESEARCH STUDY
Research Question
To provide an illustration of how the CNLSY may be used to answer important questions regarding the heritability of specific cognitive skills in both typical and low-performing samples, the present study addressed three major goals: to examine the extent to which (a) genetic influences were present in a selected sample of low performers on language, reading, and mathematics achievement tests; (b) the magnitude of the genetic influences for the total sample was similar to the magnitude of a selected sample of low performers; and (c) estimates of genetic influences on language, reading, and mathematics outcomes from a selected and an unselected sample based on representative data generalized to the findings from twin and adoption studies. We hypothesized that (a) a selected sample of low-ability (defined as the lowest 20th percentile) performers within the CNLSY would have significant and substantial effects that are attributable to genetic influences for language, reading, and mathematics achievement; (b) the unselected sample of the nationally representative CNLSY would have genetic estimates of similar magnitude to the selected sample for language, reading, and mathematics achievement; and (c) in total, the genetic estimates of both the selected and unselected sample from the CNLSY would be within range of those that were previously published from twin and adoption studies measuring cognitive domains.
METHOD
Sample
Due to an effort to include all available children in the 2,400 sampled homes from the NLSY79, the sample included full siblings (including twins), half-siblings, and cousins (see Figure 1). In previous studies, Rodgers and colleagues used all available information within the CNLSY data to assign genetic relatedness coefficients to each pair available within the data (Rodgers, Johnson, & Bard, 2005; Rodgers, Rowe, & Li, 1994; Rodgers, Rowe, & May, 1994). These identified pairs represent approximately all of the possible relationship pairs known in the CNLSY through to the 2002 cycle, meaning that all kinship pairings in the CNLSY up until that cycle have received a coefficient of relatedness (Van Hulle, Rodgers, D’Onofrio,Waldman, & Lahey, 2007). Briefly, twins were identified by having the same birth date for two siblings with zygosity determined by specific survey questions. Full and half-siblings were determined by survey questions concerning paternity. When sibling classification could not be assured, the pair received a genetic coefficient of the midpoint between full and half-siblings (“unknown siblings”). Finally, cousins were identified by determining the children of sisters in the original NLSY79 database. A more complete discussion of the linking algorithm and the logic behind the classification criterion may be found elsewhere (Rodgers et al., 2005; Van Hulle et al., 2007).
To date, there are 12,431 pairs who have been identified across the waves of analyses (see Figure 1). It should be noted that an individual child can contribute to multiple pairings, therefore resulting in a greater total functional sample size for these analyses than is present in the CNLSY sample without the pairings. For example, a family with four siblings would represent six pairings; therefore, the total number of pairings is not reflective of the total number of children in the data set. Given the large number of waves, the present analyses come from the 1994 wave of the CNLSY, which includes interviews of 7,862 “younger children” (younger than 15 years old) who were available and were in the correct age range for surveying. The present analyses are based on only the “younger children” of the 1994 wave because of the following benefits this afforded: more accurate scoring of the achievement tests due to the introduction of the CAPI technology, and the most available data based on the psychometric batteries for any wave (Center for Human Resource Research, 2004). Therefore, once the kinship algorithm was applied to the 1994 wave of the CNLSY, 7,681 pairs of children were assigned genetic relatedness coefficients, of which there are five kinship levels: monozygotic (MZ) twins (17 pairs), full siblings/dizygotic (DZ) twins (3589 pairs), unknown siblings (1158 pairs), half-siblings (1515 pairs), and cousins (1402 pairs).
In 1994, the mothers of the children were between the ages of 29 and 37 years. In general, most of the mothers had at least two or more children (40% with two, 40% with more than two, and 20% with one). Of the 3,363 mothers who were included, approximately 50% were White (1645), 30% were Black (1040), and 20% were Hispanic (658). The mothers of the children present in 1994 also represented a wide range of educational attainment, with 18.7% of the sample having less than 12 years of education, 45.2% having 12 years of education, 32.2% having up to 4 years of college, and the remaining 3.9% having more than 4 years of college. The children available from the 1994 wave of assessment have a mean age of 9.57 years (SD = 2.70 years, range = 4.92–14.83).
Measures
Four individual achievement measures of ability were given during in-depth home-based testing that was administered by trained field workers. Three of the measures came from the full Peabody Individual Achievement Test (PIAT; Dunn & Markwardt, 1970), specifically, the Reading Comprehension, Reading Recognition, and Mathematics subtests. The fourth test administered was the Peabody Picture Vocabulary Test—Revised (PPVT–R; Dunn & Dunn, 1981). Published median test–retest reliabilities for all measures are moderate to high: Reading Comprehension, r = .64; Reading Recognition, r = .89; Mathematics, r = .74 (Dunn & Markwardt, 1970); and PPVT–R, r = .78 (Dunn & Dunn, 1981). Some testing parameters reduced the range of children tested for some of the measures, thus resulting in different sample sizes depending on the test. For example, only children over the age of 5 years who had scored greater than 19 on the Reading Recognition subtest were administered the Reading Comprehension subtest. Also, the PPVT–R was only administered to children between the ages of 10 and 11 years, unless they had not been previously sampled (Center for Human Resource Research, 2004).
All scores for individual children were standardized to age and gender norms, for a population mean of 100 and a standard deviation of 15. It should be noted, however, that the norming sample for the CNLSY PIAT achievement subtests was drawn from the 1968 version of the PIAT, meaning that the norming occurred approximately 30 years before sampling of the CNLSY (see Center for Human Resource Research, 2004). In general, this has had the effect of the entire CNLSY sample having a mean standard score of slightly greater than 100 for the PIAT subtests, which is most likely reflective of social changes toward earlier preparation and education of mathematics and reading skills (see Center for Human Resource Research, 2004). Rodgers and Wänström (2007) also provide a related alternative reasoning for the increase in the mean standard score, namely the influence of the Flynn effect (e.g., Flynn, 1984). The Flynn effect describes the phenomenon of a general increase in test scores across generations due to many potential factors (Flynn, 1984).
All batteries were standardized for age and gender, but no further covariates concerning possible sample bias (e.g., maternal education) were controlled for in the present analyses. Although this may seem atypical for a large-scale sample, the nature of the methodology of between-pair analysis based on genetic relatedness serves as an implicit control for almost all covariates that could be identified in a sample with individual units of measurement. Each member of the kinship pairing serves as a statistical control for variables that are most likely shared between them, which are typically not shared between singular units of analysis, such as family-level effects. Moreover, by controlling for influences such as maternal education within the present analyses, the effect would be to inflate the estimates of heritability, as the between-family environmental variance would be diminished.
RESULTS
Descriptive Statistics
Means, standard deviations, and the ranges for each of the four achievement battery subtests’ standardized scores as measured in 1994 are presented in Table 1 for both the selected and unselected samples. These samples are based on the available individuals after the kinship algorithm was applied to the CNLSY 1994 wave with available data for the specific measure. In general, this subsample of the CNLSY scored close to the population mean of 100 and standard deviation of 15 for each subtest of the PIAT. However, the sample in general scored below the mean on the PPVT–R (M = 85.89) and above the average standard deviation (SD = 20.75) than would be expected from the general population.
Table 1.
Descriptive findings for the selected and unselected National Longitudinal Survey of Youth 1979 Children’s (CNLSY79) database sample.
| Selected sample <20th %tile | Unselected sample | |||||||
|---|---|---|---|---|---|---|---|---|
| Variable | Mean | SD | Range | n | Mean | SD | Range | n |
| PIAT–RC | 77.99 | 6.71 | 65–86 | 1,666 | 97.97 | 14.07 | 65–135 | 7,912 |
| PIAT–RR | 79.54 | 7.06 | 65–88 | 1,902 | 100.92 | 15.23 | 65–135 | 9,353 |
| PIAT–M | 77.71 | 6.73 | 65–86 | 1,885 | 97.82 | 14.00 | 65–135 | 9,376 |
| PPVT–R | 56.03 | 13.32 | 20–70 | 924 | 85.89 | 20.75 | 20–160 | 4,401 |
Note. PIAT–RC = Peabody Individual Achievement Test—Reading Comprehension subtest, PIAT–RR = Peabody Individual Achievement Test—Reading Recognition subtest, PIAT–M = Peabody Individual Achievement Test—Mathematics subtest, and PPVT–R = Peabody Picture Vocabulary Test—Revised.
Genetic Analysis
We employed a DeFries Fulker model (DF; DeFries & Fulker, 1985) to examine the genetic influence on low and unselected language, reading, and mathematics performance, analogous to Rodgers, Rowe, and May (1994). DF analysis is also based on the logic of increased genetic relatedness being associated with increased familiality. The original form of the DF model (DeFries & Fulker, 1985) was designed for examination of the genetic influences on the extremes of a population using twin data. This model can be extended to any pair of related individuals in which a proband is selected for an extreme score on a measure, with the second member of the pair score regressing to the population mean (DeFries & Fulker, 1985). From a DF analysis, it is possible to measure the genetic influence on an outcome in an extreme sample, such as low performers on a test. Additionally, the model can be extended to measure the genetic influences on an unselected sample. Following the measurement of genetic influences on both the selected and unselected samples, the DF analysis allows for an examination of the possible similarities between the magnitudes of the genetic estimates of a selected sample and an unselected sample.
Similar to the 1994 work by Rodgers, Rowe, and May on a smaller sample of available pairings, the present analysis extended the DF twin model to incorporate the five levels of relatedness that are available in the CNLSY: MZ twins (Relatedness [R] = 1.0), full siblings /DZ twins (R = .50), unclassified siblings (R = .375), half siblings (R = .25), and cousins (R = .125; Rodgers et al., 2005; Rodgers, Rowe, & Li, 1994). Therefore, using the CNLSY, it is possible to compare the degree of similarity in score, or concordance, of the various related pairs. From this, it is assumed that the higher the genetic relatedness of the pair, the greater the concordance should be, if genetics are important to the outcome. Therefore, if genetic effects are influencing the language, reading, and mathematics measures, then the identical twins (R = 1.0) should show greater concordance with each other over the full siblings (R = .50), who will in turn show greater concordance over the half-siblings (R = .50), and so on. Similarly, any extent to which the concordance is not explained by the genetic relatedness, environmental influences are assumed.
Selected Sample
The first step in the present analyses was to select any individual who scored at or below the 20th percentile and examine the extent of the similarity in scoring the other member of the pairing had. If genetic influences on the trait are indicated, the less genetically related the kinship pair is, the closer to the mean the other member of the pair should score, essentially widening the gap between their scores. Therefore, by measuring this differential second member of the pair’s regression to the mean according to genetic relatedness, it is possible to use quantitative genetic techniques to estimate “group” genetic influences. These estimates are group estimates in that they measure a selected group’s mean score on an outcome versus the rest of the population. For example, these group estimates of genetic influences explain why the mean of the selected group is 80 and the mean of the unselected group is 100, but they do not explain why these two may be different from one another. The same logic is applied for environmental influences. Any extent to which genetic influences cannot explain the regression to the mean by the second member of the pair, group environmental effects are assumed. This basic DF model based on selection of a proband is represented by the following multiple regression model:
| (1) |
where K1 is the second member of the pair’s score on the outcome, K2 is the proband’s score, R is the degree of genetic relatedness, bo is the intercept, b2 is the influence due to genetics on the selected group, and e is the error term. Finally, the b1 term is an indicator of the independent effects on the proband not including influences due to genetics (LaBuda, DeFries, & Fulker, 1986).
As previously stated, if genetic effects are important, higher familial resemblance on outcomes of interest should be correlated with higher levels of genetic relatedness (Plomin et al., 2008). Table 2 displays the result from the group correlations between the members of the same degree of genetic relatedness on each of the cognitive achievement tests. In general, as the degree of relatedness increases across a specific measure, so does the degree of correlation between the individuals in most cases. For example, for the PIAT Reading Comprehension subtest, the group correlation for the cousins is lower (.34) than that for the full siblings (.47), which is in itself lower than that for the identical twins (.86). This would suggest that there is genetic variance underlying each of the achievement test scores. However, it should be noted that the group correlation for the unknown siblings is higher in most cases than in the full siblings, which may suggest environmental influences.
Table 2.
Group correlations based on the degree of genetic relatedness (R) between kinship pairs for each of the cognitive achievement tests.
| Degree of relatedness | |||||
|---|---|---|---|---|---|
| Variable | Cousins R =.125 |
Half-siblings R =.25 |
Unknown siblings R =.375 |
Full siblings R =.50 |
Identical twins R =1.00 |
| PIAT–RC | .34 | .28 | .52 | .47 | .86 |
| PIAT–RR | .29 | .35 | .46 | .42 | .83 |
| PIAT–M | .24 | .19 | .40 | .40 | .72 |
| PPVT–R | .45 | .25 | .65 | .61 | .91 |
Therefore, specific genetic estimates derived from selecting a proband based on the cutoff of less than or equal to the 20th percentile represent the group heritability (hg2), which represents the extent to which the mean differences between the extreme group and the rest of the population are due to genetic effects (Plomin et al., 2008). As suggested above, this group heritability is based on the degree of relatedness, in that if in the CNLSY, the means between the proband and the second member of a pairing of full siblings were more similar than the same means in cousins, the greater the group heritability influence that would be expected. Similarly, it is possible to estimate the group shared environment estimates (cg2), which is defined as the extent to which the mean differences between the selected group and the typical population are due to environmental effects. These influences are assumed by the extent to which not all of the mean differences can be explained by genetic effects (e.g., if full siblings are not as less similar to each other than identical twins, as would be expected by genetic effects only). DF modeling also allows for standard errors to be estimated for the point estimates. It should be noted that the analyzed data set contains double entered data, meaning that all individuals have the opportunity to be the “proband” in order to get both members of the pair included, which effectively doubles the sample size. This is done by allowing for two lines of data for each twin pair, with the outcome estimate for Child 1 on one line switched to the outcome estimate for Child 2 on the second line, and vice versa. This allows each child in the pairing to have the chance to be K1 or K2. Therefore, the standard errors derived from the DF analysis are overly liberal, as each pairing contributes two observations to the model. This results in errors being correlated, violating the assumption of independence of errors (see Rodgers & Kohler, 2005). Given this, a correction for this was applied using the following formula:
| (2) |
where S.E. is the standard error, DE is the total number of pairs where both members are selected as probands, SE is the total number of pairs where only one member of the pairing is a proband, and k is the total number of elements in the regression formula. From this corrected standard error, statistical tests of significance can be applied on the estimates of group heritability and shared environment. This involves multiplying the corrected standard error by 1.96 and using this as the confidence interval of the point estimate. If the confidence interval does not bound zero, then the estimate is significant.
Results of group heritability and shared environment from the selection of probands who scored in the lowest 20th percentile on each of the various achievement tests available in the CNLSY79 are presented in Table 3. The confidence intervals, as well as the results from the significance tests, are also displayed. The PIAT Reading Comprehension subtest suggested moderate and significant group heritability and shared environment (hg2 = .32, cg2 = .46). The Reading Recognition subtest of the PIAT indicated moderate and significant effects of group heritability and modest shared environment (hg2 = .47, cg2 = .32). The PIAT Mathematics subtest revealed a small to moderate and significant estimate for group heritability, hg2 = .39, and for shared environment, cg2 = .28. Finally, the PPVT–R test suggested a large and significant estimate of group heritability and shared environment (hg2 = .69, cg2 = .59).
Table 3.
Group heritability (hg2) and group shared environment (cg2) for the selected sample at the 20th percentile, heritability (h2) and shared environmental (c2) estimates of the unselected sample, confidence intervals (C.I.), and significance levels for each of the specific achievement batteries.
| Selected sample ≤20th %tile | Unselected sample | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Variable | hg2 | C.I. | p < .05 | cg2 | C.I. | p < .05 | h2 | C.I. | p < .05 | c2 | C.I. | p < .05 |
| PIAT–RC | .32 | .13 | * | .46 | .12 | * | .43 | .20 | * | .26 | .19 | * |
| PIAT–RR | .47 | .14 | * | .32 | .12 | * | .33 | .14 | * | .26 | .12 | * |
| PIAT–M | .39 | .09 | * | .28 | .10 | * | .49 | .12 | * | .16 | .11 | * |
| PPVT–R | .69 | .22 | * | .59 | .23 | * | .51 | .23 | * | .35 | .19 | * |
Unselected sample
As described above, one issue is whether genetic effects in low and unselected samples are similar in magnitude (e.g., Plomin & Kovas, 2005). DF analysis for selected populations can be applied to an unselected population (Rodgers & Kohler, 2005). However, there are two differences to the formulation of the DF analysis for an unselected population. First, there is no selection of a proband based on a cutoff score. Instead, the similarity in scores between every individual in the sample by relationship is considered. Second, the basic DF regression formula is expanded to include an interaction term, which in the unselected population represents the broad sense heritability (h2) of the sample. This results in a simple extension of the DF formula (1), which is represented by the following formula:
| (3) |
where K1 is the first member of the pair’s score on the outcome, K2 is the second member’s score on the outcome, R is the degree of genetic relatedness, bo is the intercept, b3 is the heritability (additive genetic effects; h2) of the trait in the total sample, and b2 is a direct estimate of shared environmental influences (c2; Rodgers & McGue, 1994). Just as in the selected sample formulation, standard errors are produced but are based on an essential doubling of the sample size due to double entry. Therefore, these liberal standard errors are corrected for based on the actual sample size using the same formula as shown above (2), and then statistical tests of significance are used against the point estimates. All of the available subtests of achievement in the CNLSY were re-analyzed without the selection criterion for estimates of genetic and shared environmental influences on the whole sample. Again, genetic influences are implied if the similarity in score between a pairing increases as the degree of relatedness increases. For example, if genetic influences are implied, then identical twins should have a mean score closer to their co-twin than full sisters have to each other. If the mean differences between the degree of relatedness are not as great as would be assumed by genetic effects only, than environmental influences are implicated. The results from this unselected sample DF analysis are presented in Table 3, along with the confidence intervals and significance levels for each of the available achievement tests in the CNLSY. The PIAT Reading Comprehension subtest indicated small to moderate and significant heritability and shared environment (h2 = .43, c2 = .26). The PIAT Reading Recognition subtest also suggested small to moderate and significant effects due to genetics and shared environment (h2 = .33, c2 = .26). The PIAT Mathematics subtest suggested small to moderate and significant heritability and shared environment estimates, h2 = .39, c2 = .16. Finally, the PPVT–R test revealed a moderate and significant estimate of heritability (h2 = .51), as well as for the shared environment (c2 = .35).
CONCLUSION
The purpose of the present work was twofold. Our first intent was to provide an illustration of use of the CNLSY database. The second intent was to use this database to seek convergent evidence regarding the genetic effects influencing low and typical performers on measures of language, reading, and mathematics collected outside of the typical twin and adoption study paradigms. In doing so, three goals were addressed. First, we examined the extent to which genetic influences were significant in impaired language, reading, and mathematics performance in the children in the CNLSY. Next, we examined the extent to which the magnitude of the genetic influences in the unselected sample was similar to the magnitude of the genetic influences in the selected sample of low performers. Third, we examined whether the genetic influences on language, reading, and mathematics achievement outcomes from the present nationally representative selected and unselected samples generalized to the findings on similar outcomes from the extant twin and adoption studies. Using the CNLSY, five degrees of genetic relationships were identified between all pairs of children available who had been administered psychometric batteries of language, reading, and mathematics.
We tested three specific hypotheses. The first was that the selected sample of the lowest 20th percentile of scorers on each of the four achievement measures available in the CNLSY would indicate substantial and significant influences attributable to genetic effects. The results for each of the vocabulary, decoding, reading comprehension, and general mathematics tests suggested that this was the case in this sample. For all of the achievement tests, the point estimates for group heritability were significantly different from zero, and all were moderate to high in magnitude. It should be noted that the cutoff of the 20th percentile was chosen because it implies a general low performance on the measure, it is in the range of commonly used cutoffs in the literature using DF analyses (see Plomin & Kovas, 2005), and it has previously been suggested to be similar in results to other more stringent cutoffs (e.g., Petrill et al., 2001).
The second hypothesis predicted that similar significant estimates for genetic influences would be found in the unselected sample across the measures of achievement. This hypothesis was also found to be supported by the data, with vocabulary, decoding, reading comprehension, and general mathematics achievement tests all indicating moderate and significant estimates of heritability in the unselected sample. Moreover, this hypothesis stated that the unselected sample estimate of heritability would be of similar magnitude to the group heritability of the lowest 20th percentile. Importantly, this was the case. For all four measures, both group heritability and broad-sense heritability were significant and were within confidence intervals of each other. Therefore, although the point estimates derived in the present model are slightly different from each other in magnitude, they are well within the same range of potential estimates given the bounds of probability sampling. This lends credence to both the phenotypic literature’s movement toward conceptualizing disability in language, reading, and mathematics to be on the same continuum as typical performance (Bishop & Snowling, 2004), and the quantitative genetic movement toward accepting the QTL hypothesis (Plomin &McGuffin, 2003). That is, similar genes influence all variation within the cognitive performance spectrum, including the extreme ends (Plomin & McGuffin, 2003).
The third hypothesis stated that the selected and unselected estimates for genetic influences on all four of the achievement measures would be similar in magnitude to the broader literature derived from the classic twin and adoption studies. In a review of the literature concerning the extremes and unselected sample estimates for genetic effects on cognition across many different twin and adoption projects, a common theme of moderate and significant genetic estimates was determined (Plomin & Kovas, 2005). The present analyses suggest that even outside of the typical twin and adoption study methodology, within a data set that is largely representative of the population of the United States, similar estimates were found. These were similar in both magnitude and significance to the existing quantitative genetics literature. Although in some cases, the present estimates were somewhat on the lower end of the range of magnitudes in the literature, the present estimates are well within the confidence intervals of previous work. For example, the present estimate for Reading Recognition of h2 = .33 is lower than many individual point estimates in the literature. However, it is within the confidence intervals of many of these previous estimates, such as Foch and Plomin (1980), who suggested a range of heritability estimates from .09 to .82 (see Plomin et al., 2008). Along with Rodgers et al. (1994), who examined an earlier and less complete version of the kinship linkage file for the CNLSY, this is the first known example of heritability estimates for cognitive achievement tests outside of twin and adoption studies. The high degree to which the present results concur with the previously published quantitative genetic literature gives support for the results found by the twin and adoption paradigms. This is despite the concerns of generalizability (e.g., Eaves et al., 2003; Stoolmiller, 1999) due to the potential overinflation of the genetic estimates in these sample designs. Although the present analyses did not directly test these issues, by showing consistency of results, these analyses implicate that they may be in fact more of a theoretical concern than a practical concern.
There are, however, limitations to the present study that should be noted. First, an examination of the descriptive means for each of the subtests from the present sample of the CNLSY79 1994 wave shows that the PPVT–R mean is almost 1 SD below what would be expected in a population survey, given that the standardization of the test is around a population mean of 100. It seems as though the sampling procedure of the CNLSY for administering this specific test to only 10- to 11-year-olds (unless not previously sampled) has resulted in some sampling bias toward lower than typically performing children in receptive vocabulary as measured by the PPVT–R. This possible sample constriction can also be seen in the lower sample size of this test in the 1994 wave, and may be limiting the generalizability of this performance measure. It may also be the case that the outcomes of the children available in the 1994 wave are being influenced by the intrinsic sampling bias that is present in the CNLSY (e.g., Chase-Lansdale et al., 1991). Although the present sample contains only the younger children of the total available sample, it may be the case that the oldest of this group systematically have a greater chance of having mothers who have lower educational attainment and lower socioeconomic status (Center for Human Resource Research, 2004). This would increase the chance of the sample scoring lower on cognitive performance outcomes. Along these same lines, the means of the PIAT subtests were all lower than what was expected by the CNLSY total sample, which previous reports have suggested means closer to 110 for all of the tests. This higher than normal total sample mean has been previously explained as being due to the use of a standardization paradigm that was built 30 years before the children being tested (Center for Human Resource Research, 2004). The present sample means being lower than expected would appear to be due to an introduction of a slight sampling bias by the linking algorithm. Although all possible kinship pairs are identified in the present sample, this naturally precludes any children who cannot be matched to a pair (i.e., only children with no cousins). In general, these limitations highlight the fact that the CNLSY sample is representative at inception only to all children of women who were between the ages of 14 and 22 in 1979. Moreover, application of the linking algorithm may be introducing some sampling bias due to it only representing children with some sort of pairing available in the data. However, in general, the CNLSY is closest to a truly nationally representative sample that has been used within the quantitative genetics framework. By the high consistency of the present results with twin and adoption studies focusing on cognitive achievement is confidence given not only for those more classic designs, but also to the generalizability of these results.
Future work should seek to replicate these findings for each cognitive performance measure in other waves of the CNLSY, as well as vary the cutoff points (e.g., lowest 10%) for the selected analyses to determine if estimates change depending on how low performance is quantified. Also, there is an implication that the genetic coefficient of many of the unknown siblings should in fact be higher than assigned, given that the group correlation for these pairs was higher than the correlation for the full sibling group in all cases. More work in properly identifying these pairs, or using analyses that allow for an unknown rather than a set genetic coefficient, may be called for in the future.
The present analyses can only speak to the significance and relative magnitude of genetic estimates within and between the selected and unselected samples for individual tests of language, reading, and mathematics. Therefore, these analyses do not test whether the same or overlapping genes are influencing the selected and unselected groups across domain. Future research should analyze multivariate models that would allow for such an examination of the overlap to occur (e.g., Kovas & Plomin, 2006). Another interesting question for future research would be to examine why the scores for the PIAT measures seemed to fall toward the population mean in the present sample of the CNLSY with the kinship algorithm applied. This seems to suggest that there are some unmeasured factors that are influencing a selection effect of lower mean scores for “larger” families.
Despite these limitations, the present study is compelling in its consistency with not only the previous literature from twin and adoption studies, but also in its suggestion of similar levels of influence due to genetics across performance levels. Again, this seems to substantiate the work of twin and adoption studies despite the special populations that they focus on. This is not to say that environmental influences are not important to these domains. In fact, environmental effects tend to be similar in magnitude and significance as genetic effects for achievement outcomes, as can be seen in the present analyses. Further examination of these environmental effects in the CNLSY, specifically with a focus on measuring direct aspects of the environment (e.g., neighborhood and home effects; e.g., Rodgers, Rowe & May, 1994), is also important. Twin and adoption studies are powerful ways to examine these genetic and environmental effects, and the present results not only collaborate with these designs but are powerful in their own right. The continuing support for the role of genetics and environments within and across the cognitive domains and levels of performance has far-reaching significance for educational and clinical intervention and prevention work.
ACKNOWLEDGMENT
The NLSY kinship links were provided by Joe Rodgers, Department of Psychology, University of Oklahoma. The creation of the links occurred through the support of research grants from NIH/NICHD on which Dr. Rodgers was the PI. Others who wish to use the NLSY kinship links can obtain copies of these kinship links by writing Dr. Rodgers at jrodgers@ou.edu. We also wish to thank Reanne Frank for comments on an earlier draft of this manuscript.
REFERENCES
- Alarcón M, DeFries JC, Light JG, Pennington BF. A twin study of mathematics disability. Journal of Learning Disabilities. 1997;30:617–623. doi: 10.1177/002221949703000605. [DOI] [PubMed] [Google Scholar]
- Baker P, Keck C, Mott F, Quinlan S. NLSY child handbook. rev ed. Columbus, OH: Center for Human Resource Research; 1993. [Google Scholar]
- Baumrind D. The average expectable environment is not good enough: A response to Scarr. Child Development. 1993;64:1134–1156. [PubMed] [Google Scholar]
- Bishop DVM, Bishop SJ, Bright P, James C, Delaney T, Tallal P. Different origin of auditory and phonological processing problems in child with language impairment: Evidence from a twin study. Journal of Speech, Language, and Hearing Research. 1999;42:155–168. doi: 10.1044/jslhr.4201.155. [DOI] [PubMed] [Google Scholar]
- Bishop DVM, Snowling MJ. Developmental dyslexia and specific language impairment: Same or different? Pscyhological Bulletin. 2004;130:858–886. doi: 10.1037/0033-2909.130.6.858. [DOI] [PubMed] [Google Scholar]
- Brooks A, Fulker DW, DeFries JC. Reading performance and general cognitive ability: A multivariate genetic analysis of twin data. Personality and Individual Differences. 1990;11:141–146. [Google Scholar]
- Byrne B, Olson RK, Samuelsson S, Wadsworth S, Corley R, DeFries JC, et al. Genetic and environmental influences on early literacy. Journal of Research in Reading. 2006;29(1):33–49. [Google Scholar]
- Castles A, Bates T, Coltheart M, Luciano M, Martin NG. Cognitive modelling and the behaviour genetics of reading. Journal of Research in Reading. 2006;29(1):92–103. [Google Scholar]
- Center for Human Resource Research. NLSY79 Children and Young Adult data users guide. [Retrieved September 15, 2007];2004 from ftp://www.nlsinfo.org/pub/usersvc/Child-Young-Adult/2004ChildYA-DataUsersGuide.pdf.
- Center for Human Resource Research. NLSY79 users guide. [Retrieved September 15, 2007];2006 from ftp://www.nlsinfo.org/pub/usersvc/NLSY79/NLSY79%202004%20User%20Guide/79text/front.htm.
- Chase-Lansdale PL, Mott FL, Brooks-Gunn J, Phillips DA. Children of the National Longitudinal Survey of Youth: A unique research opportunity. Developmental Psychology. 1991;27(6):918–931. [Google Scholar]
- DeFries JC, Fulker DW. Multiple regression of twin data. Behavior Genetics. 1985;15(5):467–473. doi: 10.1007/BF01066239. [DOI] [PubMed] [Google Scholar]
- DeThorne LS, Petrill SA, Hart SA, Channell R, Campbell R, Deater-Deckard K, et al. Estimates of genetic and environmental effects on children’s conversational language measures. Journal of Speech, Language, and Hearing Research. 2008;51:423–435. doi: 10.1044/1092-4388(2008/031). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dunn LM, Dunn LM. PPVT-R revised manual. Circle Pines, MN: AGS; 1981. [Google Scholar]
- Dunn LM, Markwardt FC. Examiner’s manual: Peabody Individual Achievement Test. Circle Pines, MN: AGS; 1970. [Google Scholar]
- Eaves L, Foley D, Silberg J. Has the “equal environments” assumption been tested in twin studies? Twin Research. 2003;6(6):486–489. doi: 10.1375/136905203322686473. [DOI] [PubMed] [Google Scholar]
- Evans DM, Martin MG. The validity of twin studies. GeneScreen. 2000;1:77–79. [Google Scholar]
- Flynn JR. The mean IQ of Americans: Massive gains 1932 to 1978. Psychological Bulletin. 1984;95:29–51. [Google Scholar]
- Foch TT, Plomin R. Specific cognitive abilities in 5- to 12-year-old twins. Behavior Genetics. 1980;10(6):507–520. doi: 10.1007/BF01066220. [DOI] [PubMed] [Google Scholar]
- Gayan J, Olson RK. Genetic and environmental influences on individual differences in printed word recognition. Journal of Experimental Child Psychology. 2003;84(2):97–123. doi: 10.1016/s0022-0965(02)00181-9. [DOI] [PubMed] [Google Scholar]
- Harlaar N, Dale PS, Plomin R. Reading exposure: A (largely) environmental risk factor with environmentally-mediated effects on reading performance in the primary school years. Journal of Child Psychology and Psychiatry. 2007;48(12):1192–1199. doi: 10.1111/j.1469-7610.2007.01798.x. [DOI] [PubMed] [Google Scholar]
- Harlaar N, Hayiou-Thomas ME, Plomin R. Reading and general cognitive ability: A multivariate analysis of 7-year-old twins. Scientific Studies of Reading. 2005;9(3):197–218. [Google Scholar]
- Hart SA, Petrill SA, Thompson LA, Plomin R. The ABCs of math: A genetic analysis of mathematics and its links with reading ability and general cognitive ability. Journal of Educational Psychology. 2009;101(2):388–402. doi: 10.1037/a0015115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hawke JL, Wadsworth SJ, Olson RK, Defries JC. Etiology of reading difficulties as a function of gender and severity. Reading and Writing. 2007;20(1–2):13–25. [Google Scholar]
- Knopik VS, DeFries JC. Etiology of covariation between reading and mathematics performance: A twin study. Twin Research. 1999;2:226–234. doi: 10.1375/136905299320565906. [DOI] [PubMed] [Google Scholar]
- Kovas Y, Plomin R. Generalist genes: Implications for the cognitive sciences. Trends in Cognitive Sciences. 2006;10(5):198–203. doi: 10.1016/j.tics.2006.03.001. [DOI] [PubMed] [Google Scholar]
- LaBuda MC, DeFries JC, Fulker DW. Multiple regression analysis of twin data obtained from selected samples. Genetic Epidemiology. 1986;3(6):425–433. doi: 10.1002/gepi.1370030607. [DOI] [PubMed] [Google Scholar]
- Light JG, DeFries JC. Comorbidity of reading and mathematics disabilities: Genetic and environmental etiologies. Journal of Learning Disabilities. 1995;28:96–106. doi: 10.1177/002221949502800204. [DOI] [PubMed] [Google Scholar]
- Light JG, DeFries JC, Olson RK. Multivariate behavioral genetic analysis of achievement and cognitive measures in reading disabled and control twin pairs. Human Biology. 1998;70:215–237. [PubMed] [Google Scholar]
- Oliver B, Harlaar N, Hayiou-Thomas ME, Kovas Y, Walker SO, Petrill SA, et al. A twin study of teacher-reported mathematics performance and low performance in 7-year-olds. Journal of Educational Psychology. 2004;96:504–517. [Google Scholar]
- Petrill SA, Deater-Deckard K, Thompson LA, DeThorne LS, Schatschneider C. Reading skills in early readers: Genetic AND shared environmental influences. Journal of Learning Disabilities. 2006;39(1):48–55. doi: 10.1177/00222194060390010501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petrill SA, Johansson B, Pederson NL, Berg S, Plomin R, Ahern F, et al. Low cognitive functioning in nondemented 80+-year-old twins is not heritable. Intelligence. 2001;29:75–83. [Google Scholar]
- Plomin R, Kovas Y. Generalist genes and learning disabilities. Psychological Bulletin. 2005;131(4):592–617. doi: 10.1037/0033-2909.131.4.592. [DOI] [PubMed] [Google Scholar]
- Plomin R, DeFries JC, McClearn GE, McGuffin P. Behavioral genetics. 4th ed. New York: W. H. Freeman; 2008. [Google Scholar]
- Plomin R, McGuffin P. Psychopathology in the postgenomic era. Annual Review of Psychology. 2003;54:205–228. doi: 10.1146/annurev.psych.54.101601.145108. [DOI] [PubMed] [Google Scholar]
- Plomin R, Rende R. Human behavioral genetics. In: Rosenzweig MR, Porter LW, editors. Annual review of psychology. Palo Alto, CA: Annual Reviews; 1991. pp. 161–190. [DOI] [PubMed] [Google Scholar]
- Rodgers JL, Johnson AB, Bard DE. NLSY—children/young adult (1986–2000) kinship linking algorithm. Norman: University of Oklahoma; 2005. Unpublished manuscript. [Google Scholar]
- Rodgers JL, Kohler H. Reformulating and simplifying the DF analysis model. Behavior Genetics. 2005;35(2):211–217. doi: 10.1007/s10519-004-1020-y. [DOI] [PubMed] [Google Scholar]
- Rodgers JL, McGue M. A simple algebraic demonstration of the validity of DeFries-Fulker analysis in unselected samples with multiple kinship levels. Behavior Genetics. 1994;24(2):259–262. doi: 10.1007/BF01067192. [DOI] [PubMed] [Google Scholar]
- Rodgers JL, Rowe D. IQ similarity in twins, siblings, half-siblings, cousins and random pairs. Intelligence. 1987;11:199–206. [Google Scholar]
- Rodgers JL, Rowe D, Li C. Beyond nature vs. nurture: DF analyses of nonshared influences on problem behaviors. Developmental Psychology. 1994;30:374–384. [Google Scholar]
- Rodgers JL, Rowe D, May K. DF analysis of NLSY IQ/achievement data: Nonshared environmental influences. Intelligence. 1994;19:157–177. [Google Scholar]
- Rodgers JL, Wänström L. Identification of a Flynn effect in the NLSY: Moving from the center to the boundaries. Intelligence. 2007;35:187–196. [Google Scholar]
- Stoolmiller M. Correcting estimates of shared environmental variance for range restriction in adoption studies using a truncated multivariate normal model. Behavior Genetics. 1998;28(6):429–441. doi: 10.1023/a:1021685211674. [DOI] [PubMed] [Google Scholar]
- Stoolmiller M. Implications of the restricted range of family environments for estimates of heritability and nonshared environment in behavior-genetic adoption designs. Psychological Bulletin. 1999;125(4):392–409. doi: 10.1037/0033-2909.125.4.392. [DOI] [PubMed] [Google Scholar]
- U.S. Department of Labor, Bureau of Labor Statistics. NLS Web-Investigator, 2007 [Data file] 2007 Available from http://www.bls.gov/nls/nlsdata.htm.
- U.S. Department of Labor, Bureau of Labor Statistics. National Longitudinal Surveys. [Retrieved November 24, 2009];2009 from http://www.bls.gov/nls/publications.htm.
- Van Hulle CA, Rodgers JL, D’Onofrio BM, Waldman ID, Lahey BB. Sex differences in the causes of self-reported adolescent delinquency. Journal of Abnormal Psychology. 2007;116(2):236–248. doi: 10.1037/0021-843X.116.2.236. [DOI] [PubMed] [Google Scholar]
- Viding E, Spinath FM, Price TS, Bishop DVM, Dale PS, Plomin R. Genetic and environmental influence on language impairment in 4-year-old same-sex and opposite-sex twins. Journal of Child Psychology and Psychiatry. 2004;45:315–325. doi: 10.1111/j.1469-7610.2004.00223.x. [DOI] [PubMed] [Google Scholar]
- Wadsworth SJ, Corley RP, Hewitt JK, DeFries JC. Stability of genetic and environmental influences on reading performance at 7, 12, and 16 years of age in the Colorado Adoption Project. Behavior Genetics. 2001;31(4):353–359. doi: 10.1023/a:1012218301437. [DOI] [PubMed] [Google Scholar]