Revisiting the Ramachandran plot from a new angle

Abstract

The pioneering work of Ramachandran and colleagues emphasized the dominance of steric constraints in specifying the structure of polypeptides. The ubiquitous Ramachandran plot of backbone dihedral angles (φ and ψ) defined the allowed regions of conformational space. These predictions were subsequently confirmed in proteins of known structure. Ramachandran and colleagues also investigated the influence of the backbone angle τ on the distribution of allowed φ/ψ combinations. The “bridge region” (φ ≤ 0° and −20° ≤ ψ ≤ 40°) was predicted to be particularly sensitive to the value of τ. Here we present an analysis of the distribution of φ/ψ angles in 850 non-homologous proteins whose structures are known to a resolution of 1.7 Å or less and sidechain B-factor less than 30 Ų. We show that the distribution of φ/ψ angles for all 87,000 residues in these proteins shows the same dependence on τ as predicted by Ramachandran and colleagues. Our results are important because they make clear that steric constraints alone are sufficient to explain the backbone dihedral angle distributions observed in proteins. Contrary to recent suggestions, no additional energetic contributions, such as hydrogen bonding, need be invoked.

Introduction

The “Ramachandran plot” is an iconic image of modern biochemistry. In the late 1950s and early 1960s, Ramachandran and colleagues investigated the inter-atomic separations between nonbonded atoms in crystal structures of amino acids and related compounds.^1,2 For different types of atom pairs, for example between C and C, C and O, and so on, they specified two sets of allowed inter-atomic separations, the “normally allowed” and a smaller, “outer limit.” Subsequently, they assessed all possible combinations of backbone φ, ψ angles for an alanyl dipeptide mimetic (N-acetyl-l alanine-methylester) (Fig. 1), and identified those φ/ψ combinations that are consistent with allowed inter-atomic separations (where φ is the dihedral angle defined by rotation around the N-C_α bond of the backbone atoms C′-N-C_α-C′, and ψ is the dihedral angle defined by rotation about the C_α-C′ bond involving the backbone atoms N-C_α-C′-N). Plotting the allowed φ/ψ combinations yields Ramachandran plots, which are typically made for both the normal and outer limits.

Figure 1.

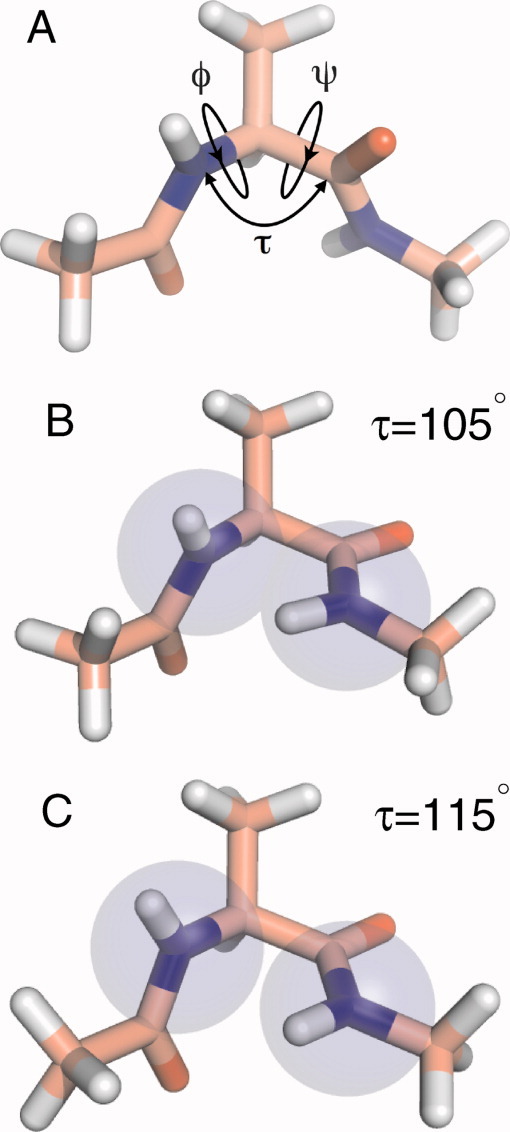
Stick representation of alanyl dipeptide mimetics. Atom types are color-coded: carbon = pink, nitrogen = blue, oxygen = red, hydrogen = white. A: The backbone dihedral angles φ and ψ and the bond angle τ are indicated. B: τ = 105°, φ = −90°, ψ = 0° (i.e., bridge region values of φ and ψ). Blue-shaded spheres indicate steric overlap between main-chain nitrogens for this value of τ. C: τ = 115°, φ = −90°, ψ = 0° (i.e., bridge region values of φ and ψ). Blue-shaded spheres indicate no steric overlap between main-chain nitrogens for this value of τ. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

In this article, we will investigate how the main chain angle τ, which is defined by the backbone bond angle C′-C_α-N, affects the conformation of a peptide backbone. For an ideal tetrahedral sp³ carbon, τ = 109.5° (Fig. 1). Ramachandran and colleagues realized that the allowed combinations of φ and ψ angles in a peptide backbone are influenced by the value of τ, and indeed they published plots showing this dependence for the Ala dipeptide.^1,2 Thus, in fact, there are many Ramachandran plots because the allowed regions of φ and ψ depend on the value of τ for which the map is calculated (Fig. 2). The crystal structures of proteins confirmed that the φ/ψ combinations predicted by Ramachandran, for an “average” value of τ = 110°, were indeed those populated by amino acids within proteins.² Nowadays, Ramachandran plots are the “gold standard” against which new crystal structures are evaluated.³ The remarkable finding of Ramachandran et al. is that they were able to predict the φ and ψ dihedral angles of known protein structures without considering electrostatic, solvent-mediated or any other interactions.

Figure 2.

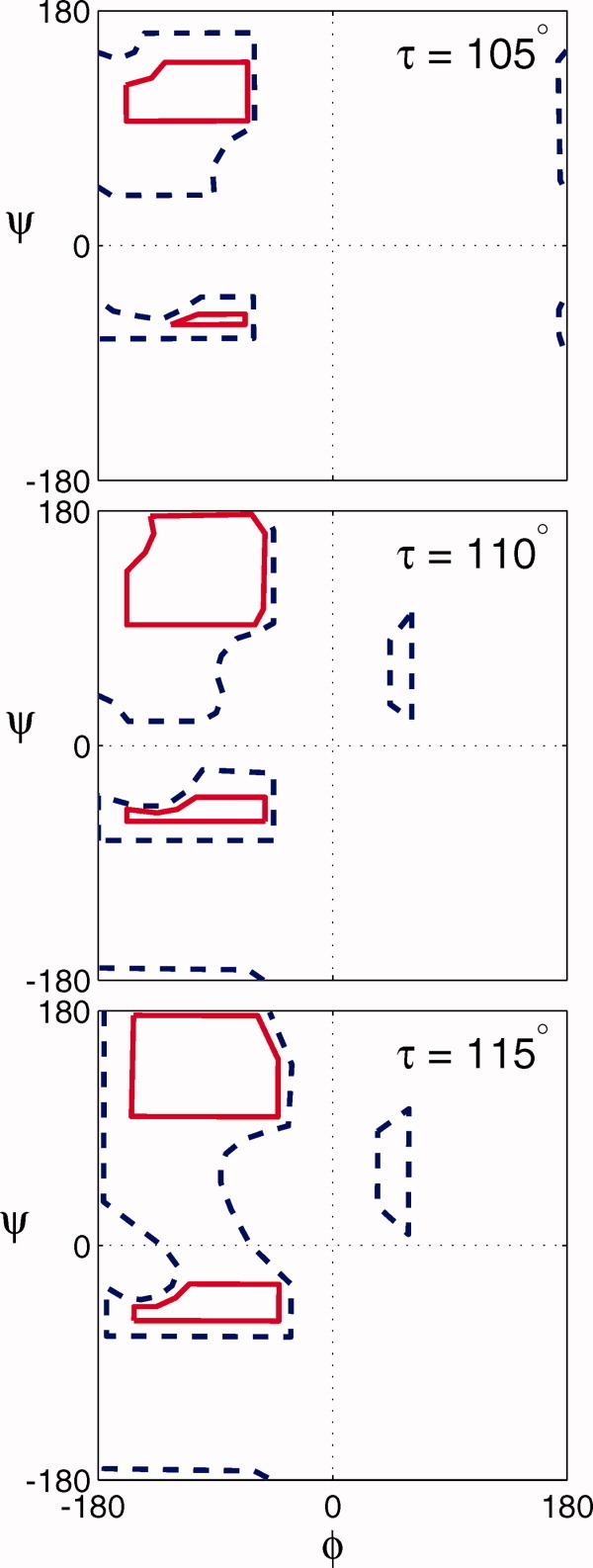
Calculated Ramachandran Plots. Ramachandran plots of allowed φ/ψ combinations for three values of τ.² The solid red lines enclose the “normally allowed” φ/ψ combinations and the dashed blue line indicates the “outer limit”. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Results and Discussion

With the large number of high resolution crystal structures of proteins now available, it is appropriate to revisit the Ramachandran plot, to examine the relationship between allowed φ and ψ angles and the backbone bond angle τ. Evidently, this angle can be widened or contracted significantly from the tetrahedral geometry to accommodate various other strains in the structure.^4–6 Figure 3(A) shows a histogram of the values of τ for 86,299 residues in 850 nonhomologous proteins, which we will refer to as the Dunbrack database.⁷ The distribution is centered on τ = 110.8°, with a range between 100° and 120° (which includes more than 99% of the data points). Figure 3(B) shows a similar plot, but for each residue individually. It is evident that the distribution of τ is similar for each amino acid. There is no systematic dependence of either the mean value or standard deviation of τ with respect to amino acid type.

Figure 3.

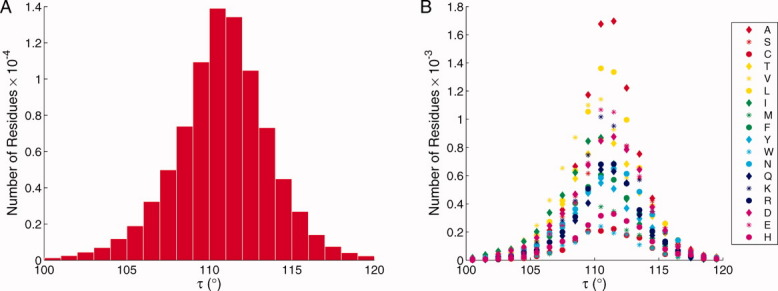
Distribution of the bond angle τ. A: Distribution of τ for all 86,299 residues in the Dunbrack data base (excluding Gly and Pro). Number of residues plotted against the indicated τ ranges. B: Distribution of τ for each type of residue in the Dunbrack data base (excluding Gly and Pro). The residue types are identified using the single letter code. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

For all amino acids in the Dunbrack database, we constructed φ/ψ plots for different ranges of τ: 100°–104°, 104°–108°, 108°–112°, 112°–116°, and 116°–120° (Fig. 4). For ease of viewing in Figure 4, we show the scatter plots of φ/ψ angles from amino acids in the Dunbrack database overlaid on an average Ramachandran plot.⁸ Of particular note are the residues with φ/ψ values in the so-called “bridge region” (φ ≤ 0° and −20° ≤ ψ ≤40°).⁹ It is clear that the fraction of residues with φ/ψ angles in the bridge region (F_bridge) increases as a function of τ [(Fig. 5(A)]. This increase in F_bridge (roughly by a factor of 3) from τ = 105° to 115° is consistent with the increase in area of the allowed part of the bridge region relative to the area of the total allowed region of the φ/ψ map predicted by Ramachandran and colleagues from their hard-sphere models of dipeptides. Figure 5(B) shows a similar plot, but for each residue individually. It is evident that the increase in the fraction of residues with φ/ψ values in the bridge region as a function of τ is similar for each amino acid type.

Figure 4.

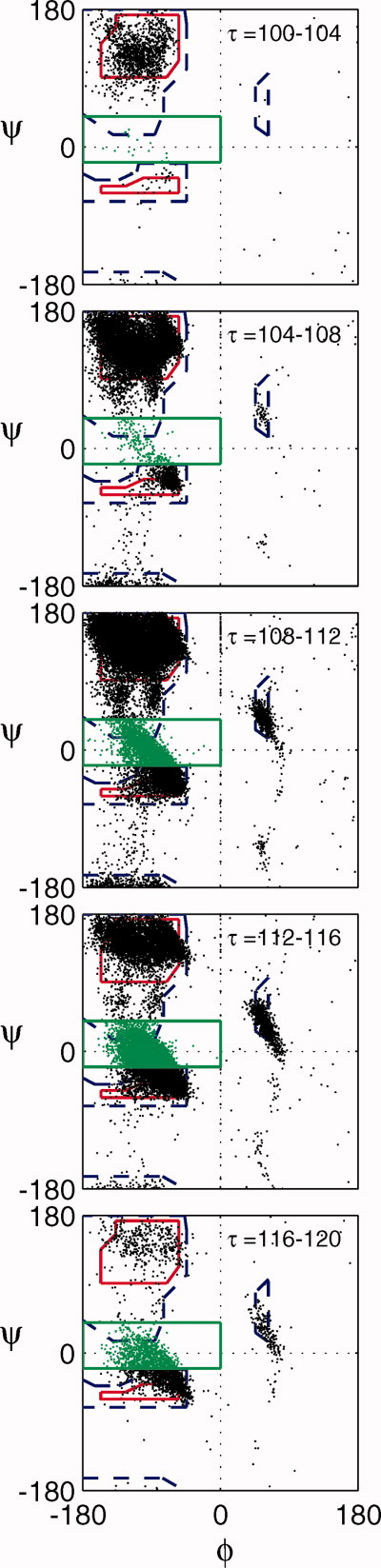
Observed φ/ψ combinations for all residues. The observed φ/ψ distribution as a function of the indicated ranges of τ for residues in the Dunbrack database (excluding Gly and Pro). The data are overlaid on an average Ramachandran plot.⁸ The solid red lines enclose the “normally allowed” φ/ψ combinations and the dashed blue line indicates the “outer limit”. Residues within the bridge region are colored in green. The bridge region is defined by the area within the solid green lines. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Figure 5.

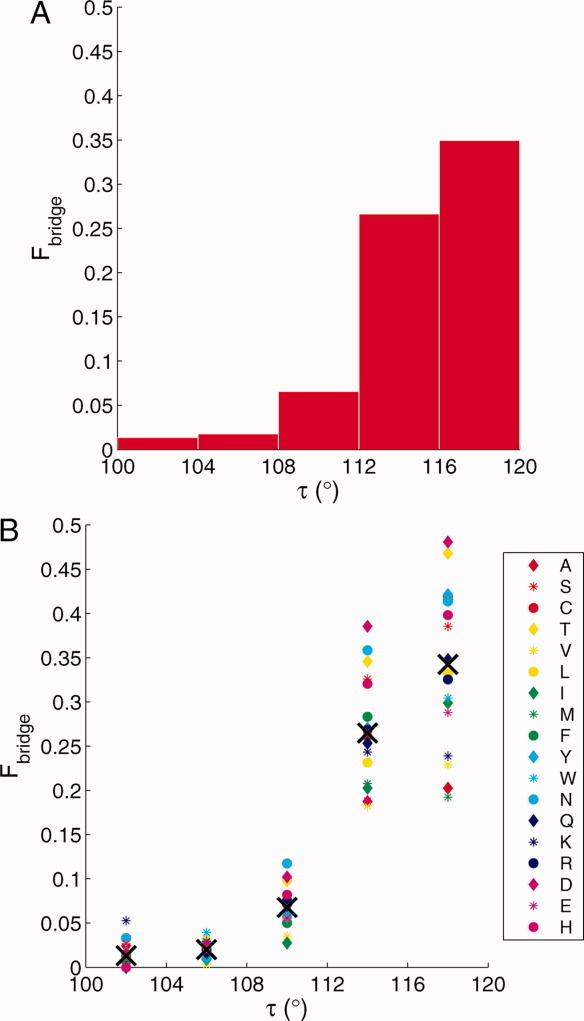
Fraction of residues with φ/ψ angles in bridge region. A: Fraction of residues, F_bridge, with φ/ψ angles in the bridge region as a function of the indicated τ ranges. B: The fraction, F_bridge, of each residue type with φ/ψ angles in the bridge region as a function of the indicated τ ranges. The residue types are identified using the single letter code. The crosses indicate the average value for each range of τ.

Porter and Rose⁹ recently suggested that it might be advantageous to “re-draw the conventional Ramachandran plot by applying a hydrogen-bonding (H-bonding) requirement as an additional energetic criterion.” They argued that the φ/ψ combinations in the bridge region prevent water from H-bonding with the backbone nitrogen of the neighboring residue. They thus speculated that even though the φ/ψ combinations in the bridge region are sterically allowed, the penalty for nitrogen not H-bonding with water excludes residues from occupying the bridge region unless they form intra-peptide H-bonds in the folded protein.

They also noted, however, that in proteins of known structure, many residues are found with φ/ψ angles in the bridge region (Fig. 4). They rationalized this apparent contradiction by suggesting that “almost all the 30,924 residues in the disfavored bridge could be classified readily into one of three local hydrogen bonded motifs.” In other words, they suggested that the reason that φ/ψ angles corresponding to the bridge region are adopted by amino acids in folded proteins is because they are always associated with H-bonding to polar groups other than water, for example, the carboxyl group on a nearby residue.

In light of our findings concerning the τ dependence of the φ/ψ distribution, we chose two different amino acid types: Serine, which is capable of intra-peptide H-bonding, and Leucine, which is not, and tracked the distribution of allowed φ/ψ angles as a function of τ for both residue types. These results, shown in Figure 6, make clear that the same trend—increasing τ correlates with increasing percentage of residues with φ/ψ angles in the bridge region—applies to both Serine and Leucine equally.

Figure 6.

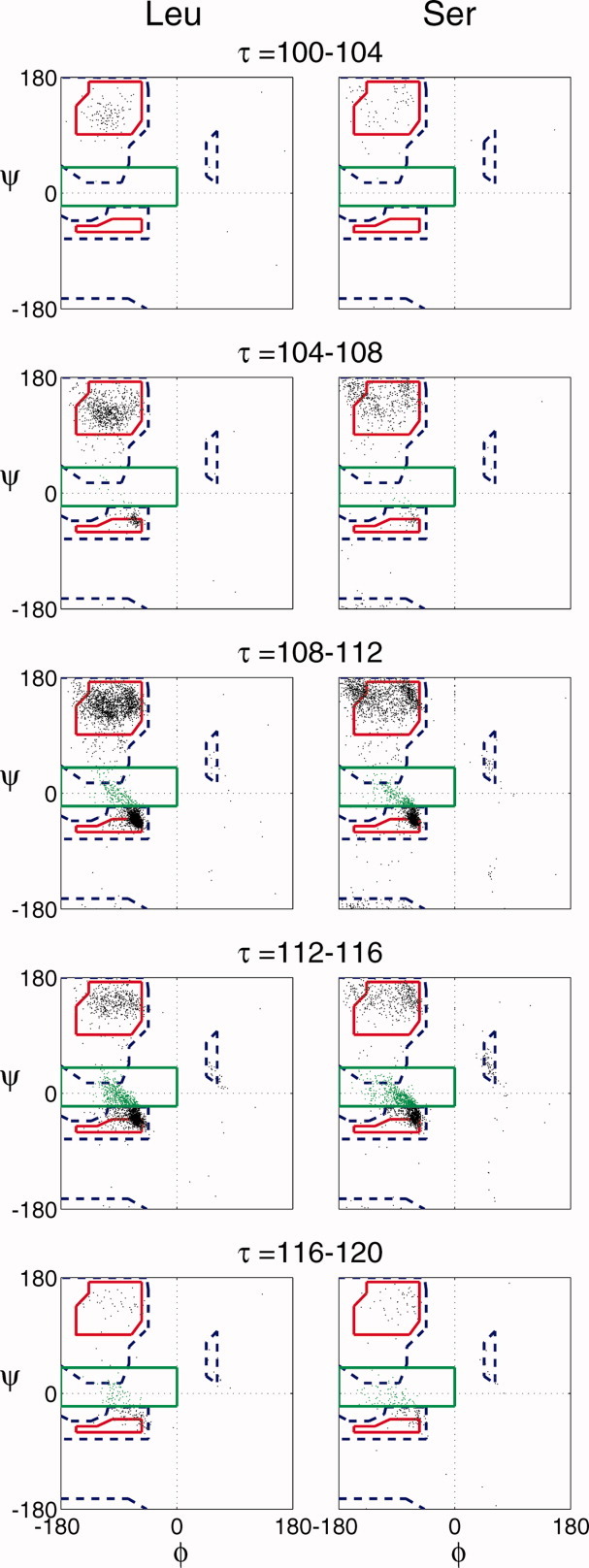
Observed φ/ψ combinations for Serine and Leucine. The observed φ/ψ distribution as a function of the indicated ranges of τ for all Ser (left column) and all Leu (right column) residues in the Dunbrack database. The data are overlaid on an average Ramachandran plot. The solid red lines enclose the “normally allowed” φ/ψ combinations and the dashed blue line indicates the “outer limit.” Residues within the bridge region are colored in green. The bridge region is defined by the area within the solid green lines.

In summary, we have shown that the distribution of backbone dihedral angles observed in proteins of known structure is well explained by Ramachandran and coworker's original analysis of an alanyl dipeptide, where only repulsive hard-sphere interactions together with bond length and angle constraints determine the allowed φ/ψ angles. Particularly, the original analysis showed an increase in the region of allowed φ/ψ dihedral angles (predominantly in the bridge region) as τ increases. For φ/ψ dihedral angles in the bridge region, larger τ relieves the clashes between N and N_i+1 and N_i and HN_i+1 [Figs. 1B,C]. Our analysis shows that in proteins of known structure the relationship between the regions of allowed φ/ψ dihedral angles and the bond angle τ is predicted by the original calculations of Ramachandran and coworkers. We find no need to invoke additional interactions to explain the backbone conformations of proteins.

Materials and Methods

Protein database

850 high-resolution non-homologous protein structures solved by X-ray crystallography (resolution ≤1.7Å, B-factor of sidechains <30Ų, R-factor ≤ 0.25, sequence identity <50%) were obtained from the Protein Data Bank (PDB) and prepared by R. L. Dunbrack, Jr. as follows: Hydrogen atoms were added to the structures using the REDUCE program.¹⁰ Side chains with atom-atom clashes were either flipped to satisfy hydrogen-bonding requirements or removed by the PROBE program.¹¹ The placement of the hydrogen atoms does not affect the backbone conformation. The list of PDB chains is available at http://dunbrack.fccc.edu/bbdep/bbdepformat.php (May 2002 version).⁷

Calculations and nomenclature

The φ dihedral angle was defined by the clockwise rotation around the N-C bond (viewed from N to C) of the backbone atoms C′-N-C_α-C′. The ψ dihedral angle was defined by the clockwise rotation about the C_α-C′ bond (viewed from C to C′) involving the backbone atoms N-C_α-C′-N. Bridge residues were defined as those with φ ≤ 0° and −20° ≤ ψ ≤ 40°. The main chain angle τ was defined as the bond angle between N-C_α-C′. The “average Ramachandran plot” shown in Figures 5 and 6 was taken from the X-PLOR user manual.⁸ F_bridge, the fraction of residues with φ/ψ in the bridge region, is defined by

(1)

where N_bridge(τ) is the number of residues with φ/ψ angles in the bridge region for a given τ range and N(τ) is the total number of residues for a given τ range.  We exclude Glycine from all calculations because its lack of a side chain makes the distribution of φ/ψ angles significantly different from that of all other amino acid types. We also exclude Proline from all calculations because the pyrrolidine ring essentially fixes φ and thus significantly limits the distribution of φ/ψ relative to that of all other amino acids.

Glossary

Abbreviations

Ala dipeptide

N-acetyl-L-alanine-methylester

C′

carboxyl carbon