TMKink: A method to predict transmembrane helix kinks

Abstract

A hallmark of membrane protein structure is the large number of distorted transmembrane helices. Because of the prevalence of bends, it is important to not only understand how they are generated but also to learn how to predict their occurrence. Here, we find that there are local sequence preferences in kinked helices, most notably a higher abundance of proline, which can be exploited to identify bends from local sequence information. A neural network predictor identifies over two-thirds of all bends (sensitivity 0.70) with high reliability (specificity 0.89). It is likely that more structural data will allow for better helix distortion predictors with increased coverage in the future. The kink predictor, TMKink, is available at http://tmkinkpredictor.mbi.ucla.edu/.

Introduction

Roughly half of all transmembrane helices contain bends or other deviations from ideality.^1,2 Distortions in helix geometry can facilitate conformational changes required for protein function by providing sites of flexibility^3,4 and can be important for positioning key residues precisely in the structure.⁵ Kinks that open the polar backbone to alternative hydrogen bonds are often wedged by water, thereby providing a polar region within the hydrophobic core.⁶ Proline kinks can also prevent off-pathway events during the folding of membrane proteins, thereby serving as a negative design feature.⁷

Because of the common occurrence of helix breaks in membrane proteins, predicting where they occur could be an important tool for membrane protein structure prediction.^8,9 Existing structure prediction efforts have typically started with the prediction of transmembrane helices that are then packed together in a separate step.^8,10–13 Clearly, knowing where helix deviations are likely to occur would be useful information for packing together transmembrane segments, but this requires that local sequence at least partially encodes the distortion. An early indication that local sequence can provide predictive information about helix deviations was the work of Rigoutsos et al., who found predictive patterns in transmembrane sequences, although the database at the time was too small to perform rigorous cross validation.¹⁴ Langelaan et al. developed a kink prediction method exploiting the recent dramatic improvement in database size, but the performance is hard to assess because the database did not exclude homologous proteins.²

One sequence signature that is clearly a powerful indicator of helix kinking is the presence of a proline, an amino acid that is incompatible with a helix.^1,2,5,15,16 Yohannan et al. found that kinks can often be identified by looking for prolines in the aligned sequences of homologs.⁵ For 36 of 39 kinks examined, Pro occurred near the kink in at least 10% of homologous family members. More recent work with a larger database suggests that the Pro signature may much be less common than originally seen,¹ however (also see below). Nevertheless, it is clear that Pro in either the protein itself or in a homolog provides strong predictive information.

There are indications that nonproline residues can also provide information about kink formation, although the picture is much less clear. Hall et al. found that Ser, Thr, and Gly are common in kinked helices.¹ Ser and Thr may collaborate with Pro to modulate bend angle.¹⁷ Langelaan et al. did not observe the enhancement in Ser, Thr, and Gly frequencies but did find changes in the prevalence of other polar residues.² Clearly as our database expands, our understanding of residue preferences is evolving.

Here, we examine kinked helices and find that there are distinct residue preferences in kinked versus nonkinked helices in a nonredundant database. We exploit these differences and residue conservation to predict kinked helices using a neural network algorithm.

Results and Discussion

Kinked helix search space

To identify possible sequence differences between kinked and nonkinked helices, we first constructed a library of kinked and nonkinked regions from a database of 41 nonhomologous, high-resolution membrane protein structures. Although there are now many more unique structures available, we believe it is important to reduce biases as much as possible by only using unrelated proteins.

We examined nine-residue segments of transmembrane helices and identified 323 kinked and 567 nonkinked segments, defined by strict bend angle criteria as described in Methods. Using only bend angle criteria has the disadvantage of lumping together many different helix anomalies (π-helix, 3₁₀ helix, etc.).¹⁶ Moreover, some helix distortions do not lead to a change in bend angle and are ignored by this criterion. Nevertheless, we are restricted by the small data set of nonhomologous high-resolution membrane protein structures currently available, so we opted not to refine the kink type categories further.

We bolstered the limited sequence data available by adding information from homologous sequences to each segment. We counted the amino acids found at each position in the kinked and nonkinked segments, but we reduced counting biases by (1) weighting the counts by sequence divergence so as not to overcount close homologs to the protein of known structures and (2) using only 100 randomly chosen homologs per segment so that all segments were roughly equally weighted (see Methods). We were unable to find 100 homologs for 75 of the kinked segments, and these were eliminated from the residue preference analysis.

Amino acid preferences in kinked helices

The observed amino acid abundance ratios for kinked versus nonkinked helices are shown in Figure 1 (histograms corresponding to this data can be found in Supporting Information Fig. S1); the kink center was defined as position 5. As expected from prior work,^1,2,5 Pro is highly overrepresented at positions 5 through 9 of the kinks. The bias of Pro toward the C-terminus of kinks makes sense because the loss of the hydrogen bond and steric clashes occur at residues preceding the proline. The spread of Pro over many kink positions at least partly reflects the difficulty of defining the center of a kink as well as diversity of kink structures. The overall occurrence of Pro in kinks is lower than we had observed previously.⁵ In particular, we found that in a smaller, less diverse database, ∼ 90% of kinks contained Pro in 10% of homologs. In the current database, the percentage decreased to 56%. Although Pro had the most pronounced change, other residues also exhibited significant biases. Other than Pro, the residues that were at least twofold overrepresented in kinked helices were as follows: Trp at position 1, Asn at position 4, Trp at position 6, and Glu at position 8. Residues at least twofold underrepresented were Glu at position 1, Asn at position 2, Gln at position 3, Thr, Lys, and Arg at position 4, Asn at position 6, His at postion 7, Gln at postion 8, and Arg at postion 9. The relative dearth of strongly polar residues in kinked helical regions was also observed by Langelaan et al.² This result is perhaps surprising as polar side chains might be expected to help satisfy any broken backbone hydrogen bonds¹ or support hydrogen bonding to water molecules that often wedge kinks.⁶ We do not see the preferences for Gly, Ser, and Thr observed by Hall et al.¹ nor the dramatic enhancement of Asp noted by Langelaan et al.,² perhaps because of differences in our database construction. Because of the variety of kinks and the likely variety of kinking mechanisms, however, understanding the reason for the residue preferences in kinks is not straightforward. Nevertheless, the results indicate that there are differences in amino acid composition in kink positions that could be exploited for kink prediction.

Figure 1.

Amino acid composition differences in kinked and nonkinked transmembrane segments. The ratio of residue frequencies in kinked versus nonkinked nine-residue segments from the strict database is shown. Darker regions signify residues that are overrepresented when comparing kinked to nonkinked structures. The position in the segment is labeled along the horizontal axis, and residue type is labeled along the vertical axis. A numerical scale has been provided in the bottom half of the figure. A more quantitative view of this data is provided by histograms in the Supporting Information. This heatmap was generated using Matrix2png.¹⁸

A kink predictor

We developed a neural network analogous to secondary structure prediction algorithms.^19–21 A feedforward network consisting of an input, hidden, and output layer was constructed as shown in Figure 2. The network inputs were amino acid sequence composition at each position and a measure of sequence conservation as described under Methods. The weights were adjusted using back propagation,²¹ and we employed early stopping to prevent overtraining of the network.²² Network performance was assessed using the leave-one-out method. We found that five hidden nodes provided the best performance on the strict set of training kinks and nonkinks. We also tested performance with 7, 9, 15, and 19 residue window sizes and found that a nine-residue window resulted in the best network performance.

Figure 2.

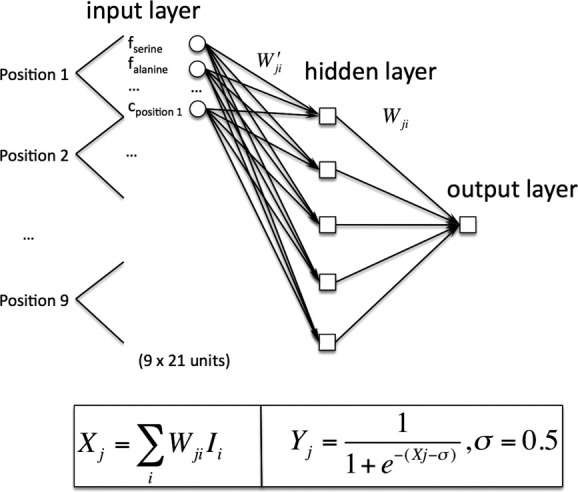
Neural network design. The neural network consisted of three layers: input, hidden, and output. The inputs are the weighted fractions of each residue type and a conservation score for each position in a set of homologous sequences (see Methods). The total number of inputs was 189 because of 9 positions × 20 residues for each candidate, and nine conservation score inputs. Two sets of weight matrices were evolved through learning: one between the input and hidden layers and the other between the hidden and output layers. For the output layer, the corresponding expressions are highlighted below and have been left general so as to also apply to the hidden layer. I_i denotes input (i.e., output from hidden node i) and W_ji its corresponding weight. i denotes the hidden node number and j the output node number into which it goes. Y_j denotes the output from a given output node. Sigma is the threshold of a neuron. The expressions are similar for the hidden layer, with weights W_ji′ used in place of the previous weights.

The performance of the network can be seen in the receiver–operator characteristic plot shown in Figure 3. We defined a network output threshold that maximized the Matthews correlation coefficient for the strict and relaxed kink databases. The threshold point for the strict database is shown in Figure 3 and yields a Matthews correlation coefficient of 0.40. At this threshold, the sensitivity is 0.46 and the specificity is 0.99. Thus, about half of all kinks are predicted and those that are predicted are almost always correct.

Figure 3.

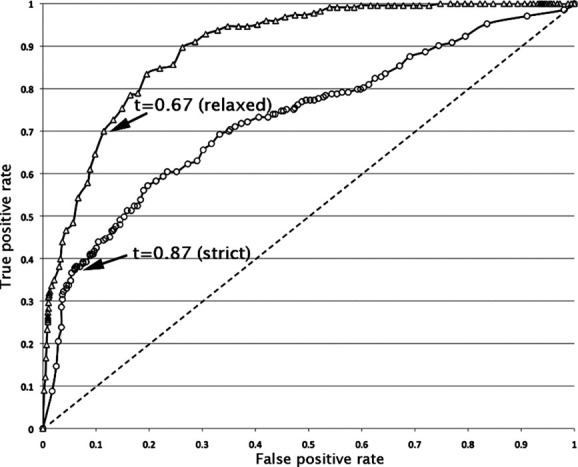
Receiver–operator characteristic plots for prediction performance. The black solid lines represent the receiver–operator curves for leave-one-out validation on the strict and relaxed databases. Statistics are provided in Table I.

We next tested the kink predictor with more realistic criteria. The training data set employed strict criteria to rigorously separate kinks and nonkinks, but it omits visually obvious kinks. We therefore tested our kink predictor using more relaxed criteria for kink identification that more accurately reflect what is seen by eye (see Methods). We also assessed prediction performance more accurately in practice by performing predictions across all possible protein windows rather than just selected nine-residue windows in our strict database. Using the relaxed criteria, the sensitivity increased to 0.70 and the specificity diminished somewhat to 0.89. The statistics described in Table I indicate that the majority of kinks are predicted, and when a kink is predicted, it is almost always a correct prediction. As there were no known freely available TM kink prediction algorithms with which to compare our method, we compared our prediction algorithm to a well-known secondary structure prediction algorithm developed for soluble proteins PSIPRED.²³ We defined predicted kinks as a predicted coil or strand and nonkinks as predicted helices. The results using the relaxed kink criteria are shown in Table I. Considering the very different physicochemical basis of helix formation in soluble and membrane proteins, PSIPRED does surprisingly well. Nevertheless, our method clearly outperforms PSIPRED.

Table I.

Statistical Summary of Prediction Performance

Structures	Sensitivity	Specificity	Jack-knife correlation coefficient	Training correlation coefficient	Kink prediction	Nonkink prediction
Strict	0.46	0.99	0.40	0.57	96%	78%
Relaxed	0.70	0.89	0.56	—	62%	92%
PSIPRED relaxed	0.64	0.81	0.42	—	54%	86%

Prediction performance was assessed using the leave-one-out method for the strict set of kink and nonkink structures as well as for the relaxed set of kink and nonkink structures. The PSIPRED results are considered equivalent to a jack-knifed procedure because none of the proteins used in the current database were included in the original soluble protein training database.

The performance for our neural network predictions is illustrated for two known structures in Figure 4. These examples were chosen to simply highlight the types of correct and incorrect predictions possible. To give a fuller picture, predictions for all structures in the database are given in the supplement. The predicted segments were always excluded during network training (see Methods). For the structure 1OTS [Fig. 4(A)], seven kinks were correctly identified (highlighted in red; true positives), four were missed (dark green; false negatives), three nonkinked helices were correctly predicted as nonkinked (true negatives), and there were no false positives. Looking at the four kinks that were missed, it appears from Figure 4(A) that these are relatively subtle bends and may have less distinctive sequence signatures. For the structure 1H2S [Fig. 4(B)], two kinks were correctly identified, one was missed, and the algorithm predicts kinks at five positions that are not kinked. The seventh helix illustrates an error in kink identification. We predict a kink at a point where the helix clearly breaks, but the bend angle does not change. Thus, we would argue that the algorithm actually predicted this deviation correctly, but our method of identifying true kinks in structures is not foolproof. The one missed kink and five mispredicted kinks that are not in fact kinked may be attributed to the fact that 1H2S chain A had only 118 homologs compared to other structures that often had thousands of homologs.

Figure 4.

Examples of predictions. Illustration of kink prediction results using the relaxed database. (A) PDB code 1OTS, chain A and (B) PDB code 1H2S, chain A. The upper section of each figure illustrates the prediction results as a one-dimensional sequence. Transmembrane regions have been highlighted in gray. Regions highlighted in red correspond to correctly predicted regions (true positives), and blue exclamation points to incorrectly predicted positions (false positives). The maximum bend angle in each kinked region has been indicated by a Δ. The center of each kink prediction has been marked with a *, and overlap of a prediction center and the maximum bend angle has been marked with a •. Kinked regions not predicted have been highlighted in green (false negatives). The bottom of the figure shows the structures of the individual transmembrane helices. The coloring scheme is the same as for the upper figure. The correctly predicted kinks are highlighted in red, and the center of each kink prediction is indicated by a red ball at the Cα position. False negatives are highlighted in dark green. False-positive predictions are indicated by a blue ball at the Cα position.

Conclusion

Our results indicate that there are significant sequence differences between kinked and nonkinked transmembrane helices and that these differences can be exploited to predict kinks. This does not mean that kinks are generated only by local sequence, however, as we cannot necessarily link cause and effect. For example, certain residue types may provide stronger long-range contacts that can distort helices. Alternatively, if kink occurrence is more frequent at functional sites, the residue preferences could reflect the likelihood of being in functional sites rather than kinks. It is likely that prediction results could be greatly improved with more structures. Sequence preferences other than proline are much more subtle and seem to vary with database construction. Some of the more subtle sequence pattern information is likely masked because of the limited number of kink classifications we can use. Clearly not all helix distortions are the same, but because of the small dataset, we used a simple binary classification of kinked or nonkinked based solely on bend angle. Ideally, one would like to parse helix bends into distinct classes as the sequence signatures may be quite different. In spite of these limitations, we have been able to develop a prediction method that provides useful information that can be incorporated into helix packing algorithms.^8,11,24 Kink prediction will only improve in accuracy and refinement as more structures become available.

Methods

Structure database

A nonredundant database of membrane proteins was used as the source from which all kinks and nonkinks were identified. None of the sequences shared more than 30% sequence identity, and only structures solved at a resolution of 2.5 Å or better resolution were retained. This resulted in a total of 41 membrane protein structures: 1C3W, 1EHK, 1H2S, 1JB0, 1K4C, 1KB9, 1KQF, 1NKZ, 1OKC, 1OTS, 1Q16, 1SU4, 1U19, 1V54, 1XIO, 1XQF, 1Z98, 2A65, 2AHY, 2BHW, 2BL2, 2BS2, 2F2B, 2FBW, 2J58, 2J7A, 2J8C, 2NQ2, 2RH1, 2UUI, 2VPZ, 2W2E, 2WGM, 2Z73, 2ZXE, 3B45, 3B9W, 3BKD, 3C02, 3DDL, and 3KCU.

Kinked and nonkinked transmembrane helix identification

Kink and nonkink identification was performed differently for training and for validation purposes. To ensure that we only trained on the clearest, most well-defined kinks, we were particularly strict in our training set definitions. Subsequently, to more accurately assess our prediction performance, we relaxed the criteria to identify all genuine kinks and nonkinks. The strict and relaxed criteria are described below.

Kinked and straight helices were identified by measuring bend angles of nine-residue stretches of transmembrane helices. Only unique chains for each structure were used. For each chain, the transmembrane regions defined in the Orientations of Proteins in Membranes (OPM) database²⁵ were used as a starting point. The transmembrane region was then extended to the end of the helix if the region was defined as helical by DSSP.²⁶ These extended helices constituted the template from which the nine-residue segments were extracted, although only segments with a center residue within at least one residue of the transmembrane region (as defined by OPM) were retained. Kinks and nonkinks for transmembrane helical regions were identified using bend angles measured using the ProKink plug-in available for Simulaid.²⁷

To extract kinked segments using strict criteria for training purposes, the nine-residue segments were filtered using several steps. First, the bend angle of all segments was sorted from largest to smallest. Beginning with the largest bend angle segment, nearby segments were eliminated if they overlapped. This process was repeated for every remaining structure in order of decreasing bend angle. Those segments that remained were then filtered using two criteria. The average bend angle over four neighboring sliding windows was required to be greater than (or equal to) 13°, or the bend angle for any individual window was required to be greater than 24°. If only three or fewer neighboring windows were available because they were at a helix end, then any candidate with a bend angle of 13° or less was thrown out. Ultimately, using the strict criteria, 323 kinked structures were obtained.

To identify clear nonkinked segments, we also employed strict criteria. First, the bend angle of all segments was sorted from smallest to largest. Any window exceeding 20° in bend angle was immediately discarded. Beginning with the smallest bend angle segment, nearby segments were eliminated if they overlapped. This process was repeated for every remaining structure in order of increasing bend angle. Those structures that remained were then filtered using two criteria: the average bend angle over four neighboring segments was required to be less than 8°, and the bend angle for every individual segment had to be less than 20°. In this manner, 567 nonkinked segments were obtained.

For prediction assessment we employed relaxed criteria that identified more visually obvious bends. A kink was identified as an authentic kink if the average bend angle over three neighboring windows was greater than (or equal to) 10° or the bend angle of an individual window was greater than 18°. A total of 2048 relaxed kink windows were extracted. This does not mean that there are 2048 kinks because overlapping windows can contain the same kink. We wanted to identify all kink windows for assessment of predictions because all possible windows are tested in kink prediction. Nonkink regions were identified as all regions other than the identified kink regions above.

Family building

Similar sequences in RefSeq's nonredundant protein sequence database²⁸ were identified using PSIBLAST with one iteration, and a P-value cutoff of 1e − 10 to ensure close similarity between the known structure and its sequence homologs. The number of sequences identified was limited to 30,000. Any aligned sequences with an alignment length less than 70% of the length of the original sequence were discarded. All nonnative gapped regions were discarded.

To count amino acid frequencies at each position, the counts were weighted by (1-% identity) to incorporate some information about the likelihood a residue might have changed in the homologous sequence (% identity refers to the whole protein). Thus, when a homolog sequence is 100% identical to the sequence of the known structure, the new amino acid is not counted. In this manner, close homologs do not overweight the counting statistics.

For input to the neural network, each residue at a given position of the original candidate sequence was added at full weight a fixed number of times per homolog. The number of times was optimized to maximize network performance; this value was 2.

This weighting scheme is described by the following equation for the 180 inputs corresponding to the 9 positions × 20 amino acids:

Use of sequence conservation

Sequence conservation scores were used as inputs to the neural network in addition to the primary sequence. Conservation scores were calculated for the nine-residue segment belonging to each candidate sequence window. This was accomplished by using the PSIBLAST data produced by the family building step described above. From all pairwise alignments for each PDB/chain, 3000 were randomly selected and conservation scores calculated using SCORECONS with the Trident scoring method.²⁹ For this purpose, ClustalW-formatted pseudo-alignments were constructed.³⁰ Positions with excessive gaps were assigned a score of 0.

Neural network design

A feedforward neural network consisting of an input, hidden, and output layer was constructed. There were 9 (positions) × 20 (amino acids) = 180 inputs to the network related to the fractional occurrence of all possible residue/position combinations (as described by the input equation above). In addition, we used nine inputs corresponding to the conservation scores of the nine residues in the native sequence. Two sets of weight matrices were evolved through learning: one between the input and hidden layers and the other between the hidden and output layers. Weights were randomly assigned to values between −0.5 and 0.5 to start. The number of hidden nodes was optimized according to network performance, and the best performance was found to occur using five hidden nodes. The output layer is governed by the following equations, which have been left general so as to also apply to the hidden layer. I_i denotes the input (i.e., output from hidden node i) and W_ji its corresponding weight. i denotes the hidden node number (e.g., 3) and j the output node number into which it goes. Y_j denotes the output from a given output node. Sigma is the threshold of a neuron and was set to 0.5²¹:

The expressions are similar for the hidden layer, with weights W′_ji used in place of the previous weights. For each cycle, the weight matrices were adjusted once for each example in the training set. Training was performed over 1000 cycles. The order of training examples during weight adjustments was shuffled every cycle to reduce any noise due to ordering.

Weight adjustment was performed in the following fashion. The output layer consisted of a single node predicting whether a candidate sequence was a kink (maximum output value of 1) or a nonkink (minimum output value of 0). The error in this output value for each training example was computed as follows:

where D is the correct value and Y is the predicted value.²¹ Adjustments to the weight matrix between the hidden and output layers were made according to the expression:

where η is the learning rate. The optimal learning rate was found to be 0.1 (according to how far training progressed). The weight matrix between the input and hidden layers was adjusted by first back propagating the error according to the expression²¹:

The weight layer adjustments were then made using the W_ji (t + 1) expression above but with weights W′_ji used in place of the previous weights, error δ_I′ in place of the previous error, and inputs to the appropriate layer.

Early stopping was used to prevent overtraining. To find the point at which overtraining occurs, we evaluated the network every 10th cycle (of 1000 cycles) for its ability to predict structures in a test set that was not used for training. The test set consisted of 50 kinked and 50 nonkinked structures. The total error over all test set examples was computed as follows:

The training network for which the lowest total error occurred on the test set was taken as the best network.²²

Training and test set creation

To ensure no bias in the datasets used for training and early stopping, kink and nonkink selection was randomized. Test set kink selection was done by selecting 50 structures at random from the total number of identified strict kinks. Similarly, test set nonkink selection was done by selecting 50 structures at random from the total number of identified strict nonkinks. These two groups became the test set used for early stopping. The remaining strict structures (273 kinks and 517 nonkinks) were retained for training of the neural network.

Evaluation

Because of limited data for membrane proteins, we chose to use the jack-knife or leave-one-out method to evaluate our strict and relaxed predictions. The threshold for each database (strict or relaxed) was chosen using a receiver–operator plot where the Matthews correlation coefficient was maximized (see Fig. 3). Relaxed predictions were done across all possible protein windows in transmembrane segments. Relaxed evaluation was done using the jack-knife approach for trained examples from the strict database and the best network (i.e., one with lowest total error) for all other structures. Assessment of kinks and nonkinks using the relaxed criteria was done separately. Because it is difficult to unambiguously separate the transition region between kinked and nonkinked regions, a buffer region of four residues to the left and right of the original kinked region centers was created. We only evaluated nonkinked region centers that were more than four intervening residues from this unambiguously defined transition kink area. These residue separations were arrived at after visual evaluation of many structures.

Kinked regions that passed the relaxed criteria were merged together to form contiguous regions when separated by one residue or less. These merged regions defined the contiguous kink regions that would be checked to see if they contained predicted kinks or not. If a contiguous kinked region contained a single kink prediction, it was recorded as a single true positive. If a contiguous kinked region did not contain a single kink prediction, it was recorded as a single false negative.

Nonkinks were evaluated differently. When evaluating a nonkink region, every single nine-residue window contained within the contiguous region was evaluated individually (rather than as a continuous region). If a given window was correctly predicted as a nonkink, it was recorded as a single true negative. If it was incorrectly predicted as a kink, it was recorded as a single false positive. All of these true and false negatives and positives were summed over all predictions. Predictions using the secondary structure prediction algorithm PSIPRED²³ were evaluated in the same way except that predicted coils or strands were defined as kinks. As with kink prediction, a nine-residue window around the predicted coil or strand was defined as the kink region.

Website predictor

De novo prediction by our web application available online is done solely using the primary amino acid sequence of entire proteins. The transmembrane helical regions can be input manually or determined automatically by Proteus2.³¹

We ran three trials of our neural network using five hidden nodes. This resulted in jack-knife networks with correlation coefficients of 0.39, 0.38, and 0.40. We chose to use the network with the highest correlation coefficient. We looked at all networks making up this jack-knife network and retained the network with the lowest total error when early stopped using the test set. This network was installed for use in online predictions.

The network threshold for online predictions was chosen to be that determined by the receiver–operator curve analysis for the relaxed database (t = 0.67). This was done because the relaxed database most closely mirrors practical usage of the prediction software on entire proteins.