Abstract
The traditional method for extracting electron density and other transmembrane profiles from molecular dynamics simulations of lipid bilayers fails for large bilayer systems, because it assumes a flat reference surface that does not take into account long wavelength undulations. We have developed what we believe to be a novel set of methods to characterize these undulations and extract the underlying profiles in the large systems. Our approach first obtains an undulation reference surface for each frame in the simulation and subsequently isolates the long-wavelength undulations by filtering out the intrinsic short wavelength modes. We then describe two methods to obtain the appropriate profiles from the undulating reference surface. Most combinations of methods give similar results for the electron density profiles of our simulations of 1024 DMPC lipids. From simulations of smaller systems, we also characterize the finite size effect related to the boundary conditions of the simulation box. In addition, we have developed a set of methods that use the undulation reference surface to determine the true area per lipid which, due to undulations, is larger than the projected area commonly reported from simulations.
Introduction
Molecular dynamics (MD) simulations can provide more detailed structural and dynamic descriptions of membranes than experiments, although the simulations must first be validated by agreement with whatever experimental data that is available (1–6).
This article deals with an artifact that occurs when comparing large-scale simulations of lipid bilayers consisting of many lipids to experimental x-ray and neutron scattering data. Traditional algorithms for analyzing simulated bilayers have treated them as if they were flat (1–3,7). This has been a reasonable assumption for the small patches that have been simulated on older/slower machines. However, increased computer speed has enabled simulations of laterally larger membrane patches. Larger systems are less vulnerable to finite size artifacts and exhibit true undulations from which the important bending modulus (kc) can be obtained and compared to experiment (8,9). However, as the simulated membrane is made larger, undulations develop and create an artifact in the profiles along the transverse direction, perpendicular to the membrane, when using the flat-patch method. We will focus on electron density profiles (EDP) of lipid bilayers, keeping in mind that neutron scattering length, density, and mass density are all subject to the same artifact, and that the issue is relevant to more complex membranes than just lipid bilayers.
We also note that direct comparison of undulating simulations and undulating experimental systems is not possible due to the much different length scales and/or the multilamellarity in some experimental samples (10,11). The appropriate comparison is to remove the quantitatively different effect of undulations from both simulations and experiment to provide a common reference consisting of profiles along the perpendicular to the local membrane.
In simulations, the flat-patch method defines a flat reference plane that represents the average center of the membrane. Each atom is then binned along the z dimension of a periodic simulation box, according to its distance from a flat plane (1,7,12), usually referenced as z = 0. We refer to EDPs determined under this flat-patch assumption as resulting from the z-bin method. It is not obvious how small a simulated patch must be for the flat-patch assumption to hold, but the general criterion is clear: simulated systems must be small enough that the undulations in the z direction are small compared to the average variations inherent in the EDP. As we will show, this requires fewer lipids than of the order of 100, corresponding to lateral dimensions L ≈ 6.0 nm. Because the bilayer is ∼4.0-nm thick, finite size effects (13) cannot be discounted. Calculated EDPs and corresponding form factors from the z-bin method applied to small bilayer systems are quite capable of accurately reproducing experimental data (1,3–5) by setting the force-field parameters, area or surface tension, but it is important that the values of these fundamental parameters are independent of system size.
Fig. 1 A shows a snapshot from a simulation of a bilayer with 64 dimyristoylphosphatidylcholine (DMPC) lipids that illustrates the flat-patch character of small bilayer simulations. In contrast, Fig. 1 B shows a snapshot from a 1-μs-long MD simulation of a bilayer with 1024 DMPC lipids that exhibit undulations inherent in equilibrated systems. The presence of undulations becomes clear when comparing the global flat bilayer reference plane (dashed-black line) and local bilayer reference surface (wavy line) in the 64-lipid and 1024-lipid systems. In the 64-lipid system, there is negligible difference between the local and global references, whereas in the 1024-lipid system there is considerable difference.
Figure 1.
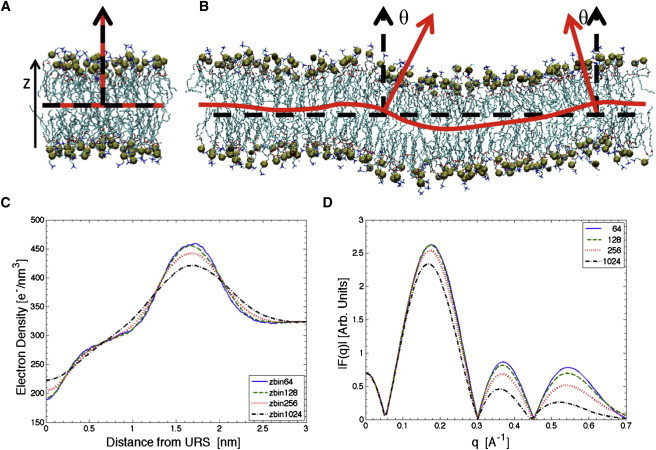
Snapshots of DMPC bilayers with (A) 64 lipids and (B) 1024 lipids. Water is not displayed, but phosphorus atoms are shown (enlarged spheres, emphasizing the top and bottom monolayers). (Dashed lines) Global bilayer reference planes, defined at the z position of the bilayer center of mass. (Solid lines) Local bilayer reference surfaces. Local bilayer normals (solid arrows) and global bilayer normals (dashed arrows) emphasize that the local orientation of the bilayer normals varies for the larger system size in panel B. (C) EDP and (D) form factors, F(q), for 64, 128, 256, and 1024 lipids, all obtained by the artifact-prone z-bin method.
When the EDP is determined via the z-bin method, as shown in Fig. 1 C, a dramatic difference develops as the system size is increased. We will show that this difference is mostly an artifact induced by undulations. Fig. 1 D presents the corresponding form factors, F(q), obtained by Fourier transformation of the EDP; this is the simulation result that should be compared directly to x-ray scattering data. Experimental comparison is greatly compromised when undulations are ignored.
In addition to corrupting the EDP and the F(q), ignoring undulations affects the quantitative evaluation of molecular areas. Often, the simulation box dimensions in the xy plane are used, which is just a projected area Ap and not the true area AL, following an undulating surface (14). Instead, undulations need to be accounted for to determine the actual area per lipid (aL = AL/N) along the bilayer surface (10,15,16), where N is the number of lipids per monolayer. Although this is a small artifact, our methods correct for it.
To extract accurate EDP and AL from simulations of undulating membranes, we first determine the undulation reference surface (URS) depicted in Fig. 1 B. We have developed two different methods to define the URS: the direct Fourier (DF) method and the real-space interpolation (RI) method. For both approaches, we apply a filter in q-space to remove the short wavelength fluctuations intrinsic to disordered membranes and retain the undulation modes that define the URS. Then, to obtain the true EDP, we have developed two methods that determine the local distance of each atom from the URS. Lastly, we employ three methods to determine AL. Comparison of results from the redundant methodologies allow us to assess which are the better methods.
Methods
Simulation methods
Specifics for the construction and simulation of the μs-long, 1024-lipid DMPC (14:0) system are detailed in Section I in the Supporting Material and in the accompanying article by Brandt et al. (17). Additional simulations for systems with 32, 64, 128, and 256 DMPC lipids were run for 500 ns to allow for equilibration and development of undulations. All systems were hydrated with 23 waters per lipid and only the last 10 ns from each system were analyzed for EDP determination by sampling every 2 ps (5000 frames).
Algorithm Development
Calculation of the undulating reference surface
Direct Fourier method
Each frame (snapshot) in the simulation provides values of xk, yk, and zk for the kth atom, where z is the direction along the normal to a flat bilayer, as indicated in Fig. 1 A. Any subset of lipidic atoms can be used in the DF method, but computer time is saved by selecting only one atom type from each lipid. Following Brandt et al. (17), for every frame the Fourier coefficients for the URS are calculated as
| (1) |
where N is the number of lipids per monolayer, and the values in the expression are the lateral atomic coordinates for atom k in monolayer j, with height zjk, where the bilayer is recentered in each frame so that Consistent with periodic boundary conditions, u(q) is defined for wave vectors with (excluding the zero mode with m = n = 0), where Lx and Ly are the lateral dimensions of the periodic simulation box. In the isobaric ensemble simulation with a fixed mean pressure of 1 atm, Lx and Ly were subject to small fluctuations.
Filtering out the nonundulation modes
As described by Brandt et al. (17), u(q) has a contribution from small q = |q| undulatory modes that account for the q−4 part of the fluctuation spectrum For large q the spectral intensity increases and reaches finally a constant value (different for different atoms) at ∼10 nm–1 (17). This part of the spectrum is due to the detailed molecular structure of the lipid bilayer that is not present in a continuum representation. Fig. 2 A shows results for Su(q) when the selected atoms are phosphorus (P) or the terminal SN1 methyl carbon (TC). It is clearly seen that the large q part of the spectrum is sensitive to atom selection, which is further evidence that these modes should not contribute to the URS. In contrast, the q−4 dependence for the small q undulation modes is conserved across atom choice, so those are the modes that should be retained to construct the URS.
Figure 2.
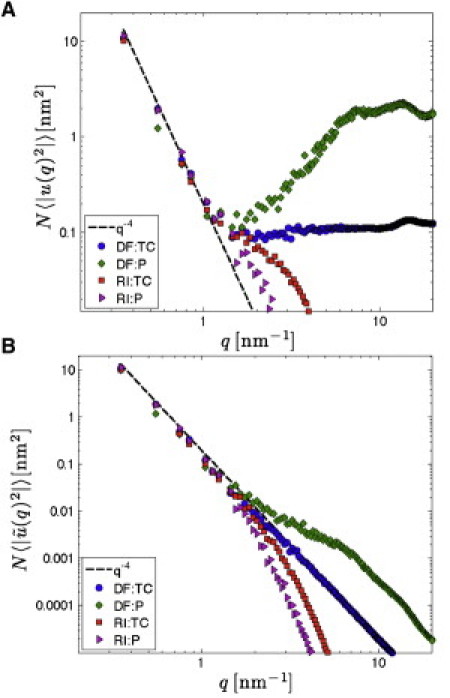
(A) Log-log plot of the one-dimensional unfiltered spectrum Su(q) = N〈|u(q)|2〉 determined using the DF and RI methods for selected atoms P and TC (terminal carbons) versus the magnitude of the wave vector q, for the last 10 ns from the μs-long simulation of the 1024-lipid DMPC system. (B) L4 filtered spectra. Undulations theoretically follow the dashed q−4-lines.
Extraction of the undulatory modes from the u(q) for the URS is accomplished by a filter function G(q/q0), such that
| (2) |
and
| (3) |
There are two issues to address: first is the choice of filter function G, and second is the value of the filter parameter q0 that marks the boundary between lightly and more heavily filtered q values.
A very sharp boundary is given by the simplest ideal (ID) filter function, namely, G(q/q0) = 1 for q/q0 ≤ 1 and G(q/q0) = 0 for q/q0 > 1. An ID filter is usually discouraged in signal processing applications because it results in ringing, i.e., the conspicuous appearance of ripples corresponding to the shortest wavelength not filtered. (Similar behavior appears in the Fourier reconstruction of electron density profiles using a finite set of Bragg orders (18).) However, significant ringing does not occur in the URS when suitable values of q0 are chosen because the amplitude of the largest remaining mode is quite small. Nevertheless, we have constructed URS with conventional filters, particularly the Hamming (HA) filter, and this makes negligible difference with the URS from the ideal filter (see Section II in the Supporting Material).
Another interesting alternative is inspired by the result for the spectrum calculated for the TC atoms, shown in Fig. 2 A, which is closely approximated by
| (4) |
Defining q0−4 = kcB, we introduce the L4 filter function,
| (5) |
which has the property that the filtered undulation spectrum (shown in Fig. 2 B) adopts a pure q−4 shape predicted by continuum theory of undulations (19,20) when q0 is chosen to be 1.15 nm–1. Interestingly, this is the same value of q0 that was derived in our previous article (17). We therefore choose this value of q0 for the ID filter.
We generate the URS, , through the inverse two-dimensional Fourier transform of . Fig. 3, A and B, shows the filtered surfaces obtained using the L4 and ID filters where the large q modes (for example, those seen in Fig. S6 B in the Supporting Material) are either removed by the ID filter or attenuated by the L4 filter. Implementation of each filter treatment highlights a computational benefit of the ID filter. There is an order-of-magnitude decrease (from 60 s to 6 s per frame) in the computation cost for the ID filter, relative to both the L4 and HA filters, due to the reduced number of q-modes required by the ID filter for the Fourier transformation used to generate the URS.
Figure 3.
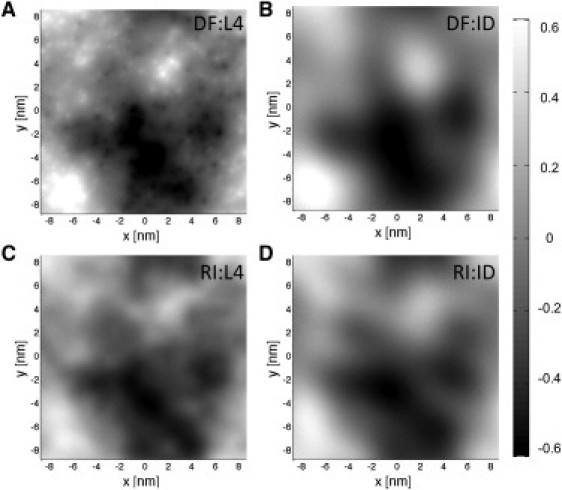
Single frame URS for 1024 DMPC lipids, selecting the TC atoms and using q0 = 1.15 nm−1. (A and B) Using the DF method. (C and D) Using the RI method. (A and C) Using the L4 filter. (B and D) Using the ID filter.
Real-space interpolation method
In addition to the DF method, we have adapted real-space interpolation (RI) methods that generate surfaces over a uniform-grid in real-space (8,21–24). Our particular approach employs a biharmonic spline interpolation (25) using equal number of fitting coefficients as lipids per monolayer to first obtain an undulation surface for each of the upper, z1(rmn), and lower, z2(rmn), monolayers separately, as shown in Fig. S6 A, with where xm = mΔx and yn = nΔy, with m and n being integers and Δx and Δy are determined for each frame to maintain periodicity (for our DMPC systems, we chose mmax = nmax = 91, which gives Δx = Δy ≈ 0.2 nm).
We then average the two monolayer surfaces to obtain an unfiltered URS, u(rmn) shown in Fig. S6 B as
| (6) |
From u(rmn), we calculate u(q) through a two-dimensional fast-Fourier transform, and determine the filtered value as in the DF method (Eq. 3). The primary advantage of the RI method is that the molecular structure contribution to the undulation spectrum is left out by averaging surfaces in real space (17). The primary disadvantage of the RI method is that we rely on a spline interpolation, which reduces and prefilters the undulations defining the URS.
Fig. 2 A shows good agreement in the undulation regime (q ≲ 1 nm–1) between the unfiltered one-dimensional spectra obtained from both the DF and RI methods for both P and TC selection atoms. Fig. 3, C and D, shows snapshots of the URS obtained using the RI method with the L4 and ID filters, respectively. The roughness of the surfaces increases from RI:ID to DF:ID to RI:L4 to DF:L4 because L4 leaves larger q modes than ID and RI prefilters the larger q modes relative to DF. Detailed examination of root mean-squared differences (RMSD) between treatments, including selection of the P atom instead of the TC atom, is given in the Supporting Material.
Two methods for calculating the EDP
Given a URS, we have developed two approaches for extracting the EDP: surface referencing with orientation approximation (OA), and surface referencing with undulation correction (UC). Both methods reference all atoms to the URS determined for each frame of the simulation. They differ in their treatment of the local orientation, which is highlighted in Fig. 1 B by the angle θ.
Surface referencing
What is convenient about the z-bin method for flat-patch bilayers is that it is obvious how to assign the distance of each atom k from the flat reference plane placed at the mean 〈z〉 for the bilayer. Assignment is more challenging for undulating bilayers because we need to obtain the distance of each atom k from the URS. We first define to be the unique position on the URS that has the same rk = (xk, yk) coordinates as the kth atom as shown in Fig. 4. We then assign a reference z value to each atom k as
| (7) |
Although this is already better than the simple z-bin method, Fig. 4 makes clear that it can be improved by taking into account the local orientation.
Figure 4.
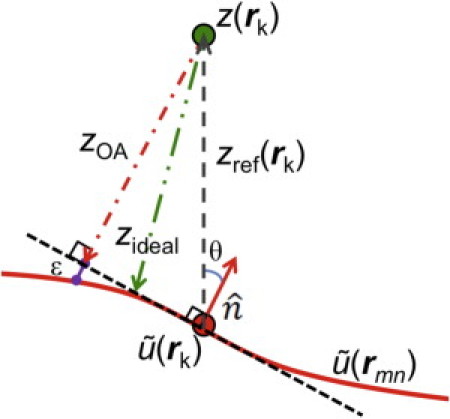
Definitions for surface referencing. (Upper circle) The kth atom [z(rk)]. (Lower circle) Reference position on the URS (, undulating solid line) with normal vector (solid arrow) that deviates from the z axis by angle θ. The OA method assigns the distance from the URS to be zOA (dashed-dotted arrow).
We use the unit normal vector, obtained relative to , as indicated in Fig. 1 B. These normal vectors are determined as
| (8) |
where
| (9) |
The angle between the z axis and for particle k is then θk = arccos (nz(rk)) (see Fig. 4).
Surface referencing with orientation approximation
For each atom k, the OA method uses the local bilayer surface orientation vector (Eq. 8). evaluated at the rk on the URS. We then approximate the distance of atom k from the URS by
| (10) |
Fig. 4 illustrates both and zOA relative to the URS. Either of these distances takes into account the local displacement from a flat reference plane at the average 〈z〉. For long wavelength undulations, the local membrane follows the wavy surface in Fig. 4 and then it is clear that zOA(rk) takes into account the local orientation, whereas zref(rk) does not. The number of electrons on each k atom is then added to that bin interval in an array that includes (bin width Δz = 0.01 nm). The ensuing histogram of electrons/bin is normalized by the scaled volume, ApΔz/〈cos θ〉. An even higher order correction equal to a fraction of ɛ in Fig. 4 would also take into account the local curvature. As shown in Section V in the Supporting Material, such a correction is not needed because θ is small due to the combination of long wavelengths and small amplitudes of the undulations. We also note that the finite size of atoms can be accounted for when computing the F(q) by using the atomic form factors and then taking the inverse Fourier transform to obtain the EDP with the finite size of the atoms included (26).
Surface referencing with undulation correction
The UC method was motivated by the treatment of undulations in the analysis of experimental x-ray scattering data (10). The experimental form factor is defined using the values in Fig. 4. However, a bilayer with orientation θ is thicker by 1/cos θ when measured along the average bilayer normal. Experimentally, the correction factor is usually applied to the form factor in reciprocal space. The equivalent correction factor in real-space scales by cos θ, which is equivalent to the OA approximation. However, one must average over all orientations experimentally; for small angles, the correction factor has then been approximated as 1 − 〈θ2〉/2, where 〈θ2〉/2 has been determined from the experimental values of the bending modulus (10).
MD simulations explicitly provide the θ-distribution, thereby allowing direct calculation of the average correction factor in the UC method. The atoms are first binned according to (Δz = 0.01 nm bin-width) with a weighting that corresponds to the number of electrons in atom k. These zref-bins are normalized by ApΔz to generate a surface-referenced EDP. We then apply the undulation correction factor by scaling the z axis by 〈cos θ〉. This is computationally less expensive than the OA method because the θ-distribution can be determined from a subset of time frames and then only , and not , have to be determined for each k. In addition, comparison of results to those of the more accurate OA method allows an evaluation of the experimental correction procedure. The direct calculation of 〈cos θ〉 = 0.9891 for the present DMPC simulation agrees with the approximate (1 − 〈θ2/2〉) to four significant digits, and corresponds to an average angle θ ≈ 8.5°.
Determining AL for undulating bilayers
The difference between the true (aL) and the projected area (ap) per lipid is
| (11) |
where N is the number of lipids per monolayer and is the z coordinate of the undulating surface. We have developed three methods to determine ΔaL.
Our first method (Method a1) evaluates Eq. 11 numerically on a regular grid, with by inverse Fourier transformation of . The discrete element approximation to the surface area is
| (12) |
where the partial derivatives are calculated using Eq. 9. After averaging over all simulation frames, 〈aL(1)〉 is obtained by extrapolating ΔaL(1)(δ) to δ = 0 using several nonzero values of δ.
The second method (Method a2) uses the Fourier definition of the derivatives (from Eq. 9) in Eq. 11 with the average mean-squared amplitudes of the Fourier amplitudes to obtain
| (13) |
Expansion of the square-root in Eq. 13 followed by use of Parseval's theorem gives
| (14) |
where the average 〈aL(2)〉 is determined over all simulation frames (14). ΔaL can be calculated using either method (a1 or a2) with just slight differences in the end result if the high-q cutoff is set equal to 2π divided by the grid size of the real-space methods.
Our third method (Method a3) uses the analytical form of the undulation spectrum, kBT/NaLkcq4, predicted by the Helfrich model (19,20). Inserting this into the expanded form of Eq. 13 and approximating the sum with an integral gives
| (15) |
Here it is clearly seen that the q−4 decay of the spectrum is not fast enough to give a convergent integral for the area without using a large-q cutoff.
Results
Electron density profiles
Results are presented for electron density profiles (EDPs) from several binary choices in methodology: the URS method (DF or RI), the atom selection method (TC or P), the filter method (ID or L4), and the surface referencing method (OA or UC). Comparisons in this subsection are for the system with 1024 DMPC lipids. We begin in Fig. 5 by comparing the OA and UC results using DF and RI methods, keeping the same choices for the other binary options (TC:ID). Clearly, it makes negligible difference whether the OA or the UC surface referencing method is used. We quantify differences in two EDPs by the RMSD averaged over all z values. A benchmark value is the RMSD = 18.2 e−/nm3 obtained by comparing the z-bin and DF:TC:ID:UC results for 1024 lipids, which is ∼6% of the mean value along the bilayer normal. Comparing DF:TC:ID:OA with DF:TC:ID:UC gives the much smaller RMSD = 0.33 e−/nm3 (∼0.1% of the mean value along the normal). This confirms that the less theoretically justifiable UC method required for experiment analysis is satisfactory, and it allows for less costly computation from simulations.
Figure 5.
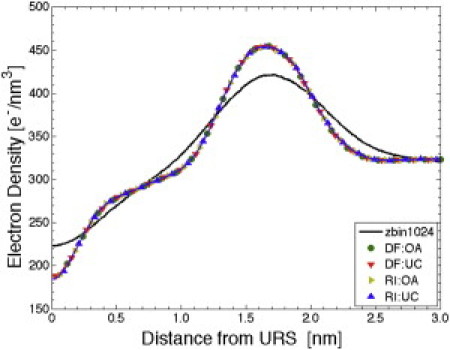
Comparisons of EDP for 1024 DMPC lipids upon variation of URS methods (DF versus RI) and surface referencing methods (OA versus UC) using q0 = 1.15 nm−1 and not varying TC:ID. (Black line) From z-bin 1024.
Fig. 5 also shows that there is little difference (RMSD = 0.91 e−/nm3) using the DF and RI methods to obtain the URS when the other binary choices (TC:ID:UC) are the same. As discussed in the previous article (17), the RI method is inferior for obtaining the undulation spectrum; subsequent comparisons focus on the DF method.
When the L4 filter is employed, there is a small, but discernible difference when the TC atom is selected (RMSD = 4.2 e−/nm3 for DF:TC:ID:UC versus DF:TC:L4:UC), and a considerably larger difference when the P atom is selected (RMSD = 43.1 e−/nm3 for DF:P:ID:UC versus DF:P:L4:UC) that is even larger than the benchmark RMSD obtained by the flawed flat-patch z-bin method. This outcome for the DF:P:L4:UC combination can be attributed to the increased intensity in the fluctuation spectrum from the molecular structure, shown in Fig. 2 for large q; this broadens the θ-distribution, which increases the subsequent scaling of the EDP's z axis. Similar comparison using the RI method, shown in Fig. S10 C, shows better agreement across atom selection and filter treatment due to the absence of molecular structure in the RI method.
Based upon these results, along with the consideration of computational efficiency, we have chosen DF:TC:ID:UC as our preferred method for obtaining EDP from the 16 possible combinations. Additional figures in the Supporting Material show results for other combinations not shown here (see, e.g., Fig. S9). Except for the two DF:P:L4:(UC and OA) combinations, results for the EDP have acceptably small RMSD differences.
It is also important to investigate the sensitivity of the calculated EDP to uncertainty in the value of q0 used in the filter. Fig. 6 plots, for several combinations of our methods, the RMSD obtained by comparing the EDP obtained at q0 = 1.15 nm–1 to the EDP obtained at different values of q0. Fig. 6 shows that the EDP is insensitive to q0 in the range 1.0–1.3 nm–1, which includes all reasonable uncertainties. Of course, as q0 goes to zero, one reverts to the z-bin method and so the RMSD increases. On the other hand, because q0 is allowed to become too large, the URS becomes very rough on a short length-scale and all surface-referencing methods break down. RMSD for the L4 filter increase more rapidly as q0 increases due to the residual intensity present at large q, whereas the ID filter affords little change in the EDP over a greater range of q0. RMSD comparisons for DF:OA, RI:OA, and RI:UC are shown in Fig. S8.
Figure 6.
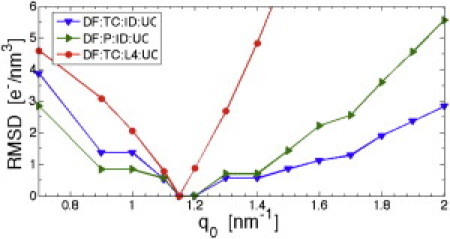
RMSD measuring the difference between EDP determined for a range of q0 values compared to the EDP obtained at q0 = 1.15 nm−1 for the methods indicated in the legend.
Size dependence
Fig. 7 compares the EDP obtained using our DF:TC:ID:UC method for DMPC systems with 32, 64, 128, 256, and 1024 lipids. The EDP of the smallest (32-lipid) system differs clearly from those of the other systems. It has a shoulder on the inner side of the headgroup peak which is shifted toward the interior of the membrane. The details of the top of the headgroup peak shown in the inset indicate that there are also smaller differences between the EDP of the 64 and 128 lipid systems and the larger ones. Fig. 7 shows no discernible finite size effect between our EDP for systems with 256 and 1024 lipids. RMSD results in Table 1 also suggest that there is a small, but systematic size effect remaining even when undulations are taken into account. The RMSDs presented in Table 1 compare the EDP using the DF:TC:ID:UC method on the 1024-lipid system to the uncorrected z-bin EDP as well as the DF:TC:ID:UC corrected EDP from each system size. It may be noted that RMSD for the 64-lipid and 32-lipid systems are the same for both corrected and uncorrected comparisons. No undulation corrections are made to these small systems because the smallest q for any undulatory mode is larger than the q0 = 1.15 nm–1 of our ID filter (Table 1), so the resulting URS is a flat reference plane that only takes into account the u(0, 0) mode that gives the average z displacement. Finally, Fig. S13 shows the corresponding finite size effect on the form factor, F(q).
Figure 7.
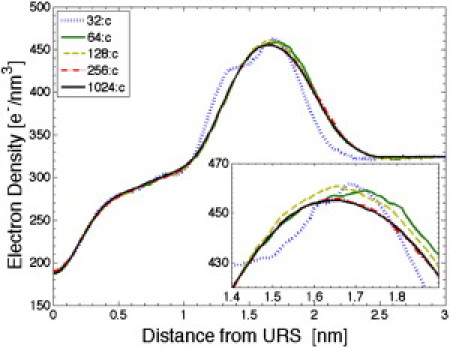
Comparison of DF:ID:TC:UC results for 32, 64, 128, 256, and 1024-lipid systems with q0 = 1.15 nm−1. (Inset) Subtle differences near the maximum of the EDP, highlighting finite size effects for the smaller systems.
Table 1.
System size comparisons: 2N is total number of DMPC lipids, Lx is average lateral size, and qmin = 2π/Lx is the minimum q
| 2N | Lx [nm] | qmin[nm–1] | RMSD-u | RMSD-c |
|---|---|---|---|---|
| 32 | 3.2 | 1.95 | 12.4 | 12.4 |
| 64 | 4.4 | 1.43 | 2.7 | 2.7 |
| 128 | 6.2 | 1.01 | 2.7 | 2.0 |
| 256 | 8.8 | 0.72 | 7.3 | 1.4 |
| 1024 | 17.7 | 0.36 | 18.2 | 0.0 |
Reference for the RMSD values is the EDP obtained for the 2N = 1024 system using the DF:TC:ID:UC method. RMSD-u compares to the uncorrected z-bin EDP and RMSD-c compares to the DF:TC:ID:UC corrected EDP. (RMSD units are e−/nm3.)
Excess area per lipid (ΔaL)
Table 2 shows results for ΔaL obtained from our three methods applied to our 1024-lipid simulation, using q0 = 1.15 nm–1. (Trends in ΔaL for a range of q0 are reported in Fig. S12). Methods a1 and a2 give similar results for each method of obtaining the URS. Different URS methods give somewhat different results when the P atom was selected, but the results for DF:ID:TC and RI:ID:TC agree and suggest that the ΔaL ≈ 0.006 nm2 correction to ap ≈ 0.6 nm2 is of ∼1%. This is in excellent agreement with the correction suggested by our use of continuum theory with our q0 cutoff, 〈Δa(3)〉 = 0.006 nm2.
Table 2.
Excess areas 〈ΔaL〉 from Methods a1, a2, and a3 (×10−3 nm2)
| Method | 〈ΔaL(1)〉 | 〈ΔaL(2)〉 |
|---|---|---|
| DF:ID:TC | 6.63 ± 0.71 | 6.73 ± 0.72 |
| RI:ID:TC | 6.06 ± 0.66 | 6.14 ± 0.67 |
| DF:ID:P | 5.34 ± 0.44 | 5.41 ± 0.44 |
| RI:ID:P | 7.00 ± 0.60 | 7.10 ± 0.61 |
| ΔaL(3) | 6.03 ± 0.82 | |
Discussion and Conclusions
We have demonstrated that undulations in fluid-phase DMPC lipid bilayers must be properly accounted for to obtain true electron density profiles and the corresponding form factors to compare directly to experiment (Fig. 1). To deal with this we have developed a redundant set of correction methods. Among these, we prefer the DF:TC:ID:UC method, but Fig. 5 shows that many other choices lead to similar results. In particular, instead of forming the URS reference surface in Fourier space (DF), a real space (RI) treatment makes little difference. This is unlike the previous article where substantially different conclusions were drawn depending upon whether Fourier or real-space calculation was employed. Those differences involved mostly the modes with larger q and those are filtered out to obtain the URS, especially when using filters with sharp cutoffs, such as the ideal (ID) filter or the Hamming (HA) filter.
When the ideal filter is employed, the results for the electron density profile are insensitive to numerical values of the q0 cutoff that fall within its uncertainty range. A much more gradual filter (L4) allows one, when the TC atom is selected, to obtain an independent estimate of the filter parameter q0 = 1.15 nm–1, which agrees well with the previous estimate (17). However, the gradual L4 filter leaves too much noise in the large q modes, especially when the phosphorus (P) atom is selected. It is especially encouraging that our two ways (OA and UC) to reference the atoms to the URS agree so well. The UC method is more approximate in principle, but it is a correction that is applied to reference experimental data to the local normal of the membrane (10,11). Therefore, the results of this article support that experimental approximation, at least for systems that have kc of ∼20 kBT, for which the underlying small angle approximation is accurate.
When corrected for undulations, the DMPC electron density profiles obtained from simulations of different sizes become much more similar (Fig. 7) than the uncorrected profiles (Fig. 1 C). There remains, however, a discernible finite size effect that is quite apparent for the system with 32 lipids and that becomes systematically smaller as the number of lipids increases (Fig. 7 and Table 1). However, the finite size effect is sufficiently small for our DMPC simulation of 64 lipids that it would make negligible difference when comparing to experimental data (27). Therefore, the standard procedure of analyzing a small simulation using the flat-patch z-bin method can be justified, with two caveats:
First, there will be finite size effects if the size is too small, as we see in our 32 DMPC lipid simulation; the size Nmin above which finite size effects are negligible may be different for different membranes.
Second, larger system sizes will be subject to the undulation effect as we begin to see in our 128 DMPC lipid simulation; the size Nmax below which the undulation effect is negligible may be different for different membranes. Lipids with a larger bending modulus than DMPC will exhibit a decreased undulation artifact, increasing the Nmax where the undulation correction should be employed.
Combining these caveats, there may be a range of system sizes, Nmin < N < Nmax within which one need not be concerned about either a finite size effect or the undulation effect. Although we know of no method to estimate Nmin except empirically, we can estimate Nmax by imposing the condition that the smallest q be larger than the q0 cutoff obtained from Eq. 18 of the previous article (17).
The URS that is necessary for obtaining electron density and other trans-membrane profiles is also useful to obtain the true undulating surface area AL which is larger than the projected area Ap. In agreement with previous results (14), we find this to be an ∼1% correction for bilayers with 1024 DMPC lipids. Although this is within the experimental uncertainty (10), it is a systematic correction that should be made when larger systems are simulated.
Software availability
The code was developed using the software MATLAB (7.9.1:R2009b, Service Pack 1; The MathWorks, Natick, MA) with the signal processing toolbox, and our code is available for download at http://sachslab.umn.edu/downloads.html. At publication time, the current MATLAB code was being ported for use within both GROMACS and CHARMM software packages.
Acknowledgments
This work has been supported by the Swedish National Infrastructure for Computing with computer time at the High Performance Computing Center North, and has been funded by the Swedish Research Council with a grant to O.E. Additional computer resources were provided by the Minnesota Supercomputer Institute. J.F.N. acknowledges support from US National Institutes of Health grant No. GM 44976.
Supporting Material
References
- 1.Sachs J.N., Petrache H.I., Woolf T.B. Interpretation of small angle x-ray measurements guided by molecular dynamics simulations of lipid bilayers. Chem. Phys. Lipids. 2003;126:211–223. doi: 10.1016/j.chemphyslip.2003.08.001. [DOI] [PubMed] [Google Scholar]
- 2.Benz R.W., Castro-Román F., White S.H. Experimental validation of molecular dynamics simulations of lipid bilayers: a new approach. Biophys. J. 2005;88:805–817. doi: 10.1529/biophysj.104.046821. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Klauda J.B., Kuĉerka N., Nagle J.F. Simulation-based methods for interpreting x-ray data from lipid bilayers. Biophys. J. 2006;90:2796–2807. doi: 10.1529/biophysj.105.075697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kuĉerka N., Perlmutter J.D., Sachs J.N. The effect of cholesterol on short- and long-chain monounsaturated lipid bilayers as determined by molecular dynamics simulations and x-ray scattering. Biophys. J. 2008;95:2792–2805. doi: 10.1529/biophysj.107.122465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Perlmutter J.D., Sachs J.N. Experimental verification of lipid bilayer structure through multi-scale modeling. Biochim. Biophys. Acta. 2009;1788:2284–2290. doi: 10.1016/j.bbamem.2009.07.006. [DOI] [PubMed] [Google Scholar]
- 6.Pan J., Tieleman D.P., Tristram-Nagle S. Alamethicin in lipid bilayers: combined use of x-ray scattering and MD simulations. Biochim. Biophys. Acta. 2009;1788:1387–1397. doi: 10.1016/j.bbamem.2009.02.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hess B., Kutzner C., Lindahl E. GROMACS 4: algorithms for highly efficient, load-balanced, and scalable molecular simulation. J. Chem. Theory Comput. 2008;4:435–447. doi: 10.1021/ct700301q. [DOI] [PubMed] [Google Scholar]
- 8.Lindahl E., Edholm O. Mesoscopic undulations and thickness fluctuations in lipid bilayers from molecular dynamics simulations. Biophys. J. 2000;79:426–433. doi: 10.1016/S0006-3495(00)76304-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Brannigan G., Brown F.L. A consistent model for thermal fluctuations and protein-induced deformations in lipid bilayers. Biophys. J. 2006;90:1501–1520. doi: 10.1529/biophysj.105.075838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Nagle J.F., Tristram-Nagle S. Structure of lipid bilayers. Biochim. Biophys. Acta. 2000;1469:159–195. doi: 10.1016/s0304-4157(00)00016-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Liu Y., Nagle J.F. Diffuse scattering provides material parameters and electron density profiles of biomembranes. Phys. Rev. E. 2004;69:040901. doi: 10.1103/PhysRevE.69.040901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Feller S.E., Venable R.M., Pastor R.W. Computer simulation of a DPPC phospholipid bilayer: structural changes as a function of molecular surface area. Langmuir. 1997;13:6555–6561. [Google Scholar]
- 13.Klauda J.B., Brooks B.R., Pastor R.W. Dynamical motions of lipids and a finite size effect in simulations of bilayers. J. Chem. Phys. 2006;125:144710. doi: 10.1063/1.2354486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Waheed Q., Edholm O. Undulation contributions to the area compressibility in lipid bilayer simulations. Biophys. J. 2009;97:2754–2760. doi: 10.1016/j.bpj.2009.08.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.den Otter W.K. Area compressibility and buckling of amphiphilic bilayers in molecular dynamics simulations. J. Chem. Phys. 2005;123:214906. doi: 10.1063/1.2132287. [DOI] [PubMed] [Google Scholar]
- 16.Noguchi H., Gompper G. Meshless membrane model based on the moving least-squares method. Phys. Rev. E. 2006;73:021903. doi: 10.1103/PhysRevE.73.021903. [DOI] [PubMed] [Google Scholar]
- 17.Brandt E.G., Braun A.R., Edholm O. Interpretation of fluctuation spectra in lipid bilayer simuluations. Biophys. J. 2011;100:2104–2111. doi: 10.1016/j.bpj.2011.03.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Tristram-Nagle S., Liu Y., Nagle J.F. Structure of gel phase DMPC determined by x-ray diffraction. Biophys. J. 2002;83:3324–3335. doi: 10.1016/S0006-3495(02)75333-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Helfrich W. Elastic properties of lipid bilayers: theory and possible experiments. Z. Naturforsch. C. 1973;28:693–703. doi: 10.1515/znc-1973-11-1209. [DOI] [PubMed] [Google Scholar]
- 20.Helfrich W., Servuss R.M. Undulations, steric interaction and cohesion of fluid membranes. Il Nuovo Cimento D. 1984;3:137–151. [Google Scholar]
- 21.Goetz R., Gompper G., Lipowsky R. Mobility and elasticity of self-assembled membranes. Phys. Rev. Lett. 1999;82:221–224. [Google Scholar]
- 22.Marrink S.J., Mark A.E. Effect of undulations on surface tension in simulated bilayers. J. Phys. Chem. B. 2001;105:6122–6127. [Google Scholar]
- 23.Song Y., Guallar V., Baker N.A. Molecular dynamics simulations of salicylate effects on the micro- and mesoscopic properties of a dipalmitoylphosphatidylcholine bilayer. Biochemistry. 2005;44:13425–13438. doi: 10.1021/bi0506829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Allen W.J., Lemkul J.A., Bevan D.R. GridMAT-MD: a grid-based membrane analysis tool for use with molecular dynamics. J. Comput. Chem. 2009;30:1952–1958. doi: 10.1002/jcc.21172. [DOI] [PubMed] [Google Scholar]
- 25.Sandwell D.T. Biharmonic spline interpolation of Geos-3 And Seasat altimeter data. Geophys. Res. Lett. 1987;14:139–142. [Google Scholar]
- 26.Kuĉerka N., Katsaras J., Nagle J.F. Comparing membrane simulations to scattering experiments: introducing the SIMtoEXP software. J. Membr. Biol. 2010;235:43–50. doi: 10.1007/s00232-010-9254-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Kuĉerka N., Liu Y., Nagle J.F. Structure of fully hydrated fluid phase DMPC and DLPC lipid bilayers using x-ray scattering from oriented multilamellar arrays and from unilamellar vesicles. Biophys. J. 2005;88:2626–2637. doi: 10.1529/biophysj.104.056606. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


