Membrane Adhesion via Homophilic Saccharide-Saccharide Interactions Investigated by Neutron Scattering

Abstract

Solid-supported membrane multilayers doped with membrane-anchored oligosaccharides bearing the LewisX motif (Le^X lipid) were utilized as a model system of membrane adhesion mediated via homophilic carbohydrate-carbohydrate interactions. Specular and off-specular neutron scattering in bulk aqueous electrolytes allowed us to study multilayer structure and membrane mechanics at full hydration at various Ca²⁺ concentrations, indicating that membrane-anchored Le^X cross-links the adjacent membranes. To estimate forces and energies required for cross-linking, we theoretically modeled the interactions between phospholipid membranes and compared this model with our experimental results on membranes doped with Le^X lipids. We demonstrated that the bending rigidity, extracted from the off-specular scattering signals, is not significantly influenced by the molar fraction of Le^X lipids, while the vertical compression modulus (and thus the intermembrane confinement) increases with the molar fraction of Le^X lipids.

Introduction

Cell-surface glycans in the form of glycolipids, glycoproteins, and glycocalix polysaccharides (1) serve not only as stabilizers for the integrity of cell membranes but also as specific ligands to communicate with neighboring cells. Although most of the receptors for cell-surface carbohydrates are proteins (e.g., lectins (2,3)), there are several examples of specific interactions between complementary carbohydrate motifs (4,5). For example, the homophilic interactions of membrane-bound saccharides bearing the neutral LewisX (Le^X) trisaccharide motif

$$\text{D-Gal}\beta \left(1\to 4\right)\left[\text{L-Fuc}\alpha \left(1\to 3\right)\right]\text{D-GlcNAc}\beta \left(1\to \text{R}\right)$$

were reported to play key roles in the aggregation of cells during the embryonic development (6,7). Although the capability of carbohydrate-carbohydrate interactions to induce cell aggregation was demonstrated by in vitro studies, it has been difficult to quantify such interactions that are weaker than carbohydrate-protein interactions. There have been several approaches to establish model systems to study the carbohydrate-carbohydrate interactions on the molecular level. For example, Geyer and co-workers (8,9) incorporated Le^X lipids in planar micelles (called bicells) for NMR spectroscopy. Hernáiz et al. (10) coupled Le^X via alkylthiolate to Au nanoparticles and Si₃N₄ tips coated with Au and studied the interactions with planar Au substrates functionalized with Le^X thiols using surface plasmon resonance and atomic force microscopy (5), respectively. Gourier et al. (11) incorporated Le^X lipids into giant vesicles and measured the adhesion energy using micropipette aspiration.

In contrast to other high-resolution probing methods (e.g., scanning and electron microscopy), x-ray and neutron scattering is not limited to free surfaces, but has also access to buried structures. Ricoul et al. (12) carried out small-angle x-ray scattering and small-angle neutron scattering experiments to determine the influence of lacitol glycolipids on the interaction of charged DDAB membranes, which only form stable multilayers under high osmotic pressures. McIntosh and Simon (13) incorporated GM1 glycolipids into egg-PC membrane multilayers and reported that the contribution of the saccharides to the membrane interactions is purely repulsive.

While scattering from isotropic suspensions generally does not allow for the distinct determination of structures parallel and perpendicular to the membrane planes, planar sample geometries enable one to identify specular and off-specular scattering signals (14–16). To date, this method has been commonly used for the physical characterization of planar stacks of phospholipid membranes using x-rays and neutrons (17–21).

In our previous accounts, we have demonstrated the potential of this technique to determine structure and mechanics of planar membrane stacks of synthetic glycolipids and bacterial lipopolysaccharides (22,23). In this study, we prepared stacks of planar phospholipid membranes incorporating lipids with Le^X headgroups (Le^X lipids). To shed light on the role of saccharide-saccharide interactions in membrane adhesion processes, we studied the influence of specific Le^X-Le^X pairs on the structural ordering and mechanics of the membranes in aqueous buffers using specular and off-specular neutron scattering.

Materials and Methods

Molecules and sample preparation

Fig. 1 shows the chemical structure of the Le^X lipid, which consists of a terminal Le^X trisaccharide epitope connected to the membrane anchor via a lactose disaccharide spacer. The naturally occurring ceramide was replaced by a 1,2-di-O-hexadecyl glycerol moiety (24) with perdeuterated hydrocarbon chains (23,25) to optimize the scattering length density contrast. The anchor lipid was coupled to the pentasaccharide moiety to give the Le^X lipid after removal of the protecting groups (26).

Figure 1.

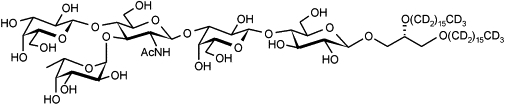
Chemical structure of the synthetic Le^X lipid.

To optimize the miscibility of Le^X lipid and lipid matrix, we used phosphatidylcholine with the same chain length, 1,2-dipalmitoyl-D62-sn-glycero-3-phosphocholine (d-DPPC), purchased from Avanti Polar Lipids (Alabaster, AL). All other chemicals were purchased from Fluka (Taufkirchen, Germany) and used without further purification. The buffers contained 100 mM NaCl, 5 mM HEPES, and selected concentrations of CaCl₂ at pH 7.4. A description of the preparation of solid-supported membrane multilayers is given in Text S1 in the Supporting Material.

Neutron scattering

Neutron scattering experiments were carried out at D16 of the Institut Laue-Langevin (Grenoble, France). Fig. 2 (left) shows the geometry of the experiment. A monochromatic (Δλ/λ = 1%) neutron beam of λ = 4.54 Å or λ = 4.73 Å reaches the sample through the aluminum windows of the sample chamber, whereas the incident angle Ω (i.e., the angle between the incident beam and the sample plane) is adjusted by a rotation stage. The intensity of the diffracted beam is recorded by a two-dimensional position-sensitive ³He detector with 128 × 128 channels and 2 mm spatial resolution. Γ denotes the angle between the scattered and the incident beams.

Figure 2.

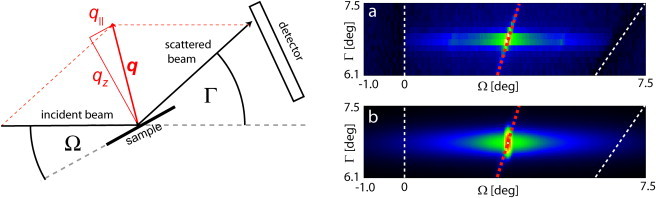
(Left) Geometry of the scattering experiments. From geometrical considerations, the angular coordinates Γ and Ω can be translated into the reciprocal space coordinates q_z and q_‖ (see expressions in Eq. 1). (Right) (a) Measured and (b) simulated Bragg sheet intensity in angular coordinates. (Dashed red line) Specular axis. Data points near the sample horizons (indicated with dashed white lines) were not used for the comparison.

The beam, focused to the sample in the vertical plane, had a horizontal width of 2 mm and was 25 mm in height at the sample position. For each measurement at an angle Ω, the detector readout was normalized to the intensity of the incident beam (via an in-beam monitor), the channel sensitivity, and the illuminated sample area. Subsequently, the two-dimensional detector readout was integrated in the vertical direction, which resulted in a one-dimensional intensity projection as a function of the horizontal detector channel position (corresponding to Γ). Thus, one Ω-scan yielded the recorded intensity as a function of Γ and Ω. The datasets in angular coordinates can be transformed into reciprocal space maps:

$$\begin{array}{l}{q}_z=\frac{2\pi }{\lambda }\left[\sin \left(\Gamma -\Omega \right)+\sin (\Omega )\right],\\ {\mathit{q}}_{\Vert }=\frac{2\pi }{\lambda }\left[\cos \left(\Gamma -\Omega \right)-\text{cos}(\Omega )\right].\end{array}$$ (1)

Here, q_z and q_‖ denote the scattering vector components perpendicular and parallel to the sample plane (see Fig. 2, left).

For the scattering experiments, we used a liquid cell designed for membrane stacks (22,23). Two Si wafers (Si-Mat, Landsberg/Lech, Germany), with one coated with the membranes, confining a thin layer of aqueous buffer, are separated by glass slide pieces (thickness: 0.10 mm). During measurements, the cell was placed in a climate chamber at controlled temperature and high relative humidity (>95%) to minimize water evaporation.

Simulation of the scattering signals based on mechanical parameters

Realistic sets of membrane-displacement correlation functions were modeled in a continuum approximation based on the discrete smectic Hamiltonian (14). Within this framework, the vertical compressibility of the membrane stacks is characterized by the compression modulus B, whereas the resistance of the membranes against bending is characterized by the membrane bending modulus κ. The membrane-displacement correlation functions g_k(r) can be expressed with the Caillé parameter η and the de Gennes parameter λ of smectic liquid crystals (14) (see Eq. 2). Here, k = 0 corresponds to the membrane self-correlation and k > 0 to the cross-correlations of the membranes with their k^th neighbors. The value r denotes the in-plane distance between two points. As shown in our previous article (23), the effect of the finite sample size can be taken into account with an effective cut-off radius R, which coincides with an upper limit for the wavelength of the membrane fluctuations. Mathematically, R defines a lower integration limit in the calculation of the correlation functions,

$$g_k\left(r\right)=\frac{d^2}{{\pi }^2}\eta \underset{2\pi /R}{\overset{\infty }{\int }}\frac{\left[1-J_{\mathit{o}}\left(q_{\Vert }r\right)\exp \left(-\lambda \mathit{k}{\mathit{q}}_{\Vert }^{\mathit{2}}d\right)\right]}{q_{\Vert }\sqrt{1+\frac{{\lambda }^2{d}^2}{4}{\mathit{q}}_{\Vert }^{\mathit{4}}}}d{q}_{\Vert },$$ (2)

where

$$\eta =\frac{\pi k_{\text{B}}T}{2d^2\sqrt{\kappa B/d}}$$

and

$$\lambda =\sqrt{\frac{\kappa }{\mathit{Bd}}}.$$

For known lamellar periodicities d, the correlation functions are fully determined by the three free parameters η, λ, and R. The scattering signals were modeled in kinematic approximation, which requires that the intensity of the scattered beam is much weaker than the incident illumination. To guarantee the validity of this assumption, only the second Bragg sheets, whose intensity nowhere becomes comparable to the incident intensity, were considered. In kinematic approximation, the scattering from periodical membrane stacks can be expressed (23,27) as a function of the membrane displacement correlation functions g_k(r):

$$S\left(q_z,q_{\Vert }\right)\propto \frac{1}{q_{\mathit{z}}^2}\left[N\underset{-\infty }{\overset{\infty }{\int }}{\mathit{e}}^{-{\mathit{q}}_{\mathit{z}}^{\mathit{2}}{g}_0\left(r\right)/2}{e}^{-i{q}_{\Vert }r}dr+2\sum _{k=1}^N\left(N-k\right)\cos \left(k{q}_{z}d\right)\underset{-\infty }{\overset{\infty }{\int }}{\mathit{e}}^{-{\mathit{q}}_{\mathit{z}}^{\mathit{2}}{g}_{\mathit{k}}\left(r\right)/2}{e}^{-i{q}_{\Vert }r}dr\right].$$ (3)

Based on this expression, which includes specular and diffuse contributions, the scattering signals were modeled in the angular coordinates of the experiment to maintain a uniform grid of points both in experimental and simulated datasets. Instrumental resolution was included by convolution of the signal in Ω- and Γ-directions with Gaussian functions, representing the point spread function of the measurement resulting from the finite angular width and the wavelength spread of the neutron beam. The convolution in Ω-direction was achieved using the Fourier convolution theorem in the computation of the Fourier integrals in Eq. 3, while the convolution in Γ-direction was applied to the simulated intensity maps. In the simulations, η, λ, and R were varied to minimize deviations from the experimental results for 1), the Γ-integrated Bragg sheet intensity and 2) the Γ-width of the sheets simultaneously. Subsequently, κ and B were calculated from η and λ.

Modeling of intermembrane interaction forces

DPPC membranes in Ca²⁺-free buffer

The interaction of neutral DPPC membranes in L_α-phase in Ca²⁺-free buffer was modeled considering three force contributions and a suited definition of the membrane separation d_W:

• 1.van der Waals (vdW) forces. For lipid membranes, several models have been developed (28,29). To account for the van der Waals attraction between the phospholipid membranes in fluid L_α phase, we used the “double film model” from Demé et al. (30) with one Hamaker constant A = 5.1 × 10⁻²¹ J. The value d_W is defined as the lamellar periodicity d minus the hydrophobic membrane thickness d_H. For the lipids with dihexadecyl chains (DPPC and Le^X lipid) studied here, d_H was estimated referring to the corresponding value reported by Janiak et al. (31) for DMPC with ditetradecyl chains (d_H = 35.5 Å). By adding four times the average projected length of a hydrocarbon C-C bond in L_α phase membranes (0.8 Å) (32), we obtained d_H = 38.7 Å.
• 2.Hydration repulsion. This force obeys an exponential decay (33) characterized by the extrapolated pressure Π₀ at d_W = 0 and a decay length λ_HYD. We used the values reported by Demé et al. (30), λ_HYD = 2.0 Å and Π₀ = 4.5 × 10⁹ Pa.
• 3.
  Undulation repulsion. This interaction was modeled according to the classical expression derived by Helfrich (34,35):

  $${\Pi }_{UND}\left(d_W\right)={\alpha }_{\infty }\frac{2{\left(k_{\text{B}}T\right)}^2}{\kappa {\mathit{d}}_{\mathit{W}}^{\mathit{3}}}.$$ (4)

  Here, d_W was defined as the periodicity d minus the steric thickness, d_S . For DPPC membranes in L_α-phase, we used the value reported by Kucerka et al. (36), d_S = 45.9 Å.

In our calculations, the prefactor α_∞ = 0.10 was taken according to the results obtained using Monte Carlo simulations (37,38), and we used the bending rigidity that we measured for DPPC membranes at 60°C, κ = 18 k_BT (see Fig. S1 and Table S1 in the Supporting Material).

The correct description of undulation interactions in membrane stacks is still under debate (39). Despite the notion that the strength of the undulation repulsion is correlated to the other interfacial forces, accurate treatments explicitly accounting for this interplay are still missing. An approach by Evans and Parsegian (40) resulted in an overestimation of the repulsion strength. To date, Helfrich's classical treatment has been most successful in reproducing experimental data (39,41). In this study, we compared the results to alternative calculations using α_∞ = 0 and α_∞ = 0.23 (Helfrich's original estimate), and confirmed that our general conclusions are independent of the exact choice of α_∞ within this interval.

DPPC membranes in Ca²⁺-loaded buffer

Several studies have reported that the presence of Ca²⁺ ions significantly increases the lamellar periodicity of phospholipid membranes (42,43). Deuterium magnetic resonance experiments have evidenced the binding of Ca²⁺ to phosphatidylcholine headgroups (44). This would alter the net charge of the membrane from neutral to positive, resulting in electrostatic repulsions. Therefore, electrostatic repulsion has to be considered in the theoretical modeling of force balance to reveal the effect of Ca²⁺. For this purpose, the Ca²⁺ ions adsorbed to the membranes were represented as homogeneously charged plates located at the center of the phosphocholine headgroup. Accordingly, d_W was defined as d minus the headgroup-headgroup distance d_HH of DPPC for the description of the electrostatic interaction. Here, d_HH = 37.8 Å was used according to the results of Kucerka et al. (36). The calculation of the repulsion between the two charged surfaces across the mixed electrolyte is presented in Text S2 in the Supporting Material.

Results and Discussion

Fig. 3 shows the reciprocal space map of DPPC membrane multilayers doped with 25 mol % Le^X lipid measured at 60°C in Ca²⁺-free buffer. The alignment of the membranes parallel to the substrate surface can be evidenced from the sharp central specular maximum along q_‖ = 0, most prominently seen in the Γ-integrated Bragg sheet intensities (see Fig. 8, a and c).

Figure 3.

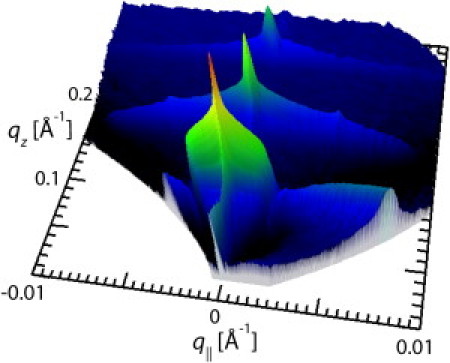
Reciprocal space map recorded by specular and off-specular neutron scattering from planar stacks of DPPC membranes doped with 25 mol % Le^X lipid at 60°C in Ca²⁺-free buffer. The intensity axis is scaled logarithmically and color-coded.

Figure 8.

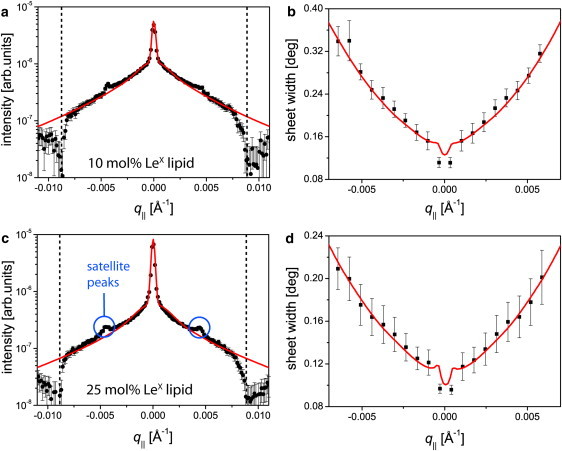
Measured (data points) and simulated (solid lines) scattering signals from the second Bragg sheets of membranes with 10 mol % (a and b) and 25 mol % (c and d) Le^X lipid at 60°C in Ca²⁺-free buffer. (a and c) Intensities integrated along Γ plotted as a function of q_‖. (Vertical dashed lines) Position of the sample horizons, separating reflection from transmission. (b and d) Width of the sheets along Γ plotted as a function of q_‖.

Lamellar periodicities of DPPC multilayers and the influence of Le^X

Fig. 4 summarizes the influence of Le^X lipid on the equilibrium lamellar periodicity d in the absence and presence of Ca²⁺, calculated from the q_z-positions of the Bragg peaks in the scattering signals. As presented in the figure, Ca²⁺ has a significant influence on the periodicity of pure DPPC membranes: d = 66.1 Å in the absence of Ca²⁺, while d = 90.0 Å in the presence of 5 mM CaCl₂.

Figure 4.

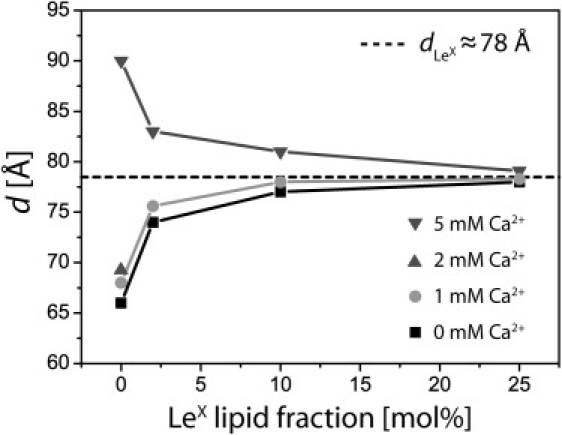
Lamellar periodicity d of DPPC membranes doped with various molar fractions of Le^X lipid in buffers containing 0, 1, 2, and 5 mM CaCl₂. The periodicity values approach to a saturation level ($d_{L{e}^X}\approx 78\mathrm{\AA }$) with increasing Le^X lipid concentration.

We found that the lamellar periodicity strongly depends on the molar fraction of Le^X lipids. The incorporation of 2 mol % of Le^X lipid already results in an increase in the periodicity in Ca²⁺-free buffer (from ≈66 Å to ≈74 Å) and a sharp decrease in buffer containing 5 mM Ca²⁺ (from ≈90 Å to ≈83 Å). This finding indicates that the opposing membranes are cross-linked by the trans-homophilic interactions between Le^X headgroups even at a low surface density (≈0.03 Le^X lipids per nm²). According to the increase in the molar fraction of Le^X lipid up to 25 mol %, the periodicities in the presence and absence of Ca²⁺ converge to a saturation level of $d_{L{e}^X}\approx 78\AA$ (indicated with a dashed line in Fig. 4), which seems optimal for the formation of homophilic pairs that cross-link the membranes.

In fact, this periodicity is in good agreement with the sum of the thickness of the hydrocarbon chain region (≈40 Å) and the thickness of two saccharide headgroups (≈2 × 22 Å = 44 Å), if one assumes a slight interdigitation of the opposing saccharide pairs. The convergence of the lamellar periodicities at all Ca²⁺ concentrations according to an increase in molar fraction of Le^X lipid can be attributed to a strengthening in membrane confinement around the optimal periodicity $d_{L{e}^X}$ as a result of an increased density of trans-homophilic Le^X pairs.

Intermembrane potential under external stress

At low Ca²⁺ concentrations, the lamellar periodicities of the pure DPPC membranes (d ≈ 68 Å for 1 mM and d ≈ 69 Å for 2 mM) are ≈10 Å smaller than the saturation level ($d_{L{e}^X}\approx 78\AA$). Here, the increase in the periodicity with increasing Le^X lipid fraction suggests that Le^X pairs expand the membrane separation while they are subject to a compression force. In contrast, at a higher Ca²⁺ concentration (5 mM), the incorporation of Le^X lipids leads to a decrease in the periodicity: pure DPPC membranes exhibit a spacing of d ≈ 90 Å, which is much larger than $d_{L{e}^X}$. Here, Le^X pairs attract the opposing membranes against a tensile force. These findings indicate that experiments at various Ca²⁺ concentrations offer a unique possibility to study the specific Le^X-Le^X interaction under defined external stresses. The strength of these compressional and tensile stresses exerted under various buffer conditions is discussed in the following.

Interactions between DPPC membranes

At first, the interaction between pure DPPC membranes is quantified, which is necessary for the further investigation of the trans-homophilic interaction of Le^X saccharide motifs. Although DPPC membranes are commonly studied model systems that have been characterized in detail (36), the comprehensive theoretical description of intermembrane interactions is still challenging (41). The interaction of electrically neutral DPPC membranes can be described as the sum of three force contributions (30)—vdW attraction, hydration repulsion, and undulation repulsion (see Materials and Methods). In Fig. 5 a, the modeled interaction contributions are plotted as a function of the lamellar periodicity d.

Figure 5.

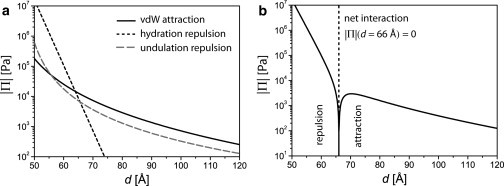
Modeled interactions of pure DPPC membranes in Ca²⁺-free buffer. (a) Absolutes of individual interaction forces (vdW attraction, hydration repulsion, and undulation repulsion). (b) Absolute of the net interaction (disjoining pressure) Π. The equilibrium lamellar periodicity can be found at |Π| = 0.

As can be seen, for low d-values corresponding to short membrane separations, the interaction is dominated by hydration repulsion, whereas vdW attraction is dominant at larger separations. Fig. 5 b represents the absolute of the modeled disjoining pressure Π (i.e., the sum of all interaction contributions). |Π| is zero at d = 66.0 Å, which corresponds to the equilibrium separation between DPPC membranes. This theoretically predicted equilibrium separation is in excellent agreement with the experimentally obtained lamellar periodicity of DPPC membranes in Ca²⁺-free buffer, d = 66.1 Å.

Note that in pure H₂O, d ≈ 65 Å is observed. As predicted by Petrache et al. (39), we found that the influence of NaCl is very weak (Δd ≈ 1 Å for 100 mM NaCl). Therefore, this effect is neglected in the following considerations.

Influence of Ca²⁺Ions on Interactions between DPPC membranes

As shown in Fig. 4, we observed a remarkable influence of Ca²⁺ on the lamellar periodicities of DPPC membranes: the addition of 1 mM Ca²⁺ already causes an increase in lamellar spacing by Δd = 1.8 Å (d = 67.9 Å). At 5 mM Ca²⁺ the spacing is increased by as much as Δd = 23.9 Å (d = 90.0 Å). The summary of the effect of Ca²⁺ on the periodicity is presented in Table 1.

Table 1.

Characteristics of DPPC membranes subject to various Ca²⁺ concentrations: lamellar periodicities, charge densities, number of DPPC molecules per adsorbed Ca²⁺, and affinity constants

Ca2+ concentration	d	Δd	Charge density σ	Number of DPPC molecules per Ca2+	Affinity Ka
0 mM	(66.1 ± 0.1) Å	0 Å	—	—	—
1 mM	(67.9 ± 0.1) Å	(1.8 ± 0.1) Å	(39 ± 1) mC/m2	126 ± 3	(7.9 ± 0.2) M−1
2 mM	(69.1 ± 0.1) Å	(3.0 ± 0.1) Å	(46 ± 1) mC/m2	107 ± 2	(4.6 ± 0.1) M−1
5 mM	(90.0 ± 0.1) Å	(23.9 ± 0.1) Å	(84 ± 1) mC/m2	59 ± 1	(3.3 ± 0.1) M−1

Within the chosen model, the errors in σ, number of DPPC, and K_a follow solely from the error in Δd.

To model the electrostatic repulsion caused by the adsorption of Ca²⁺ ions at the membrane surfaces, we used the corresponding positive surface charge density σ as a free model parameter to achieve the experimentally obtained Δd values. Fig. 6 a shows the electrostatic repulsion required to match the experimentally determined Δd values for 1, 2, and 5 mM CaCl₂. In the inset, the surface charge density σ corresponding to each condition is given. Fig. 6 b represents the absolute of the net interactions calculated from the sum of all four interfacial forces. As a clear trend, an increase in the charge density with increasing Ca²⁺ concentration is observed (from σ ≈ 39 mC/m² at 1 mM to σ ≈ 84 mC/m² at 5 mM; see Table 1). Within the model, the errors in σ (±1 mC/m²) solely result from the error in the determination of Bragg peak positions and the corresponding error in Δd (±0.1 Å). Systematic errors introduced by the model, especially in the treatment of undulation forces, are more significant, but do not influence the obtained order of magnitude (see Materials and Methods).

Figure 6.

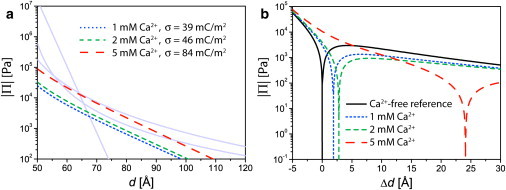
(a) Modeled electrostatic interactions in Ca²⁺-loaded buffers. The other force contributions are shown in the same plot in light shading. (b) The points of vanishing disjoining pressure represent the resulting change Δd in equilibrium lamellar periodicity.

For each Ca²⁺ concentration, the number of DPPC molecules per adsorbed Ca²⁺ ion was calculated from the charge densities by assuming that the area occupied by one DPPC molecule is 65 Å² (45). This enables us to calculate the affinity constant K_a of the DPPC-Ca²⁺ interaction (39),

$${\mathit{K}}_{\mathit{a}}=\left[\mathit{DPPC}\mathrm{\oplus }\mathit{C}{\mathit{a}}^{2+}\right]/\left(\left[\mathit{DPPC}\right]\left[\mathit{C}{\mathit{a}}^{2+}\right]\right),$$ (5)

where [DPPC ⊕ Ca²⁺] denotes the molar fraction of DPPC molecules that are associated with a Ca²⁺ ion, [DPPC] the molar fraction of free DPPC molecules, and [Ca²⁺] the bulk Ca²⁺ concentration in M. The calculated values are summarized in Table 1. The binding affinities are quite weak, of the order of several M⁻¹. Furthermore, the affinity constant decreases with increasing Ca²⁺ concentration. This tendency can be understood from the increase in σ according to the increase in Ca²⁺ concentrations, which would make the adsorption of further Ca²⁺ electrostatically less favorable.

Cross-linking the membranes: forces and energies

To estimate the forces and energies involved in the cross-linking of neighboring membranes by transhomophilic Le^X-Le^X interactions, DPPC membranes doped with 2 mol % Le^X lipid at 5 mM CaCl₂ are discussed in detail. Compared to the periodicity of pure DPPC membranes, the presence of 2 mol % Le^X lipid causes a reduction in membrane periodicity from d_0% = 90.0 Å to d_2% = 83.0 Å. The value d_0% denotes the lamellar spacing of DPPC membranes without Le^X lipids and represents the electrostatic repulsion between the membranes at a given Ca²⁺ concentration. Here, Le^X-Le^X pairs attract the opposing membranes against tensile stress. Due to the low molar fraction of Le^X lipid, the nonspecific intermembrane forces can be approximated by the disjoining pressure between pure DPPC membranes (solid curve, Fig. 7). To decrease the periodicity from d_0% to d_2%, an additional pressure of ΔΠ_2% ≈ 350 Pa (indicated by an arrow in Fig. 7) is required. Moreover, the work required for this compression can be estimated by integrating the curve in Fig. 7 between d_0% and d_2% (shaded area in Fig. 7): ΔU_2% = 110 nJ/m².

Figure 7.

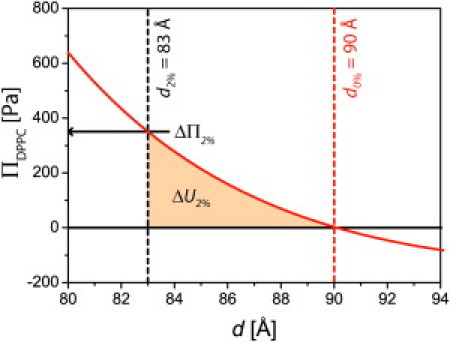
Disjoining pressure between DPPC membranes Π_DPPC for 5 mM Ca²⁺ plotted as a function of the periodicity d. To reduce the periodicity from d_0% = 90.0 Å to d_2% = 83.0 Å, an additional pressure of ΔΠ_2% ≈ 350 Pa (indicated by an arrow) is required. The work ΔU_2% that has to be performed for this compression is obtained by the integration of the pressure-distance curve between d_0% and d_2% (shaded area).

By assuming that all available Le^X groups are involved in the cross-linking, the lowest required binding force F and binding energy E per molecular pair can be calculated from ΔΠ_2% and ΔU_2% multiplied by the mean area per Le^X group (65 Å²/0.02 = 3250 Å²): F ≈ 10 fN and E ≈ 10⁻³ k_BT, respectively. However, it is likely that not all Le^X lipids but rather a small fraction are involved in the formation of pairs, and thus typical forces and energies per formed pair are significantly higher. In fact, the binding energy and force of individual Le^X pairs estimated from AFM experiments and molecular dynamics simulation are of the order of several k_BT and 10 pN, respectively (5,46). Thus, even low densities of membrane-anchored Le^X (corresponding to one Le^X motif per thousands of square nanometers) should be sufficient for the cross-linking of membranes at calcium concentrations used in this study.

Influence of Le^X on the mechanics of interacting membranes

The mechanical properties of the interacting membranes (characterized by the membrane bending modulus κ and the vertical compression modulus B) can be calculated from the off-specular scattering signals. Fig. 2 (right) shows the measured (a) and the simulated (b) intensity of a typical second Bragg sheet. Because effects of refraction and absorption, which are not considered in kinematic approximation, become important in the vicinity of the sample horizons (Yoneda wings) at Ω = 0 and Γ − Ω = 0, this angular region (indicated with dashed lines in the figure) was excluded from the comparison.

To highlight the influence of trans-homophilic Le^X pairs on the membrane mechanics, we compared membranes with 10 mol % and 25 mol % Le^X lipid in Ca²⁺-free buffer that exhibit lamellar periodicities very close to the saturation value of $d_{L{e}^X}\approx 78\AA$ (see Fig. 4). Thus, differences in the obtained mechanical parameters can be directly related to the different lateral densities of Le^X lipid molecules but not to a difference in equilibrium membrane periodicity. Fig. 8 shows the comparison of the measured and modeled scattering signals from membranes with 10 mol % (Fig. 8, a and b) and 25 mol % (Fig. 8, c and d) Le^X lipid in two characteristic representations. The sheet intensities integrated along Γ plotted as a function of q_‖ (Fig. 8, a and c) represent the displacement self-correlation function of an average membrane in the solid-supported stack, whereas the widths of the sheets along Γ plotted as a function of q_‖ (Fig. 8, b and d) represent the de Gennes parameter λ(20) independent of the other parameters.

Due to the close relation between Γ and q_z, this is valid not only for the q_z-integrated intensity and the q_z-width of the Bragg sheets, but also for the Γ-integrated intensity and the Γ-width, in good approximation. The modeled signals (solid lines) corresponding to the best matching parameters are superimposed onto the experimental data points. Here, the thick (0.1 mm) layer of H₂O buffers in the liquid cell leads to incoherent scattering by ¹H and results in a high absorption of the neutron beam in the transmission regime.

Therefore, the reflection regimes (Ω > 0 and Γ − Ω > 0) between the vertical dashed lines in Fig. 8, a and c, were used for the comparison. Another feature of the scattering signals not captured by the models is the existence of satellite peaks (indicated in Fig. 8 c, but also seen in Fig. 8 a and Fig. 3). From their position in q_z and q_‖, they were identified as results of double-scattering processes (see Text S3 and Fig. S3 in the Supporting Material). Therefore, experimental and modeled signals are not compared in the close vicinity of the satellite peaks. As presented in the figure, the models are in excellent agreement with the experimental data within the analyzed range. It should be noted that the almost perfect matching of the sheet widths (Fig. 8, b and d) enables the precise experimental determination of the de Gennes parameter λ (Δλ/λ < 10%) and the Caillé parameter η (Δη/η < 10%). This leads to a high accuracy in the calculation of the mechanical parameters κ and B (Δκ/κ < 20%, ΔB/B < 20%). The dips at q_‖ ≈ 0 in Fig. 8, b and d, in both experiment and model are result of the distorted shape of the Bragg sheets around their intersection with the specular axis.

The best-matching model parameters are summarized in Table 2. The cut-off radii R are in the range of 1 μm, consistent with those found for other membrane multilayer systems (22,23). Interestingly, the bending rigidities obtained for 10 mol % (κ ≈ 16 k_BT) and 25 mol % (κ ≈ 17 k_BT) are identical to that of pure DPPC membranes, κ ≈ 18 k_BT (Fig. S1 and Table S1) within the error. This indicates that the membrane-anchored oligosaccharides do not significantly contribute to the membrane bending rigidity even at the highest Le^X lipid density used in this study (25 mol %, corresponding to a lateral density of 0.3 saccharide headgroups per nm²).

Table 2.

Parameters of the best matching models for DPPC membrane multilayers doped with 10 mol % and 25 mol % Le^X lipid at 60°C in Ca²⁺-free buffer

LeX lipid fraction	η	λ [Å]	R [μm]	κ [kBT]	B [MPa]
10 mol %	0.085 ± 0.005	65 ± 5	0.8 ± 0.1	16 ± 3	0.22 ± 0.05
25 mol %	0.046 ± 0.005	38 ± 5	0.7 ± 0.1	17 ± 3	0.7 ± 0.1

The addition of 5 mM Ca²⁺ did not significantly alter the obtained parameters. Errors in κ and B follow from the errors in η and λ.

On the other hand, the compression moduli obtained for 10 mol % (B = 0.22 MPa) and 25 mol % (B = 0.70 MPa) show a clear difference: The higher density of Le^X motifs results in a much stronger confinement of the membranes between their neighbors. This finding can be interpreted as result of the cross-linking of the membranes via trans-homophilic Le^X pairs, which is strengthened according to an increase in the number of cross-linkers.

The addition of 5 mM Ca²⁺ did not have a significant influence on the off-specular scattering intensity and thus on the obtained parameters of the continuum mechanical model (see Fig. S2). Although the intermembrane water layer is ≈40 Å thick in the studied systems, the observed compression moduli are still comparable to those of pure phospholipid membranes with much thinner water layers (<20 Å), where the values were found to decay rapidly with increasing water layer thickness (47). This finding highlights the substantial stiffening achieved by the cross-linkers.

Influence of Ca²⁺ on membrane adhesion

As presented in Fig. 4, the lamellar periodicities in the presence and absence of Ca²⁺ converge to a saturation value ($d_{L{e}^X}\approx 78\AA$) according to the increase in the molar fraction of Le^X lipids toward the physiological level of glycolipids in eukaryotic membranes (>10 mol %) (48). The observed tendency suggests that the molar fraction of Le^X lipids significantly influences the membrane adhesion via homophilic saccharide-saccharide interactions, but the presence of Ca²⁺ does not seem to be crucial. From the analysis of the off-specular scattering signals, we also found that both bending rigidity and compression modulus of the membranes were not influenced by the presence of Ca²⁺.

To date, it has commonly been assumed that divalent cations, preferably Ca²⁺, are prerequisite for homophilic Le^X-Le^X interactions (8,9,25,49). In contrast to these results, there have been several experimental studies reporting that homophilic Le^X interaction can occur even in the absence of Ca²⁺. For example, AFM experiments suggested that the presence of Ca²⁺ does not contribute significantly to the binding forces (5). Nishimura et al. (50) and Su et al. (51) observed Le^X aggregates in the absence of Ca²⁺ by time-of-flight mass spectroscopy and molecular beam spectroscopy, respectively. Moreover, using molecular dynamics simulations, Gourmala et al. (46) reported that the Le^X dimer is stable both in the presence and absence of Ca²⁺, but that the interactions are strengthened by Ca²⁺. Although neutron scattering is not sensitive to the individual molecular interactions, the formation of trans-homophilic Le^X pairs suggested by our experiments is in good agreement with these reports.

Conclusions

Stacks of membranes doped with Le^X lipids on solid substrates were used for the study of membrane adhesion via specific carbohydrate-carbohydrate interactions. Specular and off-specular neutron scattering provided quantitative insights into the influence of surface density of Le^X motifs and Ca²⁺ concentration on the structure and mechanics of interacting membranes. The obtained results demonstrate that neighboring membranes are tightly confined by even a low density of carbohydrate cross-linkers.

In comparison to the significant influence of the surface density (molar ratio) of Le^X motifs, we found that Ca²⁺ does not significantly affect the formation of trans-homophilic pairs. The approach is promising for a systematic investigation of the membrane adhesion mediated via weak, but specific carbohydrate-carbohydrate interactions.