Hypochromicity in red blood cells: an experimental and theoretical investigation

Abstract

Multiwavelength UV-visible transmission spectrophotometry is a useful tool for the examination of micron-size particle suspensions in the context of particle size and chemical composition. This paper reports the reliability of this method to characterize the spectra of purified red blood cells both in their physiological state and with modified hemoglobin content. Previous studies have suggested the contribution of hypochromism on the particle spectra caused by the close electronic interaction of the encapsulated chromophores. Our research shows, however, that this perceived hypochromism can be accounted for by considering two important issues: the acceptance angle of the instrument and the combined scattering and absorption effect of light on the particles. In order to establish these ideas, spectral analysis was performed on purified and modified red cells where the latter was accomplished with a modified hypotonic shock protocol that altered the hemoglobin concentration within the cells. Moreover, the Mie theory was used to successfully simulate the spectral features and trends of the red cells. With this combination of experimental and theoretical exploration, definition of hypochromism has been extended to two subcategories.

1 Introduction

Multiwavelength ultraviolet-visible (UV-vis) spectrophotometry is a rapid, reliable and effective tool for the qualitative and quantitative characterization of macroscopic particles in suspension [1–5]. The optical density (OD) spectrum of turbid systems depends on both its absorption and scattering components [6,7]. While an OD transmission spectrum of a small chromophore in solution is composed mainly of absorption, large particles in a suspension exhibit more pronounced scattering along with absorption [6–8]. Such properties make suspended particle systems more complex to model in terms of their physical attributes and make interpretation of the spectrum equally problematic. The light scattering theory of electromagnetic radiation has been shown to provide an effective approach to examining the particle suspensions including polymers [9], molecular aggregates [10–12], and microorganisms [13–15]. Successful use of the theory to model multiwavelength spectra of particles requires the knowledge of several important parameters including the chemical composition, particle number, particle size, and particle size distribution (PSD), all of which can be acquired experimentally.

From a clinical standpoint, a rapid and dependable blood screening method for determining hematologic parameters and detecting abnormalities that surpasses current technology would be medically useful. Accurately interpreted multiwavelength UV-vis technology shows the promise of providing such improvements. Whole blood is a complex particle suspension with erythrocytes (red blood cells [RBC]) being the major particle component (~45% v/v) [16]. The erythrocytes contain mainly hemoglobin, a strongly chromophoric protein that constitutes approximately 98% (w/w) of the total encapsulated protein [16]. The optically dense nature and the abundance of erythrocytes make it the focus for the spectral characterization of whole blood.

In order to obtain a more comprehensive understanding of whole particle absorption and scattering on a macroscopic level, a combination of experimental techniques and mathematical modeling was used to examine data on the spectral characteristics of erythrocytes. Studies had indicated the significance of hemoglobin concentration on the red cell spectrum [17,18]. Thus, the strategy of this research has been to explore the optical behavior of dilute isolated red cells not only at physiological hemoglobin levels (33% w/v), but as cells modified to contain reduced hemoglobin concentrations. Modeling the red cell spectra using the theory of electromagnetic radiation to account for the combined absorption and scattering components of the spectra provides the ability to predict qualitative spectral changes by manipulating important parameters such as the hemoglobin concentration and particle size to successfully estimate a spectrum that is in good agreement with experimental data [6,8]. In order to achieve this level of realization, it is important to understand both how the data is obtained and processed, and to make informed assumptions about the intermolecular interactions of the hemoglobin under physiologically concentrated conditions. Hence, two important issues have been considered in this investigation: 1) hypochromism and 2) instrumental setup.

Hypochromism, or more appropriately observed hypochromism is a general term used to describe the attenuation of the absorption component (and hence that of the observed extinction coefficient) typically associated with the presence of a chromophore in high concentrations [19,20]. Historically, certain strongly absorbing chromophores capable of close association have been shown to exhibit molecular hypochromism, a reduction in the absorption when the molecules are in close proximity of one another [20]. The phenomenon has been suggested to be present in strongly absorbing biological constituents such as chlorophyll [21,22], polynucleotides [23], and hemoglobin [24,25]. In the most well studied system, polynucleotides, the molecular hypochromic effect has been explained in terms of absorptive distortions due to molecular dipolar interactions [21] or the physical overlap of π orbitals of stacked chromophores [26]. It has also been attributed to the screening of radiation by adjacent molecules [27]. Regardless of the mechanism, the fundamental cause of the hypochromism of the polynucleotides stems from their close, stacked nature. This fixed juxtaposition of the nucleotide bases has been shown to evoke a hypochromic effect of up to 28% (λ_max = 260 nm) for an oligoadenine [28] or up to 60% for a helical polynucleotide [29]. For hemoglobin in erythrocytes, Vekshin (1999) reported a decrease in absorption of up to 70% (λ_max ~415nm) [24]. Contrary to the closely packed and relatively fixed nucleotides of a double helix where the partially stacked bases are in Van der Waals contact [30], hemoglobin encapsulated in red blood cells presumably exist as independent proteins with their intermolecular distance estimated to be 62–75 Å (approximately the width of one molecule) [31]. Under such conditions, random collisions are prevalent but the effect of organized molecular hypochromism is perhaps questionable.

The second issue in the characterization of erythrocytes is related to the setup of the spectrophotometer and the manner in which the transmission data is captured. Multiwavelength spectra is generally a more powerful tool compared to single wavelength analysis since given its greater information content, it offers the ability to elucidate multiple parameters for the characterization of a suspended system. Optical scattering analyses of erythrocytes have typically been limited to a single wavelength [32] or to a small number of select wavelengths [17,33,34], while multiwavelength representations have been reported as diffuse spectra [24,25]. Diffuse spectra results from the acquisition of a large amount of scattered light in colloidal systems and is typically defined by a wide angle of acceptance of the detector [35]. The collection of diffuse scattering plays an important role in the features of an optical density spectrum of a macro-particulate system. Differences in the amount of captured light (due to differences in instrumental arrangement) are represented by variations in spectral features in terms of overall intensity and changes in absorbance peaks. As the spectrophotometer is modified to collect more of the scattered light, the arrangement approaches the characteristics of an integrating sphere, a limiting case were scattered light at essentially all angles is captured [6]. The resulting spectrum from the integrating sphere would represent the absorption component of the particulate sample with the scattering component being accounted for as background. Here the absorption bands of the encapsulated hemoglobin show hypochromicity when compared to the spectrum of free hemoglobin in solution. This phenomenon is a scattering-related effect of large particles that can be accounted for by using the scattering theory and is classified under a novel category of observed hypochromism designated as macroscopic hypochromism (see Theory section for formal definition). Our experimental evidence as well as previous work done on macromolecules (polystyrene, proteins) [9,12] support the notion that instances of perceived molecular hypochromism reported in encapsulated particle systems can be explained in terms of light scattering and instrumental configuration.

Herein, we examine the use of multiwavelength scattering and absorption data of red blood cells measured with both large and small angles of acceptance using commercially available UV-visible spectrophotometers. The data presented suggest that what has been described as hypochromicity for erythrocytes can be explained by 1) considering the angle of acceptance and 2) implementing a model based on the theory of electromagnetic radiation which accounts for the absorption and scattering components of the cell suspension. Application of the model shows that the calculated spectra of unmodified and hypotonically modified erythrocytes are in good agreement with the empirical spectra in terms of their trends and spectral features.

1.1. Experimental approach

A protocol for the red cell permeabilization (by hypotonic shock) experiments was established where the conditions of the modifications were controlled in such a manner so that the resulting concentration of the encapsulated hemoglobin could be manipulated as desired. Similar methods have been reported of using hypotonic exchange to render red blood cells transiently permeable to enable the passing of high-molecular weight molecules across the membrane [36–39]. In contrast, the aim of our modified protocol was to allow the hemoglobin to permeate out of the cells to different degrees, achieving resealed cell samples over a range hemoglobin mass fractions. While the erythrocytes are suspended in an isotonic phosphate buffered saline (PBS), the internal osmotic pressure (P_i) is constant with that of the external medium (P_e). When a hypotonic buffer is introduced to the cells (P_i > P_e), basic colligative property states that the water will flow into the cell to achieve equilibrium. If the buffer is sufficiently hypotonic, the force of the expanding cell membrane will initiate transient pores of 200–500 Å to allow the hemoglobin to pass out of the cell [39]. In order to reseal the cells, the osmotic pressure of the medium is reversed such that the pores are closed and the system returns to osmotic equilibrium. The resulting encapsulated hemoglobin concentration of the resealed cells is controlled by the volume of the administered hypotonic buffer and the duration of the hypotonic shock. It has been suggested that of the initial cell population, approximately 45–60% of the permeabilized cells maintain the capability reseal depending on the temperature of the experiment [40]. The ability obtain encapsulated hemoglobin concentrations from physiological values (~0.33 mass fraction) down to very low mass fractions of ~0.05 provides a valuable opportunity for the fundamental investigation of hypochromism.

2. Materials and methods

2.1. Erythrocyte harvesting

EDTA-treated whole blood units from human donors were obtained by gracious contribution from the Florida Blood Services (St. Petersburg, FL). Typically, the blood samples were used for experiments within 48 hours of the donation. The erythrocytes were isolated from each unit by a standard two-step protocol performed by blood bank personnel. The first was a leukocyte depletion step in which the whole blood unit was passed through a standard leuko-reducing filter (Sepacell Pre-Storage Leukocyte Reduction Set for Red Cells, Baxter Healthcare Corp., Fenwal Division, IL). The second step was a thorough washing that removed platelets and replaced the plasma and its components with isotonic (0.9%, pH 7.0-7.2) phosphate buffered saline (PBS) (Nerl Diagnostics, RI) by employing cycles of centrifugation (1500 x g) and re-suspension in PBS.

2.2. Hypotonic modification of erythrocytes

Hypotonic permeation/restoration of red cells was accomplished using a modified version of previously published procedures [40,41]. Briefly, the washed red cells (~5 ml) were gently packed by centrifugation for approximately 5 minutes. The packed cells were then carefully aliquotted to varying volumes of hypotonic 7 mM PB (phosphate buffer (pH 7.2)). For example the ratios of hypotonic buffer volume to packed cell volume ranged from 0.75:1 to 8:1. The higher the hypotonic buffer volume, the lower the resulting concentration of the hemoglobin was in the resealed cells. In order to obtain the most dilute hemoglobin concentrations, the packed cells were treated with large amounts of hypotonic buffer and kept in ice for 20 minutes. Following the permeation and equilibration of the cells, a high concentration PBS (typically 1.0–2.0%) was used to adjust the sample tonicity back to 0.9% and the cells were allowed to reseal for 45 minutes in 37°C. The restored cells were harvested via centrifugation and washing (three cycles). After the third washing, the packed cells were re-suspended in isotonic PBS to an approximate volume ratio of 1:1 and kept at room temperature during the spectrophotometric analysis. The samples were typically analyzed within an hour post-preparation. Spectral reproducibility of the samples was confirmed by performing replicates of the resealing experiment in parallel reaction vessels.

2.3. Spectrophotometric analysis of whole blood and resealed cells

Multiwavelength UV-visible spectrophotometric data (190–1100 nm) were collected for whole blood and washed red cell samples which were diluted to 4000 cells/μl in isotonic PBS. This is a concentration that was determined to give the maximum intensity for the optical density without departing from the linear range of the instrument (upper OD limit ~1.2). The Agilent 8453 diode array spectrophotometer was used to acquire a majority of the data and has an acceptance angle of approximately 2°. The integration time (time of scan) was adjusted to 15 seconds with spectra being acquired 10 times in one second, hence the resulting spectra was an average of 150 scans. Samples were read in a standard 3.5 ml quartz cuvette with a 1 cm pathlength (Starna Cells Inc., CA) at room temperature. Prior to sampling, the spectrophotometer was first blanked to correct for ambient light conditions. The sample was then solvent-corrected by taking a spectrum of approximately 2 ml of the solvent and programming the software to subtract this solvent spectrum from each scanned sample. Suspensions of resealed red cells were treated in the same manner as unmodified red cells for consistency.

2.4. Diffuse transmission spectra

Diffuse spectra were obtained using the Perkin-Elmer Lambda 900 (Perkin-Elmer, CT) spectrophotometer. The sample cuvette was placed in front of an integrating sphere module and the diffuse spectra was acquired by the light being transmitted across the sphere (acceptance angle > 2°). The Perkin-Elmer Lambda 18 fitted with an integrating sphere module (RSA-PE-18, Labsphere, NH) was used to collect all of the scattered light by the cell suspension. The spectra acquired by the three modes of data collection were compared and analyzed for a better understanding of instrumental configuration.

2.5. Standard hematology analysis

Blood samples were also examined using a hematology analyzer model 9010+ (Serono-Baker, PA) for corroboration with spectral data. The instrument uses an impedance based technology for cell counting and provides parameters such as red blood cell counts, mean corpuscular volume (MCV), hematocrit (HCT), and mean corpuscular hemoglobin concentration (MCHC). The hematology analyzer provides independent corroborating data for the spectroscopy methods.

3. Theory

3.1. Angular scattering predictions

The interaction of light with particles results in absorption and scattering phenomena; particles scatter light in all directions and, depending on the experimental set-up, changes in the properties of the scattered light relative to the incident light may be measured as function of the observation angle. For finite aperture detectors, the angular resolution of the scattered light depends on the acceptance angle of the detector. Therefore the detector response is proportional to a weighted average of the scattered intensity over the angles defined by its aperture; a limiting case being measurements with an integrating sphere where essentially all scattered light is measured and subtracted from the transmitted light to obtain estimates of the attenuation due to absorption. The angle of acceptance is defined in Fig. 1 and it is related to the radius of the detector and the distance of the sample to the detector. Particles larger than the wavelength of the incident radiation are known to forward scatter light [6,7] and in the case of erythrocytes upwards of 97% of the scattered light will fall within 5° relative to the direction of the incident light. This is demonstrated in Fig. 2 where the predicted angular scattering spectrum calculated using Mie theory is shown. In this case zero degrees represent the direction of incident light. The inset shows a semi-logarithmic plot elucidating the oscillatory features of scattering at larger angles. It is evident that careful consideration must be given to the acceptance angle of the detector when interpreting transmission data, particularly because the shape and amplitude of the spectral features can be considerably affected and thus lead to erroneous conclusions [6,35]. The implications of the acceptance angle when measuring red blood cells are seen in our experiments (Figs. 7 –9 below); notice that the spectral features for a small angle of acceptance spectrometer and for an integrating sphere are quite different and distinct from the spectrum of free hemoglobin in solution. It is also evident that spectral comparisons for the assessment of hypochromicity should be conducted on the same basis (i.e., with equivalent instrumentation). Furthermore, given that considerable scattered light is admitted into the detector is appropriate to redefine hypochromicity at two levels:

Fig. 1.

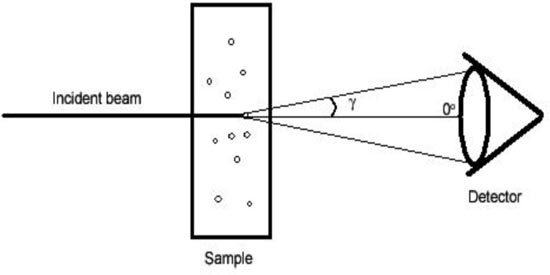
Schematic representation of the angle of acceptance. The radius of the detector and the distance of the sample to the detector determine the amount of scattered light captured by the spectrophotometer.

Fig. 2.

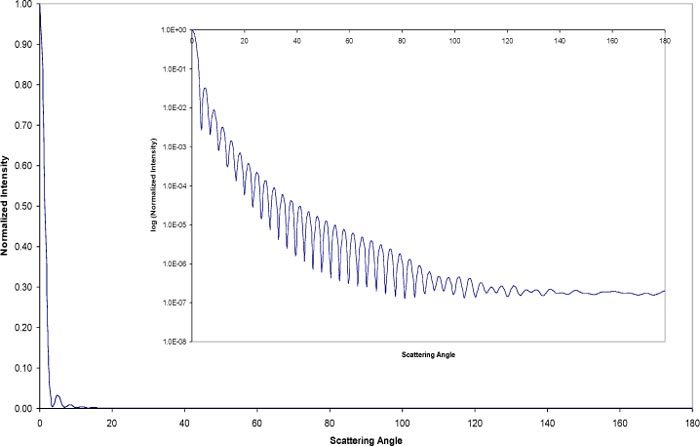
Angular scattering prediction for an equivalent sphere red cell. The large plot is a linear plot and the inset represents a semi-logarithmic depiction of the same plot. A majority of the scattered light is directed in the forward direction within five degrees.

Fig. 7.

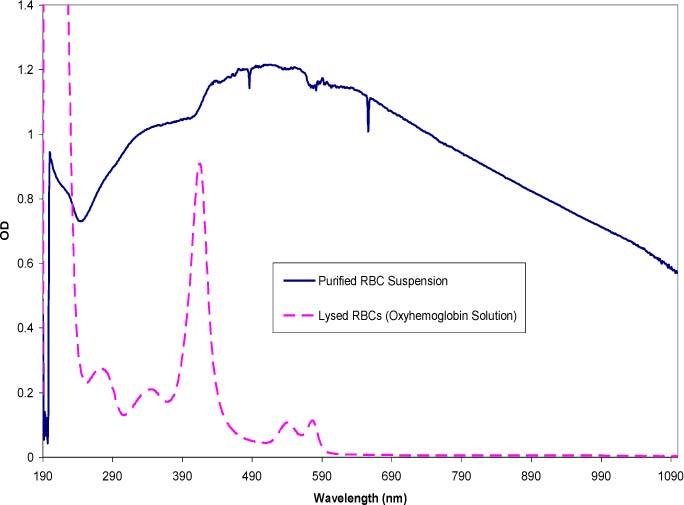
Small acceptance angle spectra comparing purified red cells and hemoglobin in solution acquired from an Agilent 8453 spectrophotometer with an acceptance angle of 2°. The RBCs were purified by washing whole blood by centrifugation and passing the suspension through a leuko-reduction filter. The RBC concentration is approximately 4000 cells/μl. The spectrum of the hemoglobin solution represents a concentration of ~0.12 mg/ml.

Fig. 9.

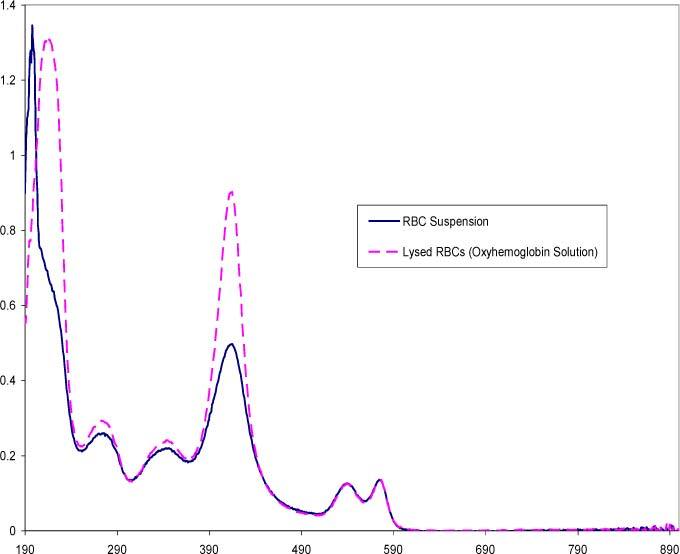
Diffuse integrating sphere spectra comparing purified red cells and hemoglobin in solution acquired from a Perkin-Elmer Lambda 18 spectrophotometer fitted with an integrating sphere. The RBC concentration is approximately 4000 cells/μl and the concentration for the hemoglobin in solution is ~0.12 mg/ml.

• • Macroscopic hypochromicity which is due to changes in scattered light and as consequence is proportional to the size of the scattering elements.
• • Microscopic or molecular hypochromicity which is due to the electronic interactions resulting from close proximity of chromophoric groups and therefore a function of the chromophore concentration within the particle.

Based on the above definitions, a chromophoric group within a particle (i.e., hemoglobin in red blood cells) will experience hypochromicity when the observed absorption coefficient of the encapsulated chromophore is smaller than the absorption coefficient of the same chromophore in dilute solution. The implication of dilute solution is that, statistically, the likelihood of one molecule screening other molecules is negligible. Given that finite acceptance angle detectors admit a considerable amount of scattered light, to assess hypochromicity the interpretation of the spectral data should be done within the context of a scattering model.

3.2. Mie theory

First published in 1907, Mie theory provides an exact solution to Maxwell’s equations for spherical particles [6–8] and contains information on the refractive index and the absorption coefficient of the materials constituting the particles, as well as, on the absorption and scattering components of the transmitted light. The material properties are defined through the complex index of refraction m(λ) such that:

$$m(\lambda )=\frac{n(\lambda )+i\kappa (\lambda )}{n_0(\lambda )}$$ (1)

where n(λ) is the refractive index of the particle, n₀(λ) is the refractive index of the medium, and κ(λ) is the absorption coefficient of the particle; n(λ) and κ(λ) constitute the optical properties of the particle. The equation that relates the particle size and the complex refractive index to the absorption and scattering components of the transmitted light at a given wavelength (τ(λ)) is given by:

$$\tau =N_p{\displaystyle \underset{0}{\overset{\infty }{\int }}\frac{\pi }{4}}{D}^2{Q}_{sca}(\alpha ,m(\lambda ))f(D)dD+N_p{\displaystyle \underset{0}{\overset{\infty }{\int }}\frac{\pi }{4}}{D}^2{Q}_{abs}(\alpha ,m(\lambda ))f(D)dD$$ (2)

where N_p is particle number per unit volume, D is the particle equivalent sphere diameter, f(D) is the particle size distribution (PSD), Q_sca(α,m) and Q_abs(α,m) are the Mie efficiencies. Mie theory is ideally suited to explore possible hypochromic effects because it has no limitations relative to the size of the particles and no constraints relative to the magnitude of the optical properties. Furthermore, the absorption coefficient of chromophores in solution ε(λ), or Beer-Lambert absorption coefficient is directly related to the Mie absorption coefficient κ(λ) through Bouger’s law (ε(λ) = 4πκ(λ) /λ) enabling direct comparison of the magnitude of the absorption coefficients for encapsulated chromophores and chromophores in solution.

3.3. Simulations of erythrocytes

The Mie-based turbidity calculations described in Eq. (2) (and assuming a 2° acceptance angle) were implemented as a computer program capable of predicting the multiwavelength spectrum of red cells as well as the resealed cells. The simulation model required inputs for parameters that describe the red cell suspension including the cell volume fraction, the cell concentration in the cuvette, the equivalent sphere diameter of the cell, the mass fraction of the protein component, the optical properties (complex refractive index) of the protein component, and the refractive index of the medium. Where applicable, the simulations (as well as experimental data) were normalized by dividing through the entire wavelength range by the area under the curve. The benefits of normalization were to eliminate the effects of concentration on the spectra, and to visually elucidate features of spectra (in comparison to each other) that are not readily apparent on a linear scale.

3.4. Estimation of optical properties

Since hemoglobin is the dominant chromophore in red cells, it was important to obtain reliable optical properties for the protein. Absorption spectra of oxyhemoglobin (Sigma-Aldrich, Inc., St. Louis, MO) were obtained across a broad wavelength range (190–1100 nm) in numerous replicates. Statistical analysis ensured a small standard deviation of the samples (within 1–2% error) and the generated extinction coefficient (ε(λ)) was found to be in good agreement with published data [42]. The experimentally obtained ε(λ) was converted to (κ(λ)) (using Bouger’s Law) which was then was used to calculate the refractive index (n(λ)) part of m(λ) (Eq. (1) using the Kramers-Kronig transform [6] to give the complete optical properties of hemoglobin. Figure 3 illustrates the two components of the complex refractive index of hemoglobin as well as the refractive index of water. The latter was obtained from values reported by Thormaehlen et al. (1985) [43].

Fig. 3.

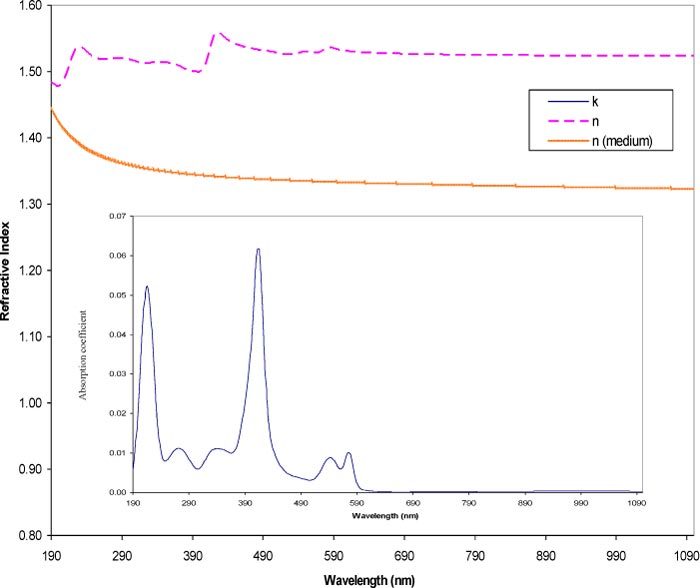
Optical properties of oxyhemoglobin and the medium. Plot of the contents of an optical properties file for oxyhemoglobin over the wavelength range of 190-1100 nm. Plots include the absorption coefficient (κ(λ)) and refractive index (n(λ)) of hemoglobin and the refractive index (n₀(λ)) of water.

3.5. Sensitivity analysis: varying MCV

The theoretical calculations based on Mie theory were used to examine the sensitivity of the spectra to changes in the cell size (MCV). The simulation varied the MCV over the physiological range of 80–100 fl [44]. The MCHC (0.33 mass fraction) and the hematocrit (0.45 volume fraction) were both held constant throughout the simulations. The MCV were represented using the diameters of spheres of equivalent volume (e.g. 80 fl has a spherical diameter of 5.35 x 10⁴ cm). Figure 4 shows the result of the simulation, normalized to eliminate effects due to particle concentration differences. As the sizes increased, the trend in the optical density showed a flattening of the spectra. The overall features stayed the same but the region above 600 nm showed small but consistent decreases in the slope with increasing particle size. In the 190–600 nm region, the larger cells exhibited a lower OD than the smaller cells. Thus, changes in the MCV within the physiological range had a detectable impact on the simulated spectra when the hemoglobin concentration was high (0.33 mass fraction). Varying the MCV at low MCHCs in the low range of ~0.05 mass fraction (Fig. 5 ) showed smaller changes in the overall spectra compared to the changes seen in Fig. 4. The hemoglobin peaks were well defined with the low MCHC. Overall, the spectra of the different MCVs overlapped across the entire wavelength range with the exception of the two large peaks at 223 and 417 nm. The intensity of these peaks increased with smaller particle sizes, however, the differences were slight.

Fig. 4.

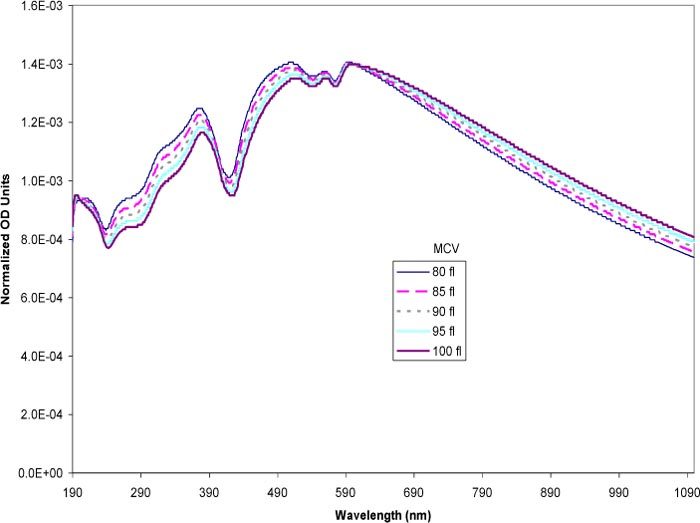
Simulated spectra of erythrocytes at varying MCV at constant high MCHC (0.33 mass fraction). The MCV was varied in the physiological range of 80–100 fl. The volumes were expressed in the model as the equivalent sphere diameter. The spectra were normalized to eliminate the effects of number based cell concentration.

Fig. 5.

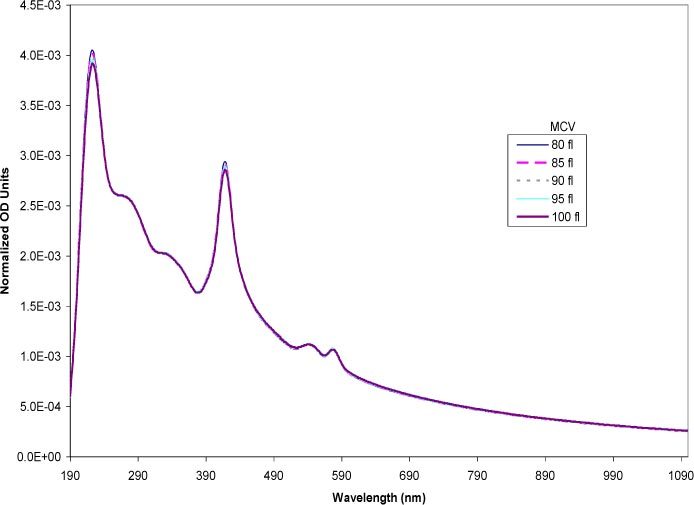
Simulated spectra of erythrocytes at varying MCV at constant low MCHC (0.05 mass fraction). The MCV was varied in the physiological range of 80–100 fl. The volumes were expressed in the model as the equivalent sphere diameter. The spectra were normalized to eliminate the effects of number based cell concentration.

3.6. Sensitivity analysis: varying MCHC

It was also of interest to examine how variations in the encapsulated hemoglobin concentration would affect the spectra as the MCV was held constant at 80 fl and the MCHC value was varied from the high physiological mass fraction (0.33) down to a mass fraction of 0.05 (Fig. 6 ). The hematocrit value was also held constant at the physiological volume fraction of 0.45 thus the cell number was invariant throughout the simulation. The most compelling trend was the overall increase in the intensity the spectra across the entire wavelength range as the MCHC increased. At the low MCHC values (0.05 and 0.09), the characteristic spectral features of free hemoglobin were visible [singlet at (417 nm) and the doublet (500~600 nm)] (compare to spectrum of free hemoglobin in solution in Figs. 7–9). Even a small difference in mass fractions between 0.05 and 0.09 lead to a substantially elevated spectrum for the 0.09 mass fraction. The features of the simulated spectrum were markedly affected as the mass fraction hemoglobin was increased from 0.09 to 0.20 with the hemoglobin peaks becoming less prominent. At physiological MCHC (0.33 mass fraction) the overall optical density was increased and further masked the characteristic hemoglobin peaks.

Fig. 6.

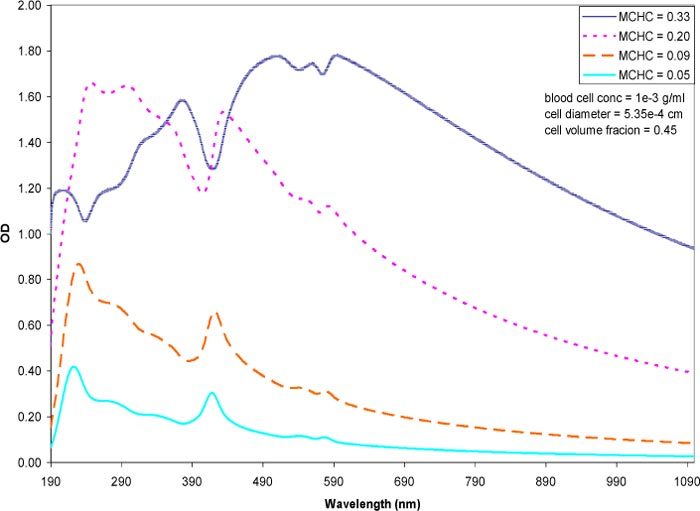
Simulated spectra of erythrocytes at varying MCHC and constant MCV. The MCV was held constant at 80 fl and the hematrocrit at 0.45 mass fraction. The MCHC was varied from the physiological value of 0.33 (high range) and decreased to medium and low ranges. The spectra are expressed per unit cell.

4. Results

4.1. Effects of instrumental setup on the spectra of erythrocytes and hemoglobin

In combination with the simulations, the effect of changes in the MCV and MCHC was also examined experimentally. To this end, it was necessary to first study the effects on the spectrum of spectrophotometer systems that captured different amounts of scattered light. Three commercially available instruments were examined: 1) the Agilent 8453 diode array spectrophotometer captured the transmitted light at a small (2°) acceptance angle, 2) the Perkin-Elmer Lambda 900 spectrophotometer acquired data at larger (> 2°) angles (referred to as diffuse transmission spectra), and 3) the Perkin-Elmer Lambda 18 spectrophotometer was fitted with an integrating sphere module to collect light scattered at all angles by the sample. Figure 6 shows a solid curve representing a spectrum of purified, diluted red cells (4000 cells/μl) containing a physiological hemoglobin concentration (33% w/v) taken with an Agilent spectrophotometer. The dashed curve shows the spectrum of a free hemoglobin solution obtained by lysing the same concentration of red cells in a hypotonic buffer (7mM phosphate buffer), thus the total mass of the hemoglobin was constant between the two samples. All the spectra presented in this section were obtained in replicates of three with good reproducibility. The spectrum of the encapsulated hemoglobin exhibits a significantly greater OD throughout the entire wavelength range compared to the spectrum of the hemoglobin solution, however it lacks the prominent absorption peaks that define free hemoglobin (characteristic hemoglobin peaks at 270, 337, 417, 547, and 575 nm).

Figure 8 illustrates spectra of a blood sample diluted to the same concentration as Fig. 7 but measured with Perkin-Elmer Lambda 900 spectrophotometer with a larger acceptance angle than the Agilent. Two features are immediately apparent compared to the spectra in the previous figure. First is the presence of prominent hemoglobin peaks in the diffuse transmission spectrum of the red cell suspension, whereas these peaks in Fig. 7 were combined with scattering features of the red cell. Second, the diffuse transmission spectrum of the suspension shows an overall lower spectral intensity across the entire wavelength range compared to the red cell spectrum taken with the smaller, 2° acceptance angle (Fig. 7). This is expected since more of the scattered light is received by the detector but the features of the scattered light are averaged over all angles accepted.

Fig. 8.

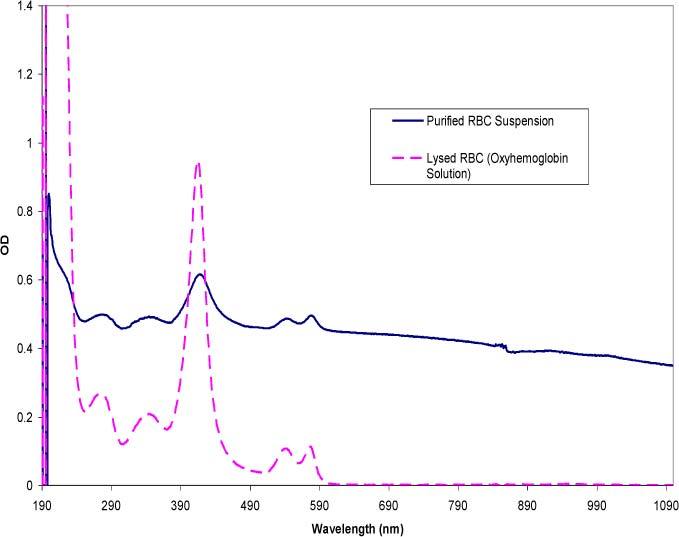
Diffuse spectra comparing purified red cells and hemoglobin in solution acquired from a Perkin-Elmer Lambda 900 spectrophotometer with an acceptance angle >2°. The RBC concentration is approximately 4000 cells/μl and the concentration for the hemoglobin in solution is ~0.12 mg/ml.

Figure 9 represents spectra acquired with an integrating sphere. In this arrangement, essentially all of the scattered light was collected, hence the resulting transmission spectrum reflected solely the absorption component (hence it can be referred to as an absorption spectrum). The baseline of the absorption spectrum of the red cells overlapped that of the spectrum of the true hemoglobin solution, contrary to the elevated nature of the diffuse transmission spectrum shown in Fig. 7. As expected, the hemoglobin peaks of the red cell absorption spectrum were more pronounced with the integrating sphere in comparison to the diffuse red cell spectrum, however, the peaks at 270, 337 and 417 nm were less intense than the peaks of the hemoglobin solution. The doublet at 547 and 575 nm showed good overlap between the whole and lysed red cell spectra. The differences in intensity have been attributed to molecular hypochromicity by several authors [24,25].

Note that the disparities in the spectra of identical cell suspensions were based solely on the differences of the spectrophotometer configuration, bringing to light the importance of understanding the instrumental arrangement in relation to data interpretation. It should also be noted that the dissimilarities in spectra due to the spectrophotometers were only manifested with large scatterers (such as RBCs) whereas the spectrum of small particles like those of hemoglobin in solution were essentially the same with all three instruments and that this behavior is consistent with the scattering theories [6,7]. Most importantly, the spectrum obtained from the smaller acceptance angle contains more scattering-related information (size, refractive index of the particle) and can be readily modeled with the appropriate scattering theory.

4.2. Comparisons of spectra between experimental and simulated data

As indicated in the theory section, Mie theory has no limitations relative to the size of the particles and no constraints relative to the magnitude of the optical properties. Given the size of the red blood cells and that that hemoglobin is a strong chromophore, Mie theory has been used as an effective tool to examine the relationship between the spectral features and the physical parameters of the experimental red cell data. The experimental system was composed of spectra of purified, unmodified red blood cells as well as red cells containing hypotonically altered hemoglobin concentrations. The data was obtained using the 2° acceptance angle to maximize information content of the spectra relative to the absorption and scattering components of the red blood cells. The experimental and simulated spectra were compared closely for consistencies in features and trends. Moreover, replicates of the resealed cells samples indicated reproducibility of relevant hematologic parameters (MCV, MCHC) and the features of the accompanying spectra.

Figure 10 is a summary of experimental spectra of purified red blood cells selected for similar MCHCs in the physiological range, but with varying MCVs. The spectra were normalized to eliminate effects due to particle concentration. A free hemoglobin spectrum scaled to fit the normalized plot was included as a reference for comparison of the features. For comparison with the experimental data, the same MCHC/MCV values were simulated using the Mie theory (Fig. 11 ).

Fig. 10.

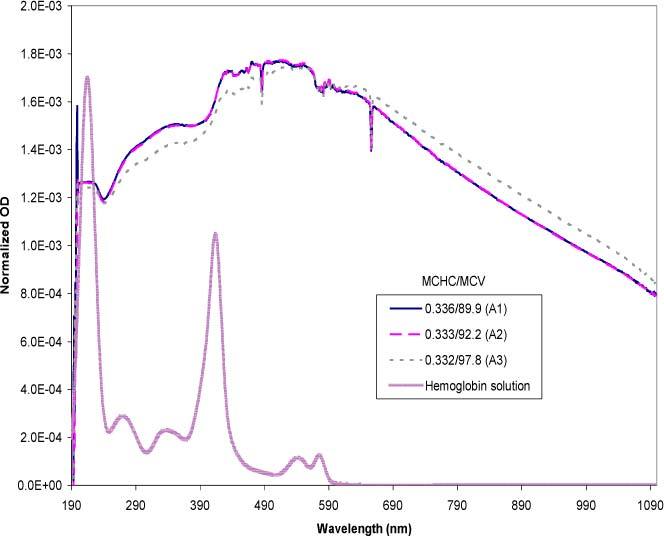
Experimental data set of purified red cells in the high MCHC range with varying MCV values. The data set is normalized in the 230-900 nm range using the area under the curve method. The MCHC is expressed in mass fractions and the MCV in fl. The free hemoglobin solution spectrum is included as a reference.

Fig. 11.

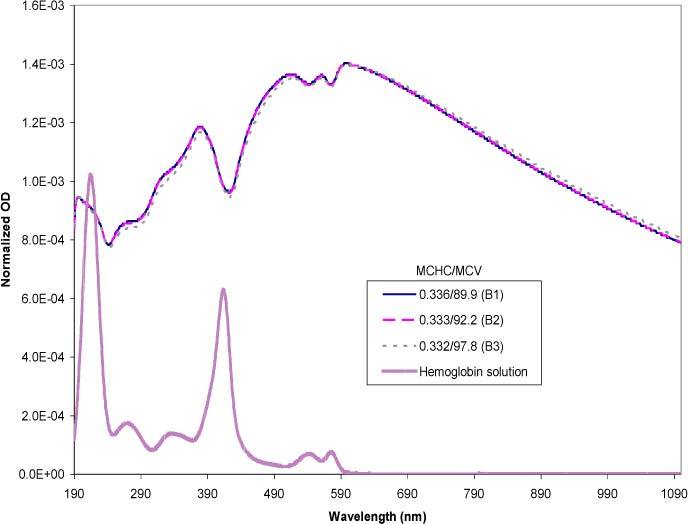
Simulated spectra mimicking the experimental data set from Fig. 6, normalized on a per cell basis. The MCHC is expressed in mass fractions and the MCV in fl. The free hemoglobin solution spectrum is included as a reference.

A comparison between the curves A1 and A2 in Fig. 10 show a direct overlap of the two spectra, as well as in the simulated spectra (curves B1 and B2 of Fig. 11). Consistent with this data, examination of the hematologic parameters for the red cell samples revealed that the MCHC and MCV values were also similar for both curves. The trend of the experimental spectrum of 0.332/97.8 (A3) compared to the other samples was also simulated accurately (B3). Compared to A2, the quantitative difference of A3 was significant in terms of the volume. Although the magnitude of difference between A2 and A3 was greater than their simulated counterparts (B2 and B3), the direction of the spectral change was the same. Consistent with trends shown by the simulations section, the A3/B3 spectrum was slightly flattened as a result of its higher MCV. The successful simulations of the MCV differences presented here were experimentally reproducible.

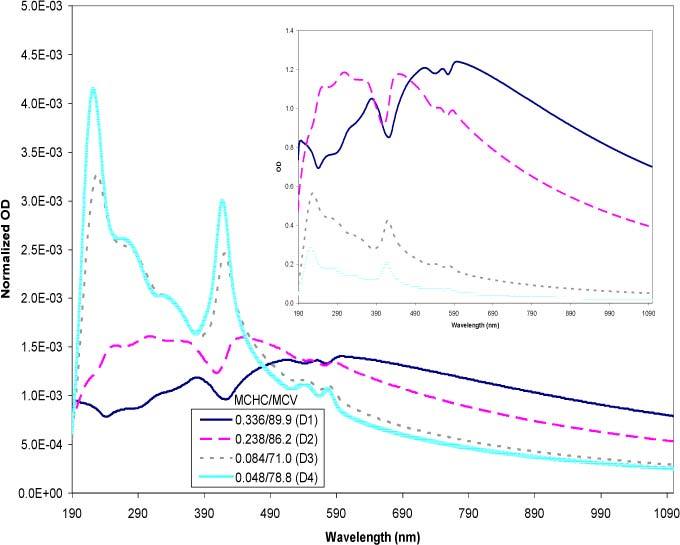
The next step was to test the ability of the model to accurately simulate combinations of varying MCHC and MCV. Figure 12 represents a group of experimental data selected over a range of MCHCs (0.048–0.336 mass fraction) each accompanied by varying MCV quantities. The inset shows raw data with each sample diluted to a concentration of approximately 4000 cells/μl. The large plot is normalized data designed to amplify the features of the spectra to facilitate visual qualitative comparisons. As the MCHC increased, the overall optical density increased (inset). The differences in the MCV provided a more subtle contribution to the spectra. The normalized plot helped to show the emergence of the hemoglobin peaks as the encapsulated hemoglobin concentrations decrease. The lowest MCHC sample (C4) showed the highest, most pronounced hemoglobin peaks whereas the highest MCHC sample (C1) exhibited a near absence of the characteristic peaks. The observed behavior is expected and consistent with the scattering theory; as the concentration of hemoglobin within the cell is decreased, so is the contrast of the particle relative to the suspending medium, which results in a decrease of the scattering contribution [6,7].

Fig. 12.

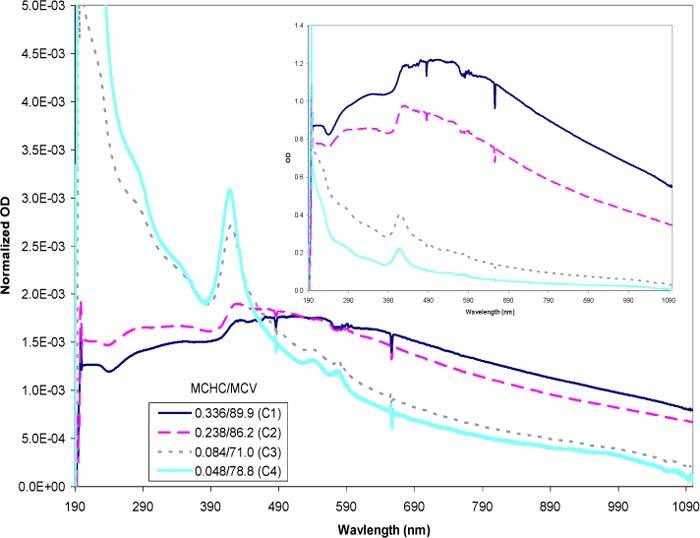
Experimental spectra of resealed cells with varying MCHC and MCV values. The MCHC is expressed in mass fractions and the MCV in fl. The inset represents the raw experimental data with each sample adjusted to a concentration of approximately 4000 cells/μl. The large plot represents the normalized data where each raw data was divided through by the area under their respective curve. The normalized plot amplifies the features of the curves to facilitate visual comparison.

Figure 13 presents the simulations of the experimental spectra using the same MCHC and MCV values. The empirical trends are evident in the simulated spectra: 1) there is a flattening in the curve with increasing MCHC, 2) the hemoglobin peaks become more apparent with decreasing MCHC, and 3) the inset plots show that with a constant cell count, the increase in MCHC generates a dramatic increase in the intensity of the overall spectrum. The good agreements seen between the experimental and simulated spectra of the unmodified and hypotonically modified erythrocytes indicate the effectiveness of the scattering theory in describing the spectral features as functions of the size and the hemoglobin concentration.

Fig. 13.

Simulated spectra of resealed cells using the experimental MCHC and MCV values in Fig. 10. The MCHC is expressed in mass fractions and the MCV in fl. The inset represents simulations of the raw experimental data. The large plot represents the normalized data where each raw data was divided through by the area under the respective curves. The normalized plot amplifies the features of the curves to facilitate visual comparison.

5. Discussion

Historically, hypochromicity has been defined by electronic molecular interactions [21,23] and it has been hypothesized that the same effect is significant in encapsulated systems such as red cells [24,25]. Our study approached this question from the perspective of instrumental configuration and a theoretical interpretation of the combined absorption and scattering phenomenon. It is generally accepted in optics that the angle of acceptance of the detector contributes significantly to the outcome of the spectral features when particles, the size of red blood cells or mitochondria, are present [2,6,21,35,45]. Although the importance of the detector aperture has been recognized it has not been incorporated as a key parameter in the interpretation of hypochromicity. The comparison of acceptance angles presented herein shows clear differences in the spectra of red cells resulting from the amount of scattered light acquired by the detector. A configuration that collects a large amount of scattered light loses scattering information in the transmission spectrum because the intensities of the scattered light are averaged over the angles accepted by the detector. In contrast, small acceptance angle transmission spectra contain a better balance of absorption and scattering information.

Since a transmission spectrum of a large particle suspension such as red cells is dominated by the scattering component an accurate description of the scattered light is necessary. In the case of the small angle transmission spectrum, scattered light not captured by the detector can be inferred using light scattering theory (in our case, the Mie theory) to deconvolute the spectrum into its scattering (Q_sca) and absorption (Q_abs) components. Conversely, the spectrum can be modeled to simulate the features and trends of the spectra, as it was successfully demonstrated herein for red blood cells. In accordance with the theory of scattering of electromagnetic radiation, the scattering and absorption efficiencies are additive (Q_ext = Q_sca + Q_abs). Therefore, as the relative contribution of the scattering component increases, a concomitant decrease in the absorption component will be observed. This explains why the absorption spectrum obtained from the integrating sphere is lower in intensity than its free hemoglobin counterpart; the encapsulated system is dominated by scattering and thus attenuates the intensity of the absorption component (macroscopic hypochromism). Moreover, both Q_sca and Q_abs are functions of the size and complex refractive index [6–8]. It is therefore easy to see that variations in the cell volume and hemoglobin content affect the spectra as shown both experimentally and theoretically in this study.

The fundamental concepts underlying the interpretation of the optical spectra of red blood cells bring to light the need to extend the definition of observed hypochromicity on two levels. The results in this study clearly show the presence of macroscopic hypochromism, which is an effect of scattered light. Thus far, simulations based on the Mie theory closely match experimental spectra, suggesting that the more commonly referenced molecular hypochromism plays a small or perhaps an insignificant role in the optical activity of red cells and related particle systems. This remains to be seen as current work progresses to extend the scattering theory to implement an interpretation model for the quantitative assessment of red blood cells.