HAPGEN2: simulation of multiple disease SNPs

Abstract

Motivation: Performing experiments with simulated data is an inexpensive approach to evaluating competing experimental designs and analysis methods in genome-wide association studies. Simulation based on resampling known haplotypes is fast and efficient and can produce samples with patterns of linkage disequilibrium (LD), which mimic those in real data. However, the inability of current methods to simulate multiple nearby disease SNPs on the same chromosome can limit their application.

Results: We introduce a new simulation algorithm based on a successful resampling method, HAPGEN, that can simulate multiple nearby disease SNPs on the same chromosome. The new method, HAPGEN2, retains many advantages of resampling methods and expands the range of disease models that current simulators offer.

Availability: HAPGEN2 is freely available from http://www.stats.ox.ac.uk/~marchini/software/gwas/gwas.html.

Contact: zhan@well.ox.ac.uk

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Genome-wide association studies have become a powerful approach for uncovering the genetic variants that impact human phenotypes. Simulation studies are a popular and inexpensive approach to evaluate new methods for statistical analysis (Su et al., 2009) and to examine the power of different experimental designs (Spencer et al., 2009).

The traditional approach of simulating a population forwards (Lambert, 2008) or backwards (Hudson, 2002) in time ignore the large amount of observed genetic data that are available, can be computationally intensive and can struggle to match real LD patterns. To overcome these problems, Spencer et al. (2009) introduced a novel simulation approach, HAPGEN, which uses an alternative resampling approach. Given a reference panel of haplotypes, this method produces a sample of haplotypes with patterns of LD similar to those in the reference panel. Using the HapMap3 and 1000G haplotype data as reference panels, HAPGEN is able to simulate data for many populations. In addition, it is fast and can simulate a single disease SNP under a general disease model, allowing the user to specify the risk allele and heterozygote and homozygote relative risks. Other resampling methods also exist (Li and Li, 2008; Wright et al., 2007), but they and HAPGEN can only simulate a single disease SNP on the same haplotype. There are many complex diseases with multiple-associated loci on the same chromosome, some of them in close proximity (e.g. Strange et al., 2010), so the ability to simulate multiple disease SNPs on the same chromosome would be desirable. To address this issue, we have devised a new approach, extending HAPGEN, to simulate multiple nearby disease SNPs on the same chromosome.

2 METHODS

The HAPGEN2 simulation approach is similar to that of HAPGEN and is based on the Li and Stephens (LS) model (Li and Stephens, 2003) of LD. Briefly, given a reference panel of haplotypes, H^R={h₁,…,h_r} as input, where each haplotype is typed at L biallelic sites, that is h_i=(h_(i,1),…,h_(i,L)) and h_(i,j)∈{0,1}, the LS model models each newly simulated haplotype as an imperfect mosiac of the haplotypes in H^R and the haplotypes that have already been simulated (see below for more details). Simulation of case–control data is based on a set of disease SNPs, D={d_k:d_k∈{1,…,L}, k=1,…,K} with effect sizes and RR={(rr¹_k, rr²_k)}, where rr¹_k and rr²_k are the disease risks of carrying one and two copies of the 1 allele relative to carrying two copies of the 0 allele at d_k, which combine multiplicatively across the K disease SNPs. The haplotypes, H^P={h_r+1,…,h_p}, for the control individuals are simulated first, followed by the haplotypes, H^Q={h_p+1,…,h_q}, for the case individuals.

2.1 Simulating control data

We simulate the control data as population controls (so that some of them may be cases) and simulate each additional haplotype, h_i+1∈H^P, sequentially under the LS model. We use the copying states, z_(i+1,j)∈{1,…,i}, which evolve in a Markov manner, to indicate the haplotype that h_(i+1,j) copies at site j. We simulate each haplotype in three stages. First, the cross-over events, which are locations where z_(i+1,j)≠z_(i+1,j−1), are simulated according to the transition probabilities

(1)

where I_z is 1 if z=z_(i+1,j−1) and 0 otherwise, and ρ_j is genetic distance between SNPs (j−1) and j. Conceptually, the cross-over events mimicks the effect of recombination and breaks up h_i+1 into independent segments, {h_(i+1,s1),…,h_(i+1,sn)}, where each segment is a haplotype of SNPs between two cross-over events. Second, the copying state for each segment is sampled uniformly from {1,…,i}. Finally, the allele at each SNP is simulated conditional on the copying state and a mutation parameter μ_i:

(2)

Spencer et al. (2009) found that 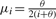, where 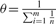, simulated amounts of novel haplotype variation similar to data simulated under the coalescent model.

2.2 Simulating case data

We simulate the case haplotypes in a similar way, but we simulate them sequentially in pairs (with each pair corresponding to a case individual) and oversample haplotypes carrying the risk alleles based on the relative risks.

Simulation of each haplotype pair, (h_i+1,h_i+2)∈H^Q, proceeds in four stages. First, the cross-over events are simulated in the same way as for the controls, according to (1). Second, the alleles at the disease SNPs are simulated. Let (h¹_D,h²_D) be the subset of (h_i+1,h_i+2) that consist of the alleles at the disease SNPs, so that h^j_D=(h_(i+j,d1),…,h_(i+j,dk)) for j=1,2. The cross−over events separate h¹_D and h²_D into segments, {h¹_s¹1,…,h¹_s¹n1} and {h²_s²1,…,h²_s²n2}. We simulate (h¹_D, h²_D) from its joint distribution, which is calculated from the relative risks and the marginal frequencies of each segment in H^P and H^R, using Bayes Theorem:

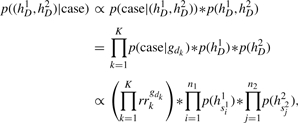where g_dk=h¹_dk+h²_dk is the genotype at d_k, and p(h_s) is the frequency of the haplotype segment h_s in H^R and H^P. Third, the copying state for each segment, h_(i+1,s), is simulated independently and is drawn uniformly from {1,…,i}, like we do for the controls, if s does not include any disease SNPs; or else it is drawn from

where I_dk is 1 if h_(i+1,dk)=h_(z,dk) and 0 otherwise. Finally, each allele for h_(i+1,s) is simulated according to (2). Copying states and alleles for h_i+2 are simulated in the same way.

3 RESULTS

To demonstrate HAPGEN2, we have simulated, using HapMap2 CEU as the reference panel, 2000 cases and 2000 controls at 880 SNPs across a 700 kb region on chromosome 21, with 3 disease SNPs, at positions d₁=25 356 790, d₂=25 390 071 and d₃=25 691 378, each under a log-additive disease model with a heterozygote relative risk of 1.3. The simulation process took <10 s on a 2.93 GHz processor laptop, and will increase linearly with the number of SNPs and individuals.

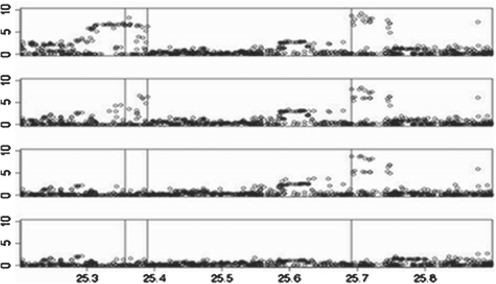
Figure 1, produced by HAPLOVIEW (Barrett et al., 2005), shows the similarity between the LD patterns of the reference panel (top) and the simulated haplotypes (bottom). The top plot in Figure 2 shows the −log₁₀(P-values), for the log-additive test, across the region, illustrating the signal of association at the disease SNPs; subsequent plots show the P-values conditioned on the genotypes at d₁, at d₁ and d₂ and at d₁, d₂ and d₃, respectively, confirming that there are indeed three independent disease SNPs.

Fig. 1.

LD patterns, in terms of r², in the HapMap reference haplotypes (top) and the simulated haplotypes (bottom).

Fig. 2.

Top plot shows the −log₁₀(P-values) under the log-additive test at each SNP in the simulated data. The location of the disease SNPs, d₁, d₂, d₃, are indicated (from left to right) by the vertical lines. Subsequent plots (from the top) show the P-values conditioned on the genotypes at d₁, at d₁ and d₂ and at d₁, d₂ and d₃.

4 DISCUSSION

We have introduced a new resampling method that can simulate multiple disease SNPs on the same haplotype, which will be particularly useful for investigating disease models involving multiple disease SNPs within close proximity. HAPGEN2 is fast, simple to use and available as a C++ package from http://www.stats.ox.ac.uk/~marchini/software/gwas/gwas.html, along with instructions and supporting resources, such as recombination rates, HapMap and 1000G reference panels.

The model described here can be easily extended to simulate interacting disease SNPs (we currently provide an R package that does this) and admixture (using reference panels from multiple populations), which we hope to implement in the future.

Funding: Wellcome Trust grants 084575/Z/08/Zand075491/Z/04/B. PD was supported in part by a Wolfson Royal Society Merit Award.J.M. was supported by United Kingdom Medical Research Council grant number G0801823.

Conflict of Interest: none declared.