Design Optimization for a 2-D Sparse Transducer Array for 3-D Ultrasound Imaging

Abstract

In 3-D ultrasound imaging where 2-D transducer arrays with more than hundreds of elements are used, sparse arrays can be used to reduce the number of active ultrasound channels. Under a restriction of desired number of active channels, we can maximize the image quality by optimally choosing the positions of active elements. Here we use the method of simulated annealing to find the optimal configuration of a 2-D sparse array. This algorithm tries to minimize the value of an objective function defined as the energy ratio between the nonfocal and focal regions in the point spread function (PSF). Optimal configurations were found for the cases of choosing 16, 20, 24, 28, and 32 transmit and receive elements from a 16×16-element rectangular transducer array. With only 32 transmit and 32 receive elements, we could achieve an energy ratio of 16%, compared to 6% of the full array, which is the gold standard utilizing all the 256 elements for both transmit and receive. Using Field II, we simulated imaging with the optimal sparse arrays, for off-axis targets as well as on-axis targets, and the resulting images were compared with those from some other configurations, such as full-transmit full-receive, full-transmit x-receive, x-transmit boundary-receive, and so on.

INTRODUCTION

In 3-D volumetric ultrasound imaging where 2-D transducer arrays with more than hundreds of elements are used, it is challenging to fabricate and interconnect as many electronic channels as the transducer elements [1], [2]. In addition, the data processing speed required in real-time imaging and the total power budget also make it difficult to use a large number of ultrasound channels [3].

In many applications, sparse arrays can be used to reduce the front-end complexity and improve the image processing speed. Since the beam pattern of an aperture is determined by its geometry, we can maximize the image quality by optimally choosing the locations of the active elements, under a restriction of desired number of active transmit and receive elements.

There have been various approaches to design sparse arrays. For example, random approaches [4]–[6], genetic algorithms [7]–[10], linear programming [11], and sparse periodic layouts [12]–[14] have been proposed as strategies for finding optimal sparse array configurations. Recently, Karaman et al. [15] developed a design method to eliminate redundancies in transmit-receive element combinations, using the concept of coarray. An alternative approach for the sparse array design is optimization by simulated annealing. This method is based on the analogy between the annealing in a solid material and the multivariate or combinatorial optimization process [16], and has produced appreciable results in previous works [17]–[21].

In this paper, we propose another application of simulated annealing algorithm for finding an optimal 2-D sparse array configuration. We defined an objective function as the energy ratio between the non-focal and focal regions in the point spread function, and implemented a simulated annealing algorithm that tries to minimize it. In each iteration of simulated annealing process, the objective function was evaluated using the Field II [22], [23] simulation results. The optimal locations of active elements were found from a 16×16-element transducer array, and we could achieve comparable image quality to that of other configurations using more number of transducers. Section II describes the methods we used, and in Section III the results of optimization are presented. The imaging simulation results with the optimal sparse arrays we found are provided in Section IV.

II. METHODS

A. Problem Definition

In the beam pattern of a sparse array, it is desirable that most of the ultrasonic energy is concentrated in the main lobe region. In other words, we want to have a point spread function (PSF) with as much energy as possible inside of the focal region, and as little energy as possible outside of that region. So our objective in this problem would be to minimize the energy ratio between the non-focal and focal regions in the PSF, by properly choosing the locations of limited number of transmit and receive elements. In summary, we define our problem as,

• -Find the optimal location of each transmit/receive element,
• -That minimizes the objective function E_out/E_in,
• -Subject to limited number of transmit/receive elements,

where E_out and E_in are the PSF energy in the non-focal region and in the focal region, respectively.

B. Evaluating the Objective Function

With the synthetic phased array (SPA) imaging technique, where a single transmit element is excited and all the receive elements are enabled at each firing event, an image obtained using an array of transducer elements can be considered as a sum of sub-images contributed by individual transmit-receive element pairs. Similarly, PSF of a transducer array can also be constructed by superposition of sub-PSFs of individual transmit-receive element pairs. Using Field II, sub-PSFs of all the transmit-receive element pairs from a dense 2-D rectangular array were simulated and saved. To construct the PSF of a sparse array, the sub-PSF data relevant to the configuration are read and added. And then we can obtain the values of E_in and E_out by simply integrating the PSF energy inside and outside of the focal volume, respectively, to calculate the energy ratio which is our objective function.

C. Simulated Annealing

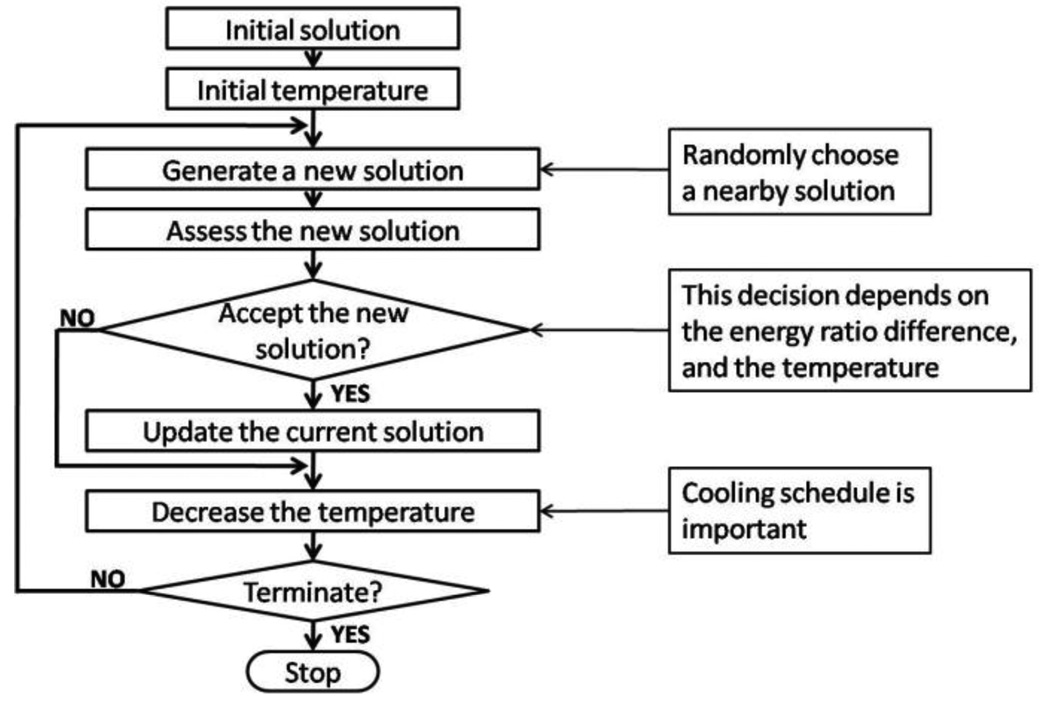
The basic algorithm of simulated annealing used in this study is shown in Fig. 1. Starting from an initial solution, which is an arbitrary sparse array configuration with required number of active transmit and receive elements, it tries to improve the solution until it finds an acceptable solution.

Figure 1.

The basic simulated annealing algorithm.

In each iteration, it perturbates the current solution, by randomly selecting one transmit or receive element, and moving it to one of its nearby positions. Since we are moving only one element at a time, the PSF of the new aperture can be quickly calculated from the PSF of the previous aperture, by replacing the contribution of the eliminated element with that of the new element, instead of recalculating the PSF from scratch.

The acceptance decision is based on the objective function value calculated from the PSF, and the current temperature. Denoting the energy ratio of the new solution by F(S_n), the energy ratio of the previous solution by F(S_n−1), and the current temperature by T, we defined our acceptance probability function P(ΔF(S), T) as

$$P(\mathrm{\Delta }F(S),T)=\begin{array}{cc}\hfill e^{-\frac{\mathrm{\Delta }F(S)}{T}},\hfill & \mathit{\text{if}}\mathrm{\Delta }F(S)>0,\hfill \\ \hfill 1,\hfill & \mathit{\text{otherwise}}\hfill \end{array}$$ (1)

where

$$\mathrm{\Delta }F(S)=F(S_n)-F(S_{n-1}).$$ (2)

Thus, if the new solution is better than the previous solution, i.e., if the new energy ratio is smaller than the previous one, the new solution is always accepted. On the other hand, if the new solution has an energy ratio larger than the previous energy ratio, the new solution is accepted with probability of P(ΔF(S), T). The smaller ΔF(S) is, and the higher the temperature is, it is more likely that the new solution is accepted, even though it is worse than the previous solution. So at high temperature, the algorithm can easily escape from a local minimum.

At the end of each iteration, we decrease the temperature, making it harder for a worse solution to be accepted. The cooling schedule is determined by the cooling factor, α. With the initial temperature T₀, the temperature becomes, after i iterations,

$$T=T_0·{\alpha }^i.$$ (3)

We can give more chances of finding the global optimum by cooling down slowly, but it also slows down the convergence of the solution. So the cooling schedule must be chosen carefully.

III. RESULTS

Assuming a 2-D 16×16-element rectangular transducer array, we implemented the simulated annealing algorithm to find the optimal sparse array configurations with 16, 20, 24, 28, and 32 active transmit and receive elements. The parameters used in the PSF simulation are listed in Table I. To simplify the problem, the symmetry of the aperture was assumed in both horizontal and vertical directions. Also, in order to reduce the front-end electronics complexity, we required that no element is used for both transmit and receive.

TABLE I.

Simulation Parameters

Parameter	VALUE
Array size	16×16 elements
Center frequency	10 MHz
Fractional bandwidth (FBW)	80%
Element pitch	60 µm
Element size	50 µm × 50 µm
Kerf	10 µm
Excitation pulse	Gaussian pulse with 80% FBW
Sampling frequency	100 MHz
Point target location	On axis, with F number of 4 (3.8 mm)
Scan volume	9 mm × 9 mm × 4.2 mm
Focal volume	1.1 mm × 1.1 mm × 0.18 mm
Voxel size	100 µm × 100 µm × 20 µm
Ultrasound velocity	1540 m/sec

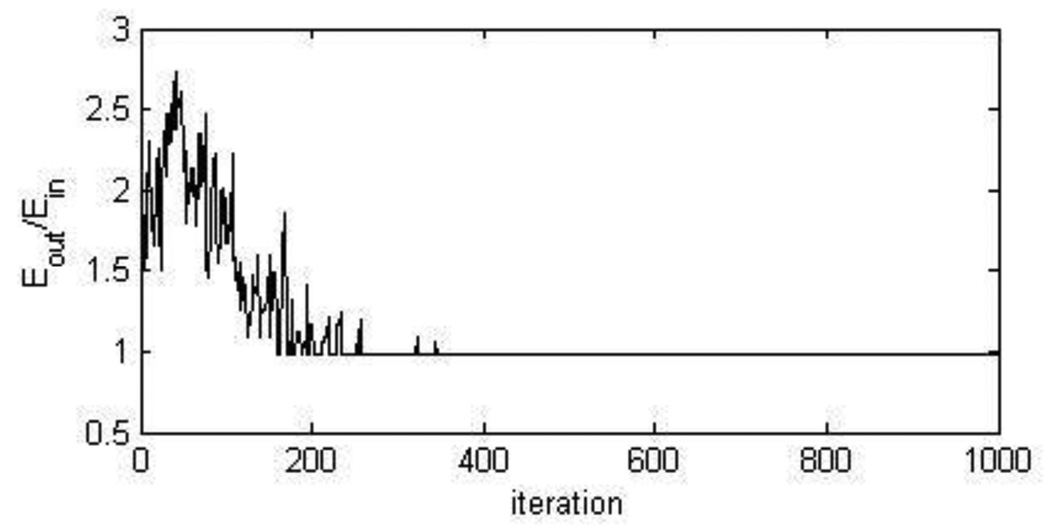
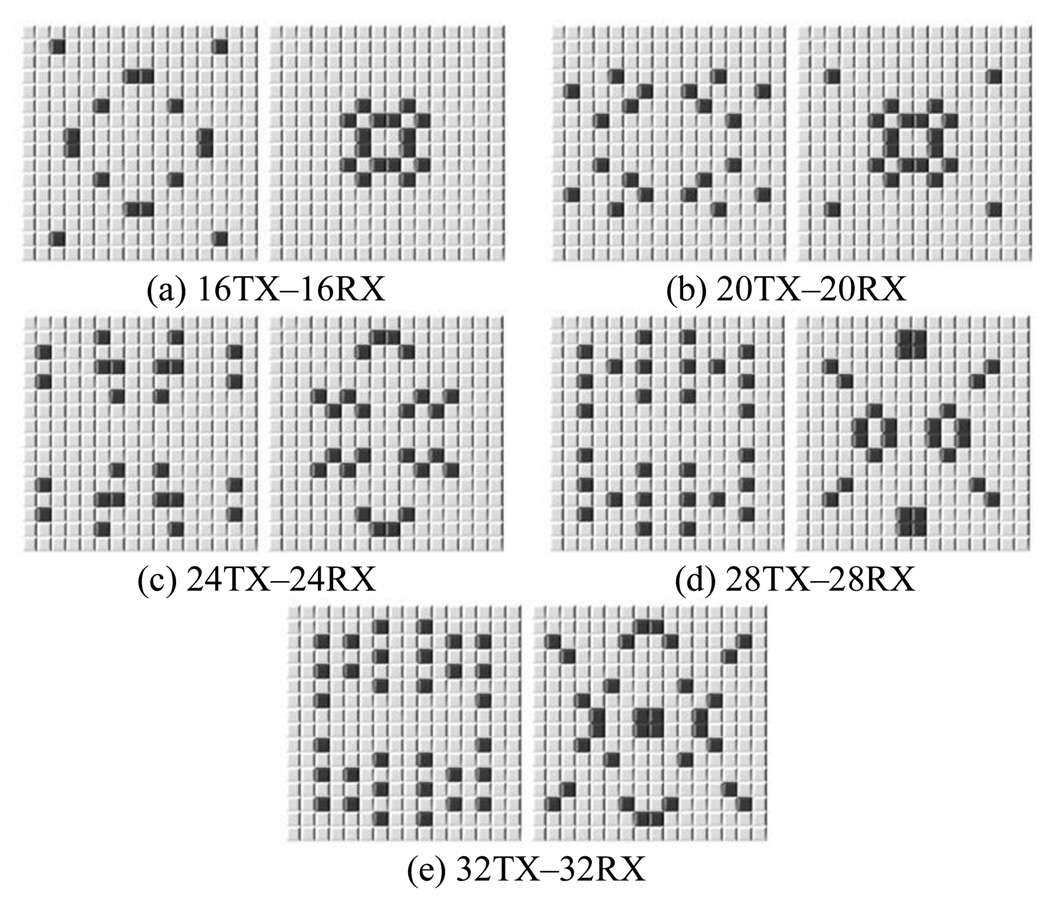
For the case of choosing 16 transmit and 16 receive elements out of 16×16 locations, the solution converges within 500 iterations (Fig. 2), with initial temperature of 1.0 and cooling factor of 0.99. The solution found in the first run of simulated annealing may not be, and usually is not, the best solution. However, it provides us a reasonably good solution in a short time, and this configuration can be used as a good starting point for another run of simulated annealing. We ran the optimization process multiple times for each problem, using the last solution as the initial configuration for the next run, and found that the solution does not improve after only a few runs. The optimal configurations found using this method are summarized in Fig. 3. It required 3 to 5 runs to reach each of these configurations. The energy ratios of these apertures are listed in Table II.

Figure 2.

Convergence of the solution. In a problem finding 16 transmit and 16 receive elements, it converges within 500 iterations.

Figure 3.

Optimal sparse array configurations (left: TX apertures, right: RX apertures) found by simulated annealing.

TABLE II.

Energy Ratio of the Optimal Sparse Arrays

Aperture	Number of TX elements	Number of RX elements	Energy Ratio
16TX–16RX	16	16	0.4427
20TX–20RX	20	20	0.3331
24TX–24RX	24	24	0.2450
28TX–28RX	28	28	0.2123
32TX–32RX	32	32	0.1613

In Table III, the energy ratios of some other apertures introduced in [15] are shown for comparison. To make the comparison fair, the same synthetic phased array (SPA) imaging technique was used for all of these apertures. So, the full transmit and full receive (FT–FR) aperture here differs from the CPA or CSA in [15], using a different imaging technique. The apertures with –NC in their names are those with no common elements between the transmit and the receive apertures.

TABLE III.

Energy Ratio of the Apertures from [15]

Aperture	Number of TX elements	Number of RX elements	Energy Ratio
FT–FR	256	256	0.0563
FT–XR–NC	224	32	0.0955
XT–BR	32	60	0.1712
XT–BR–NC	28	60	0.1870
XT–PR	32	60	0.2117
XT–PR–NC	32	56	0.3113
BRT–BCR	32	32	0.3252
BRT–BCR–NC	28	32	0.3736

–NC: No common element between TX and RX

IV. IMAGING SIMULATIONS

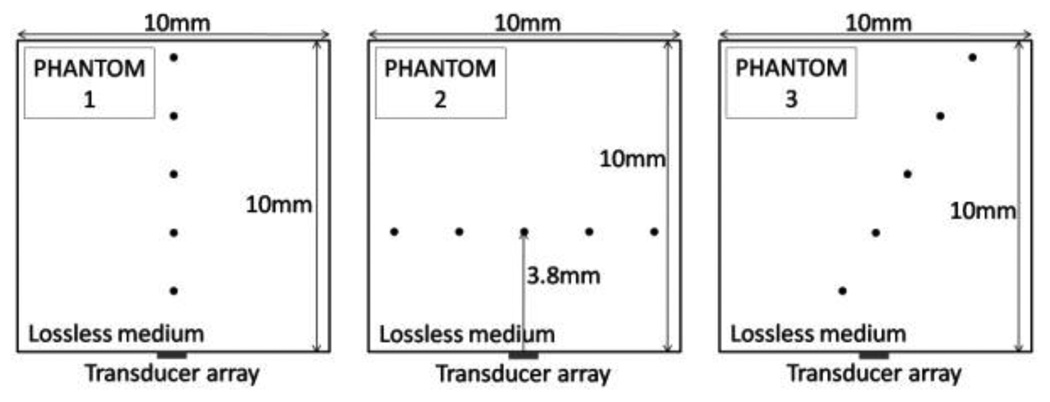
Using Field II program, we simulated imaging with the optimal sparse array configurations found by our method. Three phantoms (Fig. 4), each with 5 point targets in a lossless medium, were used to see the imaging capability of these apertures for both on-axis and off-axis targets. For comparison, the same simulations were also done with the other apertures.

Figure 4.

Three phantoms used in imaging simulations.

The simulation results show that our optimal configurations have comparable imaging capability, in a noiseless environment, to the other apertures using more number of active elements. Some of the simulation results are presented in Fig. 5.

Figure 5.

Some of the imaging simulation results. (e) and (f) are the images obtained with the optimal configurations found by simulated annealing, and (a)–(d) are from the other apertures. The display dynamic range is 40 dB.

V. CONCLUSIONS AND FUTURE WORKS

Using the method of simulated annealing, we implemented an optimization algorithm for choosing the locations of a limited number of active elements to obtain beam profiles that are comparable to those of other configurations that use a larger number of transducers. The optimal sparse array configurations were found for the cases of choosing 16, 20, 24, 28, and 32 transmit and receive elements from a 16×16-element 2-D array, and their imaging capability was examined by Field II simulations. The imaging simulation results showed that, in a noiseless environment we can achieve acceptable image quality while using only a small number of transducers.

Although sparse arrays and synthetic beamforming techniques help with the frame rate and hardware complexity, it is well known that they suffer from low SNR. One way of improving the SNR is using coded excitation [24], [25]. Currently, we are extending the presented approach to an overall system optimization for 2-D sparse arrays by including element apodization and coded excitation into consideration.