Abstract
The paper relates estimation and testing for additive interaction in proportional hazards models to causal interactions within the counterfactual framework. A definition of a causal interaction for time-to-event outcomes is given that generalizes existing definitions for dichotomous outcomes. Conditions are given concerning the relative excess risk due to interaction in proportional hazards models that imply the presence of a causal interaction at some point in time. Further results are given that allow for assessing the range of times and baseline survival probabilities for which parameter estimates indicate that a causal interaction is present, and for deriving lower bounds on the prevalence of such causal interactions. An interesting feature of the time-to-event setting is that causal interactions can disappear as time progresses i.e. whether a causal interaction is present depends on the follow-up time. The results are illustrated by hypothetical and data analysis examples.
A paper by Li and Chambless1 considered tests for additive interaction between the effects of two exposures in proportional hazards models. In this paper I will briefly relate these tests for additive interaction (along with proportional hazards survival curves) to causal interactions within the counterfactual framework.2–4 Causal interactions refer to settings in which there are persons for whom the outcome would occur (by a certain time) if both exposures were present but for whom the outcome would not occur if only one of the two exposures were present. Statistical interactions do not necessarily imply the presence of causal interactions.2 In this paper, it is shown that the tests for additive interaction in the proportional hazards model (or variants of such tests) can be used to infer the presence of a causal interaction at some point in time. To draw conclusions about the presence of causal interactions for intervals of times more generally, one can use results concerning the proportional hazard model parameters and the baseline survival function.
Methods
Let T be a time-to-event outcome and let D(t) be an indicator for the outcome having occurred by time t. Let G and E be two dichotomous exposures of interest and C a collection of covariates. Let S(t; g, e, c) and λ(t; g, e, c) denote, respectively, the survival function and hazard function at time t conditional on G = g, E = e, C = c. The proportional hazards model considered by Li and Chambless1 takes the form
| (1) |
where λ0(t) is the baseline hazard at time t and (β1, β2, β3, γ1, …, γn) are the model parameters. Note that, in the proportional hazards model in (1), we have that S(t; g, e, c) = S(t; 0, 0, c)exp(β1g+β2e+β3ge). Li and Chambless propose using as a measure of relative excess risk due to interaction5 (RERI) the quantity
which equivalently is
where HR(g, e; c) is the hazard ratio, conditional on C = c, comparing G = g, E = e with the reference group G = 0, E = 0. Li and Chambless discuss estimation, testing and confidence intervals for this quantity, RERIHR.
Now let Dge(t) denote the counterfactual outcome for a person at time t if, possibly contrary to fact, G had been g and E had been e; thus Dge(t) = 1 if the outcome for the person would have occurred by time t if G were g and E were e. We can say that there is a causal interaction between G and E at time t if for some individual D11(t) = 1 but D10(t) = D01(t) = 0 so that for that person the outcome would have occurred by time t if both exposures had been present but would not have occurred by time t if only one of the two were present. This definition generalizes the notion of a causal interaction from an outcome at a single point in time6 to a time-to-event outcome. We will take probabilities and expectations over all persons in the population.
We say that the effects of G and E are unconfounded conditional on C if P(Dge(t) = 0|C = c) = S(t; g, e, c). Essentially, if the effects of G and E are unconfounded conditional on C, then the survival curves conditional on G = g, E = e, C = c will reflect what the survival curve would have been had the exposures G and E been set to levels g and e, respectively, for the entire subpopulation with C = c. We will say that G and E have positive monotonic effects on the outcome if Dge(t) is non-decreasing in g and e for all t and all persons i.e. P(Dge(t) ≤ Dg′e′(t)) = 1 for all g ≤ g′,e ≤ e′ and all t. The exposures G and E have positive monotonic effects on the outcome if they are causative or neutral (i.e. never preventive) for all individuals. If the exposures have negative monotonic effects on the outcome (i.e. preventive or neutral for all individuals), then the exposure values could be recoded so that the recoded exposures have positive monotonic effects on the outcome. These assumptions of monotonicity concern individual-level counterfactuals and cannot be verified empirically; they must be made based on substantive knowledge. We then have the following results. Proofs are given in the Appendix (our results presuppose the technical condition that the true survival curves, S(t; g, e, c), are continuous functions of time t).
Result 1
If the effects of G and E are positive monotonic and are unconfounded conditional on C, then RERIHR > 0 in model (1) implies that there is some time t > 0 such that there is a causal interaction between G and E.
Result 1 states that if the effects of G and E are unconfounded then the tests for interaction on an additive scale given by Li and Chambless,1 i.e. concerning RERIHR, imply that a causal interaction is present at least at some point in time. However, in a proportional hazards model, RERIHR > 0 does not imply that there will be a causal interaction for all times t. We may have RERIHR > 0 in model (1) but there may be some time t > 0 for which there is no causal interaction. Result 1 requires the assumption that G and E had positive monotonic effects on the outcome. A similar result holds without employing monotonicity assumptions, but requires RERIHR > 1.
Result 2
If the effects of G and E are unconfounded conditional on C, then RERIHR > 1 in model (1) implies that there is some time t > 0 such that there is a causal interaction between G and E.
The basic intuition for Result 2 is that if RERIHR > 1 then HR(1, 1; c) − HR(1, 0; c) − HR(0, 1; c) > 0, so that the hazard ratio when both exposures are present is greater than the sum of the hazards under each of the exposures alone. If this is the case then in small intervals of time there must be some person for whom the outcome would occur if both exposures were present, but for whom it would not occur if only one of the two were present. Methods for testing the conditions on RERIHR in Results 1 and 2 and for obtaining confidence intervals for RERIHR are described by Li and Chambless.1 Results similar to those given in Results 1 and 2 hold for logistic regression with a dichotomous outcome4; the results given above generalize these results for dichotomous outcome to time-to-event outcomes. Note that Results 1 and 2 (and also Results 3 and 4 below) provide sufficient but not necessary conditions for their conclusions.
Results 1 and 2 relate only to drawing conclusions about causal interactions that may be present at a single point in time. We might also be interested in the circumstances under which one could conclude that there is a causal interaction between G and E for a range of times. The next two results give such conditions; Result 3 requires a monotonicity assumption; Result 4 does not.
Result 3
Let stc = S(t; 0, 0, c) be the survival function at time t conditional on G = 0, E = 0, C = c. If the effects of G and E are positive monotonic and are unconfounded conditional on C, then under proportional hazards model (1), there will be a causal interaction between G and E in the subpopulation C = c for all times t that satisfy
| (2) |
As an illustration of Result 3, suppose that β1 = 0.18, β2 = 0.14, β3 = −0.01 and that the effects of G and E are positive monotonic and are unconfounded conditional on C. We then have that (0.8)exp(β1+β2+β3) − (0.8)exp(β1) − (0.8)exp(β2) + (0.8) = −0.0015 < 0 and thus there would be causal interaction for all times t and c such that the baseline survival curve S(t; 0, 0, c) = 0.8. Here we also have that (0.6)exp(β1+β2+β3) − (0.6)exp(β1) − (0.6)exp(β2) + (0.6) = 0.00017 > 0, and thus we could not draw conclusions about causal interactions for t and c such that S(t; 0, 0, c) = 0.6.
In practice, one could use the parameter estimates for (β1, β2, β3) and apply Result 3 to derive a range of values of stc for which there is evidence of causal interaction by conducting a numerical search evaluating the expression in (2) for many possible values of stc to generate the range for which the inequality is satisfied. The smallest value of the baseline survival function S(t; 0, 0, c) for which this is satisfied may be of particular interest. Confidence bands for this range could be obtained by bootstrapping. If we apply this numerical-search approach to the parameter values above, we find that causal interaction would be present for all t and c such that 0.61 < S(t; 0, 0, c) < 1.
As noted in the Appendix in the proof of Lemma 1, the negation of the expression in (2) i.e. { } is a lower bound on the prevalence of individuals exhibiting a causal interaction at time t in strata C = c, provided that G and E have positive monotonic effects. The result in Lemma 1 in fact also applies to models other than the proportional hazards model. The next result allows for a similar approach but does not require assumptions about monotonicity.
Result 4
Let stc = S(t; 0, 0, c) be the survival function at time t conditional on G = 0, E = 0, C = c. If the effects of G and E are unconfounded conditional on C, then under model (1) there will be a causal interaction between G and E in the subpopulation C = c for all times t that satisfy
| (3) |
The condition in Result 4 is similar to that in Result 3 except the final stc is replaced by 1. The negation of the expression in (3), i.e. { }, is a lower bound on the prevalence of individuals exhibiting a causal interaction at time t in strata C = c without assumptions about monotonicity.
Example
Li and Chambless1 use a proportional hazards model (1) to examine possible interaction on coronary heart disease between the presence of GSTM1 susceptibility polymorphisms and smoking (ever versus never), controlling for age, cholesterol, sex, hypertension, diabetes mellitus and ethnicity. They fit model (1) to data from the ARIC cohort of 15, 792 African American and white men and women age 45 – 64 years. They obtain an estimate of RERIHR of RÊRIHR = 1.14 (95% CI: 0.05, 2.23) and estimates of (β1, β2, β3) of β̂1 = 0.05 (95% CI: −0.51, 0.61), β̂2 = 0.29 (95% CI: −0.22, 0.79), and β̂3 = 0.59 (95% CI: −0.14, 1.32). Suppose that the effects of G and E are unconfounded conditional on C. We see that the estimate of 1.14 and entire 95% confidence interval (0.05 – 2.23) for RERIHR are above 0. Thus, from their analysis, under the assumption that the GSTM1 polymorphism and smoking had monotonic effects on the outcome, we would have evidence that there is some time t > 0 such that there is a causal interaction between the effects of the GSTM1 susceptibility polymorphism and smoking, i.e. some time t at which, for some people, the outcome would have occurred if both the GSTM1 polymorphism and smoking were present, but the outcome would not have occurred by time t if just one of the two exposures was present. We see also from the analysis of Li and Chambless that, without assumptions about monotonicity, although the point estimate of 1.14 is such that RÊRIHR > 1, the 95% confidence interval (0.05 – 2.23) contains values below 1 and thus, without the assumption that G and E have positive monotonic effects on the outcome, there is only limited evidence for causal interaction.
Suppose that both the GSTM1 susceptibility polymorphism and smoking had positive monotonic effects on the outcome. Using Result 3 we can numerically search for those values of stc = S(t; 0, 0, c) for which the parameter estimates suggest that causal interaction is present. Doing so we obtain that condition (2) is satisfied (and thus the parameter estimates would suggest the presence of a causal interaction under the monotonicity assumption) for all t and c, such that 0.01 < S(t; 0, 0, c) < 1 − i.e. for almost the entire range of the baseline survival function. A similar numerical search using Result 4 without monotonicity assumptions gives the range 0.36 < S(t; 0, 0, c) < 1.
Discussion
This paper provides conditions that may be useful in helping researchers draw conclusions about causal interactions - at any time or at a range of times - when using proportional hazards models. One of the interesting features of such time-to-event settings is that causal interaction can disappear as time progresses (i.e. whether a causal interaction is present depends on the follow-up time). As shown here, the conditions for additive interaction discussed by Li and Chambless1 using the relative excess risk due to interaction in the proportional hazards model (RERIHR > 0) allow one to conclude that there is some point in time for which a causal interaction is present under an assumption that both exposures have positive monotonic effects on the outcome. To draw the same conclusion without monotonicity assumptions requires RERIHR > 1. This paper also describes a method whereby a researcher can determine the range of times and values of the baseline survival function for which the parameter estimates of the proportional hazards model suggest the presence of a causal interaction. It is also possible to estimate bounds on the prevalence of persons who exhibit causal interactions at various times. The results given here hold for the proportional hazards model; future work could examine other time-to-event models. It might also be of interest to attempt to further relate the results concerning causal interactions to the sufficient-cause framework.2, 3, 7 It has, however, been noted elsewhere4, 6 that functional-form restrictions such as those in model (1) impose certain restrictions on the sufficient-cause framework that may be difficult to evaluate in practice. The proportional hazards assumption will impose yet further restrictions.
Inverse-probability-of-treatment weighting6, 8 to control for confounding can circumvent some of the functional-form restrictions of model (1) but the proportional-hazard restriction would remain. Attempting to formulate the sufficient-cause framework so as to explicitly and formally allow for time may also face certain challenges.9 Such a formulation may be possible by using other models for time-to-event data.
Acknowledgments
Funding: Supported by National Institutes of Health grant ES017876.
Appendix
Lemma 1
If the effects of G and E are positive monotonic and are unconfounded conditional on C then there is a causal interaction between G and E at any time t such that
Without assumptions about monotonicity, if it is assumed only that the effects of G and E are unconfounded conditional on C, then there is a causal interaction between G and E at any time t such that
Proof of Lemma 1
If for some time t there is no causal interaction between G and E, then by monotonicity we would have that at time t, D11(t) − D10(t) − D01(t) + D00(t) ≤ 0 and thus
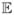 [D11(t) − D10(t) − D01(t) + D00(t)|C = c] ≤ 0 and by unconfoundedness [1− S(t; 1, 1, c)] − [1 − S(t; 1, 0, c)] − [1 − S(t; 0, 1, c)] + [1 − S(t; 0, 0, c)] ≤ 0 i.e. S(t; 1, 1, c) − S(t; 1, 0, c) − S(t; 0, 1, c) + S(t; 0, 0, c) ≥ 0. Thus if S(t; 1, 1, c) − S(t; 1, 0, c) − S(t; 0, 1, c) + S(t; 0, 0, c) < 0, then there must be a causal interaction between G and E at time t. Without assuming monotonicity, if for some time t there is no causal interaction between G and E, then we would have that at time t, D11(t) − D10(t) − D01(t) ≤ 0 and thus
[D11(t) − D10(t) − D01(t) + D00(t)|C = c] ≤ 0 and by unconfoundedness [1− S(t; 1, 1, c)] − [1 − S(t; 1, 0, c)] − [1 − S(t; 0, 1, c)] + [1 − S(t; 0, 0, c)] ≤ 0 i.e. S(t; 1, 1, c) − S(t; 1, 0, c) − S(t; 0, 1, c) + S(t; 0, 0, c) ≥ 0. Thus if S(t; 1, 1, c) − S(t; 1, 0, c) − S(t; 0, 1, c) + S(t; 0, 0, c) < 0, then there must be a causal interaction between G and E at time t. Without assuming monotonicity, if for some time t there is no causal interaction between G and E, then we would have that at time t, D11(t) − D10(t) − D01(t) ≤ 0 and thus
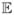 [D11(t) − D10(t) − D01(t)|C = c] ≤ 0 and by unconfoundedness [1 − S(t; 1, 1, c)] − [1 − S(t; 1, 0, c)] − [1 − S(t; 0, 1, c)] ≤ 0 i.e. S(t; 1, 1, c) − S(t; 1, 0, c) − S(t; 0, 1, c) + S(t; 0, 0, c) + 1 ≥ 0. Thus if S(t; 1, 1, c) − S(t; 1, 0, c) − S(t; 0, 1, c) + 1 < 0, then there must be a causal interaction between G and E at time t. By the same logic it follows that the extent to which S(t; 1, 1, c) − S(t; 1, 0, c) − S(t; 0, 1, c) + S(t; 0, 0, c) is less than 0 or the extent to which S(t; 1, 1, c) − S(t; 1, 0, c) − S(t; 0, 1, c) + 1 is less than 0 would serve as lower bounds for the prevalence of individuals exhibiting such causal interactions with or without the monotonicity assumption respectively.
[D11(t) − D10(t) − D01(t)|C = c] ≤ 0 and by unconfoundedness [1 − S(t; 1, 1, c)] − [1 − S(t; 1, 0, c)] − [1 − S(t; 0, 1, c)] ≤ 0 i.e. S(t; 1, 1, c) − S(t; 1, 0, c) − S(t; 0, 1, c) + S(t; 0, 0, c) + 1 ≥ 0. Thus if S(t; 1, 1, c) − S(t; 1, 0, c) − S(t; 0, 1, c) + 1 < 0, then there must be a causal interaction between G and E at time t. By the same logic it follows that the extent to which S(t; 1, 1, c) − S(t; 1, 0, c) − S(t; 0, 1, c) + S(t; 0, 0, c) is less than 0 or the extent to which S(t; 1, 1, c) − S(t; 1, 0, c) − S(t; 0, 1, c) + 1 is less than 0 would serve as lower bounds for the prevalence of individuals exhibiting such causal interactions with or without the monotonicity assumption respectively.
Proof of Result 1
Suppose that RERIHR = eβ1+β2+β3 − eβ1 − eβ2 + 1 > 0. Define Q(s) = sexp(β1+β2+β3) − sexp(β1) − sexp(β2) + s. We have that Q(1) = Q(S(t = 0; 0, 0, c)) = 1exp(β1+β2+β3) − 1exp(β1) − 1exp(β2) + 1 = 0. Furthermore
and thus if RERIHR = eβ1+β2+β3 − eβ1 − eβ2 + 1 > 0 we have that (i.e. a positive first derivative), which implies that for some ε > 0, Q(1 − ε) < Q(1) = 0. Because the survival curve S(t; 0, 0, c) is continuous in t, there exists some t > 0 such that S(t; 0, 0, c) = 1 − ε and thus for this time t,
Thus if RERIHR > 0 so that for some time t, S(t; 1, 1, c) − S(t; 1, 0, c) − S(t; 0, 1, c) + S(t; 0, 0, c) < 0 then, by the Lemma above, there must be a causal interaction between G and E at this time t.
Proof of Result 2
Suppose RERIHR = eβ1+β2+β3 − eβ1 − eβ2 + 1 > 1 so that eβ1+β2+β3 − eβ1 − eβ2 > 0. Define Q(s) = sexp(β1+β2+β3) − sexp(β1) − sexp(β2). We have that Q(1) = Q(S(t = 0; 0, 0, c)) = 1exp(β1+β2+β3) − 1exp(β1) − 1exp(β2) = −1. Also
and thus, if RERIHR > 1, so that eβ1+β2+β3 − eβ1 − eβ2 > 0, we have that , which implies that for some ε > 0, Q(1 − ε) < Q(1) = −1. Because the survival curve S(t; 0, 0, c) is continuous in t, there exists some t > 0 such that S(t; 0, 0, c) = 1 − ε and thus, for this time t,
Thus if RERIHR > 0 so that for some time t, S(t; 1, 1, c) − S(t; 1, 0, c) − S(t; 0, 1, c) < −1 then, by the Lemma above, there must be a causal interaction between G and E at time t.
Proof of Results 3 and 4
Under the proportional hazards model 1 we have that S(t; g, e, c) = S(t; 0, 0, c)exp(β1G+β2E+β3GE). Applying the Lemma above and using these proportional hazards model expressions for S(t; 1, 1, c), S(t; 1, 0, c), S(t; 0, 1, c) and S(t; 0, 0, c), implies that, if the effects of G and E are positive monotonic and are unconfounded conditional on C there will be a causal interaction between G and E for all times t that satisfy S(t; 0, 0, c)exp(β1+β2+β3) − S(t; 0, 0, c)exp(β1) − S(t; 0, 0, c)exp(β2) + S(t; 0, 0, c) < 0. This proves Result 3. Likewise, applying the Lemma above and using the proportional hazards model expressions for S(t; 1, 1, c), S(t; 1, 0, c) and S(t; 0, 1, c) implies that if the effects of G and E are unconfounded conditional on C, there will be a causal interaction between G and E for all times t that satisfies S(t; 0, 0, c)exp(β1+β2+β3) − S(t; 0, 0, c)exp(β1) − S(t; 0, 0, c)exp(β2) + 1 < 0. This proves Result 4. Note that the derivative of the expression in inequality (2) of Result 3 with respect to β3 is ; since stc ≤ 1 we have that log(stc) ≤ 0 and thus the derivative is negative. Therefore larger values of β3 will imply lower values of the left-hand-side of inequality (2); thus for larger values of β3 inequality (2) will be satisfied for more values of stc. The derivative of the expression in inequality (3) of Result 4 with respect to β3 is also and thus by the same argument, for larger values of β3 inequality (3) will be satisfied for more values of stc.
References
- 1.Li R, Chambless L. Test for additive interaction in proportional hazards models. Ann Epidemiol. 2007;17(3):227–236. doi: 10.1016/j.annepidem.2006.10.009. [DOI] [PubMed] [Google Scholar]
- 2.VanderWeele TJ, Robins JM. The identification of synergism in the sufficient-component cause framework. Epidemiol. 2007;18(3):329–339. doi: 10.1097/01.ede.0000260218.66432.88. [DOI] [PubMed] [Google Scholar]
- 3.VanderWeele TJ, Robins JM. Empirical and counterfactual conditions for sufficient cause interactions. Biometrika. 2008;95(1):49–61. [Google Scholar]
- 4.VanderWeele TJ. Sufficient cause interactions and statistical interactions. Epidemiol. 2009;20(1):6–13. doi: 10.1097/EDE.0b013e31818f69e7. [DOI] [PubMed] [Google Scholar]
- 5.Rothman KJ. Modern Epidemiology. 1. Little, Brown and Company; Boston, MA: 1986. [Google Scholar]
- 6.VanderWeele TJ, Vansteelandt S, Robins JM. Marginal structural models for sufficient cause interactions. Am J Epidemiol. 2010;171(4):506–514. doi: 10.1093/aje/kwp396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Rothman KJ. Causes. Am J Epidemiol. 1976;104(6):587–592. doi: 10.1093/oxfordjournals.aje.a112335. [DOI] [PubMed] [Google Scholar]
- 8.Robins JM, Hernán MA, Brumback B. Marginal structural models and causal inference in epidemiology. Epidemiol. 2000;11(5):550–560. doi: 10.1097/00001648-200009000-00011. [DOI] [PubMed] [Google Scholar]
- 9.Andersen PK. “Biological” interactions from a statistical point of view. Abstract. Second International Biometric Society Channel Network Conference; Ghent, Belgium. April 6, 2009. [Google Scholar]


