Semiparametric Bayesian inference for repeated fractional measurement data

Abstract

We discuss inference for repeated fractional data, with outcomes between 0 to 1, including positive probability masses on 0 and 1. The point masses at the boundaries prevent the routine use of logit and other commonly used transformations of (0, 1) data. We introduce a model augmentation with latent variables that allow for the desired positive probability at 0 and 1 in the model. A linear mixed effect model is imposed on the latent variables. We propose a Bayesian semiparametric model for the random effects distribution. Specifically, we use a Polya tree prior for the unknown random effects distribution. The proposed model can capture possible multimodality and skewness of random effect distribution. We discuss implementation of posterior inference by Markov chain Monte Carlo simulation. The proposed model is illustrated by a simulation study and a cancer study in dogs.

1. Introduction

Random effects are used to model dependence of repeated measurements on patients or other experimental units. Random effects can be thought of as unmeasured covariates whose values can be considered randomly distributed amongst study individuals. For continuous outcomes with normal errors, Laird and Ware (1982) proposed a normal linear random effects model. In this model, random effects are assumed to be centered around the mean regression coefficients for the populations, also known as the fixed effects. Conditional on random effects, repeated observations on a subject are considered independent. Goldstein (1986) and Longford (1987) developed a model that incorporates nested random effects, representing nested group-specific as well as individual-specific sources of heterogeneity (uncontrolled variation) to be modeled. Gilks et al. (1993) presented a linear multiple-random-effects model that simultaneously accommodates group-specific sources of heterogeneity for several groupings of individuals. They use Gibbs sampling to implement posterior inference. Kleinman and Ibrahim (1998a) described a semiparametric Bayesian generalization of the normal linear random effect model, where a nonparametric prior distribution is specified for the random effects.

In this article, we consider the practically important case when the outcome variable is fraction that is continuous between 0 and 1 plus positive point masses at 0 and 1. We call such data “fractional data”. Statistical modeling on fractional data of this type has not been investigated so far for longitudinal or repeated measurement data. Zero-inflated distributions have been used to model count data (Ridout et al., 1998) but would not be appropriate here. Fractional data can be seen in the cancer studies. For example, investigators may study the proportion of hypoxic cells in the cancer micoenvironment study or the proportion of stained cells in immunochemistry (ICH) studies. Such data may take the values between 0 and 1.

A standard approach for constrained data is the use of transformations to remove the constraint, such as a logit or probit transformation. Albert and Chib (1993) propose a probit regression model for binary and polychotomous outcomes. They impose a normal regression structure on latent continuous data. Values of the latent data are simulated from suitable truncated normal distributions. After the latent data have been generated, the posterior distributions of the parameters are computed using standard results from normal linear models. Draws from these posteriors are used to sample new latent data. The process is iterated leading to a Gibbs sampling scheme. For fractional data, however, we are considering, a complication arises from the fact that 0 and 1 are included in the range of possible values, with positive probabilities. This complicates the use of conventional logit or probit transformations.

In this paper, we propose a simulation-based approach to implement posterior inference for the parameters of interest in a model for fractional data. The key idea is to introduce additional latent variables to represent the awkward point masses at 0 and 1. A mixed-effects model is imposed on these latent variables. The model accommodates individual-specific sources of heterogeneity. We start with standard mixed normal linear model assumptions, as usual for continuous data, and then extend to a nonparametric Bayesian model.

The paper is organized as follows. In Section 2 we describe the proposed model for fractional data. In Section 3 we present the normal prior for the random effects in the mixed-effect model. In Section 4 we discuss the Polya tree prior for random effects distribution. We present a simulation study in Section 5 and a cancer study in Section 6. We conclude with a summary discussion in Section 7.

2. Model Formulation on Fractional Data

Suppose that a fractional outcome vector, y_i = (y_i1, …, y_ini), y_ij ∈ [0, 1] with n_i repeated measurements is observed in individual i. Responses y_ij can also be 0 or 1 with positive probability. Latent variables z_ij are introduced to address this data structure by including point masses at 0 and 1 in the model.

$$y_{ij}=\{\begin{array}{ll}0,\hfill & \text{if}{z}_{ij}\le 0;\hfill \\ z_{ij},\hfill & \text{if}0<z_{ij}<1,i=1,\dots ,n,j=1,\dots ,n_i;\hfill \\ 1,\hfill & \text{if}{z}_{ij}\ge 1.\hfill \end{array}$$ (1)

The z_ij are unknown. The distribution of z_ij is unconstrained and continuous at 0 and 1. We can therefore proceed with standard linear mixed model assumptions as is usual for continuous data, including normal distribution assumptions. If the application demands, one can use other functional forms for the latent continuous variable. Let N_p(t, S) denote a p-dimensional normal probability density function with moments (t, S). We construct the following model for ith individual:

$$z_i=X_i\beta +U_i{\theta }_i+e_i,$$ (2)

where β is a p × 1 vector of regression coefficients, commonly called fixed effects. The matrix X_i is an n_i × p design matrix of known covariates for ith individual. U_i is an n_i × q matrix of covariates for the q × 1 random effect vector θ_i, and e_i is an n_i × 1 vector of residuals. We assume that e_i and θ_i are independent and e_i ~ N_ni (0, σ²I_ni).

For the distribution of random effects, we initially assume a normal distribution. Later, we will introduce alternative and generalized models, as and if indicated by model diagnostics and criticism. We will assign nonparametric priors to the distribution of random effects.

The model includes a monotonicity assumption. We assume that P(y_ij = 1) increases as the mean of subdensity p(y_ij|0 < y_ij < 1) increases. We make an analogous assumption for P(y_ij = 0). We feel this is reasonable in most applications. For example, in an application with y_ij being the fraction of stained cells in immunohistochemistry data, it is reasonable to assume that the probability of all cells being stained (i.e., y_ij = 1) increases as the average fraction of stained cells rises.

3. Normal Linear Random Effect Model

The linear model given in Equation (2) defines the top level sampling model. Without loss of generality we assume conditional independence within experimental units (e.g., dogs), that is, a diagonal variance-covariance matrix. Little would change in the following discussion if we were to assume a non-diagonal variance-covariance matrix.

3.1 Prior specification

We complete the model with conjugate priors. For the fixed effects, we assume a conjugate multivariate normal prior

$$\beta \sim {\text{N}}_{\text{p}}({\mu }_0,{\mathrm{\sum }}_0).$$ (3)

Random effects are assumed to arise from the normal random effects model given by

$${\theta }_i\stackrel{\text{iid}}{\sim }{\text{N}}_{\text{q}}(0,{\mathrm{\sum }}_{\theta }).$$

The prior on the residual variance is specified as

$$\tau ={({\sigma }^2)}^{-1}\sim \text{Ga}\left(\frac{{\gamma }_0}{2},\frac{{\lambda }_0}{2}\right),$$ (4)

where Ga(a, b) denotes a gamma distribution with mean a/b and variance a/b². The conjugate priors of Equation (3) through Equation (4) are chosen for technical convenience. Substantial prior information might require different prior distributions. Finally, μ₀, Σ₀, Σ_θ, γ₀, and λ₀ are fixed hyperparameters.

3.2 Posterior inference

We implement posterior simulation by Gibbs sampling, resampling each of the indicated parameters conditional on the currently imputed values of all other parameters and the data. We did not use analytic forms because:

1. All priors are only conditionally conjugate. They are not conjugate for the joint posterior distribution;

2. Sampling one parameter at a time avoids manipulating an excessively large design matrix;

3. Additionally, data are truncated by 0 and 1, which breaks joint conjugacy. Moreover, the normal linear mixed model is assumed on z, not on y.

Resampling z

Conditional on other parameters, resampling the latent variable z requires truncated normal sampling. From Equations (1) and (2), we find

$$z_{ij}\{\begin{array}{ll}\sim \text{N}(X_{ij}\beta +U_{ij}{\theta }_i,{\sigma }^2)I(z_{ij}\le 0),\hfill & \text{if}{y}_{ij}=0;\hfill \\ =y_{ij},\hfill & \text{if}0<y_{ij}<1;\hfill \\ \sim \text{N}(X_{ij}\beta +U_{ij}{\theta }_i,{\sigma }^2)I(z_{ij}\ge 1),\hfill & \text{if}{y}_{ij}=1;\hfill \end{array}$$ (5)

where X_ij and U_ij are the jth row of matrices X_i and U_i, respectively. Generating random samples from a truncated normal is straightforward. Gelfand et al. (1990) provided an algorithm for sampling from truncated normal distribution.

Resampling β

We proceed as in a standard normal linear regression. Equation (2) can be re-written as

$$\underset{z_i^{★}}{\underbrace{z_i-U_i{\theta }_i}}=X_i\beta +e_i.$$

Thus conditional on other parameters, $z_i^{★}\sim \text{N}(X_i\beta ,{\tau }^{-1})$. Conditioning on z_i and θ_i, i = 1, …, n, and combining with the conjugate prior in Equation (3), we find p(β|…) = N(μ_β, v_β) with moments $v_{\beta }={({\mathrm{\sum }}_0^{-1}+\tau {\sum }_i{X}_i^{\prime }{X}_i)}^{-1}$ and ${\mu }_{\beta }=v_{\beta }({\mathrm{\sum }}_0^{-1}{\mu }_0+\tau {\sum }_i{X}_i^{\prime }{z}_i^{★})$.

We implement Gibbs sampling posterior simulation by iterating over the complete conditional posterior distributions given in the above expressions, starting with initial values for β, θ_i, i = 1, …, n, and τ. For later reference, we summarize the Gibbs sampling algorithm:

1. Generate z using Equation (5).

2. Draw β ~ p(β|…) from the multivariate normal distribution N(μ_β, v_β).

3. Draw τ ~ p(τ|…) from the inverse gamma conditional posterior distribution.

4. For i = 1, …, n, under model (1) through Equation (2), θ_i ~ p(θ_i| …) can be easily generated from a normal distribution.

Ergodic averages over the simulated parameter values approximate posterior integrals, including posterior means, posterior predictive distributions, etc. Geweke’s test (Geweke, 1992) could be used to verify the convergence of the simulations.

4. Polya Tree Random Prior for the Random Effect Distribution

The normal assumption on the random effects distribution can be restrictive. It is possible for the distribution of random effects to be multimodal and/or with unpredictable types of skewness. In biomedical data, multimodality frequently arises from patient heterogeneity, presence of outliers, exclusion of unknown but important covariates, alternative biologic mechanisms, etc. Examples of heterogenous populations include adult vs. pediatric populations, invasive vs. non-invasive tumors, strokes arising from bursting blood vessels vs. blocked vessels, and so forth. For accurate accounting of uncertainties and for improved prediction, it is clearly critical to account for such heterogeneity. Also, the nature of the heterogeneity might be of interest in itself, as, for example, in the discovery of new (sub-) types of cancer. We achieve the desired generalization with a nonparametric Bayesian model.

A commonly used technical definition of nonparametric Bayesian models is probability models with infinitely many parameters (Bernardo and Smith, 1994). In other words, a nonparametric Bayesian model is a probability model on a function space. Nonparametric Bayesian models are used to avoid critical dependence on parametric assumptions, to make parametric models more robust, and to define model diagnostics and sensitivity analysis for parametric models by embedding them in a larger encompassing nonparametric model (Müller and Quintana, 2004). Bayesian nonparametric and semiparametric approaches include mixture models (West, 1992), Dirichlet process and Dirichlet process mixture models (Ferguson, 1973; Antoniak, 1974; Escobar and West, 1995; MacEachern and Müller, 1998), and Polya tree priors (Lavine, 1992, 1994). For a recent review of nonparametric Bayesian models, see Walker et al. (1999).

In this section, we will explore the Polya tree model as a prior for the random effects distribution in models (1) and (2). Polya trees were proposed as a generalization of Dirichlet process in Bayesian data analysis by Lavine (1992, 1994). The definition, properties, and construction of Polya trees can be found in Appendix.

A random probability measure G, which is said to have a Polya tree distribution, or a Polya tree prior, with parameter (Π, ), is written as G ~ PT(Π, ). The set Π determines the partition structure of the Polya tree. The parameters α_ε in determine the smoothness of a realization of G and control how quickly the posterior predictive distribution moves from its prior mean to the empirical distribution.

4.1 Posterior predictive simulation

The joint marginal distribution of a sample (X₁, …, X_n) generated from a random distribution with a Polya tree prior has a closed form. The random probability measure G can analytically be integrated out. Suppose $x_i\stackrel{\text{iid}}{\sim }G$, i = 1, …, n and G ~ PT(Π, ). Let g be the density function of G and g₀ be the density function of the centering distribution G₀ such that E(G) = G₀ (See the appendix for the choice of g₀). The marginal joint density of (X₁, …, X_n) is given by

$$\begin{array}{l}p(x_1,\dots ,x_n)=\int p(x_1,\dots ,x_n\mid G)dp(G)\\ =\int \prod _{i=1}^{n}g(x_i)dp(G)\\ =f(x_1)\prod _{i=2}^{n}f(x_i\mid x_1,\dots ,x_{i-1}),\end{array}$$

where f(x₁) = g₀(x₁) and

$$f(x_i\mid x_1,\dots ,x_{i-1})=g_0(x_i)\underset{M\to \infty }{lim}\prod _{m=2}^M\frac{{\alpha }_{{\underset{\_}{\epsilon }}_m}^{\prime }({\alpha }_{{\underset{\_}{\epsilon }}_{m-1}0}+{\alpha }_{{\underset{\_}{\epsilon }}_{m-1}1})}{{\alpha }_{{\underset{\_}{\epsilon }}_m}({\alpha }_{{\underset{\_}{\epsilon }}_{m-1}0}^{\prime }+{\alpha }_{{\underset{\_}{\epsilon }}_{m-1}1}^{\prime })},$$ (6)

where ε_m = ε₁, …, ε_m identifies the level m subset containing x_i, i.e., x_i ∈ B_ε1,…,εm. Here ${\alpha }_{{\underset{\_}{\epsilon }}_m}^{\prime }$ is equal to α_εm plus the number of observations among x₁, …, x_i−1 that belong to B_ε1,…,εm.

In practice, we can always reduce the right side of Equation (6) to a finite product. Starting at a sufficiently large level M_xi, the sets B_ε1,…,εm, m ≥ M_xi, contain no data points x₁, …, x_i−1 and thus ${\alpha }_{{\underset{\_}{\epsilon }}_m}^{\prime }={\alpha }_{{\underset{\_}{\epsilon }}_m}$, reducing the product to M = 2, …, M_xi. Also for any fixed M, the right side of Equation (6) can be approximated by a finite product when M is large.

4.2 A semiparametric model for repeated fractional data

In this section, we improve on certain aspects of the normal linear mixed effect model introduced earlier. In particular, we discuss posterior inference for a model that assumes a Polya tree prior for an unknown random effect distribution. The Polya tree prior is centered around a parametric probability distribution. With this approach, random effects can be directly sampled and inference will be based on the predictive density.

As before, let the observed outcome be y_ij and assume that the distribution of the latent variable z_ij for the jth measurement from ith individual follows models (1) and (2). Given β and θ_i, z_i is normally distributed. The prior specification in a conjugate model for β and τ are the same as before, namely, Equations (3) and (4), respectively.

The random effect model is generalized by assuming a nonparametric random effect prior. That is,

$${\theta }_i\stackrel{\text{iid}}{\sim }G,G\sim \text{PT}(\mathrm{\Pi },\mathcal{A}).$$

We center the Polya tree distribution around a normal distribution G₀ with median (mean) 0 and a fixed large variance ${\sigma }_{\theta }^2$ (i.e. $G_0=\text{N}(0,{\sigma }_{\theta }^2)$). A fixed partition at level m is generated by taking

$$B_{{\epsilon }_1,\dots ,{\epsilon }_m}=\left(G_0^{-1}\left(\frac{j}{2^m}\right),G_0^{-1}\left(\frac{j+1}{2^m}\right)\right],$$

where j = 0, 1, …, 2^m − 1. is assumed as

$$\mathcal{A}=\{{\alpha }_{{\epsilon }_1,\dots ,{\epsilon }_m}={\text{cm}}^2:{\epsilon }_1,\dots ,{\epsilon }_m\in {\{0,1\}}^m\},$$

with a pre-specified value of c.

To implement Gibbs sampling posterior simulation, we need to generate from the conditional posterior distribution as in Section 3.2. The relevant full conditional posterior distributions include p(β|z, θ, σ²), p(σ²|z, β, θ), and p(θ_i|z, θ_−i, β, σ²), where θ_−i = (θ₁, …, θ_i−1, θ_i+1, …, θ_n), i = 1, …, n. Samples can be obtained using an MCMC algorithm and in particular a Metropolis-Hastings within Gibbs methods.

Conditional on β and the θ_i’s, z_ij can be generated by Equation (5) as before. Similarly, β can be sampled from N(μ_β, v_β) given z, θ = (θ₁, …, θ_n), and σ². The full conditional posterior distribution for τ is easily found to be an inverse gamma distribution, allowing random variable generation.

Now we describe how to update θ. Let z_i = (z_ij, j = 1, …, n_i). The likelihood for θ_i, given z, σ², β, and θ_−i, is given by

$$l(z_i\mid \beta ,{\theta }_i,{\theta }_{-i},{\sigma }^2)=\prod _{j=1}^{n_i}\text{N}(z_{ij}\mid \beta ,{\theta }_i,{\sigma }^2).$$

The conditional posterior distribution for θ_i can be written, up to a constant of proportionality, as

$$p({\theta }_i\mid z,{\theta }_{-i},\beta ,{\sigma }^2)\propto l(z_i\mid \beta ,{\theta }_i,{\sigma }^2)p({\theta }_i\mid {\theta }_{-i}),$$ (7)

for each i = 1, …, n. This motives the following Metropolis-Hastings transition probability.

A proposed value ${\theta }_i^{(p)}$ is generated from the prior predictive distribution p(θ_i|θ_−i). The prior predictive can be written as

$${\theta }_i^{(p)}\sim p({\theta }_i\mid {\theta }_{-i})=\int G({\theta }^{(p)})dp(G\mid {\theta }_{-i})\text{with}p(G\mid {\theta }_{-i})=\text{PT}({\mathcal{A}}^{★},\mathrm{\Pi }),$$

using the posterior PT, conditional on θ_−i, with ${\mathcal{A}}^{★}=\{{\alpha }_{\epsilon }^{★}={\alpha }_{\epsilon }+n_{\epsilon }\}$. Here n_ε = Σ_h≠i I(θ_h ∈ B_ε) counts the number of θ_h, h ≠ i, that fall into the partitioning subset B_ε.

We proceed as follows to generate ${\theta }_i^{(p)}$. Recall the definition of Y_ε as the random splitting probabilities in the constructive definition of the PT. Starting with Y₀, we generate the sequence of random probabilities for G ~ PT(, Π), and set ε₀ = 0 with probability Y₀, etc. We continue generating random probabilities Y_ε0,…,εm and ε_m until we reach a level m with ${\alpha }_{{\epsilon }_0,\dots ,{\epsilon }_m}^{★}={\alpha }_{{\epsilon }_0,\dots ,{\epsilon }_m}$, i.e., until we reach a partitioning subset B_ε0,…,εm that does not contain any of the currently imputed random effects θ_h, h ≠ i. Finally, we generate ${\theta }_i^{(p)}$ from the base measure G₀ restricted to this set B_ε0,…,εm. This generates ${\theta }_i^{(p)}\sim p({\theta }_i\mid {\theta }_{-i})$.

The Markov chain moves to the candidate point ${\theta }_i^{(p)}$ with probability

$$min\left\{1,\frac{l(z_i\mid \beta ,{\theta }_i^{(p)},{\sigma }^2)}{l(z_i\mid \beta ,{\theta }_i^{(c)},{\sigma }^2)}\right\},$$

where ${\theta }_i^{(c)}$ is the current sample.

5. A Simulation Study

In this section, we fit a mixed fractional data model to simulated data. Normal and Polya tree priors are considered as priors of the distributions of random effects, and we compare the resulting inference. We simulated n = 100 random effects from

$${\theta }_i\stackrel{\text{iid}}{\sim }0.5\text{N}(-0.2,{0.15}^2)+0.5\text{N}(0.2,{0.15}^2),i=1,\dots ,n.$$

We introduce one covariate, $X_{ij}\stackrel{\text{iid}}{\sim }\text{N}(0.5,{0.3}^2)$, i = 1, …, n, j = 1, 2. The simulation truth for the regression coefficient was set at β = (β₀, β₁) = (0.8, −0.6), and the random residual e was generated from N(0, 0.1²). Let z_ij = β₀ + X_ijβ₁ + θ_i + e_ij, i = 1, …, n, j = 1, 2. The observed fractional data are recorded as y_ij = 1 if z_ij ≥ 1; y_ij = z_ij if 0 < z_ij < 1; and y_ij = 0 if z_ij ≤ 0.

The histogram of the observed data y is displayed in Figure 1. From this figure, note the point masses at the boundaries. We analyze the data using model (1) through Equations (3) and (4), with z_ij = β₀ + X_ijβ₁ + θ_i + e_ij, and random effects ${\theta }_i\stackrel{\text{iid}}{\sim }G$, and residuals $e_{ij}\stackrel{\text{iid}}{\sim }\text{N}(0,{\sigma }^2)$, i = 1, …, n, j = 1, 2.

Figure 1.

Histogram of y.

Assuming a flat normal prior on β = (β₀, β₁), and β ~ N₂((0, 0), 100I₂), the random effects distribution is modeled by the following two different approaches.

The distribution of the random effect θ is first modeled with normal distribution, that is, $G(\theta )=\text{N}(0,{\sigma }_{\theta }^2)$ with a hyper-prior $1/{\sigma }_{\theta }^2\sim \text{Ga}(0.01,0.01)$. We carry out the posterior simulation as described in Section 3.2. The MCMC simulation was repeated 20,000 times. The first 5,000 iterations were discarded as burn-in. The point estimates and 95% posterior intervals of β and selected random effects are presented in Table 1. Figure 2(a) shows the posterior predictive density for y_{new, 1} under normal random effect prior when X_{new, 1} takes the average of all observed X’s. It shows normal appearance but does not capture the bimodal feature in the data, which suggests that a normal random effects prior is not appropriate in this example.

Table 1.

Posterior 2.5%th, 50%th, and 97.5%th percentiles for selected parameters under semiparametric and the parametric normal random effects model. β₀ is the intercept, β₁ is the fixed effect, and σ is the residual standard deviation. θ_i is random effect for ith subject.

Parameter	Normal prior	Polya tree prior (c = 0.1)
β0	0.830(0.768, 0.890)	0.847(0.723, 0.943)
β1	−0596(−0.659, −0.534)	−0.599(−0.661, −0.533)
σ	0.093(0.080, 0.108)	0.093(0.081, 0.109)
θ69	0.272(0.133, 0.401)	0.259(0.085, 0.396)
θ99	−0.200(−0.338, −0.051)	−0.219(−0.378, −0.039)
σθ	0.247(0.194, 0.350)

Figure 2.

(a) Predictive density of y_{new, 1} under normal random effect distribution, (b) Predictive density of y_new,1 under PT prior for random effects distribution (note the bimodal feature) and (c) Estimated random effect distribution Ḡ = E(G|z) (dashed line) vs. the simulation truth (solid line)

We specify a Polya tree prior for the random effect distribution to allow for multimodality. Priors for other parameters remain unchanged.

We construct the Polya tree prior with a Polya tree centered around N(0, 5²). At the mth partition level, α_ε1,…,εm is taken to be cm², with c fixed at 0.1. Posterior simulation was run for 25,000 iterations, with the first 5,000 being discarded as burn-in period. Every 20th iteration was saved. Posterior summary statistics for the estimated parameters are presented in Table 1. The point estimates for β₀ and β₁ are fairly close to the simulation truth. Figure 2(b) shows the posterior predictive density for y_{new, 1} under the Polya tree prior for the random effects distribution. It demonstrates the bimodal feature in the data. The posterior predictive density of θ_n+1 is plotted in Figure 2(c). It shows that inference on G captures the bimodal nature of random effect distribution very well.

As expected, point estimates of the fixed effects are similar for both models. Posterior intervals for β₁ are wider under the Polya tree priors. The increased posterior uncertainty under the Polya tree random effects model is due to the additional randomness in the later model.

The posterior medians for two θ_i, shown in Table 1, are slightly different under the two models. This is to be expected. The semiparametric model allows multiple shrinkage. Under the normal model, all estimates for θ_j are shrunk towards the common mean, E(θ_j) = 0.

6. Application

In cancer studies, some characteristics of the tumor microenvironment are often assessed by histologic evaluation of tumor biopsies. These include oxygenation and proliferation, two important features of the tumor environment that may influence the response to treatment. One approach to measure tumor oxygenation is to measure bound nitroimidazoles based on information from tumor biopsies. The accuracy of biopsy-based methods, however, is related to how precisely the information derived from the biopsies represents the overall tumor microenvironment. Thrall et al. (1997) studied binding of CCI-103F and pimonidazole, both 2-nitroimidazole compounds, in canine solid tumors to assess pretreatment oxygenation and changes in oxygenation during irradiation.

The study reports data for n = 9 dogs, each with a primary solid tumor. Twenty-four hours before the first radiation treatment, CCI-103F was administered intravenously. Immediately prior to the first radiation treatment, up to eight biopsies were obtained from different geographic regions of the tumor. One to four sections from each biopsy sample were placed on glass slides. Slides from four out of eight biopsies were measured 20 minutes after injecting the dye. Slides from the rest of biopsies in the same tumor were measured 24 hours after injecting the dye. The volume fraction of hypoxic tumor tissue was reported by measuring the CCI-103F labelled area in each slide. Responses are recorded as

$$y=\frac{(\text{CCI}-103\text{F}\text{labelled}\text{counts})}{(\text{CCI}-103\text{F}\text{labelled}\text{counts})+(\text{unlabelled}\text{counts})}.$$

An important feature of the data is that the volume fraction of hypoxic tumor tissue can be 0 or 1 in some slides. Raw cell counts are not reported, only the fraction y, resulting in the fractional data format discussed earlier. The questions of interest include: “What is the average fraction of hypoxic cells in a tumor”; “How variable is the fraction within a tumor and between dogs?”; and “How is the measurement of hypoxic cells in the same tumor affected by different measuring times?”.

Figure 3 presents the average fraction of hypoxic cells in each biopsy for each dog. The x-axis denotes the biopsy label. Biopsies labelled as 1, 2, 3, and 4 were measured 20 minutes after injecting the dye. The fraction of hypoxic cells from biopsies labelled as 5, 6, 7, and 8 were measured 24 hours after injecting the dye.

Figure 3.

Average fraction of hypoxic cells in each biopsy for each dog.

We use conventional Bayesian and Bayesian semiparametric random effect models to fit the above fractional data. Let y_ijk denote the fraction of hypoxic cells in kth slide from jth biopsy of ith dog. Time t_ij is the measurement time for the jth biopsy from the ith dog, v_i is the volume of tumor from the ith dog, d_i denotes a random dog effect and b_j(i) a random biopsy effect nested within the ith dog. To include point mass probabilities for y_ijk = 0 and y_ijk = 1, we introduce a latent variable z_ijk into the model. As in Equation (1):

$$y_{\mathit{ijk}}=\{\begin{array}{ll}0,\hfill & \text{if}{z}_{\mathit{ijk}}\le 0;\hfill \\ z_{\mathit{ijk}},\hfill & \text{if}0<z_{\mathit{ijk}}<1;\hfill \\ 1,\hfill & \text{if}{z}_{\mathit{ijk}}\ge 1.\hfill \end{array}$$

The mixed-effects model (2) becomes z_ijk = β₀+β₁t_ij +β₂v_i+d_i+b_j(i)+ ε_ijk, with residuals ${\epsilon }_{\mathit{ijk}}\stackrel{\text{iid}}{\sim }\text{N}(0,{\sigma }^2)$, i = 1, …, 9, j = 1, …, 8, k = 1, …, 4.

The model is completed with conjugate priors: β = (β₀, β₁, β₂) ~ N(0, 4I₃), $d_i\stackrel{\text{iid}}{\sim }\text{N}(0,{\sigma }_d^2)$, and a random effect distribution for the biopsy effects: $b_{j(i)}\stackrel{\text{iid}}{\sim }F$. As hyper priors, we assume $1/{\sigma }_d^2\sim \text{Ga}(0.01,0.01)$ and 1/σ² ~ Ga(0.01, 0.01).

Because of the small number of dogs, the distribution of random dog effect is assumed to be normal. Two types of random effects distributions are considered for the distribution of biopsy effect. First, a normal prior $F=\text{N}(0,{\sigma }_b^2)$ is specified. From other studies, we expect more variability within tumors than between subject-specific averages. Then the parametric prior assumption is relaxed by specifying a nonparametric Polya tree prior, i.e., F ~ PT(Π, ).

6.1 Normal prior for the biopsy effect

Assume $b_{j(i)}\stackrel{\text{iid}}{\sim }\text{N}(0,{\sigma }_b^2)$ and $1/{\sigma }_b^2\sim \text{Ga}(0.01,0.01)$. We ran the Gibbs sampler over 35,000 iterations, with the first 5,000 being discarded as a burn-in period. In addition, because of high autocorrelation, only every 12th iteration was saved and the rest discarded, leading to a total Monte Carlo sample size of 2,500.

The histogram of posterior mean estimated biopsy effects is presented in Figure 4. The distribution of biopsy effects does not show normal appearance. The non-normality may be due to heterogeneity across dogs, or biopsies, or other covariates that are not recorded.

Figure 4.

Histogram of mean biopsy effects under the parametric model.

Posterior estimates of model parameters are summarized in Table 2. The results indicate that the proportion of hypoxic cells is strongly related to time but not significantly associated with tumor volume.

Table 2.

Posterior median and central 95% posterior intervals for various parameters from the parametric normal model and Polya tree model. Here, β₀ is the intercept, β₁ is the slope over time, β₂ is the volume of tumor effect, σ is the error standard deviation, σ_d is the standard deviation of dog effect, and σ_b is the standard deviation of biopsy.

Parameter	Normal model	Polya tree model
β0	0.303(0.127, 0.507)	0.347(0.173, 0.553)
β1	0.113(0.019, 0.212)	0.054(−0.051, 0.169)
β2	−0.001(−0.003, 0.003)	−0.001(−0.003, 0.002)
σ	0.093(0.085, 0.103)	0.093(0.085, 0.102)
σd	0.252(0.154, 0.527)	0.263(0.158, 0.510)
σb	0.197(0.163, 0.241)

6.2 Polya tree prior for the biopsy effect

Suppose the biopsy effect arises from a random probability measure F, and we assume a Polya tree prior for F. We use a Polya tree with centering distribution F₀ = N(0, 3²). We place the same priors on fixed effects and random dog effects as before. The parameters of the Polya tree prior are fixed as follows. The partitioning points to define Π are chosen to be the percentiles of F₀, and c is set to 0.1.

Posterior simulation was run for 38,000 iterations, with the first 4,000 being discarded as burn-in period. Every 20th iteration was saved. Convergence of the posterior distributions of parameters was assessed using Geweke’s method. The parameter estimates are presented in Table 2. Note that the time effect is no longer significant under the Polya tree prior.

The posterior mean of F is shown in Figure 5, which indicates high between-biopsy variability. The posterior mean is centered around 0, as we would expect.

Figure 5.

Estimated random biopsy effect distribution F… = E(F|z).

7. Discussion

We have proposed Bayesian nonparametric modeling for a class of important inference problems arising in biomedical data analysis. We developed a model and corresponding inference for repeated fractional data model. Proposed techniques included specifying a nonparametric Polya tree prior for the random effects distribution. We provided appropriate posterior simulation schemes.

In the fractional data model, Polya tree priors avoid assuming a specific parametric distribution for random effects. This allows us to estimate the distribution of random effects, which provides insight into population heterogeneity and honestly accounts for related uncertainties.

Polya trees have some practical limitations, however. First, the resulting random probability measure depends on the specific partition sequence adopted. Second, using a fixed partitioning sequence Π results in discontinuities in the predictive distributions. Third, implementations for higher dimensional distributions require extensive housekeeping and are impractical.

Paddock et al. (2003) and Hanson and Johnson (2002) introduced randomized Polya trees to mitigate problems related to the discontinuities. The idea is based on dyadic rational partitions, but instead of taking the nominal half-point, Paddock et al. (2003) randomly chose a cutoff centered around the cutoff point. This construction is shown to mitigate the first two limitations noted above. Hanson and Johnson (2002) consider a mixture with respect to a hyperparameter that defines the partitioning tree. A prior was placed on the spread of the prior distribution of G, which can be learned from the data. Doing so eliminates the need to choose a centering distribution with adequate spread in ad hoc way.

In the fractional data discussed in the paper, the fractional response outcome was measured at two time points. In other applications the fractional measurements might be obtained from the same biopsy or sample at more than two time points, or the measurement might be made at several time points per cycle for multiple cycles for each subject. The proposed model can be generalized to incorporate the additional random effects, such as nested cycle effect, which is a topic of future research.

Appendix

A.1 Definition and Basic Properties of Polya Trees

Let E = [0, 1],E⁰ = ∅, E^m be the m-fold product E × E × ··· × E, $E^{★}={\cup }_{m=0}^{\infty }{E}^m$ and E^N be the set of infinite sequences of elements of E. Let Ω be a separable measurable space, π₀ = Ω and Π = {π_m; m = 0, 1, …} be a separating binary tree of partitions of Ω; that is, let π₀, π₁, … be a sequence of partitions such that ${\cup }_{m=0}^{\infty }{\pi }_m$ generates the measurable sets and such that every B ∈ π_m+1 is obtained by splitting some B′∈ π_m into two subsets. Let B₀ = Ω and, for all ε = ε₁, …, ε_m ∈E^★, let B_ε0 and B_ε1 be the two subsets into which B_ε is split.

Definition 7.1 [Lavine (1992)]

A random probability measure G is said to have a Polya tree distribution, or a Polya tree prior, with parameter (Π, ), written as G ~ PT(Π, ), if there exist non-negative numbers = (α₀, α₁, α₀₀, …) and random variables 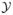= (Y₀, Y₁, Y₀₀, …) such that all random variables in 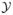are independent; for every ε, (Y_ε0, Y_ε1) ~ Beta(α_ε0, α_ε1); and for every m = 1, 2, …, and every ε = ε₁, …, ε_m,

$$G(B_{{\epsilon }_1,\dots ,{\epsilon }_m})=\left(\prod _{j=1,{\epsilon }_j=0}^m{Y}_{{\epsilon }_1,\dots ,{\epsilon }_{j-1}0}\right)\left(\prod _{j=1,{\epsilon }_j=1}^m(1-Y_{{\epsilon }_1,\dots ,{\epsilon }_{j-1}0})\right)$$

where the first term, i.e. for j = 1, is interpreted as Y₀ or 1 − Y₀.

The random variable Y_ε0 is the conditional probability of partition subset B_ε0 given B_ε. For instance, for m = 2, G(B₀₀) = Y₀Y₀₀, G(B₀₁) = Y₀(1−Y₀₀), G(B₁₀) = (1−Y₀)Y₁₀, and G(B₁₁) = (1 −Y₀)(1 −Y₁₀). The set Π determines the partition structure of the Polya tree. The parameters α_ε in determine the smoothness of a realization of G and control how quickly the posterior predictive distribution moves from its prior mean to the empirical distribution.

Several properties facilitate the use of the Polya tree for nonparametric Bayesian inference. Polya trees are conjugate under i.i.d sampling. Assume p(G|Π, ) = PT(Π, ) and $x_i\stackrel{\text{iid}}{\sim }G$, i = 1, …, n. Then p(G|x, Π, ) = PT(Π, ). The parameters α_ε are updated by adding the count of points in B_ε, i.e., ${\mathcal{A}}^{★}=\{{\alpha }_{\epsilon }^{★}={\alpha }_{\epsilon }+n_{\epsilon }:\epsilon \in E^{★}\}$ and n_ε = the number of x_i’s in B_ε. In words, the posterior distribution of G under i.i.d sampling is also Polya tree with the same fixed partition sequence. The partitioning probability (Y_ε) is generated from beta distribution with updated parameters ${\alpha }_{\epsilon }^{★}$, where ${\alpha }_{\epsilon }^{★}$ is equal to α_ε plus the number of x₁, …, x_n in subset B_ε.

The Polya tree includes the Dirichlet process as a special case. A Polya tree is a Dirichlet process if α_ε = α_ε0 + α_ε1 for every ε ∈ E^★ (Ferguson, 1974).

The parameters of a Polya tree can be chosen such that G is absolutely continuous with probability 1. In particular, any α_ε1,…,εm = ρ(m) such that ${\sum }_{m=1}^{\infty }\rho {(m)}^{-1}<\infty$ guarantees G to be absolutely continuous. For example, Walker and Mallick (1999) and Paddock et al. (2003) consider α_ε1,…,εm = cm², where c > 0.

A.2. Construction of a polya tree

Two parameters specify a Polya tree prior, the partition Π and the set . Through choosing Π, we may center the Polya tree prior around a particular continuous distribution G₀. To do so, we take the partition points to align with percentiles of G₀. For instance, if $B_0=(-\infty ,G_0^{-1}(\frac{1}{2})]$ (hence $B_1=(G_0^{-1}(\frac{1}{2}),\infty )),B_{00}=(-\infty ,G_0^{-1}(\frac{1}{4})]$, … and α₀ = α₁, α₀₀ = α₀₁, …, then since G(B₀) = Y₀ ~ Be(α₀, α₁), $\text{E}(G(B_0))=\frac{1}{2}=G_0(B_0)$. Also, e.g., G(B₀₀) = Y₀Y₀₀ implies $\text{E}(G(B_{00}))=\frac{1}{4}=G_0(B_{00})$ and for any B ∈ Π, E(G(B)) = G₀(B). We need not confine ourselves to quartiles of the form $G_0^{-1}\left(\frac{j}{2^r}\right)$.

Figure 6 shows an example of the construction of a Polya tree prior on (0, 1] = Ω (Ferguson, 1974). At the top level of the tree, Ω is split in half at the dyadic rational, 0.5. Thus B₀ = (0, 0.5], B₁ = (0.5, 1] and Ω = B₀ ∪ B₁. At the second level, B₀ and B₁ are again split at 0.25 and 0.75, respectively, which result in subsets B₀₀ = (0, 0.25], B₀₁ = (0.25, 0.5], B₁₀ = (0.5, 0.75], and B₁₁ = (0.75, 1], so on.

Figure 6.

Construction of a Polya tree prior on (0,1] (Ferguson, 1974)

One also has to choose the parameters in . The parameters α_ε in control how quickly the updated predictive distribution moves from the centering distribution G₀ to the empirical distribution. If the α_ε’s are large, then the distribution of x_n+1|x₁, …, x_n is close to G₀. If the α_ε’s are small, then the distribution of x_n+1|x₁, …, x_n is close to the empirical distribution function. The parameters α_ε also express the belief about the smoothness of G. Ferguson (1974) provides conditions on which yield discrete, continuous singular, and absolutely continuous distributions with probability one. For instance, for level m = 1, 2, …, α_{ε1, …, εm} = 2^−m implies a Dirichlet process, α_ε = 1 yields a random probability G of a type considered by Dubins and Freedman (1966) and shown to be continuous singular with probability one, and α_ε1…εm = m² implies an absolutely continuous distribution with probability 1. Walker and Mallick (1999) and Paddock et al. (2003) considered α_{ε1, …, εm} = cm², where c > 0.

Therefore, through selection of and G₀, one can center the Polya tree prior around G₀ arbitrarily close, as determined by , in a manner analogous to the specification of baseline measure and precision parameter in the Dirichlet process. can be thought of as a precision parameter and G₀ as a base measure.