Subjective and model-estimated reward prediction: Association with the feedback-related negativity (FRN) and reward prediction error in a reinforcement learning task

Abstract

In this study, we examined whether the feedback-related negativity (FRN) is associated with both subjective and objective (model-estimated) reward prediction error (RPE) per trial in a reinforcement learning task in healthy adults (n = 25). The level of RPE was assessed by 1) subjective ratings per trial and by 2) a computational model of reinforcement learning. As results, model-estimated RPE was highly correlated with subjective RPE (r = .82), and the grand-averaged ERP waves based on the trials with high and low model-estimated RPE showed the significant difference only in the time period of the FRN component (p < .05). Regardless of the time course of learning, the FRN was associated with both subjective and model-estimated RPEs within subject (r = .47, p < .001; r = .40, p < .05) and between subjects (r = .33, p < .05; r = .41, p < .005) only in the Learnable condition where the internal reward prediction varied enough with a behavior-reward contingency.

1. Introduction

To respond optimally to our environment it is critical that we modify our predictions about the world following mistakes. Understanding how we use information about mistakes (henceforth “feedback”) to subsequently modify our behaviors is critical for learning, behavioral modification, and maximizing future rewards in any situation with discernable contingencies. Yet, how we respond to the knowledge that we have made an error, and particularly, whether subsequent adjustments in behavior are necessarily conscious or explicit is not well understood. The state-of-the-art in decision literature, derived primarily from animal models, is to use computational models which assess responses to reward to estimate a participant’s subjective understanding of the meaning of error feedback. Yet, the crucial assumption that decision models reflect conscious processes has not been tested. Positive results would suggest that error modeling in animal studies may accurately reflect subjective processes in humans, allowing model based work to proceed in humans with interpretability. Negative results would suggest a dissociation between observed environmental contingencies and how humans subjectively use them, which could have important implications for how we understand people’s awareness of their decision processes. Thus, this study examined how brain response to negative feedback is modulated by reward expectation using both subjective ratings and objective model estimation.

Brain responses to negative feedback, that is, the “feedback-related negativity” (FRN) in response to negative feedback is an event-related potential (ERP) component observed at central locations (Cz or FCz) around 200-400 ms after the presentation of external feedback (Gehring and Willoughby, 2002; Luu et al., 2003; Ruchsow et al., 2002; Taylor et al., 2007). The FRN has been regarded to reflect neural processes associated with violation of expectation (Holroyd and Coles, 2002; Nieuwenhuis et al., 2002).

Violation of expectation has been operationalized as “reward prediction error” (RPE), or the difference calculated between one’s internal prediction of what feedback they will receive and the actual feedback received from the environment (e.g., Holroyd and Coles, 2002). This theory is based on animal single-unit recording studies which suggest that the activity of midbrain dopamine neurons encodes reward prediction error (Schultz, 1998; 2002; 2006). These results are consistent with decision making in the reinforcement learning (RL) models (e.g., Montague et al., 2004). Human neuroimaging studies (Knutson and Wimmer, 2007; Samejima and Doya, 2007; Ullsperger and von Cramon, 2003) have suggested that prediction error calculated by computational modeling is associated with the functional activity of medial prefrontal cortex (MPFC), basal ganglia, specifically ventral and dorsal striatum, and cingulate cortex, which have been regarded as possible sources of FRN signal. Although generally ERP indices do not have good spatial resolution, the FRN would be the prospective and practical neural index with good time resolution to explore human decision making process. In addition, the merit of human study is that in contrast to animal studies that are constrained by forced choice behavior (e.g., to choose, or not to choose), we can ask participants to report on gradations of subjective reward prediction, allowing insight into the extent to which responses to feedback are conscious. Put another way, examining relationships between subjective RPE and objective (model-estimated) RPE in human study can help to understand the extent to which model estimates, which are the staple of animal research, represent conscious information. Such subjective reports on the internal RPE might be a better index than a behavioral output which is influenced by many other processing other than the internal RPE.

Subjective ratings on the level of reward prediction in each trial would allow prediction of trial-by-trial differences in the FRN based on internal reward prediction magnitude. Only a few previous studies have used subjective reports in each trial. Hajcak et al. (2005, 2007) used subjective confirmation (i.e., “Do you think you will win on this trial? - ”yes or no.”), and Yeung et al. (2005) showed that change of subjective ratings on task involvement was associated with FRN reduction during the task in which participants were required no active choice or no overt action. However, no previous study has tested on the relationships between subjective ratings on the level of internal reward prediction and FRN magnitude.

A key point to differentiate the studies which clearly supported the association between the FRN and RPE from others might be subjectively perceived frequency of reward feedback during a task, or reward contingency. The previous studies which showed a larger FRN in the higher reward prediction condition compared to the lower reward prediction condition have manipulated reward prediction by the frequency of reward feedback during gambling tasks as a bottom-up experience (Holroyd et al., 2003; Yasuda et al., 2004). In contrast, the studies that didn’t clearly show a relationship between the FRN and RPE manipulated reward prediction by top-down information on the reward probability using a cue stimulus presented at the beginning of each trial in gambling tasks (Hajcak et al., 2005, 2007) except one study which used cue stimuli showing extreme differences in reward probability and gave twenty choices in each trial (Holroyd et al., 2009; Experiment 1). If reward contingency or perceived reward frequency is associated with the internal subjective reward prediction to maximize the association between the FRN and RPE, then such an association would be the strongest in the situation where we can learn the choice behavior-reward contingency compared to the other situation where we get a random reward regardless of our choice behavior. In that case, the association between the FRN and RPE would be stronger in the situation where a reward contingency is “learnable” compared to the other situation where a reward contingency is “unlearnable”.

In order to examine whether reward contingency is critically important to the association between the FRN and RPE, we used a reinforcement learning task in which reward prediction would be naturally formed based on the history of choice and reward for each participant (i.e., reward contingency is learnable). As a secondary analysis, the data were contrasted with an unlearnable condition (i.e., reward contingency is unlearnable) which is more analogous to gambling tasks in the extant literature.

To examine the association between FRN and reward prediction, we focused only on trials in which a reward was expected but not received. Our conceptual question regards how people respond to negative information which is associated with reward omission. Trials in which an unexpected reward is received are affectively ambiguous in the point that negative information is being provided (i.e., having committed an error regarding information), but also positive reward is achieved. Thus, brain processes associated with such trials may be more difficult to understand. Increasingly data suggests that unexpected rewards are a function of different brain processes potentially involving reward receipt and positive affect which our model does not account for (Holroyd et al., 2008), and thus different brain regions may be involved in positive and negative prediction error (e.g., different subregions of striatum; Seymour et al., 2007). More technically, mechanisms for negative and positive reward prediction error might be different as these prediction errors may be associated with different patterns of modification of internal reward prediction.

Our hypothesis is that the FRN magnitude would be associated with both of subjective and model-estimated (objective) RPE at each trial. The subjective and objective RPEs were assessed by 1) subjective ratings in each trial and by 2) the prior history of choice and reward feedback using a computational reinforcement learning model. In addition, as it is possible that people learn over time, thereby creating systematic time-varying changes in reward prediction error (e.g., Holroyd and Coles, 2002), we checked whether observed reward prediction effects may be better explained by variation in the time course of learning by comparing the FRN in the first third of trials to that in the last third. In addition, a behavior-reward contingency would be important to vary the reward prediction enough to yield detectable change in the association between the FRN and RPEs.

1.1. Formulation Using Computation Modeling

Because prediction error can not be measured from observable responses directly, we used a well-known computational modeling approach to reinforcement learning in which prediction error is estimated from the history of choice behavior and reward feedback. Many such models calculate the estimated reward value of a selected choice option in each trial. We hypothesized this could be equal to the internal reward prediction value in the computational reinforcement learning model (e.g., Samejima et al., 2005; Samejima and Doya, 2008). In order to get the model-estimated reward prediction, we applied the reinforcement learning model by Samejima et al. (2005) to our data, in which action values are updated by a Rescorla-Wagner model; parameters were estimated using Sequential Monte Carlo (SMC) methodology. As our instructions to participants did not include information regarding rules governing outcomes or the structure of task, it would be appropriate to apply this type of model to our data instead of using a simple Rescorla-Wagner model without any randomness in choice behavior (see section 2.3 for details).

In a Rescorla-Wagner type of reinforcement learning model, the model-estimated value of choice a (action) in t-th trial is defined as Qa (t). As shown in equations 1 and 2, the prediction error is defined as the difference between the value of reward feedback and the model-estimated value of choice. The model-estimated value of choice is updated using both the learning rate and prediction error. We assumed that the model-estimated value of choice for the selected action in trial t (Qa (t)) would be approximated as internal prediction, and used it as the model-estimated reward prediction value.

$$\mathrm{Prediction\; Error}(t)=\mathrm{Reward\; Feedback}(t)­\mathit{Qa}(t)$$ (1)

$$\mathit{Qa}(t+1)=\mathit{Qa}(t)+\mathrm{Learning\; Rate}\ast \mathrm{Prediction\; Error}(t)$$ (2)

If the FRN is associated with prediction error, it should largely be based on the external reward feedback value itself such that it would not be susceptible to information values determined by the learning rate. Generally, the learning rate finds solutions quickly with the exponential decay in well-behaved spaces (e.g., Kirkpatrick et al., 1983) so that it has been used for optimization in the computational modeling. Thus, if the FRN is primarily driven by the learning rate, it would decrease throughout an experiment since the amount of learning available decreases. If the FRN is primarily driven by prediction error, it might increase with errors as expectation of reward increase with learning (i.e., larger FRN to the negative feedback with higher subjective reward prediction compared to the one with lower subjective reward prediction). This would lead to comparatively smaller prediction error early in an experiment because expectations are low, but large changes in learning rate with error. Later it is expected there will be increased prediction error, but fewer changes in learning rate given the more stable acquired task representation. Alternately, if both of these factors operate in parallel and both affect the FRN, the net effect could be no observed change in the FRN with time, as has been observed and discussed in previous studies (Eppinger et al., 2008; Santesso et al., 2008). This experiment is designed to quantify the effects of prediction error on the FRN using a simple task in which the learning rate was observed to stabilize within a few trials (see Figure 3C for an example of model-estimated learning rate). To the extent that the model accurately estimates the learning rate, we assume that we will be able to examine prediction error effects on the FRN rather than learning rate related effects.

Figure 3.

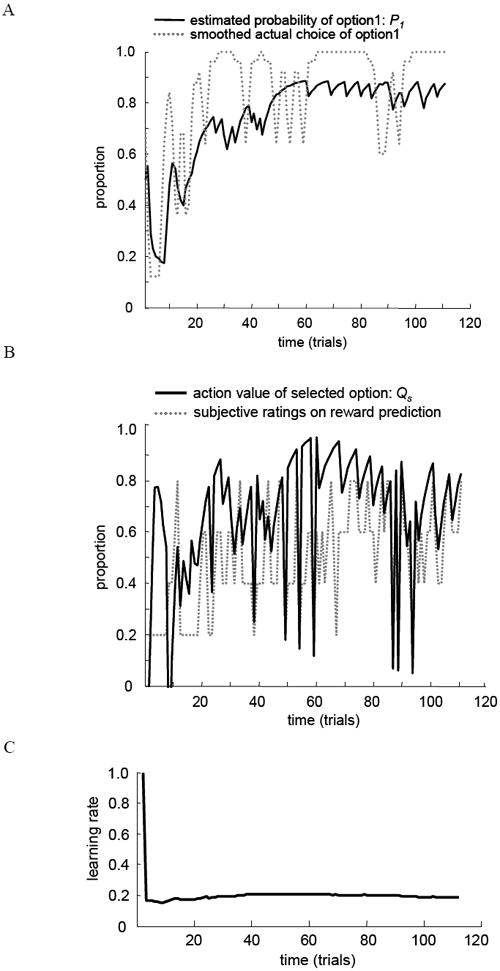
Model-estimated values and fittings to behavioral data in the Learnable condition (80/20 %). (A) An example of the time course of model estimated probability of option1 (P₁) and smoothed actual choice of option1 (r = .69; single subject). (B) An example of the time course of model estimated predicted value of choice of selected option (Q_s) and smoothed subjective ratings on reward prediction (r = .55; single subject). (C) An example of the time course of model estimated learning rate (single subject).

1.2. Study Summary

In this study, we used a simple two-alternative reinforcement learning task paradigm with two types of feedback (Gain, No-Gain), which is similar to stochastic tasks that has been used in previous studies (e.g., Hampton et al., 2006; Ohira et al., 2010). First, we hypothesized that the FRN magnitude would be associated with both of subjective and objective RPEs. Using subjective ratings or model-estimated values on reward prediction allows estimation of prediction error as a continuous value over time. Second, choice response would be more biased to the advantageous stimulus in a “learnable” condition (80 % contingency of the advantageous choice and 20 % for the alternative disadvantageous choice), and it would be associated with a reward prediction bias to positive feedback (Gain) as the reinforcement learning process goes on. Although such a reward prediction bias might be fluctuating during a task, the larger FRN amplitude would be associated with larger subjective reward prediction error only in the Learnable condition compared to an “unlearnable” condition (50 % contingency for both of two alternative choices). This would be because the ratings on subjective reward prediction are not expected to change in time course and vary enough to yield detectable changes in the Unlearnable condition. Because RPEs would not be large enough without confidence on a choice behavior-reward contingency in the Unlearnable condition.

In summary, we examined the trial-to-trial relationships of the FRN magnitude and reward prediction error by averaging ERPs based on 1) subjective RPE by ratings in each trial and 2) model-estimated RPE by a computational reinforcement learning model.

2. Methods

2.1. Participants

Twenty-five healthy volunteers (16 males and 9 females; Mean 22.1 years old, S.D. 2.2 yrs.) who were undergraduate or graduate students in Nagoya University participated in the experiment. They reported that they have no history of any kind of psychiatric disease or brain injury. All study participants provided written informed consent. Data from one subject was excluded from ERP analyses because of technical problems in recording their EEG.

2.2. Task Design and Procedures

Stimuli

Target stimuli were selected from the set of Novel Shapes (Endo et al., 2001), which is based on evaluation of the level of verbalization, association, and simpleness. Two different shapes were used as the target stimuli in each session (Learnable, Unlearnable), and only those two shapes were presented on the left or right side of the central fixation all through the session.

Task

A stochastic learning task which involved probabalistic mapping of target stimuli to responses was employed (see Figure1A). After a fixation cue was presented for 500 milliseconds (ms), two types of the target shapes are presented on the left or right side of the fixation for 500 ms. Participants were asked to choose either of the two shapes by responding with their right hand within 500 ms after the target onset; the index finger was used to choose the shape on the left side, and the middle finger was used to choose the shape on the right side. After a blank screen was presented for 1000 ms, participants were asked to rate the probability they would get a monetary reward in that trial on a 4-point scale (20 %, 40 %, 60 %, or 80 %) within 2000 ms using the index, middle, ring, or little finger of the right hand. The extreme options, including 0 % and 100 %, were not used because of a tendency to avoid extremes found in the previous studies (e.g., Hersen et al., 1984 for review). After a blank screen was presented for 2000 ms, positive (Gain: + 10 yen) or negative (No-Gain: 0 yen) feedback associated with the participant’s choice in a trial was presented for 700 ms and followed by a blank screen for 2300 ms (9 seconds per trial). In the task instructions, participants were told that their goal was to maximize the amount of money they accumulated and that they would receive that amount after the experiment.

Figure 1.

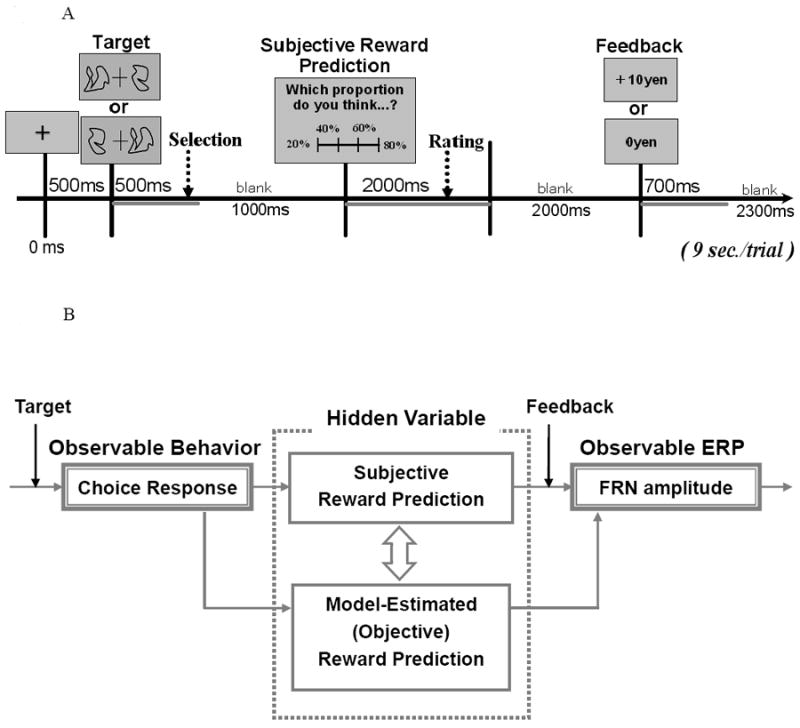
Conceptual and experimental time course of the task. (A) Reinforcement learning task: Time course of a single trial. (B) Concept of this study. We used two different ways to make “hidden variable” observable. We asked participants to rate their subjective reward prediction in the experiment, and then we estimated the predicted reward value of selected option (Q_s) from the history of choice and reward by using a computational model of reinforcement learning. We hypothesized that the model-estimated (objective) reward prediction would be associated with the subjective ratings on reward prediction.

Conditions

In a Learnable condition, selection of the advantageous shape led to a monetary reward (10 yen) with probability of 0.8 and no reward (0 yen) with the probability of 0.2, while selection of the disadvantageous shape led to a monetary reward (10 yen) with probability of 0.2 and no reward (0 yen) with the probability of 0.8. In an Unlearnable condition, there was no optimal selection strategy; selection of both the shapes led to a monetary reward or no reward with probability of 0.5 There were 120 trials (20 trials × 6 blocks) in each condition. The entire task for a single condition took approximately 20 minutes. Between the blocks, participants could take a short break or elect to continue by themselves. There was a rest for 10 minutes between the conditions. The order of the conditions was counterbalanced between the participants.

2.3. Computational Model

In order to estimate the objective value of internal reward prediction, we applied the computational reinforcement learning model by Samejima et al. (2005; model code available at http://www.tamagawa.ac.jp/sisetu/gakujutu/brain/tanji/samejima/samejima-e/Codes.html) to our data.

Samejima et al’s (2005) model was applied to a reinforcement learning two-alternative choice task. The two model-estimated values of choices were updated by a type of Rescorla-Wagner rule. One of the choices was selected based on a Boltzman distribution which defines the ‘inverse temperature’ to regulate the randomness of choice. Their model uses Bayesian inference via Monte Carlo approximation to estimate the hidden variables (model-estimated value of choice for each choice, see Figure 1B), and two parameters (learning rate, inverse temperature). A detailed explanation of the computational model is in the supplement of Samejima et al’s (2005) paper (http://www.sciencemag.org/cgi/content/full/310/5752/1337/DC1).

In our study, we calculated the model-estimated values of choices individually for each option in each trial as recommended by Cohen (2006) which compared the results using individual learning parameters with the results using fixed learning parameters. Model-estimated reward prediction error was calculated as the difference between the feedback value and model-estimated value of the choice for each trial. We compared model parameters to subjective ratings on reward prediction as follows:

$$\begin{array}{l}\mathrm{Feedback\; value}(\mathrm{FB}):\mathrm{Gain}=+1,\mathrm{No­Gain}=0\\ \mathrm{Subjective\; rating}(\mathrm{SR}):\mathrm{Four\; choices\; from\; lower\; to\; higher}=0.2,0.4,0.6,0.8\\ \mathrm{Model­estimated\; value\; of\; choice\; for\; selected\; option}(\mathrm{Qs})=[0,1]\\ \mathrm{Model­estimated\; reward\; prediction\; error}(\mathrm{modelRPE})=\mathrm{FB}-\mathrm{Qs}\\ \mathrm{Subjective\; reward\; prediction\; error}(\mathrm{subjRPE})=\mathrm{FB}­\mathrm{SR}\end{array}$$

We sorted the trials based on the subjRPE or modelRPE, and made ERP waves separately for each individual using the third of trials with the highest values and the third of trials with the lowest values. ANOVA analyses examined the effect of subjRPE and modelRPE.

2.4. Physiological Measures and Data Analyses

Recordings

Electroencephalogram (EEG) data was recorded from Ag/AgCl electrodes placed on five mid-line scalp sites (Fz, Cz, Pz, C3, C4) using the 10-20 system. All the electrodes were referenced to nose tip. Vertical electrooculogram (EOG) was recorded through two electrodes placed above and below the left eye in order to monitor eyeblink activity and remove associated noise from EEG data. Electrocardiogram (ECG) was collected simultaneously though we will not report the results of it in this paper. All the electrophysiological data were recorded by BIOPAC MP-100 Systems at 250Hz, low-pass filtered at 35Hz and high-pass filtered at 0.01Hz. EEG Electrode impedance was kept below 10kohm.

ERP Definition and Analyses

FRN amplitude was defined as the mean value of the signal 250–350 ms following the feedback stimuli, relative to a 200 ms pre-feedback baseline. To analyze the FRN, EEG segments were extracted offline, cut around the reward feedback onset, from 1000 ms before to 2000 ms after the feedback onset. We averaged the time period from 200 ms to 0 ms before the feedback presentation as a baseline, using EEGLAB 4.311 (Delorme and Makeig, 2004) and MATLAB^®. Then, EEG trial epochs from 200 ms pre to 500 ms post reward feedback onset in which the amplitude deviation exceeded 50 microvolts in a 100 ms interval were regarded as containing EOG or motion artifacts, and were removed before averaging. The artifact-free EEG data were low-pass filtered at 15 Hz off-line and averaged for each participant and each condition. ERP data were analyzed using repeated measures analysis of variance (ANOVA) with factors of electrode (Fz, Cz, Pz), condition (Learnable, Unlearnable), and feedback (Gain, No-Gain) or time (Former third, Latter third) or negative reward prediction error (High third, Low third). To account for violations of sphericity in our ANOVAs, a Greenhouse-Geisser correction was applied where appropriate. For the comparisons between high and low of the subjective reward prediction, model estimated reward prediction, and the comparisons between early and late period of the time course, we averaged the third of highest (or earliest) and lowest (or latest) data for analyses. In order to explore relationships between the FRN and RPE within single subjects, first, the EEG data was preprocessed and divided into single-trial EEG epochs. Second, we sorted those epochs from high to low by the value of RPE calculated based on subjective ratings, and did the same thing using the value of model-estimated RPE. Third, we applied a 10-trial moving average to increase signal-to-noise ratio (SNR) for the FRN and RPE single-trial waveforms. This technique allowed us to correlate RPE with FRN magnitude within subjects. ERP and behavioral results were statistically evaluated using SPSS (ver. 16.0).

3. Results

3.1. Behavioral Measures

As a manipulation check, we examined the results of response bias on choice behavior, subjective ratings, and model-estimation on reward prediction. Group results are shown in Figure 2 and examples of individual results are shown in Figure 3. In the group results, a repeated measures ANOVA (condition × block) on the choice rate of a certain stimulus (with an 80 % contingency in the Learnable condition, or, with a 50 % contingency in the Unlearnable condition) revealed that a response bias to the advantageous stimuli was formed only in the Learnable condition (see Figure 2A, main effect of condition F(1, 24) = 27.91, p < .0005, Partial Eta Squared = .54). Subjective ratings of reward prediction were high only in the time course of Learnable condition compared to that of Unlearnable condition (Figure 2B illustrates the interaction of condition × block: F(5.42, 130) = 2.92, p < .05, Partial Eta Squared = .11 with Greenhouse-Geisser correction). We checked the distribution of subjective ratings to make sure that this four-alternative rating method did work. Both of the average and standard deviation (SD) of subjective ratings in the Learnable condition (Average: M(SE) = 2.35 (.12), SD: M(SE) = .87 (.04)) and those in the Unlearnable condition (Average: M(SE) = 2.05 (.13), SD: M(SE) = .74 (.05)) were significantly different (Average: t(24) = 5.09, p < .001; SD: t(24) = 3.11, p < .005). Model-estimated reward prediction increased only in the Learnable condition compared to the Unlearnable condition as well as subjective ratings on reward prediction (see Figure 2C, the interaction of condition × block: F(6.98, 168) = 2.66, p < .05, Partial Eta Squared = .10 with Greenhouse-Geisser correction). As subjective and model-estimated reward prediction showed the similar pattern of time course in a group level. We computed the Pearson’s correlation coefficient between subjective and model-estimated RPE for each subject. The correlation of subjective and model-estimated RPE was lower in the Learnable condition (M(SE): r = .82 (.02)) compared to that in the Unlearnable condition (M(SE): r = .91 (.01)) ; t(23) = 7.05, p < .001; see the distribution of correlation in Figure S5 in the supplementary material). Although subjective and model-estimated RPE seemed to show high correlation described above, in the following ERP analysis, just around half of the trials overlapped each other between subjective RPE and model-estimated RPE conditions both in the Learnable condition (overlapped trials: High-RPE M(SE) = 5.9 (.5) trials, Low-RPE M(SE) = 6.4 (.5) trials) and in the Unlearnable condition (overlapped trials: High-RPE M(SE) = 7.0 (.5) trials, Low-RPE M(SE) = 6.3 (.6) trials). This is because we used only the highest third and the lowest third trials for High and Low RPE conditions in the ERP analysis in order to get clear contrast of the FRN result.

Figure 2.

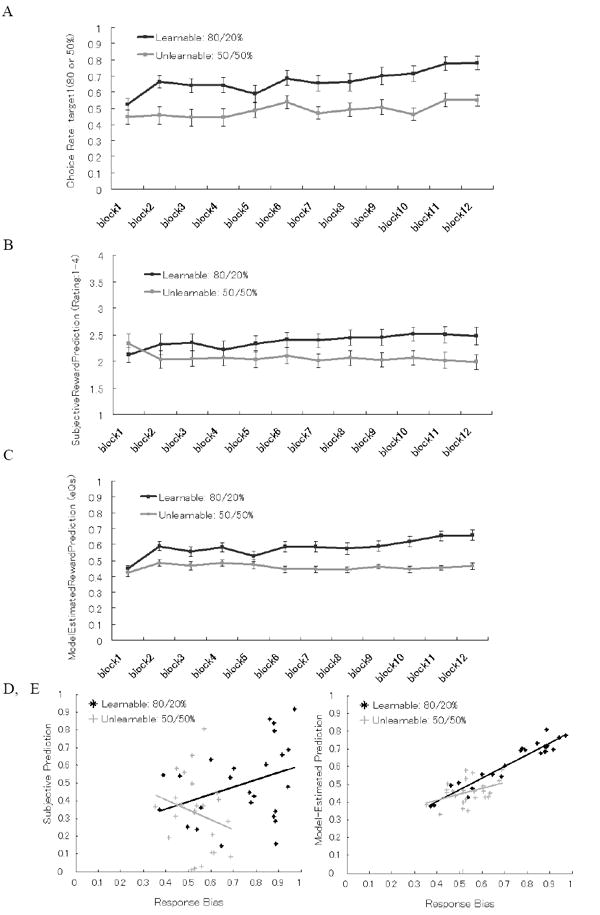
(A, B, and C) Behavioral results averaged per 10 trials in the Learnable (80/20 %) and Unlearnable (50/50 %) conditions. (A) Choice rate of option1. (B) Subjectively perceived reward prediction in each trial. (C) Model-estimated value of reward prediction. (D and E) Correlation plots of response bias (average of choice rate) in the last third session and each reward predictions between subjects. (D) Subjective reward prediction in the Learnable condition (r = .35, p < .10) and Unlearnable condition (n.s.). (E) Model-estimated reward prediction in Learnable condition (r = .96, p < .001) and Unlearnable condition (r = .41, p < .05).

To examine the relationships between choice behavior and reward prediction, we smoothed the actual choice and subjective ratings on reward prediction via a 10 trial kernel moving average filter, as previous studies have used (e.g., Cohen and Ranganath, 2007; Samejima et al., 2005). Because the actual choice (measured as 0 or 1) and subjective ratings on reward prediction (four alternative choices) are discrete values whereas the model-estimated choice probability and reward prediction are continuous values, this method had the effect of allowing those values to slowly accumulate and decay rather than varying from 0 to 1 between trials. The smoothing method was applied only to the discrete values (i.e., actual choices, subjective ratings) when we computed correlations between the time courses of choice behavior (i.e., actual choice vs. model-estimated choice probability), reward prediction error (i.e., subjective RPE vs. model-estimated RPE), or correlations across both choice behaviors and RPEs.

In order to check whether the task order was not critical for participants to form a response bias successfully, we made two groups, ‘learners (n = 12)’ who successfully formed a response bias and ‘non-learners (n = 12)’ who did not, as shown in previous studies (Krigolson et al., 2009; Santesso et al., 2008). Those two groups were defined based on their response bias in the last third (9-12 blocks) in the Learnable condition. One subject who had no ERP data because of a recording problem was not included in either of the groups. As a result, the task order didn’t seem to have a serious carry-over effect for learning performance because 58 % of “non-learners” and 50 % of “learners” got the Learnable condition first. In addition, only “learners” showed an interaction of condition × block (F(3.84, 42.3) = 2.96, p < .05, Partial Eta Squared = .21 following Greenhouse-Geisser correction), whereas “non-learners” did not (F(5.30, 58.3) = .70, n.s., Partial Eta Squared = .06 with Greenhouse-Geisser correction. The time course of subjective ratings was associated with that of choice behavior (M(SE): r = .36 (.06)), and increased for ‘learners’ (M(SE): r = .51 (.07)) compared to ‘non-learners’ (M(SE): r = .23 (.08); t(22) = 2.59, p < .01, after converting in Fisher Z’ scores). Moreover, model-estimated reward prediction value (Q_s) and subjective ratings on reward prediction (SR) were correlated (M(SE): r = .30 (.05)); correlations were stronger for ‘learners’ (M(SE): r = .43 (.06)) compared to ‘non-learners’ (M(SE): r = .19 (.06); t(22) = 2.77, p < .01, after converting in Fisher Z’ scores).

Figures 2D and 2E shows the between-subjects correlations between response bias (i.e., average of choice rate) and either subjective reward prediction (i.e., average of subjective ratings), or model-estimated reward prediction during the last third of trials (i.e., average of action value of selected choice option; showing that the computational model is working as a manipulation check). The correlation between response bias and reward prediction was significant for model-estimated prediction (Learnable condition: r = .96, p < .001; Unlearnable condition: r = .41, p < .05) but it was not significant for subjective prediction (Learnable condition: r = .35, p < .10; Unlearnable condition: n.s.). One subject in Unlearnable condition was removed from this correlation analysis and the following ERP analysis as an outlier which has too low response bias in Unlearnable condition (Response Bias = .10), it was smaller than the mean minus three standard deviations.

Figure 3 shows examples from one participant whose choice behavior fit well to the model-estimated probability of advantageous choice in the Learnable condition (Figure 3A; r = .69). The time course of subjective ratings (SR) and model-estimated value (Q_s) on reward prediction also fit well (Figure 3B; r = .55). The time course of the estimated learning rate is shown in Figure 3C. Model fits to behavior were moderate on average (M(SE): r = .23 (.05)). They were significantly better for ‘learners’ (M(SE): r = .37 (.08)) compared to ‘non-learners’ (M(SE): r = .12 (.06); t = 2.66, p < .01, after converting in Fisher Z’ scores).

3.2. ERPs

Grand-averaged, feedback-locked ERPs are shown in Figure 4A-D for the Learnable condition and in Figure 5A-D for the Unlearnable condition. In order to check if there is a clear difference between these conditions only in the time period of FRN, the time points with significant differences (p < .05) between conditions are highlighted in different colors (as in Siegle et al., 2008). To control Type I error for the large number of tests, as recommended by Guthrie and Buchwald (1991), differences between conditions were considered significant only when there were at least 10 significant contiguous tests in a row at p < .05 (40 ms), which exceeds the expected threshold given the autocorrelation of component waveforms (r = .96) in the length of simulated time interval for FRN (200-400 ms). The period which is significant above the contiguous threshold was marked with asterisk (“*”; p < .05). The same number of trials was used to make ERP waves for both High-RPE and Low-RPE, Early and Late, in each condition (Learnable: Figure 4B, 4C, and 4D; Unlearnable: Figure 5B, 5C, and 5D).

Figure 4.

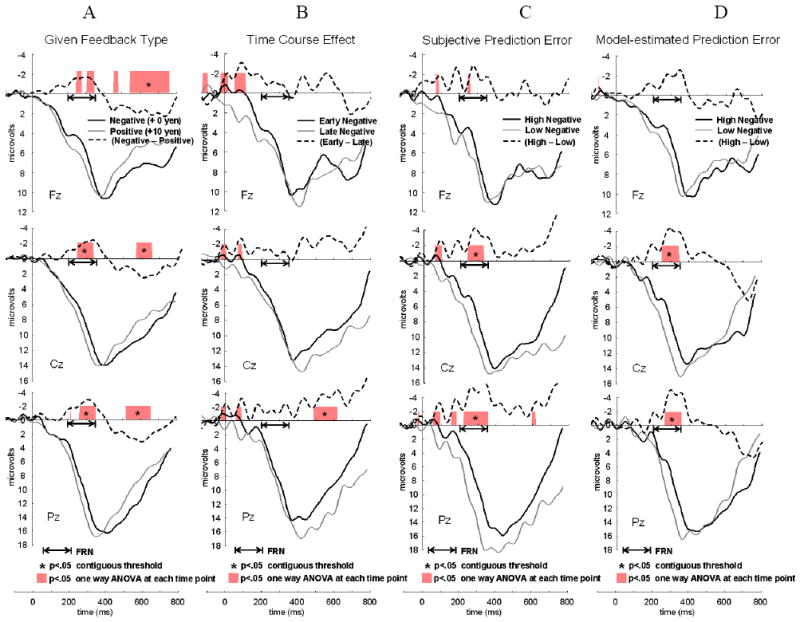
Feedback-locked, grand-averaged ERPs at Fz, Cz, and Pz in the Learnable condition (80/20 %, n = 24). Significant condition-related differences at each time point was highlighted over the x-axis (p < .05, see text for detail) and significant time periods at the contiguous threshold (p < .05) was marked as “*”. A dotted black line shows a difference wave between two conditions for each figure (a solid black line minus a thin gray line). (A) ERPs elicited by given feedback type in conventional method. Negative feedback (+ 0 yen; a solid black line) versus positive feedback (+ 10 yen; a thin gray line). (B) ERPs elicited by time course effect. Early negative feedback trials in the first third session (a solid black line) versus Late negative feedback trials in the last third session (a thin gray line). (C) ERPs elicited by subjective reward prediction error (subjRPE). High prediction error (trials in the highest third; a solid black line) versus low prediction error (trials in the lowest third; a thin gray line) with negative feedback. (D) ERPs elicited by model-estimated reward prediction error (modelRPE). High prediction error (trials in the highest third; a solid black line) versus low prediction error (trials in the lowest third; a thin gray line) with negative feedback.

Figure 5.

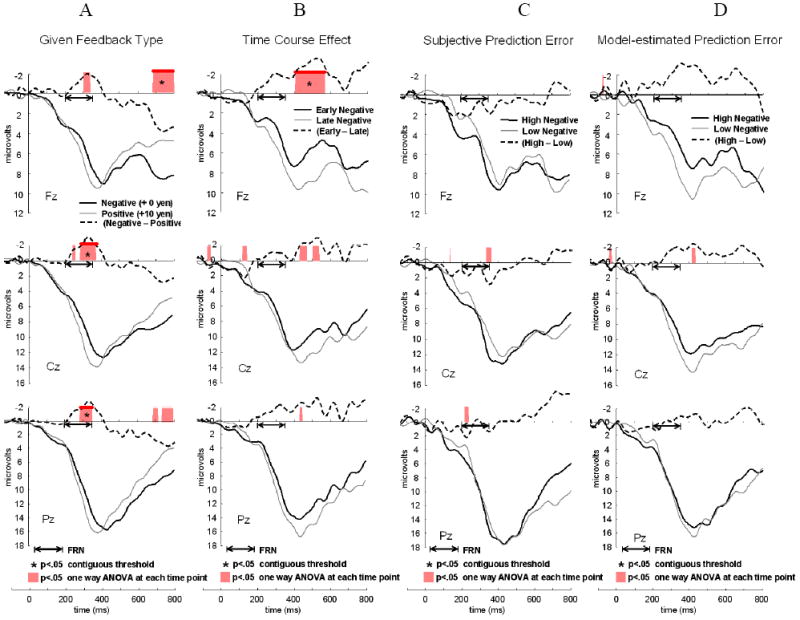
Feedback-locked, grand-averaged ERPs at Fz, Cz, and Pz in Unlearnable condition (50/50 %, n = 23). In Unlearnable condition, subjective ratings on reward prediction and model-estimated reward prediction didn’t vary enough to assess the difference (see Figure 2D, 2E) and there was no significant difference observed in Figure 5C and 5D. Significant condition-related differences at each time point was highlighted over the x-axis (p < .05, see text for detail) and significant time periods at the contiguous threshold (p < .05) was marked as “*”. A dotted black line shows a difference wave between two conditions for each figure (a solid black line minus a thin gray line). (A) ERPs elicited by given feedback type in conventional method. Negative feedback (+ 0 yen; a solid black line) versus positive feedback (+ 10 yen; a thin gray line). (B) ERPs elicited by time course effect. Early negative feedback trials in the first third session (a solid black line) versus Late negative feedback trials in the last third session (a thin gray line). (C) ERPs elicited by subjective reward prediction error (subjRPE). High prediction error (trials in the highest third; a solid black line) versus low prediction error (trials in the lowest third; a thin gray line) with negative feedback. (D) ERPs elicited by model-estimated reward prediction error (modelRPE). High prediction error (trials in the highest third; a solid black line) versus low prediction error (trials in the lowest third; a thin gray line) with negative feedback.

3.2.1. Number of Trials Needed to Achieve a Reliable FRN

To achieve stable and reliable error-related ERP analysis, Olvet and Hajcak (2009) suggested that a minimum of between 6 and 8 error trials for single subject ERPs are required. As they examined response-onset ERPs (i.e., error-related negativity: ERN), we checked whether the similar number of negative feedback trials is required for single subject feedback-onset ERPs (i.e., FRN). We computed Cronbach’s alpha for the FRNs at Cz as increasing number of trials which were pseudorandomly selected from the trials with negative feedback in the Learnable condition in which subjects had smaller number of negative feedback trials compared in the Unlearnable condition. Our results were consistent with those of Olvet and Hajcak (2009). A minimum of 6 negative feedback trials were required for single subject FRNs to achieve moderate internal reliability (alpha from .50 to .70; Olvet and Hajcak, 2009). That is, Cronbach’s alpha increased from -.037 with 2 trials (n = 24) to .48 with 4 trials (n = 24), .65 with 6 trials (n = 24), .74 with 8 trials (n = 23), .75 with 10 trials (n = 19), .78 with 12 trials (n = 10), and .80 with 14 trials (n = 6); see Figure S1 in the supplemental material). We also computed Pearson’s correlation coefficient between the FRNs based on increasing number of negative feedback trials and the FRN averaged with all the negative feedback trials. The correlation was high with 6 negative feedback trials (r = .94, p < .001); As shown in Supplementary Figure S2, the correlation increased with the number of trials.

Thus, we believe our results to be reliable, as the average number of the trials we used for making individual ERPs was 11.9 trials (SE = 0.8, max = 23, min = 7) in the Learnable condition, and 16.6 trials (SE = 0.8, max = 23, min = 9) in the Unlearnable condition. These trial numbers for averaging were different between conditions because participants received more negative feedbacks in Unlearnable condition compared to Learnable condition.

3.2.2. Feedback effects

As a manipulation check, we compared ERPs with Negative and Positive feedback to make sure that we could find FRN as the previous studies have suggested. Figure 4A and 5A show ERPs averaged by feedback type, using the conventional method for computing the FRN.

In the Learnable condition (Figure 4A), a two-way feedback (Negative: 0 yen, Positive: +10 yen) × location (Fz, Cz, Pz) ANOVA suggested that the interaction effect was not significant (F(1.35, 31.1) = 1.62, n.s.) and the FRN was larger to negative feedback compared to positive feedback as a main effect of feedback (F(1,23) = 6.86, p < .05, Partial Eta Squared = .23), and larger in the following order, Fz, Cz, and Pz as a main effect of electrode (F(1.47, 33.9) = 8.76, p < .005, Partial Eta Squared = .28).

In the Unlearnable condition (Figure 5A), the same two-way ANOVA (feedback × location) suggested that the feedback × location interaction was not significant (F(2, 44) = .867, n.s.) and the FRN was larger to negative feedback compared to positive feedback as a main effect of feedback (F(1, 22) = 7.62, p < .05, Partial Eta Squared = .26), and larger in the following order, Fz, Cz, and Pz as a main effect of electrode (F(2, 44) = 14.26, p < .001, Partial Eta Squared = .39).

3.2.3. Time Course of Learning effects

Figure 4B and 5B show the ERPs with negative feedback for the first third of trials versus the last third of trials. We examined the temporal change of FRN amplitude, focusing on the early and late periods in order to see whether the results were similar to those of subjective prediction or not. As we were interested in the time course of learning effect especially on the trials with negative feedback, we checked the results of a two-way ANOVA of time course (Early, Late) × location on the FRN amplitude in the trials with negative feedback.

In the Learnable condition (Figure 4B), The results showed that there was no significant interaction effect associated with the time course of learning effect on the FRN in the trials with negative feedback (F(2, 46) = .72, n.s., Partial Eta Squared = .03). No statistical test at each time point for the temporal range of FRN was significant.

In the Unlearnable condition (Figure 5B), there was no significant interaction effect associated with the time course of learning effect on the FRN in the trials with negative feedback (F(2, 44) = .25, n.s., Partial Eta Squared = .01). But the FRN was larger in the following order, Fz, Cz, and Pz as a main effect of electrode (F(2, 44) = 15.77, p < .001, Partial Eta Squared = .42).

3.2.4. Subjective Prediction Effects

Figure 4C and 5C show the ERPs to trials with negative feedback averaged by the third of trials with the highest versus lowest subjective RPE.

In the Learnable condition (Figure 4C), a two-way ANOVA of subjective RPE (High, Low) × location on the FRN amplitude in the trials with negative feedback showed an interaction effect of subjective RPE and location (F(1.34, 30.84) = 4.23, p < .05, Partial Eta Squared = .16). The following pairwise comparisons with Bonferroni correction showed that there was a significant difference of FRN magnitude between Fz and Pz (p < .05) with low RPE while there was no difference in FRN among electrodes with high RPE. The difference between high and low subjective RPE was significant on Pz (p < .05).

In the Unlearnable condition (Figure 5C), there was no significant interaction effect (F(1.35, 29.7) = .52, n.s., Partial Eta Squared = .02). The FRN was larger in the following order, Fz, Cz, and Pz as a main effect of electrode (F(2, 44) = 13.90, p < .001, Partial Eta Squared = .39).

3.2.5. Model estimated reward prediction effects

Figure 4D and 5D show the ERPs from trials with negative feedback, contrasting the highest and lowest third of trials averaged by model-estimated RPE.

In the Learnable condition (Figure 4D), a two-way ANOVA of model-estimated RPE (High, Low) × location didn’t show an interaction effect (F(1.42, 32.65) = 1.41, n.s., Partial Eta Squared = .06) and all of the main effects were significant. High model-estimated RPE was associated with a large FRN compared to low model-estimated RPE (F(1, 23) = 6.35, p < .05, Partial Eta Squared = .22). FRN magnitude was more negative in the following order, Fz, Cz, and Pz as main effect of electrodes (F(2, 46) = 7.33, p < .005, Partial Eta Squared = .24).

In the Unlearnable condition (Figure 5D), there was no significant interaction effect (F(1.36, 30.0) = 1.21, n.s., Partial Eta Squared = .05). The FRN was larger in the following order, Fz, Cz, and Pz as a main effect of electrode (F(2, 44) = 12.7, p < .001, Partial Eta Squared = .37).

3.2.6. Correlations between FRN and subjective RPE, model-estimated RPE

As previously described, in order to test our primary hypotheses, we focus here on the results of the Learnable condition because both of subjective and model-estimated reward prediction didn’t vary enough in the Unlearnable condition (see Figure 2D, 2E) so that the FRN amplitudes based on the trials with high and low reward prediction error didn’t show any differences in the Unlearnable condition (see Figure 5C, 5D). The scatter plots of FRN magnitude and RPEs (i.e., subjective, model-estimated) between subjects in the Learnable condition are shown in Figure 6A. These plots are based on the FRNs from the trials with the highest and lowest thirds of negative RPE for each subject. The middle third trials were excluded because they had higher variability on both indices. The FRN magnitudes were significantly associated with subjective RPE (r(23) = .33, p < .05) and model-estimated RPE (r(23) = .41, p < .005) across participants. These relationships were not significantly different by the test of dependent r’s (t(21) = -.62, n.s.).

Figure 6.

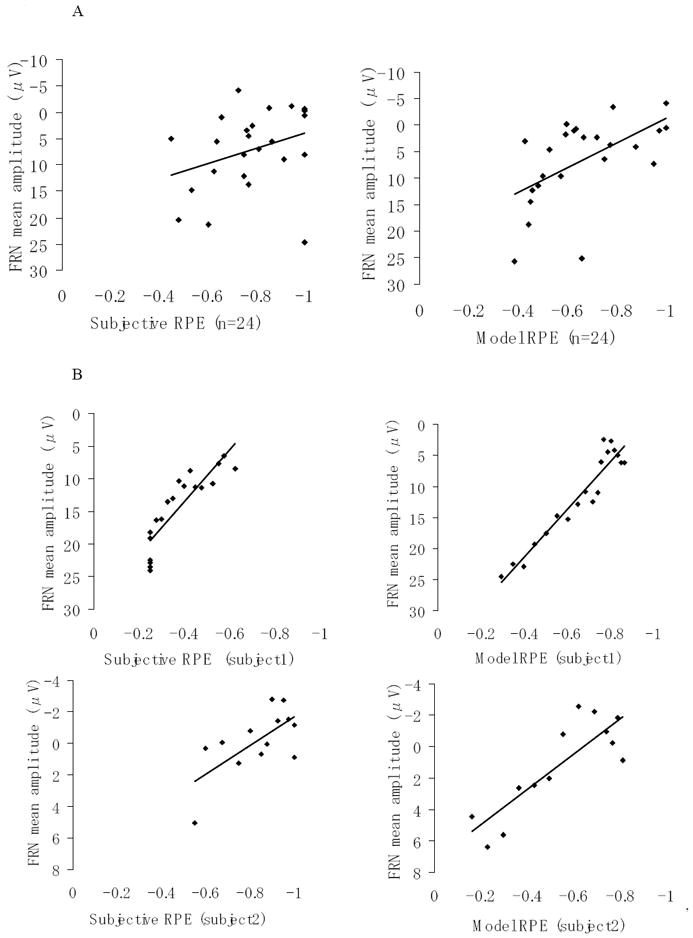
(A) Scatter plots of FRN and RPEs (subjective, model-estimated) between subjects in the Learnable condition (n = 24). Left: Subjective RPE assessed by subjective ratings on reward prediction (r = .33, p < .05). Right: Model-estimated RPE assessed by a computational reinforcement learning model (r = .41, p < .005). (B) Examples of scatter plot from two single subjects. Left: Subjective RPE and FRN (upper: subject1, r = .88; lower: subject2, r = .67). Right: Model-estimated RPE and FRN (upper: subject1, r = .96; lower: subject2, r = .85).

To test correlations between the FRN and RPE within subjects, we made moving-averaged ERP waves using every ten trials of the single-trial EEG data sorted by RPE value from high to low. Using the FRN magnitudes from those moving-averaged ERP waves, we calculated Pearson’s product-moment correlation coefficients between FRN and RPE individually for each single subject. Examples of scatter plots within subject are shown in Figure 6B (two examples of single subject results). We conducted one sample t-tests on the correlation coefficients of all the subjects after Fisher’s z transformation. The correlations within subjects were significant between FRN magnitude and subjective RPE (M(SE): r = .47 (.13); t(23) = 3.69, p < .001), and between FRN magnitude and model-estimated RPE (M(SE): r = .40 (.19); t(23) = 2.11, p < .05). These relationships were not significantly different (t(23) = .44, n.s.).

4. Discussion

In this study, at first we examined whether the model-estimated RPE is highly correlated with the subjective RPE assessed by ratings in each trial in a reinforcement learning task. Then, we examined whether the FRN is associated with both RPEs (subjective, model-estimated) in the Learnable condition where RPEs would vary enough with the confidence on a choice-reward contingency. We used enough error trials to assure reliability of our estimates.

As we hypothesized, both subjective and model-estimated RPEs were significantly correlated with each other, and the FRN magnitude was associated with both RPEs (subjective, model-estimated) between and within subjects in the Learnable condition. The FRN magnitude was larger in the trials with larger negative RPE, and this was consistent with the explanation of a reinforcement learning theory. As predicted, these differences were not observed in the Unlearnable condition and that is consistent with a role of reinforcement learning. For a secondary analysis, we examined whether or not the FRN is associated with RPE even regardless of reward contingency in the Unlearnable condition. As results, there were no differences between high and low prediction error related FRNs in the Unlearnable condition, for both of subjective and objective model-estimated prediction error. This could be because both of subjective and objective reward predictions didn’t vary enough to assess differences in the Unlearnable condition (see Figure 2D, 2E) or experience of reward contingency might be associated with FRN amplitudes.

For subjective prediction error, little research has focused on relationships between the FRN and internally generated prediction error. Hajcak et al. (2005, 2007) suggested that the FRN might be sensitive to reward prediction error and that it may depend on the close coupling of prediction and outcome. They compared two separate gambling experiments in which subjective prediction ratings were acquired before or after a choice response. Moser and Simons (2009) further examined relationships between the FRN and change of subjective prediction before and after the task-related choice response in a gambling task. They found that the FRN was largest when subjective reward prediction increased during the trial (i.e., predicted ‘no-win’ before their choice, but predicted ‘win’ after their choice). Our results are consistent with these results, in that higher subjective reward prediction rated after choice response was associated with a larger FRN.

We applied a computational reinforcement learning model to estimate the internal reward prediction (Samejima et al., 2005). The unique point of this study is that we used the model only for calculating objective RPE, and our goal was not simulating FRN itself (e.g., Holroyd and Coles, 2002; Nieuwenhuis et al., 2002). Our results regarding to model-estimated RPE were as follows. First, the objectively estimated RPE by the reinforcement learning model showed high correlation with the RPE based on subjective ratings. Second, the ERP wave based on the trials with high model-estimated RPEs was significantly different from the ERP wave based on the trials with low RPEs regardless of the time course of reinforcement learning. The FRN differences associated with prediction error was observed more clearly only in the time period of FRN based on the model-estimated RPE (Figure 4D) compared to when we used time course of learning (Figure 4B) or subjective ratings method (Figure 4C). For the concern whether the “dynamic” learning rate that we used in this paper was appropriate, we also checked the FRN results at Cz based on the model-estimated RPE computed by the model with the “fixed” learning rate (fLR = 0.05, 0.1, 0.15, 0.2, 0.25, 0.3; analogous to Figure 4D) and showed them in the supplementary material (Figure S3). As a result, the models with a fixed learning rate did not seem to show clearer results compared to the model with a dynamic learning rate. In addition, we compared the original model with a dynamic learning rate to the model with an optimized-fixed learning rate (optimized for each individual’s data). The results suggested that the issue of dynamic vs. fixed learning rate did not critically affect model fit (see Figure S4 in the supplementary material for more details). Thus, whether the learning rate parameter was dynamic or fixed was not critical to our primary conclusions regarding the association between prediction error and FRN.

Differences in FRN amplitude between conditions could reflect contributions from early P300 responses in part. In fact, for “subjective” reward prediction error, high and low prediction error related FRN showed significant difference on Pz so that the FRN observed here might contain not only the prediction error signal from anterior cingulate cortex as the previous reinforcement learning hypothesized (Holroyd and Coles, 2002) but also influenced by some other signals from different brain regions which are associated with a reinforcement learning. However, it is also hard to say that these results just reflect the influence of P300 because of the following two reasons. First, the narrow time-window of condition-related differences (250-350 ms after feedback-onset) observed in our sample-wise tests which did not seem to include the P300 latency (Figure 4C, 4D). Second, if these FRN results were really overlapped with P300, the time course effects (Figure 4B) should show clear differences between early and late negative feedback trials in the same latency of FRN (250-350 ms) instead of the latency of P300. In that case, Figure 4B should show larger P300 in Late negative feedback trials compared to Early negative feedback trials because participants received less negative feedback in the late third compared to the early third in the Learnable condition as we see in the figure of choice rate of the Learnable condition (Figure 2A). As we see in the ERP results on Pz in Figure 4, the significant time periods (p < .05) in Figure 4C (240-380 ms) and 4D (270-370 ms) seem to be overlapping with the earlier significant time period of FRN latency in Figure 4A (270-360 ms). The significant time period in Figure 4B (500-640 ms) seems to be overlapping with the late significant time period of Figure 4A (520-660 ms). Although it would be hard to say whether the late significant period is P300 or late positive component (LPP), this component doesn’t seem to be overlapping with the latency of FRN.

For the differences of the ERPs during the pre-stimulus and early post-stimulus period observed in Figure 4, they might not be due to noise, but instead they might reflect the condition differences of prediction or expectation of the feedback that occurred in the long pre-stimulus interval. The stimulus-preceding negativity (SPN; Brunia, 1988) has been occurred prior to the feedback stimulus, and it might be associated with these differences. The SPN has been enhanced when participants expected more negative (noise) or more positive (reward) feedback compared to less negative (pure tone) or less positive (no reward) feedback (Kotani et al., 2001). Furthermore, the SPN has been associated with the motivational significance of the previous outcomes (Masaki et al., 2006) so that it would be possible that there would be differences between the ERPs with High RPE and Low RPE regarding the SPN. However, we focused on the FRN in this study and used the pre-feedback period (from -200 to 0 ms) as a baseline, we will examine the association between reward prediction and the SPN separately in the future study.

There were a number of limitations to this study. The low number of employed electrodes prevented source localization which would be interesting to examine in a future study. The collection of subjective prediction data could have biased the natural course of feedback-related reactivity, though this request came long after the examined components were generated. We tried to avoid extreme choices of 100 % and 0 % in the four-alternative subjective ratings on reward prediction by using 20, 40, 60, and 80 % because of a tendency to avoid extremes (e.g., Hersen et al., 1984). However, even the highest and the lowest confident predictions on reward were rated as only 80 % or 20 %, and these could be new extreme choices. The employed computational model made the standardly applied assumption that people have a moderate learning rate (i.e., not changing their behavior completely based on one trial, but eventually acquiring the rule); this convention appeared acceptable as model fits were generally good. As we were using a published model, we made only standard assumptions associated with this model. We showed that a minimum of 6 negative feedback trials were required for single subject FRNs using the same methods employed by (Olvet and Hajcak, 2009). However, the replication of this result with larger numbers of negative feedback trials would be needed in the future study.

In summary, our results suggest that the model-estimated reward prediction error (RPE) was highly correlated with subjective RPE assessed by ratings in each trial, and the FRN was associated with both subjective and model-estimated RPEs regardless of the time course of learning, only in the Learnable condition where the internal reward prediction varies enough with the confidence of choice-reward contingency.

Highlights.

• FRN was associated with both subjective and model-estimated RPEs.

• FRN was not associated with the time course of learning.

• Subjective RPE was correlated with model-estimated RPE.