Force scanning: A rapid, high-resolution approach for spatial mechanical property mapping

Abstract

Atomic force microscopy (AFM) can be used to co-localize mechanical properties and topographical features through property mapping techniques. The most common approach for testing biological materials at the micro-and nano-scales is force mapping, which involves taking individual force curves at discrete sites across a region of interest. Limitations of force mapping include long testing times and low resolution. While newer AFM methodologies, like modulated scanning and torsional oscillation, circumvent this problem, their adoption for biological materials has been limited. This could be due to their need for specialized software algorithms and/or hardware. The objective of this study is to develop a novel force scanning technique using AFM to rapidly capture high-resolution topographical images of soft biological materials while simultaneously quantifying their mechanical properties. Force scanning is a straight-forward methodology applicable to a wide range of materials and testing environments, requiring no special modification to standard AFMs. Essentially, if a contact mode image can be acquired, then force scanning can be used to produce a spatial modulus map. The current study first validates this technique using agarose gels, comparing results to the standard force mapping approach. Biologically relevant demonstrations are then presented for high-resolution modulus mapping of individual cells, cell-cell interfaces, and articular cartilage tissue.

1. Introduction

Atomic force microscopy (AFM) is a high-resolution type of scanning probe microscopy that has great versatility with the materials it can image. AFM is widely used to characterize the nanoscale topographical structure of biological and non-biological materials but has also found popularity as a force measurement device. In addition to surface imaging and mechanical testing, AFM can be expanded to assess additional material properties, including electrical conductance, magnetism, and resistivity. Combining multiple techniques is also possible so that spatial arrangements of mechanical or electrical properties can be assessed at high resolution. A major strength of AFM is its compatibility with biological environments, allowing living organisms to be tested without requiring extensive or damaging sample preparation. High-resolution imaging and force measurement of cells and tissues can help elucidate changes that occur in response to injury or disease, as well as shed light on the phenomena of mechanotransduction. Of particular importance is developing an effective method for evaluating the co-localization of surface topography and mechanical properties, allowing for a single assay to produce both structural and functional information on the molecular, cellular, and tissue levels.

Spatial property mapping combines the high-resolution scanning and force spectroscopy capabilities of AFM. These approaches are especially important for biological materials that have highly complex mechanical characteristics coupled to biological responses. Mechanical imaging has been implemented through different approaches in the past. Force mapping is one common technique in which the mechanical compliance of a surface is simultaneously reported with its height features [1, 2]. Basic protocols involve applying individual force curves at discrete sites across a sample surface. These data are analyzed separately, and the resulting mechanical properties are mapped over the surface topology. Force mapping is a simple, straight-forward approach that provides high-resolution force curves at the expense of longer testing times and lower lateral resolution. Fitting a mathematical model to the force-indentation data is simple and typically involves a geometrically appropriate form of the Hertz equation[3]. Force mapping has been used successfully in the past for probing molecules [2, 4, 5], cells [6–8], tissues [9–17], and various biomaterials [18, 19]. Fast, high-resolution imaging options have been developed in recent years to improve upon force mapping [20–23]. These techniques often capitalize on phase changes in the cantilever deflection signal to determine the relative mechanical properties of a sample. Unfortunately, extensive modeling that takes into account tip-sample interactions is often necessary to interpret the measurements [24]. While most commercial AFM setups have the capability to perform these approaches, it is unclear whether they all can be used successfully for testing soft materials in physiological, fluid environments. Furthermore, the complexity of these techniques limits their large-scale adoption in the biological sciences.

The objective of this study was to develop a force scanning technique using AFM to rapidly capture high-resolution topographical images of soft biological materials while simultaneously quantifying their mechanical properties. Prior property mapping approaches have either lacked spatial resolution, required long testing times, were restricted to certain materials or testing environments, needed specialized equipment, or resulted in non-quantitative results. Our proposed technique is intended as an easy to understand approach for general use in biological applications. To achieve our goal, we first validated the high-resolution force scanning technique for its ability to accurately measure the spatial distribution and mechanical properties of an agarose gel. The mapping technique was subsequently applied to samples of biological relevance, illustrating an ability to measure the elastic properties of individual living cells, cell-cell interactions, and the extracellular matrix of murine articular cartilage.

2. Materials and Methods

2.1. Mechanical characterization via AFM

Surface images and force measurements were collected using an atomic force microscope (MFP-3D-BIO, Asylum Research, Santa Barbara, CA). To facilitate conformal contact, borosilicate glass spheres (5 μm diameter) were attached to the tip of AFM cantilevers (Novascan Technologies, Inc., Ames, IA). Cantilever spring constants (typically 0.03 N/m for cell and agarose experiments, 4.5 N/m for cartilage matrix experiments) were determined from the power spectral density of the thermal noise fluctuations [25] prior to experimentation. Multiple testing sessions were conducted for the various samples to account for systematic errors. Force vs. indentation data were analyzed using custom MATLAB scripts (The MathWorks, Natick, MA) utilizing the Hertz contact model. All experiments were carried out at room temperature in fluid environments. The AFM was allowed to equilibrate before tests to minimize deflection laser and/or piezo drift.

2.1.1. Force mapping

Spatial modulus maps were collected for a variety of samples using the previously established force mapping technique [2, 19]. In brief, individual force curves were taken at discrete points across a region of interest. During analysis, the spatial arrangement of the data was retained to create a matrix of elastic modulus values that could be overlaid onto a height image. Force-indentation data were sampled at 5 kHz with an approach velocity of 15 μm/s. Region size, force trigger, and resolution were varied based on sample type and experimental goal, and as such, these parameters are stated explicitly within each section. Region size typically ranged from 20 to 90 μm, force trigger from 0.5 nN to 500 nN, and resolution from 4×4 pts to 40×40 pts. In addition to elastic modulus values, these experiments were evaluated for time to completion, accuracy of fits, and quality of image.

2.1.2. Force scanning

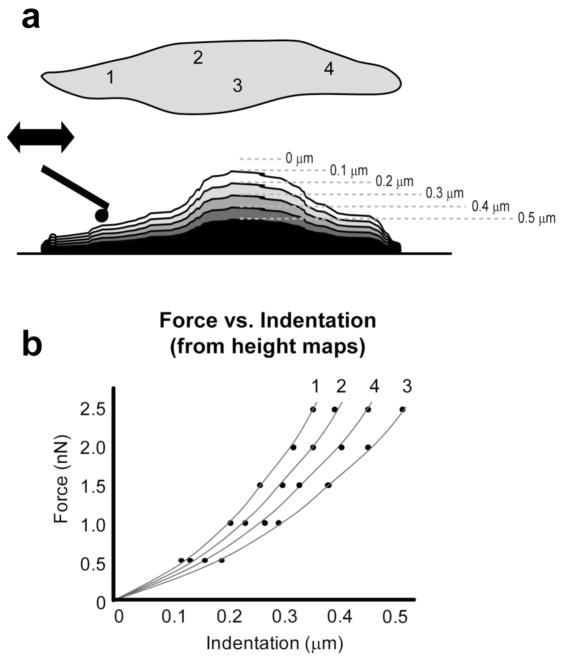
Spatial modulus maps were also created using a novel force scanning approach. In its most basic sense, the AFM functions by raster scanning a flexible cantilever across a surface to capture topographical features. By applying a downward force (setpoint), the cantilever tip presses into the sample material, effectively indenting it while tracing a faithful representation of the surface. For the force scanning technique, a consecutive series of contact mode surface scans were taken using incrementally greater setpoint forces. The number of scans and maximum force varied by sample but typically 5–7 scans were used for each test (setpoints: 4 – 12 nN for agarose, 0.5 – 4.5 nN for cells, 150 – 500 nN for cartilage). Cantilever deflection and depth of indentation were dependent on the relative stiffness of the cantilever and sample. Therefore, setpoints were determined prior to force scanning experiments using single indentation curves on each sample to be tested. These curves were used to define upper and lower force limits that would result in physically appropriate deformations. For example, a setpoint of 0.1 nN used on a cell might not produce a consistent measure of cantilever deflection, while a setpoint of 5 nN might result in too large of compressive strain, violating the limits of the mathematical model. Best spatial mapping results were achieved when surface images were clear and sharp with minimal smearing or loss of surface contact. Data collected during scans included height (z-piezo position), normal deflection, and lateral deflection, all of which were used to calculate the applied force and indentation into the sample. For analysis, a combination of trace and retrace channel data was used to more accurately define surface topography by selecting for the minimal height value between the two channels. Since each consecutive height scan was taken with a different setpoint force, the resulting data could be transformed into a spatial map of low resolution force-indentation curves using a custom MATLAB script (figure 1).

Figure 1.

For the force scanning technique, multiple contact-mode images were taken at incrementally greater setpoint forces (i.e. 0.5, 1, 1.5, 2, 2.5 nN). Topographical height data were converted into “indentations” for each data point on the sample surface (a). In this example, four locations were identified by number, but typical analyses include 4,000 to 65,000 distinct locations. These force-indentation curves (b) were used to calculate elastic moduli at each point. This method quickly provided high-resolution images with spatially matched modulus values. Measured mechanical properties for agarose, single cells, and cartilage were all comparable to previously reported values.

In brief, for each topographical image, the z-piezo value of a single point was combined into an array that defined that location’s indentation values. Corresponding force values were calculated using the setpoint force for the corresponding topographical image. For example, a surface might be scanned using four setpoint forces (e.g. 0.5, 1, 1.5, 2 nN) which produce four topographical images defined by a set of z-piezo values distributed across a region of interest:

$$\left[\begin{array}{ccc}& F=0.5\text{nN}& \\ 45& \cdots & 37\\ ⋮& \ddots & ⋮\\ 44& \cdots & 40\end{array}\right]\left[\begin{array}{ccc}& F=1\text{nN}& \\ 43& \cdots & 36\\ ⋮& \ddots & ⋮\\ 42& \cdots & 39\end{array}\right]\left[\begin{array}{ccc}& F=1.5\text{nN}& \\ 40& \cdots & 34\\ ⋮& \ddots & ⋮\\ 39& \cdots & 38\end{array}\right]\left[\begin{array}{ccc}& F=2\text{nN}& \\ 35& \cdots & 32\\ ⋮& \ddots & ⋮\\ 36& \cdots & 37\end{array}\right]$$

These data are then converted into force-indentation data by combining all z-piezo values from the same location into a single, height array:

$$\left[\begin{array}{c}\mathit{Force}\mathit{Array}\\ 0.5\\ 1\\ 1.5\\ 2\end{array}\right]\left[\begin{array}{c}\mathit{Point}(1,1)\\ 45\\ 43\\ 40\\ 35\end{array}\right]\left[\begin{array}{c}\mathit{Point}(1,\dots Y)\\ 37\\ 36\\ 34\\ 32\end{array}\right]\left[\begin{array}{c}\mathit{Point}(\dots X,1)\\ 44\\ 42\\ 39\\ 36\end{array}\right]\left[\begin{array}{c}\mathit{Point}(\dots X,\dots Y)\\ 40\\ 39\\ 38\\ 37\end{array}\right]$$

To define actual indentation changes, the height values in each array are subtracted from an arbitrary contact-point height (e.g. 50), which does not affect computation of the final Young’s modulus values:

$$\left[\begin{array}{c}\mathit{Force}\mathit{Array}\\ 0.5\\ 1\\ 1.5\\ 2\end{array}\right]\left[\begin{array}{c}\mathit{Point}(1,1)\\ 5\\ 7\\ 10\\ 15\end{array}\right]\left[\begin{array}{c}\mathit{Point}(1,Y)\\ 3\\ 4\\ 6\\ 8\end{array}\right]\left[\begin{array}{c}\mathit{Point}(X,1)\\ 6\\ 8\\ 11\\ 14\end{array}\right]\left[\begin{array}{c}\mathit{Point}(X,Y)\\ 10\\ 11\\ 12\\ 13\end{array}\right]$$

The slope of the force-indentation curves for each point is then fit with a linearized Hertz model to determine an elastic modulus corresponding to spatial locations in the height image. Providing quantitative values for the mechanical properties is an important advantage over previous attempts [1]. Linear corrections were made for AFM laser and piezo drift, if present. Contributions from lateral forces were also incorporated into the data analysis, although results indicated these were minor (~1%) compared to applied forces in the normal direction. For some samples, regions not of interest were removed using height and/or force thresholding (i.e. glass substrate around cells). Force scanning experiments were evaluated for their ability to produce high-resolution mechanical property maps in addition to other parameters like quality of fit and total testing time.

2.2. Data analysis and evaluation

As mentioned previously, data collected during repeated indentations, force mapping, and force scanning techniques were analyzed using custom MATLAB scripts. For all approaches, elastic moduli were determined by fitting a linearized Hertz model to force-indentation curves [26]. This method does not require knowledge of the contact point, since modulus values are calculated directly from the slope of the linearized force-indentation curves (see supplemental materials of [26] for derivation):

$$F^{2/3}={\left[\frac{4{ER}^{1/2}}{3(1-{\nu }^2)}\right]}^{2/3}\mathrm{\Delta }+C^{\ast }$$ (1)

where F is force, E is Young’s modulus, R is effective indenter radius, ν is Poisson’s ratio, Δ is the difference between piezo movement and cantilever deflection, arbitrary of the contact point, and C^* is the y-intercept. When presented in this manner, the Young’s modulus is directly related to the slope:

$$E=\left[\frac{3(1-{\nu }^2)}{4R^{1/2}}\right]{\mathit{Slope}}^{3/2}.$$ (2)

Data generated by the force scanning technique only includes points within the indentation phase of the curve, so methodologies requiring a priori knowledge of the contact point, like the commonly used Oliver and Pharr method [27], would be problematic to implement. Since the compressive, elastic modulus was of primary interest to the current study, all analyses focused on the indentation phase, rather than the retraction phase, of the force-indentation curve. Custom MATLAB scripts allowed rapid assessment of collected data, which for some cases included over 65,000 curves for a single sample (256×256 force scan). In brief, the scripts converted raw cantilever deflection and z-piezo movement data into two arrays: force and indentation. The Young’s modulus was calculated for each curve using Eqn. 2, and values were mapped to corresponding topographical points. The Poisson’s ratio (ν) was assumed to be 0.04 for articular cartilage tissue, determined by previous studies [28, 29], and 0.5 for agarose gels and cells. Parametric studies showed that varying ν from 0.3 to 0.5 altered the measured properties by less than 20%. If desired, a “reduced modulus”, E* = E/(1 − ν²), can be calculated by dividing the reported values by (1 − ν²).

Results from the MATLAB programs were output in multiple formats, including numerical matrices, property arrays, means and standard deviations, and three-dimensional images. Spatial modulus maps were created by overlaying topographical surface images with heat maps representing point-specific elastic moduli. These results emphasized the similarities and differences between force mapping and force scanning techniques and highlighted possible sources of errors during analysis (i.e. high strains in lamellipodial regions could artificially increase measured moduli values).

2.5. Sample preparation and testing

To validate the force scanning technique and illustrate its versatility, we conducted experiments for three distinct samples: agarose hydrogels, cells in monolayer, and articular cartilage tissue. All samples were tested in physiologically appropriate, fluid environments.

2.5.1. Agarose gels

Validation experiments were conducted on 2% (wt/vol) agarose gels (Fisher Scientific, Pittsburgh, PA) to determine the accuracy and consistency of force scanning, force mapping, and single indentation techniques (table 1). To better understand how velocity, force, and cycle number influenced measured mechanical properties, a series of repeated indentations was applied at a single point on the gel. Ten indentation curves were taken for each velocity (0.5, 2, 5, 10, 15, 25, 35, 50, 75, and 100 μm/s) and force (2.7, 8.0, and 13.4 nN) condition, with the resulting elastic modulus values being analyzed for trends or anomalies. Following these control experiments, force mapping (4×4 pts) was conducted three times in succession across a 20×20 μm test region using three different force triggers (1.3, 5.4, and 10.7 nN). These tests aimed to assess load-dependency and reproducibility for the widely used force mapping technique. Lastly, force scanning experiments (64×64 pts) were conducted across the same region as the force mapping tests (20×20 μm). Three consecutive runs were made for each of three different scanning rates (3, 4, and 5 Hz). Similar to the force mapping analysis, these tests aimed to determine any scanning rate dependency as well as the overall consistency of the force scanning technique. All experiments were conducted at room temperature in distilled water using a spherically tipped, soft (k ~ 0.03 N/m) AFM cantilever.

Table 1.

Testing parameters for comparison of force mapping, force scanning, and repeated indentation techniques on 2% agarose gels.

	Approach velocity (μm/s)	Scan rate (Hz)	Maximum force (nN)	Region size (μm × μm)	Scan resolution (rows × columns)
Force mapping	10	N/A	1.3, 5.4, 10.7	40×40	4×4
Force scanning	N/A	3, 4, 5	12	40×40	64×64
Repeated indentations	0.5, 2, 5, 10, 15, 25, 35, 50, 75, 100	N/A	2.7, 8.0, 13.4	N/A	N/A

2.5.2. Single cell imaging

Individual cells were assessed for their mechanical properties in relationship to their subcellular contents. Two cell types were examined: NIH3T3 fibroblasts (ATCC, Manassas, VA) and adipose-derived stem cells (ASCs, ZenBio Inc., Research Triangle Park, NC). ASCs were grown in expansion media containing DMEM/F12 (Gibco, Carlsbad, CA), 10% FBS (ZenBio), 1% penicillin-streptomycin-fungizone (Gibco), 0.25 ng/ml transforming growth factor-β1 (R&D Systems, Minneapolis, MN), 5 ng/ml epidermal growth factor (Roche Diagnostics, Indianapolis, IN), and 1 ng/ml basic fibroblast growth factor (Roche Diagnostics) as described previously [30]. NIH3T3 cells were grown in DMEM, 10% FBS, and 1% penicillin-streptomycin-fungizone. Prior to testing, cells were seeded onto glass coverslips and allowed to attach and spread overnight. Both force mapping and force scanning techniques were used on healthy, living cells, which resulted in elastic moduli distributions that corresponded to spatial markers. Of particular interest was how increased resolution affected the measured mechanical properties at points across the surface of a cell. While most runs were conducted on whole cells or portions of individual cells, feasibility tests were also carried out for assessing the mechanical properties present at cell-cell interfaces. All tests were done at room temperature in culture media using a spherically tipped, soft (k~0.03 N/m) AFM cantilever.

2.5.3. Articular cartilage

In addition to biomaterials and cells, the force scanning technique was evaluated for use in quantitatively assessing the mechanical properties of biological tissues. Articular cartilage was harvested from the femoral heads of 2-wk old, C57BL/6 mice and subsequently sectioned using a cryostat to expose the extracellular (ECM) and pericellular (PCM) matrices for mechanical testing [19]. The cartilage slices were placed on negatively charged glass slides and rinsed thoroughly with PBS containing protease inhibitors to remove the water soluble embedding medium and cellular fragments. As with the cell samples, both force mapping and force scanning techniques were assessed for their abilities to determine the spatial mechanical properties of a biological tissue. During data analysis, a Poisson’s ratio of 0.04 was used for both ECM and PCM based on previously published findings for articular cartilage [28, 29].

2.6. Statistical analyses

Regression analyses were used to determine whether cycle number significantly affected the measured mechanical properties of single-point, iterative mechanical tests. One-factor ANOVA with Fisher’s LSD post hoc analysis was performed to determine whether significant differences (α = 0.05) in elastic moduli existed for force, velocity, and iteration (single indentations), force and iteration (force mapping), and scan rate and iteration (force scanning). Additionally, comparisons between force mapping and force scanning properties were assessed quantitatively using a Student’s t-test for agarose and cartilage samples and qualitatively using spatial stiffness maps for cell samples. All data are presented as mean ± standard deviation.

3. Results and Discussion

3.1. Agarose gel validation

Single indentations, force mapping, and force scanning tests on 2% agarose gels resulted in similar average elastic moduli (18.7 ± 2.6 kPa, 17.2 ± 6.1 kPa, and 19.3 ± 0.9 kPa, respectively), which are in agreement with previously published findings [15, 17, 31]. The Hertz model for elastic deformation fit force vs. indentation data well for all tests (single indentations, R² = 0.9587; force mapping, R² = 0.8388; force scanning, R² = 0.9987). Experiments on agarose gels provided a uniform surface that allowed comparison across methodologies.

3.1.1. Repeated indentations

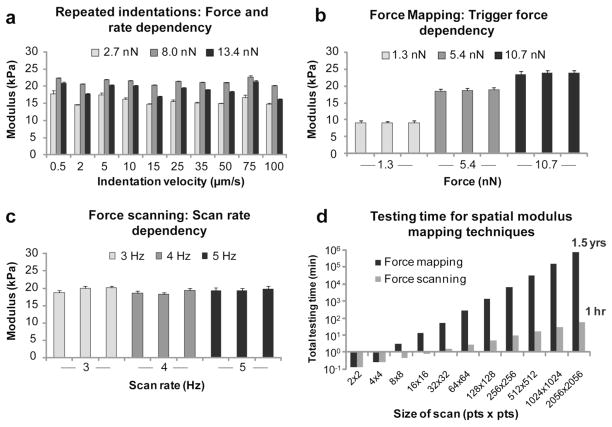
Single indentation tests showed that the maximum force applied during indentation influenced the measured elastic modulus, whereas indentation velocity did not (figure 2a). Repeated indentations at the same site had an average test-to-test error of 1.3%, with more error associated with a trigger force of 2.7 nN (2.7%) than either an 8.0 nN (0.7%) or 13.4 nN (0.8%) trigger force. The applied force dependency was expected since agarose is not purely an elastic material. The viscoelastic characteristics of the gel influenced the measured moduli values, since larger applied forces had the result of indenting deeper into the material, encountering a larger contribution from fluid pressurization. The elastic measurements were generally consistent, though, even across force trigger and indentation velocity values.

Figure 2.

AFM-based mechanical testing was evaluated on 2% agarose gels using repeated indentations, force mapping, and force scanning techniques. All methods provided similar elastic moduli values with excellent run-to-run consistency. Individual, repeated indentations showed no dependency on trigger force or indentation rate (a). Force mapping provided spatial mechanical property information but exhibited a dependency on trigger force, with larger forces/indentations resulting in higher measured moduli (b). Force scanning also provided spatial property mapping and was influenced by maximal applied force (data not shown) but showed no dependency on scanning rate (c). Based on temporal trends observed during testing, very high-resolution images could only be achieved using force scanning within a reasonable time frame (d).

3.1.2. Force mapping

Force mapping results showed a strong dependency on the maximum applied force during testing (p<0.0001), with higher forces producing higher elastic moduli (figure 2b). No significant differences were observed among consecutive test runs at each force trigger (p=0.31). Point-by-point analysis for force mapping tests showed good consistency with an average error of 1.1%. As with the repeated indentation tests, force dependency was expected due to the viscoelastic characteristics of agarose gels. However, the measured elastic moduli fell within an acceptable range and were consistent with previously published values [31].

3.1.3. Force scanning

Force scanning on agarose gels produced clear topographical images with spatially matched elastic moduli values that were comparable to other testing methods. Due to the large number of data points taken for each test (64×64 = 4096), all scan rate and iteration comparisons were statistically significant (p<0.0001). However, the magnitude of the differences among all runs was minor (~2.5%) in comparison to the overall elastic modulus of the gel (figure 2c). Unlike force mapping, no major dependency was observed for testing parameters like scan rate and resolution (data not shown). Maximal applied force could still influence elastic modulus values, but this effect could easily be corrected by excluding higher-force scans during analysis. Point-by-point accuracy for force scanning was similar for the 3 and 4 Hz scan rates (2.5% variation) and slightly higher for 5 Hz scan rates (7.7% variation). This finding was expected since the quality of surface imaging in contact-mode is dependent on scan rate, setpoint force, and feedback gain values. Raising the scan rate too high resulted in loss of contact for regions with sharp height changes. If neither the trace nor retrace curves were contacting the surface, this would translate into an erroneous indentation depth during analysis. Lower scan rates (i.e. 2 or 3 Hz) resulted in the best combination of speed and tracing fidelity.

3.2. Force scanning vs. force mapping

A direct comparison of point-specific moduli was difficult to achieve, especially since the actual “indentation” for the two methods was dissimilar. Force mapping involved actual indentations as described by the Hertz model, whereas force scanning “constructed” force-indentation curves under the assumption that similar physical deformations in the z-direction occurred at discrete points. Interestingly, the elastic moduli measured using the force scanning technique were comparable to those measured using the force mapping technique, regardless of sample type. These values correlated with spatial markers across the sample surface, which supports the assertion that force scanning is a reliable method for measuring elastic properties. One explanation for the high-quality fits observed with force scanning data is that contact time at each point is extremely short. This does not allow for relaxation of the surrounding material and effectively produces a snapshot of indentation at a given depth. The deformation geometry is still that of a sphere indenting a flat surface, so the Hertz model accurately represents the collected data.

The major strengths of force scanning are its speed and simplicity. While both testing methods are theoretically capable of producing high-resolution images, force mapping requires individual force curves to be taken at each point, resulting in exponentially longer testing times than force scanning (figure 2d). Strikingly, a 2056×2056 scan would take approximately an hour using force scanning but almost a year and a half with standard force mapping. Testing time is critically important for many situations, particularly for single-cell experiments of living, motile samples. Force scanning is quick enough that a series of images can be taken before significant changes occur. This is often infeasible with force mapping unless very low resolution tests are used. The simplicity of force scanning allows it to be implemented with any scanning force microscope, as well as any cantilever type. No additional hardware is necessary, and a variety of cantilever compliances and shapes can be used to equal effectiveness. Limitations are similar to those that exist for contact-mode imaging. Samples with large height changes or non-accessible features cannot be accurately tested. Additionally, property artifacts can occur for specimens that move during imaging (see supplementary figure 2).

3.3. Cellular and subcellular modulus mapping

3.3.1. Single-cell imaging

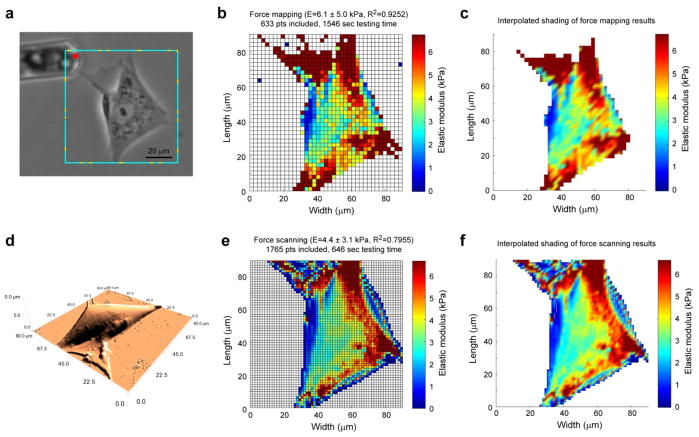
The simplest approach to using force scanning on living cells was to image an entire cell adhered to a rigid substrate (figure 3). Individual cells were imaged using either force mapping or force scanning techniques over a predefined area. Contract-mode imaging resulted in high-resolution surface features, even when using a 5 μm, spherically tipped cantilever at a 0.5 Hz scan rate. Comparisons between force mapping and force scanning techniques showed good similarity between the locations of high- or low-modulus areas. However, the increased resolution possible with force scanning allowed better identification of subcellular structures present underneath the cell membrane. Cell nuclei were clearly defined and typically exhibited a lower modulus than other regions of the cell. Stress fiber distributions could be identified in the perinuclear regions of the cell, and lamellipodial extensions could be tentatively assessed for their compressive stiffness. It is important to note that strains calculated for these thin regions can exceed the limitations in the Hertz model if too high of a setpoint force is used. In these cases a contribution from the underlying rigid substrate might exist (see supplementary figure 1). Future iterations of the force scanning technique will incorporate a correction factor to account for this contribution [31]. A small increase in resolution (40×40 pts to 64×64 pts) resulted in much better imaging results for single cells, as evidenced by switching from force mapping to force scanning (figure 3c, e). Concomitant with this improvement was a reduction in testing time by approximately 40%. High-resolution depictions of three-dimensional cells were created by overlaying mechanical property maps onto AFM height data (figure 4). Both testing time and resolution are critical for quantitative assessment of living cells since movement can occur on the order of seconds to minutes for many cell types (see supplementary figure 2). Since high-resolution force mapping is incapable of collecting data this quickly, an alternative spatial imaging technique such as force scanning is needed.

Figure 3.

Spatial modulus mapping of spread cells. A representative ASC (a) was imaged using contact-mode AFM (d) and then mechanically tested using a 40×40 pt force map (b, c) and a 64×64 pt force scan (e, f). Images from the more rapid, higher-resolution force scanning technique could depict the underlying cytoskeletal structure in greater detail in a shorter time. The force mapping images shown above took 2.4 times longer to capture than the force scanning images (25.8 vs. 10.8 minutes).

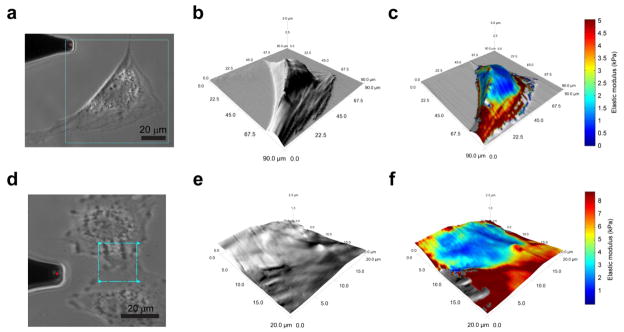
Figure 4.

High-resolution elastic modulus mapping of cells. AFM height images were overlaid with elastic modulus maps to determine localized mechanical properties for single cells and cell-cell interfaces. These 128×128 pt. scans were collected within six minutes using a scan rate of 2 Hz and demonstrate the possible applications of the force scanning technique. The single ASC exhibited lower moduli (0.5–1 kPa) over the nucleus and perinuclear region and higher moduli near its edges (3–10 kPa) (a–c). The interface between two NIH3T3 fibroblasts is difficult to discern using either phase contrast microscopy (d) or AFM height images (e). However, by mapping mechanical properties to the height image, a clearer distinction between the cells can be detected (f). In this case, the filopodia of adjacent cells exhibited variable elastic moduli depending on their immediate, underlying material (i.e. glass, 6–10 kPa or cell, 3–4 kPa).

3.3.2. Cell-cell interfaces

Another interesting application of the force scanning technique is assessing the mechanical property distribution present at cell-cell interfaces. Filopodial extensions from one cell can interact with another cell at relatively fast rates. Capturing three-dimensional images of these structures coupled with their elastic moduli can provide valuable information on the mechanical properties present when cells interact. Feasibility studies indicated that a cell’s filopodial modulus decreased when moving on top of another cell (figure 4d–f). We hypothesize that the cytoskeletal structure within the filopodia is driving the measured mechanical properties. Formation of F-actin bundles “stiffens” a cell, but without a strong binding site, these structures cannot form, which helps explain the current results. The upper filopodial projection has no means of forming focal adhesions with the glass substrate, except where it is not overlapping the lower cell. In the non-overlapping regions, a higher modulus is measured, similar to values exhibited by the lower cell, which has no impediments to forming focal adhesions. Coupling the force scanning technique with optical imaging of fluorescently labeled cytoskeletal structures could help define these interactions and will be implemented in future studies.

3.4. Biomaterial and tissue modulus mapping

The mechanical properties of biological materials are often difficult to assess using scanning force microscopes. These materials are typically soft, exhibit viscoelastic characteristics, and require a fluid environment during testing. This is non-ideal for many previously developed stiffness mapping techniques. In the current study, articular cartilage from mouse femoral heads was tested using the force scanning technique (figure 5). As with agarose gels and single cells, measured elastic moduli for cartilage samples were comparable to force mapping results (134 ± 28 kPa vs. 119 ± 24 kPa, respectively).

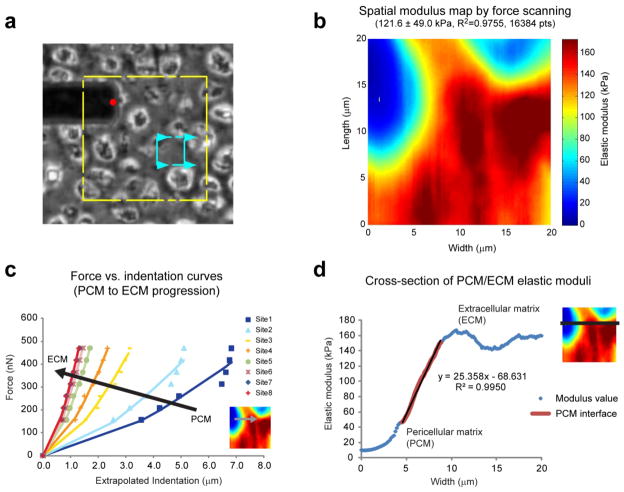
Figure 5.

Cartilage matrix properties. The spatial distribution of elastic moduli in sectioned mouse cartilage was rapidly assessed using the force scanning technique at 3 Hz. Phase contrast images were used to identify regions of interest (a, yellow box depicts maximum scan area, blue box depicts sample region). Force scanning produced high-resolution, modulus maps that highlighted the mechanical differences between extracellular and pericellular matrices (b). The increased resolution allows detailed assessment of the extracellular-pericellular matrix interface. A series of individual, force-indentation curves illustrates the increase in stiffness from PCM to ECM (c). These plots also show that if too large a force is used, the underlying material (i.e. ECM) will contribute to the measured modulus. Cross-sectional examination of elastic moduli showed a linear increase of 25 kPa/μm through the pericellular matrix region (d).

Articular cartilage exhibits a zonal structure from its surface to the subchondral bone, as well as a regional structure extending outward from each sparsely distributed cell [32]. The tissue is primarily fluid, with its solid fraction being composed of collagen II and proteoglycans. Extracellular matrix dominates the overall structure of articular cartilage and comprises the bulk of the tissue. However, immediately surrounding each chondrocyte is a special type of tissue termed the pericellular matrix. This material is hypothesized to transduce external forces propagating through cartilage so that resident chondrocytes experience appropriate strains [28]. Understanding the mechanical transition from extracellular matrix to pericellular matrix to chondrocyte can help elucidate mechanotransduction for both healthy and diseased/damaged tissue.

Experimental results showed a clear transition from the extracellular region through the pericellular region to where the chondrocyte would be in intact cartilage (figure 5b, c). The gradual change in mechanical properties effectively minimizes interfacial shearing that otherwise might occur in the regional structure of the matrices. Articular chondrocytes exhibit elastic moduli of ~1 kPa [33]. Without a transducing region, the stiff extracellular matrix would completely shield the cells from strains in the tissue. Experimental results indicated the extracellular regions of immature mouse cartilage had moduli of ~200 kPa, while the innermost pericellular regions had moduli of ~10 kPa (see supplementary figure 3 for moduli distribution). Cross-sectional analysis of the interfacial region showed a 25 kPa/μm slope, with more gradual changes in modulus occurring at either end (figure 5d). Future work will investigate whether this transition is consistent across donors and age groups for healthy and damaged cartilage. Mechanical property measurements are comparable to previous findings for mouse cartilage of the same age and location [19]. Discrepancies do exist in the literature, however, with several groups reporting much higher modulus values for articular cartilage [17, 34]. Possible reasons for these differences are animal age, freezing effects on the tissue, and analysis method. In the present study, mouse cartilage was only two weeks old, whereas other published reports typically used more mature tissue. Past studies show that cartilage stiffness can vary significantly with age and joint location [35]. Likewise, the process of freeze-thawing tissues can affect measured stiffness values by disrupting the microstructure in the specimen. Analysis method could also be a contributing source of discrepancy. This study used a linearized Hertz model to extract modulus values from the indentation portion of the data. Another common approach is to use the Oliver and Pharr method [27], which fits a similar geometrical model of indentation, but targets the retraction portion of the data. This method has been used extensively for mechanical characterization of metals and films that exhibit elastic-plastic deformation [36]. Since the current study focuses on the compressive properties of soft biomaterials, cells, and tissues that exhibit minimal plastic deformation, the Oliver and Pharr approach is non-ideal. Furthermore, its implementation with force scanning data is problematic since a full indentation-retraction curve is never actually recorded and a contact point never exists.

4. Conclusion

This novel force scanning method allows rapid assessment of the mechanical properties of any material that can be imaged using AFM. The technique is broadly applicable to stiff and soft samples, fluid or air environments, and can be implemented on any atomic force microscope without need for additional hardware. Force scanning is especially useful for biological samples that are otherwise difficult to assess mechanically using traditional means, either because the sample is too soft or moves during imaging. Limitations do exist, but are similar to those present when running simple, contact-mode images. In comparison to force mapping, force scanning has higher spatial resolution and shorter testing times. These benefits are achieved through a reduction in force curve resolution. However, for the presented examples, high force resolution does not appear to be necessary to accurately describe mechanical properties. The current results demonstrated the suitability of force scanning for studying basic materials, living cells, and structured tissues. While this work was limited to topographical and elastic modulus data, future extensions to the technique could include functionalizing the cantilever tip for quantifying spatial adhesion forces or extracting the frictional properties of the sample using lateral force data. Force scanning is a useful technique for rapidly assessing the mechanical properties of a biological sample via AFM and can be adopted for a variety of fields using existing technology.

Supplementary Material

Supplemental Figure 1. Estimated compressive strains were calculated across a sample cell. The height of each point on the cell was determined by AFM topographical data. Probe-cell contact points were extrapolated by extending fits to the linearized Hertz model through the x-axis. These estimated contact points provided gross height and indentation measurements that could be used to calculate local compressive strains. As predicted, higher strains are observed for the outer regions of the cell where it is thinnest (A). If a thin-layer correction factor is used that accounts for the underlying rigid substrate [1], then the resulting modulus map exhibits much lower values for the peripheral regions of the cell (B vs. C). Future work will incorporate thin-layer modeling into the full analysis rather than using an a priori correction. It should be noted that the general trends observed without correction still exist: cytoskeletal elements have higher moduli than cytoplasmic and nuclear regions. This finding has been observed for other cell types, including fibroblasts [2], astrocytes [3], and kidney cells [4].

Supplemental Figure 2. Force scanning with a pyramidal tip showed a detailed mechanical property map for two touching ASCs (a, yellow box depicts maximum scan area, blue box depicts sample region). Assuming the pyramid-modified Hertz model holds for a sharp tip indenter during force scanning, this approach could help decrease convolution effects while increasing resolution. However, this image emphasizes the difficulty in capturing accurate representations of living cells. Movement of cell filopodia is revealed by discrepancies between the height image (b) and modulus map (c). The trade-off between testing duration and image quality is a common concern when imaging living samples.

Supplementary Figure 3: Force-indentation curves (Force^2/3 vs. Delta) were generated for every point across the cartilage ECM-PCM region shown in Figure 5. The force scanning data (a) show 16,384 curves (128 × 128 pts), while the force mapping data (b) show 100 curves (10 × 10 pts). The slope of each individual curve defines the Young’s modulus for that point. For presentation purposes, the contact point was also extrapolated from the slope of the data. If discontinuities existed, such as for the right-most points in (a), the total indentation distance could be incorrectly estimated (i.e. 6 μm of indentation instead of 1–2 μm). Fortunately, the calculated modulus values do not depend on this extrapolated contact point, so the error is contained only to graphical aberrations as seen in the data above. Histograms depicting the frequency of Young’s modulus values across the sample regions are shown for force scanning (c) and force mapping (d). The large peaks on the right represent the stiffer ECM regions, which comprise the majority of the area tested, and hence, greater frequencies. The low stiffness peak represents the inner portion of the PCM, while the transition region between PCM-ECM is represented by the range of middle-stiffness values.