An Extension of SIC Predictions to the Wiener Coactive Model

Abstract

The survivor interaction contrasts (SIC) is a powerful measure for distinguishing among candidate models of human information processing. One class of models to which SIC analysis can apply are the coactive, or channel summation, models of human information processing. In general, parametric forms of coactive models assume that responses are made based on the first passage time across a fixed threshold of a sum of stochastic processes. Previous work has shown that that the SIC for a coactive model based on the sum of Poisson processes has a distinctive down-up-down form, with an early negative region that is smaller than the later positive region. In this note, we demonstrate that a coactive process based on the sum of two Wiener processes has the same SIC form.

1. Introduction

One of the fundamental goals in modeling cognitive processing is determining how multiple sources of information are processed together. One major component of this determination is the distinction between parallel processing, in which sources are processed simultaneously, and serial processing, in which the sources are processed one at a time (e.g., Sternberg, 1966; Townsend, 1974). A special case of parallel processing is of particular interest to psychologists, coactive processing, in which information is accumulated in parallel, then pooled (Bernstein, 1970; Miller, 1982; Townsend & Ashby, 1983; Grice et al., 1984; Schwarz, 1989, 1994). Distinguishing among these processing types based on observable data can be difficult. However, under certain conditions, the Survivor Interaction Contrast (SIC) predicted by each processing type are distinct (Townsend & Nozawa, 1995). SIC predictions for independent serial and parallel systems are based on very general theorems, however the SIC prediction for the coactive model is specific to a Poisson accumulator model. In this paper we show that the predicted SIC for coactive models given by the sum of two Wiener processes is qualitatively the same as the predicted SIC of the Poisson coactive model. By demonstrating that the same SIC form is predicted by a coactive model based on a different stochastic process, we hope to add credence to the claim that this SIC is a signature of coactive processing in general.

Coactive processing models are generally used to describe systems in which information is gathered from multiple sources in parallel and is pooled toward a single decision. This type of model has been alternately described in the literature as ‘coactive,’ (Miller, 1982; Townsend & Ashby, 1983; Townsend & Nozawa, 1995)‘superposition’ (Schwarz, 1989, 1994) and ‘energy summation/integration’ (Bernstein, 1970; Nickerson, 1973). The key feature is that the summed activation level across sources is compared to a single threshold.

The coactive model is often used to model performance when there are multiple sources of information that contain redundant information about the appropriate response. Participants are normally faster and more accurate when there is redundant information than when an individual source is presented (e.g., Hershenson, 1962; Kinchla, 1974). This phenomenon is known as the redundant target effect (e.g., Miller, 1982). As it turns out, a redundant targets effect is not necessarily enough to indicate coactive processing. Raab (1962) demonstrated that a redundant target effect can be produced by an independent, separate decision, parallel model due to statistical facilitation alone.¹ Essentially his argument was that the probability that either of two processes is finished is higher than the probability that one specific process has finished. Nonetheless, there are methods of ruling out statistical facilitation as an explanation of the redundant target effect.

Miller (1982) developed one method of ruling out statistical facilitation as an explanation for faster response times in a redundant target design. He showed that, under certain assumptions, a parallel, separate-decision model must have a smaller CDF of completion times in the redundant trials (F_AB(t)) than the sum of the CDFs of completion times in single target trials (F_A(t), F_B(t)),

$$F_{AB}\left(t\right)\le F_A\left(t\right)+F_B\left(t\right).$$ (1)

If Equation 1 is violated for some t, then this is taken as evidence of coactive processing (see Maris & Maris, 2003 for a statistical test). One issue with this test is that it conflates the workload capacity with architecture (e.g., Townsend & Wenger, 2004). For example, if there are more resources dedicated to processing A and B when they are presented together rather than apart, then even an independent parallel model of processing could predict violations of Equation 1. The applicability of the Miller inequality depends on the assumption of context invariance, i.e., the processing time of one source of information does not depend on the presence of another source of information.

To rule out an independent parallel model that may have more resources available when both sources are presented together, we can measure the SIC. The SIC is defined as the contrast between changes in processing speed of one source of information to changes in processing speed of the other source. Unlike the Miller inequality, this measure is based on equal processing loads for each component of the contrast. We use S(t) to denote the survivor function of a random variable and F(t) to denote the cumulative distribution function, i.e., S(t) = Pr{T > t} = 1 − Pr{T ≤ t} = 1 − F(t). The different distributions associated with the processing speeds are indicated by subscripts on S(t) and F(t), so for example the survivor function of response times when the first source is processed at high speed and the second source is processed at the lower speed is denoted by S_HL(t). Using this notation, the SIC is given by,

$$\begin{array}{cc}\hfill \mathrm{SIC}\left(t\right)& =\left[{\mathrm{S}}_{\mathrm{H}\mathrm{H}}\right(t)-{\mathrm{S}}_{\mathrm{H}\mathrm{L}}(t\left)\right]-\left[{\mathrm{S}}_{\mathrm{L}\mathrm{H}}\right(t)-{\mathrm{S}}_{\mathrm{L}\mathrm{L}}(t\left)\right]\hfill \\ \hfill & =\left[{\mathrm{F}}_{\mathrm{L}\mathrm{H}}\right(t)-{\mathrm{F}}_{\mathrm{L}\mathrm{L}}(t\left)\right]-\left[{\mathrm{F}}_{\mathrm{H}\mathrm{H}}\right(t)-{\mathrm{F}}_{\mathrm{H}\mathrm{L}}(t\left)\right].\hfill \end{array}$$ (2)

Data for the calculation of the SIC is often elicited within the double factorial paradigm. In this design two sources of information can independently be present or absent and, when present, can be independently presented at two levels of salience.² This gives four different redundant target conditions, one for each of the four high-low salience combinations on the two channels, which are used to calculate the SIC from Equation 2. By comparing the target present and absent conditions we can also test the Miller inequality and the capacity coefficient (Townsend & Nozawa, 1995; Townsend & Wenger, 2004). The capacity coefficient is another way to test for coactive processing (Townsend & Wenger, 2004) and is related to the Miller inequality (Townsend & Eidels, 2010).

Independent parallel models, like independent serial models, predict specific SIC forms depending on whether processing of one or both sources must be completed before a response is made. We refer to models of processing in which processing of only one source must be completed as first-terminating, or OR systems. We refer to models of processing in which processing of both sources must be completed as exhaustive, or AND systems.

The mean interaction contrast (MIC; Equation 3) is also important in distinguishing among certain processing types. With M indicating the mean response time and the subscripts as defined above, the MIC is given by,

$$\mathrm{MIC}=[{\mathrm{M}}_{\mathrm{H}\mathrm{H}}-{\mathrm{M}}_{\mathrm{H}\mathrm{L}}]-[{\mathrm{M}}_{\mathrm{L}\mathrm{H}}-{\mathrm{M}}_{\mathrm{L}\mathrm{L}}].$$ (3)

The MIC was originally used as a test of serial independent processing. Sternberg (1969) showed that, assuming selective influence of the salience manipulations, this type of processing would lead to MIC = 0. Schweickert & Townsend (1989) extended the use of the MIC by showing Parallel-AND models have a negative MIC. Townsend & Nozawa (1995) further extended these results to Parallel-OR processes and the Poisson coactive model which both predict MIC > 0. Note that, due to the linearity of the integral, the fact that response times are always positive, and the integral of the survivor function of a positive random variable is its expected value, the integrated SIC is equal to the MIC, i.e., ${\int }_0^{\infty }\mathrm{SIC}\left(t\right)dt=\mathrm{MIC}$.

The SIC and MIC predictions of the four standard models are shown in Figure 1. In the upper left panel the SIC for the Parallel-AND model is shown; it is always negative, so the MIC is also negative. The Serial-AND model prediction is shown in the upper right panel: first negative, then positive with equal positive and negative areas so the MIC is zero. On the bottom row the Parallel- and Serial-OR model predictions are shown. The Parallel-OR model is always positive with a positive MIC and the Serial-OR model SIC and MIC are zero.

Figure 1.

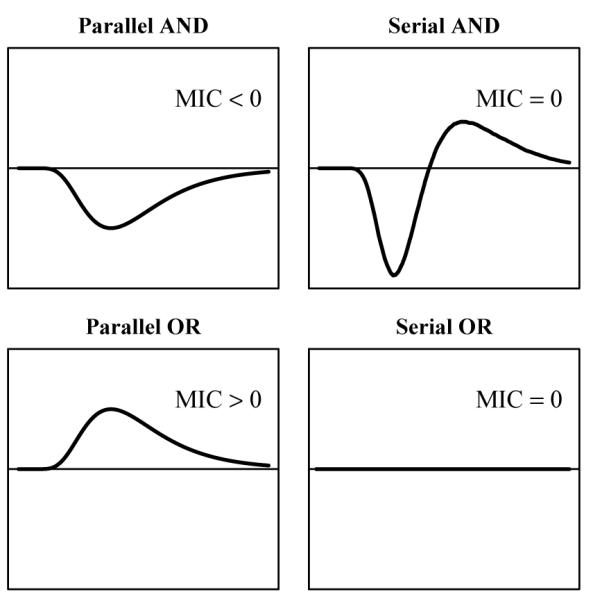
Predicted survivor interaction contrast forms for Parallel-AND (top-left), Serial-AND (top-right), Parallel-OR (bottom-left), and Serial-OR (bottom-right) processing models. In each graph, the relation between zero and the integrated SIC, or MIC, is indicated for that processing model.

In contrast, Townsend & Nozawa (1995) show that a specific case of the coactive model, based on the Poisson process (cf. Schwarz, 1989) predicts an SIC of the form depicted in Figure 2. In this case, the SIC is negative for early times, then positive for later times, much like the SIC for the Serial-AND model. The difference between this coactive SIC and the Serial-AND SIC is in the relative positive and negative areas under the SIC: the coactive SIC has more positive than negative area whereas the Serial-AND SIC has equal positive and negative areas. Thus, the integrated SIC, i.e., the MIC, can distinguish between these two models. Note that despite the similarities in the form of the SIC, the Serial-AND model is a very different process than a coactive process.

Figure 2.

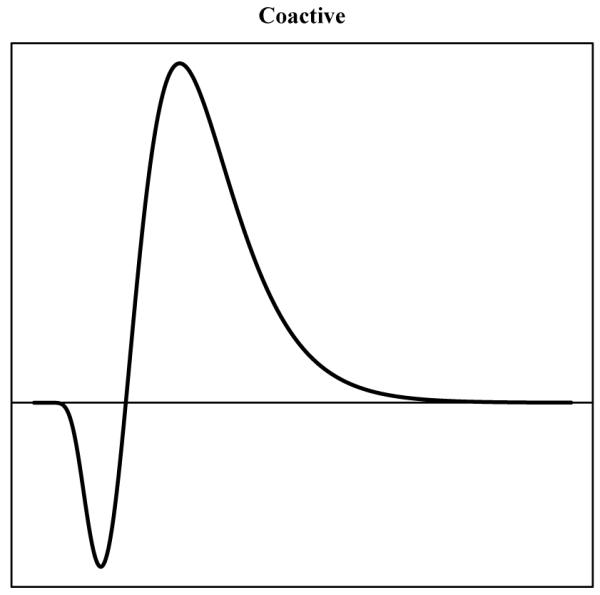
Predicted survivor interaction contrast form for Poisson and Wiener coactive models. As indicated in the figure, these models have a positive MIC.

Although these differences are qualitative, there are statistical tests available for determining if the collected data are enough to rule out any class of models. Houpt & Townsend (2010) show that a version of the Kolmogorov-Smirnov test can be used to check the positive and negative parts of an empirical SIC are significantly different from zero. This test is similar to the Maris & Maris (2003) test of the Miller inequality.

In the next section, we show that the distinguishing properties of the Poisson coactive SIC (down–up–down form and positive MIC) generalize to another class of coactive models, defined as the sum of two Wiener processes.

The Wiener process is formally defined as a stochastic process W(t) such that:

1. W (0) = 0,

2. {W (t), t ≥ 0} has stationary and independent increments,

3. for every t > 0, W (t) is normally distributed with mean 0 and variance t (Ross, 1996, pg. 357).

In contrast, a Poisson process, N(t), is defined by:

1. N(0) = 0,

2. {N(t), t ≥ 0} has stationary and independent increments,

3. the number of events in any interval of length t is Poisson distributed with mean λt (Ross, 1996, pg. 60).

Note that the Poisson process takes on discrete values while the Wiener process is real valued. Furthermore, the Poisson process can only increase as time increases, whereas the Wiener process increases and decreases.

2. Theory

The coactive model we consider here consists of two processing streams modeled by two (possibly dependent) Wiener processes which are summed together. In general each channel can have its own drift rate (ν₁; ν₂) and discusion coefficient (${\sigma }_1^2$; ${\sigma }_2^2$). Furthermore, the processes can have arbitrary correlation (q₁₂). Processing continues until the summed activation reaches a fixed, positive threshold (α). Note that this is the model of coactive processing proposed by Schwarz (1994).

Let {X₁(t), t ≥ 0} and {X₂(t), t ≥ 0} be the stochastic processes representing the processing state of channel 1 and 2 respectively. Then, if {W(t), t ≥ 0} is a standard Wiener process, i.e., with drift 0 and disscusion coefficient 1,³

$$X_1\left(t\right)\stackrel{\mathcal{D}}{=}{\nu }_{1}t+{\sigma }_{1}W\left(t\right)$$ (4)

$$X_2\left(t\right)\stackrel{\mathcal{D}}{=}{\nu }_{2}t+{\sigma }_{2}W\left(t\right).$$ (5)

The process of interest is the sum of the two individual channel processes,

$$\begin{array}{cc}\hfill X_{12}\left(t\right)& =X_1\left(t\right)+X_2\left(t\right)\hfill \\ \hfill & \stackrel{\mathcal{D}}{=}({\nu }_1+{\nu }_2)t+\sqrt{{\sigma }_1^2+{\sigma }_2^2+2q_{12}{\sigma }_a{\sigma }_b}W\left(t\right).\hfill \end{array}$$ (6)

This process is equal in distribution to a Wiener process with drift ν₁ + ν₂ and discusion coefficient ${\sigma }_{12}^2={\sigma }_1^2+{\sigma }_2^2+2q_{12}{\sigma }_a{\sigma }_b$. The first passage time of a Wiener process with positive drift has an inverse Gaussian distribution (Borodin & Salminen, 2002, pg. 295), i.e., with T₁₂ as the random variable for the completion time of the process,

$$T_{12}(\alpha ,{\nu }_1+{\nu }_2,{\sigma }_{12})=\inf \{0<t\mid X_{12}(t)=\alpha \}\sim \mathrm{IG}\left(\frac{\alpha }{{\nu }_1+{\nu }_2},\frac{{\alpha }^2}{{\sigma }_{12}^2}\right).$$ (7)

Therefore, with Φ(·) denoting the standard normal CDF, the CDF of the completion time is given by,

$${\mathrm{F}}_{12}(t;\alpha ,{\nu }_1+{\nu }_2,{\sigma }_{12}^2)=\Phi \left[\sqrt{\frac{{\alpha }^2}{t{\sigma }_{12}^2}}\left(\frac{({\nu }_1+{\nu }_2)t}{\alpha }-1\right)\right]+\exp \left(\frac{2({\nu }_1+{\nu }_2)\alpha }{{\sigma }_{12}^2}\right)\Phi \left[-\sqrt{\frac{{\alpha }^2}{t{\alpha }_{12}^2}}\left(\frac{({\nu }_1+{\nu }_2)t}{\alpha }+1\right)\right].$$ (8)

Within this distribution, neither the individual processing rates nor the individual discusion coefficients are identifiable. Although this is not the target of SIC analysis, there are other methods that may be more conducive to discovering the contribution of each of the underlying distributions. For example, along with the assumption of context invariance, examining each of the processes in isolation (e.g., Miller, 1982), or offsetting the presentation of the stimulus components (e.g., Schwarz, 1994).

We begin by demonstrating that the MIC is over-additive and hence the SIC will have larger positive area under the curve than negative area. We then demonstrate that the SIC is negative for small t and positive for large t. Finally, we show that there are only two t ∈ (0, ∞) such that the derivative of the SIC with respect to t is zero, and hence the curve only changes direction twice. These three properties are those described in Townsend & Nozawa (1995) and hence Wiener coactive model makes qualitatively equivalent SIC predictions to the Poisson coactive models.

2.1. Mean interaction contrast

The mean first passage time of a Wiener process is given by the mean of the inverse Gaussian distribution which, in the parameterization above, is simply the first parameter,

$$\mathrm{E}\left[T_{12}\right(\alpha ,{\nu }_1+{\nu }_2,{\sigma }_{12}\left)\right]=\frac{\alpha }{{\nu }_1+{\nu }_2}.$$ (9)

To determine the sign of the MIC, we examine the partial derivative of the expected completion time, first with respect to ν₁, then with respect to ν₂.⁴

$$\frac{{\partial }^2}{\partial {\nu }_1\partial {\nu }_2}\mathrm{E}=\frac{2\alpha }{{\nu }_1+{\nu }_2}$$ (10)

Because α, ν₁ and ν₂ must be positive, this function will always be positive. Thus, from the definition of the derivative and the smoothness of the function in Equation 9, the change in expected completion time between two values of ν₂ increases as ν₁ increases. The MIC is just that: a measure of the change due to an increase in processing rate in the difference of mean completion time across the change in the other processing rate. Thus, the MIC must be positive.

2.2. Survivor interaction contrast

For the SIC, we examine the second partial derivative of the CDF, first with respect to ν₁, then with respect to ν₂.

$$\frac{{\partial }^2{F}_{12}}{\partial {\nu }_1\partial {\nu }_2}=\frac{1}{\sqrt{\pi }{\sigma }_{12}^4}\exp \left[\frac{{(-t({\nu }_1+{\nu }_2)+\alpha )}^2}{2t{\sigma }_{12}^2}\right]\left(4{\alpha }^2\sqrt{\pi }\exp \left[\frac{{\left(t\right({\nu }_1+{\nu }_2)+\alpha )}^2}{2t{\sigma }_{12}^2}\right]\Phi \left[-\frac{t({\nu }_1+{\nu }_2)+\alpha )}{\sqrt{t{\sigma }_{12}^2}}\right]-\sqrt{\frac{2{\alpha }^{2}t}{{\sigma }_{12}^2}}\right)$$ (11)

By examining the derivative with respect to t, we can understand the basic shape of the function.

$$\frac{{\partial }^3{F}_{12}}{\partial {\nu }_1\partial {\nu }_2\partial t}=\frac{\alpha }{\sqrt{2\pi t^3{\sigma }_{12}^{1}0}}\exp \left(-\frac{{(\alpha -t({\nu }_1+{\nu }_2\left)\right)}^2}{2t{\alpha }_{12}^2}\right)[{(\alpha -t({\nu }_1+{\nu }_2\left)\right)}^2-t{\sigma }_{12}^2]$$ (12)

This function has only two zeros (below), so across time it only changes direction twice.

$$t=\frac{\alpha ({\nu }_1+{\nu }_2)+2{\sigma }_{12}^2\pm 2{\sigma }_{12}\sqrt{\alpha ({\nu }_1+{\nu }_2)+{\sigma }_{12}^2}}{{({\nu }_1+{\nu }_2)}^2}.$$ (13)

Both of these solutions must be positive because α, ν₁, ν₂ and ${\sigma }_{12}^2$ must all be positive, so t must be positive for $\alpha =t{({\nu }_1+{\nu }_2)}^2+t{\sigma }_{12}^2$ to hold.

Furthermore, for small t, $\left[\right(\alpha -t{({\nu }_1+{\nu }_2)}^2-t{\sigma }_{12}^2]>0$ so Equation 11 starts with a positive slope, changes to a negative slope at the first zero, and is then positive again after the second zero.

By the same reasoning we used for the MIC, if the second partial is negative (positive), then the interaction contrast of the CDFs must be negative (positive). That is, the correspondence between the interaction contrast and the second partial derivative for the sign follows from the definition of “derivative.” The usual contrast operator is simple the discrete version of the second, mixed, partial derivative. Under standard assumptions of smoothness, the result follows. Because the SIC is the negative of the interaction contrast of the CDFs, this implies that the SIC does have the down–up–down form shown in Figure 2.

3. Conclusions

The coactive model has been of particular interest, mainly as a model of redundant target effects. Determining whether a redundant target effect is due merely to statistical facilitation or to coactive processing of the stimulus information can be difficult. The Miller inequality, Equation 1, is one possible method, but can fail if the assumption of context invariance fails. The SIC is a powerful measure for distinguishing among certain classes of information processing systems. Information about SIC forms predicted by coactive models had previously been limited to a particular class of models, a sum of two Poisson processes (Schwarz, 1989; Townsend & Nozawa, 1995). In this paper we have demonstrated that the SIC form predicted by the Poisson coactive model is also predicted by a distinct class of models, based on the sum of two Wiener processes (Schwarz, 1994). These new results hold regardless of the correlation between the two channels.

When data are collected within the double factorial paradigm, it is possible to test both the Miller Inequality and the SIC for evidence of coactive processing. These data may also be used to calculate the capacity coefficient (Townsend & Nozawa, 1995; Townsend & Wenger, 2004). Coactive processing architectures also have distinctive capacity coefficient patterns. In fact, the capacity coefficient is closely related to the Miller Inequality and can be thought of as a more fine grained measure of the same concept (Townsend & Eidels, 2010).

Despite the generality of this demonstration within the class of Wiener models, the coactive SIC predictions are still quite limited compared with the serial and parallel models. In part this is due to the lack of a clear definition of a general coactive model. In future work we would like to find a sensible, quantitatively well specified, general definition of a coactive model. Based on this, we would like to determine whether the distinguishing SIC characteristics discussed in this work are in fact always produced by coactive processing.

Nonetheless, we have demonstrated that the SIC form associated with the Poisson coactive model does generalize beyond that particular case. This is an important step in the direction of tying coactive processing to the early negative–late positive SIC. This, in turn, will aid in future experimental work in which experimenters are interested in discerning coactive psychological processes.