Objective Comparison of Quantitative Imaging Modalities Without the Use of a Gold Standard

Abstract

Imaging is often used for the purpose of estimating the value of some parameter of interest. For example, a cardiologist may measure the ejection fraction (EF) of the heart in order to know how much blood is being pumped out of the heart on each stroke. In clinical practice, however, it is difficult to evaluate an estimation method because the gold standard is not known, e.g., a cardiologist does not know the true EF of a patient. Thus, researchers have often evaluated an estimation method by plotting its results against the results of another (more accepted) estimation method, which amounts to using one set of estimates as the pseudogold standard. In this paper, we present a maximum-likelihood approach for evaluating and comparing different estimation methods without the use of a gold standard with specific emphasis on the problem of evaluating EF estimation methods. Results of numerous simulation studies will be presented and indicate that the method can precisely and accurately estimate the parameters of a regression line without a gold standard, i.e., without the x axis.

I. Introduction

There are many approaches in the literature to assessing image quality, but there is an emerging consensus in medical imaging that any rigorous approach must specify the information desired from the image (the task) and how that information will be extracted (the observer). Broadly, tasks may be divided into classification and estimation and the observer can be either a human or a computer algorithm [1]–[3].

In medical applications, a classification task is to make a diagnosis, perhaps to determine the presence of a tumor or other lesion. This task is usually performed by a human observer and task performance can be assessed by psychophysical studies and receiver operating characteristic (ROC) analysis. Scalar figures of merit such as a detectability index or area under the ROC curve can then be used to compare imaging systems.

Often, however, the task is not directly a diagnosis but rather an estimation of some quantitative parameter from which a diagnosis can later be derived. An example is the estimation of cardiac parameters such as blood flow, ventricular volume, or ejection fraction (EF). For such tasks, the observer is usually a computer algorithm, though often one with human intervention, for example defining regions of interest [4], [5]. Task performance can be expressed in terms of the bias and variance of the estimate, perhaps combined into a mean-square error as a scalar figure of merit.

For both classification and estimation tasks, a major difficulty in objective assessment is lack of a believable standard for the true state of the patient. In ROC analysis for a tumor-detection task, we need to know if the tumor is really present and for estimation of ejection fraction we need to know the actual value for each patient. In common parlance, we need a gold standard, but it is rare that we have one with real clinical images.

For classification tasks, biopsy and histological analysis are usually accepted as gold standards, but even when a pathology report is available, it is subject to error; the biopsy can give information on false-positive fraction but if a lesion is not detected on a particular study and, hence, not biopsied, its contribution to the false-negative fraction will remain unknown [6].

Similarly, for cardiac studies, ventriculography, or ultrasound might be taken as the gold standard for estimation of EF and nuclear medicine or dynamic magnetic resonance imaging might then be compared with the supposed standard [7]. A very common graphical device is to plot a regression line of EFs derived from the system under study to ones derived from the standard and to report the slope, intercept, and correlation coefficient (r) for this regression [8]–[12]. Another comparison approach is the use of a Bland–Altman plot, a measure of agreement between two different modalities [8], [10]–[13]. Neither of these approaches allows for objective performance rankings of the imaging systems, a point we expand upon in the next section. Even a cursory inspection of papers in this genre reveals major inconsistencies. In reality, no present modality can lay claim to the status of gold standard for quantitative cardiac studies. Indeed, if there were such a modality, there would be little point in trying to develop new modalities for this task.

Because of the lack of a convincing gold standard for either classification or estimation tasks, simulation studies are often substituted for clinical studies, but there is always a concern with how realistic the simulations are. Researchers who seek to improve the performance of medical imaging systems must ultimately demonstrate success on real patients.

A breakthrough on the gold-standard problem was the 1990 paper by Henkelman et al. on ROC analysis without knowing the true diagnosis [14]. They showed, quite surprisingly, that ROC parameters could be estimated by using two or more diagnostic tests, neither of which was accepted as the gold standard, on the same patients. Recent work by Beiden et al. has clarified the statistical basis for this approach and studied its errors as a function of number of patients and modalities as well as the true ROC parameters [15].

The goal of this paper is to examine the corresponding problem for estimation tasks. For definiteness, we cast the problem in terms of estimation of cardiac ejection fraction and we pose the following question: If a group of patients of unknown state of cardiac health is imaged by two or more modalities and an estimate of EF is extracted for each patient for each modality, can we estimate the bias and variance of the estimates from each modality without regarding any modality as intrinsically better than any other? Stated differently, can we plot a regression line of estimated EF versus true EF without knowing the truth?

II. Current Methods of Comparison

As stated above, the two most common methods of comparison used currently in the literature consist of plotting regression lines of EFs to calculate slope, intercept, and r and Bland–Altman analysis. Calculating the correlation coefficient for the regression plot is not particularly informative when comparing two estimation tasks [16]–[18]. A nonzero value of implies correlation which is of very little help considering the two estimators are attempting to measure the same quantity. Rather, researchers would like to state that a large r value implies strong agreement. This is not necessarily true. The value of r depends on the magnitude of the spread of the data points around the regression line and the variance of the true parameter across the subjects. As a result, the interpretation of r can be very misleading. For example, if for a given comparitive study we were to measure the EFs for 100 patients with true EFs between 0.6 and 0.7 using two different modalities we would very likely have a lower r value than if we were to run the same study, using the same modalities to measure the EFs for 100 patients with EFs between 0.4 and 0.9.

The slope and intercept of the regression line between two modalities may also be misleading. If one of the methods was an actual gold standard, then the slope and intercept could be used to calibrate the “new” system. This is rarely the case, however, leaving us wondering why we calculated the slope and intercept in the first place.

Bland and Altman presented a simple approach to this problem in 1983 which attempts to quantify the level of agreement between two methods for calculating the same quantity [16]. Given two sets of estimates for the same paramater the Bland–Altman plot depicts the difference between the estimates versus the mean of the estimates. If 95% of the estimates fall within two standard deviations of the mean of the differences, then the two methods of estimation are said to “agree” and, thus, one method could, in theory, replace another.

A shortcoming of this approach lies in the definition of agreement which appears to be rather arbitrary. Their definition implies that if the differences of the estimates follow a Gaussian distribution then “agreement” is achieved independent of how big or small those differences are. Furthermore, whether or not Bland–Altman plots are useful when determining agreement, they do not tell us which method is performing better. In this paper, we describe a method which allows us to determine just that: Which method is better? Our method estimates the relative accuracy and consistency of the methods used without assuming a priori that one method is the gold standard.

III. Approach

We begin with the assumption that there exists a linear relationship between the true EF and its estimated value. We will describe this relationship for a given modality m and a patient p using a regression line with a slope a_m, intercept b_m, and noise term ε_pm. We represent the true EF for a given patient with Θ_p and an estimate of the EF made using modality m with θ_pm. The linear model is, thus, represented by

$${\theta }_{\mathit{\text{pm}}}=a_m{\mathrm{\Theta }}_p+b_m+{\epsilon }_{\mathit{\text{pm}}}.$$ (1)

We make the following assumptions.

1. Θ_p does not vary for a given patient across modalities and is statistically independent from patient to patient.

2. The parameters a_m and b_m are characteristic of the modality and independent of the patient.

3. The error terms, ε_pm, are statistically independent and normally distributed with zero mean and variance ${\sigma }_m^2$.

Using assumption 3) we write the probability density function (pdf) for the noise ε_pm for a given patient p and M modalities as

$$\mathit{\text{pr}}(\{{\epsilon }_{\mathit{\text{pm}}}\})={\displaystyle \prod _{m=1}^M}\frac{1}{\sqrt{2\pi {\sigma }_m^2}}\text{exp}\left(-\frac{1}{2{\sigma }_m^2}{\epsilon }_{\mathit{\text{pm}}}^2\right)$$ (2)

where the term {ε_pm} signifies the set of M noise terms. In other words, we assume a multivariate noise model with a diagonal covariance matrix. We could relax this assumption by adding nonzero terms in the off-diagonal components of the covariance matrix. One could also assume a different noise model, even one that is signal dependent. Solving for ε_pm in (1), we rewrite (2) as the probability of the estimated EFs for multiple modalities and a specific patient given the linear model parameters (a_ms, b_ms, and σ_ms) and the true EF as

$$\mathit{\text{pr}}(\{{\theta }_{\mathit{\text{pm}}}\}|\{a_m,b_m,{\sigma }_m^2\},{\mathrm{\Theta }}_p)={\displaystyle \prod _{m=1}^M}\frac{1}{\sqrt{2\pi {\sigma }_m^2}}\text{exp}(-\frac{1}{2{\sigma }_m^2}{({\theta }_{\mathit{\text{pm}}}-a_m{\mathrm{\Theta }}_p-b_m)}^2).$$ (3)

The notation {θ_pm} represents the estimated EFs for a given patient p over M modalities. Using the following property of conditional probability:

$$\mathit{\text{pr}}(x_1,x_2)=\mathit{\text{pr}}(x_1|x_2)\mathit{\text{ pr }}(x_2)$$ (4)

as well as the marginal probability law

$$\mathit{\text{pr}}(x_1)={\displaystyle \int }{\mathit{\text{dx}}}_2\mathit{\text{pr}}(x_1,x_2)$$ (5)

we write the probability of the estimated EF for a specific patient across all modalities given the linear model parameters as

$$\mathit{\text{pr}}(\{{\theta }_{\mathit{\text{pm}}}\}|\{a_m,b_m,{\sigma }_m^2\})={\displaystyle \int }d{\mathrm{\Theta }}_p\mathit{\text{pr}}({\mathrm{\Theta }}_p)·S\text{ exp }({\displaystyle \sum _{m=1}^M}-\frac{1}{2{\sigma }_m^2}{({\theta }_{\mathit{\text{pm}}}-a_m{\mathrm{\Theta }}_p-b_m)}^2)$$ (6)

where

$$S={\displaystyle \prod _{m=1}^M}\frac{1}{\sqrt{2\pi {\sigma }_m^2}}.$$ (7)

From assumption 1) above, the likelihood of the linear model parameters can be expressed as

$$L={\displaystyle \prod _{p=1}^P}\left[S{\displaystyle \int }d{\mathrm{\Theta }}_p\mathit{\text{pr }}({\mathrm{\Theta }}_p)·\text{exp }\left({\displaystyle \sum _{m=1}^M}\left(-\frac{1}{2{\sigma }_m^2}{({\theta }_{\mathit{\text{pm}}}-a_m{\mathrm{\Theta }}_p-b_m)}^2\right)\right)\right]$$ (8)

where P is the total number of patients. Upon taking the log and rewriting products as sums we obtain

$$\lambda =\text{ln}(L)=P\text{ln}(S)+{\displaystyle \sum _{p=1}^P}\text{ln}[{\displaystyle \int }d{\mathrm{\Theta }}_p\mathit{\text{pr}}({\mathrm{\Theta }}_p)·\text{exp}\left({\displaystyle \sum _{m=1}^M}(-\frac{1}{2{\sigma }_m^2}{({\theta }_{\mathit{\text{pm}}}-a_m{\mathrm{\Theta }}_p-b_m)}^2)\right)].$$ (9)

It is this scalar λ, the log-likelihood, that we seek to maximize to obtain our estimates of a_m, b_m, and ${\sigma }_m^2$. These estimates will be maximum-likelihood (ML) estimates for our parameters when the data matches the model. Although pr(Θ_p) may appear to be a prior term, we are not using a maximum a posteriori approach; we are simply marginalizing over the unknown parameter Θ_p which we are treating as a nuisance parameter. We are not estimating Θ_p, rather we are estimating the linear model parameters in an attempt to compare the different modalities. Thus, we have derived an expression for the log-likelihood of the model parameters which does not require knowledge of the true EF Θ_p, i.e., without the use of a gold standard. This is analogous to fitting lines without the use of the x axis.

A. True (pr_t(θ_p)) Versus Assumed (pr_a(θ_p)) Distributions

Although the expression for the log-likelihood in (9) does not require the true EF Θ_p, it does require some knowledge of their distribution pr(Θ_p). We will refer to this distribution, as it appears in (9), as the assumed distribution (pr_a(Θ_p)) of the EFs. In this paper, we will investigate the effect different choices of the assumed distributions have on estimating the linear model parameters. We first sample parameters from a true distribution (pr_t(Θ_p) and generate different estimated EFs for the different modalities by linearly mapping these values using known a_ms and b_ms, then add normal noise to these values with known σ_ms. These EF estimates form the values θ_pm, which will be used in the process of determining the estimates of the linear model parameters by optimizing (9). We will look at cases in which the assumed and true distributions match (data matches model), as well as cases in which they do not match (data does not match model).

For our experiments, we will investigate beta distributions and truncated normal distributions as our choices for both the assumed and true distributions. These distributions have been chosen because EF is bounded between zero and one and has been shown to follow a unimodal distribution [19]. The beta distribution has pdf given by

$$\mathit{\text{pr}}(\theta )=\frac{{\theta }^{\nu -1}{(1-\theta )}^{\omega -1}}{B(\nu ,\omega )}$$ (10)

where θ ∈ [0,1] and the beta function B(ν, ω) is a normalizing constant. The truncated normal distribution is given by

$$\mathit{\text{pr}}(\theta )=A(\mu ,\sigma )\text{ exp }\left(-\frac{1}{2{\sigma }^2}{(\theta -\mu )}^2\right)\mathrm{\prod }(x)$$ (11)

where A(μ, σ) is a normalizing constant involving error functions and Π(x) is a rect function which truncates the normal from zero to one. It should be noted that μ and σ are the mean and standard deviation for the normal distribution, not necessarily the mean and standard deviation of the truncated normal. While ν, ω, μ, and σ appear to be hyperparameters they are not; they are simply parameters characterizing the density, pr(Θ_p), which we used to marginalize Θ_p in (3).

Using a truncated normal for the assumed distribution in (9), we find the following closed-form solution for the log-likelihood:

$$\lambda =P\text{ln}(S)+{\displaystyle \sum _{p=1}^P}\left(\frac{{\beta }^2-4\alpha \gamma }{4\alpha }\right)·\text{ln}\left(\frac{A(\mu ,\alpha )}{2}\sqrt{\frac{\pi }{a}}[\text{erf}\left(\frac{2\alpha +\beta }{2\sqrt{\alpha }}\right)-\text{erf}(\frac{\beta }{2\sqrt{\alpha }})]\right)$$ (12)

where

$$\begin{array}{cc}\alpha \hfill & =\frac{1}{2{\sigma }^2}+{\displaystyle \sum _{m=1}^M}\frac{a_m^2}{2{\sigma }_m^2}\hfill \\ \beta \hfill & =-\frac{\mu }{{\sigma }^2}-{\displaystyle \sum _{m=1}^M}\frac{a_m({\theta }_{\mathit{\text{pm}}}-b_m)}{{\sigma }_m^2}\hfill \\ \gamma \hfill & =\frac{{\mu }^2}{2{\sigma }^2}+{\displaystyle \sum _{m=1}^M}\frac{{({\theta }_{\mathit{\text{pm}}}-b_m)}^2}{2{\sigma }_m^2}.\hfill \end{array}$$

The expression for the log-likelihood with a beta assumed distribution does not easily simplify to a closed-form solution and, thus, we used numerical integration techniques to evaluate the one-dimensional integral in (9).

We used a quasi-Newton optimization method in Matlab on a Dell Precision 620 running Linux to maximize the log-likelihood as a function of our parameters [20]. For each experiment, we generated EF data for 100 patients using one of the aforementioned distributions. We then ran the optimization routine to estimate the parameters and repeated this entire process 100 times in order to compute sample means and variances for the parameter estimates. The tables below consist of the true parameters used to create the patient data as well as the sample means and standard deviations attained through the simulations.

IV. Results

A. Estimating the Linear Model Parameters for a Given Assumed Distribution

We first investigated the results of choosing the assumed distribution to be the same as the true distribution. The asymptotic properties of ML estimates would predict that in the limit of large patient populations the estimated linear model parameters would converge to the true values [21]. The results, shown in Table I, are consistent with this prediction. For the experiment below, we have chosen ν = 1.5 and ω = 2 for the beta distribution and μ = 0.5 and σ = 0.2 for the truncated normal distribution. Fig. 1 illustrates the results of an individual experiment using the truncated normal distribution.

TABLE I.

Values of the estimated linear model parameters using matching assumed and true distributions

	a1	a2	a3	b1	b2	b3
True Values	0.6	0.7	0.8	−0.1	0.0	0.1
pr(Θ)=Beta	0.59±.03	0.69±.03	0.79±.05	−0.10±.02	0.00±.02	0.11±.03
pr(Θ)=Normal	0.58±.04	0.68±.04	0.78±.06	−0.09±.02	0.01±.02	0.11±.03
		σ1	σ2	σ3
True Values		0.05	0.03	0.08
pr(Θ)=Beta		0.048±.005	0.029±.009	0.079±.007
pr(Θ)=Normal		0.048±.006	0.028±.010	0.080±.007

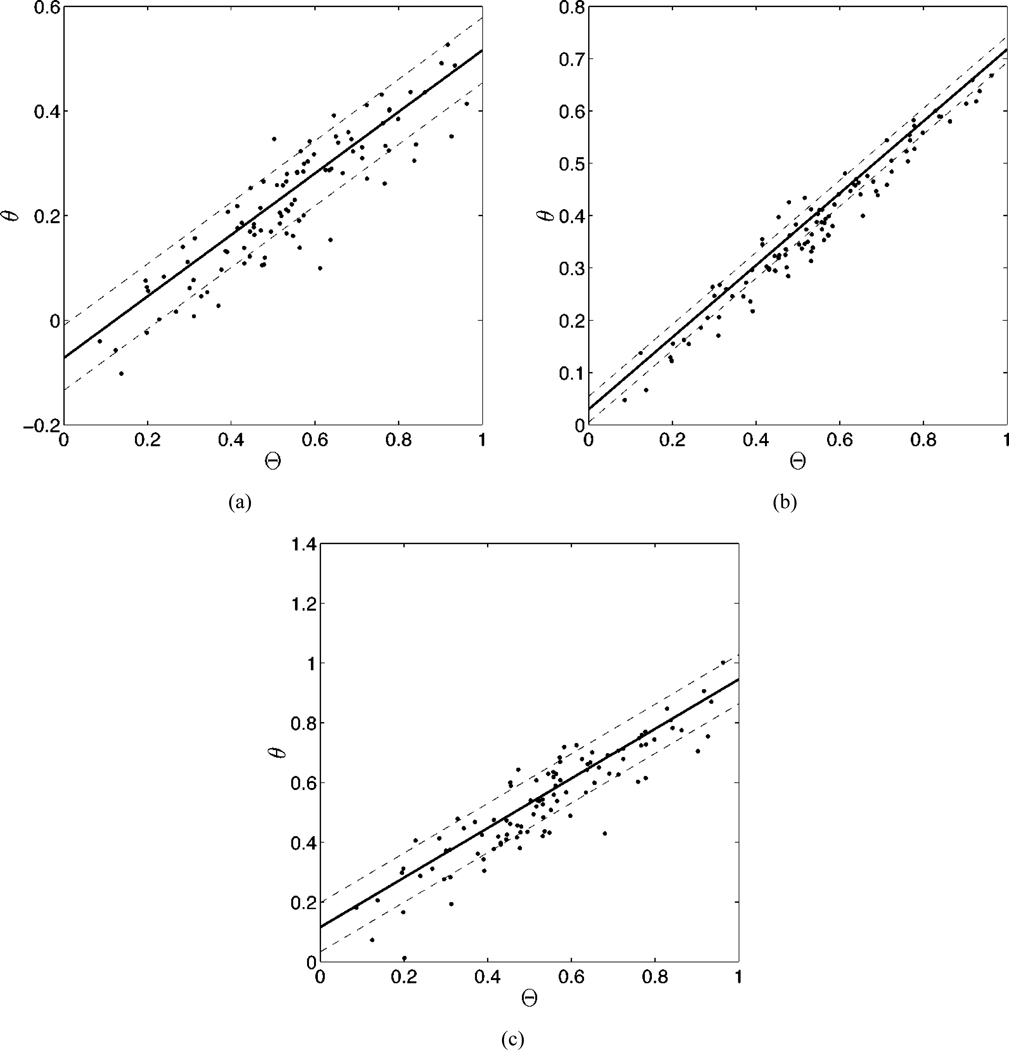
Fig. 1.

The results of an experiment using 100 patients, three modalities and the same true parameters as shown in Table I. In each graph, we have plotted the true ejection fraction against the estimates of the EF for three different modalities [(a)–(c)]. The solid line was generated using the estimated linear model parameters for each modality. the dashed lines denote the estimated standard deviations for each modality. The estimated a_m, b_m, and σ_m for each graph are (a) 0.59, −0.07, and 0.06; (b) 0.69, 0.03, and 0.025; and (c) 0.83, 0.12, and 0.082. Note that although we have plotted the true EF on the x axis of each graph, this information was not used in computing the linear model parameters.

In an attempt to understand the impact of the assumed distribution on the method, we next used a flat assumed distribution, which is in fact a special case of the beta distribution (ν = 1, ω = 1). We used the same beta and truncated normal distributions for the true distribution as was chosen in the previous experiment, namely ν = 1.5, ω = 2, μ = 0.5, and σ = 0.2. As shown in Table II, the parameters estimated using a flat assumed distribution are not as accurate as those in the experiment with matching assumed and true distributions. However, the systematic underestimation on the a_ms and the systematic overestimation on the b_ms has not affected the ordering of these parameters. In fact, the estimated parameters have been shifted roughly the same amount. It should also be noted that the estimates of the σ_ms are still accurate. We will return to this point later in the paper.

TABLE II.

Values of estimated linear model parameter using a flat assumed distribution (pr_a(Θ) = 1)

	a1	a2	a3	b1	b2	b3
True Values	0.6	0.7	0.8	−0.1	0.0	0.1
prt(Θ)=Beta	0.53±.03	0.61±.03	0.70±0.05	−0.09±.02	0.02±.02	0.13±.03
prt(Θ)=Normal	0.50±.01	0.56±.03	0.64±.08	−0.05±.02	0.07±.03	0.18±.04
		σ1	σ2	σ3
True Values		0.05	0.03	0.08
prt(Θ)=Beta		0.049±0.005	0.031±0.009	0.079±0.007
prt(Θ)=Normal		0.048±0.005	0.033±0.008	0.080±0.007

B. Estimating the Linear Model Parameters and the Parameters of the Assumed Distribution

After noting the impact of the choice of the assumed distribution on the estimated parameters it occurred to us to investigate the effect of varying this distribution. In the case of the beta distribution, this was simply a case of adding ν and ω to the list of parameters over which we were attempting to maximize the likelihood. In similar fashion, we added μ and σ to the list of parameters for the truncated normal distribution. In the case of the beta distributions, we limited the search in the region 1 ≤ ν, ω ≤ 5, since values of ν and ω between zero and one create singularites at the boundaries, an impossibility considering the nature of EF. In the case of the truncated normal distributions, we limited the search in the region 0 ≤ μ ≤ 1 and 0.1 ≤ σ ≤ 10. We began by choosing the form of the assumed distribution and the true distribution to be the same, i.e., we estimated the parameters of the beta distribution while using beta distributed data. We found that the method successfully approximated the values of all parameters, including those on the assumed distribution, as displayed in Table III. The results of an individual experiment is displayed graphically in Fig. 2.

TABLE III.

Values of estimated linear model and distribution parameters with the assumed distribution and the fixed true distribution having the same form

	a1	a2	a3
True Values	0.6	0.7	0.8
pr(Θ)=Normal	0.59±0.3	0.69±.04	0.79±.04
pr(Θ)=Beta	0.60±.09	0.70±.09	0.79±.11
	b1	b2	b3
True Values	−0.1	0.0	0.1
pr(Θ)=Normal	−0.09±.03	0.01±.03	0.11±.04
pr(Θ)=Beta	−0.10±.03	0.01±.03	0.11±.04
	σ1	σ2	σ3
True Values	0.05	0.03	0.08
pr(Θ)=Normal	0.050±.002	0.029±.004	0.080±.003
pr(Θ)=Beta	0.048±.006	0.030±.011	0.080±.006
	Distribution	Parameters
True Values	μ = 0.5, ν = 1.5	σ = 0.2, ω = 2.0
pr(Θ)=Normal	μ = 0.50±.03	σ = 0.20±.02
pr(Θ)=Beta	ν = 1.50±.53	ω = 2.08±.99

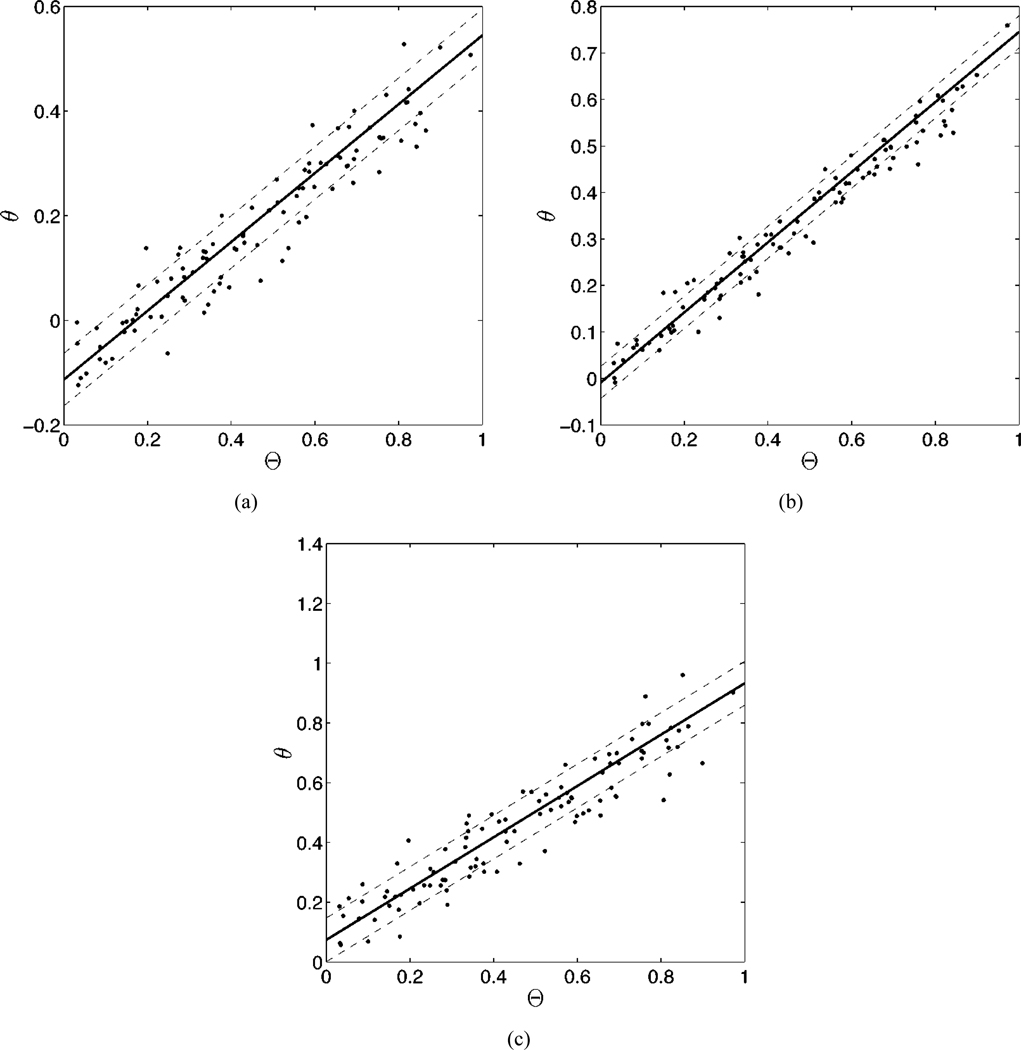
Fig. 2.

The results of an experiment using 100 patients, three modalities and the same true parameters as shown in Table III. In each graph, we have plotted the true ejection fraction against the estimates of the EF for three different modalities [(a)–(c)]. The solid line was generated using the estimated linear model parameters for each modality. The dashed lines denote the estimated standard deviations for each modality. The estimated a_m, b_m, and σ_m for each graph are: (a) 0.66, −0.11, and 0.050; (b) 0.75, 0.01, and 0.035; and (c) 0.86, 0.07, and 0.073. Note in this study the parameters of the beta distribution were estimated along with the linear model parameters.

In the previous experiment, the estimated parameters associated with both the beta and truncated normal distributions were very close to their true values. We now show the results when the assumed distribution differs from the true distribution in Table IV. We know from our previous experiment that when the form of the assumed and true distributions match, the correct distribution parameters are estimated (on average). However, it remains to be seen what distribution parameters will be estimated when the forms of the two distributions differ. Thus, in Fig. 3 we display the true distribution as well as the assumed distribution with the mean estimates of the distribution parameters. Note that the assumed distribution cannot equal the true distribution because they are from two different distribution families, i.e., beta and truncated normal. The assumed distribution does, however, take on a form which approximates the true distribution in an attempt to maximize the likelihood.

TABLE IV.

Values of estimated linear model parameters using different forms of the varying assumed distribution and the fixed true distribution

	a1	a2	a3
True Values	0.6	0.7	0.8
pra(Θ)=Normal/prt(Θ)=Beta	0.56±.04	0.65±.05	0.74±.06
pra(Θ)=Beta/prt(Θ)=Normal	0.66±.10	0.78±.09	0.89±.12
	b1	b2	b3
True Values	−0.1	0.0	0.1
pra(Θ)=Normal/prt(Θ)=Beta	−0.09±.02	0.01±.02	0.12±.03
pra(Θ)=Beta/prt(Θ)=Normal	−0.14±.06	−0.06±.06	0.03±.07
	σ1	σ2	σ3
True Values	0.05	0.03	0.08
pra(Θ)=Normal/prt(Θ)=Beta	0.050±.005	0.029±.004	0.080±.007
pra(Θ)=Beta/prt(Θ)=Normal	0.050±.007	0.025±.011	0.079±.009

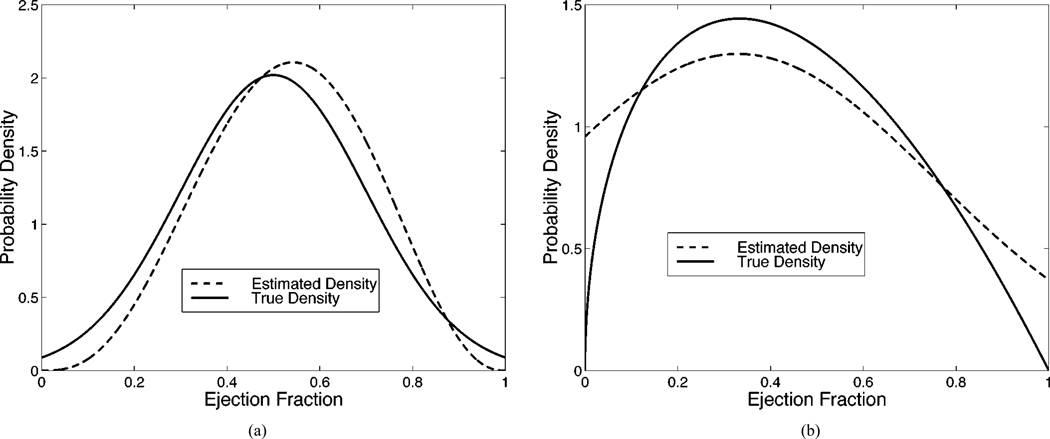
Fig. 3.

When the form of the assumed distribution does not match that of the true distribution, we see that the optimal distribution parameters are such that the form of the assumed distribution approximates the true distribution. In (a), the true distribution is a truncated normal which is approximated automatically by the method using a beta distribution (ν = 3.93, ω = 3.47). In (b), the role are reversed, as a truncated normal automatically approximates a beta distribution (μ = 0.33, σ = 0.42).

V. Discussion and Conclusion

We have developed a method for characterizing an observer’s performance in estimation tasks without the use of a gold standard. Although a gold standard is not required for this method, it is necessary to make some assumptions on the distribution of the parameter of interest (i.e., EF). We have found that when the assumed distribution matches the true distribution, the estimates of the linear model parameters are both accurate and precise. Conversely, when the assumed and true distributions do not match, we find that our linear model parameters are no longer as accurate. This led us to investigate the role of the assumed distribution in the accuracy of the linear model parameters. By optimizing both the distribution parameters and the model parameters, we found that one can effectively find both the model parameters and the form of the assumed distribution.

When comparing different imaging modalities one would typically prefer the modality with the smallest error, i.e., the smallest σ_m/a_m. Estimating σ_m/a_m facilitates modality comparisons without knowledge of a gold standard. As discussed earlier, the estimates of the slopes a_ms retained the proper ordering amongst modalities even when a bias is introduced by mismatching true and assumed distributions. The estimates of σ_m, meanwhile, were very accurate regardless of the choise of the assumed and true distributions. Combining these observations we feel confident that σ_m/a_m will serve as a good figure of merit to compare imaging systems even when the data does not match the model.

The estimates of the slope and intercept values describe the systematic error (or bias) of the modality. If one is confident in these estimates they could be employed to adjust and correct systematic error for each modality. Another interesting result of the experiments is the successful estimation of the distribution parameters to fit the form of the true distribution. This could serve as an insight into the distribution of the true parameter for the population studied, i.e., the patient distribution of EFs.

A major underlying assumption of the method proposed in this paper is that the true parameter of interest does not vary according to modality. This assumption may not be accurate in the context of estimating EF, which may vary moment to moment with a patient’s mood and/or breathing pattern. This assumption may be valid, however, for other estimation tasks. Another assumption we have made is the linear relationship between the true and estimated parameters of interest. This was chosen in large part due to mathematical simplicity, but is, nonetheless, a good first step. More complicated, nonlinear models can easily be accommodated by this method and are discussed briefly in another work [22]. Ideally, we would like to choose a model based on some sort of physical knowledge.

The major components of this work were originally presented at the 2001 conference on Information Processing in Medical Imaging (IPMI) and published in the conference proceedings [23]. Since then we have studied the effect of varying the true parameters, the number of patients and the noise and compared the performance of our method to standard linear regression with a gold standard in simulation [22]. Our method performed very well.

Those familiar with latent variable models might prefer to think of the EF Θ_p as a latent variable and to perform latent class anaylsis [24], [25]. We are not performing conventional latent class anaylsis because we do not assume the data to follow a Gaussian distribution and we do not compare covariance matrices. Rather, we work with the data directly and perform ML estimation of the linear model parameters.

In order to quantify the performance of our method, we are in the process of evaluating the Fisher information matrix for the estimates of the linear model parameters and the parameters characterizing the shape of the assumed distribution. This will allow us to determine a theoretical minimum variance for these estimated parameters. In the future, we would like to relax the independence assumption of the noise, i.e., assume a correlated Gaussian as our noise model.