Sensitivity Analysis and Bounding of Causal Effects With Alternative Identifying Assumptions

Abstract

When identification of causal effects relies on untestable assumptions regarding nonidentified parameters, sensitivity of causal effect estimates is often questioned. For proper interpretation of causal effect estimates in this situation, deriving bounds on causal parameters or exploring the sensitivity of estimates to scientifically plausible alternative assumptions can be critical. In this paper, we propose a practical way of bounding and sensitivity analysis, where multiple identifying assumptions are combined to construct tighter common bounds. In particular, we focus on the use of competing identifying assumptions that impose different restrictions on the same non-identified parameter. Since these assumptions are connected through the same parameter, direct translation across them is possible. Based on this cross-translatability, various information in the data, carried by alternative assumptions, can be effectively combined to construct tighter bounds on causal effects. Flexibility of the suggested approach is demonstrated focusing on the estimation of the complier average causal effect (CACE) in a randomized job search intervention trial that suffers from noncompliance and subsequent missing outcomes.

1 Introduction

Principal stratification (Frangakis & Rubin, 2002) is a widely used framework for causal inference considering intermediate posttreatment outcomes. Principal stratification refers to classification of individuals based on potential values of intermediate outcomes under all treatment conditions that are compared. The resulting categories (principal strata) are unaffected by treatment assignment, and therefore, the outcome difference between treatment groups within each principal stratum (principal effect) can be interpreted as a causal effect. Since principal stratification requires consideration of potential outcomes under all treatment conditions and each individual can be assigned to only one of these conditions, identification of principal effects naturally involves population values that are not directly identifiable from the observed data. Given that, it is critical to conduct sensitivity analysis and to provide reasonable ranges of principal effects to guide proper interpretation of the estimation results.

Starting from earlier work by Manski (1989) and Robins (1989), the idea of bounds has been utilized in various contexts of causal effect estimation (e.g., Balke & Pearl, 1997; Cheng & Small, 2006; Gilbert et al., 2003; Heckman & Vytlacil, 2001; Horowitz & Manski, 2000; Hotz et al., 1997; Manski, 1989; Manski, 1997, 2003; Manski & Pepper, 2000; Robins, 1989; Robins et al, 2000; Scharfstein et al., 2004; Zhang & Rubin, 2003; Grilli & Mealli, 2008). A straightforward strategy for bounding is based on allowable (in terms of natural parameter space) values of non-identified parameters. The drawback of this approach is that the resulting bounds are often impractically wide or unrealistic. Given that, beyond what data informs, it is critical to introduce external assumptions based on science (expert opinion) to narrow bounds within reasonable ranges (e.g., Manski, 1997; Manski & Pepper, 2000; Scharfstein, Manski, & Anthony, 2004). The use of science-based bounding assumptions directly benefits causal inference in the principal stratification framework, as demonstrated in Zhang & Rubin (2003) and Grilli and Mealli (2008).

In line with Zhang and Rubin (2003) and Grilli and Mealli (2008), we intend to achieve informative nonparametric large-sample bounds in the principal stratification framework by utilizing science-based assumptions. The current paper differs from the previous ones in a few aspects: (a) whereas previous studies imposed a single bounding assumption on each non-identified parameter, the current study imposes several alternative bounding assumptions on each non-identified parameter, (b) we provide confidence intervals for bounds by applying the method proposed in Imbens and Manski (2004), and (c) we utilize bounds in conducting sensitivity analysis in the current study.

The emphasis in this paper is in the use of alternative bounding assumptions to sharpen inferences in the principal stratification framework. In particular, we focus on the use of multiple assumptions that can be translated back and forth on the basis of their connection through a common non-identified parameter. Let us consider a simple example, where bounding benefits from translation across multiple assumptions that impose different restrictions on the common non-identified parameter. Let us assume that we do not know the range of A, which is the parameter of interest. There are three other parameters, B, C, and D, that are directly related to A. That is, B = 2A, C = 3A and D = 4A. Suppose scientists have strong beliefs (or evidence) in assuming that B > 2, C < 6, and D < 12. These assumptions may seem unrelated until they are translated into each other. Based on the connection through A, translation across these three assumptions is possible, and therefore each assumption can be viewed from a few different perspectives. That is, B > 2 is translated to A > 1, C > 3 and D > 4, C < 6 is translated to A < 2, B < 4 and D < 8, and D < 12 is translated to A < 3, B < 6 and C < 9. Since these assumptions impose restrictions on the same parameter A, we can also obtain the plausible range of A by combining them. For example, we may choose the tightest bounds by adopting B > 2 and C < 6. That is, 1 < A < 2. In this choice, the assumption that D < 12 (i.e., A < 3) does not directly determine the bounds, but it supports the assumption that C < 6 (i.e., A < 2).

In the above example, assumptions that can be cross-translated mutually regulate the bounds of each other, increasing the chance to narrow bounds. These assumptions are also used to cross-examine plausibility of each other, increasing the chance to adopt more plausible assumptions. In estimating principal effects considering noncompliance and missing data, several studies have in fact employed cross-translatable identifying assumptions (e.g., Frangakis & Rubin, 1999; Mealli et al., 2004; Peng, Little, & Raghunathan, 2004). However, in these studies, alternative assumptions were handled rather as competing assumptions than as assumptions that can be jointly considered to construct tighter bounds for principal effects. A more directly related example can be found in Jo (2008), where alternative missing data assumptions were jointly considered to establish a reasonable range of deviation from each assumption, and sensitivity of principal effect estimates was examined within this range. In the current paper, we explicitly utilize translatability across alternative assumptions to refine bounds for principal effects. This method can be easily extended to accommodate more complex situations that involve multiple non-identified parameters, which we will demonstrate through a simultaneous modeling of noncompliance and missing data.

The paper is organized as follows. Section 2 describes the motivating example. Section 3 defines the causal effect estimand of interest. In Section 4, nonparametric bounds of causal effects and related parameters are discussed. Section 5 presents alternative identifying assumptions. Section 6 defines point estimators. In Section 7, nonparametric bounds of causal effects are constructed based on alternative identifying assumptions. In Section 8, sensitivity analysis and model selection are discussed based on point estimators. Section 9 provides conclusions.

2 Job Search Intervention Study

The Job Search Intervention Study (JOBS II: Price et al., 1992; Vinokur et al., 1995; Vinokur & Schul, 1997) was a randomized field experiment developed at the University of Michigan to prevent poor mental health and to promote high-quality reemployment among unemployed workers. Among 1801 individuals who were randomly assigned to the experimental (1249) or to the control (552) condition, 715 (486 intervention, 229 control) were classified as at high-risk (Price et al., 1992; Vinokur et al., 1995) and were included in the analyses reported in this paper. Risk score was computed based on risk variables in the screening data (Price et al., 1992) that predict depressive symptoms at follow-up (depression, financial strain, and assertiveness). The experimental condition consisted of five 4-hour training sessions regarding the application of problem-solving and decision-making processes, inoculation against setbacks, provision of social support and positive regard from trainers, and learning and practicing job search skills. The control condition consisted of a booklet briefly describing job-search methods and tips.

The outcome used here to illustrate the proposed methodology is the employment status two months from the intervention. Individuals who work 20 or more hours per week and who report working as many hours as they need are regarded as reemployed. One of the main questions in the JOBS II trial is how large the intervention impact was on individuals who would actually abide by the intervention program. The reemployment rate was 44% in the intervention condition and 35% in the control condition. Since employment can be affected by various fundamental factors that the intervention cannot modify, such as the general status of economy and socio-political situations, a moderate increase in the reemployment rate due to the intervention may be considered as a meaningful gain. However, comparing intervention conditions based only on raw employment rates may not appropriately reflect efficacy of the program, since the trial suffered from substantial noncompliance and subsequent missing outcomes.

Table 1 shows overall and compliance-specific sample statistics of the outcome and response variables. When the receipt of intervention is defined as completing at least one out of five training sessions (the majority either attended 4–5 sessions or did not attend at all), 54% of individuals assigned to the intervention condition actually received the intervention (p_c). The sample mean outcome (reemployment) of individuals who responded at the follow-up assessment is 0.352 in the control (${\stackrel{‒}{y}}_0$), and 0.443 in the intervention condition (${\stackrel{‒}{y}}_1$), and the difference is significant (at .05 level, 2-tailed). In the intervention condition, significant difference in the employment rate between compliance types is observed. The sample mean is 0.398 for individuals who attended at least one session (${\stackrel{‒}{y}}_{1,1}$), and 0.510 for individuals who did not attend any (${\stackrel{‒}{y}}_{0,1}$). The trial also suffered from nonresponse at the follow-up. At the two-months follow-up assessment, the overall sample response rate was 0.743 in the intervention condition ($p_1^R$), and 0.782 ($p_0^R$) in the control condition. In the intervention condition, the sample response rate was 0.818 for individuals who completed at least one session ($p_{1,1}^R$) and 0.653 for individuals who did not ($p_{0,1}^R$), and the difference is significant.

Table 1.

Sample Statistics

${\stackrel{‒}{y}}_0$	${\stackrel{‒}{y}}_1$	${\stackrel{‒}{y}}_{1,1}$	${\stackrel{‒}{y}}_{0,1}$	$p_0^R$	$p_1^R$	$p_{1,1}^R$	$p_{0,1}^R$	pc
0.352	0.443	0.398	0.510	0.782	0.743	0.818	0.653	0.543

The problem of sensitivity arises in estimating causal effects, since compliance and outcome information is partly missing. In JOBS II, among individuals assigned to the control condition, compliance information could not be collected because they were not given an opportunity to receive the intervention treatment. One common way to achieve identifiability in this situation is to apply the instrumental variable approach (Angrist et al., 1996; Bloom, 1984). Using this approach and ignoring missing outcomes, the identified causal treatment effect for compliers (CACE: complier average causal effect) indicates that the JOBS II intervention was quite highly efficacious ($C\widehat{AC}E=({\stackrel{‒}{y}}_1-{\stackrel{‒}{y}}_0)∕p_c=0.168$) as reported in the previous analysis using Bloom's method (Vinokur et al., 1995). However, one may have some reservations towards this optimistic conclusion, given that JOBS II was a naturalistic field experiment, where blinding was not an option, and that study participants were unemployed workers who may experience depressive symptoms related to job loss. In other words, some deviation from the exclusion restriction is possible due to the psychological effect of treatment assignment. Similar issues also arise when imposing restrictions on the missing outcome data mechanism. Further, multiple complications (i.e., noncompliance and nonresponse) necessitate simultaneous considerations of different non-identified parameters, increasing complexity in causal effect estimation. Given this situation, our interest is in obtaining conservative, but still informative bounds of causal effects by jointly considering alternative sets of identifying assumptions.

3 Complier Average Causal Effect (CACE)

For the analyses considering compliance patterns, participants in the JOBS II trial were classified based on their intervention assignment status Z and treatment receipt status D. If individual i is randomly assigned to the intervention, Z_i = 1 (i = 1, …, N) and if assigned to the control condition, Z_i = 0. The treatment receipt status D_i = 1 if individual i completed at least one treatment session, and D_i = 0 otherwise. Let D_i(1) denote the potential treatment receipt status for individual i when Z = 1, and D_i(0) when Z = 0. The reemployment status outcome Y_i = 1 if individual i was reemployed at the follow-up, and Y_i = 0 otherwise. Let Y_i(1) denote the potential outcome for individual i when Z = 1, and Y_i(0) when Z = 0.

• Common assumption 1. Random assignment: individuals are randomly assigned to the intervention (Z = 1) or to the control (Z = 0) condition, which implies in the principal stratification context that treatment assignment is independent of potential outcomes and intermediate outcomes. That is, (D_i(1),D_i(0),Y_i(1),Y_i(0)) ⊥ Z_i.

Since individuals were prohibited from receiving a different treatment than the one that they were assigned to, only two principal strata (compliance types) are possible based on Z and D. Let C ∈ {1, 0} denote the latent principal stratum membership. The membership C_i = 1 if individual i would attend at least one session when the intervention is offered, and C_i = 0 if i would not attend any sessions regardless of the intervention assignment. That is,

$$C_i=\{\begin{array}{cc}1\left(\text{complier}\right)\hfill & \mathrm{if}{D}_i\left(1\right)=1,\mathrm{and}{D}_i\left(0\right)=0\hfill \\ 0\left(\text{noncomplier}\right)\hfill & \mathrm{if}{D}_i\left(1\right)=0,\mathrm{and}{D}_i\left(0\right)=0,\hfill \end{array}\phantom{\}}$$

which implies that C_i is observed if assigned to the intervention condition, but unobserved if assigned to the control condition.

Another critical assumption in defining the causal effect of interest is the stable unit treatment value (Rubin, 1978, 1980, 1990).

• Common assumption 2: Stable unit treatment value (SUTVA) - potential outcomes for each person are unrelated to the treatment status of other individuals. In JOBS II, SUTVA is a plausible assumption. The sample in JOBS II is a very small fraction of the local population of unemployed at the time of the study since recruitment was conducted from employment security offices that serve the entire greater Detroit area. It is also very unlikely that there was a substantial portion of individuals who participated in the trial with significant others. Although study participants were not explicitly questioned, according to the JOBS II staff who closely monitored incoming participants, none of the unemployed workers came to the recruitment sites or training sessions with close friends or relatives.

Along with SUTVA and randomization, the latent ignorability (LI: Frangakis & Rubin, 1999) provides the basis for identification of the principal effect of interest (i.e., CACE). Let R ∈ {1, 0} denote the outcome response indicator. The indicator R_i = 1 if outcome Y_i is observed, and R_i = 0 if outcome Y_i is missing. Under LI, the probability of outcome being recorded is not associated with the outcome conditional on treatment assignment and latent compliance status. That is, Y_i ⊥ R_i | Z_i, C_i. In this paper, we consistently assume that LI holds. However, this assumption is also unverifiable and may have been violated in JOBS II. A systematic consideration of LI violation is difficult because violation may occur in many different directions (see Appendix in Jo, 2008), although it is possible in principle to examine the sensitivity of inferences to deviation from this assumption in the same fashion as is done in this paper.

• Common assumption 3: Latent ignorability (LI) - the probability of outcome being recorded is not associated with the outcome, conditional on treatment assignment and principal stratum membership. This implies that E(Y_i | R_i = r, C_i = c, Z_i = z) = E(Y_i | C_i = c, Z_i = z). In other words, LI makes it possible to define principal effects, which is conditional on principal stratum membership, ignoring outcome response behavior.

Under the common assumptions 1 through 3, let μ_c,z be the population mean potential outcome given C and Z. That is, μ_c,z := E(Y_i | C_i = c, Z_i = z). In particular, the complier average causal effect (CACE) estimand is defined as

$$\mathit{CACE}={\mu }_{1,1}-{\mu }_{1,0}.$$ (1)

Since C_i is observed when Z_i = 1 and Y_i is observed when R_i = 1, μ_c,1 is directly estimable among individuals with Z_i = 1 and R_i = 1 under LI. Among individuals with Z_i = 0 and R_i = 1, additional assumptions (or restrictions) are necessary to identify μ_c,0 based on the observed data in the control condition.

Based on random assignment, it is assumed that E(C_i | Z_i = 1) = E(C_i | Z_i = 0) = E(C_i). Let the compliance probability π_c := E(C_i). From the observed data in the treatment condition, π_c is directly estimable. Let the response probability ${\pi }_z^R≔E(R_i\mid Z_i=z)$. Based on observed data, ${\pi }_z^R$ is directly estimable. Let the compliance-specific response probability ${\pi }_{c,z}^R≔E(R_i\mid C_i=c,Z_i=z)$. The response probability ${\pi }_z^R$ can be written as a mixture of response probabilities for the two compliance types as

$${\pi }_z^R={\pi }_c{\pi }_{1,z}^R+(1-{\pi }_c){\pi }_{0,z}^R.$$ (2)

Let ${\mu }_z^{\mathit{obs}}≔E(Y_i\mid R_i=1,Z_i=z)$. The observed average outcome of the control condition is

$${\mu }_0^{\mathit{obs}}=\frac{{\pi }_{1,0}^R}{{\pi }_0^R}{\pi }_c{\mu }_{1,0}+\frac{{\pi }_{0,0}^R}{{\pi }_0^R}(1-{\pi }_c){\mu }_{0,0}.$$ (3)

From (2) and (3), μ_1,0 can be written as

$${\mu }_{1,0}=\frac{{\mu }_0^{\mathit{obs}}{\pi }_0^R-{\mu }_{0,0}{\pi }_{0,0}^R(1-{\pi }_c)}{{\pi }_0^R-{\pi }_{0,0}^R(1-{\pi }_c)},$$ (4)

where ${\mu }_0^{\mathit{obs}}$, ${\pi }_0^R$ and π_c are directly estimable from the observed data. However, further restrictions are necessary to identify μ_0,0 and ${\pi }_{0,0}^R$. The same derivation of μ_1,0 has been demonstrated in Frangakis and Rubin (1999).

From (1) and (4), the CACE estimand can be written as

$$\mathit{CACE}={\mu }_{1,1}-{\mu }_{1,0}={\mu }_{1,1}-\left\{\frac{{\mu }_0^{\mathit{obs}}{\pi }_0^R-{\mu }_{0,0}{\pi }_{0,0}^R(1-{\pi }_c)}{{\pi }_0^R-{\pi }_{0,0}^R(1-{\pi }_c)}\right\}.$$ (5)

To identify CACE in (5), additional assumptions are necessary. In principle, it is possible to do analyses without imposing direct restrictions on non-identified parameters, relying on auxiliary information such as from proper priors and covariates (Hirano et al., 2000; Imbens & Rubin, 1997; Jo, 2002). However, the resulting causal effect estimates tend to be quite imprecise even when a restriction on a single parameter is relaxed. Given that, parameter bounding and sensitivity analysis play important roles in dealing with nonidentified parameters and related causal effects. Considering both nonresponse and noncompliance in sensitivity analysis has been previously explored in some studies (Robins, 1998; Rotnitzky et al., 2001), though their methods and contexts were different from those used in this study. Table 2 summarizes key parameters and corresponding sample statistics under the three common assumptions discussed above.

Table 2.

Key Parameters and Corresponding Sample Statistics

Parameter	Description	Corresponidng Sample Statistic
${\mu }_0^{\mathit{obs}}$	mean outcome if Z = 0, R = 1	${\stackrel{‒}{y}}_0$
${\mu }_1^{\mathit{obs}}$	mean outcome if Z = 1, R = 1	${\stackrel{‒}{y}}_1$
${\mu }_{1,1}$	mean outcome if C = 1, Z = 1	${\stackrel{‒}{y}}_{1,1}$
${\mu }_{0,1}$	mean outcome if C = 0, Z = 1	${\stackrel{‒}{y}}_{0,1}$
${\mu }_{1,0}$	mean outcome if C = 1, Z = 0	Not Available
${\mu }_{0,0}$	mean outcome if C = 0, Z = 0	Not Available
${\pi }_0^R$	mean response probability if Z = 0	$p_0^R$
${\pi }_1^R$	mean response probability if Z = 1	$p_1^R$
${\pi }_{1,1}^R$	mean response probability if C = 1, Z = 1	$p_{1,1}^R$
${\pi }_{0,1}^R$	mean response probability if C = 0, Z = 1	$p_{0,1}^R$
${\pi }_{1,0}^R$	mean response probability if C = 1, Z = 0	Not Available
${\pi }_{0,0}^R$	mean response probability if C = 0, Z = 0	Not Available
π c	mean compliance probability	pc

4 Large-Sample Nonparametric Bounds Without External Assumptions

Without introducing any subjective external assumptions, nonparametric bounds of causal effects can be often formulated based solely on the information from the data (e.g., Manski, 2003). Assuming a sufficiently large sample, bounds of causal effects can be constructed based on sample statistics.

Since identification of μ_0,0 is dependent on identification of ${\pi }_{0,0}^R$, as shown in (4), let us first derive the bounds for ${\pi }_{0,0}^R$. According to (2), ${\pi }_{1,0}^R=\{{\pi }_0^R-{\pi }_{0,0}^R(1-{\pi }_c)\}∕{\pi }_c$, which cannot exceed one or fall below zero. Therefore, ${\pi }_{0,0}^R$ must lie within the range

$$\mathit{max}\left[\frac{{\pi }_0^R-{\pi }_c}{1-{\pi }_c},0\right]\le {\pi }_{0,0}^R\le \mathit{min}\left[\frac{{\pi }_0^R}{1-{\pi }_c},1\right],$$ (6)

where all the involved parameters are directly estimable. by replacing π_c and ${\pi }_0^R$ with sample statistics p_c and $p_0^R$ in Table 1, the large sample bounds for ${\pi }_{0,0}^R$ are obtained as (0.522, 1.000).

The employment status is a binary variable. Therefore, the average employment rate μ_1,0 should fall between 0 and 1. With this restriction, the bounds for outcome μ_0,0 are derived from (4) as

$$\mathit{max}\left[\frac{{\mu }_0^{\mathit{obs}}{\pi }_0^R-{\pi }_0^R+{\pi }_{0,0}^R(1-{\pi }_c)}{{\pi }_{0,0}^R(1-{\pi }_c)},0\right]\le {\mu }_{0,0}\le \mathit{min}\left[\frac{{\mu }_0^{\mathit{obs}}{\pi }_0^R}{{\pi }_{0,0}^R(1-{\pi }_c)},1\right],$$ (7)

where all the involved parameters are directly estimable except ${\pi }_{0,0}^R$. By applying the allowable values of ${\pi }_{0,0}^R$ and by replacing ${\mu }_0^{\mathit{obs}}$, ${\pi }_0^R$, and π_c with sample statistics ${\stackrel{‒}{y}}_0$, $p_0^R$ and p_c, the large sample bounds for μ_0,0 are obtained. Note that the bounds for μ_0,0 vary depending on the value of ${\pi }_{0,0}^R$. The bounds for μ_0,0 are (0, 1) at the lower limit of ${\pi }_{0,0}^R$, and (0, 0.602) at the upper limit of ${\pi }_{0,0}^R$.

Given that μ_0,0 should lie between 0 and 1, from (4), the bounds for μ_1,0 are

$$\mathit{max}\left[\frac{{\mu }_0^{\mathit{obs}}{\pi }_0^R-{\pi }_{0,0}^R(1-{\pi }_c)}{{\pi }_0^R-{\pi }_{0,0}^R(1-{\pi }_c)},0\right]\le {\mu }_{1,0}\le \mathit{min}\left[\frac{{\mu }_0^{\mathit{obs}}{\pi }_0^R}{{\pi }_0^R-{\pi }_{0,0}^R(1-{\pi }_c)},1\right],$$ (8)

where all the involved parameters are directly estimable except ${\pi }_{0,0}^R$. By applying the allowable values of ${\pi }_{0,0}^R$ and sample statistics ${\stackrel{‒}{y}}_0$, $p_0^R$ and p_c, the large sample bounds for μ_1,0 are obtained. The bounds for μ_1,0 are (0.067, 0.507) at the lower limit of ${\pi }_{0,0}^R$, and (0, 0.847) at the upper limit of ${\pi }_{0,0}^R$.

Finally, the bounds on the average causal effect for compliers (CACE) are derived based on (8) and μ_1,1 as

$${\mu }_{1,1}-\mathit{min}\left[\frac{{\mu }_0^{\mathit{obs}}{\pi }_0^R}{{\pi }_0^R-{\pi }_{0,0}^R(1-{\pi }_c)},1\right]\le {\mu }_{1,1}-{\mu }_{1,0}\le {\mu }_{1,1}-\mathit{max}\left[\frac{{\mu }_0^{\mathit{obs}}{\pi }_0^R-{\pi }_{0,0}^R(1-{\pi }_c)}{{\pi }_0^R-{\pi }_{0,0}^R(1-{\pi }_c)},0\right],$$ (9)

where μ_1,1 is directly estimable from the data. By applying the allowable values of ${\pi }_{0,0}^R$ and sample statistics ${\stackrel{‒}{y}}_{1,1}$, ${\stackrel{‒}{y}}_0$, $p_0^R$ and p_c, the large sample bounds for CACE are obtained. The bounds for CACE are (−0.108, 0.331) at the lower limit of ${\pi }_{0,0}^R$, and (−0.449, 0.398) at the upper limit of ${\pi }_{0,0}^R$. Therefore, the overall large sample bounds for CACE are (−0.449, 0.398), which are not so informative. According to these bounds, even without considering any sample errors, the JOBS II intervention might have had a very positive (i.e., increase in the employment rate by 0.4), very negative(i.e., decrease in the employment rate by 0.45), or no effect at all for those who would abide by the assigned intervention treatment.

Figure 1 shows more details on how CACE changes as a function of allowable values of ${\pi }_{0,0}^R$ and μ_0,0. In the presence of nonresponse, the bounds for mean outcomes vary depending on response probabilities, as shown in (7) and (8). As a result, the bounds for CACE also vary depending on the value of ${\pi }_{0,0}^R$. Panel (a) in Figure 1 shows that the bounds for CACE get widened as ${\pi }_{0,0}^R$ increases. Panel (a) also shows that imposing restrictions on ${\pi }_{0,0}^R$ is not enough to determine the sign of CACE, implying the need for an assumption (or assumptions) that restricts the range of μ_0,0. Panel (b) shows how CACE changes as a function of μ_0,0 and how that relationship changes as a function of ${\pi }_{0,0}^R$. As ${\pi }_{0,0}^R$ increases, μ_0,0 has narrower bounds, and the CACE value is more sensitive to the change of μ_0,0.

Figure 1.

Possible CACE within the natural bounds for ${\pi }_{0,0}^R$ and μ_0,0.

5 Alternative Identifying Assumptions

To obtain scientifically plausible ranges of nonidentified parameters and tighter bounds for causal effects, this study jointly considers multiple identifying assumptions that posit alternative theories regarding each nonidentified parameter.

5.1 Response Assumptions

Three point-identifying and three bounding assumptions are considered regarding the response behavior of participants in the JOBS II intervention study. The same point-identifying assumptions have been previously used to examine sensitivity of principal effect estimates to the choice among missing data assumptions (Mealli et al., 2004).

MAR (Missing At Random)

The probability of outcome being recorded is not associated with the outcome conditional on treatment assignment and observed treatment receipt status (Y_i ⊥ R_i | Z_i, D_i), which is consistent with the MAR assumption discussed in Little & Rubin (2002). In the current setting, a sufficient restriction to satisfy this condition is that ${\pi }_{1,0}^R={\pi }_{0,0}^R$^§. Let $\delta ={\pi }_{1,0}^R-{\pi }_{0,0}^R$, which indicates a deviation from MAR. Under MAR, δ = 0.

MAR^B (MAR-Bounded)

δ ≥ 0 (i.e., ${\pi }_{1,0}^R\ge {\pi }_{0,0}^R$). In JOBS II, some deviation from MAR is expected because individuals who comply with the treatment are also more likely to comply with requests to complete questionnaires at the follow-up assessment than individuals who decide not to comply with the treatment. The observed data in the intervention condition, although indirectly, also supports the plausibility of MAR^B (i.e., compliers showed a substantially higher response rate than noncompliers).

RER (Response Exclusion Restriction)

For noncompliers, response behavior is not affected by treatment assignment status. That is, R_i ⊥ Z_i | C_i = 0, which implies that ${\pi }_{0,1}^R={\pi }_{0,0}^R$. Along with MAR, this is another assumption that has been previously suggested to model the relationship between noncompliance and nonresponse (Frangakis & Rubin, 1999). Let $\beta ={\pi }_{0,1}^R-{\pi }_{0,0}^R$, which indicates a deviation from RER. Under RER, β = 0.

RER^B (RER-Bounded)

β ≤ 0 (i.e., ${\pi }_{0,1}^R\le {\pi }_{0,0}^R$). In JOBS, some deviation from RER is possible because the trial did not employ blinding or double-blinding. If RER is violated, it is very likely that noncompliers assigned to the treatment condition and failed to comply with the treatment responded less at follow-up than their counterparts in the control condition who did not experience this negative psychological effect from failing to receive the treatment.

SCR (Stable Complier Response)

For compliers, response behavior is unaffected by treatment assignment status. In other words, compliant study participants are likely to show stable response behavior regardless of intervention assignment. In Mealli et al. (2004), this assumption is referred to as the response exclusion restriction for compliers. In the current setting, for compliers, R_i ⊥ Z_i | C_i = 1, which implies that ${\pi }_{1,0}^R={\pi }_{1,1}^R$. Let $\zeta ={\pi }_{1,1}^R-{\pi }_{1,0}^R$, which indicates a deviation from SCR. Under SCR, ζ = 0.

SCR^B (SCR-Bounded)

ζ ≥ 0 (i.e., ${\pi }_{1,1}^R\ge {\pi }_{1,0}^R$). In JOBS, there is a possibility of deviation from SCR, given that the trial was not blinded. If the assumption is violated, it is very likely that compliers respond more at the follow-up when assigned to the intervention condition than when assigned to the control condition. In JOBS II, the intervention participants evaluated the intervention program very positively. As a consequence, it is likely that they felt more inclined/obliged to reciprocate what they got by helping the researchers and by providing the follow-up data. The observed data in the intervention condition, although indirectly, also supports the plausibility of SCR^B (i.e., individuals in the intervention condition showed a substantially higher response rate than individuals in the control condition).

5.2 Outcome Assumptions

Two point-identifying assumptions and two bounding assumptions are considered regarding the reemployment outcome in the JOBS II intervention study.

OER (Outcome Exclusion Restriction)

For noncompliers, the distributions of the potential outcomes are independent of the treatment assignment (Angrist et al., 1996). That is, Y_i(1) = Y_i(0) for units with C_i = 0, which directly implies that μ_0,1 = μ_0,0 in the current setting. This assumption has been widely used in practice, although its plausibility is often questioned when applied to experiments that do not employ blinding. Let γ₀ = μ_0,1−μ_0,0, which indicates a deviation from OER, or, the assignment effect for noncompliers (NACE: noncomplier average causal effect). Under OER, γ₀ = 0.

OER^B (OER-Bounded)

γ₀ ≥ 0 (i.e., μ_0,1 ≥ μ_0,0). In JOBS, where blinding was not an option, some deviation from the exclusion restriction is possible due to the psychological effect of treatment assignment. One possible scenario is that noncompliers assigned to the treatment condition felt more optimistic about their reemployment possibility, or felt that they should take more initiative in job search given that they failed to receive the intervention treatment. Another possibility is that noncompliers assigned to the treatment condition experienced negative psychological effect of failing to receive the treatment. The two scenarios provide opposite bounding information, and it is not clear which scenario is more realistic. Given this open possibilities, OER^B(i.e., γ₀ ≥ 0) is adopted as a conservative bounding assumption because the size of CACE only gets larger as the opposite holds (i.e., γ₀ < 0).

AER (Average Effect Restriction)

The distributions of the potential causal effects are independent of the compliance status. That is, Y_i(1) − Y_i(0) ⊥ C_i, which directly implies that μ_1,1 − μ_1,0 = μ_0,1 − μ_0,0 in the current setting. This assumption is considered as a scientifically plausible worst case scenario. Let η = γ₁ − γ₀, where γ₁ = CACE (μ_1,1 − μ_1,0), and γ₀ = NACE (μ_0,1 − μ_0,0). Under AER, η =0.

AER^B (AER-Bounded)

η ≥ 0 (i.e., γ₁ ≥ γ₀). In JOBS II, even if we take into account some psychological effect of treatment assignment, AER is an unrealistic assumption meaning that intervention assignment has the same effect on the outcome regardless of individuals' compliance status. Instead, it is more reasonable to assume that the treatment assignment has a larger effect on compliers since they are the ones who would receive the intensive JOBS II intervention treatment. Given that the training program provided critical information and skills necessary for high quality reemployment and that intervention participants highly evaluated the intervention program, the opposite scenario (i.e., η < 0) is very unlikely. Besides, η < 0 means a substantial deviation from OER, which is also unlikely given that the effect of treatment assignment on noncompliers is mainly psychological.

6 Point Estimators

First, on the basis of the point-identifying assumptions, various point estimates of CACE can be obtained in a straightforward manner. Restrictions in any pair of bounding parameters in the Cartesian product sets {δ, β, ζ}×{γ₀,η} identifies ${\pi }_{0,0}^R$ and μ_0,0. Under these assumptions, μ_0,0 and ${\pi }_{0,0}^R$ in (5) can be replaced by quantities directly estimable from the observed data (see Tables 1 and 2).

Assuming one of the response (MAR, RER, SCR) and one of the outcome (OER, AER) assumptions, six estimators of CACE can be constructed from (5) as

$${\mathit{CACE}}^{\mathit{MAR}.\mathit{OER}}={\mu }_{1,1}-\left\{\frac{{\mu }_0^{\mathit{obs}}-{\mu }_{0,1}(1-{\pi }_c)}{{\pi }_c}\right\},$$ (10)

$${\mathit{CACE}}^{\mathit{RER}.\mathit{OER}}={\mu }_{1,1}-\left\{\frac{{\mu }_0^{\mathit{obs}}{\pi }_0^R-{\mu }_{0,1}{\pi }_{0,1}^R(1-{\pi }_c)}{{\pi }_0^R-{\pi }_{0,1}^R(1-{\pi }_c)}\right\},$$ (11)

$${\mathit{CACE}}^{\mathit{SCR}.\mathit{OER}}={\mu }_{1,1}-\left\{\frac{{\mu }_0^{\mathit{obs}}{\pi }_0^R-{\mu }_{0,1}({\pi }_0^R-{\pi }_{1,1}^R{\pi }_c)}{{\pi }_{1,1}^R{\pi }_c}\right\},$$ (12)

$${\mathit{CACE}}^{\mathit{MAR}.\mathit{AER}}={\mu }_{1,1}-\left\{{\mu }_0^{\mathit{obs}}+({\mu }_{1,1}-{\mu }_{0,1})(1-{\pi }_c)\right\},$$ (13)

$${\mathit{CACE}}^{\mathit{RER}.\mathit{AER}}={\mu }_{1,1}-\left\{{\mu }_0^{\mathit{obs}}+\frac{({\mu }_{1,1}-{\mu }_{01,}){\pi }_{0,1}^R(1-{\pi }_c)}{{\pi }_0^R}\right\},$$ (14)

$${\mathit{CACE}}^{\mathit{SCR}.\mathit{AER}}={\mu }_{1,1}-\left\{\frac{{\mu }_0^{\mathit{obs}}{\pi }_0^R+({\mu }_{1,1}-{\mu }_{0,1})({\pi }_0^R-{\pi }_c{\pi }_{1,1}^R)}{{\pi }_0^R}\right\},$$ (15)

Estimates of CACE based on the method of moments estimator are reported in Table 3. Standard errors were calculated using the delta method. The estimator assuming RER and AER presents the smallest CACE, whereas the estimator assuming MAR and OER presents the largest CACE, and the difference is quite large considering that the outcome is reemployment. Which estimates lie within the scientifically plausible range and which estimators are more sensitive to deviation from their point-identifying assumptions will be discussed in the following sections.

Table 3.

Point Estimates of CACE (standard error in parentheses)

MAR.OER	SCR.OER	RER.OER	MAR.AER	SCR.AER	RER.AER
0.179 (0.083)	0.166 (0.080)	0.144 (0.073)	0.097 (0.044)	0.095 (0.044)	0.089 (0.044)

7 Large-Sample Nonparametric Bounds With Alternative Bounding Assumptions

In Section 5, we considered alternative identifying assumptions that impose restrictions on two non-identified parameters (i.e., ${\pi }_{0,0}^R$ and μ_0,0). To represent deviations from these assumptions, bounding parameters were formed (δ, β, and ζ for the response, γ₀ and η for the outcome). The main message of this paper is that it is possible to narrow the bounds for CACE by making reasonable assumptions that restrict the values of a number of distinct non-identified, though easily interpretable, contrasts (the contrasts being defined by the parameters δ, β, ζ, γ₀, and η). Because of translatability across bounding parameters, knowledge of the values taken by any pair in the Cartesian product sets {δ, β, ζ}×{γ₀, η} identifies ${\pi }_{0,0}^R$ and μ_0,0 and the remaining parameters in each set of the Cartesian product. We will demonstrate that restrictions on one pair of the Cartesian product also restricts the values of the remaining pairs and that combining restrictions on the range of plausible values of each of the bounding parameters in {δ, β, ζ} and {γ₀, η} yields a refinement of the bounds for CACE.

7.1 Response Assumptions

We considered three bounding parameters (δ, β, ζ) that is commonly related to ${\pi }_{0,0}^R$. These bounding parameters and ${\pi }_{0,0}^R$ are completely cross-translatable (i.e., any of them can be expressed in terms of any of the others). Since there is one to one relationship between any pairs of δ, β, ζ, and ${\pi }_{0,0}^R$, if the value of any one of these parameters is given, the rest can be derived.

For example, from (2) and definitions of δ (i.e., ${\pi }_{1,0}^R-{\pi }_{0,0}^R$), β (i.e., ${\pi }_{0,1}^R-{\pi }_{0,0}^R$), and ζ (i.e., ${\pi }_{1,1}^R-{\pi }_{1,0}^R$),

$$\delta =\frac{{\pi }_0^R-{\pi }_{0,0}^R}{{\pi }_c},$$ (16)

$$\beta ={\pi }_{0,1}^R-{\pi }_{0,0}^R,$$ (17)

$$\zeta =\frac{{\pi }_{1,1}^R{\pi }_c+{\pi }_{0,0}^R(1-{\pi }_c)-{\pi }_0^R}{{\pi }_c},$$ (18)

where all the parameters except δ, β, ζ, and ${\pi }_{0,0}^R$ are directly estimable from the observed data. A full translation across δ, β, ζ, and ${\pi }_{0,0}^R$ is shown in Appendix A.

On the basis of cross-translatability, alternative bounding assumptions can be combined to form common bounds for ${\pi }_{0,0}^R$. From (16), MAR^B (i.e., δ ≥ 0), is translated as ${\pi }_{0,0}^R\le {\pi }_0^R$. From (17), RER^B (i.e., β ≤ 0), is translated as ${\pi }_{0,0}^R\ge {\pi }_{0,1}^R$. From (18), SCR^B (i.e., ζ ≥ 0), is translated as ${\pi }_{0,0}^R\ge ({\pi }_0^R-{\pi }_{1,1}^R{\pi }_c)∕(1-{\pi }_c)$. Then, the common bounds for ${\pi }_{0,0}^R$ are

$$\mathit{max}\left[{\pi }_{0,1}^R,\frac{{\pi }_0^R-{\pi }_{1,1}^R{\pi }_c}{1-{\pi }_c}\right]\le {\pi }_{0,0}^R\le {\pi }_0^R.$$ (19)

According to sample statistics, ${\pi }_{0,1}^R<({\pi }_0^R-{\pi }_{1,1}^R{\pi }_c)∕(1-{\pi }_c)$. Therefore, SCR^B determines the lower bound and MAR^B determines the upper bound in (19). By replacing π_c, ${\pi }_{1,1}^R$, and ${\pi }_0^R$ with sample statistics p_c, $p_{1,1}^R$, and $p_0^R$ in Table 1, the large sample bounds for ${\pi }_{0,0}^R$ are obtained as (0.738, 0.782).

Plausibility of (or deviation from) alternative assumptions can be compared and can be viewed from multiple perspectives once they are put on the same scale. Figure 2 shows the relationship among δ, β, ζ, and ${\pi }_{0,0}^R$ based on a full translation across them (see Appendix A) within the common bounds for ${\pi }_{0,0}^R$. The figure shows the importance of translation across assumptions before judging relative plausibility of competing identifying assumptions.

Figure 2.

Translation across response assumptions

Making use of sample statistics, the upper bound of ${\pi }_{0,0}^R$ based on MAR^B translates to ${\pi }_{0,0}^R\le 0.782$. MAR^B translates to ζ ≤ 0.036, indicating a slight assignment effect on compliers' response behavior. The decision on the lower bound of ${\pi }_{0,0}^R$ can be quite arbitrary if we approach from MAR^B. It is difficult to decide how large δ should be. The lower bound of ${\pi }_{0,0}^R$ can be more confidently made based on SCR^B. SCR^B translates to ${\pi }_{0,0}^R\le 0.738$, which is the lower bound of ${\pi }_{0,0}^R$. SCR (i.e., ζ ≥ 0) translates to δ ≤ 0.080, indicating that compliers' response rate was somewhat higher than noncompliers' in the absence of treatment. Translation between MAR^B and SCR^B shows that each assumption provides a reasonable scenario for response behavior when viewed from the other assumption.

Although RER^B did not directly determine the bounds for ${\pi }_{0,0}^R$, the assumption contributes to validation of MAR^B and SCR^B, which indicate reasonable deviation from RER when expressed in terms of β. That is, MAR^B (i.e., δ ≥ 0) translates to β ≥ −0.128, and SCR^B translates to β ≤ −0.085. Together, MAR^B and SCR^B imply a negative but not too large treatment assignment effect on noncompliers' response behavior, which is realistic both in terms of the size and the direction of deviation from RER. This kind of insight is hard to achieve if we only consider the plausibility of one assumption.

7.2 Outcome Assumptions

Two bounding parameters for the outcome (γ₀, η) impose restrictions on the same parameter μ_0,0. The bounding parameter γ₀ and μ_0,0 are simply cross-translatable. However, cross-translation between η and γ₀ and cross-translation between η and μ_0,0 involves ${\pi }_{0,0}^R$, which is not directly estimable.

For example, from (3) and definitions of γ₀ (i.e., ${\mu }_{0,1}-{\mu }_{0,0}$)and η (i.e., ${\gamma }_1-{\gamma }_0$, where γ₁ = μ_1,1 − μ_1,0 and γ₀ = μ_0,1 − μ_0,0),

$${\gamma }_0={\mu }_{0,1}-{\mu }_{0,0},$$ (20)

$$\eta ={\mu }_{1,1}-{\mu }_{0,1}+\frac{({\mu }_{0,0}-{\mu }_0){\pi }_0^R}{{\pi }_0^R-{\pi }_{0,0}^R(1-{\pi }_c)},$$ (21)

where all the parameters except γ₀, η, μ_0,0, and ${\pi }_{0,0}^R$ are directly estimable from the observed data. A full translation across γ₀, η, and μ_0,0 is shown in Appendix.

On the basis of cross-translation, alternative bounding assumptions can be combined to form common bounds for μ₀ 0. From (20), OER^B (i.e., γ₀ ≥ 0), is translated as μ_0,0 ≤ μ_0,1. From (21), AER^B (i.e., γ₁ − γ₀ ≥ 0), is translated as ${\mu }_{0,0}\le {\mu }_{0,1}$. From (21), AER^B (i.e.,${\gamma }_1-{\gamma }_0\ge 0$), is translated as ${\mu }_{0,0}\ge [{\mu }_0^{\mathit{obs}}{\pi }_0^R-({\mu }_{1,1}-{\mu }_{0,1})\{{\pi }_0^R-{\pi }_{0,0}^R(1-{\pi }_c)\}]∕{\pi }_0^R$. Then, the common bounds for μ_0,0 are

$$\frac{{\mu }_0^{\mathit{obs}}{\pi }_0^R-({\mu }_{1,1}-{\mu }_{0,1})\{{\pi }_0^R-{\pi }_{0,0}^R(1-{\pi }_c)\}}{{\pi }_0^R}\le {\mu }_{0,0}\le {\mu }_{0,1},$$ (22)

where AER^B determines the lower bound and OER^B determines the upper bound. The bounds in (22) require that ${\mu }_{0,1}\ge [{\mu }_0^{\mathit{obs}}{\pi }_0^R-({\mu }_{1,1}-{\mu }_{0,1})\{{\pi }_0^R-{\pi }_{0,0}^R(1-{\pi }_c)\}]∕{\pi }_0^R$, which holds in the JOBS II intervention trial according to sample statistics. By applying allowable values of ${\pi }_{0,0}^R$, and by replacing ${\mu }_0^{\mathit{obs}}$, μ_1,1, μ_0,1, π_c, and ${\pi }_0^R$ with sample statistics ${\stackrel{‒}{y}}_0$, ${\stackrel{‒}{y}}_{1,1}$, ${\stackrel{‒}{y}}_{0,1}$, p_c, and $p_0^R$, the large sample bounds for μ_0,0 are obtained as (0.416, 0.510) at the lower limit of ${\pi }_{0,0}^R$, and (0.413, 0.510) at the upper limit of ${\pi }_{0,0}^R$.

Figure 3 shows the relationship between γ₀, η, and μ_0,0 based on a full cross-translation (see Appendix A) within the common bounds for μ_0,0 and ${\pi }_{0,0}^R$. The figure shows that intuitive decisions on relative plausibility, such as which assumption seems stronger or weaker, can be quite misleading. Based on cross-translation, the comparison can be made systematically.

Figure 3.

Translation across outcome assumptions

Given that no active treatment was given to noncompliers, AER^B is considered a highly plausible assumption in JOBS II. AER^B (η ≥ 0) determines the lower bound of μ_0,0, and translates to γ₀ ≤ 0.094 at the lower limit of ${\pi }_{0,0}^R(=0.738)$, and translates to γ₀ ≤ 0.097 at the upper limit of ${\pi }_{0,0}^R(=0.782)$, implying that OER^B is correct but deviation from OER is quite small. Although it is likely that CACE > NACE, it is arbitrary to decide how much larger CACE should be. The decision on the upper bound for μ_0,0 can be more comfortably made by taking the OER perspective. OER^B translates to η ≤ 0.166 at the lower bound of ${\pi }_{0,0}^R$, and translates to η ≤ 0.179 at the upper bound of ${\pi }_{0,0}^R$. If OER^B does not hold, η > 0.166, or, η > 0.179, indicating a much larger effect of treatment assignment on compliers (CACE) than on never-takers (NACE). Therefore, OER^B can be considered as a conservative assumption compared to the assumption that γ₀ < 0.

7.3 CACE

Based on (4) and the bounds for μ_0,0 in (22), the bounds for μ_1,0 at the lower limit of ${\pi }_{0,0}^R$ (i.e., from (19), ${\pi }_{0,0}^R=({\pi }_0^R-{\pi }_{1,1}^R{\pi }_c)∕(1-{\pi }_c)$) are

$$\frac{{\mu }_0^{\mathit{obs}}{\pi }_0^R-{\mu }_{0,1}({\pi }_0^R-{\pi }_{1,1}^R{\pi }_c)}{{\pi }_{1,1}^R{\pi }_c}\le {\mu }_{1,0}\le \frac{{\mu }_0^{\mathit{obs}}{\pi }_0^R+({\mu }_{1,1}-{\mu }_{0,1})({\pi }_0^R-{\pi }_c{\pi }_{1,1}^R)}{{\pi }_0^R},$$ (23)

where all the involved parameters are directly estimable. By applying sample statistics, the large sample bounds for μ_1,0 are obtained as (0.232, 0.304).

Based on (4) and the bounds for μ_0,0 in (22), the bounds for μ_1,0 at the upper limit of ${\pi }_{0,0}^R$ (i.e., from (19), ${\pi }_{0,0}^R={\pi }_0^R$) are

$$\frac{{\mu }_0^{\mathit{obs}}-{\mu }_{0,1}(1-{\pi }_c)}{{\pi }_c}\le {\mu }_{1,0}\le {\mu }_0^{\mathit{obs}}+({\mu }_{1,1}-{\mu }_{0,1})(1-{\pi }_c),$$ (24)

where all the involved parameters are directly estimable. By applying sample statistics, the large sample bounds for μ_1,0 are obtained as (0.219, 0.301).

Based on (23), the bounds on CACE are defined at the lower limit of ${\pi }_{0,0}^R$ as

$${\mu }_{1,1}-\left\{\frac{{\mu }_0^{\mathit{obs}}{\pi }_0^R+({\mu }_{1,1}-{\mu }_{0,1})({\pi }_0^R-{\pi }_c{\pi }_{1,1}^R)}{{\pi }_0^R}\right\}\le {\mu }_{1,1}-{\mu }_{1,0}\le {\mu }_{1,1}-\left\{\frac{{\mu }_0^{\mathit{obs}}{\pi }_0^R-{\mu }_{0,1}({\pi }_0^R-{\pi }_{1,1}^R{\pi }_c)}{{\pi }_{1,1}^R{\pi }_c}\right\},$$ (25)

where the lower bound corresponds to the point estimator CACE^SCR.AER, which assumes SCR and AER, and the upper bound corresponds to CACE^SCR.OER, which assumes SCR and OER.

Based on (24), the bounds on CACE are defined at the upper limit of ${\pi }_{0,0}^R$ as

$${\mu }_{1,1}-\{{\mu }_0^{\mathit{obs}}+({\mu }_{1,1}-{\mu }_{0,1})(1-{\pi }_c)\}\le {\mu }_{1,1}-{\mu }_{1,0}\le {\mu }_{1,1}-\left\{\frac{{\mu }_0^{\mathit{obs}}-{\mu }_{0,1}(1-{\pi }_c)}{{\pi }_c}\right\},$$ (26)

where the lower bound corresponds to the point estimator CACE^MAR.AER, which assumes MAR and AER, and the upper bound corresponds to CACE^MAR.OER, which assumes MAR and OER.

Based on (25), (26), and sample statistics, the large sample bounds on CACE are (0.095, 0.166) at the lower limit of ${\pi }_{0,0}^R$ and (0.097, 0.179) at the upper limit of ${\pi }_{0,0}^R$. Given that, the overall large sample bounds on CACE are (0.095, 0.179), where the lower bound can be estimated by the point estimator CACE^SCR.AER and the upper bound by the point estimator CACE^MAR.OER (see Section 6 and Table 3). To reflect uncertainty in the estimated bounds, the bounds can be wrapped in confidence bands. Using the method to construct confidence intervals for bound estimates, suggested by Imbens and Manski (2004), the 95% confidence intervals for the overall bounds of CACE were obtained as (0.021, 0.319). See Appendix B for details of this procedure. The bounds on CACE established by combining alternative assumptions provide much narrowed range of possible CACE (compared to the natural bounds). Under informative, but still conservative assumptions, the resulting range of the CACE indicates a positive, and possibly substantial impact of the JOBS II intervention on compliers.

8 Sensitivity Analysis and Model Selection

Sometimes, instead of bounds, a point estimate with identifying assumptions we believe plausible is of primary interest. Comparing plausibility is straightforward (as shown in Figures 2 and 3) as long as alternative assumptions are connected through the same parameter. However, sensitivity analysis is still necessary in model selection, since more plausible assumptions may or may not result in less biased estimates (unless assumptions strictly hold). On the basis of cross-translation, comparing sensitivity across competing models is also straightforward even with multiple identifying assumptions.

By subtracting (5) from each point estimator, the total bias can be defined. Further, the total bias can be partitioned depending on its sources. For example, let us consider two estimators, CACE^MAR.OER and CACE ^SCR.AER.

Bias in the estimation of CACE due to deviation from MAR and OER (i.e., δ and γ) can be written as

$${\mathit{CACE}}_{\mathit{bias}}^{\mathit{MAR}.\mathit{OER}}=-\frac{\delta (1-{\pi }_c)({\mu }_0^{\mathit{obs}}-{\mu }_{0,1})}{{\pi }_c\{{\pi }_0^R+\delta (1-{\pi }_c)\}}+\frac{\gamma (1-{\pi }_c)}{{\pi }_c}-\frac{\delta \gamma (1-{\pi }_c)}{{\pi }_c\{{\pi }_0^R+\delta (1-{\pi }_c)\}},$$ (27)

where all the involved parameters are directly estimable except δ and γ.

Bias in the estimation of CACE due to deviation from SCR and AER (i.e., ζ and η) can be written as

$${\mathit{CACE}}_{\mathit{bias}}^{\mathit{SCR}.\mathit{AER}}=\frac{\zeta {\pi }_c({\mu }_{1,1}-{\mu }_{0,1})}{{\pi }_0^R}-\frac{\eta ({\pi }_0^R-{\pi }_{1,1}^R{\pi }_c)}{{\pi }_0^R}-\frac{\eta \zeta {\pi }_c}{{\pi }_0^R},$$ (28)

where all the involved parameters are directly estimable except ζ and η.

In (27) and (28), the total bias is partitioned into three parts, where the first part explains bias due to deviation from response assumptions (δ, ζ) and the second part explains bias due to deviation from outcome assumptions (γ, η). The third part explains additional bias due to interaction between deviations from the two assumptions (δγ, ηζ). For example, let us assume that μ_0,0 = 0.45 and ${\pi }_{0,0}^R=0.76$. Then, $\widehat{\delta }=0.040$, $\widehat{\zeta }=0.018$, $\widehat{\gamma }=0.060$, and $\widehat{\eta }=0.064$. According to (27) and (28), $C\widehat{AC}{E}_{\mathit{bias}}^{MAR.OER}=0.007+0.051-0.003=0.055$ and $C\widehat{AC}{E}_{\mathit{bias}}^{SCR.AER}=-0.001-0.028-0.001=-0.030$.

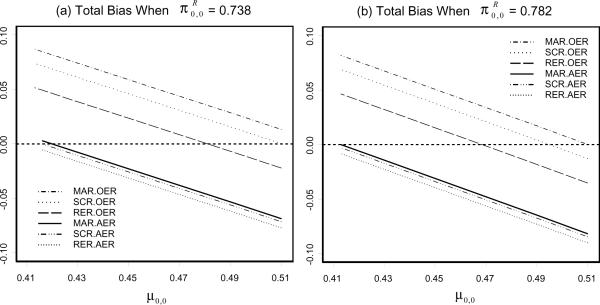
Figure 4 shows possible bias in all considered point estimators. Within the common bounds for μ_0,0 and ${\pi }_{0,0}^R$, more informative comparisons can be made. In general, estimators assuming OER tend to overestimate CACE, whereas estimators assuming AER underestimate CACE. Some interaction between response and outcome assumptions is also noticeable. Sensitivity to deviation from response assumptions (MAR, RER, and SCR) has a substantial variation when OER is imposed, whereas the variation is trivial when AER is imposed. Within the common bounds for μ_0,0 and ${\pi }_{0,0}^R$, different selections may be made depending on the purpose of the inference and the level of belief on plausibility of the assumptions. The most conservative choice would be any estimators assuming AER, with which CACE is almost never overestimated. A reasonable choice with some possibility of both overestimation and underestimation would be CACE^RER.OER.

Figure 4.

Possible bias in six point estimators of CACE within the common bounds for μ_0,0 and ${\pi }_{0,0}^R$.

9 Conclusion

It is convenient to employ common identifying assumptions in analyzing different data because properties of the assumptions are well known, and therefore there is less possibility of misunderstanding. However, this practice may lead to rigid thinking about what is possible in formulating point-identifying or bounding assumptions, and may discourage cross-examination of plausibility based on external assumptions.

This study demonstrated a flexible way of bounding and sensitivity analysis by using alternative identifying assumptions in the principal stratification framework. In particular, the emphasis was given to assumptions that can be cross-translated. Cross-translatability across assumptions is a convenient property that allows subject matter experts and analysts to explore various possible assumptions and directly compare and cross-examine their plausibility. In this framework, alternative assumptions rather jointly contribute than compete in narrowing bounds for causal effects. In the JOBS II example, based on alternative identifying assumptions, we formulated bounding parameters that can be completely cross-translated (δ, β, and ζ for the missing data indicator; γ₀ and η for the outcome). It was shown that restrictions on one pair of the Cartesian product {δ, β, ζ}×{γ₀,η} also restricts the values of the remaining pairs and that combining restrictions on the range of plausible values of each of the bounding parameters in {δ, β, ζ} and {γ₀,η} yields a refinement of the bounds for CACE.

For simplicity, the study considered a limited number of alternative assumptions in constructing tight bounds. However, alternative assumptions other than those that determine bounds can also be important for better cross-examination of plausibility and selection of less sensitive point estimators. The possibility of formulating various case-specific assumptions needs to be explored through applications in diverse settings. The number of non-identified parameters was also limited to two in this paper, focusing on a randomized experiment setting with treatment noncompliance and missing data. However, in practice, several complications may co-occur, increasing the number of non-identified parameters and increasing complexity in principal effect estimation (e.g., Barnard et al., 2003; Mattei & Mealli, 2007). Further investigation is needed to examine practicality of the proposed method in more complex situations.

Appendix A: Translation Across Bounding Parameters

From (2) and definitions of δ (${\pi }_{1,0}^R-{\pi }_{0,0}^R$), β (${\pi }_{0,1}^R-{\pi }_{0,0}^R$), and ζ (${\pi }_{1,1}^R-{\pi }_{1,0}^R$), response bounding parameters can be cross-translated as

$${\pi }_{0,0}^R={\pi }_0^R-\delta {\pi }_c,$$

$${\pi }_{0,0}^R={\pi }_{0,1,}^R-\beta ,$$

$${\pi }_{0,0}^R=\frac{\zeta {\pi }_c+{\pi }_0^R-{\pi }_{1,1}^R{\pi }_c}{1-{\pi }_c},$$

$$\delta =\frac{{\pi }_0^R-{\pi }_{0,0}^R}{{\pi }_c},$$

$$\delta =\frac{\beta +{\pi }_0^R-{\pi }_{0,1}^R}{{\pi }_c},$$

$$\delta =\frac{\zeta +{\pi }_0^R-{\pi }_{1,1}^R}{1-{\pi }_c},$$

$$\beta ={\pi }_{0,1}^R-{\pi }_{0,0}^R,$$

$$\beta =\delta {\pi }_c-{\pi }_0^R+{\pi }_{0,1}^R,$$

$$\beta =\frac{-\zeta {\pi }_c+{\pi }_{0,1}^R-{\pi }_0^R+({\pi }_{1,1}^R-{\pi }_{0,1}^R){\pi }_c}{1-{\pi }_c},$$

$$\zeta =\frac{{\pi }_{1,1}^R{\pi }_c+{\pi }_{0,0}^R(1-{\pi }_c)-{\pi }_0^R}{{\pi }_c},$$

$$\zeta ={\pi }_{1,1}^R-{\pi }_0^R-\delta (1-{\pi }_c),$$

$$\zeta =\frac{{\pi }_{1,1}^R{\pi }_c-{\pi }_0^R+({\pi }_{0,1}^R-\beta )(1-{\pi }_c)}{{\pi }_c}.$$

From (3) and definitions of γ₀ (μ_0,1 − μ_0,0) and η (γ₁ − γ₀), outcome bounding parameters can be cross-translated as

$${\mu }_{0,0}={\mu }_{0,1}-{\gamma }_0,$$

$${\mu }_{0,0}={\mu }_0+\frac{\eta -{\mu }_{1,1}+{\mu }_{0,1}}{{\pi }_0^R\{{\pi }_0^R-{\pi }_{0,0}^R(1-{\pi }_c)\}},$$

$${\gamma }_0={\mu }_{0,1}-{\mu }_{0,0},$$

$${\gamma }_0={\mu }_{0,1}-{\mu }_0+\frac{{\mu }_{1,1}-{\mu }_{0,1}-\eta }{{\pi }_0^R\{{\pi }_0^R-{\pi }_{0,0}^R(1-{\pi }_c)\}},$$

$$\eta ={\mu }_{1,1}-{\mu }_{0,1}+\frac{({\mu }_{0,0}-{\mu }_0){\pi }_0^R}{{\pi }_0^R-{\pi }_{0,0}^R(1-{\pi }_c)},$$

$$\eta ={\mu }_{1,1}-{\mu }_{0,1}\frac{({\mu }_{0,1}-{\gamma }_0-{\mu }_0){\pi }_0^R}{{\pi }_0^R-{\pi }_{0,0}^R(1-{\pi }_c)}.$$

Appendix B: Estimation of Confidence Intervals Using the Method Proposed by Imbens and Manski (2004)

Imbens and Manski's method gives a CI that asymptotically cover the true value of the estimator θ = f(λ) with unknown parameter λ (but λ ∈ Λ) with probability α. First, the bound of θ is given: L ≤ θ ≤ U,where L = min_λ∈Λ{f(λ)} and U = max_λ∈Λ{f(λ)}. Then, their Equation (6) gives the CI:

$${\mathrm{CI}}_{\alpha }^{\theta }=[L_n-{\stackrel{‒}{C}}_n{\widehat{\sigma }}_l∕\sqrt{n},U_n-{\stackrel{‒}{C}}_n{\widehat{\sigma }}_u∕\sqrt{n}],$$

where L_n and U_n are estimates of L and U, n is the size of sample data set, ${\widehat{\sigma }}_l$ and ${\widehat{\sigma }}_u$ are estimates for the standard errors of $\sqrt{n}(L_n-L)$ and $\sqrt{n}(U_n-U)$, and ${\stackrel{‒}{C}}_n$ satisfies their Equation (7):

$$\Phi ({\stackrel{‒}{C}}_n+\sqrt{n}\frac{\widehat{\Delta }}{\max \{{\widehat{\sigma }}_l,{\widehat{\sigma }}_u\}})-\Phi (-{\stackrel{‒}{C}}_n)=\alpha ,$$

where $\widehat{\Delta }=U_n-L_n$, and α is the confidence level. Finally, showed that

$$\underset{n\to \infty }{\overset{\lim }{}}\underset{\lambda \in \Lambda }{\overset{\inf }{}}\text{Prob}(\theta \in {\mathrm{CI}}_{\alpha }^{\theta })\ge \alpha$$

in their lemma 4.

Let ${\pi }_{0,0}^{R,l}$ denote the lower bound of ${\pi }_{0,0}^R$ and ${\pi }_{0,0}^{R,u}$ the upper bound of ${\pi }_{0,0}^R$ from (19). Let ${\mu }_{0,0}^l$ denote the lower bound of ${\mu }_{0,0}$ and ${\mu }_{0,0}^u$ the upper bound of μ_0,0 from (22) at the upper bound of ${\pi }_{0,0}^R$ in (19). Let L denote the lower bound of CACE, which is the LHS of and U the upper bound of CACE from (22) at the upper bound of ${\pi }_{0,0}^R$ in (19). In applying Imbens and Manski's method to our example, we replace θ by CACE, λ by {$\{{\pi }_{0,0}^R,{\mu }_{0,0}\}$}, Λ by $[{\pi }_{0,0}^{R,l},{\pi }_{0,0}^{R,u}]\times [{\mu }_{0,0}^l,{\mu }_{0,0}^u]$, L by CACE^SCR.AER (LHS of (25)), and U by CACE^MAR.OER (RHS of (26)). Let us also a for ${\stackrel{‒}{C}}_n{\widehat{\sigma }}_l∕\sqrt{n}$, and b for ${\stackrel{‒}{C}}_n{\widehat{\sigma }}_u∕\sqrt{n}$. Then we have the confidence interval [L_n − a, U_n + b] such that

$$\underset{n\to \infty }{\overset{\lim }{}}\underset{\{{\pi }_{00}^R,{\mu }_{00}\}\in [{\pi }_{0,0}^{R,l},{\pi }_{0,0}^{R,u}]\times [{\mu }_{0,0}^l,{\mu }_{0,0}^u]}{\overset{\inf }{}}\text{Prob}(\mathit{CACE}\in [L_n-a,U_n+b])\ge \alpha .$$

To get ${\widehat{\sigma }}_l∕\sqrt{n}$ and ${\widehat{\sigma }}_u∕\sqrt{n}$, we used the bootstrap with 10000 random samples. In this procedure, B random samples of size n are drawn with replacement from the original sample, and L and U are estimated from each of these samples. Thus the bootstrap estimate of the standard errors of L and U (i.e., ${\widehat{\sigma }}_l∕\sqrt{n}$ and ${\widehat{\sigma }}_u∕\sqrt{n}$) are the sample standard errors of the estimates over all the bootstrap samples. If $L_n^b$ and $U_n^b$ are estimates of L and U from the bth bootstrap sample, for b = 1, …, B, then ${\widehat{\sigma }}_l∕\sqrt{n}$ and ${\widehat{\sigma }}_u∕\sqrt{n}$ are estimated as

$$\sqrt{\sum _{b=1}^B{(L_n^b-{\stackrel{‒}{L}}_n)}^2∕(B-1)}\mathrm{and}\sqrt{\sum _{b=1}^B{(U_n^b-{\stackrel{‒}{U}}_n)}^2∕(B-1)}$$

where ${\stackrel{‒}{L}}_n={\Sigma }_{b=1}^B{L}_n^b∕B$ and ${\stackrel{‒}{U}}_n={\Sigma }_{b=1}^B{U}_n^b∕B$.