A Mathematical Approach to the Analysis of Multiplex DNA Profiles

Abstract

Multiplex DNA profiles are used extensively for biomedical and forensic purposes. However, while DNA profile data generation is automated, human analysis of those data is not, and the need for speed combined with accuracy demands a computer-automated approach to sample interpretation and quality assessment. In this paper, we describe an integrated mathematical approach to modeling the data and extracting the relevant information, while rejecting noise and sample artifacts. We conclude with examples showing the effectiveness of our algorithms.

Introduction

Our purpose is to describe a new approach to computer examination of multiplex STR DNA profiles. The approach is the foundation for the OSIRIS software program, or Open Source Independent Review and Interpretation System [1], [2], which we developed at the National Center for Biotechnology Information. It is based on a collection of mathematical algorithms inspired by a combination of theoretical and empirical understandings of the DNA analysis process. To facilitate a discussion of this approach, we now describe the uses and physical aspects of the multiplex STR DNA analyses processes in broad detail. For a more in depth exposition, see [3].

1. Background

a. Uses of DNA Profiles

Multiplex analyses of Short Tandem Repeats (STRs) are used extensively for biomedical and forensic purposes. Commercially available kits now permit the simultaneous interrogation of up to 20 genetic markers in a single examination. Automated analysis platforms can screen hundreds of samples per day per machine. This constellation of technological advances is used to support the high throughput generation of DNA profiles that can be stored in large databases and screened for matches of biomedical or forensic significance. Multiplex STR profiles for biomedical applications include cell-line authentication important to pathology and fertility investigations and population genetic assays in drug development studies. Large-scale forensic DNA data banking of multiplex STR profiles allows law enforcement to check convicted offenders’ profiles against DNA evidence from unsolved crimes to provide investigative leads. Forensic applications further cover civil paternity investigations, estimated at nearly half a million annually in the US. Medico-legal and humanitarian uses of DNA profiling include victim identification in mass fatalities where proof of death may be needed for insurance purposes as well as providing tangible proof to support the grieving process. When sufficient and appropriate DNA markers are used, a DNA profile can establish identity to statistical certainty, even among closely related individuals, although not between identical twins.

b. Analytic Processes

The analytic procedures leading to a multiplex STR DNA profile are the same whether for biomedical, forensic or humanitarian use. DNA is extracted from a biospecimen and examined for the genetic markers in question using the mainstay biochemical methods briefly described below. Besides providing a general framework for understanding multiplex STR DNA profiling, the reader should be aware that each of the steps can introduce artifactual variations in the signal output which we are mathematically modeling.

A sample is processed thermo-chemically using a technique known as the “polymerase chain reaction”, or PCR, that creates sample-dependent fragments of different sizes [3, pp. 63 – 75]. The mixture of fragments is driven electrochemically through an apparatus, or analytical platform, that separates liquid phase fragments by size using a method called electrophoresis. Finally, a human analyst examines the graphical output of electrophoresis generated by the analysis platform, often with the assistance of an expert system. The output allows the analyst to determine the genetic profile revealed by the analysis and to assess the quality of the test for reliability. The characteristics the analyst observes, called alleles, make up the profile for each genetic marker – or locus - examined. Typically, profiles are stored in databases for future mining.

For both the biomedical and forensic communities, the human element is the bottleneck in these high throughput environments. A delayed result can cause real human suffering in each arena. Misread or poor quality DNA profiles stall criminal investigations jeopardizing public safety while public health suffers when individuals’ diagnostic odysseys are confounded or delayed. We now briefly describe the uses and physical aspects of DNA profiles and associated artifacts that impact their quality and utility. For a more in depth exposition, see [3].

c. Characteristics of DNA Profiles

Multiplex DNA profiles reflect a small fraction of an individual’s genome (i.e. their entire genetic code) to identify specific landmarks. While the number and specifics of the landmarks chosen may vary between biomedical and forensic applications, the current US standard to declare identification in court or for medico-legal victim identification purposes is a core of 13 genetic loci specified by the FBI and sanctioned by law. These 13 core loci are independently inherited and each locus has a number of known variants within all known populations. These 13 core loci are required for analysis of convicted offender DNA and form the basis of the National DNA Index System (NDIS); the DNA equivalent of the federal fingerprint database [3, pp. 440 – 441]. Typically there are from 5–25 different alleles associated with each locus that are common to all known human populations, although the frequencies of these alleles may differ in different populations. Each person inherits two alleles per locus – one from each parent. The calculation of the individuality of a specific DNA profile is based on the binominal expansion of the frequency of the two alleles at a locus multiplied across all the independent loci used in the multiplex analysis. Depending on the subpopulation, the likelihood that two unrelated people would share alleles at all 13 of the required loci has been shown to be at least 1 in 2.77 × 10¹⁴ [3, p. 505].

d. Quality Concerns in DNA Profiling

By and large, DNA is a stable molecule that behaves predictably when exposed to the reagent kits and analytical platforms described above. The development of multiplex kits and robust electrophoresis platforms were the pivotal breakthroughs providing opportunities for automation and economies of scale which made high throughput analyses possible. The nearly 8 million DNA profiles of convicted offenders added to the National DNA Index System (see [4]) in the past five years alone, speak to the power of the system.

Nevertheless, optimizing a reaction so that 13 or more loci can be analyzed simultaneously on nanograms of target DNA is not without tradeoffs. The quality of the target DNA, techniques used to amplify (PCR) and separate the target DNA at the appropriate landmarks (electrophoresis), combined with accidental introduction of extraneous inhibiting materials and variations in the stability, separation, and balance of the different loci in the multiplex reaction, can all introduce artifacts in some – and sometimes many – of the loci that can render the profile, at best, difficult to interpret properly and, at worst, unusable. To be sure, the vast majority of DNA profiles generated for use in biomedicine and forensics are robust and uncomplicated, but discriminating sound profiles from ambiguous results requires automated assistance for those human reviewers charged with public health or public safety responsibilities.

2. Artifacts

The details of the causes of the artifacts are beyond the scope of this paper. However, our approach must encompass the identification of specific artifact types. The development of the profile into a usable “electropherogram” of peaks, accurately measured against control samples that can be relied upon, is not trivial. This is the central problem of multiplex DNA profiling: how to interpret the peaks that are output from electrophoresis in terms of the (STR) alleles of the original DNA sample versus the peaks that are the result of artifacts. The remainder of this paper details our mathematical and computational approach to solving this problem.

a. PCR Effects

PCR is the process of copying the target sequences of DNA by adding synthetic template DNA to the original sample in such a way that the synthetic template is incorporated into the original sample to recreate a copy of the original double helix. PCR is an amplification process. Changing the quantity of input DNA correspondingly changes the quantity of each amplified STR fragment and superposing two (or more) alleles in the input DNA, whether from the same or different loci, results in a bath with all the corresponding STR fragments. This superposition property is particularly important because it implies that an STR fragment detected following electrophoresis can be properly associated with a sample’s true genetic allele. We will see that there can be exceptions, but the exceptions can be inferred from other data.

Since there is an abundance of template DNA, in addition to the “target” original DNA more than one fragment for a given sample allele can occur. PCR can cause an artifact called “stutter”, in which secondary fragments are created during the PCR amplification process that, most often, have a size that is one repeat less than the input allele [3, pp. 123–126]. More rarely, the stutter peak is one repeat more than the input allele. Stutter products can be caused by many conditions during PCR, but they are made more likely by an increase in the quantity of input DNA. Typically, stutter products amount to 15% or less of the primary fragment from which they arise [3, pp. 125–126]. In a multiplex mix, different loci show different tolerances to the formation of stutter products during PCR.

Another PCR-induced artifact, called “non-template addition” or “partial adenylation” [3, pp. 127–129], occurs when higher-than-optimal quantities of DNA are amplified. The resulting artifact manifests itself as duplicate fragments, one base pair apart, corresponding to a single input allele, although, in practice, the extraneous peak is usually “small” (in height) compared to the primary peak. Because of their proximity to the true allele’s peak in the electropherogram, peak morphology can be compromised with split or “crater” peaks, explained below, confounding the analysis.

Finally, fragments of random size amplified to a lesser but non-repeatable extent produce an effect that shows up in the output electropherogram as apparent noise. While background noise at baseline is not difficult to identify, more extensive background noise can cause quality concerns and profile misinterpretation.

b. Other Sources of Artifacts

While PCR of multiplex STR DNA profiles is a common opportunity for these two important artifact classes (stutter and adenylation) to occur, there are a number of other artifact-inducing factors. DNA extraction, electrophoresis and the interactions among sample alleles lend themselves to other, specific artifact signatures that also must be assessed in determining the quality of each sample.

Other artifacts associated with electrophoresis are “dye blobs” and “spikes”. A dye blob arises when the fluorescent dye comes off its primer and migrates independently [3, p. 383]. Dye blobs have a characteristic shape that is different from an allelic peak. Spikes are sharp peaks that appear equally intense across all channels and can arise from a variety of conditions, such as urea crystals migrating in the buffer, that are usually not reproducible [3, p. 383].

In case of over-amplification during PCR, the laser sensor becomes saturated in any or all of its measured spectra during electrophoresis. This can cause artifacts because of the manner in which the dye colors are isolated. The dyes that are used to distinguish the channels have independent but overlapping spectra. Hence, an empirically determined color separation matrix is used to resolve the color spectrum measured by the laser at each observation time into the components that correspond to the dye values. This dye intensity matrix process works well as long as none of the fragments is sufficiently amplified that its dye input saturates the laser. Otherwise, the process falls outside the linear model range and applying the color separation matrix has the effect that artificial peaks appear in “secondary” channels, at virtually the same time as the over-amplified peaks in the “primary” channel. This phenomenon is called “pull-up” or “bleed-through” [3, pp. 335–337]. The pull-up peaks are numerical artifacts with no relationship to the physical presence of DNA in the sample.

An over-amplified peak and the resulting saturation of the laser can lead to a further manifestation called a “crater” or a “split peak”. Craters are often associated with pull-up, although not necessarily.

Other possible artifacts include poor peak morphology, which can be due to many causes beyond the scope of this article. Even if a peak has an appropriate shape, it may be either wider or narrower than expected, which should be flagged for human review.

Finally, as will be explained in greater detail below, certain control fragments with known sizes are routinely intermixed with the sample to help to calibrate the subsequent analysis. Because of ambient conditions at the time of electrophoresis, it is possible for one or more of the resulting control peaks to migrate in a manner such that their position, if used, may adversely effect the accuracy of the analysis.

While the in depth causes of these issues are beyond the scope of this article, nevertheless their manifestations are part of our model. We note that a new analysis technique may produce, as a side benefit, new metrics by which the quality of a peak may be assessed. Later, we will point out ways in which this occurs for the algorithms we have developed.

3. Defining the Mathematical Model

While the user communities require electropherogram results to be assessed in terms of their base-pair alleles, the data are actually time snapshots of the moment the fragment passed by the laser that measures fragment density during electrophoresis. We emphasize that there is no single continuous map across all loci that converts STR fragment size to an associated allelic repeat number because, within each locus,

$$\text{Fragment Length}=\text{Primer Length}+(\text{Core Repeat Number})\times (\text{Number of Repeats}),$$

and both primer length and core repeat number are dependent on the particular locus. The primers for each locus are designed to be distinguishable in a multiplex mixture. It is customary to identify alleles within a locus either by the number of repeats or by the fragment length.

We denote by ℓ² [1, ∞) the space of all vectors (a₁, a₂, …) such that ${\displaystyle {\sum }_{i=1}^{\mathrm{\infty }}{a}_i^2<\mathrm{\infty }}$. Then, each STR locus of a quantity of DNA (or mixture of DNA) corresponds to an element (a₁, a₂, …) of ℓ² [1, ∞), where a_i is the quantity of STR fragment with fragment length i.

In typical multiplex DNA reagent kits, samples are tagged with different fluorescent dyes so they may be separated through the application of a color matrix during electrophoresis, in order to reveal their alleles in a multi-channeled electropherogram. The typical dye kit, with three or four dyes, devotes one channel to a kit – a control channel consisting of a known quantity of pre-sized fragments which are included with the unknown sample DNA [3, p. 375]. Called the “internal lane standard”, or ILS, it, too, corresponds to an element of ℓ² [1, ∞). For example, if an ILS were to have pre-sized fragments at lengths of 75, 100, 150 and 200, then its vector would consist entirely of zero-valued components except for {a₇₅, a₁₀₀, a₁₅₀, a₂₀₀}.

We note that, with some care, we could restrict ourselves to finite (but large) dimensional vector spaces, but we will soon find ourselves dealing with outputs in infinite dimensional spaces, so we have judged the effort not to be worthwhile.

If N is the number of loci in the multiplex reagent kit, D is the number of dyes or channels and P is the mathematical map denoting PCR, and including the ILS control, then

$$P:{[{\ell }^2[1,\mathrm{\infty })]}^{N+1}\to {[{\ell }^2[1,\mathrm{\infty })]}^D.$$

4. The Electrophoresis Process

During electrophoresis, STR fragments of a given length essentially map into unimodal peaks on the appropriate dye channels, which are then sampled discretely. Later, we will discuss the shape and significance of these peaks. For this model, the amplification process of PCR, as well as electrophoresis are mapped linearly onto the observed output. Electrophoresis preserves superposition and, up to saturation, scaling. In practice, analysis by electrophoresis is run until some final time t_f. If L²[0, t_f] denotes the space of square integrable functions on the interval [0, t_f], and E is the map for electrophoresis, then

$$E:{[{\ell }^2[1,\mathrm{\infty })]}^D\to {[L^2[0,t_f]]}^D.$$

The overall PCR / electrophoresis process, S, is represented by the composition S ≡ E ∘ P, and

$$S:{[{\ell }^2[1,\mathrm{\infty })]}^{N+1}\to {[L^2[0,t_f]]}^D.$$

Pull-up, dye blobs and spikes, in addition to other peak-specific artifacts described above, all manifest themselves in the output in easily recognized ways and can be tested in a straightforward manner, which we will elaborate further below..

Hence, we can conclude that a single peak in the output of the electrophoresis stage, in the absence of clear evidence of an artifact, as above, can be linked to an STR fragment that must have occurred in the output of the PCR stage, and therefore to an allele of genetic origin in the original sample. Furthermore, because these peaks are unimodal, in theory we can link a particular time, the time of a peak’s mode, with an STR fragment. We postpone the exposition of how this is to be done until Section 7. First, we show how we can use the time of the mode of a peak to assess the fragment sizes, which, in turn, are assigned allele names.

It should be noted that a traditional theoretical model-based approach, in which a mathematical model of PCR and electrophoresis is formulated, validated and inverted, may not be practical. Even if a resolution of the difficulties of formulation and inversion were to fall into place, both PCR and electrophoresis are highly sensitive to ambient conditions, many of which are not measured. For example, samples are run in parallel capillary tubes each containing the same electrophoresis substrate on several of the analytical platforms commonly used in labs. However, there can be microhabitat differences in each of these capillary environments that can cause subtle but distinct differences in sample analysis outputs. Thus, validation for any particular sample run would be problematic. Before we can discuss a possible solution to these limitations, we must introduce the issues associated with comparing two different samples.

5. Comparing Different Samples Using the ILS

As suggested above, even if both PCR and then electrophoresis are run simultaneously on two different samples in parallel capillaries, it is known that their time signals are not directly comparable. Because of differences in the ambient micro-conditions within the separate analysis locations, for unknown samples, all that is known is that, for each sample individually, peaks are size sorted by the electrophoresis process, so that peaks occurring later in the sample run correspond to longer STR fragments.

However, every sample is electrophoresed with the internal lane standard (ILS), which consists of STR fragments of predetermined and known size. The ILS is assigned a unique dye and therefore occupies a single channel in the electrophoresis output. Since the choice of channel numbers is arbitrary, without loss in generality, we may assume that the ILS occupies the last channel.

Let us assume, for the moment, that for any sample ILS, we can determine the time associated with each ILS peak. Indeed, let us assume, for now, that for any sample peak, we can determine the time associated with that peak. We will return to the peak identification issue later. If M is the number of ILS peaks in the multiplex kit, then the set of peak times is an M-tuple:

$$T=\{t_1,t_2,\dots ,t_M\}.$$

Given an electrophoresis process that maps the ILS into the time M-tuple T, we write the electrophoresis map E as E_T and the corresponding overall map as the composition

$$S_T=E_T\circ P.$$

In general, two different samples will give rise to two different time M-tuples, T₁ and T₂, and thus, to two different maps S_T1 and S_T2.

Conventional approaches to forensic analysis use the ILS directly. Each peak in the ILS arises from an STR fragment of known size or length, calibrated in units of base pairs. Thus, the set of peak times married to the corresponding fragment sizes provides a crude map of time into base pairs. This map can be interpolated for intermediate values to give an approximate base pair equivalent for any peak in the sample. Traditionally, there have been two common choices of interpolation function – the local Southern and the global Southern. Both use linear interpolation when the true relationship between time and fragment length is not known to be linear. Issues with the local and global Southern techniques, including sensitivities to temperature fluctuations by different ILS peaks, are described in [3, p. 380].

Our approach, by contrast, does not use the ILS to map time into base pairs. Rather, we use the peak times of two different sample ILS’s to build a coordinate transform that maps the time axis of one into that of the other.

First, we define some notation. For a map c,

$$c:[0,t_f]\to [0,t_f],$$

having square integrable second derivatives, we define a (pseudo) norm

$${\Vert c\Vert }_2^2={\displaystyle \underset{0}{\overset{t_f}{\int }}{\left|c″(t)\right|}^2\mathit{\text{dt}}.}$$

By this definition, a map c has zero norm if and only if c is a linear function. Also, in some sense, the smaller the norm of c, the closer c is to being linear. We denote the space of such functions c by $L_2^2[0,t_f]$. We denote by $M_2^2[0,t_f]$ the subset of $L_2^2[0,t_f]$ which consists of functions that are monotone increasing and we think of such functions as coordinate transforms between two time frames. For an element $c\in M_2^2[0,t_f]$ and an element f ∈ L²[0,t_f], we define the transform

$$W_c(f)(t)=f(c(t)).$$

Evidently, W_c is a linear transformation and, if |c′(t)| ≥ K > 0 for some constant K, then it is bounded as well. We can extend W_c to vectors of functions by applying it to individual components so, we choose not to rename the operator for use on a vector domain.

Finally, for a given peak time set T, coordinate transform c, and corresponding combined experimental PCR/electrophoresis map S_T, we define a transformed experimental map:

$$S_{c(T)}^c=W_c\circ E_{c(T)}\circ P.$$

The new transformation defined as above maps its ILS onto the new peak time set c(T) and the other channels of measurement functions are similarly transformed into the new time coordinates.

If we have two different samples with ILS peak time sets T₁ and T₂, and we have a coordinate transform $c\in M_2^2[0,\mathrm{\infty })$ such that c(T₁) = T₂, then the map $S_{c(T_1)}^c$ effectively transforms the first sample into the time frame of the second, where they are directly comparable and, in particular, their respective ILS’s align with each other. That is, a peak in sample one, when transformed, must have a length less than any sample two peak to its right. We need more than just this qualitative information, however.

In general, there are many coordinate transforms in $M_2^2[0,t_f]$ that map T₁ onto T₂, and, for quantitative comparisons between two samples, we must employ a criterion that gives us the “best” coordinate transform for our purposes. What is desired is to find the coordinate transform that manages to minimize a measure of the distortion, both of the transformed signals and of the transformed spaces between signals. The shape of a signal is distorted in proportion to the magnitude of the second derivative of a coordinate transform and therefore we choose the coordinate transform c such that c(T₁) = T₂, the $M_2^2[0,t_f]$ norm is minimized, effectively minimizing the average second derivative, and such that

$$c″(t_{11})=c″(t_{1M})=0,$$

where t₁₁ and t_1M are the first and last points of the ILS peak time set, respectively (i.e., no distortion at the endpoints).

The solution to this minimization is known to be [5, pp. 95–96] the natural cubic spline with knots at the peak time points

$$T_1=\{t_{11},t_{12},\dots ,t_{1M}\}.$$

Furthermore, given two peak time sets T₁ and T₂, it is a straightforward computation to build the coefficient set for the spline c.

Empirically, we have observed that, for two different samples, the natural cubic spline mapping one set of ILS peak times onto another is very close to linear. Fortunately, and unlike the global Southern technique, the cubic spline approach does not rely on linearity for its accuracy. By [6], the optimal bound on the magnitude of the approximation error can be calculated as follows. Let L be the maximum of the 4^th derivative of the true time transform and let K be the maximum distance between adjacent peak times in the peak time set that is the domain. By the optimal bound derivation in [6], if c = 5 / 384, then, the approximation error e is bounded by:

$$e\le {\mathit{\text{cLK}}}^4.$$

As an example to illustrate the utility of this formula, for two particular ILS’s from samples using the ABI Identifiler multiplex DNA profile kit, we have

$$T_1=\{2822.07,3171.66,3711.73,3846.02,3972.5,4507.04,5115.08,5795.23,6275.93,6414.74,7046.32,7639.15\}$$

and

$$T_2=\{2842.33,3192.9,3735.18,3869.82,3996.37,4532.01,5139.7,5820.96,6301.32,6440.76,7073.44,7667.07\},$$

where all units are in seconds.

For the map from T₁ onto T₂, it is estimated that L ≤ 7.2 × 10⁻¹³, and we can see that K ≤ 680. We calculate that the error bound satisfies

$$e\le 0.0021\text{seconds}.$$

Since, depending on the speed of the electrophoresis, a base pair is equivalent to anywhere from 8.0 to 16.0 seconds, we conclude that our approximation is extremely accurate, easily accurate enough for our analysis purposes.

We note that a peak (or peaks) of the ILS may be susceptible to migration, as described above. In particular, the Applied Biosystem Corporation’s ILS “250” peak is known to migrate readily [3, p. 380]. Clues that suggest a migratory ILS peak will be discussed below. In our algorithm, dropping a single ILS peak would have a small effect on the overall error. In the example above, at worst, K would be doubled, leading to a new bound for e of less than 0.04 seconds, still easily accurate enough for our analysis purposes.

We also note that this approach to “shifting” one time frame into another could be regarded as a particular example of a process called “time-warping”, described in [7]. There are significant differences, however. In our algorithm, there is a well-defined rationale for choosing corresponding times, or knots, in the two time frames and we choose to use a cubic spline rather than piece-wise linear approximation because the spline minimizes curve distortion.

As a final note in this section, we point out that the selection of the “correct” peaks comprising the ILS may not be a trivial task. In general, more peaks are found in the ILS channel than make up the ILS itself. Also, identifying the ILS peaks is the first stage in the orientation of the fitted peaks and the assignments to loci. The only real clue that we have to the identities of the measured ILS peaks is the spacing between them and the relationship of that spacing with the corresponding assignments, expressed in base pairs.

Specifically, if the ILS consists of M points, whose base pair values are

$$B=\{b_1,b_2,\dots ,b_M\},$$

we denote by ΔB the M − 1 vector whose components are the differences Δb_i = b_i+1 − b_i. Similarly, for a time set

$$T=\{t_1,t_2,\dots ,t_M\},$$

we write ΔT for the M − 1 vector whose components are the differences Δt_i = t_i+1 −t_i. We then choose the set of M peaks such that the normalized dot product between ΔB and ΔT is maximized. Effectively, we are choosing the peaks with the maximum correlation in spacing with the ideal set.

In the next section, we show how to use our natural coordinate transform to make quantitative calls using the so-called “allelic ladder” sample.

6. The Allelic Ladder

The allelic ladder, or, simply, the ladder, is a special sample, usually provided by the manufacturer of the multiplexing kit. The ladder consists of a collection of the most common alleles for each sample locus in the kit. For forensic work, at least one ladder sample is required to be analyzed within each sample run and no sample can be accepted without at least one acceptable ladder in the universe of samples analyzed in a single electrophoresis event. Essentially, the allelic ladder sample provides a solution, or output, given a known input. Using the technique of coordinate transform from Section 5, we will use the ladder as a yardstick to calibrate the interpretation of unknown samples.

Within the ladder, each locus n has a designated number of alleles with repeat numbers

$$\{l_1,l_2,\dots ,l_{M_n}\}.$$

These are mapped to STR segments of corresponding lengths and these, in turn, are mapped during electrophoresis individually to L²[0, t_f] functions

$$\{f_1(t),f_2(t),\dots ,f_{M_n}(t)\}$$

which are added into the appropriate channel as

$$f_1(t)+f_2(t)+\dots +f_{M_n}(t).$$

This sum presents as a collection of known peaks in the output of the electrophoresis process with associated times

$$\{{\tau }_1,{\tau }_2,\dots ,{\tau }_{M_n}\}.$$

The ordered pairs (τ_i, l_i), for i = 1,2, …M_n, allow us to form a map from time to base pairs. Typically, because of the relatively short interval of time spanned by a single locus, this map is very nearly linear, but, for accuracy, we build a natural cubic spline q_n(τ) with the τ_i as knots. Such a spline minimizes the number of concavity changes and, as with the coordinate transforms, minimizes distortion. We note that q_n(τ) is valid only for the n^th locus. To extend the locus beyond the ladder peaks requires extrapolation and so accuracy suffers outside the boundaries of the ladder times, but, because of the typical close spacing of the ladder locus peaks and the near linearity, it is possible to use q_n(τ) for values of τ a short distance outside of the interval [τ₁, τ_Mn]. The extrapolated distance must be defined for each locus and will constitute the “extended locus”. A future study will establish reasonable limits.

We note that, for each ladder locus, we face a similar problem in choosing peaks, in the likely event that there are too many, to represent the “true” ladder peaks. The prior existence of the ILS helps us to localize a region within the channels for each locus. Beyond that, we use the same strategy as for the ILS, in which we form the vector of differences of times and compare that vector with the differences of the base pair values of the true ladder alleles. In particular, we select the set of peaks whose times {τ₁, τ₂,…, τ_Mn} give rise to the maximum spacing correlation with the spacing of the ladder alleles.

Here, then, is our strategy for an unknown sample. We assume, for now, that we can identify a peak and discover its peak time. We assume that we have an acceptable ladder, as above, and that the sample has an ILS with peak times

$$T=\{t_1,t_2,\dots ,t_M\}.$$

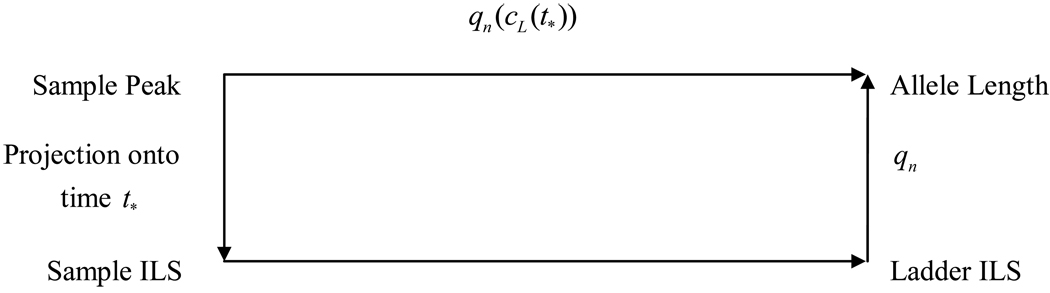
We assume that we have constructed the ideal coordinate transform c_L(t) which maps T onto the ILS peak times for the ladder. Under the transform c_L(t), each peak time t_* in the sample time frame maps to a peak time c_L(t_*) in the ladder time frame. Assuming this time falls within the n^th locus, then a length of q_n(c_L (t_*)) results. Because lengths are expressed in units of base pairs, this value must be an integer, so we accept the computed value rounded to the nearest integer. The residual distance between a computed length and its nearest integer can be regarded as a measure of the quality of the sample and ladder. Residuals exceeding a specified threshold can be flagged for human review. A commutative diagram, below, illustrates this process:

Almost all the time, the computed integer value should coincide with one of the ladder values, in which case we have simply fit the transformed sample to the ladder. In the comparatively rare case that the value falls between or outside the ladder peaks, the sample allele is termed “off-ladder” and flagged for scrutiny. Using the ladder peaks, with their known allelic sizing, as a basis for a (nearly linear) cubic spline map, intermediate values can be sized using interpolation and, for short distances, peaks beyond the ladder in either direction can be sized using extrapolation.

Often, more than one ladder may be associated with a given sample. In this case, we choose the ladder file for which the ILS cubic spline time transform above has the lowest maximum second derivative. In other words, we choose the ladder that minimizes the maximum distortion of time transformation. Thus, in theory, each sample could have its own unique ladder.

It now remains for us to describe the manner in which peaks are analyzed and peak times calculated.

7. Analyzing Peaks and Calculating Peak Times

It is important to remember that the data output from the electrophoresis process is sampled at discrete times (typically, at a 1 sec. interval) and is noisy. Therefore, any use of numerical derivatives is inadvisable. Furthermore, while conventional approaches tend to associate a peak with its maximum value, its mode, this may be unreliable, again because of noise. Hence, the safest approach is to use as much data as possible, i.e., the entire peak, to try to calculate either a mean value or a mode value. Ideally, these two values coincide.

A human reviewer, examining the output of electrophoresis, perceives a collection of unimodal, symmetric peaks superposed over a background of low level noise that is primarily visible at the base of the peaks. Magnifying an individual peak shows essentially a bell-shaped curve and comparing different peaks on the same channel shows that the apparent width of the peaks increases with time.

The data are suggestive of Gaussian peaks with standard deviations that increase with increasing mean. A qualitative description of the physical phenomena embodied by electrophoresis implies that this could be a correct inference. If we imagine that, at time 0, the sample that is to be input to electrophoresis (and that will shortly be migrating up the capillary toward the measuring laser) contains quantities of various molecules of different lengths. Initially, all of these fragments concentrate at the mouth of the capillary. With time, the fragments separate by length and, for a given length, the fragments tend to migrate at constant speed – faster for those of lesser length and slower for those of greater length. For a given length l, the fragments of that length migrate together. But, in addition to the force of the electric field and the counter-balancing force of the gel in the capillary, the fragments of length l also experience inter-molecular forces and they tend to disperse around their center of mass according to the law of diffusion (see [8] and [9]). This would result in a Gaussian function of concentration as a function of time as the mass passes the fixed laser. Furthermore, longer fragments, taking greater time to reach the laser, would diffuse more than shorter fragments and therefore, the peaks would tend to spread more with passing time, which is consistent with observation.

As a first approximation, based on this model, we attempted a Gaussian shape to fit observed electrophoresis data and, in this case, the mean and the mode do, in fact, coincide. The only problem is that the residuals between a fitted Gaussian and the empirical data tend to exhibit a uniform profile, indicating that something is missing in this perhaps overly simple model. The data suggest that the tails of a Gaussian fall off too fast compared to actual data. A more comprehensive model is needed to account for this apparently universal discrepancy from a pure Gaussian. Because the inadequacies of the pure Gaussian model are manifest equally for ILS peaks and for sample peaks, and sample peaks undergo PCR while ILS peaks do not, we conclude that a more complex model of peak broadening should be confined to the electrophoresis portion of the overall process.

By [8, p. 726], during electrophoresis, there is a surplus of cations, which accumulate at the inner surface of the capillary and therefore lead to the formation of a boundary layer. This, in turn, causes electroosmotic flow (EOF), combined with electrophoretic flow (EPF). Each type of flow contributes to band-broadening independently, as if there were two different species migrating with the same average speed, but with different diffusion coefficients (see [9], for example).

Formulas for the dispersion variance of the electroosmotic layer have been derived under various restrictive assumptions, such as cylindrical capillaries of infinite length (see [9], for example), but, in general, these conditions may not approximate real laboratory electrophoresis.

Hence, for simplicity, we have chosen to add a second Gaussian with the same mean and with a standard deviation that is a fixed multiple of that of the primary curve. This signature, which we have called a “double Gaussian”, produces extremely close fits. So that we can quantify the level of fit and provide a numerical criterion for our algorithms, we must recall some definitions.

We recognize that it may seem that using a fixed multiple of the primary standard deviation is an unnecessary and restrictive condition. However, it saves one dimension of search in our function fit optimization and it appears that the effect on the results is minimal for different choices of the fixed factor in the range of 3.0 to 5.0. If this turned out not to be the case, we could allow the multiple to be an output of the fit at the cost of some extra optimization complexity.

For two real-valued elements f and g of L²[a,b], we define the inner product (f, g) in the usual way:

$$(f,g)={\displaystyle \underset{a}{\overset{b}{\int }}f(t)g(t)\mathit{\text{dt}}},$$

and (f, g) = 0 if and only if f and g are orthogonal. Thus, as is well known,

$${\Vert f-g\Vert }^2={\Vert f\Vert }^2+{\Vert g\Vert }^2-2(f,g),$$

so, for a given f, with norm 1, say, finding a g of norm 1, to minimize the norm of the difference when g lies within some subset of L²[a, b], is equivalent to maximizing the inner product (f, g) over that subset. We will refer to the normalized inner product,

$$r=\frac{(f,g)}{\Vert f\Vert \Vert g\Vert },$$

as the correlation between f and g. When f and g each have norm 1, the correlation reduces to the inner product. In this case, the formula for the norm squared of the difference becomes

$${\Vert f-g\Vert }^2=2(1-r).$$

Hence, a perfect fit is equivalent to a correlation of 1 and the level of fit can be quantified as the degree of correlation, i.e., how close the correlation is to 1. Finally, if we project the element f onto its approximating g using

$$\tilde{f}=\frac{(f,g)g}{{\Vert g\Vert }^2},$$

then, the residual Δf = f − f̃ satisfies (f, Δf) = 0, or, in other words, f is perpendicular to Δf.

Given a sampled function f in L²[a, b], and for fixed λ, we seek a function g from the parameterized family of double Gaussian curves,

$$g(t,\mu ,\sigma ,c_1,c_2,\lambda )=c_1{e}^{-\frac{{(t-\mu )}^2}{2{\sigma }^2}}+c_2{e}^{-\frac{{(t-\mu )}^2}{2{\lambda }^2{\sigma }^2}}$$

that minimizes the normalized (f, g). Once we have found such a g = g(·, μ, σ, c₁, c₂, λ), provided (f, g) is sufficiently close to 1, we may repeat the process for every peak in the sample and then analyze the sample using the projections above, with the g chosen as the double Gaussian above. The projections f̃ then serve as substitutes for the original functions f. The mean μ and the mode of the projections f̃ are well-defined and are then stable functions of all of the points of the original data embodied by f. We use the mean μ as the “peak time”, or the location, of the peak f.

More specifically, if we write our function g in terms of its two basic functions:

$$g_1(t,\mu ,\sigma )=e^{-\frac{{(t-\mu )}^2}{2{\sigma }^2}},$$

$$g_2(t,\mu ,\sigma )=e^{-\frac{{(t-\mu )}^2}{2{\lambda }^2{\sigma }^2}},$$

so that,

$$g(t,\mu ,\sigma ,c_1,c_2,\lambda )=c_1{g}_1(t,\mu ,\sigma )+c_2{g}_2(t,\mu ,\sigma ),$$

then, we can normalize g₁ (t, μ, σ) and call it G₁(t, μ, σ). Further, since g₁(t, μ, σ) and g₂(t, μ, σ) are linearly independent, we can use g₁(t, μ, σ) and g₂(t, μ, σ) as input to the first step in the Gram-Schmidt orthonormalization process [10, pp. 67–68] to find a normalized G₂(t, μ, σ) that is orthogonal to G₁(t, μ, σ)and such that g₂(t, μ, σ) is a linear combination of G₁ and G₂. We can now deal exclusively with G₁ and G₂.

We note that all normalization and orthonormalization is performed relative to the restricted interval [a,b] because the function f is taken to be defined only on that interval. Therefore, all integral calculations are done numerically on [a, b].

We write f̄ for f/‖f‖ so that f̄ is a unit vector, and we observe that, given any values of μ and σ, there is a function n such that n is orthogonal to G₁ and G₂ and

$$\overline{f}=\alpha G_1+\beta G_2+n.$$

We seek an approximation g to f̄ so that g‖f‖ will be an approximation to f. Because of the mutual orthogonality of G₁, G₂, and n,

$$\alpha =(\overline{f},G_1)$$

and

$$\beta =(\overline{f},G_2).$$

Because f̄, G₁ and G₂ are unit vectors, α and β are each less than 1 in absolute value. We now connect G₁ and G₂ to our original function g via

$$g(t,\mu ,\sigma ,c_1,c_2,\lambda )=\alpha G_1+\beta G_2,$$

where c₁ and c₂ can be found from α and β together with the calculated relationship between G₁ and G₂ on the one hand and g₁(t, μ, σ) and g₂(t, μ, σ) on the other. Finally, we can calculate the correlation between f and g as

$$(\overline{f},g)={[{\alpha }^2+{\beta }^2]}^{1/2}.$$

This, then, is the measure of fit of the properly scaled function ‖f‖ g to the original sampled data function f.

Thus, summarizing, for every μ and σ we can calculate α and β to get a best fit to f. Now, we can iteratively search for a pair of values (μ, σ) such that the correlation above is maximized. This can be accomplished using any of a number of numerical procedures.

Next, we explain how we find the intervals [a,b] which delineate the individual peaks f above.

Ideally, since we know what shape or shapes we are seeking within the sampled data, it seems that we should be able to use a matched filter [11, pp. 156–158] based on the expected shape, the double Gaussian. However, our situation dictates that we know only the generic form of the expected shape. The width, or standard deviation, varies as a function of time and is, a priori, unknown. Also, the mix of the two Gaussians in the double Gaussian is unknown. Hence, the matched filter with double Gaussian basis will not work in our case.

Instead, for a first approximation, we simplify our “expected” shape so that, in essence, we are searching for “pulses” of data. We use a matched filter based on a square wave. Such a filter will exhibit peaks near the centers of regions of high data density. To be more precise, given a window width of W seconds, we perform the convolution

$$F(t)={\displaystyle \underset{0}{\overset{\infty }{\int }}f(t-\tau )S_W(\tau )}d\tau$$

where S_W is defined to be the characteristic function of the interval [0, W]:

$$S_W(t)=\{\begin{array}{cc}1,\hfill & 0\le t\le W\hfill \\ 0,\hfill & \mathit{\text{otherwise}}\hfill \end{array}.$$

Thus, the convolution reduces to a time average of the values of f over a time window of width W:

$$F(t)={\displaystyle \underset{0}{\overset{W}{\int }}f(t-\tau )d\tau }.$$

For a channel sample f, we evaluate the convolution F, replacing the continuous time integral by a discrete approximation, and we look for the local maxima of F that exceed a specified noise threshold. To delineate a local peak, we look for local minima, one on each side of a calculated local maximum, and the resulting interval’s data proceeds to the next level of analysis – the discovery and computation of the particular identity of the shape within the interval.

We note that the particular convolution above is efficient to compute for sampled data, for which we compute F(t) only for t = t₀, t₁,…, the sample times. For each time t_n, and using Simpson’s Rule to approximate the integral [5, pp. 126–131],

$$F(t_n)=F(t_{n-1})+0.5[f(t_n)+f(t_{n-1})]\mathrm{\Delta }t-0.5[f(t_{n-W-1})+f(t_{n-W})]\mathrm{\Delta }t,$$

independent of window size, where Δt is the assumed constant sample time update interval t_n − t_n−1.

The square wave window and the noise threshold require some tuning. Too narrow a window will tend to amplify noise, as will too low a threshold, and too wide a window will tend to wash out valid signals, as will too high a threshold. The system does not appear to be overly sensitive these values, however, and this approach has provided effective amplification of signal to noise ratio. Furthermore, our approach tolerates somewhat excessive amplification of noise in preference to over-damping because extracted peaks that are “too small” can be eliminated based on that criterion directly. In fact, a standard criterion for accepting a peak as valid is that the peak height exceed a specified minimum.

To delineate each interval [a, b] on which we perform a search for a proper double Gaussian curve, we look for local minima of the function F, above. Specifically, we seek a and b which are local minima of F, with a local maximum c in the interior of the interval [a, b] such that F(c) exceeds the noise threshold. What results is a collection of intervals and, from those, a collection of peaks.

Note that, in the sequence of the algorithm described thus far, a peak is identified, assigned to a locus and then a base pair is calculated. Because of the data itself and the approximations in the analysis, as a general rule, the calculated base pair is not an integer value, as it, in fact, must be. We call the discrepancy between the calculated base pair and the nearest integer the “residual”. The value of the residual affords an opportunity for a new measure of quality. It is a measure that assesses the overall analytic framework as it relates to this peak. That is, it reflects the accuracy of the curve fit, as well as the curve fits of the ladder and ILS peaks, and the spacing of the ladder locus and that of the ILS., If the ILS contains a migratory peak, as described above, that fact will affect the residuals, at least in the same time frame as that of the migrating peak. Thus, a systematic manifestation of “excessive” (according to a specified threshold) residuals – classed as a new artifact – is a strong indication of a migrating ILS peak.

Another artifact that can indicate a migratory ILS peak is a so-called “off-ladder” allele. A locus allele that does not coincide with a designated ladder allele is called an “off-ladder” allele. There are some common alleles that are technically off-ladder, but are accepted without the artifact designation. As with excessive residuals, a systematic manifestation of off-ladder alleles is another strong indication of a migrating ILS peak.

In cases where the double Gaussian does not fit to a minimum acceptable level, alternate signatures can be tested. For example, a so-called super Gaussian signature has been found to represent dye blobs well and spikes are closely approximated by triangular functions. A useful signature for craters, or split peaks, is a function consisting of a pair of double Gaussians, with inter-peak distance determined by the sample data.

We observe that the main intent of this algorithm has been to serve in those situations when a sample is being analyzed for comparison to another sample that is not available for analysis, e.g., in forensic work. In these cases, a ladder is required as a template to produce allele calls. However, when a sample is to be compared for identity to a known sample that is on hand, both samples may be analyzed and their respective ILS channels may be mapped by the technique described in Section 5 and the peaks of the samples may then be compared in the same time frame. Without having to make allele calls, it would be straightforward to validate if the two samples were from the same source.

Next, we summarize the steps we have described.

8. Summary

The analysis of a ladder file follows the general steps below:

1. For each channel, use the square wave convolution process to delineate data intervals with values sufficiently significant that the noise threshold is exceeded.

2. For each data interval above, attempt to fit a signature double Gaussian. If the level of fit is below an acceptance threshold, try to improve the fit using alternate signatures representative of different artifacts.

3. For the ILS channel, select the requisite number of peaks to represent the ILS based on maximizing the spacing as measured by the scaled inner product between the differences of the ideal positions (in base pairs) and the differences of the means (in time) between adjacent selected peaks.

4. For each ladder locus, use the ILS peaks located in (c) above and a pre-specified parameter list, which delineates the minimum and maximum ILS base pair for the locus, to select peaks that belong to the locus. These are chosen from the channel’s double Gaussian set found in (b).

5. For each ladder locus, select the requisite number of peaks from the set chosen in (d) based on maximizing the spacing as measured by the scaled inner product between the differences of the ideal positions (in base pairs) and the differences of the means (in time) between adjacent selected peaks.

6. For each locus, build a cubic spline interpolation function mapping the mean time of each ladder locus peak into its corresponding base pair equivalent.

The first three steps of the analysis of a sample file are essentially the same as for a ladder. The rest differ:

1. For each channel, use the square wave convolution process to delineate data intervals with values sufficiently significant that the noise threshold is exceeded.

2. For each data interval above, attempt to fit a signature double Gaussian. If the level of fit is below an acceptance threshold, try to improve the fit using one or more artifact signatures.

3. For the ILS channel, select the requisite number of peaks to represent the ILS based on maximizing the spacing as measured by the scaled inner product between the differences of the ideal positions (in base pairs) and the differences of the means (in time) between adjacent selected peaks.

4. Choose an associated ladder by building cubic spline time transformations mapping the sample ILS into each available ladder ILS, i.e., mapping the sample ILS peak time set onto the ladder ILS peak time set. Select the ladder for which the above time transformation has the smallest maximum second derivative (least distortion).

5. Using the time transformation and ladder selected in (e), map the peaks for each sample locus into corresponding peaks in the ladder time frame. Based on the time intervals for each ladder locus, assign peaks to loci.

6. Using the cubic spline interpolation function mapping ladder locus allele times into (known) ladder locus base pairs (ladder step (f)), compute the base pair equivalent of each transformed sample peak, rounded to the nearest integer, and convert to the correct allele name.

9. Examples

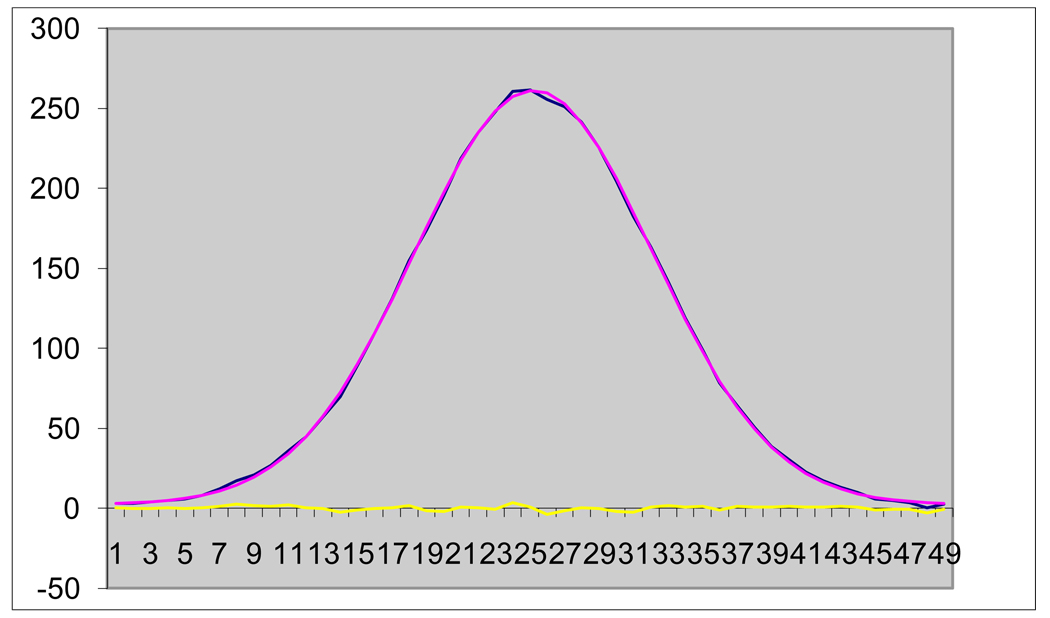
In Figure 2, below, the purple curve is a double Gaussian, fitted to the blue measurement points, and the yellow is the residual noise. As is common for this program, the correlation exceeds 0.999.

Figure 2.

Fit of Raw Data Using Double Gaussian and Residual

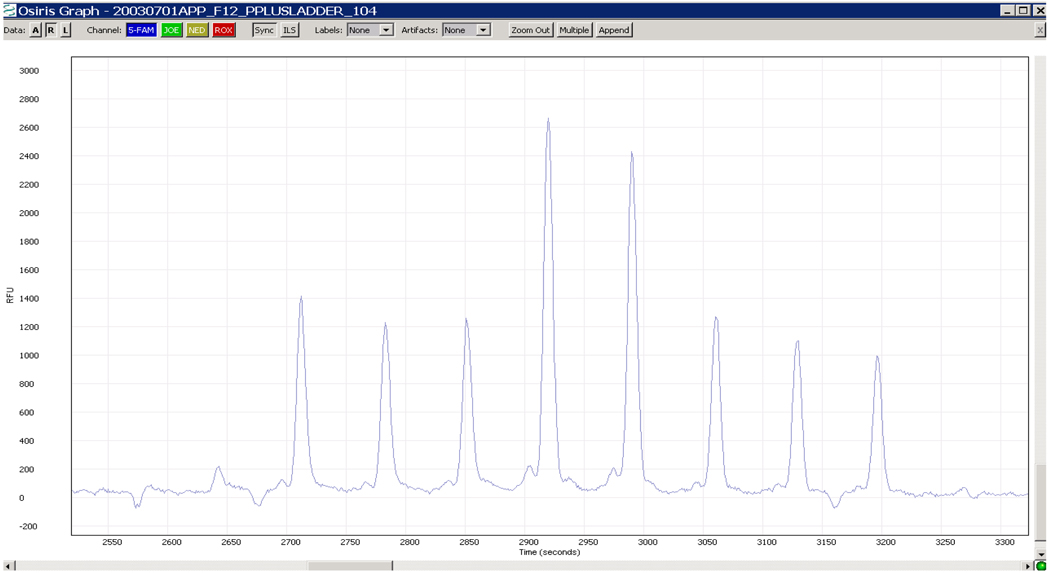
The pair of graphs below illustrates how well the techniques work in context of a ladder analysis. Figure 3 shows the raw data from the D3S1358 locus of an ABI ProfilerPlus kit ladder file.

Figure 3.

Raw data from Locus D3S1358 from a ProfilerPlus Ladder File

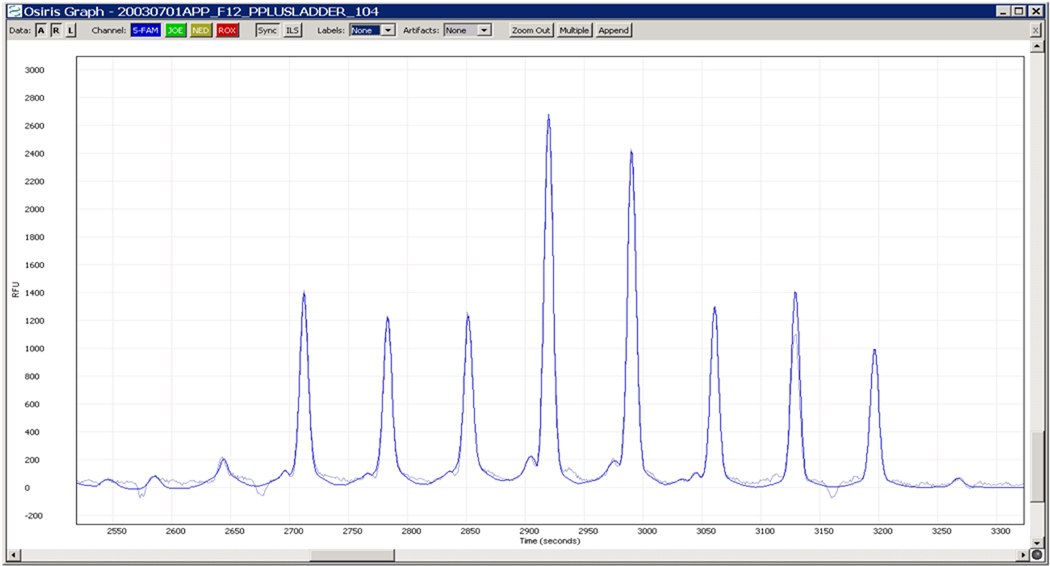
Figure 4 shows the fitted signals superimposed on top of the raw data from Figure 3. Note that in Figure 4, the fit is virtually identical to the measurements except in the low level noise regions between peaks. Note also that a region of over 800 point measurements has been reduced to four parameters per peak (mean, variance and scaling parameters) times 8 peaks, or 32 numbers. Given the accuracy of the fits, mean values (or peak locations) and peak heights may be confidently calculated from the fitted curves with minimal sensitivity to noise and time series discretization issues.

Figure 4.

Fitted Signals Superimposed on Top of Raw Data

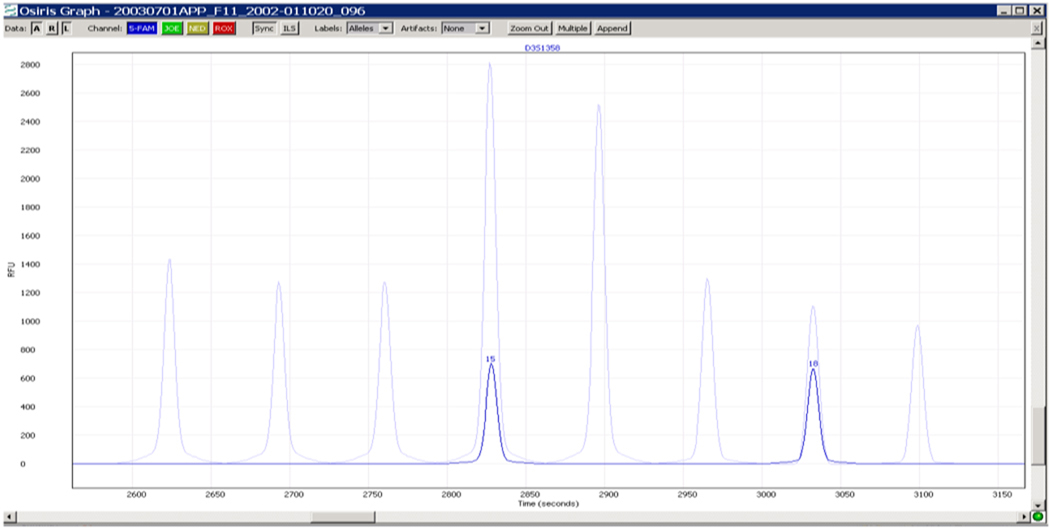
In Figure 5, a fit of the raw data for an ABI ProfilerPlus sample has been mapped into the time space of the above ladder which has been used to quantify the size(s) of the sample alleles. The result shows that this sample aligns accurately with the 4^th and 7^th ladder peaks.

Figure 5.

Sample Superimposed on Ladder: fit typically within 0.05 bp

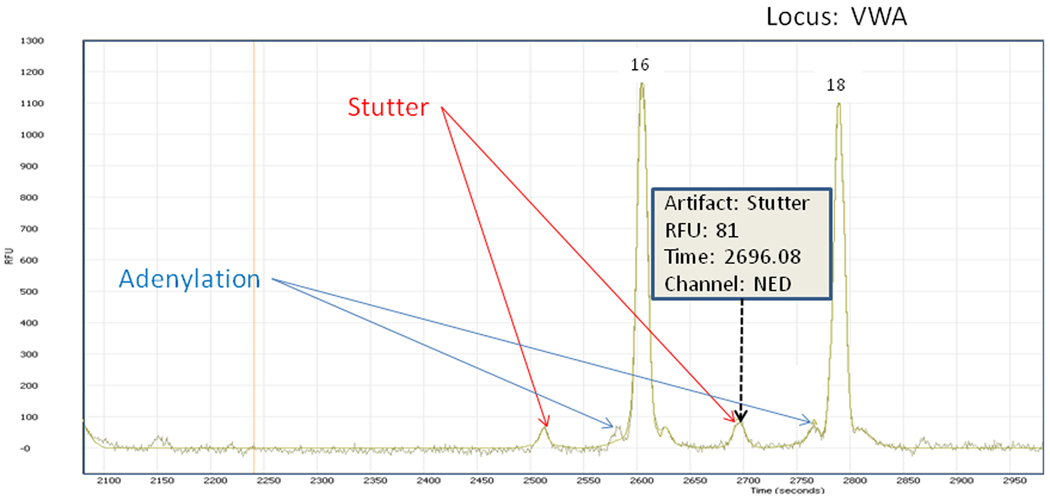
In Figure 6, we show a fit of the raw data for an ABI Identifiler sample, in which the program has identified both stutter and adenylation sites. Note the rejection of the prevalent noise from the original sample.

Figure 6.

Sample showing rejection of noise and identification of stutter and adenylation artifacts

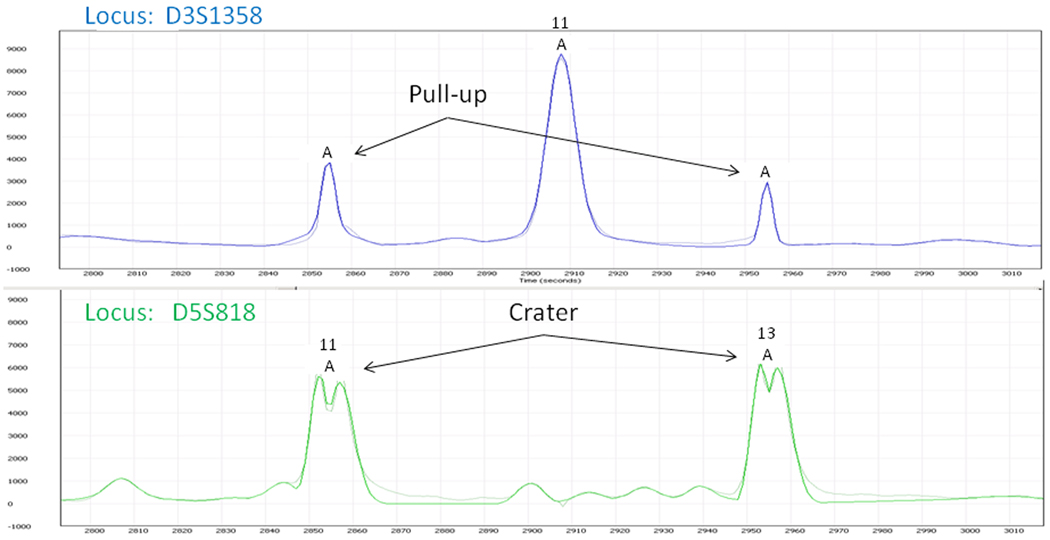
In Figure 7, we show a portion of a sample with craters and pull-up identified by the algorithm. The “A” at a peak indicates an artifact. The two uncalled peaks in the “blue” channel have been analyzed by the algorithm to be pull-up and, if called, to have excessive residual. Thus, they are deemed not to be true alleles. Nevertheless, they are flagged for human review, as are the craters. The large peak in the “blue” channel has been flagged as an artifact because it is the cause of pull-up in another (undisplayed) channel.

Figure 7.

Sample showing craters and pull-up identified by software algorithm

10. Conclusions

We have designed an integrated mathematical framework, based on function space concepts, for modeling and processing DNA profile data from multiplexes of short tandem repeat loci. The algorithms derived from this framework have been realized as a software package called OSIRIS that has been demonstrated to work accurately and robustly. The software has been tested on the 700 National Institute for Science and Technology (NIST) population samples for concordance studies. Manufactured reagent kits from both Applied Bioscience and Promega were used. (See [2].) From [2], “OSIRIS development also relied on thousands of samples representing all commonly used reagent kits and analytical platforms through state and local laboratory collaborations.” (Also, see [12].) The NIST concordance studies were completed with perfect scores. As suggested by the examples above, OSIRIS works not only with clean data, but with marginal data and even with highly problematic samples. An in-depth description of OSIRIS’s ability to handle a wide range of artifacts will be the subject of a future publication.

OSIRIS is publicly available by download from: http://www.ncbi.nlm.nih.gov/projects/SNP/osiris/.

Figure 1.

Commutative Diagram for Coordinate Transform