Adaptive Surrogate Modeling for Expedited Estimation of Nonlinear Tissue Properties Through Inverse Finite Element Analysis

Abstract

Simulation-based prediction of specimen-specific biomechanical behavior commonly requires inverse analysis using geometrically consistent finite element (FE) models. Optimization drives such analyses but previous studies have highlighted a large computational cost dictated by iterative use of nonlinear FE models. The goal of this study was to evaluate the performance of a local regression-based adaptive surrogate modeling approach to decrease computational cost for both global and local optimization approaches using an inverse FE application. Nonlinear elastic material parameters for patient-specific heel-pad tissue were found, both with and without the surrogate model. Surrogate prediction replaced a FE simulation using local regression of previous simulations when the corresponding error estimate was less than a given tolerance. Performance depended on optimization type and tolerance value. The surrogate reduced local optimization expense up to 68%, but achieved accurate results for only 1 of 20 initial conditions. Conversely, up to a tolerance value of 20 N², global optimization with the surrogate yielded consistent parameter predictions with a concurrent decrease in computational cost (up to 77%). However, the local optimization method without the surrogate, although sensitive to the initial conditions, was still on average seven times faster than the global approach. Our results help establish guide-lines for setting acceptable tolerance values while using an adaptive surrogate model for inverse FE analysis. Most important, the study demonstrates the benefits of a surrogate modeling approach for intensive FE-based iterative analysis.

INTRODUCTION

Computational predictions of specimen-specific tissue mechanics require accurate geometric representation, boundary conditions, and material behavior. From evaluating intervention strategies for pressure-relieving footwear to assessing the effects of anterior cruciate ligament reconstruction on cartilage stress, biomechanical applications of computational modeling are far reaching.^3,9,11,16,29 In addition to direct biomechanical analysis, simplified and efficient models have also been developed for surgical simulation and image-guided surgery, where the haptic behavior of tissue and organs are simulated for the surgeon or trainee.^{4,10,23,24,27} Varying platforms have been used to develop models, ranging from the relatively complex finite element (FE)-based continuum approach to more simplified but efficient statistical or mechanical surrogates. Computational expense can be a significant concern, whether it is for real-time feedback or development of specimen-specific material behavior for biomechanical evaluation. Whatever the application is, without accounting for appropriate material response, the usefulness of such simulations is limited.

Successful material models addressing patient and specimen specificity have been developed, but these highlighted a large computational cost dictated by iterative optimization using nonlinear FE representations.^8,21 In most inverse FE analyses of soft tissue, experimental data were compared against predictions of a geometrically consistent model, which traditionally adopted an elastic or a hyperelastic material definition.^5,8 Inverse modeling is generally employed when the material stress–strain response is desired, and isolated material testing is not practical or feasible, as can be the case for many biological tissues. Within an inverse framework, the mechanical response of the model can be controlled through easily updated parameters, generally termed “material coefficients.” Assuming a given constitutive model is appropriate to capture the mechanical behavior, material coefficients can be found through an iterative optimization scheme to reproduce the response of the given subject or specimen. However, combining a time-consuming FE analysis, representative of the specimen geometry and complex boundary conditions with an iterative optimization procedure may result in significant computational expense.⁸

A number of studies have looked to overcome this computational burden. Through the use of a radialbasis interpolation approach, rapid identification of dental-implant tissue elastic moduli has been performed.³⁰ Assumed values were used to train the radial-basis model, and a computationally efficient neural network was built to predict accurate tissue stiffness. Lin et al.²² developed a model for efficient contact modeling of a total knee replacement. The static “surrogate” model proved very efficient for motion, contact force, and wear prediction when compared to a more costly elastic foundation approach. For haptic feedback during surgical simulation, Zhong and Peters³¹ developed an exponential model to simulate a human liver biopsy procedure. Calibrated parameters for the model were used to predict the necessary force feedback information and results compared well with a corresponding FE representation. Also, Einstein et al.⁶ utilized a successive response surface method combined with gradient-based optimization to estimate material parameters of biological tissues. Their approach was effective, and the semi-global optimization framework, including the response surface method and the leap-frog algorithm,²⁸ fit nonlinear anisotropic material behavior to the available experimental data. Although not necessarily developed to decrease computational expense, the authors found the method to be efficient and in a subsequent study optimized complex material behavior able to reproduce vascular mechanics.⁵ These promising studies proved well suited for development of static (nonadaptive) surrogate models, but required a predetermined bounding of the input space or additional optimization routines⁶ to achieve desired accuracy and speed. This approach may not be ideal for all applications, especially when real-time feedback is not required or a well-defined input space is not available. Implementing a robust, adaptive surrogate modeling approach would not only minimize costly FE-based simulations during iterative analysis, i.e., during optimization, it would also be advantageous for parametric or specimen-specific studies. An adaptive surrogate model utilizes previous FE results to interpolate a desired output and bypasses the need to rely solely on computationally expensive FE simulations and thus has the potential to save significant computational cost.¹

In many inverse FE studies, computational concerns have driven the choice to use more efficient gradient-based optimization methods for material parameter determination.^8,13,17 As opposed to a global approach, i.e., SA or particle swarm,^12,18 gradient-based methods potentially suffer from solutions found at a local minimum and are thus sensitive to the initial guess values. Well-behaved problems may not exhibit these shortcomings, but more complex analyses will result in greater demand on the optimization approach. Due to the dramatic increase in function calls, a more robust global method is often overlooked for inverse FE applications, but adoption may become advantageous if the disparate computational investment can be overcome. Of course, when the underlying model itself is costly, the number of function evaluations plays a prohibitive role in gradient-based optimization as well. Regardless of the optimization type, decreasing the number of expensive FE simulations through informed utilization of previous solutions will facilitate implementation of specimen-specific constitutive models, as opposed to the generic models often found in the literature. As these issues can be problem specific, it is important to evaluate any proposed methodology using an established and efficient problem.

The goal of this study was to assess the potential benefits of implementing a regression-based adaptive surrogate modeling approach to decrease computational cost for both global and local optimization using a previously published inverse FE application.⁸ Nonlinear-elastic material parameters for heel-pad tissue were found for a patient-specific force–displacement indentation data set using sequential quadratic programming (SQP) and simulated annealing (SA) optimization routines, both with and without the adaptive surrogate model to illustrate the capacity of the coupled computational framework.

METHODS

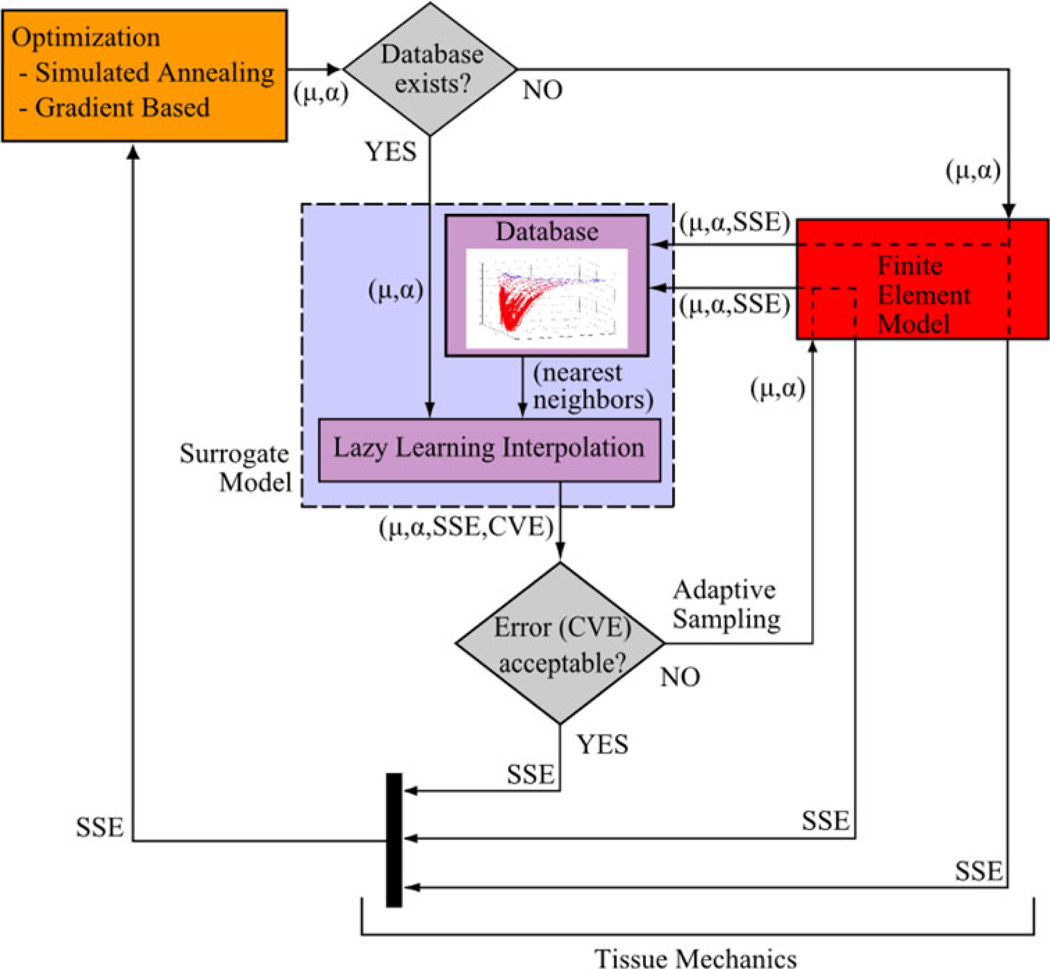
The adaptive surrogate modeling framework is described below with the data flow outlined in Fig. 1. To briefly summarize, optimization is used to minimize a sum of squared error between known experimental data and FE predicted behavior. Normally, in an inverse style optimization framework, FE prediction alone is relied on to quantify model response for a given set of material parameters. To increase efficiency, a local linear regression-based surrogate model was included to potentially bypass the need to rely solely on expensive FE simulations. In this framework, the optimization routine supplies parameters to the surrogate model (“Lazy Learning” in Fig. 1) to efficiently predict the model response based on previous FE solutions (“Database” in Fig. 1). Important to the accuracy of this approach, the surrogate also predicts a cross-validation error (CVE, explained below) to assess the relative accuracy of the regression results. If deemed accurate, based on the CVE prediction, the FE simulation is bypassed thus saving computational expense. A previously published inverse FE problem⁸ was chosen to develop and assess the capacity of this surrogate modeling framework. The inverse analysis was targeted at the characterization of in vivo heel-pad tissue properties.⁸ The components of Erdemir et al.⁸ used in our study are summarized in the “Experimental Data” and “Finite Element Representation” sections.

FIGURE 1.

Coupled simulation of inverse material parameter optimization focusing on the adaptive surrogate modeling approach. Material parameters are μ and α, and SSE is the corresponding model vs. experimental squared error (Eq. (2)). Note that when a finite element (FE) analysis is requested, SSE is returned back to the optimization loop and also to the surrogate model with the corresponding material parameters to expand the database. Data handling was performed in Matlab (Mathworks, Inc., Natick, MA), in which a script was developed to link the optimization with the FE through file input/output and with the surrogate representation directly. Note that the cross-validation error (CVE), as predicted by the surrogate model, was used as measure of surrogate SSE prediction accuracy. The CVE was compared with a given tolerance value (“Error (CVE) acceptable?”) to achieve the adaptive nature of the computational framework.

Experimental Data

In vivo displacement–load data from indentation testing of heel-pad plantar tissue was used to drive the optimization. Data were obtained from a custom experimental apparatus designed to hold a subject’s foot in place while a 25.4-mm indenter compressed the heel-pad to ~50% thickness of the unloaded state at a rate of 5.7 mm/s. Ultrasound images and force were recorded during the testing.⁸ Data from the right heel of a single subject from the study of Erdemir et al.⁸ were used. The subject was a healthy 68-year-old woman. Patient information has been de-identified (made untraceable), and data collection procedures were approved by the Institutional Review Board, as described in Erdemir et al.⁸

Finite Element Representation

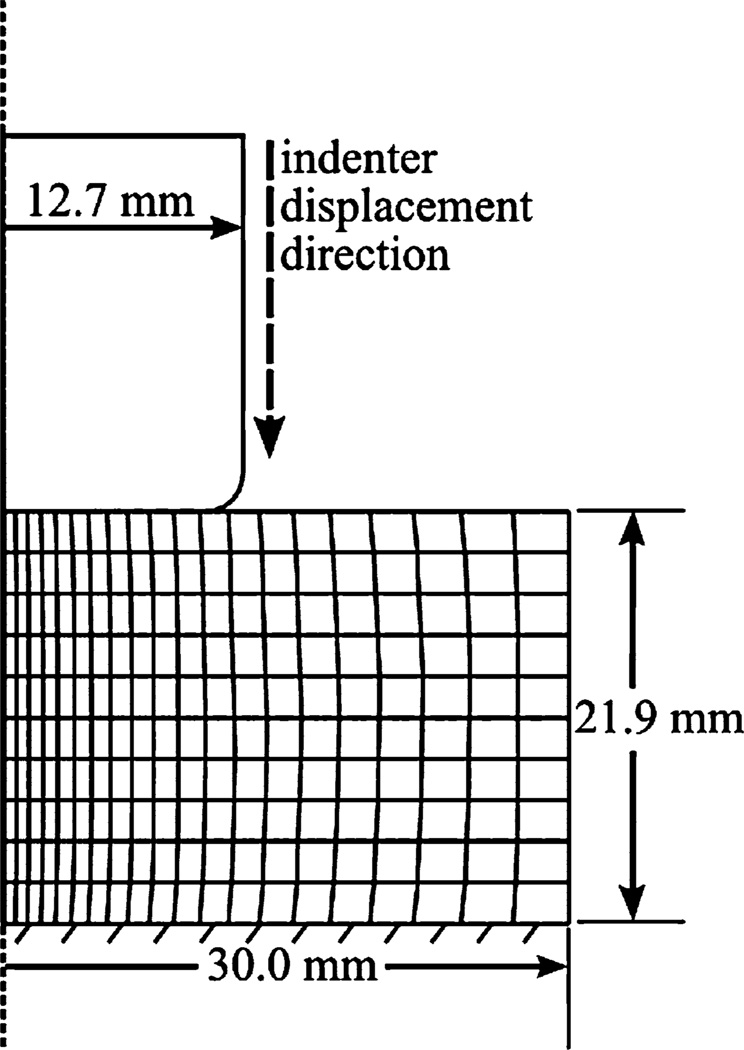
A displacement driven axisymmetric FE representation of the indenter and heel-pad tissue was used⁸ (Fig. 2). Heel thickness was tailored to the subject, and the indenter was modeled as rigid. The soft-tissue material definition used an incompressible Ogden strain energy potential function available in Abaqus/Standard version 6.9.²⁵

$$U=2\frac{\mu }{{\alpha }^2}({\lambda }_1^{\alpha }+{\lambda }_2^{\alpha }+{\lambda }_3^{\alpha }-3),$$ (1)

where λ_1–3 are the deviatoric principle stretches, and μ and α represent the hyperelastic heel-pad behavior. Boundary conditions were specified to reproduce the experimental kinematic conditions. For a given μ and α, the model was driven with indenter displacement, and the corresponding force was monitored and compared with experimental results. Ten evenly spaced points, for every millimeter of indenter displacement up to the maximum value of 10 mm, were used to calculate the model vs. experimental sum squared error (SSE, note that zero displacement is not a data point),

$$\mathit{\text{SSE}}={\displaystyle \sum _{i=1}^{10}}{(F_{\text{Model},i}-F_{\text{Experiment},i})}^2,$$ (2)

where F_Model and F_Experimental are the model and experimental forces imparted at data point i, respectively. A more complete description of the model can be found in Erdemir et al.⁸

FIGURE 2.

The axisymmetric finite-element model of the heel pad and indenter to obtain heel-specific material properties. Patient-specific heel-pad thickness (21.9 mm) was defined based on the initial thickness measured by ultrasound imaging. Indenter to heel-pad contact was defined as frictionless.

Surrogate Model

The Lazy Learning Toolbox^1,2 for Matlab (Mathworks, Inc., Natick, MA) was used as the surrogate modeling tool with inputs defined as μ and α from the Ogden constitutive equation (Eq. (1)).²⁵ Lazy Learning is a local regression method based on the use of nearest neighbor input/output sets present in the database. Effectively, a linear regression model is fit to a subset of existing training data (input/output sets), decided upon by a prescribed number of closest neighbors to a given query point. The output of this locally weighted regression was utilized as an approximate of the system, for which a surrogate model was sought. For this application, output from the surrogate model was a predicted model vs. experimental SSE. The distance from the query point X_q to candidate neighbors X_i was defined as the “Manhattan” distance:

$$d(X_i,X_q)={\displaystyle \sum _{j=1}^m}{w}_j|X_{\mathit{\text{ij}}}-X_{\mathit{\text{qj}}}|$$ (3)

where X_ij and X_qj are the jth coordinates of the database point and query point, respectively. In the present application, m = 2 is the number of dimensions in the input space and w_j are the weighting factors that define its distance metric. Weights were set to 1.0, and inputs were adaptively normalized using the current database range. The number of nearest neighbors was allowed to range from 6 to 15 and for each set of neighbors, model vs. experimental SSE was approximated through linear regression, and a leave-one-out cross validation error (CVE) was also computed (not to be confused with the experimental vs. model SSE). In summary, to calculate the CVE, individual input/output data points were excluded and subsequently used to calculate the difference between the regression result and the excluded data point, yielding a measure of regression accuracy as a function of nearest neighbor sets (6–15 in this study). The minimum CVE among each set of neighbors was chosen as the best fit and, when compared to a tolerance value, determined whether to utilize the regression result or perform a FE simulation (Fig. 1). We refer the reader to Atkeson et al.¹ for a more complete description of the CVE calculation. To avoid regression in sparsely populated areas of the input space, a vector was defined of distances, up to the maximum number of neighbors N, from each data point to the average of the N nearest neighbors, X_i,

$$S(X_i)={\displaystyle \sum _{i=1}^N}\sqrt{{\displaystyle \sum _{j=1}^m}{({\overline{X}}_j-X_{\mathit{\text{ij}}})}^2}.$$ (4)

The standard deviation of S(X_i) was used as a measure of spread of the data set used for regression. If the distance from the query point to X̄_j was greater than two times the standard deviation of S(X_i), a FE simulation was deemed necessary, regardless of the CVE. Especially for SA, which experiences large jumps in the input space, this feature avoided unsupported regions of the database. Additionally, unlike the direct calculation of SSE using FE-based results, the surrogate predicted SSE, as it was based on regression, has the potential to return a negative value if the existing input/output sets (real FE-based results) were sparse or the surrogate was asked to extrapolate (only possible while still satisfying Eq. (4)). If this condition was realized, it was also deemed necessary to perform a FE simulation.

When the above conditions were met, the minimum CVE of the local regression model was compared to a prescribed tolerance value. A systematic progression was defined to test the computational cost and relative accuracy of the results for a range of tolerance values and initial guesses. To evaluate the sensitivity to the tolerance, optimization routines (described below) were performed with values ranging from 0 N² up to 30 N², in 5 N² increments. A tolerance of 0 N² represents strict utilization of FE results for each optimization function call. To evaluate the sensitivity to the initial guess values, 20 runs at each tolerance value were performed with random initial guess values for material coefficients, with ranges loosely based on literature reported values (1–50 kPa for μ and 5–30 for α).^8,15 A relatively wide range of initial values was chosen to test the robustness of the computational framework, and at every tolerance setting, the 20 optimization runs used the same initial guesses (see “Appendix A” section for a list of the values). When the minimum CVE was below the specified tolerance, the Lazy Learning predicted SSE was used to continue the inverse analysis procedure, thus bypassing the computationally more expensive FE simulation. If the CVE was above the specified tolerance, a FE simulation was completed, and the results (FE predicted SSE) were supplied to both the optimization routine and saved in the database (Fig. 1). A complete description of the Lazy Learning algorithms can be found in Atkeson et al.¹

Optimization

Optimization was performed to minimize the SSE difference between model and experimental results. Material parameters μ and α from the hyperelastic material model (Ogden, Eq. (1)) were the control variables and both SA,¹² a global search method, and an unconstrained sequential quadratic programming (SQP) algorithm (fminunc, available in Matlab, Mathworks, Inc, Natick, MA),²⁶ a gradient-based approach, were implemented. The adaptive surrogate model (tolerance values greater than 0 N²) actively populated the database as the optimization proceeded. It should be noted that for every tolerance value and for each of the 20 runs with unique initial guess values, the database was cleared before the simulations. This allowed the contribution of the surrogate model to be accurately assessed for all runs. In practice, it would be more efficient to save FE results for use in subsequent simulations.

Solutions were compared for relative accuracy and computational expense against optimization with FE simulations performed for every function evaluation (0 N² tolerance). At the end of optimization, FE simulations were performed to calculate experimental vs. model RMSE values to illustrate the suitability of optimized material coefficients to represent specimen-specific behavior:

$$\mathit{\text{RMSE}}=\sqrt{\frac{\mathit{\text{SSE}}}{10}},$$ (5)

and SSE (Eq. (2)) was calculated using optimized material coefficients and the FE model. For optimizations which used the surrogate model (tolerance > 0 N²), RMSE values indicate the effectiveness of the surrogate model to reflect the corresponding FE behavior during the inverse analysis process, at least for the respective tolerance value. Due to the non-normal distribution of the results, RMSE values at each tolerance value were also split into quartiles to assess the potential spread of data. Finally, for evaluation of the resulting material behavior, stress–strain curves up to 50% compressive strain were calculated for each material coefficient combination found during optimization.

RESULTS

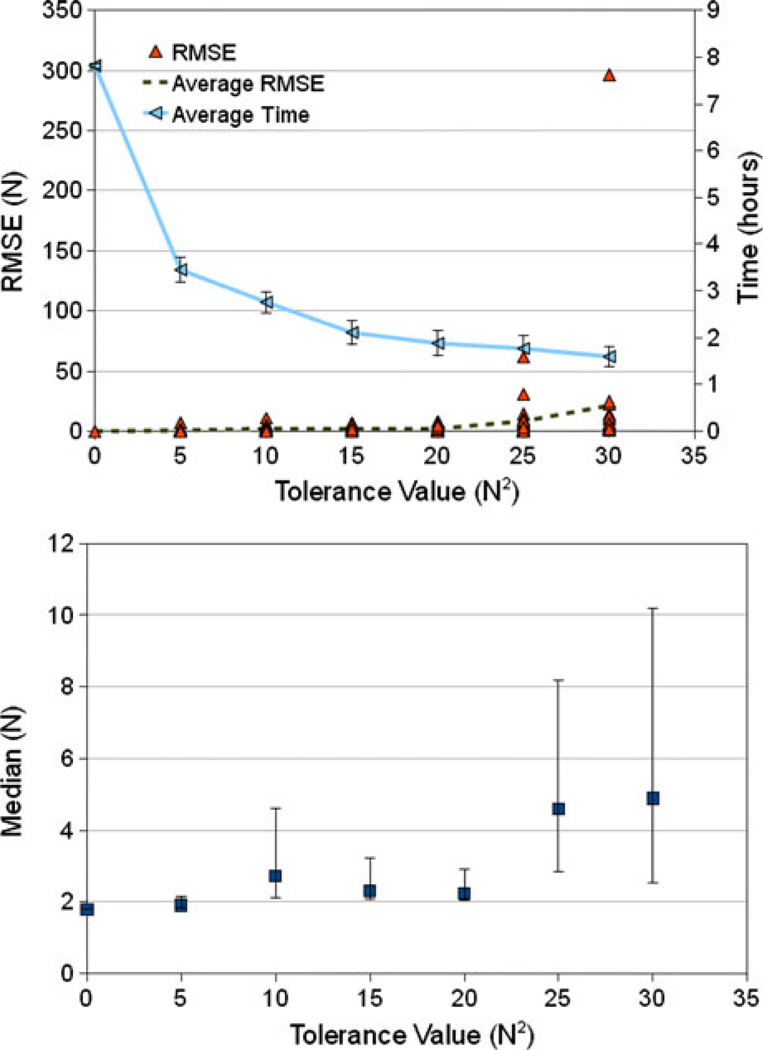
Even for the relatively stringent tolerance value of 5 N², surrogate modeling reduced the average computation time of the SA optimization from nearly 8 h to under 3.5 h (on an Intel^® 2.0 GHz Xeon processor with 2 GB of RAM) (Fig. 3). Hereafter, “computational cost” refers to wall clock time on the aforementioned computational hardware. Adaptive surrogate modeling reduced the number of FE calls by an average of 59.5 ± 3.3% (811 vs. 2001) at 5 N² tolerance, which grew to 77 ± 3.4% at 20 N² tolerance (467 vs. 2001). The corresponding average computation time at 20 N² was 1.9 h. An acceptable balance between accuracy and efficiency for the SA optimization was found at the threshold value of 20 N², beyond which the average solution error and the upper limits of the quartile ranges began to increase (Fig. 3). Considering all SA results below the 25 N² tolerance, the average RMSE was 2.5 N (4% of peak experimental load) with a peak value of 12.5 N (19.5% of peak load). At 25 N², the average RMSE increased to almost 10 N or nearly 16% of the maximum load with the subsequent 30 N² tolerance realizing an even greater 23.3 N (36% of peak load) average RMSE. The distribution of results was non-normal; as a result, quartiles were calculated using all 20 runs at each tolerance value (Fig. 3). A wider spread of the results was realized above 20 N² tolerance, demonstrated by the upper quartile (75th percentile) increasing from 3 to 8.2 to 10.2 (5, 13, and 16% peak load) for the 20, 25, and 30 N² tolerance values, respectively (Fig. 3).

FIGURE 3.

Root mean square errors (RMSE) and computational cost. (Top) Using simulated annealing (SA), model vs. experimental RMSE (see Eq. (5)) were calculated for each of the 20 results at every tolerance value. Average RMSE values as a function of tolerance were included and show consistent results up to a tolerance value of 25 N². Average computation time with corresponding standard deviations was also plotted and demonstrates a decrease in expense with increasing tolerance. (Bottom) Quartile breakdowns for the SA RMSE results as a function of tolerance value. Values for the 25th percentile, median (squares), and 75th percentile were included, and results demonstrated increasing values above a tolerance of 20 N². For clarity, the quartile breakdowns were calculated using the raw data (triangles) in the top plot.

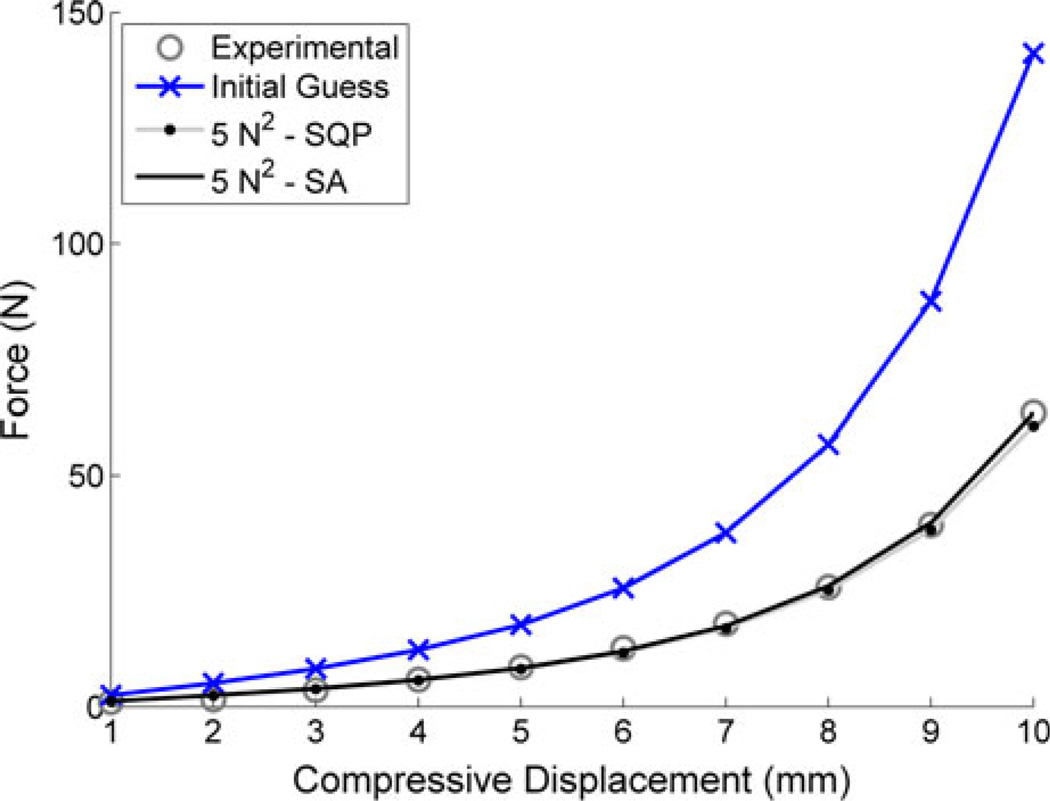
The SQP optimization, as might be expected, was very sensitive to the initial guess value. Even at a tolerance of 0 N² (no surrogate), of the 20 random initial guess values, only 11 realized model vs. experimental RMSE values within 2.5 N (4% of peak load) of the experimental data (SA average error below 25 N² tolerance). For tolerance values greater than zero, only one initial guess value was capable of recreating a similar result with an RMSE of 1.8 N (Fig. 4). All other results were influenced by the surrogate model with RMSEs ranging from 6 up to 1500 N (9 up to 2300% of the peak load). For the single adequate initial guess, the surrogate model produced a 68% drop in computational cost (3.5 vs. 11 min) with 42 and 36 function calls for the 0 and 5 N² tolerance values, respectively. As these results were consistent for each tolerance setting, it is apparent that the SQP results with the surrogate model were more sensitive to the initial guess than the choice of tolerance value. SA proved far more robust for the given initial guess values, with relatively accurate solutions found for every simulation below a tolerance value of 20 N² (Fig. 3).

FIGURE 4.

Compressive displacement vs. force: experimental; FE predictions with μ and α as 16.6 kPa and 11.24, respectively, as the initial guess; FE predictions with μ and α calculated by inverse analysis using sequential quadratic programming (5 N² − SQP); FE predictions with μ and α calculated by inverse analysis using simulated annealing (5 N² − SA). The highlighted SQP results are for the single surrogate model optimization that converged to a model vs. experimental error of 1.8 N. Note that the 5 N² − SQP line lies very close to the data points for the experimental results. The presented SA result is a typical curve at a tolerance value of 5 N².

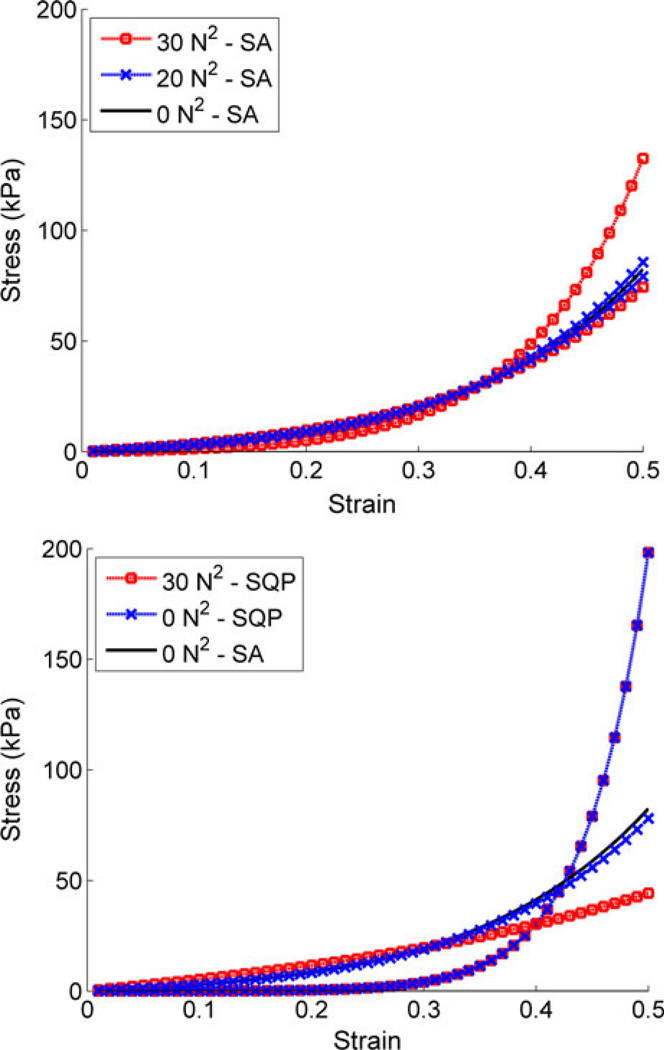
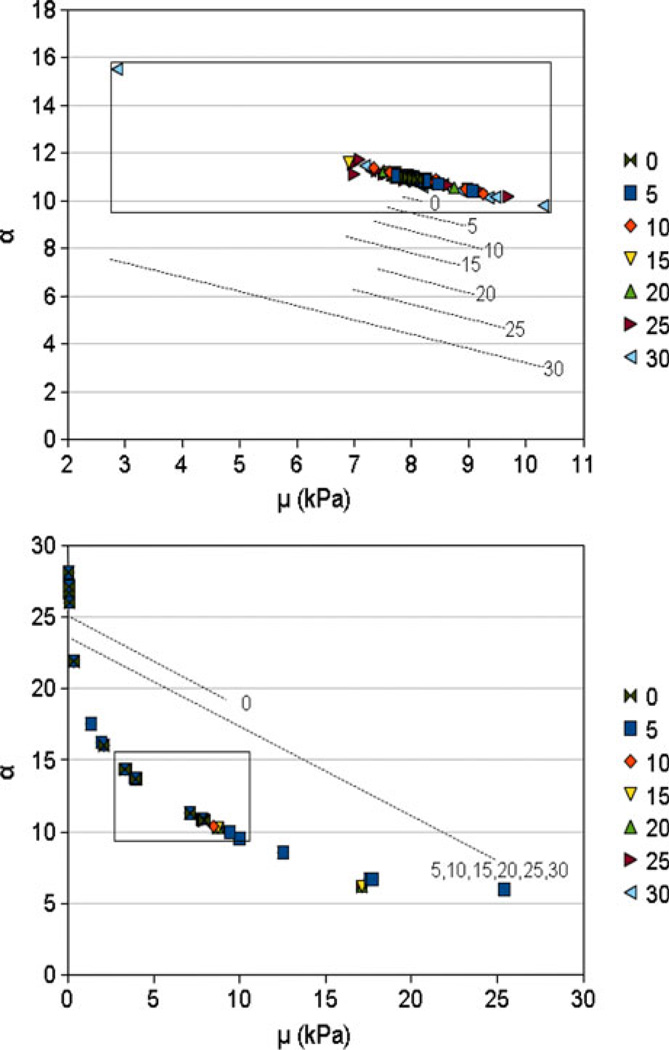
Beyond simply evaluating the model vs. experimental displacement–load behavior, stress results are of primary interest for predictions of internal tissue mechanics. Parameter predictions for the SA optimizations resulted in relatively tight spread of stress–strain response, especially below a tolerance value of 25 N² (Fig. 5). SQP, conversely, demonstrated increased variability in the stress–strain response, as might be expected from the wide range of corresponding parameter results (Figs. 5, 6). Still, for the single SQP result that did converge to an adequate representation of experimental displacement–load behavior, the stress–strain behavior was also well in line with the optimal results from the SA runs (Fig. 5 and as indicated in Fig. 4). The relative spread of results was also demonstrated through a two-dimensional (2D) plot of the material coefficients (Fig. 6). Overall, the SA material coefficients demonstrated a much tighter spread of coefficients as opposed to the SQP results.

FIGURE 5.

Bounded range of the stress–strain response. These values were determined by maximum and minimum stress results at 0.5 strain (defined as worst-case scenarios), for all 20 nonlinear material parameters at tolerance values of (top) 0, 20, and 30 N² using simulated annealing (SA) and (bottom) 0 and 30 N² tolerance values using sequential quadratic programming (SQP). Note that two lines were required to represent each data set, and 0 N² tolerance corresponds to strict utilization of FE-predicted behavior. At 0 N² tolerance, SA predicted stress–strain response proved very consistent while SQP results displayed an approximate 125 MPa range of stress results (at 0.5 strain). SA results at 0 N² tolerance were also included in the bottom plot for comparison.

FIGURE 6.

Scatter plots of the μ and α values at each tolerance setting for the (top) simulated annealing and (bottom) sequential quadratic programming optimizations. Bounding boxes, placed in the same positions and sized for consistent height and width, were included in each plot to give a reference of the relative spread between the two sets of results in the material parameter space. The dotted lines represent ranges of results at each tolerance (lines are labeled and offset for clarity).

DISCUSSION

Using a previously published inverse FE application, the study was successful in assessing the computational benefits of a local adaptive surrogate modeling approach for identification of nonlinear elastic material parameters. Overall, the implementation of the surrogate model resulted in marked improvements in computational expense for both the global SA approach as well as the SQP method if an adequate initial guess was provided in the latter case. The robustness of the global SA method over the SQP approach was demonstrated through 20 successive runs, each with a unique initial guess. This result is of particular importance when feature rich models are necessary and an approximate initial guess is unavailable, as a solution found at a local minimum can be a concern. Implementation of the surrogate model resulted in a nearly 60% decrease in computational expense while using SA with a tolerance value of 5 N². Computational cost continued to decrease beyond 5 N², achieving a 77% reduction at a tolerance of 20 N², but the initial cost savings were the most substantial. Reducing the expense of a global method such as SA is worthwhile as many problems are difficult to bound and may contain local minimums. On the contrary, when problems are well behaved and a gradient-based optimization approach is desired, computational benefits are still possible with this surrogate model, as evidenced from our previous study,¹⁵ and from a solution obtained by one of the initial guess values in the current study. Overall, however, the SQP optimizations using the proposed range of start values demonstrated an obvious sacrifice in reliability, as measured by the RMSE results and the spread of material parameters (Figs. 5, 6).

While it is generally true that gradient-based optimization is sensitive to the starting condition, it appears to be even more sensitive if a time-saving approach, such as the included surrogate model, is adopted. Using SQP, 11 initial guess values out of 20 converged to a relatively accurate solution without the surrogate model implemented. Of the 11 acceptable solutions, only one similar result was found above a tolerance of 0 N² (with the surrogate). The nature of SQP optimization, where small perturbations to the optimization variables are relied on for gradient calculations, may have contributed to the decline in performance with the surrogate. Qualitative post-processing revealed that the gradient calculations followed by a line search approach led to unrealistically low CVE predictions and misrepresentation of the underlying FE model. It is possible that benefits of a combined SQP and surrogate framework may be realized after careful assessment including informed initial guess values and more elaborate regression schemes. That particular investigation, however, was beyond the scope of the current study but will need to be performed before future work uses an SQP and surrogate framework.

Obviously, this study benefited from utilization of a previously published 2D simulation.⁸ Adoption of a known test problem was necessary to develop and quantify performance of the surrogate modeling approach. The realized material coefficients were consistent with the previous study. It is noteworthy though that results presented in Erdemir et al.⁸ were averaged over 20 subjects, whereas this study used data from a single subject from the healthy population. It is expected that similar conclusions on the utility of surrogate modeling would be obtained for all the subjects, but this remains a future endeavor. Future work will also include utilizing the proposed framework for patient and specimen-specific assessment of tissue behavior, including application to more physiologically consistent and computationally expensive three-dimensional (3D) analysis.⁷ Given that a 3D simulation may easily require hours to complete, as opposed to an average 14 s FE computation time for this study, surrogate modeling has the potential to curtail significant computational expense. For example, at the current SA optimization settings, a 1-h FE simulation of a 3D heel-pad model would result in 2001 h (83 days) of computation time. With the surrogate, this expense could reduce to approximately 460 h (19 days) (77% fewer FE simulations, as found in this study). As demonstrated, the absolute time savings will depend on the optimization type, and our current results facilitate informed application of these methods to more computationally intense models.

Even without the surrogate model, the SQP optimization could be performed nearly seven times before it equals the computational cost for SA results at 20 N² tolerance (average SQP computation time at 0 N² was 18 min). Understandably, this might deter the use of a global approach but it is possible that the chosen SA parameters were stringent for this application. There is a potential for further computational savings, without sacrificing accuracy, through tailoring of the SA parameters, which as defined, required 2001 function evaluations. For this study, SA parameters included the maximum temperature (50), minimum temperature (0.0001), cooling rate (0.5), and the number of iterations at each temperature (20), all applied using an exponential mode of decreasing temperature.¹²

Parameters associated with the Lazy Learning local regression algorithm could also affect the results. The number of nearest neighbors used in regression was allowed to range from 6 points up to 15 and is potentially a wide range of the necessary data points to achieve accurate results. Given the disproportionate computational cost of the FE simulations vs. the surrogate model (approximately 14 vs. 6 × 10⁻⁴ s per result), this choice does not result in a large computational investment for this problem. Nevertheless, if performance on this order of magnitude becomes important, it is recognized that efficiency gains are possible through informed setting of the regression model parameters.

Beyond the specific method used in this study, the type of adaptive surrogate modeling may also significantly influence the performance of the system. Our approach was based on our experience with Lazy Learning,^14,15 but it is recognized that alternative methods, especially with regard to the SQP optimization, may yield better results. This initial investment, however, found the relatively straightforward Lazy Learning method to perform well for the SA optimizations. SA’s inherent random generation of inputs (material parameters in this case) produced sufficient database support and adequate regression. A relatively wide input range was accommodated, and the database was populated on an as-needed basis, indicating potential value when a problem may not be well characterized a priori. Additionally, as previously demonstrated, this approach is suited to handle other computationally expensive iterative processes such as a musculoskeletal or probabilistic analysis.^14,19,20

In practice, surrogate tolerance setting requires insight into the behavior of the underlying model, and sensitivity was evaluated through systematic changes to this parameter. For the SA optimization, significant time savings were found for all tolerance values but beyond 20 N², variability in solution results was evident (Figs. 3, 6). While the tolerance values of 25 and 30 N² proved capable of finding acceptable solutions, the spread of values did not lend confidence in the predictions. In addition, in terms of computational expense, only minimal benefit was realized. It is recognized that 20 runs of the SA optimization may not be sufficient to demonstrate the true variability, but it is also apparent that results were affected above 20 N² tolerance. For other applications, and in lieu of a systematic study of tolerance values, there are many approaches for choosing an acceptable tolerance value. Tolerance setting can be achieved through comparison of the surrogate model with actual FE results on a limited input space. This approach previously served as an acceptable starting point for simulations.¹⁴ Iteratively changing the tolerance value(s) until accurate results are realized is another approach, but potentially defeats the benefits of a more conservative but reliable estimate, where less time is spent in model and optimization interaction. On the contrary, a loose initial tolerance value may result in wide database support and benefit future analyses, but potentially comes at the cost of decreased solution reliability (Fig. 3). This controlled study obviously did not exploit that benefit. Whatever approach is adopted for setting the tolerance, actively evaluating the performance of the surrogate model for a given application is advisable.

To the authors’ knowledge, this is the first study to systematically evaluate the use of an adaptive regression-based surrogate model during inverse nonlinear material parameter optimization using different optimization procedures. Performance of the computational framework was found to depend on the type of optimization, in this case SA and SQP. The SQP method’s sensitivity to initial guess was amplified with surrogate modeling. Nonetheless, one surrogate and SQP optimization demonstrated promising results and might indicate potential value in this approach, if the method is further refined. For SA, the application of the surrogate model consistently decreased computational cost of the SA optimizations while retaining reliable parameter predictions. This study effectively demonstrates the benefits of a surrogate modeling framework for intensive FE-based iterative analysis, particularly for global search problems, and helps elucidate potential for application to other coupled, computationally expensive systems.

APPENDIX A

LIST OF INITIAL GUESS VALUES

Initial guess values for the Ogden material parameters used during optimization were generated using the “rand” random number generator in Matlab (Mathworks, Inc., Natick, MA). The 20 results from the “rand” function were found on the ranges 1–50 kPa for μ and 5–30 for α, as presented under “Methods” section.

μ (kPa)	α
11.933	10.081
49.725	11.08
37.221	13.073
5.569	26.762
45.404	17.04
16.57	11.239
48.647	18.534
12.543	28.542
10.975	9.5657
33.533	17.92
13.84	27.587
37.493	6.4607
4.893	16.3
6.688	17.612
12.824	10.084
21.529	14.471
43.99	7.8168
34.203	28.344
22.415	22.856
27.103	6.5119