How mutation affects evolutionary games on graphs

Abstract

Evolutionary dynamics are affected by population structure, mutation rates and update rules. Spatial or network structure facilitates the clustering of strategies, which represents a mechanism for the evolution of cooperation. Mutation dilutes this effect. Here we analyze how mutation influences evolutionary clustering on graphs. We introduce new mathematical methods to evolutionary game theory, specifically the analysis of coalescing random walks via generating functions. These techniques allow us to derive exact identity-by-descent (IBD) probabilities, which characterize spatial assortment on lattices and Cayley trees. From these IBD probabilities we obtain exact conditions for the evolution of cooperation and other game strategies, showing the dual effects of graph topology and mutation rate. High mutation rates diminish the clustering of cooperators, hindering their evolutionary success. Our model can represent either genetic evolution with mutation, or social imitation processes with random strategy exploration.

1. Introduction

Understanding the emergence of cooperation is of great interest in evolutionary biology. Cooperative behaviors have been observed in microbes, animals, plants, and humans. For these behaviors to evolve, some evolutionary mechanism must be present enabling cooperators to overcome the fitness disadvantages they incur (Nowak, 2006). Spatial structure is one such mechanism (Nowak & May, 1992). Local reproduction and limited dispersal can lead to spatial assortment of cooperators. Since interaction is also local, the benefits of cooperation are received mostly by other cooperators. This clustering can promote evolution of cooperation (Nakamaru et al., 1997; Killingback & Doebeli, 1996; van Baalen & Rand, 1998; Mitteldorf & Wilson, 2000; Le Galliard et al., 2003; Santos & Pacheco, 2005; Ohtsuki et al., 2006; Taylor et al., 2007; Szabó & Fáth, 2007; Helbing & Yu, 2009; Roca et al., 2009a; Wu et al., 2010b). A recent and powerful approach to studying such questions is provided by evolutionary graph theory (Lieberman et al., 2005; Santos & Pacheco, 2005; Ohtsuki et al., 2006; Taylor et al., 2007; Szabó & Fáth, 2007; Pacheco et al., 2006; Roca et al., 2009b; Perc & Szolnoki, 2010).

Here we investigate how mutation affects evolutionary games on graphs. The interplay between mutation rate and spatial selection has previously been investigated in games on sets (Tarnita et al., 2009a), games in phenotype space (Antal et al., 2009), and various general approaches (Tarnita et al., 2009b; Nowak et al., 2010a). But most studies of games on graphs assume either no mutation (Ohtsuki et al., 2006; Szabó & Fáth, 2007) or the limit of very small mutation rates (Taylor et al., 2007). Intuitively, mutation can be expected to dilute spatial assortment and thus hinder the evolution of cooperation.

To explore how mutation affects spatial clustering, we use mathematical methods from statistical physics and coalescent theory (Wakeley, 2009). Through generating function analysis of coalescing random walks, we obtain exact expressions for the probability that two individuals are identical-by-descent (IBD), depending on their relative positions, the mutation rate, and the graph topology.

Using these results, we obtain exact conditions for cooperation to succeed under weak selection. Our results show the effects of graph degree (number of neighbors per individual), mutation rate, and higher-order features of the graph topology. As expected, cooperation becomes more difficult to achieve as the mutation rate increases. Simulations confirm our results.

For genetically evolving populations, the mutation rate between cooperator and defector phenotypes may be rather small. But cultural evolution and learning on social networks may occur with substantial rates of strategy exploration, analogous to mutation (Traulsen et al., 2009, 2010).

2. The basic model: neutral drift on graphs

2.1. Graph structure

We model population structure as a graph G (Ohtsuki et al., 2006; Taylor et al., 2007; Szabó & Fáth, 2007; Lieberman et al., 2005). Interaction and replacement occur between neighboring nodes. We focus on graphs with strong internal symmetry, which we characterize in terms of the automorphisms of G (Beineke & Wilson, 2004). An automorphism is a bijection of the node set of G which preserves the graph structure. That is, if nodes i and j are neighbors and T is an automorphism, then nodes T(i) and T(j) are neighbors as well.

We require the following two symmetry conditions:

• Bi-transitivity (Taylor et al., 2007): For every pair of nodes i and j, there is an automorphism T that interchanges them: T(i) = j, T(j) = i.

• Rotational symmetry: For any node i, and any pair of neighbors j and j′ of i, there is an automorphism T that fixes i and maps j to j′ : T that fixes i and maps j to j′: T(i) = i, T(j) = j′.

Less formally, bi-transitivity asserts that the graph “looks the same” from the vantage point of any node. Rotational symmetry asserts that each neighbor of a given node is equivalent with respect to the graph structure. In particular, all our graphs are regular: each node has the same number k of neighbors.

We focus on the examples of lattices (finite or infinite, of any dimension) and Cayley trees. A Cayley tree (or Bethe lattice) is an infinite regular graph with no cycles. Lattices correspond to spatially structured populations, whereas a Cayley tree can model a homogeneous, weakly interconnected social network.

2.2. The neutral drift model

We first consider a process of neutral drift. Our results apply to any number n of evolving types. Each time-step, a random node is chosen as a “parent”, and a random neighbor of the parent is chosen as the “offspring”. The order in which parent and offspring are selected does not matter for this neutral model. With probability u, a mutation occurs and the type of the offspring is sampled from some mutation kernel. Otherwise, with probability 1 – u, reproduction is faithful. In this case the offspring adopts the type of the parent, and the two are said to be identical-by-descent (IBD). This model is a discrete-time analogue of the “noisy voter” model in statistical physics (Granovsky & Madras, 1995).

Strategy updating can represent either asexual genetic reproduction or imitation of social partners. In the latter case, mutation represents random strategy exploration (Traulsen et al., 2009).

This process, as described, is well-defined only for finite graphs. For infinite graphs, it is not possible to randomly choose a parent so that each node has equal probability of being chosen. However, the mathematical techniques we use extend naturally to infinite graphs. Our results for infinite graphs can be considered as limits, as the population size approaches infinity, for certain classes of graphs. For example as N → ∞, the local structure of a random k-regular graph of size N increasingly resembles that of a Cayley tree (Szabó & Fáth, 2007). Thus our results for Cayley trees apply to random regular graphs in the limit of large population size.

2.3. Coalescing random walks

We analyze neutral drift on graphs using coalescing random walks (CRWs) (Cox, 1989; Cox & Durrett, 2002), as illustrated in figure 1. The basic idea is to trace the evolutionary process backwards through time until lineages coalesce at a common ancestor (Kingman, 1982; Wakeley, 2009). For spatial evolution, lineages are traced through space as well as time. The path traced back to an individual’s ancestors is the realization of a random walk backwards in time.

Figure 1.

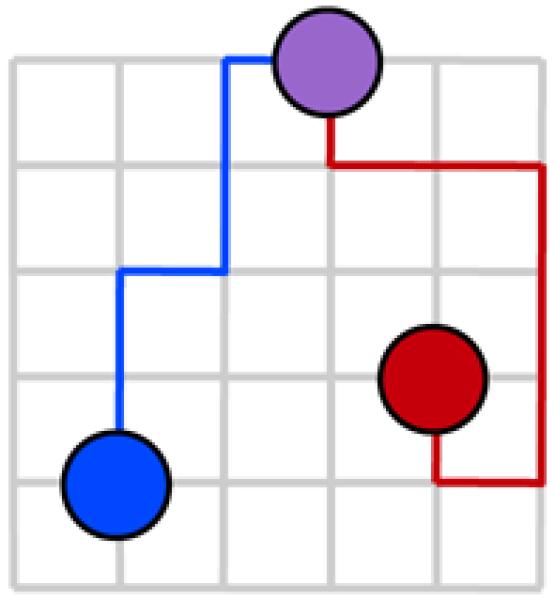
To analyze the relatedness of two individuals (marked by red and blue circles), we consider a coalescing random walk (CRW). One walker starts at each initial position. At each time step, either walker steps to an adjacent node. The process terminates when the walkers coalesce (purple circle). The two trajectories represent the locations of the ancestors of the two individuals. The point of coalescence represents the most recent common ancestor.

The CRW models the co-ancestry of two individuals at locations i and j by considering a pair of random walkers. The state of the CRW is the pair (h, ℓ) representing the current walker positions. The initial state is (i, j). Each time step, one of the two walkers may step to an adjacent node. Thus (h, ℓ ) may transition to either (h′, ℓ ), where h′ is a neighbor of h, or (h, ℓ′ ), where ℓ′ is a neighbor of ℓ. Each transition occurs with equal probability (this is not the case for non-regular graphs). The CRW terminates when the walkers occupy a site simultaneously, at which point they have coalesced. The point of coalescence represents the divergence of the two lineages.

We use CRWs to obtain IBD probabilities. Suppose that for each step in a CRW, a mutation occurs with probability u. The equilibrium probability q_ij that the occupants of nodes i and j are IBD equals the probability that no mutations occur in the CRW from i and j.

By symmetry, we can choose a focal node ● and restrict attention to the IBD probabilities q_●i between ● and other nodes i. For lattices and Cayley trees there is an additional simplification: in place of the coalescing random walk we can consider a single walk that starts at ● and terminates upon hitting i. The displacement from the walker’s location to i in the single walk represents the displacement between the two walkers in the CRW. We formalize this argument in Appendix A.

For finite graphs other than lattices, the underlying Markov process of the CRW can be represented by a stochastic matrix. IBD probabilities can be obtained numerically by inverting this matrix. This approach was explored by Seshadri (2007).

2.4. Generating function analysis

Consider a random walk of n steps starting at ●. Let p⁽ⁿ⁾(i) be the probability that the walk terminates at i, and let q⁽ⁿ⁾(i) denote the probability that it terminates at i without having visited i at any previous step.

We analyze CRWs using two generating functions (Woess, 2009; Lawler & Limic, 2010): the Green’s generating function

$$\tilde{p}(i;z)=\sum _{n=0}^{\infty }{p}^{\left(n\right)}\left(i\right)z^n,$$

and the first visit generating function

$$\tilde{q}(i;z)=\sum _{n=0}^{\infty }{q}^{\left(n\right)}\left(i\right)z^n.$$

By the symmetry argument of the previous section, q⁽ⁿ⁾(i) equals the probability that the lineages of ● and i coalesce in exactly n steps. Since each step in the coalescent process is faithful with probability 1 – u, the probability that ● and i are IBD is

$$q_{•i}=\sum _{n=0}^{\infty }{q}^{\left(n\right)}\left(i\right){(1-u)}^n=\tilde{q}(i;1-u)$$ (1)

A random walk that terminates at i after n steps must (a) visit i for the first time after m steps, for some 0 ≤ m ≤ n, and (b) return to i after n – m further steps. For a particular value of m, event (a) has probability q^(m)(i) and event (b) has, by symmetry, probability p^(n–m)(●). This implies the relation

$$p^{\left(n\right)}\left(i\right)=\sum _{m=0}^n{q}^{\left(m\right)}\left(i\right)p^{(n-m)}\left(•\right),$$

which can be conveniently expressed using generating functions:

$$\tilde{p}(i;z)=\tilde{q}(i;z)\tilde{p}(•;z).$$ (2)

We also have the relation

$$\tilde{p}(i;z)=\{\begin{array}{cc}1+\frac{z}{k}\sum _{\underset{j\text{of}i}{\text{neighbors}}}\tilde{p}(j;z)\hfill & \text{if}i=•\hfill \\ \frac{z}{k}\sum _{\underset{j\text{of}i}{\text{neighbors}}}\tilde{p}(j;z)\hfill & \text{if}i\ne •\hfill \end{array}\phantom{\}}$$ (3)

This asserts that a random walk terminating at i either has length zero (possible only if i = ●) or else passes through one of the k neighbors of i before arriving at i.

The Green’s generating function on lattices was investigated by Montroll & Weiss (1965). For a point x = (x₁,…,x_n) on a finite periodic n-dimensional lattice of side length m, they obtained

$$\tilde{p}(x;z)=\frac{1}{m^n}\sum _{y\in G}\frac{\exp \left(-\frac{2\pi \sqrt{-1}}{m}x\cdot y\right)}{1-\frac{z}{2}\sum _{i=1}^n\cos \frac{2\pi y_i}{m}}.$$ (4)

For an infinite lattice, the sum is replaced by an integral:

$$\tilde{p}(x;z)=\frac{1}{{\left(2\pi \right)}^n}{\int }_{-\pi }^{\pi }\cdots {\int }_{-\pi }^{\pi }\frac{\exp (-\sqrt{-1}\sum _{i=1}^n{x}_i{\theta }_i)}{1-\frac{z}{2}\sum _{i=1}^n\cos {\theta }_i}d{\theta }_1\dots d{\theta }_n.$$ (5)

For the two-dimensional infinite lattice in particular, Shore & Tyler (1993) derived

$$\tilde{p}(•;z)=\frac{1}{\mathrm{agm}(1+z,1-z)}.$$ (6)

The symbol agm(x, y) denotes the arithmetic-geometric mean of x and y, which equals the common limit of two recursively defined sequences, {a_n} and {g_n}. The initial terms a₁ and g₁ are the arithmetic and geometric means, respectively, of x and y: a₁ = (x + y)/2, $g_1=\sqrt{xy}$. Subsequent terms a_n+1 and g_n+1 are set equal to the arithmetic and geometric means, respectively, of a_n and g_n.

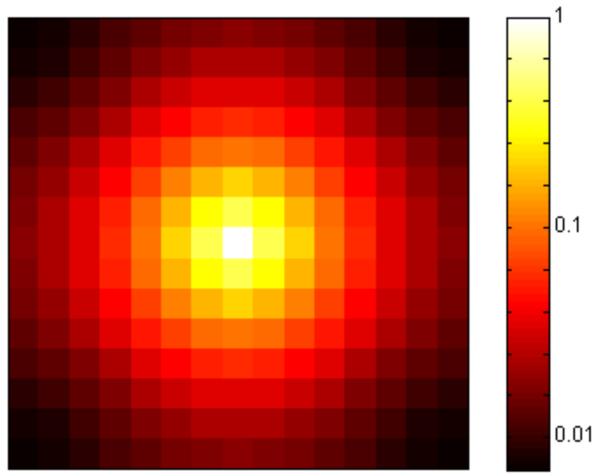
Exact IBD probabilities between any pair of points on a lattice can be obtained using (1), (2), and (4) or (5). The spatial pattern of IBD probabilities on a finite lattice is illustrated in figure 2.

Figure 2.

IBD probabilities q_i for neutral evolution on a 15 × 15 lattice, calculated using the Green’s generating function (4) and the relation (2) between the Green’s generating function and the first visit generating function. The mutation rate is u = 0.05. The likelihood of identity by descent decreases with distance from the focal individual (center).

We now turn to Cayley trees. Cayley trees are distance-transitive (Beineke & Wilson, 2004), which means informally that, with respect to the graph structure, any pair of nodes distance d apart is equivalent to any other pair the same distance apart. We therefore write $\tilde{p}(d;z)$ and $\tilde{q}(d;z)$ as a short-hand for the generating functions $\tilde{p}(i;z)$ and $\tilde{q}(i;z)$ corresponding to any particular node i that is distance d from ●.

The tree structure of Cayley trees implies the relation

$$\tilde{q}(d_1+d_2;z)=\tilde{q}(d_1;z)\tilde{q}(d_2;z),$$ (7)

reflecting the fact that, to reach a node i that is distance d₁ + d₂ from ●, a walk must first pass through the node that is d₁ steps along the (unique) path from ● to i. In particular

$$\tilde{q}(2;z)=\tilde{q}{(1;z)}^2.$$ (8)

Furthermore, (3) implies that

$$\tilde{p}(1;z)=\frac{z}{k}\left(\tilde{p}(0;z)+(k-1)\tilde{p}(2;z)\right).$$

Dividing both sides by $\tilde{p}(0;z)$ and invoking (2) we obtain

$$\tilde{q}(1;z)=\frac{z}{k}\left(1+(k-1)\tilde{q}(2;z)\right).$$

Combining with (8) yields a quadratic equation for $\tilde{q}(1;z)$, whose solution is

$$\tilde{q}(1;z)=\frac{k-\sqrt{k^2-4z^2(k-1)}}{2z(k-1)}.$$

From (7) we have

$$\tilde{q}(d;z)=\tilde{q}{(1;z)}^d={\left(\frac{k-\sqrt{k^2-4z^2(k-1)}}{2z(k-1)}\right)}^d$$

Substituting z = 1 – u yields the IBD probability for any pair of nodes distance d apart on the Cayley tree.

In our subsequent analysis, we only need the probability q that immediate neighbors are IBD. These values are presented in table 1 and illustrated in figure 3.

Table 1.

Neighbor IBD probabilities on graphs

Graph family	Neighbor IBD probability q	Low-mutation approximation
Infinite 1D lattice	$\frac{1-\sqrt{u(2-u)}}{1-u}$	$1-\sqrt{2u}+\mathcal{O}\left(u\right)$
Finite 1D lattice	$\frac{q_{\infty }^{N∕2-1}+q_{\infty }^{1-N∕2}}{q_{\infty }^{N∕2}+q_{\infty }^{-N∕2}}$ *	$1-(N-1)u+\mathcal{O}\left(N^3{u}^2\right)$
(Infinite) k-Cayley tree	$\frac{k-\sqrt{k^2-4{(1-u)}^2(k-1)}}{2(1-u)(k-1)}$	$\frac{1}{k-1}\left(1-\frac{k}{k-2}u\right)+\mathcal{O}(u^2∕k^2)$
Infinite 2D lattice	$\frac{1-\mathrm{agm}(u,2-u)}{1-u}$ **	$1-\frac{\pi }{\ln (8∕u)}+\mathcal{O}\left(u\right)$
Other finite graphs	see text	$1-(N-1)u+\mathcal{O}\left(u^2\right)$ ***

^*Due to Grafen (2007). The notation $q_{\infty }=\frac{1-\sqrt{u(2-u)}}{1-u}$ represents the q value for the infinite 1D lattice.

^**Obtained using equations (1), (6), and (3) in the case i = •.

^***Due to Taylor et al. (2007). The magnitude of the error term with respect to N depends on the graph structure.

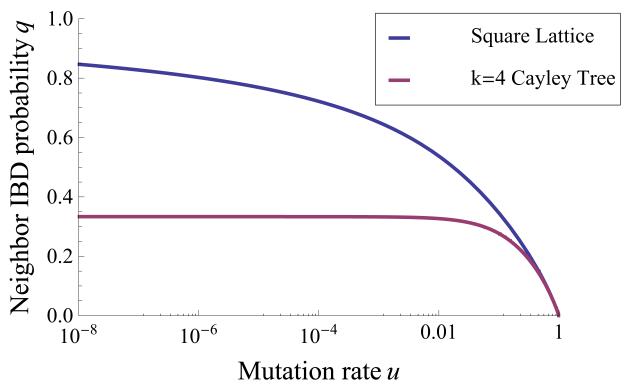
Figure 3.

Neighbor IBD probabilities q on the infinite square lattice and degree 4 Cayley tree. As the mutation rate u increases, neighbors are less likely to be IBD. Though both graphs have degree 4, the IBD probabilities for small u are quite different, reflecting the differences in graph topology. q approaches 1 for the lattice, and $\frac{1}{k-1}=\frac{1}{3}$ for the Cayley tree, as u → 0. In the limit of low mutation, lattice neighbors are necessarily IBD, but Cayley tree neighbors are not. This is because on the lattice (or on any finite graph), any pair of lineages will coalesce in finite time with probability 1. However, on the Cayley tree, there is a nonzero probability that a CRW never coalesces. In other words, individuals on the Cayley tree do not necessarily have a common ancestor in the finite past. This counterintuitive property arises only for infinite graphs.

Other statistics of spatial assortment can be obtained from IBD probabilities. If there are two evolving types, labeled 0 and 1, then q_ij is the correlation coefficient between the types of i and j. More generally, if there are n types, all equally likely to result from any mutation, then q_ij+(1–_qij)/n is the equilibrium probability that i and j have the same type.

3. Cooperation on graphs with mutation

We study cooperation via the additive (simplified) Prisoner’s Dilemma game. We consider two strategies, cooperators, C, and defectors, D. A cooperator pays a cost c to give a benefit b > c to the other player, while a defector pays no costs and gives no benefits. This yields the payoff matrix

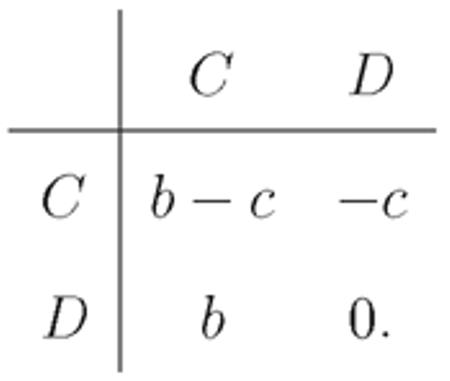Every time step, each individual plays this game with each neighbor, obtaining an average payoff π. This payoff is transformed into fecundity (reproductive rate) by a map π ↦ F(δπ). F can be any increasing differentiable function satisfying F(0) = F′(0) = 1, for example F(δπ) = 1 + δπ (Nowak et al., 2004; Ohtsuki et al., 2006) or F(δπ) = e^δπ (Traulsen et al., 2008). The parameter δ > 0 quantifies the strength of selection, i.e. the extent to which fecundity depends on payoff. We consider only weak selection, so that only the first-order behavior of F is relevant (Wu et al., 2010a). Under weak selection, neutral IBD probabilities can be used in determining whether cooperators are favored. The range of δ values for which weak selection results are accurate depends on the update rule (see section 3.1).

We consider the cooperator type to be favored if they have greater than 50% abundance in mutation-selection equilibrium (Antal et al., 2009). Nowak et al. (2010b) showed that (under conditions which are satisfied for evolution on finite fixed graphs) this success condition is equivalent to

$${\langle \frac{\partial (b_{•}-d_{•})}{d\delta }\rangle }_{\begin{array}{c}\hfill \delta =0\hfill \\ \hfill s_{•}=C\hfill \end{array}}-u{\langle \frac{\partial b_{•}}{d\delta }\rangle }_{\begin{array}{c}\hfill \delta =0\hfill \\ \hfill s_{•}=C\hfill \end{array}}>0.$$ (9)

Above, b_● and d_● are the reproduction and death probabilities, respectively, of the focal individual ●. The notation ${\langle \dots \rangle }_{\begin{array}{c}\hfill \delta =0\hfill \\ \hfill s_{•}=C\hfill \end{array}}$ indicates an expectation over the stationary distribution of states of the neutral process, conditioned on the focal individual ● being of type C. The first term of (9) represents the fitness effect of being a cooperator (including fitness benefits acquired from neighboring cooperators). The second term represents a mutational bias due to different birth rates of C and D types. This second term vanishes if either birth rates or death rates are constant over all individuals, or if the limit of low mutation is considered (Nowak et al., 2010b).

3.1. Update rule

In contrast to the neutral case, outcomes for non-neutral evolution depend on how the nature of local population regulation (Ohtsuki et al., 2006). We consider two different update rules (replacement schemes). For “death-birth” (DB) updating, a random site is chosen for replacement (with neutral probability). A neighbor is chosen to reproduce into this site, with probability proportional to fecundity. For “birth-death” (BD) updating, an individual is chosen from the entire population with probability proportional to fecundity. This individual reproduces into a neighboring site chosen at random (with neutral probability).

These two update rules have different effects on local competition. For BD updating, there is a conflict between neighbors: if a neighbor of a focal individual ● is chosen to reproduce, there is a 1/k chance that the new offspring will displace ● For DB updating, there is a conflict between neighbors-of-neighbors: if a neighbor of ● is chosen for replacement, ● competes with its neighbors-of-neighbors for the opportunity to reproduce. These differences in local competition affect the success of cooperation, as we show in the following section and in Appendix C.

Each reproduction event is faithful with probability 1 – u. With probability u, a mutation occurs, and the type (C or D) of the offspring is assigned at random.

For δ = 0 on a regular graph, both DB and BD reduce to the neutral drift process described in section 2.2.

3.2. Conditions for the evolution of cooperation

We now present conditions for the success of cooperation, based on the mutation rate, graph topology, and update rule. We assume weak selection, δ ⪡ 1/m, where m is the number of individuals who affect a given individual’s fitness. For BD updating, m is the number of nodes within distance two of a given node (an individual’s fitness is affected by the payoffs of neighbors, which depend in turn on the types of neighbors-of-neighbors). For DB m is the number within distance 3. This assumption allows the use of neutral IBD probabilities in determining the direction of selection.

Consider a symmetric graph of degree k, whose neighbors have probability q to be IBD. For DB updating, we show in Appendix C.1 that cooperators are favored if and only if

$$\frac{b}{c}>\frac{k(1-u)(1-u-q)}{1-u-q-qu(2-u)(k-1)}.$$ (10)

This condition is derived for finite graphs, but can be applied to any lattice or Cayley tree by substituting the appropriate value of q (table 1).

For any fixed graph, as the mutation rate u increases, q decreases and the threshold (10) increases. Thus the requirements for successful cooperation become increasingly stringent with u. In short, mutation weakens the spatial benefit to cooperation.

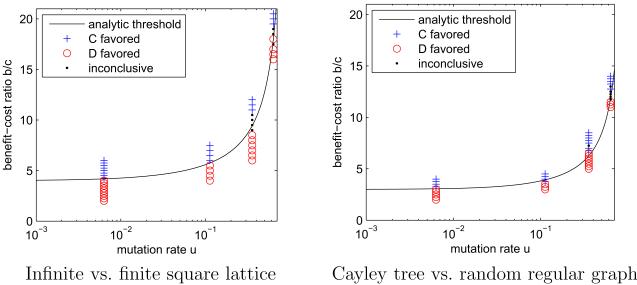
The increase in the cooperation threshold (10) with u is illustrated in figure 4. As this figure shows, our analytic results for infinite graphs correctly predict the outcomes of simulations on large finite graphs with weak selection.

Figure 4.

Theoretical cooperation thresholds, and simulation results on related graphs, as a function of mutation rate. Left: Comparison of analytical results for an infinite square lattice with simulation results on a 20 × 20 lattice with periodic boundary. Right: Comparison of analytical results on the k = 3 Cayley tree with simulation results for a random regular graph of degree 3 with 400 nodes. Random regular graphs locally approximate Cayley trees (Szabó & Fáth, 2007); however, some deviations between analytical and simulation are expected due to the possible presence of short loops in random regular graphs. A + (○) indicates that cooperators are favored (disfavored) with 98% confidence after 1000 simulation runs. A dot (·) indicates that neither statement could be made with 98% confidence. In each case the cost c is 1 and the selection strength δ is 0.01. Simulation procedures are described in Appendix D.

If we instead consider a particular family of graphs (such as lattices or Cayley trees) and increase the degree k while holding u constant, then q decreases and the threshold (10) increases. Thus, cooperation is more successful when individuals have fewer neighbors, as was previously known for the low-mutation limit (u → 0) (Ohtsuki et al., 2006; Taylor et al., 2007).

For BD replacement, we find that cooperation is never favored (Appendix C.2). This generalizes the result that was previously known for the low-mutation limit (Ohtsuki et al., 2006; Taylor et al., 2007). This can be explained by noting that any benefit given to a neighbor increases the chance of being displaced by that neighbor’s offspring (see also Ohtsuki et al., 2006; Ohtsuki & Nowak, 2008).

For finite graphs of size N our results reduce, in the limit of low mutation, to those of Taylor et al. (2007). They showed that, for DB updating, cooperation is favored if and only if

$$\frac{b}{c}>\frac{k(N-2)}{N-2k}.$$ (11)

This condition can be obtained from ours (10) by substituting q ≈ 1 – (N – 1)u, which is accurate for Nu ⪡ 1 (Taylor et al., 2007). If we additionally take the limit of large population size (letting N → ∞ while maintaining Nu ⪡ 1), we recover the condition of Ohtsuki et al. (2006),

$$b∕c>k.$$

Table 2 shows how the critical benefit-to-cost threshold increases with u, for various graph structures. For the infinite 1D and 2D lattice, the b/c thresholds have infinite u-derivative at u = 0. This means that, when u is near zero, these thresholds increase faster than any linear function of u.

Table 2.

Thresholds for cooperation on infinite graphs with low mutation

Graph	b/c threshold
1D lattice	$2+\sqrt{8u}+\mathcal{O}\left(u\right)$
2D lattice	$4-\frac{24}{\pi }u\ln u+\mathcal{O}\left(u\right)$
k-Cayley tree (k ≥ 3)	$k+\frac{k^2}{k-2}u+\mathcal{O}\left(k{u}^2\right)$

For Cayley trees (including the infinite 1D lattice), the condition (10) reduces to

$$\frac{b}{c}>\frac{k}{(k-1)q}.$$

This rule has a simple interpretation, generalizing earlier interpretations of the b/c > k rule (Ohtsuki et al., 2006; Ohtsuki & Nowak, 2008). The C neighbors of a vacant site have, on average, q(k–1)/k more C’s among their k – 1 other neighbors than do D neighbors of the vacant site. Thus in the competition to fill this site, C’s receive an extra bq(k – 1)/k in benefit. This extra benefit is weighed against the cost c of cooperation, implying the above rule.

4. Other evolutionary games

We now consider general 2 × 2 games. Tarnita et al. (2009b) proved that for any population structure, mutation rate, and update rule satisfying certain fundamental assumptions (Tarnita et al., 2009b), there is an invariant $\sigma \in \mathbb{R}$ which is independent of the evolutionary game under consideration. Given an evolutionary process with a particular value of σ, and a game

strategy A will succeed (have greater abundance than B in mutation-selection equilibrium) if and only if

$$\sigma a_{11}+a_{12}>a_{21}+\sigma a_{22}.$$ (12)

This and related results are reviewed by Nowak et al. (2010a).

Evolutionary games on finite graphs, with BD or DB updating, satisfy the conditions of this theorem. Since the condition (12) applies to all games, the value of σ can be inferred from analysis of any particular game. Using our results for the Prisoner’s Dilemma, we find that

$$\sigma =\frac{(k+1-ku)(1-u-q)-qu(2-u)(k-1)}{(k-1-ku)(1-u-q)+qu(2-u)(k-1)}$$

for DB updating, and

$$\sigma =\frac{(N+2-Nu)(1-u-q)-(N-2)qu(2-u)}{N(1-u)(1-u-q)+Nqu(2-u)}$$

for BD updating (see Appendix C.3). With these values of σ, condition (12) gives an exact threshold for success in any evolutionary game on any graph with any rate of mutation.

5. Discussion

We have derived the first analytic results for evolutionary games on graphs with mutation. As the mutation rate increases, spatial assortment decreases and the conditions for cooperation become more stringent.

The IBD probabilities obtained here characterize evolutionary assortment on graphs. They show how correlation of type decreases with distance (fig. 2), in qualitative agreement with other spatial evolutionary models (Malécot, 1955; Kimura & Weiss, 1964; Granovsky & Madras, 1995). Moreover, they serve as a starting point for analysis of local frequency-dependent selection on graphs. Potential applications include the evolution of predation rates (Gilpin, 1975) and virulence (Boots & Sasaki, 1999), and persistence of ecological communities (Hassell et al., 1994; Bonsall et al., 2002).

Our results can also be applied in the framework of inclusive fitness theory (Taylor & Frank, 1996; Rousset, 2004). While inclusive fitness theory is usually formulated only in the limit of low mutation, Nowak et al. (2010b) derived inclusive fitness conditions for evolutionary success under any mutation rate. Thus the IBD probabilities derived here provide a basis for inclusive fitness analysis on graphs with mutation.

Coalescing random walks are a powerful tool for studying spatial evolution (Berestycki, 2009). They have been used to understand coalescence (Cox & Durrett, 2002) and fixation (Cox, 1989) times, spatial assortment (Granovsky & Madras, 1995), and biodiversity patterns (Durrett, 1999; Rauch & Bar-Yam, 2004). Because CRWs yield exact results, they improve on the pair approximation method (Matsuda et al., 1992; Iwasa, 2000), which has become standard in spatial evolutionary game theory (Ohtsuki et al., 2006; Szabó& Fáth, 2007). Interestingly, for the neutral drift process described above, pair approximation for a k-regular graph reproduces our exact results for the k-Cayley tree (calculation not shown).

Our findings may be useful for studying behaviors that spread through imitation of social contacts (Holme et al., 2003; Fu et al., 2007; Perc & Szolnoki, 2008; Santos et al., 2008). The outcomes of such imitation processes depend on how individuals adopt new strategies. A recent empirical study of humans playing the Prisoner’s Dilemma game on a lattice (Traulsen et al., 2010) found that the resulting dynamics could not be explained by assuming pure strategies with faithful imitation of neighbors. Incorporating mixed strategies or random strategy exploration is an important refinement to imitation-only models (Traulsen et al., 2009). Our work shows that increased rates of strategy exploration can reduce the benefit that spatial structure gives to cooperation.

Appendix A. Coalescing random walks

As discussed in section 2.3, CRWs can be used to determine stationary IBD probabilities. For Cayley trees and lattices, a major simplification occurs: in place of the CRW from ● and i, a single random walk can be considered, recording the distance or displacement between the two walkers. More precisely, we can consider a random walk starting at ● that terminates upon hitting i. Suppose a mutation event occurs with probability u at each step. The probability of no mutation in a CRW from ● and i equals the probability of no mutation in the ordinary random walk from ● to i.

We explore the reasons for this simplification separately for lattices and Cayley trees.

Appendix A.1. Reduction to ordinary random walk: Cayley trees

Cayley trees are distance-transitive, meaning that if i and i′ are distance d apart, and j and j′ are also distance d apart, there is a graph automorphism taking i to i′ and j to j′.

Distance transitivity implies that the CRW from ● and i reduces to a Markov process on the natural numbers $\mathbb{N}$. The state of the reduced Markov process is the current distance between walk positions. The initial state is the distance d(●, x). At each time step, the distance decreases by one with probability 1/k and otherwise increases by one. The process terminates when the distance equals zero.

The same reduction applies to an ordinary random walk that starts at ● and terminates upon hitting i. In this case the state of the reduced process is the current distance to i. Since these two processes reduce to the same underlying Markov process, they are equivalent. It follows that the probability of mutation in a CRW from ● and i equals the probability of a mutation event in the ordinary random walk terminating at i.

Appendix A.2. Reduction to ordinary random walk: lattices

For our purposes, we define a lattice to be a symmetric graph L which is also an Abelian group. Without any loss of generality, we identify the focal node ● as the identity element of this group. Examples of lattices include infinite square lattices of any dimension, finite periodic square lattices of any dimension, and the two-dimensional triangular lattice. Lattices have the essential property that the displacement between any two points x, x′ ∈ L is itself a lattice point: x′ – x ∈ L.

The CRW from ● and i can be reduced to an ordinary random walk on L. If the state of the CRW is(j, j′), we define the state of the corresponding ordinary random walk to be i–(j′–j). It is clear that the ordinary random walk starts at ● and terminates upon hitting i. It again follows that the probability of mutation in a CRW from ● and i equals the probability of a mutation event in the ordinary random walk terminating at i.

Appendix B. IBD relations

Our derivation of conditions for the evolution of cooperation makes use of simple relations between IBD probabilities, which we derive here. This section generalizes the approach of Taylor et al. (2007) to arbitrary mutation rates.

Consider the neutral drift process of section 2.2. For i ≠ j, we have the recurrence relation

$$q_{ij}=\frac{N-2}{N}{q}_{ij}+\frac{1-u}{Nk}\sum _{h\in n\left(i\right)}{q}_{hj}+\frac{1-u}{Nk}\sum _{\ell \in n\left(j\right)}{q}_{i\ell }.$$ (B.1)

k is the degree of the graph and n(i) denotes the set of neighbors of node i. This relation (B.1) reflects the fact that, in a single time step, i and j are replaced with probability $\frac{1}{N}$ for each, or else with probability $\frac{N-2}{N}$ both survive. If both survive, the IBD status of i and j is unchanged. If one (say j) is replaced, we must consider the IBD status of i with the parent of j, which is equally likely to be located at any of j′s neighbors. i and j will be IBD only if (a) i is IBD to the parent of j, and (b) no mutation occurs during reproduction.

Relation (B.1) can be rewritten as

$$\frac{1}{2k}\left(\sum _{h\in n\left(i\right)}{q}_{hj}+\sum _{\ell \in n\left(j\right)}{q}_{i\ell }\right)=\frac{q_{ij}}{1-u}.$$ (B.2)

According to bi-transitivity, there must be a graph automorphism T with T(i) = j and T(j) = i. Such an automorphism must preserve IBD probabilities. This implies that

$$\sum _{h\in n\left(i\right)}{q}_{hj}=\sum _{T\left(h\right)\in n\left(T\right(i\left)\right)}{q}_{T\left(h\right)}{T}_{\left(j\right)}=\sum _{\ell \in n\left(j\right)}{q}_{i\ell }.$$

Substituting this identity into (B.2) and re-indexing in terms of the focal individual, we have

$$\frac{1}{k}\sum _{j\in n\left(i\right)}{q}_j=\frac{q_i}{1-u},$$ (B.3)

for i ≠ ●.

Rotational symmetry implies that all neighbors of ● are equivalent with respect to the graph structure. Thus q_i is equal to a constant value q for each i ∈ n(●). We trivially have

$$\frac{1}{k}\sum _{i\in n\left(•\right)}{q}_i=q.$$ (B.4)

Appendix C. Evolutionary games

We turn now to evolutionary game competition, starting with the Prisoner’s Dilemma game introduced in section 3. We denote the payoff to individual at node i by π_i, and its fecundity by F_i = F(δπ_i). F_i is not the same as i’s fitness. Fecundity is a direct function of an individual’s payoff, whereas fitness depends also on the payoffs of others in the population, according to the update rule.

Given that ● is a cooperator, the probability that i is a cooperator is

$${\langle s_i\rangle }_{\begin{array}{c}\hfill \delta =0\hfill \\ \hfill s_{•}=C\hfill \end{array}}=\frac{1+q_i}{2}.$$

Fecundity under weak selection is described by

$$\begin{array}{cc}\hfill {\langle \frac{\partial F_i}{\partial \delta }\rangle }_{\begin{array}{c}\hfill \delta =0\hfill \\ \hfill s_{•}=C\hfill \end{array}}& =-c\frac{1+q_i}{2}+\frac{b}{k}\sum _{j\in n\left(i\right)}\frac{1+q_j}{2}\hfill \\ \hfill & =\frac{b-c}{2}+\frac{1}{2}\left(-c{q}_i+\frac{b}{k}\sum _{j\in n\left(i\right)}{q}_j\right)\hfill \end{array}$$ (C.1)

Appendix C.1. Conditions for cooperation: DB

We can now derive exact conditions for cooperation to be favored. For DB updating, death rates are constant across the population (d_i = 1/N for all i), so condition (9) reduces to

$${\langle \frac{\partial b_{•}}{\partial \delta }\rangle }_{\begin{array}{c}\hfill \delta =0\hfill \\ \hfill s_{•}=C\hfill \end{array}}>0.$$

We calculate:

$$\begin{array}{cc}\hfill {\langle \frac{\partial b_{•}}{\partial \delta }\rangle }_{\begin{array}{c}\hfill \delta =0\hfill \\ \hfill s_{•}=C\hfill \end{array}}=& \frac{1}{N}\sum _{i\in n\left(•\right)}{\langle \frac{\partial }{\partial \delta }\frac{F_{•}}{\sum _{j\in n\left(i\right)}{F}_j}\rangle }_{\begin{array}{c}\hfill \delta =0\hfill \\ \hfill s_{•}=C\hfill \end{array}}\hfill \\ \hfill =& \frac{1}{N}\left({\langle \frac{\partial F_{•}}{\partial \delta }\rangle }_{\begin{array}{c}\hfill \delta =0\hfill \\ \hfill s_{•}=C\hfill \end{array}}-\frac{1}{k^2}\sum _{i\in n\left(•\right)}\sum _{j\in n\left(i\right)}{\langle \frac{\partial F_j}{\partial \delta }\rangle }_{\begin{array}{c}\hfill \delta =0\hfill \\ \hfill s_{•}=C\hfill \end{array}}\right),\hfill \end{array}$$

since ∑_j∈n(i) F_j∣_δ=0 = k. This expression shows how DB updating induces spatial competition between neighbors-of-neighbors (see section 3.1). Applying (C.1) and simplifying, we obtain

$$\begin{array}{cc}\hfill 2N{\langle \frac{\partial b_{•}}{\partial \delta }\rangle }_{\begin{array}{c}\hfill \delta =0\hfill \\ \hfill s_{•}=C\hfill \end{array}}=& -c\left(1-\frac{1}{k^2}\sum _{i\in n\left(•\right)}\sum _{j\in n\left(i\right)}{q}_j\right)\hfill \\ \hfill & +b\left(\frac{1}{k}\sum _{i\in n\left(•\right)}{q}_i-\frac{1}{k^3}\sum _{i\in n\left(•\right)}\sum _{j\in n\left(i\right)}\sum _{h\in n\left(j\right)}{q}_h\right).\hfill \end{array}$$

Making use of (B.3) and (B.4), the coefficient of −c reduces to

$$1-\frac{1}{k(1-u)}\sum _{i\in n\left(•\right)}{q}_i=1-\frac{q}{1-u}.$$

The coefficient of b simplifies as

$$\begin{array}{cc}\hfill & q-\frac{1}{k^3}\sum _{i\in n\left(•\right)}\left(\sum _{h\in n\left(•\right)}{q}_h+\sum _{\begin{array}{c}\hfill j\in n\left(i\right)\hfill \\ \hfill j\ne •\hfill \end{array}}\sum _{h\in n\left(j\right)}{q}_h\right)\text{using}\left(\mathrm{B}.4\right)\text{and rearranging}\hfill \\ \hfill & =q-\frac{1}{k^2}\sum _{i\in n\left(•\right)}\left(q-\sum _{\begin{array}{c}\hfill j\in n\left(i\right)\hfill \\ \hfill j\ne •\hfill \end{array}}\frac{q_j}{1-u}\right)\text{using}\left(\mathrm{B}.3\right)\text{and}\left(\mathrm{B}.4\right)\hfill \\ \hfill & =q-\frac{q}{k}-\frac{1}{k^2(1-u)}\sum _{i\in n\left(•\right)}\left(\sum _{j\in n\left(i\right)}{q}_j-1\right)\text{simplifying and using}{q}_{•}=1\hfill \\ \hfill & =\frac{(k-1)q}{k}-\frac{1}{k(1-u)}\left(\sum _{i\in n\left(•\right)}\frac{q_i}{1-u}-1\right)\text{using}\left(\mathrm{B}.3\right)\text{and simplifying}\hfill \\ \hfill & =\frac{(k-1)q}{k}-\frac{q}{{(1-u)}^2}+\frac{1}{k(1-u)}\text{using}\left(\mathrm{B}.4\right)\text{and simplifying}.\hfill \end{array}$$

Comparing these coefficients, we see that cooperation is favored if and only if

$$\frac{b}{c}>\frac{k(1-u)(1-u-q)}{1-u-q-(k-1)qu(2-u)}.$$ (C.2)

Appendix C.2. Conditions for cooperation: BD

For BD updating, the effect of weak selection on the birth rate of cooperators is given by

$$\begin{array}{cc}\hfill {\langle \frac{\partial b_{•}}{d\delta }\rangle }_{\begin{array}{c}\hfill \delta =0\hfill \\ \hfill s_{•}=C\hfill \end{array}}=& {\langle \frac{\partial }{d\delta }\frac{F_{•}}{\sum _h{F}_h}\rangle }_{\begin{array}{c}\hfill \delta =0\hfill \\ \hfill s_{•}=C\hfill \end{array}}\hfill \\ \hfill =& \frac{1}{N}{\langle \frac{\partial F_{•}}{d\delta }\rangle }_{\begin{array}{c}\hfill \delta =0\hfill \\ \hfill s_{•}=C\hfill \end{array}}-\frac{1}{N^2}\sum _h{\langle \frac{\partial F_h}{d\delta }\rangle }_{\begin{array}{c}\hfill \delta =0\hfill \\ \hfill s_{•}=C\hfill \end{array}},\hfill \end{array}$$

using the fact that ∑_j F_j∣_δ=0 = N. Applying (C.1) and simplifying using (B.4),

$$\begin{array}{cc}\hfill 2N{\langle \frac{\partial b_{•}}{d\delta }\rangle }_{\begin{array}{c}\hfill \delta =0\hfill \\ \hfill s_{•}=C\hfill \end{array}}=& -c+\frac{b}{k}\sum _{i\in n\left(•\right)}{q}_i-\frac{1}{N}\sum _h\left(-c{q}_h+\frac{b}{k}\sum _{\ell \in n\left(h\right)}{q}_{\ell }\right)\hfill \\ \hfill =& -c+bq-(b-c)\stackrel{‒}{q}\hfill \end{array}$$ (C.3)

Above, $\stackrel{‒}{q}$ is the average IBD probability of the population to ●:

$$\stackrel{‒}{q}=\frac{1}{N}\sum _i{q}_i.$$

Later, we will express $\stackrel{‒}{q}$ in terms of N, q, and u.

For the death rate we obtain

$$\begin{array}{cc}\hfill {\langle \frac{\partial d_{•}}{d\delta }\rangle }_{\begin{array}{c}\hfill \delta =0\hfill \\ \hfill s_{•}=C\hfill \end{array}}=& {\langle \frac{1}{k}\frac{\partial }{d\delta }\sum _{i\in n\left(•\right)}\frac{F_{•}}{\sum _j{F}_j}\rangle }_{\begin{array}{c}\hfill \delta =0\hfill \\ \hfill s_{•}=C\hfill \end{array}}\hfill \\ \hfill =& \frac{1}{Nk}\sum _{i\in n\left(•\right)}{\langle \frac{\partial F_i}{d\delta }\rangle }_{\begin{array}{c}\hfill \delta =0\hfill \\ \hfill s_{•}=C\hfill \end{array}}-\frac{1}{N^2}\sum _h{\langle \frac{\partial F_h}{d\delta }\rangle }_{\begin{array}{c}\hfill \delta =0\hfill \\ \hfill s_{•}=C\hfill \end{array}}.\hfill \end{array}$$

The first term above represents the spatial competition between neighbors under BD updating, as described in section 3.1. Applying (C.1) and simplifying using (B.3) and (B.4),

$$\begin{array}{cc}\hfill 2N{\langle \frac{\partial d_{•}}{d\delta }\rangle }_{\begin{array}{c}\hfill \delta =0\hfill \\ \hfill s_{•}=C\hfill \end{array}}=& -\frac{c}{k}\sum _{i\in n\left(•\right)}{q}_i+\frac{b}{k^2}\sum _{i\in n\left(•\right)}\sum _{j\in n\left(i\right)}{q}_j-\frac{1}{N}\sum _h\left(-c{q}_h+\frac{b}{k}\sum _{\ell \in n\left(h\right)}{q}_{\ell }\right)\hfill \\ \hfill =& -cq+b\frac{q}{1-u}-(b-c)\stackrel{‒}{q}.\hfill \end{array}$$ (C.4)

Cooperator success is determined by the condition (9), which can be rewritten as

$$(1-u){\langle \frac{\partial b_{•}}{d\delta }\rangle }_{\begin{array}{c}\hfill \delta =0\hfill \\ \hfill s_{•}=C\hfill \end{array}}-{\langle \frac{\partial d_{•}}{d\delta }\rangle }_{\begin{array}{c}\hfill \delta =0\hfill \\ \hfill s_{•}=C\hfill \end{array}}>0.$$

Invoking (C.3) and (C.4), cooperators succeed if and only if

$$-c(1-u-q+u\stackrel{‒}{q})+bu\left(\stackrel{‒}{q}-q-\frac{q}{1-u}\right)>0,$$ (C.5)

We now show that the coefficient of −c is positive and the coefficient of b is negative. This implies that condition (C.5) is never satisfied for nonnegative b and c. For −c, the identity (B.3) in the case i ∈ n(●) becomes

$$\frac{1}{k}\sum _{j\in n\left(i\right)}{q}_j=\frac{q}{1-u}.$$

The left-hand side above is less than one for u > 0, implying q < 1 − u. Thus the coefficient $1-u-q+u\stackrel{‒}{q}$ of −c is positive. The coefficient $\stackrel{‒}{q}-q-q∕(1-u)$ of bu can be written as

$$\frac{1}{N}\sum _h{q}_h-\frac{1}{k}\sum _{i\in n\left(•\right)}{q}_i-\frac{1}{k^2}\sum _{i\in n\left(•\right)}\sum _{j\in n\left(i\right)}{q}_j.$$

Since the largest q-values in the population are those corresponding to ●, its neighbors, and its neighbors-of-neighbors, the above quantity is negative. Both terms on the left-hand side of (C.5) are therefore negative for all b, c, u > 0. We conclude that cooperation is not favored under BD updating for any mutation rate.

As a side-note, we can obtain the average IBD probability $\stackrel{‒}{q}$ in terms of q, u, and N via the following calculation:

$$\begin{array}{cc}\hfill \stackrel{‒}{q}=& \frac{1}{N}\sum _i{q}_i\hfill \\ \hfill =& \frac{1}{Nk}\sum _i\sum _{j\in n\left(i\right)}{q}_j\hfill \\ \hfill =& \frac{1}{Nk}\sum _{i\in n\left(•\right)}{q}_j+\frac{1}{N}\sum _{i\ne •}\frac{1}{k}\sum _{j\in n\left(i\right)}{q}_j\hfill \\ \hfill =& \frac{q}{N}+\frac{1}{1-u}\frac{1}{N}\sum _{i\ne •}{q}_i\hfill \\ \hfill =& \frac{q}{N}+\frac{1}{1-u}\frac{1}{N}\left(\sum _i{q}_i-1\right)\hfill \\ \hfill =& \frac{q}{N}+\frac{\stackrel{‒}{q}}{1-u}-\frac{1}{N(1-u)}.\hfill \end{array}$$

Solving for $\stackrel{‒}{q}$,

$$\stackrel{‒}{q}=\frac{1-q(1-u)}{Nu}.$$

Substituting into (C.5) we obtain the equivalent condition

$$\begin{array}{c}-c\left((N+1-nu)(1-u-q)+qu(2-u)\right)\hfill \\ \hfill +b\left(1-u-q-(N-1)qu(2-u)\right)>0.\end{array}$$ (C.6)

Appendix C.3. Other evolutionary games

Success in any pairwise evolutionary game can be determined from the value of σ associated to the population structure (Tarnita et al., 2009b; Nowak et al., 2010a), as described in section 4. The value of σ for a specific population structure, update rule, and mutation rate can be determined from the critical benefit-to-cost ratio ${\left(\frac{b}{c}\right)}^{\ast }$ needed for cooperation to be favored. (Note that ${\left(\frac{b}{c}\right)}^{\ast }$ can be negative, as is the case for BD updating. This indicates that the cost c must be negative for cooperation to evolve.) The formula relating σ and ${\left(\frac{b}{c}\right)}^{\ast }$ is

$$\sigma =\frac{{\left(\frac{b}{c}\right)}^{\ast }+1}{{\left(\frac{b}{c}\right)}^{\ast }-1}.$$

Using (C.2) and (C.6) we find that

$$\sigma =\frac{(k+1-ku)(1-u-q)-(k-1)qu(2-u)}{(k-1-ku)(1-u-q)+(k-1)qu(2-u)}$$

for DB updating, and

$$\sigma =\frac{(N+2-Nu)(1-u-q)-(N-2)qu(2-u)}{N(1-u)(1-u-q)+Nqu(2-u)}$$

for BD updating.

Appendix D. Simulations

We simulated the Prisoner’s Dilemma DB process on (a) a periodic 20×20 lattice and (b) on random regular graphs of degree 3 with 400 nodes. We used selection strength δ = 0.01, cost c = 1, and varied the benefits of cooperation. We used the exponential payoff-to-fecundity map F(δπ) = e^δπ.

We said cooperators were favored for given parameters if they reproduced more frequently than defectors. This condition is theoretically equivalent to the average cooperator abundance exceeding 50%. Frequency of reproduction is less subject to random mutational noise, making it a better test of favorability than average abundance.

More precisely, after a simulation achieved relaxation (see below) we recorded the number of times cooperators and defectors reproduced. We regarded these as independent Bernoulli trials in which cooperators are chosen to reproduce with probability p_C. Combining data from multiple simulation runs, we judged cooperators successful if the claim $p_C>\frac{1}{2}$ could be made with 98% confidence, using a normal approximation to a binomial test. We judged them unsuccessful if $p_C<\frac{1}{2}$ with 98% confidence. If neither condition held we deemed the results inconclusive.

Each simulation run was allowed a relaxation time of 3.5 * n/u time steps (n being the number of nodes), and then run for an additional 2000 time steps to collect data. Between 400 and 40,000 runs were performed for each data point. Greater numbers of runs were used for larger mutation rates in order to achieve conclusive results. Random regular graphs were generated by the matgraph toolbox for MATLAB, available at http://www.ams.jhu.edu/~ers/matgraph/. Random regular graphs were regenerated every $\sqrt{R}$ runs, (R being the total number of runs), in order to minimize the effects of particular graph structures that might skew results.