T₁-corrected fat quantification using chemical shift-based water/fat separation: application to skeletal muscle

Abstract

Chemical shift based water/fat separation, like iterative decomposition of water and fat with echo asymmetry and least-squares estimation (IDEAL), has been proposed for quantifying intermuscular adipose tissue (IMAT). An important confounding factor in IDEAL-based IMAT quantification is the large difference in T₁ between muscle and fat, which can cause significant overestimation in the fat fraction. This T₁ bias effect is usually reduced by employing small flip angles. T₁-correction can be performed by employing at least two different flip angles and fitting for T₁ of water and fat. In the present work, a novel approach for the water/fat separation problem in a dual flip angle experiment is introduced and a new approach for the selection of the two flip angles, labeled as the unequal small flip angle approach, is developed, aiming to improve the noise efficiency of the T₁-correction step relative to existing approaches. It is shown that the use of flip angles, selected such the muscle water signal is assumed to be T₁-independent for the first flip angle and the fat signal is assumed to be T₁-independent for the second flip angle, has superior noise performance to the use of equal small flip angles (no T₁ estimation required) and the use of large flip angles (T₁ estimation required).

INTRODUCTION

Muscular fat has been associated with different metabolic abnormalities including obesity and insulin resistance (1–3). The non-invasive assessment of skeletal muscle lipids would be an important alternative to the highly invasive muscle biopsies, and it would allow analysis of muscles, which are less accessible to biopsy. Different MRI techniques have been proposed for assessing the different compartments of muscular fat (4). Specifically, skeletal muscle fat includes intramyocellular lipids (IMCLs) and extramyocellular lipids (EMCLs). IMCLs are located within muscle fibers in the form of cytosolic triacyglycerols. EMCLs represent adipocytes located between muscle fibers and muscle fiber bundles and can be divided into two compartments: intermuscular fat and intramuscular fat. Intramuscular fat corresponds to adipocytes present between muscle fibers and muscle fiber bundles within individual muscles. Intermuscular fat corresponds to adipocytes present between muscle groups and beneath the muscle fascia. According to the literature, the superposition of intermuscular fat and intramuscular fat that is visible on T₁-weighted images constitutes the intermuscular adipose tissue (IMAT) compartment (3). Volume localized spectroscopy and low resolution spectroscopic imaging techniques have been widely used for the quantification of IMCLs and EMCLs (5,6). However, the spatial distribution of IMAT cannot be assessed accurately by low resolution spectroscopic imaging techniques and requires high spatial resolution imaging (7).

Because of the high resolution requirement, the distribution and the total area/volume of IMAT have been traditionally assessed using T₁-weighted imaging (8). However, quantification of IMAT based on T₁-weighted imaging is limited by residual partial volume effects and requires effective and accurate segmentation procedures (9). Some alternative techniques that have been proposed for measuring total intramuscular lipid content combine fat selective excitation with gradient echo imaging (7,10) or high spatial resolution spectroscopic imaging (11–13). Fat selective gradient echo imaging requires a reliable reference signal and fat selective high spatial resolution spectroscopic imaging suffers from prolonged scan times. Chemical-shift based water/fat separation (14–16) has recently received considerable attention for fat quantification in different body parts (17,18). Therefore, chemical shift-based water-fat separation techniques could be used to derive quantitative IMAT fat fraction maps. Three-point Dixon techniques (14) and iterative decomposition of water and fat with echo asymmetry and least-squares estimation (IDEAL) (19) have been recently implemented to measure fat content in dystrophic skeletal muscle (20,21).

In order to get accurate fat content measurements with quantitative IDEAL multiple confounding factors have to be taken into consideration. Specifically, the spectral complexity of fat (17,18), the T₂* decay (17,22) and the T₁ bias effects (23) have to be considered. Multi-peak T₂* IDEAL based on at least 6 time-point measurements has been proposed to overcome the two first confounding factors (18). Regarding the T₁ bias effect, the large T₁ difference (values at 3 T) between muscle (1500 ms) and fat (360 ms) can cause a significant overestimation in the fat fraction (17,23). The acquisition of data at small flip angle (SFA) has been proposed to reduce T₁ weighting (17,23) and the acquisition of data at two flip angles (dual flip angle-DFA) or multiple flip angles has been used to correct for T₁ weighting (23–25). However, the SFA method can be limited by low SNR and a method that corrects for T₁ effects based on multiple flip angles suffers from prolonged scan times (23,25). At least two flip angles are required to fit for the proton-density weighted signal and the T₁ of both the water and fat compartments. Therefore, the dual flip angle (DFA) acquisition can correct for T₁ bias effects at the cost of increasing the minimum scan time, but the introduction of additional unknowns increases the signal model complexity and may degrade the noise performance of the fat fraction estimation (23,25). This problem of noise degradation in the fat fraction estimation of the DFA acquisition has been assessed in the case of tissues with small T₁ differences between water and fat compartments (i.e. liver) (23,25), but it has not been studied in the case of tissues with large T₁ differences between water and fat compartments (i.e. skeletal muscle).

In the present work, the problem of T₁-unbiased estimation of fat fraction from dual flip angle multi-peak T₂* IDEAL data is separated into a water/fat separation problem and a T₁-correction problem. In terms of the water/fat separation problem, a new approach, labeled as joint fieldmap estimation IDEAL, is introduced for the implementation of IDEAL algorithm on dual flip angle data. Specifically, it is investigated whether performing a joint water/fat separation at the two employed flip angles improves the noise performance of the water signal, fat signal and fat fraction estimates relative to the traditional approach of performing the water/fat separation separately at every flip angle. In terms of the T₁-correction problem, a new approach, labeled as the unequal small flip angle approach, is introduced in the selection of the employed flip angles. Specifically, it is investigated whether the use of two small unequal flip angles, selected such the water signal is assumed to be T₁-independent for the first flip angle and the fat signal is assumed to be T₁-independent for the second flip angle, provides superior noise performance to the use of the same small flip angle twice (no T₁ estimation required) and the use of two unequal large flip angles (T₁ estimation required). Therefore, a thorough comparison of the accuracy and noise performance of the different water/fat separation approaches and the different T₁ bias reduction and correction procedures is presented in the context of IMAT quantification, using numerical simulations and water/fat phantom measurements. Finally, the noise performance of the different approaches is qualitatively compared in the calf muscle region of a healthy volunteer.

THEORY

Signal model

The multi-peak T₂* IDEAL signal model (18) can be enhanced by using a multi-peak fat spectrum that takes into account the T₁ weighting of the individual fat peaks. If a_p is the proton density-weighted relative amplitude of the p-th fat peak (p=1,…,P, such that ${\displaystyle \sum _{\mathrm{p}=1}^{\mathrm{P}}{\mathrm{a}}_{\mathrm{p}}=1}$), and a_p,cor is the T₁-weighted relative amplitude of the p-th fat peak, the signal model of a voxel containing water (ρ_w) and fat (ρ_f) in a spoiled gradient echo (SPGR) experiment with echo time t, repetition time TR and flip angle α can be written as:

$$\mathrm{S}(\mathrm{t},\mathrm{\alpha })=\left[{\mathrm{\rho }}_{\mathrm{w}}\frac{(1-\text{exp}(-\text{TR}/{\mathrm{T}}_{1\mathrm{w}}))\text{sin}(\mathrm{\alpha })}{1-\text{exp}(-\text{TR}/{\mathrm{T}}_{1\mathrm{w}})\text{cos}(\mathrm{\alpha })}+{\mathrm{\rho }}_{\mathrm{f}}\left({\displaystyle \sum _{\mathrm{p}=1}^{\mathrm{P}}{\mathrm{a}}_{\mathrm{p}}}\frac{(1-\text{exp}(-\text{TR}/{\mathrm{T}}_{1\text{fp}}))\text{sin}(\mathrm{\alpha })}{1-\text{exp}(-\text{TR}/{\mathrm{T}}_{1\text{fp}})\text{cos}(\mathrm{\alpha })}\right){\displaystyle \sum _{p=1}^P{\mathrm{a}}_{\mathrm{p},\text{cor}}(\mathrm{\alpha })\text{exp}(j2\mathrm{\pi }\mathrm{\Delta }{\mathrm{f}}_{\mathrm{p}}}\mathrm{t})\right]\text{exp}(\mathrm{j}2\mathrm{\pi }\mathrm{\psi }\mathrm{t})\text{exp}(-\mathrm{t}/{\mathrm{T}}_2^{*})$$ [1]

where Δf_p is the resonance frequency difference of the p-th peak with respect to water, ψ is the local fieldmap frequency offset and T_1w and T_1fp are the T₁ relaxation times of water and p-th fat peak, respectively. It should be noticed that Eq. [1] assumes that T₂* values of water and all fat peaks are equal.

The T₁-weighted relative amplitudes of the fat peaks are in general flip angle dependent:

$${\mathrm{a}}_{\mathrm{p},\text{cor}}(\mathrm{\alpha })=\frac{{\mathrm{a}}_{\mathrm{p}}\frac{(1-\text{exp}(-\text{TR}/{\mathrm{T}}_{1\text{fp}}))\text{sin}(\mathrm{\alpha })}{1-\text{exp}(-\text{TR}/{\mathrm{T}}_{1\text{fp}})\text{cos}(\mathrm{\alpha })}}{{\displaystyle \sum _{\mathrm{p}=1}^{\mathrm{P}}{\mathrm{a}}_{\mathrm{p}}\frac{(1-\text{exp}(-\text{TR}/{\mathrm{T}}_{1\text{fp}}))\text{sin}(\mathrm{\alpha })}{1-\text{exp}(-\text{TR}/{\mathrm{T}}_{1\text{fp}})\text{cos}(\mathrm{\alpha })}}}$$ [2]

and such that ${\displaystyle \sum _{\mathrm{p}=1}^{\mathrm{P}}{\mathrm{a}}_{\mathrm{p},\text{cor}}(\mathrm{\alpha })=1}$.

The problem of extracting the fat fraction from the above measurements can be considered a two-step problem. First, the T₁-weighted water and fat signals are separated by solving the following water/fat separation problem:

$$\mathrm{S}(\mathrm{t},\mathrm{\alpha })=\left[{\mathrm{M}}_{\mathrm{w}}(\mathrm{\alpha })+{\mathrm{M}}_{\mathrm{f}}(\mathrm{\alpha }){\displaystyle \sum _{\mathrm{p}=1}^{\mathrm{P}}{\mathrm{a}}_{\mathrm{p},\text{cor}}(\mathrm{\alpha })\text{exp}(\mathrm{j}2\mathrm{\pi }\mathrm{\Delta }{\mathrm{f}}_{\mathrm{p}}}\mathrm{t})\right]\text{exp}(\mathrm{j}2\mathrm{\pi }\mathrm{\psi }\mathrm{t})\text{exp}(-\mathrm{t}/{\mathrm{T}}_2^{*})$$ [3]

Second, the proton density weighted water and fat signals can be extracted based on the SPGR signal expressions:

$${\mathrm{M}}_{\mathrm{w}}(\mathrm{\alpha })={\mathrm{\rho }}_{\mathrm{w}}\frac{(1-\text{exp}(-\text{TR}/{\mathrm{T}}_{1\mathrm{w}}))\text{sin}(\mathrm{\alpha })}{1-\text{exp}(-\text{TR}/{\mathrm{T}}_{1\mathrm{w}})\text{cos}(\mathrm{\alpha })}$$ [4]

$${\mathrm{M}}_{\mathrm{f}}(\mathrm{\alpha })={\mathrm{\rho }}_{\mathrm{f}}\left({\displaystyle \sum _{\mathrm{p}=1}^{\mathrm{P}}{\mathrm{a}}_{\mathrm{p}}}\frac{(1-\text{exp}(-\text{TR}/{\mathrm{T}}_{1\text{fp}}))\text{sin}(\mathrm{\alpha })}{1-\text{exp}(-\text{TR}/{\mathrm{T}}_{1\text{fp}})\text{cos}(\mathrm{\alpha })}\right)$$ [5]

The fitting of the T₁ of the different fat peaks would require in general the acquisition of a very high number of flip angles. A spectroscopy-based precalibration of the T₁ of the different fat peaks would require the repetition of the spectroscopy experiment with multiple TRs. Instead, it is proposed to assume that for the range of the employed flip angles the effect of modeling the T₁ of different fat peaks equal to the T₁ of the dominant fat peak (T_1fp=T_1f) can be neglected. This simplifying assumption leads to the result that a_p,cor (α) = a_p and Eq. [5] becomes:

$${\mathrm{M}}_{\mathrm{f}}(\mathrm{\alpha })={\mathrm{\rho }}_{\mathrm{f}}\frac{(1-\text{exp}(-\text{TR}/{\mathrm{T}}_{1\text{fp}}))\text{sin}(\mathrm{\alpha })}{1-\text{exp}(-\text{TR}/{\mathrm{T}}_{1\text{fp}})\text{cos}(\mathrm{\alpha })}$$ [6]

T₁-bias minimization/correction

The extraction of the proton-density weighted water and fat signal values, based on Eqs. [4] and [6], requires in general the estimation of T₁ of water and fat. However, Eqs. [4] and [6] can be roughly considered T₁-independent at flip angles sufficiently smaller than the Ernst flip angles of water and fat, respectively. Therefore, T₁-bias minimization/correction can be performed following three approaches, when two flip angles are collected in a dual flip angle IDEAL experiment:

Equal small flip angles (ESFA) approach

First, the two flip angles can be selected to be equal and substantially smaller than the Ernst flip angles of both water and fat, such that the T₁ weighting in both Eqs. [4] and [6] can be neglected. This first method of minimizing the T₁-bias effect is labeled in the present study as equal small flip angles (ESFA) approach and it is equivalent to the small flip angle approach with two averages proposed in previous studies (17,23,26,27).

Specifically, if the two flip angles are equal α₁ = α₂ = α and have been selected such that M_w (α) ≈ ρ_wα and M_f (α) ≈ ρ_fα, there is no T₁-correction step required since the fat fraction is

$$\mathrm{\eta }=\frac{{\mathrm{M}}_{\mathrm{f}}(\mathrm{\alpha })}{{\mathrm{M}}_{\mathrm{f}}(\mathrm{\alpha })+{\mathrm{M}}_{\mathrm{w}}(\mathrm{\alpha })}\approx \frac{{\mathrm{\rho }}_{\mathrm{f}}}{{\mathrm{\rho }}_{\mathrm{f}}+{\mathrm{\rho }}_{\mathrm{w}}}$$ [7]

Therefore, the ESFA approach has two unknowns M_w (α₁), M_f (α₁).

Unequal large flip angles (ULFA) approach

Second, in the general case that both flip angles are not sufficiently smaller than the Ernst flip angles of water and fat, T₁ estimation of both compartments is required. This second method of correcting the T₁-bias effect is labeled in the present study as unequal large flip angles (ULFA) approach it is equivalent to the dual flip angle approach proposed in previous studies (23,25).

Specifically, in the most general case that the two flip angles have been selected such that neither of the water nor the fat SPGR signal expressions is T₁-independent, the proton-density weighted water and fat signals can be computed based on Eqs. [4] and [6]:

$${\mathrm{\rho }}_{\mathrm{w}}=\frac{{\mathrm{M}}_{\mathrm{w}}({\mathrm{\alpha }}_1){\mathrm{M}}_{\mathrm{w}}({\mathrm{\alpha }}_2)(\text{cos}({\mathrm{\alpha }}_1)-\text{cos}({\mathrm{\alpha }}_2))}{{\mathrm{M}}_{\mathrm{w}}({\mathrm{\alpha }}_1)\text{sin}({\mathrm{\alpha }}_2)(\text{cos}({\mathrm{\alpha }}_1)-1)-{\mathrm{M}}_{\mathrm{w}}({\mathrm{\alpha }}_2)\text{sin}({\mathrm{\alpha }}_1)(\text{cos}({\mathrm{\alpha }}_2)-1)}$$ [8]

$${\mathrm{\rho }}_{\mathrm{f}}=\frac{{\mathrm{M}}_{\mathrm{f}}({\mathrm{\alpha }}_1){\mathrm{M}}_{\mathrm{f}}({\mathrm{\alpha }}_2)(\text{cos}({\mathrm{\alpha }}_1)-\text{cos}({\mathrm{\alpha }}_2))}{{\mathrm{M}}_{\mathrm{f}}({\mathrm{\alpha }}_1)\text{sin}({\mathrm{\alpha }}_2)(\text{cos}({\mathrm{\alpha }}_1)-1)-{\mathrm{M}}_{\mathrm{f}}({\mathrm{\alpha }}_2)\text{sin}({\mathrm{\alpha }}_1)(\text{cos}({\mathrm{\alpha }}_2)-1)}$$ [9]

Therefore, the ULFA approach has four unknowns M_w (α₁), M_f(α₁), M_w (α₂), M_f (α₂).

Unequal small flip angles (USFA) approach

Third, the two flip angles can be selected to be unequal and such that one (α₁) is sufficiently smaller than the Ernst flip angle of water and the other one (α₂) is sufficiently smaller than the Ernst flip angle of fat. Because T_1f is typically shorter than T_1w, α₁ < α₂. Then, Eq. [6] can be approximately considered T₁-independent for both flip angles and Eq. [4] can be considered T₁-independent only for the smaller flip angle (α₁).

Specifically, if the flip angles are not equal and have been selected such that M_w(α₁) ≈ ρ_wα₁ and M_f(α₂) ≈ ρ_fα₂ (which means that also M_f(α₁) ≈ ρ_fα₁), then the proton density weighted water signal can be computed from the first flip angle (α₁) data and the proton density weighted fat signal can be computed from both flip angles (α₁ and α₂) data in the least squares sense:

$${\mathrm{\rho }}_{\mathrm{w}}\approx \frac{{\mathrm{M}}_{\mathrm{w}}({\mathrm{\alpha }}_1)}{{\mathrm{\alpha }}_1}$$ [10]

$${\mathrm{\rho }}_{\mathrm{f}}\approx \frac{{\mathrm{\alpha }}_1{\mathrm{M}}_{\mathrm{f}}({\mathrm{\alpha }}_1)+{\mathrm{\alpha }}_2{\mathrm{M}}_{\mathrm{f}}({\mathrm{\alpha }}_2)}{{{\mathrm{\alpha }}_1}^2+{{\mathrm{\alpha }}_2}^2}$$ [11]

Therefore, the USFA approach has three unknowns M_w(α₁), M_f(α₁), M_w(α₂), since M_f(α₂) = (α₂ / α₁) M_f(α₁).

Water/fat separation

The water/fat separation problem involves in general the extraction of the T₁-weighted water and fat signals M_w(α₁), M_f(α₁) and M_w(α₂), M_f(α₂) at two flip angles based on the multi-echo source signals {S (t₁, α₁),…, S(t₆, α₁)} and {S(t₁, α₂),…, S(t₆, α₂)}, respectively. In the present work, the following two options are investigated for the water/fat separation problem at two flip angles described by Eq. [3].

Independent fieldmap estimation (IFE) IDEAL

The water/fat separation step can be performed independently for the two different flip angles employing the multi-peak T₂* IDEAL algorithm (18) separately for each flip angle. The fieldmap is estimated based on a region growing scheme for every flip angle separately as in (28). This approach is labeled as independent fieldmap estimation IDEAL.

Joint fieldmap estimation (JFE) IDEAL

The fieldmap ψ and T₂* values are common unknowns for the independent fieldmap estimation IDEAL problem at both flip angles. Therefore, it is proposed to use the T₁-weighted multi-echo source signals at both flip angles to jointly estimate the T₁-weighted water, fat signals at both flip angles. The approach of joint estimation of the T₁-weighted water, fat signals at both flip angles, is labeled as joint fieldmap estimation IDEAL. Appendix A1 presents the matrix formulation of the multi-peak T₂* IDEAL problem with joint fieldmap estimation at two flip angles extending the formulation presented by Yu et al. (18,22). The matrix formulation of the joint fieldmap estimation IDEAL can also be modified to take into account the constraints imposed by the employed T₁ bias minimization/correction approach (see Appendix A1). The joint fieldmap estimation IDEAL is performed in two steps: Independent fieldmap estimation IDEAL is performed first to extract initial estimates for the water/fat separation problem at the two flip angles separately. The derived field map ψ and T₂* values from the implementation of independent fieldmap estimation IDEAL at the two different flip angles are averaged and introduced as initial estimates of the joint fieldmap estimation IDEAL problem.

The magnitude discrimination approach is applied to the T₁-weighted water and fat signals after the water/fat separation step and before the T₁-correction step in order to remove noise bias effects at high and low fat fractions as previously proposed by Liu et al. (23).

Selection of flip angles

If the T₁ values of water and fat are constant and known and there are no variations of the actual flip angle across the field-of-view relative to the nominal flip angle, the problem of T₁-correction becomes straightforward as ρ_w and ρ_w can be calculated directly from Eq. [4] and Eq. [6] for a given flip angle and estimated M_w and M_f. In the present work, it is assumed that T₁ of water is unknown and varying in the range between T_1wmin and T_1wmax and the T₁ of fat is considered to be unknown and constant. The maximum T₁-induced fat fraction bias occurs for a nominal fat fraction approximately equal to 50%. Therefore, the flip angles for the above two approaches that do not correct but minimize the T₁ bias effect (namely the ESFA and USFA approaches) are selected such that the T₁-induced fat fraction bias is minimized for a nominal fat fraction of 50%.

Equal small flip angles (ESFA)

As the employed flip angles increase, the result of Eq. [7] is not any more valid and the T₁ bias effect increases. At very small flip angles, the bias effect is minimized but the SNR for both the water and fat signal is low, degrading the noise properties of the fat fraction measurement. A common approach to select the small flip angle is to allow a T₁ biased fat fraction η at a nominal fat fraction f. The optimal small flip angle resulting in T₁-biased fat fraction η for a nominal fat fraction f is described by the equation:

$$\text{cos}(\mathrm{\alpha })=\frac{(1-\text{exp}(-\text{TR}/{\mathrm{T}}_{1\mathrm{f}}))\mathrm{f}(1-\mathrm{\eta })-(1-\text{exp}(-\text{TR}/{\mathrm{T}}_{1\mathrm{w}}))\mathrm{\eta }(1-\mathrm{f})}{(1-\text{exp}(-\text{TR}/{\mathrm{T}}_{1\mathrm{f}}))\text{exp}(-\text{TR}/{\mathrm{T}}_{1\mathrm{w}})\mathrm{f}(1-\mathrm{\eta })-(1-\text{exp}(-\text{TR}/{\mathrm{T}}_{1\mathrm{w}}))\text{exp}(-\text{TR}/{\mathrm{T}}_{1\mathrm{f}})\mathrm{\eta }(1-\mathrm{f})}$$ [12]

The results of Eq. [12] are equivalent to the ones presented by Hines et al (29) but the final mathematical expression (Eq. [12]) is simpler in the present derivation than the one in (29).

The maximum T₁-induced fat fraction bias occurs for a nominal fat fraction f approximately equal to 50% and for T₁ equal to T_1wmax. Therefore, the flip angle of the ESFA approach is selected such that the worst case of T₁-induced fat fraction when f=50% and for T₁=T_1wmax is equal to a given fat fraction bias (in our case set to 2%). The flip angle of the ESFA approach is then derived by Eq. [12] with T_1w=T_1wmax, η=52% and f=50%. For the parameters used in the simulations and the phantom experiments (TR=40ms, T_1wmin=500 ms, T_1wmax=2000 ms, T_1f=360 ms), the optimal flip angle for the ESFA approach is 3.7°.

Unequal large flip angles (ULFA)

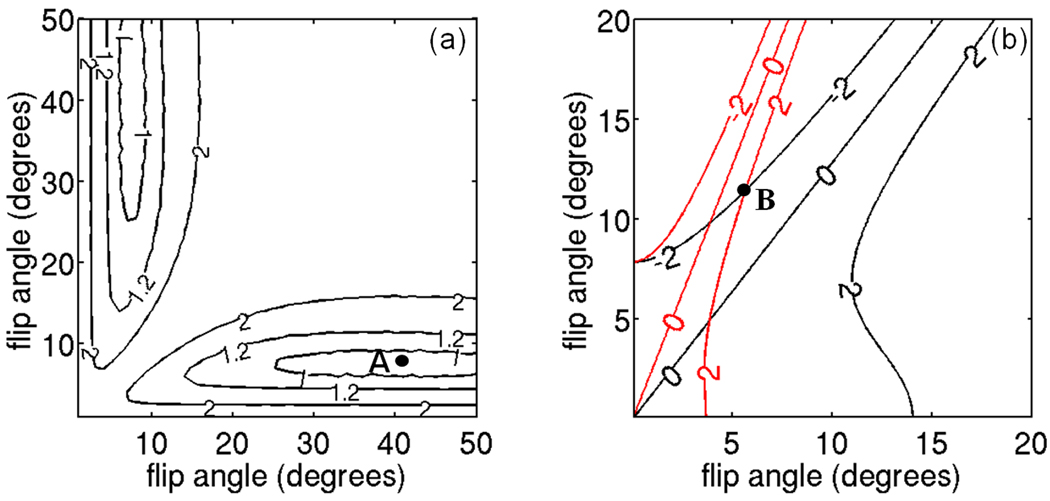
The ULFA approach totally removes the T₁ bias and the optimal flip angles are derived such that the noise performance of the T₁-correction procedure is maximized. The derivation of the flip angles that maximize the noise performance for the ULFA approach requires the performance of numerical simulations of both the water/fat separation and the T₁-correction step. Numerical simulations are performed using 6 echoes, TE_min=1.27 ms, ΔTE=0.65 ms, TR=40 ms, the multi-peak fat spectrum of the phantom excluding the glycerin peak (see below), T_1w=1500 ms, T_1f=360 ms, for fat fraction values between 0% and 100% and flip angles in the range between 1° and 50°. Gaussian noise is added in quadrature to the simulated data assuming SNR=50 for the fat signal at the flip angle of the ESFA approach and 1000 repetitions are performed. The optimal flip angles are computed so that the mean variance of the estimated fat fraction over the entire nominal fat fraction range (0 to 100%) is minimized. Figure 1a shows the isocontours of the mean variance of the fat fraction as a function of the two employed flip angles. Point A (Fig. 1a) corresponds to the optimal flip angles (7.2° and 42°) for the ULFA approach (for the parameters used in the simulations and phantom experiments).

Figure 1.

Design criteria for selection of flip angles in ULFA and USFA approaches. (a) ULFA approach: isocontour lines of mean variance of fat fraction for ULFA approach (values in arbitrary units). The selected flip angles (Point A) correspond to the flip angles that maximize noise performance. (b) USFA approach: isocontour lines of fat fraction bias at 50% fat fraction for T_1w=T_1wmin (black lines) and T_1w=T_1wmax (red lines) (values in %). The selected flip angles (Point B) correspond to the flip angles that minimize fat fraction bias over the range of T_1w.

Unequal small flip angles (USFA)

The optimal flip angles of the USFA approach are computed, similar to the ESFA approach, such that the SNR is maximized with the constraint that the worst case fat fraction bias does not exceed a given threshold. The isocontours of the fat fraction bias as a function of the two employed flip angles are plotted in Figure 1b for T_1wmin and T_1wmax. The optimal flip angles pair is selected as the maximum flip angles pair, to maximize SNR, for which the maximum absolute bias is Df=2% for both T_1wmin and T_1wmax. Specifically, the two flip angles are selected so that the T₁-induced bias is equal to −Df=−2% for T_1wmin and +Df=+2% for T_1wmax. Point B (Fig. 1b) corresponds to the optimal flip angles (5.7° and 11.6°) for the USFA approach (for the parameters used in the simulations and phantom experiments).

MATERIALS AND METHODS

Numerical simulations

Numerical simulations are performed to examine the noise performance of the following alternatives for T₁ unbiased estimation of fat fraction:

• T₁ bias correction/minimization step: three options are examined including ESFA, ULFA and USFA approaches.

• Water/fat separation step: two options are examined including independent fieldmap estimation IDEAL and joint fieldmap estimation IDEAL.

The simulation parameters are 6 echoes, TE_min=1.27 ms, ΔTE=0.65 ms, TR=40 ms (values for 3 T experiments), the employed flip angles are equal to the optimal flip angles for the ESFA, ULFA and USFA approaches. The multi-peak fat spectrum measured in the phantom excluding the glycerin peak (see below) is employed. Gaussian noise is added in quadrature to the simulated data assuming SNR=50 for the fat signal at the flip angle of the ESFA approach. 1000 repetitions are generated for every fat fraction. The data is then analyzed using all the alternatives for the water/fat separation step and the T₁ bias correction/minimization step (six options in total). The mean and standard deviation of fat fraction are computed after extreme outlier removal. A fat fraction value is considered to be an extreme outlier if its distance to the interquartile interval (i.e. interval between the 25^th and 75^th percentiles) exceeds three times the length of the interquartile interval.

Central to any approach that estimates or corrects for T₁ weighting in SPGR experiments is the sensitivity of the approach to absolute flip angle variations. Absolute flip angle variations can occur due to calibration errors and transmit B₁ inhomogeneities. The effect of absolute flip angle variations is tested for all three T₁ bias correction/minimization approaches using numerical simulations.

Phantom experiment

A water/fat phantom with varying fat fraction and T_1w was built to validate the simulations results. A spin-echo experiment with multiple repetition times (0.25 s, 0.5 s, 0.75 s, 1 s, 1.5 s and 2s) was performed in five 55-ml water vials with variable concentration of CuSO₄ (1 mM, 1.25mM, 1.67 mM, 2.5 mM and 5 mM) to measure the dependence of the T₁ of a Cu-doped aqueous solution with the Cu concentration. The derived calibration curve was T₁=1.51/C where T₁ is in s and C in mM.

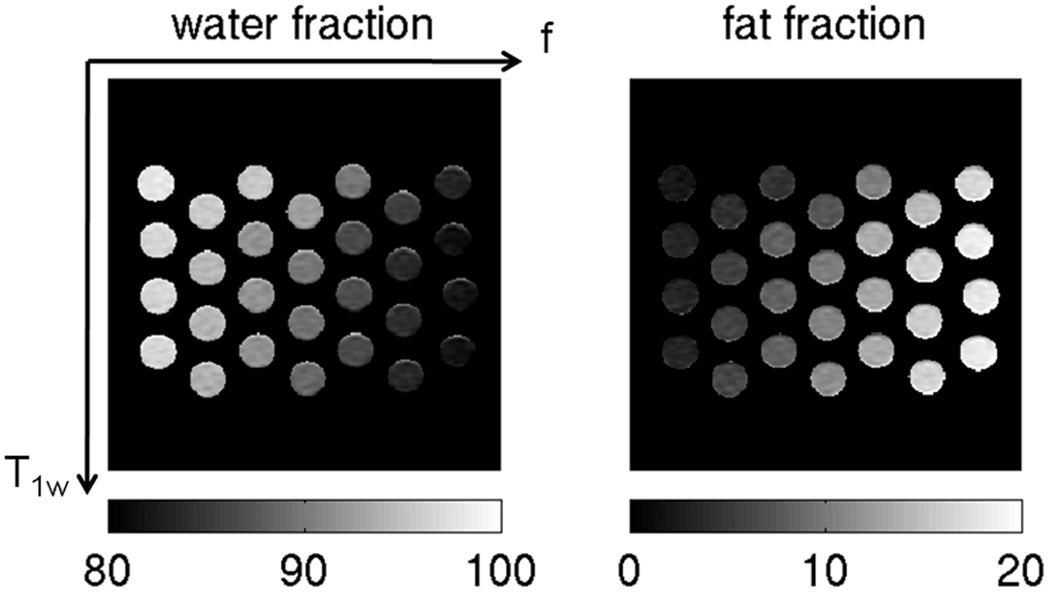
A water/fat phantom with Cu doping was constructed containing 28 16-ml plastic vials with fat content by weight (2.5%, 5.0%, 7.5%, 10%, 12.5%, 15% and 17%) and Cu concentration (0.75 mM, 1.0 mM, 1.5 mM and 3 mM). The varying fat fraction was achieved by diluting with a 20% Intralipid fat emulsion (Baxter Healthcare Corporation, Deerfield, IL, USA) and the varying Cu concentration was achieved by diluting with a 20 mM CuSO₄ stock solution. The labeled fat fraction of Intralipid is 20% soybean oil by weight and 1.2% glycerin by weight. The proton density weighted fat and glycerin fraction of Intralipid in the phantom vials was computed taking into account the formulas in (30) and was equal to (2.7%, 5.4%, 8.1%, 10.8%, 13.6%, 16.3% and 18.6%). The 28 vials of the water/fat phantom with Cu doping were arranged such that 4 rows (corresponding to the different concentration of Cu) and 7 columns (corresponding to the different fat fractions) were formed, as shown in Fig. 2.

Figure 2.

Water fraction and fat fraction maps in the phantom with the ESFA approach flip angle (3.7°). The fat fraction increases from left to right and the T₁ of water increases from the top to the bottom (values of water and fat fraction are in %).

MRI measurements

Precalibration of fat spectrum

Single voxel magnetic resonance spectroscopy measurements (PRESS sequence, TE=28 ms, TR=6000 ms, 10×10×20 mm³ voxel, 64 averages, no water suppression) were performed on a separate vial with 20% fat Intralipid without any further dilution. 8 different peaks were identified in frequency locations [−69 148 257 327 353 404 442 493] Hz at 3 T. The peak at 148 Hz corresponded to the glycerin and the rest of the peaks corresponded to the soybean oil. The area of the peaks was corrected for T₂ effects resulting in relative peak areas [7.7 5.1 5.6 9.3 6.9 3.9 56 5.5] %. Single voxel spectroscopy experiments were also performed on separate vials with 20% and 10% fat Intralipid and no Cu doping with different TR values (TR= 1080, 2000, 3000, 4000 and 5000 and 6000 ms) to evaluate the dependence of T₁ of fat with fat content in the phantom. The results showed small variation of T₁ of the methylene fat peak with the fat content. Specifically, the saturation recovery fitting results gave a T₁ of the methylene fat peak equal to 356 ms and 374 ms for the phantom vials with fat fraction 10% and 20%, respectively.

For the in vivo data, the precalibrated fat spectrum from (31) was used. Single voxel spectroscopy experiments were also performed on regions with different IMAT content with different TR values similarly to the phantom in order to evaluate the dependence of T₁ of fat with fat content in vivo. The results showed again small variation of T₁ of the methylene fat peak with the fat content (the T₁ of the methylene fat peak varied between 430 ms and 500 ms).

IDEAL measurements

A quadrature knee coil was used to scan the variable fat fraction/T₁ phantom and the middle-calf muscle region of a healthy female volunteer (age 30) on a 3 T Signa HDx system (GE Healthcare, Waukesha, WI, USA). An investigational version of 6-point IDEAL in a 3D SPGR sequence with a monopolar readout gradient was used. The imaging parameters in the phantom experiments were: TR=40 ms, TE_min=1.27 ms, ΔTE=0.65 ms, 2 echoes per TR (3 shots), flip angles= [3.7°, 3.7°, 5.7°, 7.2°, 11.6°, 42°], bandwidth=83.5 kHz, FOV=16×16 cm², acquisition matrix size 128×64 (reconstruction matrix 256×256), 6 slices with 4 mm slice thickness. The phantom IDEAL experiment was repeated 32 times to assess noise performance as in (26,32). The total scan time for the phantom experiment was 4 hours and 7 minutes (there was a dead time equal to 30 ms after every repetition of every flip angle). The imaging parameters in the in vivo experiments were: TR=10 ms, TE_min=1.09 ms, ΔTE=0.58 ms, 2 echoes per TR (3 shots), flip angles= [2.7°, 2.7°, 3.3°, 5.4°, 6.0°, 31°], bandwidth=83.5 kHz, FOV=20×20 cm², acquisition matrix size 128×64 (reconstruction matrix 256×256), 6 slices with 4 mm slice thickness. The in vivo IDEAL experiment was repeated 10 times to assess noise performance. The total scan time for the in vivo experiment was 20 minutes (there was a dead time equal to 8 ms after every repetition of every flip angle). In the in vivo experiment, a shorter TR was used than in the phantom experiment to minimize the total scan time. The flip angles of the in vivo experiment were selected based on the same flip angle selection arguments as in the phantom experiment but with TR=10 ms.

RESULTS

Numerical simulations

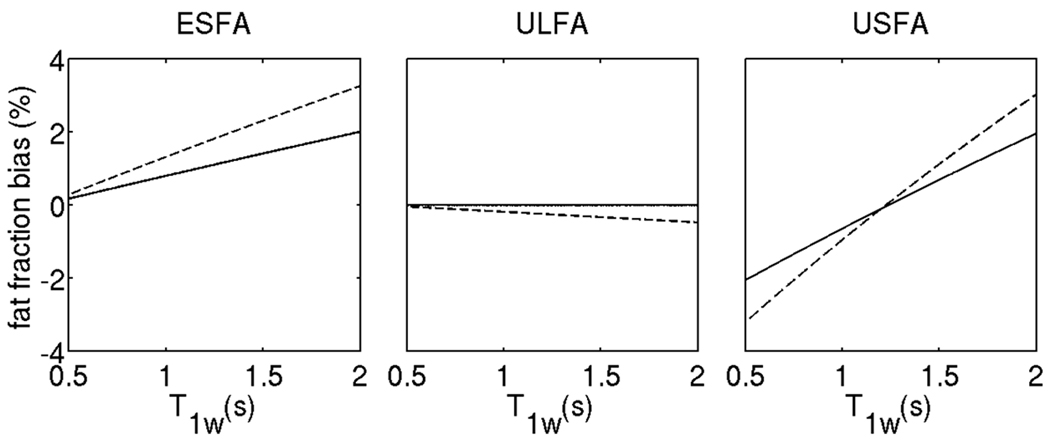
Figure 3 shows a plot of fat fraction bias at 50% fat fraction for the 3 employed T₁-correction approaches as a function of T_1w with no absolute flip angle variation and with absolute flip angle increase equal to 30% of the nominal value. The results show only a relatively small increase in the T₁ induced fat fraction bias in the presence of absolute flip angle variations for all three employed T₁ bias correction/minimization approaches. This result can be explained by the theoretical analysis of the three approaches. In the case of the small equal flip angles approach, the effect of absolute flip angle variations cancels out for the flip angle range that Eq. [7] is valid. However, in the presence of absolute flip angle variations that result in higher flip angle than the nominal one, the deviation from the small flip angle approximation increases and the T₁ induced fat fraction bias increases (ESFA approach in Fig. 4). As it has been shown by Liu et al. (23), in the case of the unequal large flip angles approach, the effect of absolute flip angle variations totally cancels out in the fat fraction estimates for flip angles sufficiently small such that sin (α) ≈ α and cos (α) ≈ 1 − α²/ 2 (as shown in Appendix A2). However, in the presence of absolute flip angle variations that result in higher flip angles than the nominal ones, such that the results of Appendix A2 are not valid, the T₁ induced fat fraction bias increases (ULFA approach in Fig. 3). In the case of the unequal small flip angles approach, the effect of absolute flip angle variations also cancels out for the flip angle range that Eqs. [10] and [11] are valid. However, in the presence of absolute flip angle variations that result in higher flip angles than the nominal ones, the deviation from the approximations of Eqs. [10] and [11] increases and the T₁ induced fat fraction bias increases (USFA approach in Fig. 3). The results in Fig. 3 show that for all 3 approaches (ESFA, USFA and ULFA), the increase of the T₁ induced fat fraction bias does not overcome 1% even in the presence of absolute flip angle variations that result in flip angles higher by 30% than the nominal ones.

Figure 3.

Sensitivity of fat fraction estimates to absolute flip angle variations: plot of fat fraction bias at 50% fat fraction for the 3 employed T₁-correction approaches as a function of T_1w with no absolute flip angle variation (solid line) and with absolute flip angle variation such that the actual flip angle is 30% higher than the nominal flip angle (dashed line).

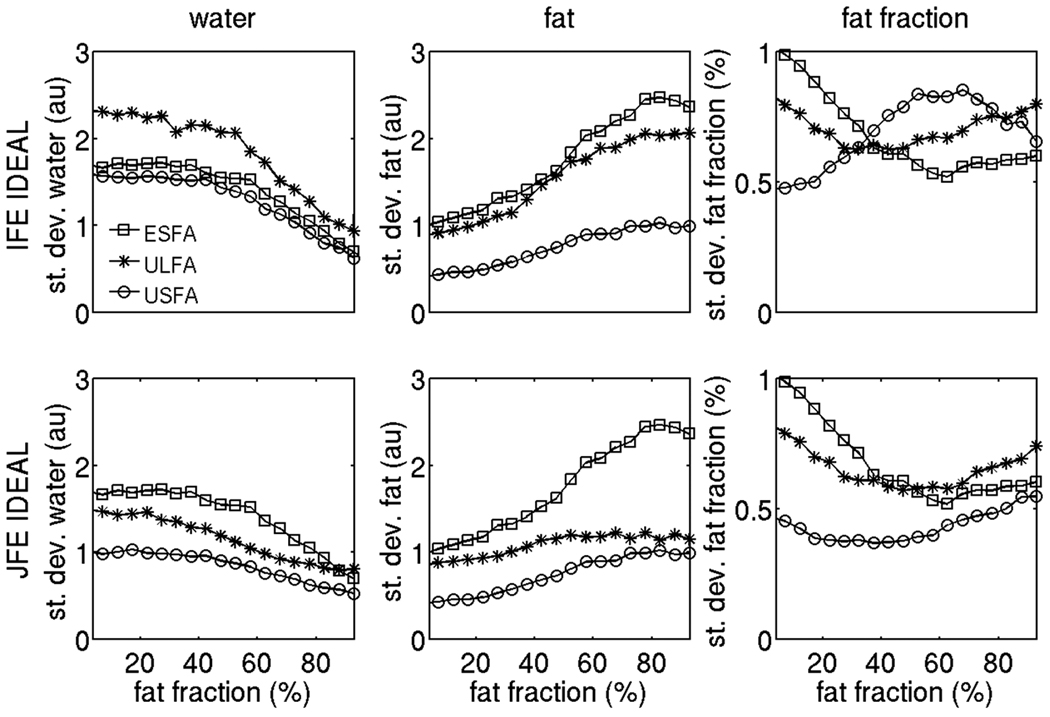
Figure 4.

Noise performance of proton density weighted water signal, proton density weighted fat signal and fat fraction using the 6 options under study on the simulated data. The squares correspond to ESFA approach results, the stars correspond to ULFA approach results and the circles correspond to USFA approach results. The first row shows independent fieldmap estimation IDEAL results and second column shows joint fieldmap estimation IDEAL results.

Figure 4 shows the comparison of the of noise performance for the 6 methods under study on the simulation data. The first and second column of Fig. 4 show the standard deviation results for the water and fat signal, respectively. In the case of independent fieldmap estimation IDEAL, the USFA approach shows reduced standard deviation in the water and fat signal when compared to ESFA and ULFA approaches. Specifically, a significant reduction in the standard deviation of the fat signal is observed by using the USFA approach at small fat fractions compared to ESFA and ULFA approaches. Furthermore, the joint fieldmap estimation IDEAL method reduces overall the standard deviation in the estimation of water signal and fat signal compared to the independent fieldmap estimation IDEAL method for all three T₁ bias correction/minimization approaches. Specifically, the joint fieldmap estimation IDEAL method considerably improves the noise performance in the estimation of the water signal for the ULFA approach and the USFA approach, compared with independent fieldmap estimation IDEAL approach. Similarly, joint fieldmap estimation IDEAL shows much superior noise performance in the estimation of the fat signal for the ULFA approach, compared with independent fieldmap estimation IDEAL approach. The third column of Fig. 4 shows the standard deviation results for the fat fraction. Since the fat fraction is a non-linear function of the water and fat signal and the water and fat signal estimates are dependent, the fat fraction standard deviation results are a little less intuitive than the water and fat signal standard deviation results. In the case of independent fieldmap estimation IDEAL, the standard deviation in the fat fraction is lower with the USFA approach than with the ESFA and ULFA approaches but only for fat fractions between 0 and 35%. However, in the case of joint fieldmap estimation IDEAL the noise performance of the USFA approach in the estimation of the fat fraction at moderate fat fraction values is much improved compared to the independent fieldmap estimation IDEAL and ends up being superior to the ESFA and ULFA approaches. Therefore, based on the simulation results in Fig. 4, the USFA approach combined with joint fieldmap estimation IDEAL shows the lowest standard deviations for the water signal, the fat signal and the fat fraction in the entire range of fat fraction values.

Phantom measurements

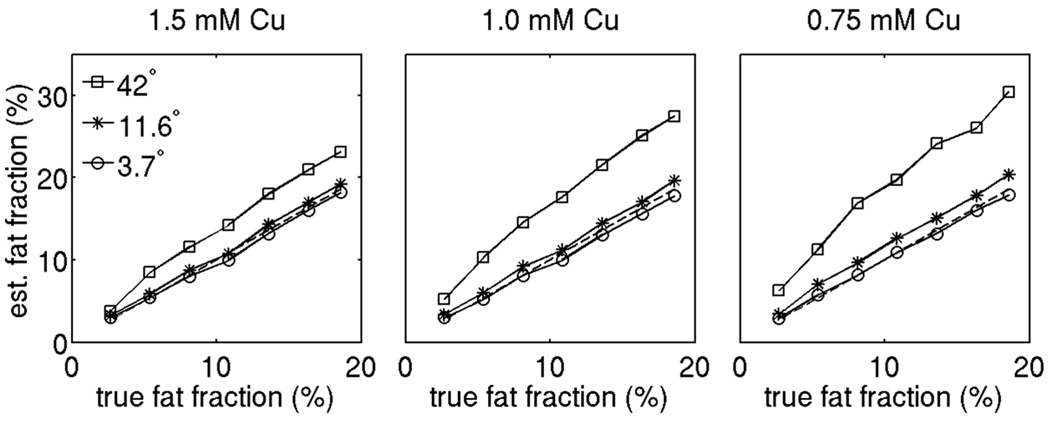
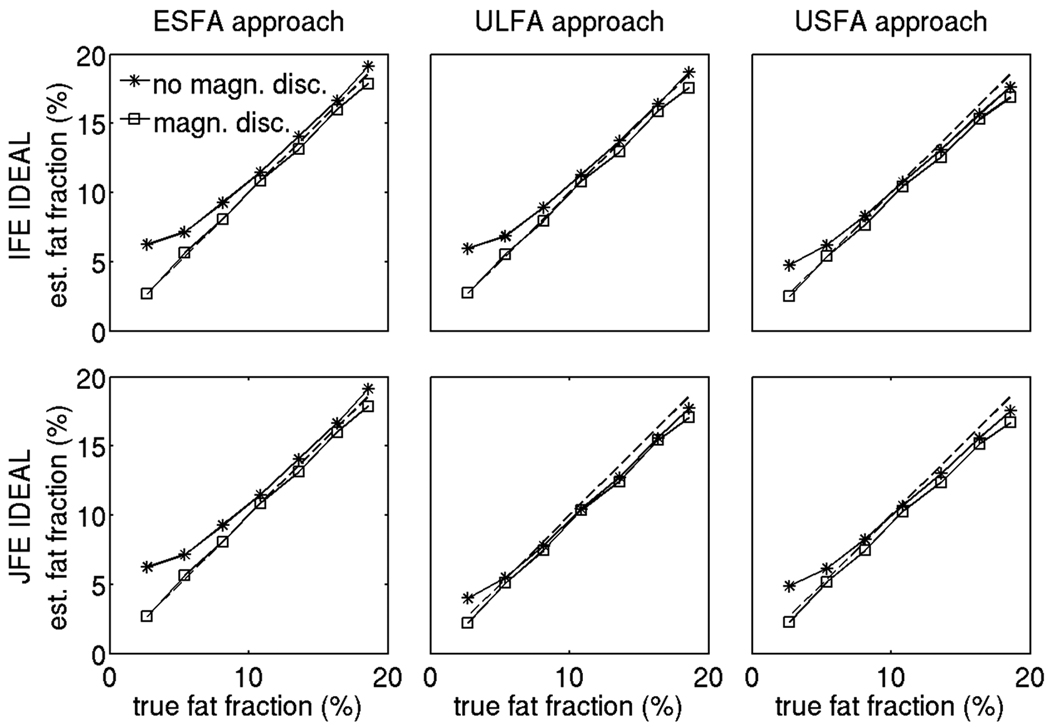
Figure 5 shows the T₁ bias effect over the phantom fat fraction range for three different concentrations of Cu. For a given flip angle, as the concentration of Cu decreases, the T₁ of water increases and the T₁ difference between the water and fat compartments also increases leading to a stronger T₁ bias effect (the Cu concentration increases from left to right in Fig. 5). For a given Cu concentration, as the flip angle increases, a stronger T₁ bias in fat fraction is also observed (the different symbols correspond to different flip angle data in Fig. 5). Figure 6 shows the T₁ corrected fat fraction estimates over the phantom fat fraction range for the 0.75 mM concentration in Cu vials. All three T₁ bias correction/minimization approaches (ESFA, ULFA, and USFA) reduce the T₁ bias effect and result in fat fraction values very close to the nominal ones. The fat fraction values have been computed with and without the magnitude discrimination approach (23) to remove noise bias at the small fat fraction range. The estimated fat fraction results at the low true fat fraction in Fig. 6 show that the noise bias correction is essential for all three T₁ bias correction/minimization approaches (ESFA, ULFA and USFA) and all two water/fat separation approaches (independent fieldmap estimation IDEAL and joint fieldmap estimation IDEAL).

Figure 5.

T₁ bias effect on phantom fat fraction values for different flip angles without any T₁ correction. The squares, stars and circles correspond to the uncorrected fat fraction values with flip angles 42°, 11.6° and 3.7° respectively. The dashed line corresponds to the nominal fat fraction values (identity line).

Figure 6.

Noise bias effect on fat fraction of phantom vials with 0.75 mM concentration in Cu for all 6 options under study. The stars show the results without applying the magnitude discrimination approach, the squares show the results with applying the magnitude discrimination approach, and the dashed line shows the nominal fat fraction values (identity line).

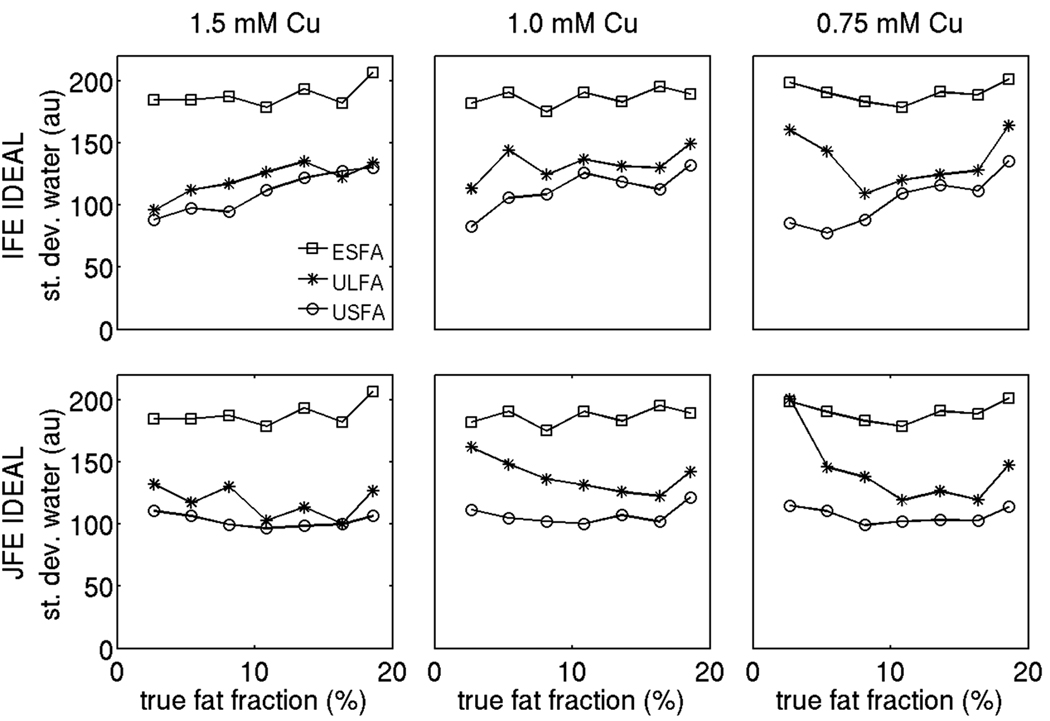
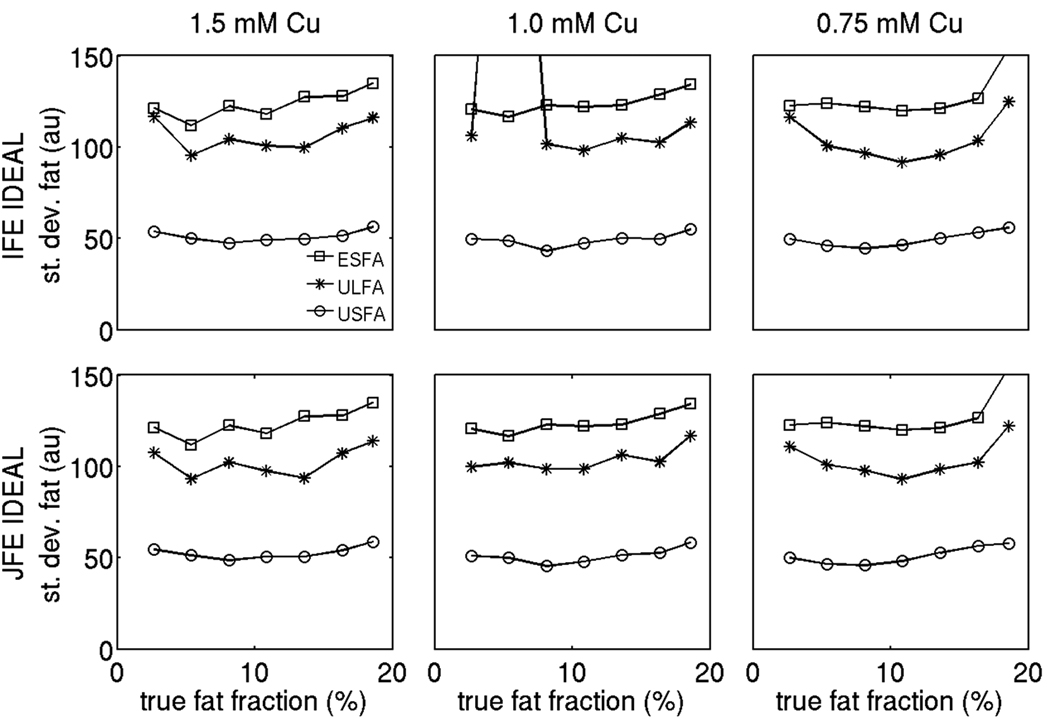
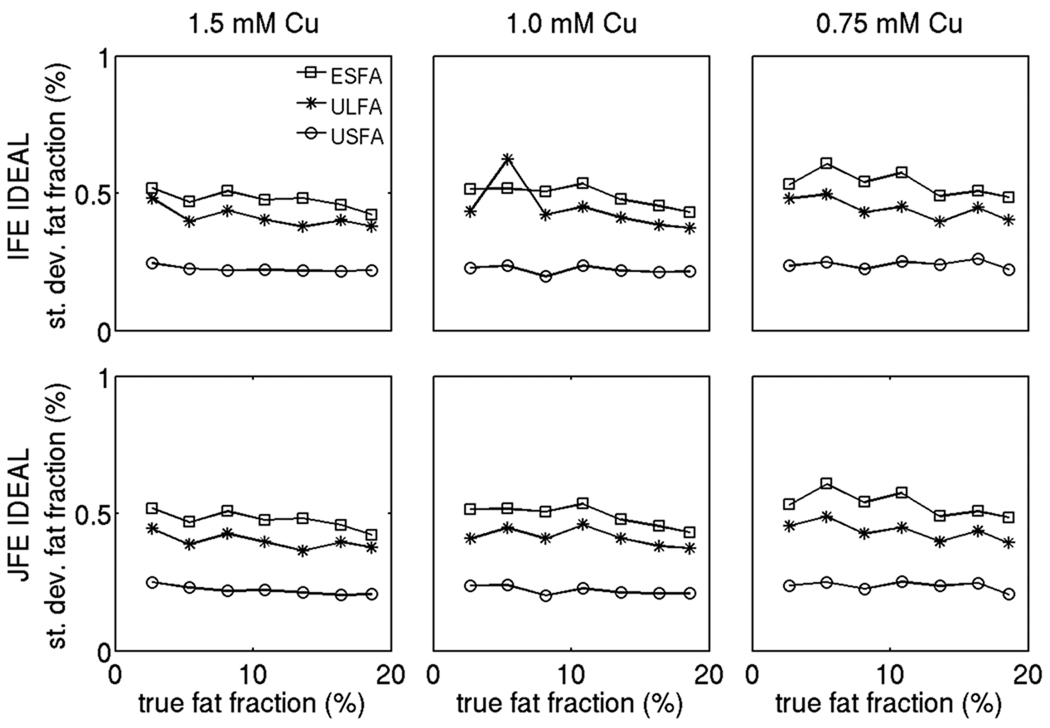
Figures 7, 8 and 9 show the standard deviation results for the proton density weighted water signal, the proton density weighted fat signal and the fat fraction respectively employing the 6 alternatives under study on the phantom data. In the fat fraction range and T₁ range of the phantom, the USFA approach has the lowest standard deviation for the water signal, the ULFA approach has a moderate standard deviation for the water signal, and the ESFA has the highest standard deviation for the water signal (Fig. 7). The joint fieldmap estimation IDEAL approach improves the noise performance of the water signal estimates relative to the independent fieldmap estimation IDEAL approach for all three T₁ bias correction/minimization approaches (ESFA, ULFA, and USFA) in the fat fraction range between 10% and 17%. Furthermore, in the fat fraction range and T₁ range of the phantom, the USFA approach has the lowest standard deviation for the fat signal, the ULFA approach has a moderate standard deviation for the fat signal, and the ESFA has the highest standard deviation for the fat signal (Fig. 8). The joint fieldmap estimation IDEAL approach does not alter significantly the noise performance of the fat signal estimates relative to the independent fieldmap estimation IDEAL approach for all three T₁ bias correction/minimization approaches (ESFA, ULFA, and USFA). Finally, in the fat fraction range and T₁ range of the phantom, the USFA approach has the lowest standard deviation for the fat fraction, the ULFA approach has a moderate standard deviation for the fat fraction, and the ESFA has the highest standard deviation for the fat fraction (Fig. 9). Specifically, Fig. 9 shows that the USFA approach leads to a decrease in the standard deviation of fat fraction up to 50% compared with the ESFA approach. In summary, the phantom measurements show a superior noise performance in water, fat and fat fraction estimation for the USFA approach when compared to the ESFA and ULFA approaches in the fat fraction range and T₁ range of the phantom, which is consistent with the simulation results in Fig. 4.

Figure 7.

Comparison of standard deviation of the proton density weighted water signal using the 6 options under study on the phantom data (for three different concentrations in Cu). The squares correspond to ESFA approach results, the stars correspond to ULFA approach results and the circles correspond to USFA approach results. The first row shows independent fieldmap estimation IDEAL results and second column shows joint fieldmap estimation IDEAL results.

Figure 8.

Comparison of standard deviation of the proton density weighted fat signal using the 6 options under study on the phantom data (for three different concentrations in Cu). The squares correspond to ESFA approach results, the stars correspond to ULFA approach results and the circles correspond to USFA approach results. The first row shows independent fieldmap estimation IDEAL results and second column shows joint fieldmap estimation IDEAL results.

Figure 9.

Comparison of standard deviation of fat fraction using the 6 options under study on the phantom data (for three different concentrations in Cu). The squares correspond to ESFA approach results, the stars correspond to ULFA approach results and the circles correspond to USFA approach results. The first row shows independent fieldmap estimation IDEAL results and second column shows joint fieldmap estimation IDEAL results.

In vivo measurements

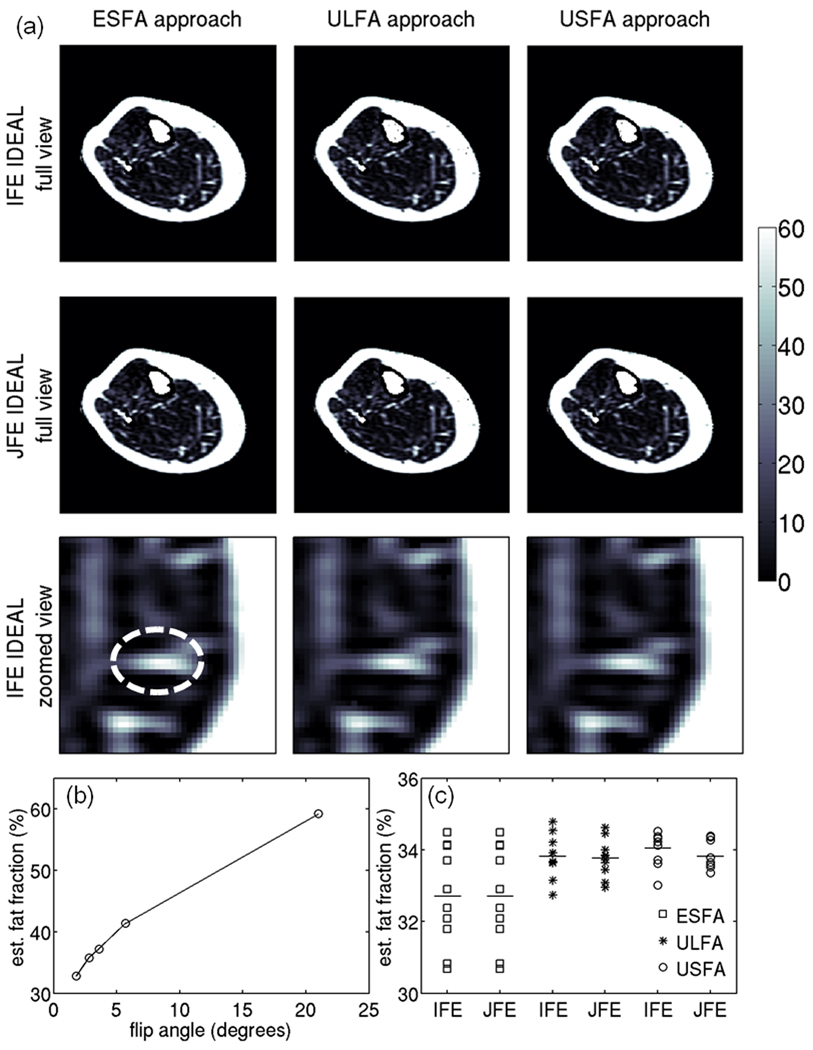
Figure 10a shows the fat fraction maps from the middle-calf slice of a healthy volunteer for all three T₁ bias correction/minimization approaches and two water/fat separation approaches. It is difficult to identify any differences in the estimated fat fraction values even in the zoomed view of Fig. 10a due to the strong spatial variation of fat fraction within the muscular regions. Figure 10b shows the flip angle dependence of the estimated fat fraction in an ROI in the medial gastrocnemius, highlighting the significance of the T₁ bias effect (the five presented flip angles data points correspond to the data from the ESFA, ULFA and USFA flip angles). Figure 10c includes a scatter plot of the estimated fat fraction values using all three T₁ bias correction/minimization approaches and two water/fat separation approaches for the 10 repetitions of the in vivo experiment. It can be noticed that the USFA approach combined with either the joint fieldmap estimation IDEAL or independent fieldmap estimation IDEAL shows the lowest dispersion of the 10 repetitions of the fat fraction measurements around their mean values, which is consistent with the simulation results (Fig. 4).

Figure 10.

In vivo results. (a) Fat fraction maps using the 6 options under study (values in %). First two rows show the fat fraction maps for the full FOV and the third row shows the fat fraction maps for a zoomed region in the medial gastrocnemius muscle. (b) Dependence of uncorrected mean fat fraction over the shown ROI with the employed flip angle. (c) Scatter plot of the corrected mean fat fraction over the shown ROI using the 6 options under study for the 10 repetitions of the in vivo experiment. The squares correspond to results of the ESFA approach, the stars correspond to results of the ULFA approach and the circles correspond to results of the USFA approach.

DISCUSSION

The correction of the various confounding factors in quantitative water/fat separation can improve the accuracy of the measurement by removing systematic biases, but it can also degrade the noise performance when the complexity of the signal model is increased and more unknowns are introduced. Typical example of degrading the noise properties of the model by increasing the number of unknowns in quantitative water/fat separation is the modeling of T₂* decay as a two T₂* decay instead of a single T₂* decay (26,33,34). The correction of T₁ bias is another example where a trade-off between improving the accuracy and degrading the noise performance must be considered. Specifically, the minimization of the T₁ bias effect on fat fraction measurements derived from chemical/shift based water/fat separation requires the use of small flip angles that lead in general to low SNRs (ESFA approach) (23,25). The correction of the T₁ bias effect on fat quantification measurements requires the acquisition of the IDEAL data at least at two different flip angles, introducing more unknowns and increasing the complexity of the signal model (ULFA approach) (23,25). Instead a novel approach is proposed in this work with the acquisition of the IDEAL data at two small flip angles such that the water signal is assumed to be T₁-independent for the first flip angle and the fat signal is assumed to be T₁-independent for the second flip angle (USFA approach). Although the USFA approach discards the information for the water signal at the second flip angle, the USFA approach benefits from the use of the T₁-independent equations for estimating the water and fat signals. Taking into account the information for the water signal at the second flip angle would require the estimation of T₁ of water and increase the complexity of the model with the potential of degrading the noise performance of the water signal estimation.

The presented simulations, phantom and in vivo results show that the USFA approach can minimize the T₁ bias with improved noise performance over the ESFA and ULFA approaches in tissues with large T₁ difference between water and fat. In the case of tissues with small T₁ difference between water and fat, the noise efficiency of the ESFA approach is higher than the noise efficiency of ULFA approach (25). Therefore, it should be emphasized that the presented arguments related to the selection of flip angles refer to the case of tissues with large T₁ difference between water and fat. Furthermore, the acquisition of two flip angles as in the ULFA and the USFA approaches or the acquisition of two averages for the same small flip angle as in ESFA approach can be prohibitive in the case of quantitative water/fat separation in body parts where the data acquisition has to be performed within a single breath hold or respiratory gating is required. In that case, the small flip angle approach with a single average will be preferred. However, the present results show that in the case of tissues large T₁ difference between water and fat and where two averages of the same flip angle can be acquired it is preferable to acquire the IDEAL data at two different flip angles (selected as in the USFA approach) than to acquire the IDEAL data at the same flip angle two times (as in the ESFA approach). Similar arguments might be applicable for more than two averages and more than two flip angles, but such an analysis was outside the scope of the present study.

An additional consideration when comparing the different T₁ bias correction/minimization procedures on quantitative chemical shift based water/fat separation is the instability at low and high fat fractions, as previously reported by Liu et al (23). Specifically, the ULFA approach suffers from instabilities due to erroneously estimated T₁ values occurring when the fraction of one of the species (water or fat) is small. The ESFA and the USFA approaches do not suffer from this type of instability, since T₁ estimation is not required to remove the T₁-bias effect in the estimation of the fat fraction (23). In the present work, outlier removal is employed in the analysis of the numerical simulations and averaging over ROIs is employed in the analysis of the phantom and in vivo data, reducing the effect of the instabilities in fat fraction estimation with the ULFA approach at low and high fat fractions due to erratic estimates of T₁. However, the instability of the T₁ correction step in the ULFA approach should be always considered when comparing the different T₁ bias correction/minimization procedures on quantitative chemical shift based water/fat separation.

A further improvement of the noise performance of IDEAL data acquired at multiple flip angles can be achieved by joint estimation of the T₁-weighted water signal, the T₁-weighted fat signal, the fieldmap and T₂* values based on the multi-echo source signals at multiple flip angles. The joint estimation approach, labeled as joint fieldmap estimation IDEAL, has the advantage of improving the noise performance of the estimated water and fat signals relative to the approach of solving the water/fat separation problem at every flip angle separately. This improvement occurs since the approach of joint estimation reduces the total number of unknowns. It should be pointed out that, in the present implementation, fieldmap smoothing is used in solving the independent fieldmap estimation IDEAL problem at every flip angle, as previously proposed (28). The fieldmap values from the solution of the independent fieldmap estimation IDEAL problem at every flip angle are averaged and used as initial guess for solving the joint field map estimation IDEAL problem. There is no additional fieldmap smoothing applied when solving the joint field map estimation IDEAL problem. However, fieldmap smoothing is an operation that can be always performed as an additional regularization during the joint field map estimation IDEAL reconstruction.

The goal of the present work was not to study the T₁ dependence of the water and fat compartments on fat fraction, but its implications should be discussed. Hu et al. (35) have recently reported a strong dependence of the T₁ of the main fat peak with the fat fraction in water/fat mixtures based on single-voxel spectroscopy measurements in oil-water emulsions and pork-kidney lard mixtures. Specifically, in Hu’s study (35) the T₁ of the main fat peak approaches the T₁ of water in water/fat mixtures with very low fat fractions (of the order of 10%). This result contradicts with the results of previous in vivo studies (36,37) measuring the T₁ of skeletal muscle metabolites showing a rather constant value for the T₁ of the methylene peak of extramyocellular lipids (of the order of 360 ms). The present phantom results also show a very small change of the T₁ of the main fat peak for the phantom emulsion between 10% and 20% fat fraction. The above differences could be attributed to the observation that the spectra shown in Hu’s work are characterized by much broader linewidths than the spectra measured in the present water/fat phantom (38) or the in vivo spectra measured routinely in skeletal muscle regions with low fat content. Broad linewidths in MR spectra can affect the peak area calculation and may induce peak area values for the water and fat peaks dependent on the fat fraction. Nevertheless, the issue of the fat fraction dependence of the T₁ of fat could be dependent on the type of fat depot under study and further work in that direction would be necessary.

The presented ESFA, ULFA and ESFA approaches have been designed for T₁ bias correction and minimization in quantitative water/fat separation, but are not suitable, in their current implementation, for T₁ mapping of water and fat. A detailed analysis of the T₁ variation of water and fat compartments with fat fraction would require the addition of a robust absolute flip angle mapping approach to the present ULFA approach (39). However, single voxel spectroscopy experiments confirmed the small variation of the T₁ of the main fat peak both in phantom and previous in vivo measurements of the T₁ of the methylene peak of extramyocellular lipids support this hypothesis (36,37). A rather wide range of variation was also selected for the T_1w (between 500 ms and 2000 ms) in an effort to take into account the dependence of T_1w on muscle fiber composition (40) and to include potentially severely altered T_1w values in diseased muscles. Therefore, the variation of the T_1w in a given range and the relative constancy of the T_1f of the fat are the only constraints for which the presented ESFA and USFA approaches minimize the T₁ bias effect. The implementation of the ULFA approach is not accompanied by any constraint since it exactly corrects for the T₁ effect, although the optimal flip angles selection would obviously depend on the T₁ values of water and fat.

The present work has some limitations. The precalibrated fat spectrum used in the water/fat separation of the in vivo data was borrowed from the literature (31). The accuracy of the precalibrated fat spectrum is an important factor that can affect the accuracy of quantitative chemical shift based water/fat separation. Further work would be needed to understand the variation of muscular fat spectrum with fat fraction and muscle region for a given subject and its variation among subjects, including potential variable levels of unsaturated fatty acids. Furthermore, the following confounding factors in the quantitative water/fat separation have not been taken into consideration: eddy currents effects (41), T₂* difference between water and fat compartments (42) and different T₁s for the different fat peaks (38). Regarding the eddy currents compensation, eddy currents induced phase errors can be assessed using a magnitude tuning approach as in (41). The phase contribution from eddy currents was studied in the phantom and found to be not significant. However, the noise performance of the magnitude tuning approach in dual flip angle acquisitions would require further analysis. Regarding the need to model different T₂* for water and fat, the muscle T₂* value is expected to be in the range 24–29 ms at 3 T (43) and the fat T₂* is expected to be close to 26 ms at 3 T (18). Therefore, the single T₂* decay model might be adequate in muscle applications of quantitative water/fat separation. Regarding the difference in T₁ values among the different fat peaks, the effect of different T₁ values for the different fat peaks should be important primarily at high flip angles and high fat fractions. A separate experiment in a vial containing only fat showed that the use of the same T₁ for the different fat peaks in the fat only region lead to an underestimation of the fat fraction by 2–3% relative to the use of different T₁s for the different fat peaks with the ULFA approach.

The present analysis focused on examining the noise performance of different T₁ bias correction/minimization procedures for 3D IDEAL-SPGR data. Chemical shift based water/fat separation methods can use either 2D or 3D sequences. 2D sequences lead to longer in general TR values for the same slice coverage as the 3D sequences and use thus higher flip angles than the 3D sequences (44). The arguments analyzed in the present work can be generalized for the 2D acquisition case. However, it has to be emphasized that 2D sequences at high flip angles will suffer from slice profile effects, which can make the signal behavior deviate from the traditional SPGR signal expression (45,46). Therefore, in the case of strong slice profile effects, the insensitivity of the three T₁ bias correction/minimization approaches to absolute flip angle variations needs to be re-evaluated.

The present analysis optimizes the T₁-correction of fat fraction derived from chemical shift based water/fat separation in the case where the T₁ of fat and water are unknown. Depending on the application, alternative approaches for the T₁-correction procedure could be the a priori knowledge of the T₁ values of fat and water or the precalibration of the T₁ value of the fat compartment as in (38). In the case where the T₁ of fat and water are exactly known, Eqs. [4] and [6] could be directly used to remove T₁ effects based on the acquisition of data at a single flip angle. The flip angle that would optimize the noise performance would be between the Ernst flip angle of water and the Ernst flip angle of fat depending on the fat fraction. However, when the T₁ values of water and fat are a priori known, attention should be paid on the effect of the absolute flip angle variations on the T₁ correction step. Furthermore, in the case where the T₁ of fat is precalibrated, the ULFA approach could be used. However, when the T₁ value of fat is known and is used to reduce the number of unknowns in the T₁-correction step, the insensitivity of the ULFA approach to absolute flip angle variations (as shown in Appendix A2) does not hold. Therefore, the effect of absolute flip variations due to both transmit B₁ inhomogeneities and RF calibration errors (39) should be taken into consideration on the T₁-correction procedure when the T₁ values of fat and water are a priori known or when the T₁ value of the fat is precalibrated.

Finally, the present work focused on the application of chemical shift based fat quantification methods on the skeletal muscle, which would be important in the context of metabolic syndrome (including obesity and diabetes) (1,2) as well as in the context of muscle dystrophies (20). However, the conclusions of this analysis can be generalized in the case of other tissues with large T₁ differences between water and fat compartments. Fat quantification in the breast (47) and the red bone marrow (48,49) are potential applications where the findings of the present work could be applied.

CONCLUSION

Novel approaches for T₁ bias effect correction and minimization in quantitative chemical shift based water/fat separation have been introduced and compared with previously proposed approaches. Simulations, phantom and in vivo measurements have been employed in order to characterize the noise performance of different fat fraction T₁ bias correction/minimization approaches. A novel approach, labeled as the unequal small flip angle approach, is proposed for the minimization of the T₁ bias effect. The results show that the use of two small unequal flip angles, selected such the water signal is assumed to be T₁-independent for the first flip angle and the fat signal is assumed to be T₁-independent for the second flip angle, has superior noise performance to the use of the same small flip angle twice (no T₁ estimation required) and the use of two unequal large flip angles (T₁ estimation required). It is also shown that a novel approach performing a joint water/fat separation at the two employed flip angles can improve further the noise performance relative to the traditional approach of performing the water/fat separation separately at every flip angle.

APPENDIX A1: Matrix formulation of dual flip angle IDEAL

With the signals collected at six echoes and two flip angles, Eq. [3] can be formatted in the following matrix form:

$$\mathbf{S}=\mathbf{P}(\mathrm{\psi })·\mathbf{A}·\mathbf{T}·\mathbf{M}$$ [13]

where

$$\mathbf{P}(\mathrm{\psi })=\left(\begin{array}{cccccc}\hfill \text{exp}(j2\mathrm{\pi }\mathrm{\psi }{\mathrm{t}}_1)\hfill & \hfill \dots \hfill & \hfill 0\hfill & \hfill \text{exp}(j2\mathrm{\pi }\mathrm{\psi }{\mathrm{t}}_1)\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill \dots \hfill & \hfill \dots \hfill & \hfill \dots \hfill & \hfill \dots \hfill & \hfill \dots \hfill & \hfill \dots \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \text{exp}(j2\mathrm{\pi }\mathrm{\psi }{\mathrm{t}}_6)\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \text{exp}(j2\mathrm{\pi }\mathrm{\psi }{\mathrm{t}}_6)\hfill \end{array}\right)$$ [14]

$$\mathbf{A}=\left(\begin{array}{cccc}\hfill 1\hfill & \hfill {\displaystyle \sum _{\mathrm{p}=1}^{\mathrm{P}}{\mathrm{a}}_{\mathrm{p},\text{cor}}({\mathrm{\alpha }}_1)\text{exp}(\mathrm{j}2\mathrm{\pi }\mathrm{\Delta }{\mathrm{f}}_{\mathrm{p}}}{\mathrm{t}}_1)\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \dots \hfill & \hfill \dots \hfill & \hfill \dots \hfill & \hfill \dots \hfill \\ \hfill 1\hfill & \hfill {\displaystyle \sum _{\mathrm{p}=1}^{\mathrm{P}}{\mathrm{a}}_{\mathrm{p},\text{cor}}({\mathrm{\alpha }}_1)\text{exp}(\mathrm{j}2\mathrm{\pi }\mathrm{\Delta }{\mathrm{f}}_{\mathrm{p}}}{\mathrm{t}}_6)\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill {\displaystyle \sum _{\mathrm{p}=1}^{\mathrm{P}}{\mathrm{a}}_{\mathrm{p},\text{cor}}({\mathrm{\alpha }}_2)\text{exp}(\mathrm{j}2\mathrm{\pi }\mathrm{\Delta }{\mathrm{f}}_{\mathrm{p}}}{\mathrm{t}}_1)\hfill \\ \hfill \dots \hfill & \hfill \dots \hfill & \hfill \dots \hfill & \hfill \dots \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill {\displaystyle \sum _{\mathrm{p}=1}^{\mathrm{P}}{\mathrm{a}}_{\mathrm{p},\text{cor}}({\mathrm{\alpha }}_2)\text{exp}(\mathrm{j}2\mathrm{\pi }\mathrm{\Delta }{\mathrm{f}}_{\mathrm{p}}}{\mathrm{t}}_6)\hfill \end{array}\right)$$ [15]

$$\mathbf{S}=\left(\begin{array}{c}\mathrm{S}({\mathrm{t}}_1,{\mathrm{\alpha }}_1)\hfill \\ \dots \hfill \\ \mathrm{S}({\mathrm{t}}_6,{\mathrm{\alpha }}_1)\hfill \\ \mathrm{S}({\mathrm{t}}_1,{\mathrm{\alpha }}_2)\hfill \\ \dots \hfill \\ \mathrm{S}({\mathrm{t}}_6,{\mathrm{\alpha }}_2)\hfill \end{array}\right)$$ [16]

The matrices T, M depend on the employed T₁ bias minimization/correction approach:

For the ESFA approach: α₁ = α₂ = α:

$$\mathbf{T}=\left(\begin{array}{cc}1\hfill & 0\hfill \\ 0\hfill & 1\hfill \\ 1\hfill & 0\hfill \\ 0\hfill & 1\hfill \end{array}\right),\mathbf{M}=\left(\begin{array}{c}{\mathrm{M}}_{\mathrm{w}}(\mathrm{\alpha })\hfill \\ {\mathrm{M}}_{\mathrm{f}}(\mathrm{\alpha })\hfill \end{array}\right)$$ [17]

For the ULFA approach:

$$\mathbf{T}=\left(\begin{array}{cccc}1\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 1\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 1\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 1\hfill \end{array}\right),\mathbf{M}=\left(\begin{array}{c}{\mathrm{M}}_{\mathrm{w}}({\mathrm{\alpha }}_1)\hfill \\ {\mathrm{M}}_{\mathrm{f}}({\mathrm{\alpha }}_1)\hfill \\ {\mathrm{M}}_{\mathrm{w}}({\mathrm{\alpha }}_2)\hfill \\ {\mathrm{M}}_{\mathrm{f}}({\mathrm{\alpha }}_2)\hfill \end{array}\right)$$ [18]

For the USFA approach:

$$\mathbf{T}=\left(\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill \frac{{\mathrm{\alpha }}_2}{{\mathrm{\alpha }}_1}\hfill & \hfill 0\hfill \end{array}\right),\mathbf{M}=\left(\begin{array}{c}{\mathrm{M}}_{\mathrm{w}}({\mathrm{\alpha }}_1)\hfill \\ {\mathrm{M}}_{\mathrm{f}}({\mathrm{\alpha }}_1)\hfill \\ {\mathrm{M}}_{\mathrm{w}}({\mathrm{\alpha }}_2)\hfill \end{array}\right)$$ [19]

APPENDIX A2: Insensitivity of ULFA approach to absolute flip angle variations

For small flip angles such that sin(α) ≈ α and cos (α) ≈ 1 − α²/ 2

$${\mathrm{\rho }}_{\mathrm{i}}\approx \frac{{\mathrm{M}}_{\mathrm{i}}({\mathrm{\alpha }}_1){\mathrm{M}}_{\mathrm{w}}({\mathrm{\alpha }}_2)\left({{\mathrm{\alpha }}_2}^2-{{\mathrm{\alpha }}_1}^2\right)}{{\mathrm{M}}_{\mathrm{i}}({\mathrm{\alpha }}_2){\mathrm{\alpha }}_1{{\mathrm{\alpha }}_2}^2-{\mathrm{M}}_{\mathrm{i}}({\mathrm{\alpha }}_1){\mathrm{\alpha }}_2{{\mathrm{\alpha }}_1}^2}$$ [20]

where i=w,f.

In the presence of absolute flip angle variations by a relative factor Δα from the nominal flip angles α_1nom and α_2nom, such that the actual flip angles are α₁ = Δα α_1nom and α₂ = Δα α_2nom

$${\mathrm{\rho }}_{\mathrm{i}}\approx \frac{1}{\mathrm{\Delta }\mathrm{\alpha }}\frac{{\mathrm{M}}_{\mathrm{i}}({\mathrm{\alpha }}_1){\mathrm{M}}_{\mathrm{i}}({\mathrm{\alpha }}_2)\left({{\mathrm{\alpha }}_{2\text{nom}}}^2-{{\mathrm{\alpha }}_{2\text{nom}}}^2\right)}{{\mathrm{M}}_{\mathrm{i}}({\mathrm{\alpha }}_2){\mathrm{\alpha }}_{1\text{nom}}{{\mathrm{\alpha }}_{2\text{nom}}}^2-{\mathrm{M}}_{\mathrm{i}}({\mathrm{\alpha }}_1){\mathrm{\alpha }}_{2\text{nom}}{{\mathrm{\alpha }}_{1\text{nom}}}^2}$$ [21]

Therefore f = ρ_f / (ρ_w + ρ_f) becomes independent of Δα.