Calculating tissue shear modulus and pressure by 2D Log-Elastographic methods

Abstract

Shear modulus imaging, often called elastography, enables detection and characterization of tissue abnormalities. In this paper the data is two displacement components obtained from successive MR or ultrasound data sets acquired while the tissue is excited mechanically. A 2D plane strain elastic model is assumed to govern the 2D displacement, u. The shear modulus, μ, is unknown and whether or not the first Lamé parameter, λ, is known the pressure p = λ∇ · u which is present in the plane strain model cannot be measured and is unreliably computed from measured data and can be shown to be an order one quantity in the units kPa. So here we present a 2D Log-Elastographic inverse algorithm that: (1) simultaneously reconstructs the shear modulus, μ, and p, which together satisfy a first order partial differential equation system, with the goal of imaging μ; (2) controls potential exponential growth in the numerical error; and (3) reliably reconstructs the quantity p in the inverse algorithm as compared to the same quantity computed with a forward algorithm. This work generalizes the Log-Elastographic algorithm in [20] which uses one displacement component, is derived assuming the component satisfies the wave equation, and is tested on synthetic data computed with the wave equation model. The 2D Log-Elastographic algorithm is tested on 2D synthetic data and 2D in-vivo data from Mayo Clinic. We also exhibit examples to show that the 2D Log-Elastographic algorithm improves the quality of the recovered images as compared to the Log-Elastographic and Direct Inversion algorithms.

1. Introduction

Shear modulus imaging, often called elastography, is a non-invasive new medical imaging technology that targets detection or classification of tissue abnormalities, such as cancer or fibrotic tissue. Shear modulus contrast between normal tissue and abnormal tissue is high with ratios of two or (much) more being common, enabling high resolution images of tissue changes. The expectation is to identify and classify tissue abnormalities and to corroborate with ultrasound or MR images enhancing medical diagnosis by imaging the elastic properties of the tissue.

The first step toward making a shear modulus image is to obtain tissue displacement data. To achieve this data, a broad range of experiments have been developed to displace the tissue. These experiments are: (1) static experiment, e.g. see [38] and [45]; (2) dynamic sinusoidal excitation, e.g. see [6], [16], [18], [21], [22], [23], [29], [48], [51]; (3) acoustic radiation force localized impulse, e.g. see [11], [32], [33]; and (4) impulsive line source as in transient elastography and supersonic imaging, e.g. see [2], [3], [4], [5], [7], [15], [19], [43] and [44]. In each of these procedures an external or internal stimulus is applied to mechanically excite the region of interest. Then a movie of the interior displacement response is created from successive ultrasound or MR datasets. The movie of the interior displacement is then the data used to create biomechanical property images. The displacement represented in these movies is on the order of tens of microns. Once the movie is created, an inversion algorithm is developed to obtain tissue shear wave speed or shear modulus images.

The information in these movies can be utilized in a number of different ways. In [26] and [27], the authors developed the Arrival Time algorithm for the transient elastography experiment and supersonic imaging to recover the shear wave speed. There the data is not single frequency content but the arrival time of a propagating front at each point of the image plane. They first use a cross-correlation technique to find the arrival time surface from the displacement data. The arrival time surface satisfies the Eikonal equation. They then apply either the distance method or the level set method to solve the inverse Eikonal equation to find the wave speed. This new technique has also been successfully used in the crawling wave experiment, see [29] and [30].

In this paper, we will focus on using a single frequency content that can be extracted from the time dependent movie data obtained when the tissue is dynamically displaced either with a sinusoidal excitation or a transient pulse. Because the displacement deformations are small, the mathematical model we use for describing the tissue response during these experiments is a linear elastic equation system.

To reconstruct and image the shear wave speed or the shear modulus from single frequency content, different inversion methods have been developed. An often used method is the so-called Direct Inversion method, where a locally constant assumption on the Lamé parameters is made. In this Direct Inversion Method, the divergence of the displacement is set to zero. The elastic equation system is decoupled and reduced to a system of Helmholtz equations; each equation contains no derivatives of the shear modulus, and is for a single displacement component. The shear modulus can then be recovered through a simple algebraic inversion, see [2], [3], [4], [21], [22], [23], [24], [28], [36], [37] and [44]. This approach is very straightforward to implement. Some good reconstruction results have also been obtained. However, the locally constant assumption on the shear modulus may introduce a level of inaccuracy, especially in the regions near the boundary of stiff inclusions. We will make comparisons with this method in a later section of this paper.

Another kind of direct inversion method, see [46] and [47], is to take curl of the elastic equation system first, and then neglect all the derivatives of the shear modulus. Therefore, in this case, the reconstruction is also based on a single equation. The disadvantage of this method is that third-order spatial derivatives of the displacement data are introduced by taking curl and the locally constant assumption that eliminates all terms that contain derivatives of the shear modulus is also required here. We do not make comparison with this method; see [53] (p.107) for some of our comparison with this direct inversion method.

In [20], the authors develop two inverse algorithms: (1) an acoustic Log-Elastographic nonlinear marching scheme; and (2) a linear finite difference based elliptic scheme. There, inverse algorithms are derived assuming a single displacement component satisfies a Helmholtz equation with real parameters; derivatives of the shear modulus are included. The algorithms are tested on the Fourier Transform of synthetic data computed with a wave equation model. The authors show that both methods are convergent and stable of first order and do not require a very fine discretization to succeed.

Besides the above methods, other algorithms have also been developed. Some are based on finite element methods including iterative methods, [9], [34], [35], [49] and [50], and non-iterative methods [39]. The finite element based iterative methods use the full elastic equation system and the goal is to find the elastic modulus that minimizes the difference between the computed and measured displacements in a least squares sense. Because they require the full forward calculation and contain iterations, all the iterative methods are time-consuming. In [39], the authors developed a non-iterative finite element based method. Their method is also based on the full elastic equation system. There they use the weak form of the elastic system, and then only the first order derivatives of the measured displacement data are calculated. They then solve the remaining system for the shear modulus and pressure with the finite element method.

Another non-iterative variational method, that has similarities with the Direct Inversion Method in that it neglects derivatives of the shear modulus, is developed in [40] and [41]. This non-iterative variational method is obtained by integrating the weak form of the elastic system by parts twice, and hence avoids taking derivatives of the measured displacements; however all derivatives of the shear modulus are neglected.

In this paper, we focus on using two displacement components, u = (u₁, u₂), as a basis for our inverse problem with the assumption that they satisfy the 2D plane strain elastic equation system. The data is then the two in-plane displacement components in a single plane. The 2D plane strain elastic system contains the hydrostatic pressure term, p = λ∇ · u, where λ is the first Lamé parameter. Tissue is nearly incompressible so the term ∇ · u ≪ 1; the noise in measured data makes the computation of the value of this term unreliable; furthermore the first Lamé parameter, λ ≫ 1. The product p = λ∇ · u is, then, unreliably computed from measured data whether or not λ is known. The hydrostatic pressure, p, can be computed with a forward algorithm to show that, for an inhomogeneous medium, p is approximately first order and should not be ignored. Therefore, in this paper we develop a finite difference based 2D Log-Elastographic inverse method to reconstruct a real shear modulus and the hydrostatic pressure with two components of the measured displacement data. We will employ a few of the ideas already used in the Log-Elastographic algorithm or in the fluid dynamics paper, [14]; however the application is not a straightforward use of those ideas when our model is a first order p.d.e. system for the shear modulus and the pressure partly because the pressure does not have fixed sign and partly because the operations, log and exponential, used to create the algorithm are nonlinear. Since we solve a first order p.d.e. system, we must select good approximate values for the boundary conditions for the shear modulus. These boundary conditions are usually not known from measurements. Inspired by the estimate given in [20], we make our choice from one of the available direct inversion results. We compare our reconstructions, when the shear modulus is real, with those obtained by: (1) the Direct Inversion method; and (2) the Log-Elastographic method which uses only one displacement component. For these comparisons we use displacement components computed with a 2D plane strain model.

We also initiate a method for reconstructing a complex shear modulus from two in-plane displacement components. We test this method on measured data obtained from Mayo Clinic.

The remainder of this paper is composed as follows. The mathematical model for the forward and inverse problem is given in Section 2. Section 3 briefly discusses the Direct Inversion method. Then, the 2D Log-Elastographic algorithm for elastography is presented in Section 4. Next in Section 5, this new algorithm is tested on synthetic data and experimental data.

2. The Mathematical Model: Forward and Inverse Problem

Our target here is an appropriate 2D approximate model when our data is movies of two displacement components in a single image plane. The medium is inherently 3D and is assumed to be heterogeneous, isotropic and nearly incompressible. The 3D mathematical model for these kinds of problems is based on the 3D linear hyperbolic elastic system:

$$\rho {\mathbf{u}}_{tt}=\nabla (\lambda \nabla ·\mathbf{u})+\nabla ·(\mu (\nabla \mathbf{u}+\nabla {\mathbf{u}}^{\mathrm{T}}))+\mathbf{f}$$ (1)

where u is the 3D displacement vector, μ = μ(x₁, x₂, x₃), is the shear modulus, or second Lamé parameter, ρ is the density, which for tissue being imaged is usually assumed to be constant although it can vary as much as 10%. λ is the first Lamé parameter, and f is a source interior to the material. We assume that either there is an impulsive force (force that acts for a very short time in a localized region), with a central frequency, ω_c, or there is a single frequency, ω_c, excitation.

If we let p = λ∇ · u = λ(u_1,1 + u_2,2 + u_3,3), the elastic system becomes

$$\rho {\mathbf{u}}_{tt}=\nabla p+\nabla ·(\mu (\nabla \mathbf{u}+\nabla {\mathbf{u}}^{\mathrm{T}}))+\mathbf{f}.$$ (2)

Note that p is essentially the hydrostatic stress, or the pressure. To simplify our notation, we divide both sides of equation (2) by ρ, assumed here to be constant as mentioned above, and make the following notation: μ̃ = μ/ρ, p̃ = p/ρ, and f̃ = f/ρ, so that our model for the forward problem is: given (λ/ρ)(x₁, x₂, x₃), μ̃(x₁, x₂, x₃), f̃(x₁, x₂, x₃, t), find the 3D displacement vector u(x₁, x₂, x₃, t) and the scaled pressure p̃(x₁, x₂, x₃, t) which satisfy

$${\mathbf{u}}_{tt}=\nabla \tilde{p}+\nabla ·(\tilde{\mu }(\nabla \mathbf{u}+\nabla {\mathbf{u}}^{\mathrm{T}}))+\tilde{\mathbf{f}},$$ (3)

$$\tilde{p}=(\lambda /\rho )\nabla ·\mathbf{u},$$ (4)

together with the initial and boundary conditions.

To obtain the 2D model, there are basically two possible choices, the plane stress model or the plane strain model. Neither is completely satisfactory. A full discussion of the implications of these two choices is beyond the scope of this paper. We only comment that the plane stress assumption is more often used for thin materials. Here we use the plane strain model where the choice is driven by the lack of data in parallel image planes. The assumptions then are that the elements ε_i3 = 0, for i = 1, 2, 3, where ${\epsilon }_{ij}=\frac{1}{2}(u_{i,j}+u_{j,i})$ is the strain matrix. That is,

$$u_{1,3}+u_{3,1}=0,u_{2,3}+u_{3,2}=0,\text{\hspace{1em}and\hspace{1em}}{u}_{3,3}=0.$$

In addition, in the plane strain assumption, we ignore the third equation $\rho u_{3,tt}=\frac{\partial }{\partial z}(\lambda (u_{1,1}+u_{2,2}))+f_3$. Hence we obtain a system that can also be written as (3)–(4) if we use the notation that u is now the 2D displacement and p̃ is the scaled pressure, p̃ = p̃(x₁, x₂, t).

In the 2D forward problem, we are given (λ/ρ)(x₁, x₂), μ̃(x₁, x₂), f̃(x₁, x₂, t), together with initial and boundary conditions, and the goal is to find u(x₁, x₂, t) and p̃(x₁, x₂, t).

In the inverse problem, the 2D displacement vector u = u(x₁, x₂, t) is given and f̃ = f̃(x₁, x₂, t) is given. The goal is to solve the 2D elastic system (3) for the scaled shear modulus μ̃. In our formulation of the inverse problem, we add the additional goal of finding p̃ as even when it is assumed that λ/ρ is given the product (λ/ρ)∇ · û is unreliably computed with measured data as described in the introduction. In this paper, we will focus on the inverse problem and use the Fourier Transform û(x₁, x₂, ω) of u, evaluated at the central frequency, ω_c, where û has significant amplitude, or the frequency of excitation which we also refer to as ω_c.

Taking the Fourier transform in time of the system (3), we arrive at the following Fourier transformed system at a single frequency, where û, $\hat{\tilde{p}}$, and $\widehat{\tilde{\mathbf{f}}}$ are the transformed u, p̃, and f̃,

$$\nabla ·(\tilde{\mu }(\nabla \hat{\mathbf{u}}+\nabla {\hat{\mathbf{u}}}^{\mathrm{T}}))+{\omega }_c^2\hat{\mathbf{u}}+\nabla \hat{\tilde{p}}+\widehat{\tilde{\mathbf{f}}}=\mathbf{0}.$$ (5)

For the reasons above, we do not use equation (4) or its transform. In this paper, our main objective is to solve the equation system (5) simultaneously for the scaled shear modulus μ̃ and the scaled pressure $\hat{\tilde{p}}$ given the 2D displacements u throughout the image plane. A 2D Log-Elastographic method will be presented to solve this equation system for μ̃ and $\hat{\tilde{p}}$. This method utilizes finite difference approximations of derivatives of μ̃ and $\hat{\tilde{p}}$.

We will show that computing $\hat{\tilde{p}}$ simultaneously with μ̃, as opposed to setting $\hat{\tilde{p}}=0$, significantly improves the accuracy in our reconstruction of μ̃. Note also that it can be difficult to reconstruct $\hat{\tilde{p}}$ accurately, see [39], in an inverse algorithm, and this inaccuracy may effect the shear modulus reconstructions. We show that with the 2D Log-Elastographic algorithm we obtain good agreement between the $\hat{\tilde{p}}$ recovered with the inverse algorithm and the $\hat{\tilde{p}}$ simulated with the forward algorithm.

All of our synthetic examples are for real μ̃. We will image our reconstruction of μ̃ which is the square of the shear wave speed when μ̃ is real. For our in-vivo data, a more accurate model includes a viscoelastic term. For example we could use a linear solid model which is

$$\begin{array}{c}\rho {\mathbf{u}}_{tt}=\nabla ·\sigma \prime +\nabla p+\mathbf{f}\hfill \\ p=\lambda \nabla ·\mathbf{u}\hfill \end{array}$$ (6)

where

$$\sigma \prime =2{\mu }_0{\epsilon }_{ij}+{\mu }_1{\displaystyle {\int }_{t_0}^t{e}^{-(t-t\prime )/{\tau }_1}}\frac{d}{dt\prime }(2{\epsilon }_{ij})dt\prime ;$$

μ₀, μ₁, τ₁ depend on x, y, and τ₁ is the relaxation time. When we take a Fourier transform in time for this model we obtain equation (5) again with the property that here, for this model,

$$\tilde{\mu }=\text{Re}\tilde{\mu }+i\text{Im}\tilde{\mu }=\frac{{\mu }_0+{\mu }_1}{\rho }-\frac{{\mu }_1}{\rho (1+{\omega }^2{\tau }_1^2)}+i\frac{{\mu }_1\omega {\tau }_1}{\rho (1+{\omega }^2{\tau }_1^2)},$$

which is a complex quantity. The coefficients η₁ = τ₁μ₁, μ₁ are the viscosity and elasticity, respectively, of a Maxwell body, i.e., the coefficients corresponding to the dashpot and spring element. The coefficient μ₀ is the coefficient for the spring element that is parallel to the Maxwell element ([12]). In the linear solid model, our algorithm computes complex valued μ̃; we image the real quantities,

$$c_s^2={(\text{Re}\sqrt{1/\tilde{\mu }})}^{-2},\alpha =-\omega \text{Im}\sqrt{1/\tilde{\mu }}$$ (7)

with in-vivo data. The biomechanical properties, (7), are the square of the shear wave speed and the attenuation, respectively, for a plane wave propagating in a homogeneous viscoelastic medium modeled by (6), see [13].

3. Direct Inversion Method in Elastography

Before we present the 2D Log-Elastographic Method, we first briefly explain the Direct Inversion Method for computing the shear modulus when a single displacement component satisfies a Helmholtz equation. In later sections, we will compare the shear modulus obtained by the 2D Log-Elastographic method with the shear modulus obtained from this method. This comparison is not the same as the comparison given in [20] as here our model for the forward algorithm is a 2D plane strain elastic system. By comparison, in [20], the simulated data is based on a wave equation model.

In the Direct Inversion Method, the shear modulus is assumed to be locally constant, and hence all the terms including the derivatives of the shear modulus are neglected. Furthermore, ∇ · u is assumed to be identically zero. With these assumptions, the 2D elastic system can be decoupled. After taking the Fourier transform in time, a Helmholtz equation is obtained at single frequency as follows:

$$\hat{\mu }\mathrm{\Delta }\hat{u}+{\omega }^2\hat{u}=0$$ (8)

where û is the Fourier transform of any single component of the displacement vector û. Note that we denote the Direct Inversion approximation of μ̃ by μ̂. The method then is to solve this algebraic equation for the approximate scaled shear modulus μ̂. The frequency, ω, is usually chosen to be the central frequency, ω_c.

4. 2D Log-Elastographic Algorithm for Elastography

In this section we consider the 2D system (5). We develop a 2D Log-Elastographic algorithm to recover a real scaled shear modulus and the scaled pressure with the given 2D displacement data using an equation system based on system (5). We show that this algorithm effectively controls the exponential growth in the error of the numerical solution without a fine grid requirement. To begin, we rewrite system (5) as

$$\begin{array}{cc}-{\omega }_c^2\hat{\mathbf{u}}\hfill & =\nabla ·(\tilde{\mu }(\nabla \hat{\mathbf{u}}+{(\nabla \hat{\mathbf{u}})}^{\mathrm{T}}))+\nabla \hat{\tilde{p}}\hfill \\ \hfill & =\tilde{\mu }\mathrm{\Delta }\hat{\mathbf{u}}+\tilde{\mu }\nabla (\nabla ·\hat{\mathbf{u}})+\nabla \tilde{\mu }·(\nabla \hat{\mathbf{u}}+{(\nabla \hat{\mathbf{u}})}^{\mathrm{T}})+\nabla \hat{\tilde{p}}\hfill \end{array}$$ (9)

where we have set $\widehat{\tilde{\mathbf{f}}}\equiv 0$ as our imaging domain usually does not contain the source location. Note that (9) contains the term μ̃∇(∇ · û) and as ∇ · û ≪ 1, and μ̃ generally satisfies 1 ≤ μ̃ ≤ 20 in units m²/s², the term μ̃∇(∇ · û) is generally very small. Hence we will consider two cases: (1) where we eliminate μ̃∇(∇ · û), and (2) where we keep μ̃∇(∇ · û). We compare the reconstructions with simulated data where we can accurately compute ∇(∇ · û), and exhibit that the difference is small. We are motivated to establish this result with simulated data since, as mentioned in the introduction, this term is unreliably computed with measured data due to noise in that data.

Before developing our algorithm we give examples in Subsection 4.1 to show that when μ̃ is real, we can have exponential growth in the numerical error and when μ̃ is complex valued the exponential growth can be arbitrarily large.

4.1. Exponentially Growth in the First Order P.D.E. System: Examples

To exhibit the exponential growth we look at the canonical form of a homogeneous first order system. Let v̂ be the solution of

$${\hat{\mathbf{v}}}_{,1}+{\hat{E}}^1{\hat{\mathbf{v}}}_{,2}+{\hat{E}}^2\hat{\mathbf{v}}=\mathbf{0}$$ (10)

where for purposes of the example we assume the matrices ʹ, ʲ are constants. Then consider a solution of the form v̂ = ŵ(x₁)e^inx₂. Therefore ŵ(x₁) satisfies

$${\hat{\mathbf{w}}}_{,1}+\mathit{\text{in}}{\hat{E}}^1\hat{\mathbf{w}}+{\hat{E}}^2\hat{\mathbf{w}}=\mathbf{0}$$ (11)

Suppose ʹ is diagonalizable and the associated eigenvector matrix, Ŝ, yields Ŝʹ Ŝ⁻¹ = D, a diagonal matrix of the eigenvalues. Then $\hat{S}\hat{\mathbf{w}}=\widehat{\hat{\mathbf{w}}}$ satisfies

$${\widehat{\hat{\mathbf{w}}}}_{,1}+(\mathit{\text{in}}D+\hat{S}{\hat{E}}^2)\widehat{\hat{\mathbf{w}}}=\mathbf{0}$$ (12)

The solution can be represented by

$$\widehat{\hat{\mathbf{w}}}(x_1)=\widehat{\hat{\mathbf{w}}}(0)e^{-(\mathit{\text{in}}D+\hat{S}{\hat{E}}^2)x_1}.$$

If D has real eigenvalues, $\widehat{\hat{\mathbf{w}}}$ can have exponential growth if −Ŝʲ has at least one eigenvalue with positive real part. If this occurs we can have exponential growth but not of arbitrarily high order. To control the corresponding exponentially growing numerical error, a very small discretization, which is not the CFL condition, may be needed when a standard upwind or stable central difference scheme [8] are used.

If D has complex eigenvalues with at least one eigenvalue, $\hat{\hat{\lambda }}$, with positive imaginary part then $\widehat{\hat{\mathbf{w}}}$ grows exponentially of order $e^{n\hat{\hat{\lambda }}}$. As n can be arbitrarily large we can obtain arbitrarily large exponential error in our computed solution.

This example inspires our 2D Log-Elastographic algorithm. We develop the main ideas under the assumption that ʹ has real eigenvalues and test them when μ̃ is real. Then we propose a change in the algorithm for the case when ʹ has complex eigenvalues and apply this latter algorithm to in-vivo data where μ̃ is expected to be complex valued.

Note that these examples are not the same as those given in [14].

4.2. Case 1: Neglect the μ̃∇(∇ · û) Term

If we neglect the μ̃∇(∇ · û) term from system (9) we arrive at

$$\tilde{\mu }\mathrm{\Delta }\hat{\mathbf{u}}+\nabla \tilde{\mu }·(\nabla \hat{\mathbf{u}}+{(\nabla \hat{\mathbf{u}})}^{\mathrm{T}})+\nabla \hat{\tilde{p}}+{\omega }_c^2\hat{\mathbf{u}}=\mathbf{0}.$$ (13)

To see the structure of this first order system of equations, we rewrite it as the following equation system in matrix form

$$\left(\begin{array}{cc}\hfill 2{\hat{u}}_{1,1}\hfill & \hfill 1\hfill \\ \hfill {\hat{u}}_{2,1}+{\hat{u}}_{1,2}\hfill & \hfill 0\hfill \end{array}\right)\left(\begin{array}{c}\hfill {\tilde{u}}_{,1}\hfill \\ \hfill {\hat{\tilde{p}}}_{,1}\hfill \end{array}\right)+\left(\begin{array}{cc}\hfill {\hat{u}}_{1,2}+{\hat{u}}_{2,1}\hfill & \hfill 0\hfill \\ \hfill 2{\hat{u}}_{2,2}\hfill & \hfill 1\hfill \end{array}\right)\left(\begin{array}{c}\hfill {\tilde{\mu }}_{,2}\hfill \\ \hfill {\hat{\tilde{p}}}_{,2}\hfill \end{array}\right)+\left(\begin{array}{cc}\hfill \mathrm{\Delta }{\hat{u}}_1\hfill & \hfill 0\hfill \\ \hfill \mathrm{\Delta }{\hat{u}}_2\hfill & \hfill 0\hfill \end{array}\right)\left(\begin{array}{c}\hfill \tilde{\mu }\hfill \\ \hfill \hat{\tilde{p}}\hfill \end{array}\right)+{\omega }_c^2\left(\begin{array}{c}\hfill {\hat{u}}_1\hfill \\ \hfill {\hat{u}}_2\hfill \end{array}\right)=\mathbf{0}.$$ (14)

Denoting

$$\mathbf{v}≔\left(\begin{array}{c}\tilde{\mu }\\ \hfill \hat{\tilde{p}}\hfill \end{array}\right),A≔\left(\begin{array}{cc}\hfill 2{\hat{u}}_{1,1}\hfill & \hfill 1\hfill \\ \hfill {\hat{u}}_{2,1}+{\hat{u}}_{1,2}\hfill & \hfill 0\hfill \end{array}\right),\text{then}{A}^{-1}=\left(\begin{array}{cc}\hfill 0\hfill & \hfill \frac{1}{{\hat{u}}_{2,1}+{\hat{u}}_{1,2}}\hfill \\ \hfill 1\hfill & \hfill -\frac{2{\hat{u}}_{1,1}}{{\hat{u}}_{2,1}+{\hat{u}}_{1,2}}\hfill \end{array}\right).$$

Multiplying A⁻¹ on both sides of (14), we obtain another system of first order equations of the form

$${\mathbf{v}}_{,1}+E^1{\mathbf{v}}_{,2}+E^2\mathbf{v}+{\mathbf{E}}^3=\mathbf{0}$$ (15)

where

$$E^1=\left(\begin{array}{cc}\hfill \frac{2{\hat{u}}_{2,2}}{{\hat{u}}_{2,1}+{\hat{u}}_{1,2}}\hfill & \hfill \frac{1}{{\hat{u}}_{2,1}+{\hat{u}}_{1,2}}\hfill \\ \hfill {\hat{u}}_{2,1}+{\hat{u}}_{1,2}-\frac{4{\hat{u}}_{1,1}{\hat{u}}_{2,2}}{{\hat{u}}_{2,1}+{\hat{u}}_{1,2}}\hfill & \hfill -\frac{2{\hat{u}}_{1,1}}{{\hat{u}}_{2,1}+{\hat{u}}_{1,2}}\hfill \end{array}\right),E^2=\left(\begin{array}{cc}\hfill \frac{\mathrm{\Delta }{\hat{u}}_2}{{\hat{u}}_{2,1}+{\hat{u}}_{1,2}}\hfill & \hfill 0\hfill \\ \hfill \mathrm{\Delta }{\hat{u}}_1-\frac{2{\hat{u}}_{1,1}}{{\hat{u}}_{2,1}+{\hat{u}}_{1,2}}\mathrm{\Delta }{\hat{u}}_2\hfill & \hfill 0\hfill \end{array}\right),\text{and}{\mathbf{E}}^3=\left(\begin{array}{c}\hfill \frac{{\omega }_c^2{\hat{u}}_2}{{\hat{u}}_{2,1}+{\hat{u}}_{1,2}}\hfill \\ \hfill {\omega }_c^2{\hat{u}}_1-\frac{2{\omega }_c^2{\hat{u}}_2{\hat{u}}_{1,1}}{{\hat{u}}_{2,1}+{\hat{u}}_{1,2}}\hfill \end{array}\right).$$

Here, to obtain the linear system (15), we have assumed that the complex quantity û_2,1 + û_1,2 ≠ 0 which is almost always satisfied. With this assumption, we can interpret, for the purpose of solving the first order p.d.e. system (15) with a marching method, that the x direction is a time-like direction. In keeping with this interpretation we assume that v(0, x₂) is known. Later in this paper we will address how to get good approximations for v(0, x2). We also select one of the components û₁ or û₂ of û, which we call the leading component. Usually it is the component that is larger, e.g. the component orthogonal to the direction of propagation.

To develop this algorithm, we first rewrite system (15) back in scalar form as

$${\tilde{\mu }}_{,1}+E^1(1,1){\tilde{\mu }}_{,2}+E^1(1,2){\hat{\tilde{p}}}_{,2}+E^2(1,1)\tilde{\mu }+{\mathbf{E}}^3(1)=0$$ (16)

$${\hat{\tilde{p}}}_{,1}+E^1(2,1){\tilde{\mu }}_{,2}+E^1(2,2){\hat{\tilde{p}}}_{,2}+E^2(2,1)\tilde{\mu }+{\mathbf{E}}^3(2)=0$$ (17)

where E^k(i, j) is the component of matrix E^k at i^th row and j^th column, k = 1, 2, and E³(j) is the j^th component of the vector E³. Next for our first step we divide equation (16) by μ̃, and introduce a new variable υ = log μ̃, where we note that for our targeted υ the values are always positive since for our application requirement μ̃ ≥ 1 m²/s². Then equations (16) and (17) become, in the variables υ, $\hat{\tilde{p}}$,

$${\upsilon }_{,1}+E^1(1,1){\upsilon }_{,2}+E^1(1,2){\hat{\tilde{p}}}_{,2}{e}^{-\upsilon }+E^2(1,1)+{\mathbf{E}}^3(1)e^{-\upsilon }=0$$ (18)

$${\hat{\tilde{p}}}_{,1}+E^1(2,1)e^{\upsilon }{\upsilon }_{,2}+E^1(2,2){\hat{\tilde{p}}}_{,2}+E^2(2,1)e^{\upsilon }+{\mathbf{E}}^3(2)=0.$$ (19)

Note that at this intermediate step it appears that in the new variable, υ, we have an exponentially growing term, e^υ. This term will not be present in the final form of the algorithm.

Now we have a coupled system for υ and $\hat{\tilde{p}}$. The first step is to discretize (18) and (19) with the standard upwind scheme. Writing (18) and (19) in system form designating $\left(\begin{array}{c}\hfill \upsilon \hfill \\ \hfill \hat{\tilde{p}}\hfill \end{array}\right)=\mathbf{w}$, we obtain

$${\mathbf{w}}_{,1}+{\tilde{E}}^1{\mathbf{w}}_{,2}+{\tilde{\mathbf{E}}}^3=\mathbf{0}$$ (20)

where

$$\begin{array}{c}{\tilde{E}}^1=\left(\begin{array}{cc}\hfill \frac{2{\hat{u}}_{2,2}}{{\hat{u}}_{2,1}+{\hat{u}}_{1,2}}\hfill & \hfill \frac{1}{({\hat{u}}_{2,1}+{\hat{u}}_{1,2})e^{\upsilon }}\hfill \\ \hfill ({\hat{u}}_{2,1}+{\hat{u}}_{1,2})e^{\upsilon }-\frac{4{\hat{u}}_{1,1}{\hat{u}}_{2,1}{e}^{\upsilon }}{{\hat{u}}_{2,1}+{\hat{u}}_{1,2}}\hfill & \hfill -\frac{2{\hat{u}}_{1,1}}{{\hat{u}}_{2,1}+{\hat{u}}_{1,2}}\hfill \end{array}\right),\hfill \\ {\tilde{\mathbf{E}}}^3=\left(\begin{array}{c}\hfill \frac{\mathrm{\Delta }{\hat{u}}_2}{{\hat{u}}_{2,1}+{\hat{u}}_{1,2}}+\frac{{\omega }_c^2{\hat{u}}_2}{({\hat{u}}_{2,1}+{\hat{u}}_{1,2})e^{\upsilon }}\hfill \\ \hfill \mathrm{\Delta }{\hat{u}}_1{e}^{\upsilon }-\frac{2{\hat{u}}_{1,1}{e}^{\upsilon }}{{\hat{u}}_{2,1}+{\hat{u}}_{1,2}}\mathrm{\Delta }{\hat{u}}_2+{\omega }_c^2{\hat{u}}_1-\frac{2{\omega }_c^2{\hat{u}}_2{\hat{u}}_{1,1}}{{\hat{u}}_{2,1}+{\hat{u}}_{1,2}}\hfill \end{array}\right)\hfill \end{array}$$ (21)

both depend nonlinearly on υ. We assume that the eigenvalues of Ẽ¹ are real.

Our first step in case 1 is to apply the standard upwind scheme, [25] (p. 417–421), to discretize (20) and obtain

$${\mathbf{W}}_{i+1,j}={\mathbf{W}}_{i,j}-\frac{\mathrm{\Delta }x}{\mathrm{\Delta }y}({\tilde{E}}_{i,j}^{1,+}({\mathbf{W}}_{i,j}-{\mathbf{W}}_{i,j-1})+{\tilde{E}}_{i,j}^{1,-}({\mathbf{W}}_{i,j+1}-{\mathbf{W}}_{i,j}))-\mathrm{\Delta }x{\tilde{\mathbf{E}}}_{i,j}^3$$ (22)

where ${\mathbf{W}}_{i,j},{\tilde{E}}_{i,j}^{1,\pm },{\tilde{\mathbf{E}}}_{i,j}^3$ are the approximated values of w, Ẽ^1,±, Ẽ³, respectively, at the point (iΔx, jΔy), and W_0,j are the discretized values of the known initial conditions. Here, we decide the finite difference approximation direction according to the sign of the eigenvalues of the coefficient matrix Ẽ¹. We write Ẽ¹ as Ẽ¹ = Ẽ^1,+ + Ẽ^1,−, where Ẽ^1,+ = S̃Λ⁺S̃⁻¹ and Ẽ^1,− = S̃Λ⁻S̃⁻¹. The symbol Λ⁺ has all the nonnegative eigenvalues of Ẽ¹ on its diagonal, Λ⁻ has all the negative eigenvalues of Ẽ¹ on its diagonal, and S̃ is the eigenvector matrix. This discretization appears to require that at each step we need to recalculate the eigenvalues and eigenvectors of Ẽ¹, which contains the computed value of υ. To avoid this extra calculation which can lead to additional inaccuracies, we establish relationships between the matrix E¹ in (15) and the matrix Ẽ¹ in (20) and between E^1,± and Ẽ^1,±.

We write

$$E^1=\left(\begin{array}{cc}\hfill \frac{2{\hat{u}}_{2,2}}{{\hat{u}}_{2,1}+{\hat{u}}_{1,2}}\hfill & \hfill \frac{1}{{\hat{u}}_{2,1}+{\hat{u}}_{1,2}}\hfill \\ \hfill {\hat{u}}_{2,1}+{\hat{u}}_{1,2}-\frac{4{\hat{u}}_{1,1}{\hat{u}}_{2,2}}{{\hat{u}}_{2,1}+{\hat{u}}_{1,2}}\hfill & \hfill -\frac{2{\hat{u}}_{1,1}}{{\hat{u}}_{2,1}+{\hat{u}}_{1,2}}\hfill \end{array}\right)\text{as}\left(\begin{array}{cc}\hfill a\hfill & \hfill b\hfill \\ \hfill c\hfill & \hfill d\hfill \end{array}\right)$$ (23)

in its undiscretized form and assume the eigenvalues of E¹ are λ₁ and λ₂. λ₁ denotes the nonnegative eigenvalue and λ₂ denotes the negative eigenvalue when they have opposite signs. It is then straightforward to establish that the eigenvector matrix S of E¹ together with its inverse matrix S⁻¹ can be expressed as

$$S=\left(\begin{array}{cc}\hfill b\hfill & \hfill {\lambda }_2-d\hfill \\ \hfill {\lambda }_1-a\hfill & \hfill c\hfill \end{array}\right),S^{-1}=\frac{1}{\alpha }\left(\begin{array}{cc}\hfill c\hfill & \hfill d-{\lambda }_2\hfill \\ \hfill a-{\lambda }_1\hfill & \hfill b\hfill \end{array}\right),$$

where α = bc − λ₁λ₂ + aλ₂ + dλ₁ − ad. And hence

$$\begin{array}{c}{E}^{1,+}=S{\mathrm{\Lambda }}^{+}{S}^{-1}=\frac{1}{\alpha }\left(\begin{array}{cc}\hfill bc{\lambda }_1\hfill & \hfill b{\lambda }_1(d-{\lambda }_2)\hfill \\ \hfill {\lambda }_1({\lambda }_1-a)c\hfill & \hfill {\lambda }_1({\lambda }_1-a)(d-{\lambda }_2)\hfill \end{array}\right),\hfill \\ E^{1,-}=S{\mathrm{\Lambda }}^{-}{S}^{-1}=\frac{1}{\alpha }\left(\begin{array}{cc}\hfill {\lambda }_2({\lambda }_2-d)(a-{\lambda }_1)\hfill & \hfill b{\lambda }_2({\lambda }_2-d)\hfill \\ \hfill {\lambda }_2(a-{\lambda }_1)c\hfill & \hfill bc{\lambda }_2\hfill \end{array}\right).\hfill \end{array}$$ (24)

Note that when the eigenvalues are both positive (negative), then E^1,− (or E^1,+) is zero and E^1,+ = E¹ (or E^1,− = E¹).

From (21) and (23) we have that

$$\begin{array}{c}{\tilde{E}}^1(1,1)=E^1(1,1),{\tilde{E}}^1(1,2)=E^1(1,2)e^{-\upsilon },\hfill \\ {\tilde{E}}^1(2,1)=E^1(2,1)e^{\upsilon },{\tilde{E}}^1(2,2)=E^1(2,2).\hfill \end{array}$$

A straightforward calculation yields that E¹ and Ẽ¹ have the same eigenvalues and that the eigenvector matrix S̃ of Ẽ¹ and its inverse (S̃)⁻¹ are

$$\tilde{S}=\left(\begin{array}{cc}\hfill b/e^{\upsilon }\hfill & \hfill {\lambda }_2-d\hfill \\ \hfill {\lambda }_1-a\hfill & \hfill c{e}^{\upsilon }\hfill \end{array}\right),{(\tilde{S})}^{-1}=\frac{1}{\alpha }\left(\begin{array}{cc}\hfill c{e}^{\upsilon }\hfill & \hfill d-{\lambda }_2\hfill \\ \hfill a-{\lambda }_1\hfill & \hfill b/e^{\upsilon }\hfill \end{array}\right).$$

So we can write

$$\begin{array}{c}{\tilde{E}}^{1,+}=\tilde{S}{\mathrm{\Lambda }}^{+}{(\tilde{S})}^{-1}=\frac{1}{\alpha }\left(\begin{array}{cc}\hfill bc{\lambda }_1\hfill & \hfill \frac{b}{e^{\upsilon }}{\lambda }_1(d-{\lambda }_2)\hfill \\ \hfill {\lambda }_1({\lambda }_1-a)c{e}^{\upsilon }\hfill & \hfill {\lambda }_1({\lambda }_1-a)(d-{\lambda }_2)\hfill \end{array}\right),\hfill \\ {\tilde{E}}^{1,-}=\tilde{S}{\mathrm{\Lambda }}^{-}{(\tilde{S})}^{-1}=\frac{1}{\alpha }\left(\begin{array}{cc}\hfill {\lambda }_2({\lambda }_2-d)(a-{\lambda }_1)\hfill & \hfill \frac{b}{e^{\upsilon }}{\lambda }_2({\lambda }_2-d)\hfill \\ \hfill {\lambda }_2(a-{\lambda }_1)c{e}^{\upsilon }\hfill & \hfill bc{\lambda }_2\hfill \end{array}\right).\hfill \end{array}$$ (25)

So the following relationships between the components of E^1,± and the components of Ẽ^1,± hold:

$$\begin{array}{c}{\tilde{E}}^{1,\pm }(1,1)=E^{1,\pm }(1,1),{\tilde{E}}^{1,\pm }(1,2)=E^{1,\pm }(1,2)e^{-\upsilon },\hfill \\ {\tilde{E}}^{1,\pm }(2,1)=E^{1,\pm }(2,1)e^{\upsilon },{\tilde{E}}^{1,\pm }(2,2)=E^{1,\pm }(2,2).\hfill \end{array}$$

Because the above relationships are either linear in e^υ or e^−υ, we can then write the standard upwind scheme for (20) as follows

$${\tilde{\upsilon }}_{i+1,j}={\tilde{\upsilon }}_{i,j}-\frac{\mathrm{\Delta }x}{\mathrm{\Delta }y}(E_{i,j}^{1,+}(1,1)({\tilde{\upsilon }}_{i,j}-{\tilde{\upsilon }}_{i,j-1})+E_{i,j}^{1,+}(1,2)({\tilde{\tilde{p}}}_{i,j}-{\tilde{\tilde{p}}}_{i,j-1})e_{i,j}^{-\tilde{\upsilon }}+E_{i,j}^{1,-}(1,1)({\tilde{\upsilon }}_{i,j+1}-{\tilde{\upsilon }}_{i,j})+E_{i,j}^{1,-}(1,2)({\tilde{\tilde{p}}}_{i,j+1}-{\tilde{\tilde{p}}}_{i,j})e^{-{\tilde{\upsilon }}_{i,j}})-\mathrm{\Delta }x{\tilde{\mathbf{E}}}_{i,j}^3(1)$$ (26)

$${\tilde{\tilde{p}}}_{i+1,j}={\tilde{\tilde{p}}}_{i,j}-\frac{\mathrm{\Delta }x}{\mathrm{\Delta }y}(E_{i,j}^{1,+}(2,1)({\tilde{\upsilon }}_{i,j}-{\tilde{\upsilon }}_{i,j-1})e^{{\tilde{\upsilon }}_{i,j}}+E_{i,j}^{1,+}(2,2)({\tilde{\tilde{p}}}_{i,j}-{\tilde{\tilde{p}}}_{i,j-1})+E_{i,j}^{1,-}(2,1)({\tilde{\upsilon }}_{i,j+1}-{\tilde{\upsilon }}_{i,j})e^{{\tilde{\upsilon }}_{i,j}}+E_{i,j}^{1,-}(2,2)({\tilde{\tilde{p}}}_{i,j+1}-{\tilde{\tilde{p}}}_{i,j}))-\mathrm{\Delta }x{\tilde{\mathbf{E}}}_{i,j}^3(2)$$ (27)

where υ̃ and $\tilde{\tilde{p}}$ are the approximate values of υ and $\hat{\tilde{p}}$ determined by the discretized system.

The second step in Case 1 is to take the exponential of the first discretized equation (26). This step is similar to the one taken in [20] for the inverse problem for the acoustic equation. Here we also have a pressure term and a second equation in our discretized system, but here we do not exponentiate the second equation. We obtain

$${\tilde{\tilde{\mu }}}_{i+1,j}={\tilde{\tilde{\mu }}}_{i,j}^{\left(1-\frac{\mathrm{\Delta }x}{\mathrm{\Delta }y}\left(E_{i,j}^{1,+}(1,1)-E_{i,j}^{1,-}(1,1)\right)\right)}·{\tilde{\tilde{\mu }}}_{i,j-1}^{\frac{\mathrm{\Delta }x}{\mathrm{\Delta }y}{E}_{i,j}^{1,+}(1,1)}·{\tilde{\tilde{\mu }}}_{i,j+1}^{-\frac{\mathrm{\Delta }x}{\mathrm{\Delta }y}{E}_{i,j}^{1,-}(1,1)}·\text{exp}\left(-\frac{\mathrm{\Delta }x}{\mathrm{\Delta }y}(E_{i,j}^{1,+}(1,2)({\tilde{\tilde{p}}}_{i,j}-{\tilde{\tilde{p}}}_{i,j-1})+E_{i,j}^{1,-}(1,2)({\tilde{\tilde{p}}}_{i,j+1}-{\tilde{\tilde{p}}}_{i,j})\right)/{\tilde{\tilde{\mu }}}_{i,j})·\text{exp}\left(-\mathrm{\Delta }x\left(E_{i,j}^2(1,1)+{\mathbf{E}}_{i,j}^3(1)/{\tilde{\tilde{\mu }}}_{i,j}\right)\right)$$ (28)

$${\tilde{\tilde{p}}}_{i+1,j}={\tilde{\tilde{p}}}_{i,j}-\frac{\mathrm{\Delta }x}{\mathrm{\Delta }y}(E_{i,j}^{1,+}(2,1)({\tilde{\tilde{\mu }}}_{i,j}-{\tilde{\tilde{\mu }}}_{i,j-1})+E_{i,j}^{1,-}(2,1)({\tilde{\tilde{\mu }}}_{i,j+1}-{\tilde{\tilde{\mu }}}_{i,j})+E_{i,j}^{1,+}(2,2)({\tilde{\tilde{p}}}_{i,j}-{\tilde{\tilde{p}}}_{i,j-1})+E_{i,j}^{1,-}(2,2)({\tilde{\tilde{p}}}_{i,j+1}-{\tilde{\tilde{p}}}_{i,j}))-\mathrm{\Delta }x\left(E_{i,j}^2(2,1){\tilde{\tilde{\mu }}}_{i,j}+{\mathbf{E}}_{i,j}^3(2)\right)$$ (29)

where in equations (28) and (29) we replace ${\tilde{\mathbf{E}}}_{i,j}^3(1),{\tilde{\mathbf{E}}}_{i,j}^3(2)$ by the equivalent expressions $E_{i,j}^2(1,1)+{\mathbf{E}}_{i,j}^3(1)/{\tilde{\tilde{\mu }}}_{i,j}$ and $E_{i,j}^2(2,1){\tilde{\tilde{\mu }}}_{i,j}+{\mathbf{E}}_{i,j}^3(2)$, respectively. We have also replaced e^υ̃_i,j by the computed value of μ̃, ${\tilde{\tilde{\mu }}}_{i,j}$, so that (28) and (29) are now equations for ${\tilde{\tilde{\mu }}}_{i,j}$ and ${\tilde{\tilde{p}}}_{i,j}$.

Now we apply the approximation exp (bΔx) ≈ 1 + bΔx to the first exponential term in the first equation as our experience is that this approximation controls exponential error growth due to error in the approximation of $\hat{\tilde{p}}$. Then we get

$${\tilde{\tilde{\mu }}}_{i+1,j}=({\tilde{\tilde{\mu }}}_{i,j}^{\left(1-\frac{\mathrm{\Delta }x}{\mathrm{\Delta }y}\left(E_{i,j}^{1,+}(1,1)-E_{i,j}^{1,-}(1,1)\right)\right)}·{\tilde{\tilde{\mu }}}_{i,j-1}^{\frac{\mathrm{\Delta }x}{\mathrm{\Delta }y}{E}_{i,j}^{1,+}(1,1)}·{\tilde{\tilde{\mu }}}_{i,j+1}^{-\frac{\mathrm{\Delta }x}{\mathrm{\Delta }y}{E}_{i,j}^{1,-}(1,1)}-\frac{\mathrm{\Delta }x}{\mathrm{\Delta }y}\left(E_{i,j}^{1,+}(1,2)({\tilde{\tilde{p}}}_{i,j}-{\tilde{\tilde{p}}}_{i,j-1})+E_{i,j}^{1,-}(1,2)({\tilde{\tilde{p}}}_{i,j+1}-{\tilde{\tilde{p}}}_{i,j}))\right)·\text{exp}\left(-\mathrm{\Delta }x\left(E_{i,j}^2(1,1)+{\mathbf{E}}_{i,j}^3(1)/{\tilde{\tilde{\mu }}}_{i,j}\right)\right).$$ (30)

where on the second line of (30) we have also approximated

$${\tilde{\tilde{\mu }}}_{i,j}^{\left(1-\frac{\mathrm{\Delta }x}{\mathrm{\Delta }y}\left(E_{i,j}^{1,+}(1,1)-E_{i,j}^{1,-}(1,1)\right)\right)}·{\tilde{\tilde{\mu }}}_{i,j-1}^{\frac{\mathrm{\Delta }x}{\mathrm{\Delta }y}{E}_{i,j}^{1,+}(1,1)}·{\tilde{\tilde{\mu }}}_{i,j+1}^{-\frac{\mathrm{\Delta }x}{\mathrm{\Delta }y}{E}_{i,j}^{1,-}(1,1)}\text{by}1,$$

which is essentially accomplished by here approximating ${\tilde{\tilde{\mu }}}_{i,j\pm 1}$ by ${\tilde{\tilde{\mu }}}_{i,j}$. In (30) we have not approximate the second exponential term

$$\text{exp}\left(-\mathrm{\Delta }x\left(E_{i,j}^2(1,1)+{\mathbf{E}}_{i,j}^3(1)/{\tilde{\tilde{\mu }}}_{i,j}\right)\right).$$

The reason is that the term in the exponent is often near zero and so in practice does not appear to contribute to exponential numerical error.

For Case 1 then we solve the above two discretized equations (29) and (30) in the following way. Our solution methods differ since one equation is linear and the other one is nonlinear. First we solve the discretized equation (30) for the discretized solution ${\tilde{\tilde{\mu }}}_{i+1,j}$ with the starting condition for $\tilde{\tilde{p}}$ as $\tilde{\tilde{p}}=0$, and then we solve the discretized equation (29) for the discretized solution ${\tilde{\tilde{p}}}_{i+1,j}$ using the results of the previous calculation for $\tilde{\tilde{\mu }}$. Then we repeat the procedure using the previously calculated value of $\tilde{\tilde{p}}$ when solving equation (30). We call this method the 2D Log-Elastographic method for the reduced 2D elastic system.

4.3. Case 2: Include the μ̃∇(∇ · û) Term

In this case, the 2D elastic system including the μ̃∇(∇ · û) term, which was set to zero in Case 1, can be rewritten as

$${\mathbf{v}}_{,1}+E^1{\mathbf{v}}_{,2}+{\overline{E}}^2\mathbf{v}+{\mathbf{E}}^3=\mathbf{0}$$ (31)

where the only change from Case 1 is that now

$${\overline{E}}^2=\left(\begin{array}{cc}\hfill \frac{\mathrm{\Delta }{\hat{u}}_2+{\hat{u}}_{1,11}+{\hat{u}}_{2,12}}{{\hat{u}}_{2,1}+{\hat{u}}_{1,2}}\hfill & \hfill 0\hfill \\ \hfill \mathrm{\Delta }{\hat{u}}_1+{\hat{u}}_{1,12}+{\hat{u}}_{2,11}-\frac{2{\hat{u}}_{1,1}}{{\hat{u}}_{2,1}+{\hat{u}}_{1,2}}(\mathrm{\Delta }{\hat{u}}_2+{\hat{u}}_{1,11}+{\hat{u}}_{2,12})\hfill & \hfill 0\hfill \end{array}\right).$$

In Case 2 then we can apply the same 2D Log-Elastographic algorithm for μ̃ and $\hat{\tilde{p}}$ except that we replace E² by Ē².

We now apply our 2D Log-Elastographic method for the 2D elastic system with and without the μ̃∇(∇ · û) term and demonstrate that the difference in the recovered $\tilde{\tilde{\mu }}$ images is very small. We demonstrate the small difference in the recovered $\tilde{\tilde{\mu }}’\mathrm{s}$ using synthetic data where there is one round inclusion and one elliptic inclusion inside the computational domain. The scaled shear modulus of the background is 2 m² /s². The maximum scaled shear modulus inside the inclusion is 12 m² /s². The exact formula is

$$\tilde{\mu }(x_1,x_2)=b+a{((r-{(x_1-x_1^0)}^2-{(x_2-x_2^0)}^2)/r)}^3+a{(1-{((x_1+x_2)/\sqrt{2}-x_1^1)}^2/r_1-{((x_2-x_1)/\sqrt{2}-x_2^1)}^2/r_2)}^3$$

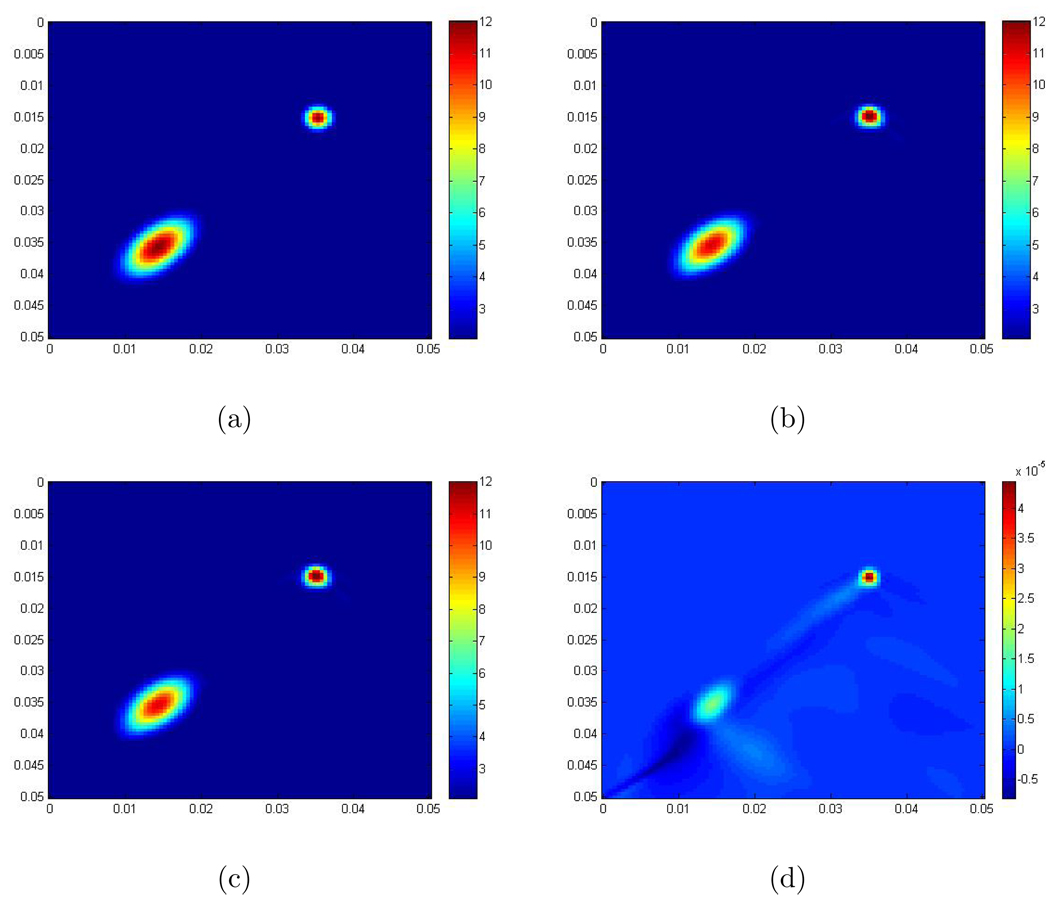
where r = 0.003, r₁ = 0.005, r₂ = 0.009, b = 2, a = 10, $(x_1^0,x_2^0)=(0.015,0.035)$, and $(x_1^1,x_2^1)=(0.035,-0.015)$. Figure 1 shows the recoveries obtained with and without the μ̃∇(∇ · û) term, and also the difference between them. From these images, you can see that the recoveries, in this case where the contrast is 6, are very similar, and the error here is of order 10⁻⁵ which is one order less than that of Δx = Δy. For these calculations we use λ/ρ = 10⁶ m²/s² which is the right order of magnitude for this ratio in tissue. While we do not show it here we observe that the error is of order 10⁻⁶ when the contrast ratio is 4 and 10⁻⁶ when the contrast ratio is 2. The error is of the same order when we add 10% and 20% noise to the data. In our remaining examples, we thus ignore the term μ̃∇(∇ · û). Note that our method for creating the simulations is described in Section 5.

Figure 1.

(a) The exact scaled shear modulus; The exact contrast between the background and the maximum value inside the inclusion is 2 to 12; (b) The recovery using the system without the μ̃∇(∇ · û) term; (c) The recovery using the system with the μ̃∇(∇ · û) term; (d) The error between recoveries obtained from neglecting the μ̃∇(∇ · û) term and including the μ̃∇(∇ · û) term. The units are m²/s².

5. Numerical Results with Synthetic Data and Experimental Data

In the previous section we introduced the 2D Log-Elastographic finite difference algorithm to reconstruct the scaled shear modulus and the scaled pressure simultaneously using a 2D plane strain elastic system and neglecting a small nonlinear term. In this section, we test this inversion algorithm with some numerical examples using synthetic data. We also use experimental data: the MR measured displacement data, taken during harmonic excitation, in the liver and the spleen. We obtained this data from Mayo Clinic. In all reconstructions, we apply the 2D Log-Elastographic method using the reduced equation. Even in the synthetic data examples cases where μ̃ is real, the eigenvalues of the coefficient matrix E¹ in the first order p.d.e. system (15) can be complex. When this occurs we determine the separation of the eigenvalues of E¹ according to the sign of the real parts of the eigenvalues.

To obtain synthetic data, we need to do the forward simulation. To do this the scaled shear modulus μ̃ and the first scaled Lamé parameter λ̃ are given; in all of our examples λ̃ will be a constant. Furthermore we derive a hyperbolic second order partial differential equation system for u and p̃ − 2∇ · u/(1 + μ̃/λ̃) and solve this system of three equations for u and p̃ in the time domain. The creation of this hyperbolic system of three equations in u and p̃ − 2∇ · u/(1 + μ̃/λ̃) eliminates making the multiplication λ̃∇ · u from a computed u. To compute u and p̃, we apply a second order finite difference method. In addition, since we are simulating experiments implemented in a much larger region of tissue, we assume outgoing boundary conditions on all boundaries of our domain. This allows only outgoing waves without reflection. To achieve this outgoing boundary condition, we apply the idea of the Perfectly Matched Layer method in [10]; see [53] for our application. We use this forward algorithm to compute synthetic data for a selection of shear moduli, which are each represented by a C¹ function. We compute for a total time of 0.054 seconds and the total number of time steps is 1800. After obtaining the space and time dependent displacement, we take the Fourier transform of the displacement data in time using Matlab’s function FFT. We then have the Fourier Transforms, û, $\hat{\tilde{p}}$ of the displacement u(x₁, x₂, t) and the scaled pressure p̃(x₁, x₂, t). Our inverse algorithms will be applied using the synthetically calculated û(x₁, x₂, ω) and the computed $\tilde{\tilde{\mu }}$ will be compared to the exact μ̃ for each example. Furthermore we will for at least one example compare the $\tilde{\tilde{p}}$ computed with inverse algorithm to the $\hat{\tilde{p}}$ computed with forward algorithm.

5.1. Imaging μ̃ with Synthetic Data

In all the examples with synthetic data, the frequency for simulation and inversion is 100Hz; the units that we are using to display the results are seconds for time, meters for length and m²/s² for the scaled shear modulus; the computational domain is

$$\{(x_1,x_2)\in R^2:0\le x_1\le 0.05,0\le x_2\le 0.05\};$$

and for the discretization, we use a 100 × 100 spatial grid. In the forward simulation, λ/ρ = 10⁶ m²/s², which is of the same order as that in [39]. We add a source in the x₂ direction, that is, the first component of the source function, f̃, is zero while the second component of the source function f̃ is given by

$$f_2(x_1,x_2,t)=5000e^{-{10}^7{(x_1-x_1^0)}^2}\frac{e^{-t^2/2{\sigma }^2}}{\sqrt{2\pi }\sigma }\text{sin}(\omega (t+\pi /2)),0\le x_2\le 0.05\},$$

where σ = 0.005, ω = 200π and $x_1^0=0.0005$. The rapid decay of the Gaussian functions makes it possible to simulate a short duration wave pulse temporally and to simulate a line source spacially. Since, in our synthetic example, μ̃ is real, (see specific formulas below), in the images we display only the real part of the recovered scaled shear modulus $\tilde{\tilde{\mu }}$.

Recall that we assume in the experiment that the wave propagation direction occurs primarily in one direction, say the x₁ direction. And following our algorithmic development we assume that the x₁ direction is a time-like direction. If the x₂ direction is the horizontal direction, then we require a Dirichlet boundary condition on the top of the computational domain. We also need a Dirichlet condition on the left and right boundaries of the computational domain when the inflow condition holds. By inflow condition we mean that at any boundary point x_b, $\tilde{\tilde{\mu }}({\mathbf{x}}_b)n_1+\tilde{\tilde{p}}({\mathbf{x}}_b)n_2<0$ for any unit vector n directed out of the computational domain at x_b. When we need boundary values, we choose the boundary values to be the results obtained from applying the Direct Inversion Method to equation (8) where û is the component of û that is orthogonal to the wave propagation direction.

First we show recoveries from synthetic data without noise. Since there is no noise, we use standard second order finite difference approximations to calculate the derivatives of the solution û; those derivatives become coefficients in our 2D Log-Elastographic method.

1. Example 1: In this example, the scaled shear modulus μ̃ is given by the following function:

   $$\tilde{\mu }(x_1,x_2)=b+a{((r-{(x_1-x_1^0)}^2-{(x_2-x_2^0)}^2)/r)}^3$$

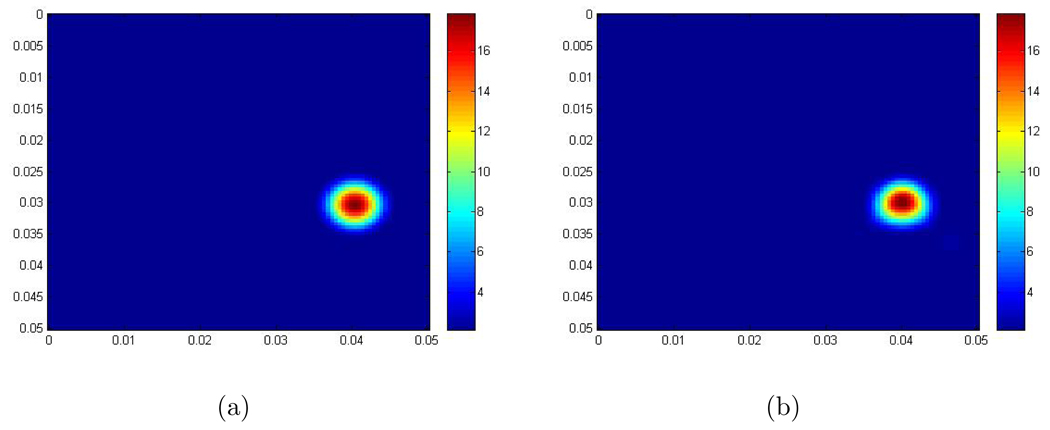
   where r = 0.006, b = 2, a = 16 and $(x_1^0,x_2^0)=(0.03,0.04)$. So there is one round inclusion inside the computational domain. The scaled shear modulus of the background is 2 m²/s². The maximum scaled shear modulus inside the inclusion is 18 m²/s². Figure 2 shows the recovery.
2. Example 2: In this example, the scaled shear modulus μ̃ is given by the following function:

   $$\tilde{\mu }(x_1,x_2)=b+a{(1-{((x_1+x_2)/\sqrt{2}-x_1^1)}^2/r_1-{((x_2-x_1)/\sqrt{2}-x_2^1)}^2/r_2)}^3+a{(1-{((x_1-x_2)/\sqrt{2}-x_1^2)}^2/r_1-{((x_1+x_2)/\sqrt{2}-x_2^2)}^2/r_2)}^3$$

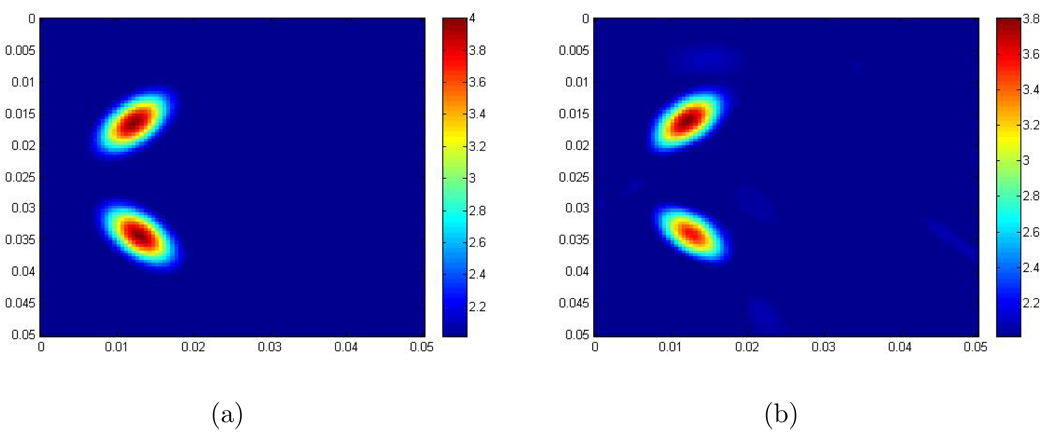
   where r = 0.003, r₁ = 0.005, r₂ = 0.009, b = 2, a = 2, $(x_1^1,x_2^1)=(0.015,0.033)$, and $(x_1^2,x_2^2)=(0.02,-0.003)$. So there are two elliptic inclusions placed one in front of the other with respect to the time like x₁ direction in the computational domain. The scaled shear modulus of the background is 2 m²/s². The maximum scaled shear modulus inside the inclusions is 4 m²/s². Figure 3 shows the recovery.
3. Example 3: In this example, the scaled shear modulus μ̃ is given by the following function:

   $$\tilde{\mu }(x_1,x_2)=b+a{((r-{(x_1-x_1^0)}^2-{(x_2-x_2^0)}^2)/r)}^3+a{(1-{((x_1+x_2)/\sqrt{2}-x_1^1)}^2/r_1-{((x_2-x_1)/\sqrt{2}-x_2^1)}^2/r_2)}^3+a{(1-{((x_1-x_2)/\sqrt{2}-x_1^2)}^2/r_1-{((x_1+x_2)/\sqrt{2}-x_2^2)}^2/r_2)}^3$$

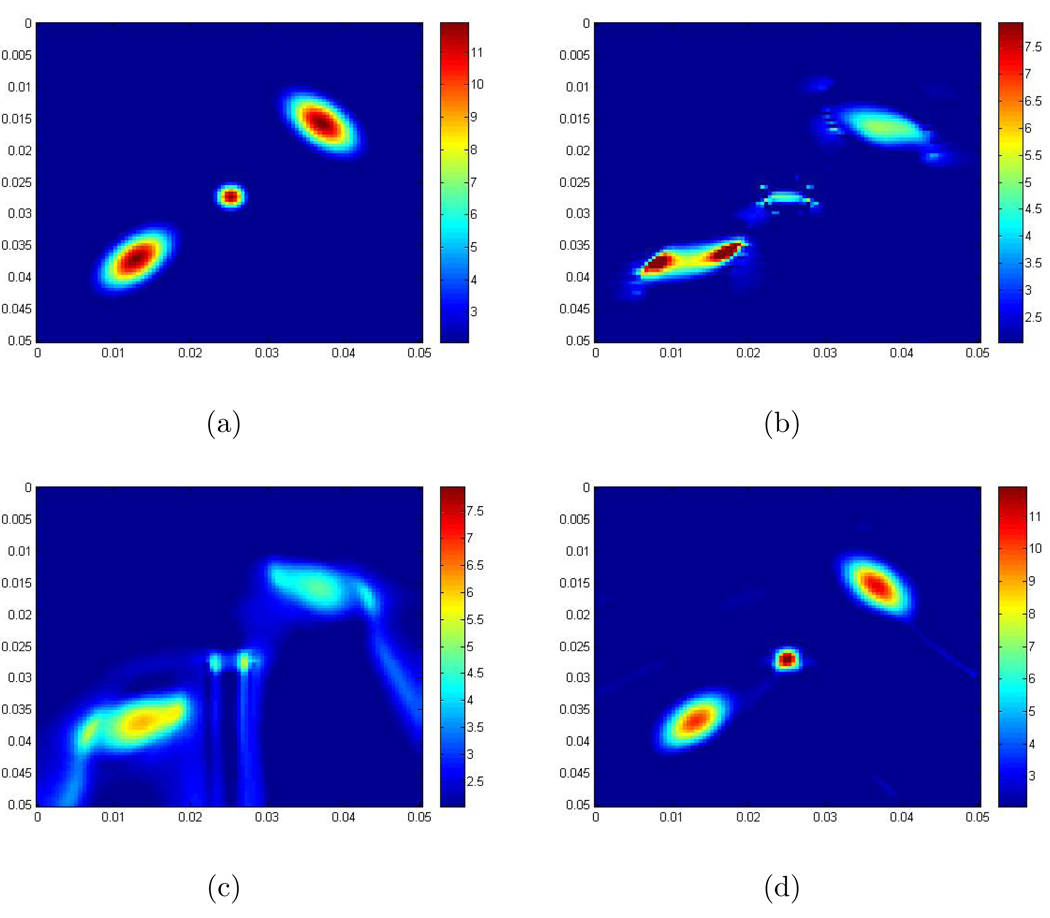
   where r = 0.003, r₁ = 0.005, r₂ = 0.009, b = 2, a = 10, $(x_1^0,x_2^0)=(0.027,0.025)$, $(x_1^1,x_2^1)=(0.035,-0.017)$, and $(x_1^2,x_2^2)=(-0.015,0.037)$. So there are two elliptic inclusions and one round inclusion inside the computational domain. The scaled shear modulus of the background is 2 m²/s². The maximum scaled shear modulus inside the inclusions is 12 m²/s².

Figure 2.

(a) The exact scaled shear modulus; (The contrast between the background and the maximum value in the inclusion is 2 to 18.); (b) The recovered scaled shear modulus obtained from the 2D Log-Elastographic scheme. The units are m²/s².

Figure 3.

(a) The exact scaled shear modulus; (The contrast between the background and the maximum value in the inclusions is 2 to 4.); (b) The recovered scaled shear modulus obtained from the 2D Log-Elastographic scheme. The units are m²/s².

We compare the recovered scaled shear modulus obtained with the 2D Log-Elastographic method with: (i) the exact scaled shear modulus; (ii) the recovered scaled shear modulus obtained by solving equation (8) with the Direct Inversion Method using the component of displacement in the direction orthogonal to the propagation direction; (iii) the recovered scaled shear modulus obtained with the (acoustic) Log-Elastographic method, [20], applied with data from only the component of displacement in the direction orthogonal to the propagation direction; note that in this method both the pressure p and the term ∇ · (μ̃∇û^T) are set to zero. Figure 4 shows the recoveries.

Figure 4.

(a) The exact scaled shear modulus; (The contrast between the background and the maximum value in the inclusions is 2 to 12.); (b) The recovered scaled shear modulus obtained from the Direct Inversion Method; (c) The recovered scaled shear modulus obtained from the (acoustic) Log-Elastographic method; (d) The recovered scaled shear modulus obtained from the 2D Log-Elastographic scheme. The units are m²/s². Note that the colorbar in each of these figures is different.

From these examples, we can see in Figure 2(b), 3(b) and 4(d) that the 2D Log-Elastographic nonlinear algorithm recovers the scaled shear modulus very well in shape and size when we have either a single inclusion or multiple inclusions. This performance occurs when we have either low or high contrast between the background medium and the maximum value in the inclusion. Comparing the images in Figure 4, we can also see that the maximum value of $\tilde{\tilde{\mu }}$ in the recovery from the Direct Inversion Method and from the (acoustic) Log-Elastographic method exhibit undershooting. The shape and size of the inclusions are not recovered as well as in the 2D Log-Elastographic method. Here we have not shown the comparison with the images obtained with a standard upwind scheme. We refer the reader to [53] (p.81–84, p.86–89, and p.93–100) for those comparisons.

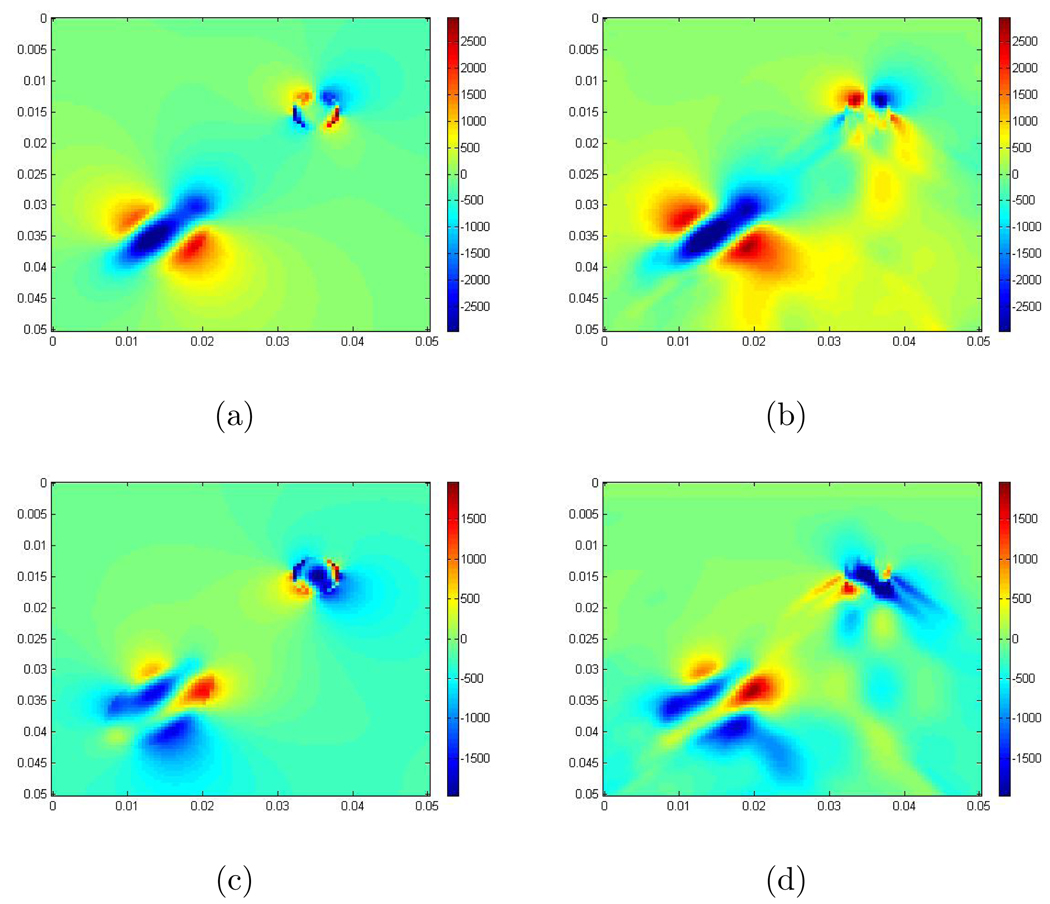
Besides the scaled shear modulus in the 2D Log-Elastographic method, we also recover the scaled pressure. In Figure 5 we compare the Fourier transformed pressure, obtained by first doing the forward calculation and then taking the Fourier transform in time for the example in Figure 1, to the scaled pressure we recover in the 2D Log-Elastographic method for the same example. These images show that besides the scaled shear modulus we can also recover the pressure at the same time, and the recovered pressure is similar to the pressure obtained from the forward simulation. This has been shown to be difficult to accomplish, see [39].

Figure 5.

(a) is the real part of the pressure simulated with the forward problem algorithm and then taking the Fourier transform; (b) is the real part of the recovered scaled pressure $\tilde{\tilde{p}}$ from the 2D Log-Elastographic scheme; (c) is the imaginary part of the pressure simulated with the forward problem algorithm and then taking the Fourier transform; (d) is the imaginary part of the recovered scaled pressure $\tilde{\tilde{p}}$ from the 2D Log-Elastographic scheme.

To test the stability and robustness of our full inversion algorithm, we add 10% and 20% Gaussian random noise to the displacement data respectively

$${\mathbf{u}}_{\mathit{\text{noisy}}}(x_1,x_2,t)=\mathbf{u}(x_1,x_2,t)+\gamma {\mathbf{u}}_{\mathit{\text{max}}}\text{rand}(x_1,x_2,t)$$

where u_max is the maximum displacement amplitude, γ is the noise level, and rand(x₁, x₂, t) is a random vector generated in Matlab from the normal distribution with mean zero and variance one. We apply the 2D Log-Elastographic algorithm to this data set with 10% and 20% noise (γ = 0.1 and 0.2) for the examples (I) and (III) in this section.

Again we need to differentiate the data. But if there is noise in the data, the errors can be strongly amplified in the standard differentiation process, which means that the differentiation process is ill-posed. Since we now have noise in the data, we apply an averaging method introduced by Anderssen and Hegland, see [1], to compute the derivatives of noisy displacement. This method averages the displacement over local windows and following that averaging procedure is then essentially based on a central difference scheme (or mid-point rule) to approximate the derivatives. The step size for the central difference is related to the local window sizes and acts as a regularization parameter to control the tradeoff between the accuracy and smoothness of the derivatives.

The recovered scaled shear moduli are shown in Figure 6. From these results, it is seen that the 2D Log-Elastographic nonlinear algorithm still performs well, which shows that it is robust with respect to noise.

Figure 6.

(a) The recovery for example I. The contrast here between the background and the maximum value in the inclusion is 2 to 18 and the noise level is 10%; (b) The recovery for example III. The contrast between the background and the maximum value in the inclusions here is 2 to 12 and the noise level is 10%; (c) The recovery for example I. The contrast here between the background and the maximum value in the inclusion is 2 to 18 and the noise level is 20%; (d) The recovery for example III. The contrast here between the background and the maximum value in the inclusions is 2 to 12 and the noise level is 20%. The units are m²/s².

5.2. Examples with Experimental Data

Next, we apply the 2D Log-Elastographic algorithm to recover the scaled shear modulus with the MR measured displacement data in the liver and the spleen. This data set is provided by R. L. Ehman’s lab from Mayo Clinic. In their experiment, low-amplitude mechanical waves at 60 Hz were generated in the abdomen, during aquisition of sequences of MR data sets, by using an acoustic driver device placed on the anterior body wall. The waves propagate along the diagonal direction of the field of view (FOV). 3D displacement data was then obtained by using a 2-dimensional gradient echo MR elastography sequence to collect axial wave images in three different orthogonal directions, see [42] and [52]. The FOV is a single 2D plane, whose size is 38 × 38 cm with 96 × 96 pixels. This displacement is given at 4 equally spaced times in a single period. The amplitude of the wave is measured in terms of microns.

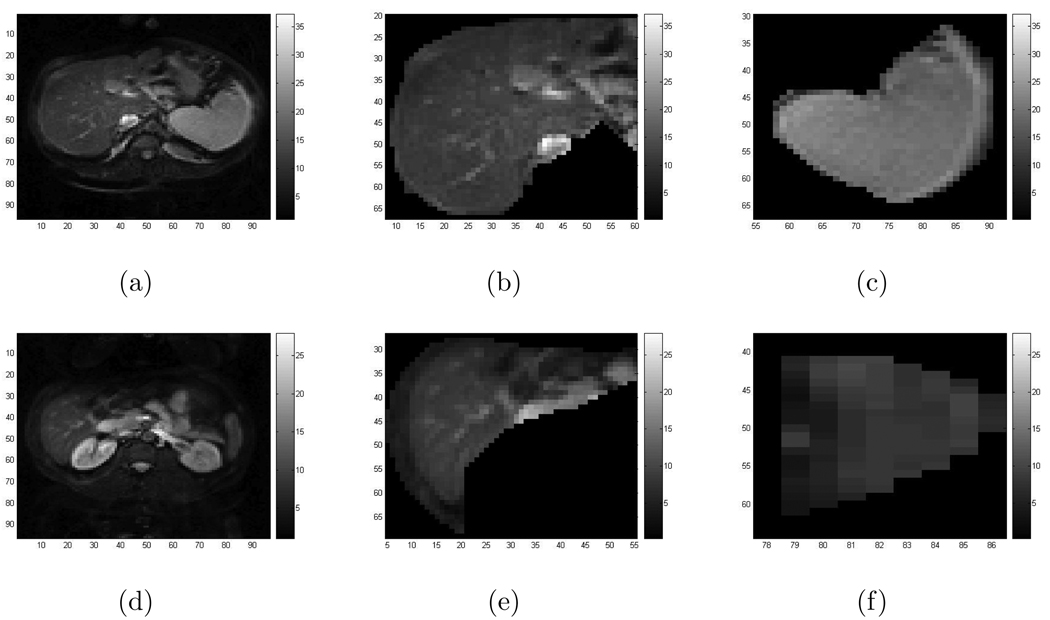
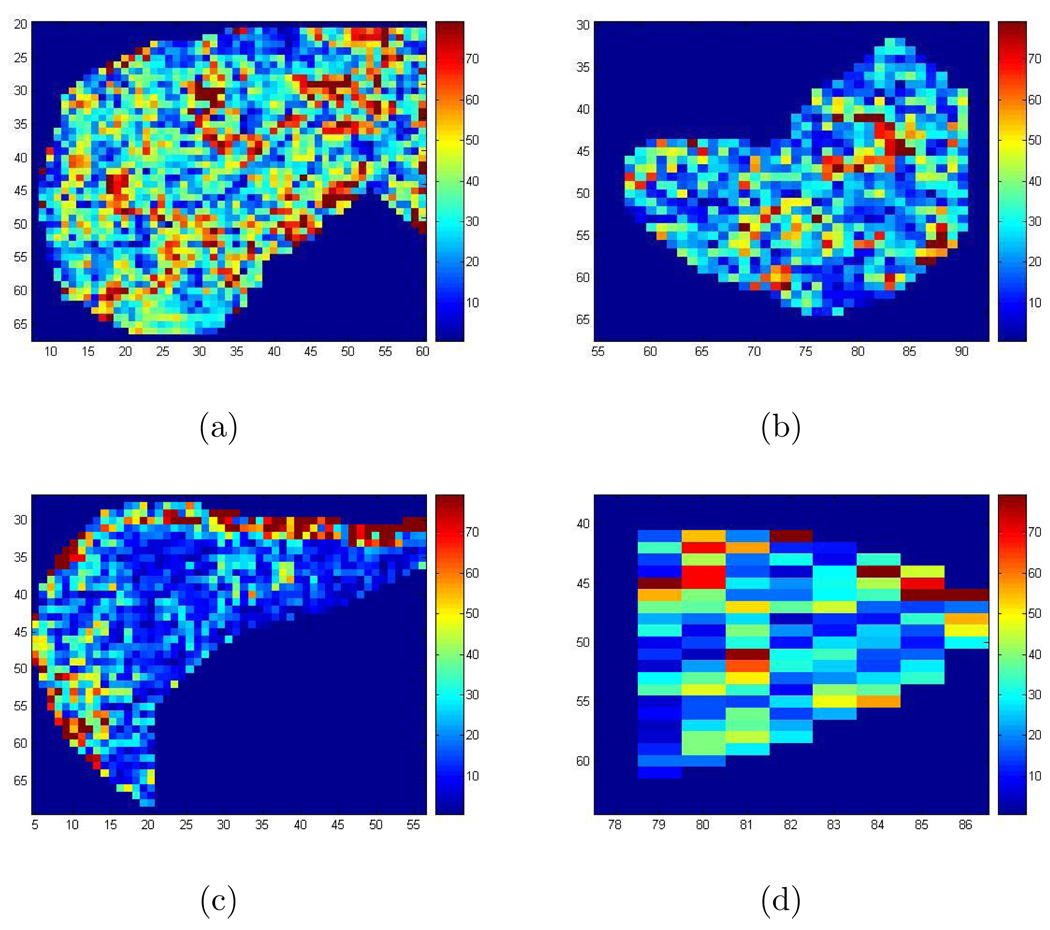
In the MR measured displacement data of the liver and spleen and the regions bounding them, there exist very noisy regions, particularly in the area surrounding those two organs. Therefore we separate the regions where we will do recovery, eliminating the surrounding regions and separately recovering the scaled shear modulus μ̃ in the liver and spleen. Figure 7 shows the MR images of these two organs where we do our recovery.

Figure 7.

(a)–(c) are images of the patient: (a) The MR image of the tissue in the image plane cross section; (b) The MR image in the liver; (c) The MR image in the spleen; (d)–(f) are images of the healthy volunteer: (d) The MR image of the tissue in the image plane cross section; (e) The MR image in the liver; (f) The MR image in the spleen. Note that the grid labeling on the axes in (b), (c) and in (e), (f) are consistent with grid labeling in (a) and (d) respectively.

The 3D displacement vector contains three components: two in-plane components u₁, u₂ and one out-of-plane component u₃. We first apply a coordinate transformation to obtain two new components from u₁ and u₂. One of these new components is along the wave propagation direction, say u_p, and the other one is orthogonal to the wave propagation direction, say u_m. They both are still in the plane and hence are assumed to satisfy the 2D plane strain elastic system. Moreover, for this data set the amplitudes of all the components are approximately the same. Therefore, in our inversion method, we first assume one of the two components, u_p, is the leading component and then the other, u_m. In our 2D Log-Elastographic inversion algorithm, we treat the variable in the wave propagation direction as a time like variable. But here the wave propagates along the diagonal. Therefore, we do the inversion in two different ways: first we treat the x₁ variable as a time like variable and then we treat the x₂ variable as a time like variable. Altogether there are 4 different possible combinations to do the inversion with the 2D Log-Elastographic algorithm. Afterwards, we take the geometric average of all these recoveries.

As for the boundary, we still require Dirichlet boundary conditions on the boundaries of the computational domain when we have the inflow condition. As before we choose the boundary values to be the results obtained from the Direct Inversion Method. Here the boundaries of the above two computational domains are curved and we compute only inside the boundary curves. Since the 2D Log-Elastographic method is a marching method, when we compute at the next line we need to add or neglect grid points along the curved boundary because of the boundary curvature. When we add grid points we set the values of μ̃ at those points to be the values obtained from the Direct Inversion Method.

In order to solve for the scaled shear modulus, we need to calculate the derivatives of the magnitudes and the phases of the in-plane components of the 3D displacement vector. Relatively speaking, from our observations, the magnitudes and the phases of those two components throughout our selected computational regions change smoothly, except at some places where the wrapped phase has discontinuities. Therefore, we take the following steps to calculate the derivatives of the magnitude and the phase for each component. First, for the phase, we shift the interval for the definition of the phase to produce an unwrapped phase; second, we do local median filtering of the magnitude and the phase; third, we calculate the derivatives at each interior point by taking the median of the second order central difference approximation and two second order one-sided approximations; then on the boundary we use only a one-sided second order approximation to the derivative at each point.

For the experimental data, the expected shear modulus is complex valued. In this case, as our example in Subsection 4.1 has shown, we could have arbitrarily high exponential error growth in our computations if the imaginary part of one of the eigenvalues of the coefficient matrix E¹ is positive. To control this unwanted growth, we apply an additional filtering step after each sweeping step. Basically, we filter out the high frequency content of the computed solution at the end of each sweeping step. Our preliminary realization is as follows: first at each sweeping step we take the Fast Fourier Transform with respect to the transverse space variable, in the direction orthogonal to the sweeping direction. This transform is taken of the computed solution ${\{{\mu }_{i,j},p_{i,j}\}}_{j=1}^N$. We obtain the vector ${\{V_{i,j}\}}_{j=1}^N=F\mathit{\text{FT}}({\{{\mu }_{i,j},p_{i,j}\}}_{j=1}^N)$; then we filter it with the formula given below

$${(f{V}_i)}_j=\{\begin{array}{cc}{V}_{i,j}\hfill & \text{if}|j|\le L\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$

where L is half of the total length, and $V_i={\{V_{i,j}\}}_{j=1}^N$ is the computed FFT at present step. Lastly we take the inverse Fast Fourier Transform of fV_i to obtain the final solution at the present step. Repeat this procedure at the next step, etc.. Generally, the frequency content ω and the total length l of the vector under FFT have the relationship given by ω(k) = 2π(k − 1)/l, where k is the index, therefore by keeping half of the total length of the vector under FFT is equivalent to keeping up to the same frequency content at each step.

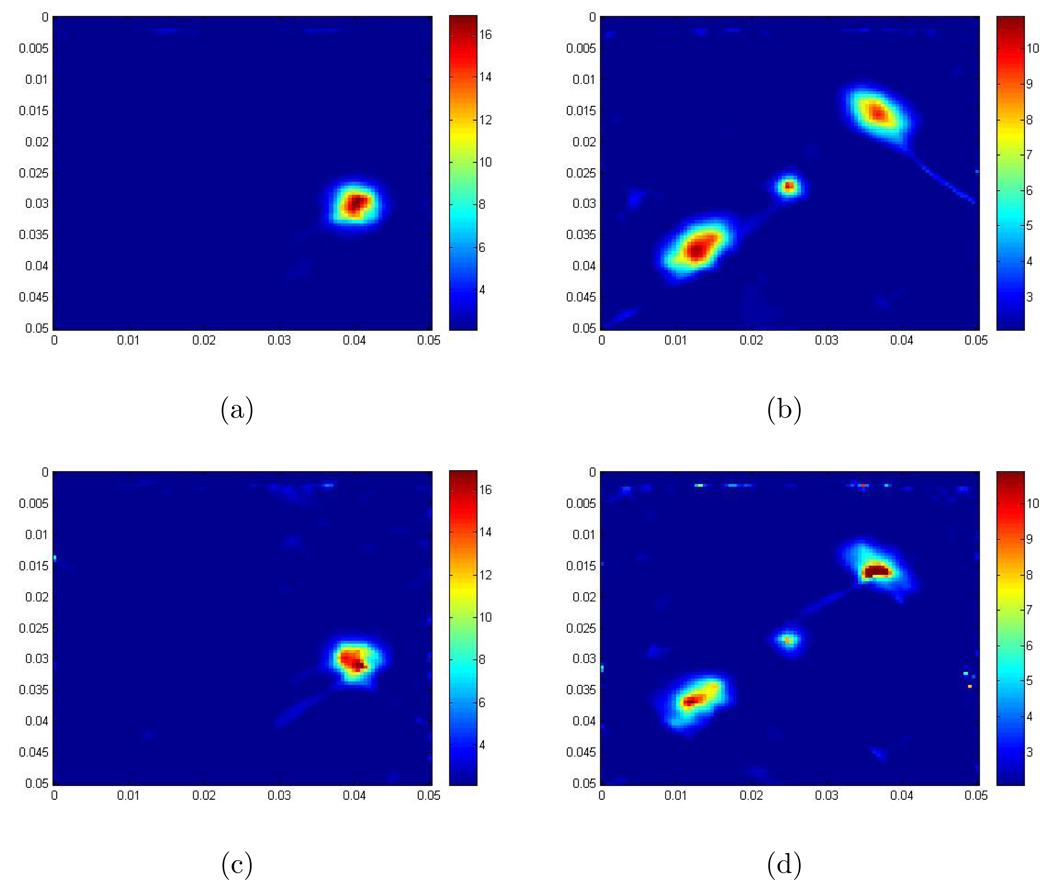
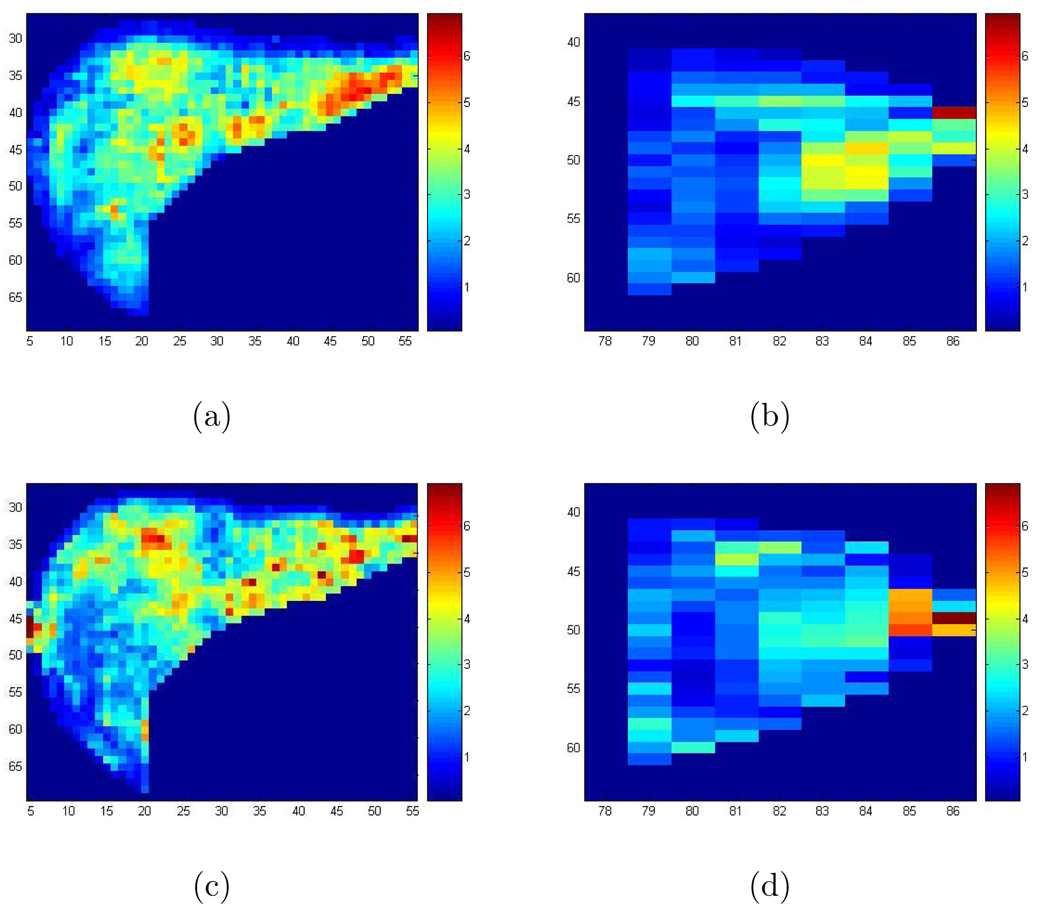
Figure 8 shows the recovered wave speed squared (see Section 2) in the liver and the spleen for a patient obtained by implementing the 2D Log-Elastographic method, with the additional filtering step, and the Direct Inversion Method. Figure 9 shows the recovered wave speed squared in the liver and the spleen for a healthy volunteer from the 2D Log-Elastographic method and the Direct Inversion Method. The Direct Inversion recovery is the geometric average of the three Direct Inversion recoveries obtained by using each of the three components separately. To compare the results from different methods, we have also calculated: (1)Average Difference: The average value of the difference between the Direct Inversion result and the 2D Log-Elastographic result; (2)L¹ Difference: The L¹ norm (sum of the absolute value of the differences, pixel by pixel divided by the number of pixels) of the difference between the Direct Inversion result and the 2D Log-Elastographic result; (3)L² Difference: The root mean square difference between the Direct Inversion result and the 2D Log-Elastographic result. The results are tabulated for the in-vivo data in Table 1 when no cutoff is applied to the imaging functionals. We only have two data sets so the data is too limited to draw firm conclusions from the tables. However, the small differences in average values indicate that diagnoses made by average values obtained from images produced with either Direct Inversion or the 2D Log-Elastographic method might be very similar. However the L¹ and L² differences indicate that the two algorithms yield different spacial distribution of disease progression as indicated by shear wave speed squared values. More data is needed to obtain further conclusions.

Figure 8.

(a) The recovered speed squared in the liver for the patient with the 2D Log-Elastographic method; (b) The recovered speed squared in the spleen for the patient with the 2D Log-Elastographic method; (c) The recovered speed squared in the liver for the patient with the Direct Inversion Method; (d) The recovered speed squared in the spleen for the patient with the Direct Inversion Method.

Figure 9.

(a) The recovered speed squared in the liver for the healthy volunteer with the 2D Log-Elastographic method; (b) The recovered speed squared in the spleen for the healthy volunteer with the 2D Log-Elastographic method; (c) The recovered speed squared in the liver for the healthy volunteer with the Direct Inversion Method; (d) The recovered speed squared in the spleen for the healthy volunteer with the Direct Inversion Method.

Table 1.

Average difference, L¹ and L² differences between the Direct Inversion image and the 2D Log-Elastographic image when no cutoff is applied to the imaging functional (which is $c_s^2$ in equation (7)).

Cases	Average Difference	L1 Difference	L2 Difference
liver of the patient	0.0066	1.3556	4.2302
spleen of the patient	−0.1970	1.2790	1.6796
liver of the healthy volunteer	0.1522	0.8766	1.6815
spleen of the healthy volunteer	0.0432	0.8175	1.1846

In Figure 8, we have put all the images on the same scale, i.e., we cut off the values larger than 7. In this case, we also calculated the three differences mentioned above. Table 2 shows the results, where the differences between the recoveries from the 2D Log-Elastographic algorithm and the Direct Inversion Method become smaller than those when there is no cutoff. This shows that most of the differences occur in the places where values are larger than 7.

Table 2.

Average difference, L¹ and L² differences between the Direct Inversion image and the 2D Log-Elastographic image when cutoff is applied to the imaging functional (which is $c_s^2$ in equation (7)).

Cases	Average Difference	L1 Difference	L2 Difference
liver of the patient	−0.2435	1.0607	1.3880
spleen of the patient	−0.2082	1.1675	1.5105
liver of the healthy volunteer	0.1108	0.8352	1.1161
spleen of the healthy volunteer	0.0413	0.8156	1.1796

The scaled shear wave speed we obtained with the data from the healthy volunteer is comparable with the recoveries in [17], where their results are obtained with the liver of five healthy volunteers. In [42] and [52], the authors have recovered the shear modulus for the liver and spleen of patients and healthy volunteers. The mean values of our recoveries with the 2D Log-Elastographic algorithm are 3.7171 m²/s² for the liver of the patient, 3.4319 m²/s² for the spleen of the patient, 2.6390 m²/s² for the liver of the healthy volunteer and 1.8437 m²/s² for the spleen of the healthy volunteer. These values times the density ≈ 10³ Kg/m³ are in the range, 1.77–2.85 kPa, of those in [52] for the healthy volunteers, and in the range, 2.76–12.01 kPa, for the group of patients, and also are comparable with those for the patients with fibrosis stage 2, where the range is 3.2±0.8 kPa.

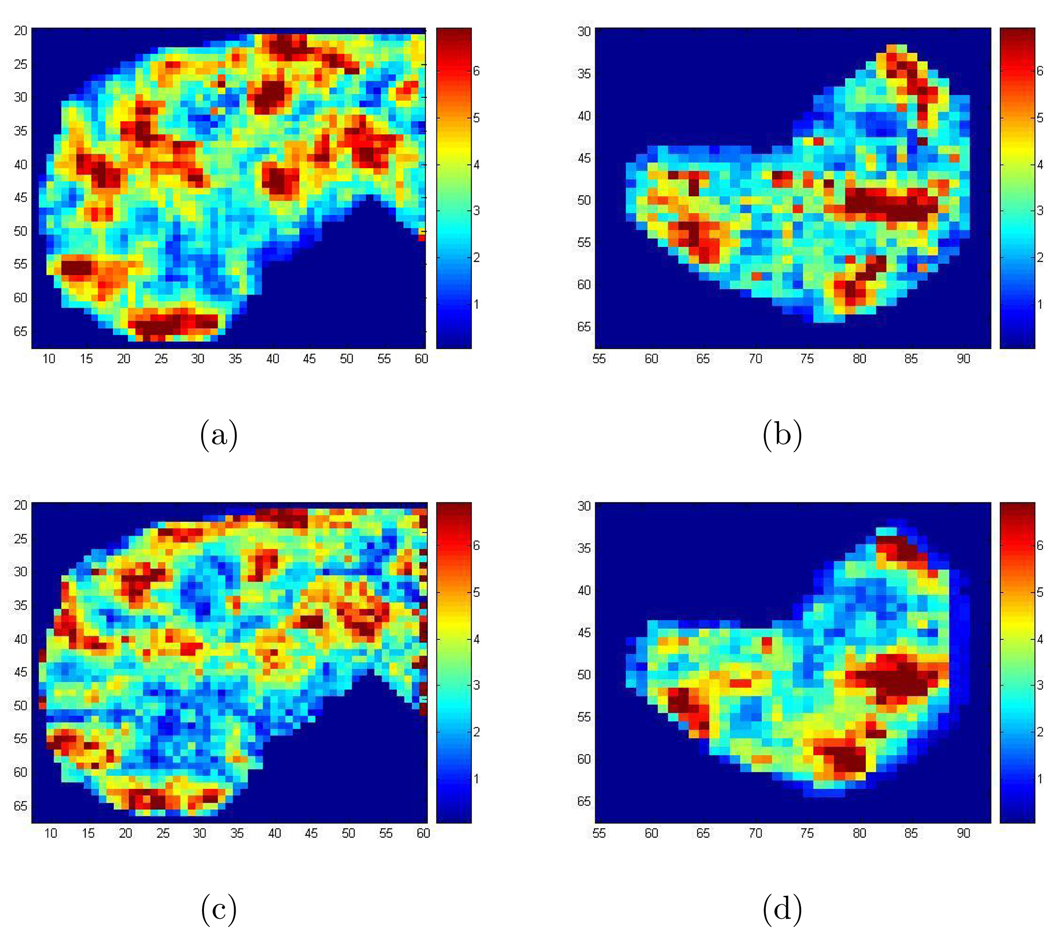
Besides the scaled shear wave speed squared, we have also calculated the attenuation with formula in [13]. In Figure 10, we show the attenuation in the liver obtained with the 2D Log-Elastographic algorithm for the patient and the volunteer. But we do not include here additional comparisons for this biomechanical property.

Figure 10.

(a) The recovered attenuation in the liver for the patient with the 2D Log-Elastographic method; (b) The recovered attenuation in the spleen for the patient with the 2D Log-Elastographic method; (c) The recovered attenuation in the liver for the healthy volunteer with the 2D Log-Elastographic method; (d) The recovered attenuation in the spleen for the healthy volunteer with the 2D Log-Elastographic method.